Thermodynamic Modeling and Performance Analysis of Vehicular High-Temperature Proton Exchange Membrane Fuel Cell System
Abstract
:1. Introduction
2. System Description
- (1)
- (2)
- The ambient air temperature is 298.15 K, the pressure is 101 kPa [60].
- (3)
- Dry air and hydrogen behave as ideal gas. Hydrogen is 100% pure and reacts completely in the fuel cell. Air is composed of 21% oxygen and 79% nitrogen [62].
- (4)
- The working temperature of the stack is uniform. The temperature rise of both gases and coolant in the stack is fixed at 10 K, and the pressure drop is fixed at 0.2 atm [60].
- (5)
- Energy loss and exergy losses during the gas flow are not considered [63].
- (6)
- All the heat generated by the stack is carried away by the coolant [63].
3. Thermodynamic Modeling and Analysis
3.1. HT-PEMFC Stack
3.2. Auxiliary Equipment
3.2.1. Compressors
3.2.2. Humidifiers
3.2.3. Heat Exchangers
3.2.4. Coolant Pump
3.2.5. Turbine
3.3. Thermodynamic Analysis
3.3.1. Energy Efficiency
3.3.2. Exergy Efficiency
3.3.3. Ecological Function
3.3.4. Improvement Potential
4. Results and Discussion
4.1. Effect of Stack Inlet Temperature
4.2. Effect of Cathode and Anode Inlet Pressures
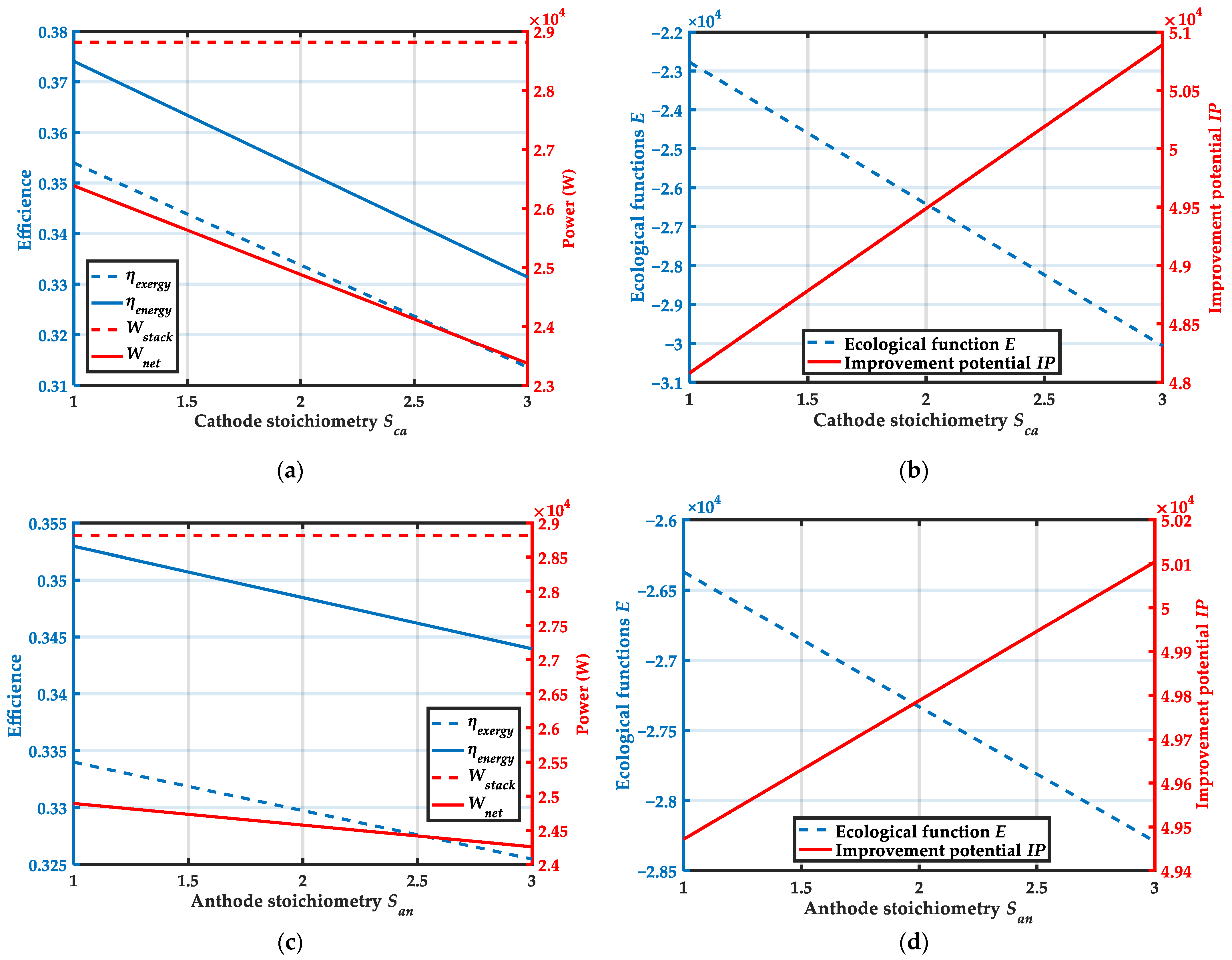
4.3. Effect of Cathode and Anode Stoichiometry
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Stephens, I.E.L.; Rossmeisl, J.; Chorkendorff, I. Toward sustainable fuel cells. Science 2016, 354, 1378–1379. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Xue, X.; Liu, G. Techno-economic evaluation for hybrid renewable energy system: Application and merits. Energy 2018, 159, 385–409. [Google Scholar] [CrossRef]
- Liu, S.Q.; Jia, L. Review on sustainable development of forest-based biodiesel. J. Nanjing For. Univ. Nat. Sci. Ed. 2020, 44, 216–224. [Google Scholar]
- Chen, J.; Jiang, J.C.; Xu, J.M.; Nie, X.A. Catalytic cracking of soybean oil via a distillation process for renewable liquid fuel. J. Nanjing For. Univ. Nat. Sci. Ed. 2011, 35, 87–90. [Google Scholar]
- Yang, H.Q.; Yu, Z.H. Research trends and future key issues of global harvested wood products carbon science. J. Nanjing For. Univ. Nat. Sci. Ed. 2021, 45, 219–228. [Google Scholar]
- Zhang, Z.G. Researches on green features and category architecture of green strategies of renewable-resource-based enterprises: A case study of forestry enterprise. J. Nanjing For. Univ. Nat. Sci. Ed. 2020, 44, 1–8. [Google Scholar]
- Zuo, S.L.; Wang, Y.F.; Zhang, Q.H. Activated carbons for the electrochemical storage of energy and electrochemical catalytic conversion of fuels: A review. J. For. Eng. 2018, 3, 1–11. [Google Scholar]
- Debe, M.K. Electrocatalyst approaches and challenges for automotive fuel cells. Nature 2012, 486, 43–51. [Google Scholar] [CrossRef]
- Wang, Y.; Diaz, D.F.R.; Chen, K.S.; Wang, Z.; Adroher, X.C. Materials, technological status, and fundamentals of PEM fuel cells—A review. Mater. Today 2020, 32, 178–203. [Google Scholar] [CrossRef]
- Jahnke, T.; Futter, G.; Latz, A.; Malkow, T.; Papakonstantinou, G.; Tsotridis, G.; Schott, P.; Gerard, M.; Quinaud, M.; Quiroga, M.; et al. Performance and degradation of Proton Exchange Membrane Fuel Cells: State of the art in modeling from atomistic to system scale. J. Power Sources 2016, 304, 207–233. [Google Scholar] [CrossRef] [Green Version]
- Lawrence, C.P.; ElShatshat, R.; Salama, M.M.A.; Fraser, R.A. An efficient auxiliary system controller for Fuel Cell Electric Vehicle (FCEV). Energy 2016, 116, 417–428. [Google Scholar] [CrossRef]
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next generation of proton-exchange membrane fuel cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef]
- Bose, S.; Kuila, T.; Thi Xuan Lien, N.; Kim, N.H.; Lau, K.-t.; Lee, J.H. Polymer membranes for high temperature proton exchange membrane fuel cell: Recent advances and challenges. Prog. Polym. Sci. 2011, 36, 813–843. [Google Scholar] [CrossRef]
- Wu, Z.; Zhu, P.; Yao, J.; Tan, P.; Xu, H.; Chen, B.; Yang, F.; Zhang, Z.; Ni, M. Thermo-economic modeling and analysis of an NG-fueled SOFC-WGS-TSA-PEMFC hybrid energy conversion system for stationary electricity power generation. Energy 2020, 192, 116613. [Google Scholar] [CrossRef]
- Haider, R.; Wen, Y.; Ma, Z.-F.; Wilkinson, D.P.; Zhang, L.; Yuan, X.; Song, S.; Zhang, J. High temperature proton exchange membrane fuel cells: Progress in advanced materials and key technologies. Chem. Soc. Rev. 2021, 50, 1138–1187. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Liu, Y.; Xu, B.; Ma, Z. Finite Time Thermodynamic Optimization of an Irreversible Proton Exchange Membrane Fuel Cell for Vehicle Use. Processes 2019, 7, 419. [Google Scholar] [CrossRef] [Green Version]
- Bazylak, A. Liquid water visualization in PEM fuel cells: A review. Int. J. Hydrogen Energy 2009, 34, 3845–3857. [Google Scholar] [CrossRef]
- Li, C.J.; Liu, Y.; Ma, Z.S. Thermodynamic Analysis of the Performance of an Irreversible PEMFC. Defect Diffus. Forum 2018, 4679, 350–360. [Google Scholar] [CrossRef]
- Devrim, Y.; Arica, E.D. Multi-walled carbon nanotubes decorated by platinum catalyst for high temperature PEM fuel cell. Int. J. Hydrogen Energy 2019, 44, 18951–18966. [Google Scholar] [CrossRef]
- Alpaydin, G.U.; Devrim, Y.; Colpan, C.O. Performance of an HT-PEMFC having a catalyst with graphene and multiwalled carbon nanotube support. Int. J. Energy Res. 2019, 43, 3578–3589. [Google Scholar] [CrossRef]
- Nalbant, Y.; Colpan, C.O.; Devrim, Y. Energy and exergy performance assessments of a high temperature-proton exchange membrane fuel cell based integrated cogeneration system. Int. J. Hydrogen Energy 2020, 45, 3584–3594. [Google Scholar] [CrossRef]
- Reddy, E.H.; Jayanti, S. Thermal management strategies for a 1 kWe stack of a high temperature proton exchange membrane fuel cell. Appl. Therm. Eng. 2012, 48, 465–475. [Google Scholar] [CrossRef]
- Altaf, F.; Batool, R.; Gill, R.; Rehman, Z.U.; Majeed, H.; Ahmad, A.; Shafiq, M.; Dastan, D.; Abbas, G.; Jacob, K. Synthesis and electrochemical investigations of ABPBI grafted montmorillonite based polymer electrolyte membranes for PEMFC applications. Renew. Energy 2021, 164, 709–728. [Google Scholar] [CrossRef]
- Lobato, J.; Canizares, P.; Rodrigo, M.A.; Ubeda, D.; Javier Pinar, F. A novel titanium PBI-based composite membrane for high temperature PEMFCs. J. Membr. Sci. 2011, 369, 105–111. [Google Scholar] [CrossRef]
- Lobato, J.; Canizares, P.; Rodrigo, M.A.; Ubeda, D.; Javier Pinar, F. Enhancement of the fuel cell performance of a high temperature proton exchange membrane fuel cell running with titanium composite polybenzimidazole-based membranes. J. Power Sources 2011, 196, 8265–8271. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Y.; Song, C.; Zhang, J. Polybenzimidazole-membrane-based PEM fuel cell in the temperature range of 120-200 degrees C. J. Power Sources 2007, 172, 163–171. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, Y.N.; Jiang, J.X.; Liu, L.J.; Duan, J.F. Preparation and characterization of PAM /PEGDA phase change energy storage conductive wood films. J. For. Eng. 2021, 6, 89–95. [Google Scholar]
- Wang, X.W.; Tang, S.W.; Wu, Z.G.; Fang, X.W.; Qin, X.Q.; Wei, L.S. Research status of biomass-based composite films with high barrier properties. J. For. Eng. 2021, 6, 13–22. [Google Scholar]
- Oono, Y.; Sounai, A.; Hori, M. Influence of the phosphoric acid-doping level in a polybenzimidazole membrane on the cell performance of high-temperature proton exchange membrane fuel cells. J. Power Sources 2009, 189, 943–949. [Google Scholar] [CrossRef]
- Qi, Z.; Buelte, S. Effect of open circuit voltage on performance and degradation of high temperature PBI-H3PO4 fuel cells. J. Power Sources 2006, 161, 1126–1132. [Google Scholar] [CrossRef]
- Bricard, M.; Lin, M.; Sanming, H.; Wajid, U.M.; Kun, C.; Lina, F.; Weiwei, Z.; Zhijun, S.; Guang, Y. Bacterial cellulose/glycolic acid/glycerol composite membrane as a system to deliver glycolic acid for anti-aging treatment. J. Bioresour. Bioprod. 2021, 6, 129–141. [Google Scholar]
- Krishnana, N.N.; Lee, S.; Ghorpade, R.V.; Konovalova, A.; Jang, J.H.; Kim, H.-J.; Han, J.; Henkensmeier, D.; Han, H. Polybenzimidazole (PBI-OO) based composite membranes using sulfophenylated TiO2 as both filler and crosslinker, and their use in the HT-PEM fuel cell. J. Membr. Sci. 2018, 560, 11–20. [Google Scholar] [CrossRef]
- Galbiati, S.; Baricci, A.; Casalegno, A.; Carcassola, G.; Marchesi, R. On the activation of polybenzimidazole-based membrane electrode assemblies doped with phosphoric acid. Int. J. Hydrogen Energy 2012, 37, 14475–14481. [Google Scholar] [CrossRef]
- Li, X.; Wang, P.; Liu, Z.; Peng, J.; Shi, C.; Hu, W.; Jiang, Z.; Liu, B. Arylether-type polybenzimidazoles bearing benzimidazolyl pendants for high-temperature proton exchange membrane fuel cells. J. Power Sources 2018, 393, 99–107. [Google Scholar] [CrossRef]
- He, Q.L.; Fu, Y.T.; Cong, H.L.; Lin, Z.X. Preparation of polyester polyols from acidic oil. J. Nanjing For. Univ. Nat. Sci. Ed. 2008, 5, 95–98. [Google Scholar]
- Xia, Z.H.; Zhao, L.Y.; Wu, W.B.; Jing, Y.; Dai, H.Q.; Fang, G.G. Performance of photocatalytic biomass fuel cells based on heteropolyacids. J. For. Eng. 2017, 2, 86–91. [Google Scholar]
- Liu, H.R.; LIu, G.B.; Li, L.J.; Liu, Y.Q.; Peng, S.Q.; Hu, D.N.; Dong, Z.H. Optimization of the manufacturing process of Pinus rigida briquette by response surface methodology. J. For. Eng. 2016, 1, 93–99. [Google Scholar]
- Mingxue, S.; Wenzhi, L.; Qiaozhi, M.; Bowen, Z. Production of jet fuel intermediates from biomass platform compounds via aldol condensation reaction over iron-modified MCM-41 lewis acid zeolite. J. Bioresour. Bioprod. 2020, 5, 256–265. [Google Scholar]
- Adeogun, A.I.; Agboola, B.E.; Idowu, M.A.; Shittu, T.A. ZnCl2 Enhanced Acid Hydrolysis of Pretreated Corncob for Glucose Production: Kinetics, Thermodynamics and Optimization Analysis. J. Bioresour. Bioprod. 2019, 4, 149–158. [Google Scholar]
- Yang, Z.; Du, Q.; Jia, Z.; Yang, C.; Xuan, J.; Jiao, K. A comprehensive proton exchange membrane fuel cell system model integrating various auxiliary subsystems. Appl. Energy 2019, 256, 113959. [Google Scholar] [CrossRef]
- Liu, Y.; Lehnert, W.; Janssen, H.; Samsun, R.C.; Stolten, D. A review of high-temperature polymer electrolyte membrane fuel-cell (HT-PEMFC)-based auxiliary power units for diesel-powered road vehicles. J. Power Sources 2016, 311, 91–102. [Google Scholar] [CrossRef]
- Guo, Y.; Guo, X.; Zhang, H.; Hou, S. Energetic, exergetic and ecological analyses of a high-temperature proton exchange membrane fuel cell based on a phosphoric-acid-doped polybenzimidazole membrane. Sustain. Energy Technol. Assess. 2020, 38, 100671. [Google Scholar] [CrossRef]
- Qin, Y.; Du, Q.; Fan, M.; Chang, Y.; Yin, Y. Study on the operating pressure effect on the performance of a proton exchange membrane fuel cell power system. Energy Convers. Manag. 2017, 142, 357–365. [Google Scholar] [CrossRef]
- Zhang, Q.; Tong, Z.; Tong, S.; Cheng, Z. Modeling and dynamic performance research on proton exchange membrane fuel cell system with hydrogen cycle and dead-ended anode. Energy 2021, 218, 119476. [Google Scholar] [CrossRef]
- Reddy, E.H.; Monder, D.S.; Jayanti, S. Parametric study of an external coolant system for a high temperature polymer electrolyte membrane fuel cell. Appl. Therm. Eng. 2013, 58, 155–164. [Google Scholar] [CrossRef]
- Lotric, A.; Sekavcenik, M.; Pahar, A.; Likozar, B.; Hocevar, S. Conceptual design of an integrated thermally self-sustained methanol steam reformer—High-temperature PEM fuel cell stack manportable power generator. Int. J. Hydrogen Energy 2017, 42, 16700–16713. [Google Scholar] [CrossRef]
- Han, J.; Im, S.; Yu, S. Air flow trajectory and surge avoidance of centrifugal compressor under variable pressure operation of automotive fuel cells. Int. J. Automot. Technol. 2016, 17, 731–738. [Google Scholar] [CrossRef]
- Kim, M.; Sohn, Y.-J.; Cho, C.-W.; Lee, W.-Y.; Kim, C.-S. Customized design for the ejector to recirculate a humidified hydrogen fuel in a submarine PEMFC. J. Power Sources 2008, 176, 529–533. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Zhao, J.; Wang, F.; Wang, J.; Miao, H.; Yuan, J. Performance evaluation of an integrated high-temperature proton exchange membrane fuel cell and absorption cycle system for power and heating/cooling cogeneration. Energy Convers. Manag. 2019, 181, 292–301. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Yuan, J.; Wang, J.; Zhao, J.; Wang, F.; Miao, H.; Hou, S. Energetic and exergetic analyses of a combined system consisting of a high-temperature polymer electrolyte membrane fuel cell and a thermoelectric generator with Thomson effect. Int. J. Hydrogen Energy 2019, 44, 16918–16932. [Google Scholar] [CrossRef]
- Chen, X.; Li, W.; Gong, G.; Wan, Z.; Tu, Z. Parametric analysis and optimization of PEMFC system for maximum power and efficiency using MOEA/D. Appl. Therm. Eng. 2017, 121, 400–409. [Google Scholar] [CrossRef]
- Chitsaz, A.; Haghghi, M.A.; Hosseinpour, J. Thermodynamic and exergoeconomic analyses of a proton exchange membrane fuel cell (PEMFC) system and the feasibility evaluation of integrating with a proton exchange membrane electrolyzer (PEME). Energy Convers. Manag. 2019, 186, 487–499. [Google Scholar] [CrossRef]
- Hwang, J.J.; Zou, M.L. Development of a proton exchange membrane fuel cell cogeneration system. J. Power Sources 2010, 195, 2579–2585. [Google Scholar] [CrossRef]
- Mert, S.O.; Dincer, I.; Ozcelik, Z. Exergoeconomic analysis of a vehicular PEM fuel cell system. J. Power Sources 2007, 165, 244–252. [Google Scholar] [CrossRef]
- Blum, L.; Deja, R.; Peters, R.; Stolten, D. Comparison of efficiencies of low, mean and high temperature fuel cell Systems. Int. J. Hydrogen Energy 2011, 36, 11056–11067. [Google Scholar] [CrossRef]
- Marandi, S.; Sarabchi, N.; Yari, M. Exergy and exergoeconomic comparison between multiple novel combined systems based on proton exchange membrane fuel cells integrated with organic Rankine cycles, and hydrogen boil-off gas subsystem. Energy Convers. Manag. 2021, 244, 114532. [Google Scholar] [CrossRef]
- Wang, G.; Yu, Y.; Liu, H.; Gong, C.; Wen, S.; Wang, X.; Tu, Z. Progress on design and development of polymer electrolyte membrane fuel cell systems for vehicle applications: A review. Fuel Processing Technol. 2018, 179, 203–228. [Google Scholar] [CrossRef]
- Zhang, C.; Yu, T.; Yi, J.; Liu, Z.; Raj, K.A.R.; Xia, L.; Tu, Z.; Chan, S.H. Investigation of heating and cooling in a stand-alone high temperature PEM fuel cell system. Energy Convers. Manag. 2016, 129, 36–42. [Google Scholar] [CrossRef]
- Kang, H.S.; Kim, M.-H.; Shin, Y.H. Thermodynamic Modeling and Performance Analysis of a Combined Power Generation System Based on HT-PEMFC and ORC. Energies 2020, 13, 6163. [Google Scholar] [CrossRef]
- Liu, G.; Qin, Y.; Wang, J.; Liu, C.; Yin, Y.; Zhao, J.; Yin, Y.; Zhang, J.; Otoo, O.N. Thermodynamic modeling and analysis of a novel PEMFC-ORC combined power system. Energy Convers. Manag. 2020, 217, 112998. [Google Scholar] [CrossRef]
- Tsatsaronis, G.; Morosuk, T. Advanced exergetic analysis of a novel system for generating electricity and vaporizing liquefied natural gas. Energy 2010, 35, 820–829. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Deng, C.; Ren, J.; Ji, F.; Sun, Y.; Xiao, Z.; Yang, S. Conventional and advanced exergy analyses of a vehicular proton exchange membrane fuel cell power system. Energy 2021, 222, 119939. [Google Scholar] [CrossRef]
- Liu, G.K.; Qin, Y.Z.; Yin, Y.F.; Bian, X.Z.; Kuang, C.C. Thermodynamic modeling and exergy analysis of proton exchange membrane fuel cell power system. Int. J. Hydrogen Energy 2020, 45, 29799–29811. [Google Scholar] [CrossRef]
- Li, D.; Li, S.; Ma, Z.; Xu, B.; Lu, Z.; Li, Y.; Zheng, M. Ecological Performance Optimization of a High Temperature Proton Exchange Membrane Fuel Cell. Mathematics 2021, 9, 1332. [Google Scholar] [CrossRef]
- Xu, B.; Li, D.; Ma, Z.; Zheng, M.; Li, Y. Thermodynamic Optimization of a High Temperature Proton Exchange Membrane Fuel Cell for Fuel Cell Vehicle Applications. Mathematics 2021, 9, 1792. [Google Scholar] [CrossRef]
- Li, Y.; Ma, Z.; Zheng, M.; Li, D.; Lu, Z.; Xu, B. Performance Analysis and Optimization of a High-Temperature PEMFC Vehicle Based on Particle Swarm Optimization Algorithm. Membranes 2021, 11, 691. [Google Scholar] [CrossRef]
- Rosli, R.E.; Sulong, A.B.; Daud, W.R.W.; Zullzifley, M.A.; Husaini, T.; Rosli, M.I.; Majlan, E.H.; Haque, M.A. A review of high-temperature proton exchange membrane fuel cell (HT-PEMFC) system. Int. J. Hydrogen Energy 2017, 42, 9293–9314. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, G.; Chen, J. Multi-objective optimisation analysis and load matching of a phosphoric acid fuel cell system. Int. J. Hydrogen Energy 2012, 37, 3438–3446. [Google Scholar] [CrossRef]
- Kim, M.; Kang, T.; Kim, J.; Sohn, Y.-J. One-dimensional modeling and analysis for performance degradation of high temperature proton exchange membrane fuel cell using PA doped PBI membrane. Solid State Ion. 2014, 262, 319–323. [Google Scholar] [CrossRef]
- Sousa, T.; Mamlouk, M.; Scott, K. An isothermal model of a laboratory intermediate temperature fuel cell using PBI doped phosphoric acid membranes. Chem. Eng. Sci. 2010, 65, 2513–2530. [Google Scholar] [CrossRef]
- Chen, H.; Wang, S.; Liu, F.; Wang, D.; Li, J.; Mao, T.; Liu, G.; Wang, X.; Xu, J.; Wang, Z. Base-acid doped polybenzimidazole with high phosphoric acid retention for HT-PEMFC applications. J. Membr. Sci. 2020, 596, 117722. [Google Scholar] [CrossRef]
- Ubeda, D.; Canizares, P.; Rodrigo, M.A.; Pinar, F.J.; Lobato, J. Durability study of HTPEMFC through current distribution measurements and the application of a model. Int. J. Hydrogen Energy 2014, 39, 21678–21687. [Google Scholar] [CrossRef]
- Sarabchi, N.; Mahmoudi, S.M.S.; Yari, M.; Farzi, A. Exergoeconomic analysis and optimization of a novel hybrid cogeneration system: High-temperature proton exchange membrane fuel cell/Kalina cycle, driven by solar energy. Energy Convers. Manag. 2019, 190, 14–33. [Google Scholar] [CrossRef]
- Yang, S.; Xiao, Z.; Deng, C.; Liu, Z.; Zhou, H.; Ren, J.; Zhou, T. Techno-economic analysis of coal-to-liquid processes with different gasifier alternatives. J. Clean. Prod. 2020, 253, 120006. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, N.; Yang, S. Thermodynamic and parametric analysis of a coupled LiBr/H2O absorption chiller/Kalina cycle for cascade utilization of low-grade waste heat. Energy Convers. Manag. 2020, 205, 112370. [Google Scholar] [CrossRef]
- Zhou, W.L.; Zheng, Y.P.; Pan, Z.J.; Lu, Q. Review on the Battery Model and SOC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Chang, C.C.; Zheng, Y.P.; Sun, W.M.; Ma, Z.S. LPV Estimation of SOC Based on Electricity Conversion and Hysteresis Characteristic. J. Energy Eng. 2019, 145, 04019026. [Google Scholar] [CrossRef]
- Ye, L.; Jiao, K.; Du, Q.; Yin, Y. Exergy Analysis of High-Temperature Proton Exchange Membrane Fuel Cell Systems. Int. J. Green Energy 2015, 12, 917–929. [Google Scholar] [CrossRef]
- Angulo-Brown, F. An ecological optimization criterion for finite-time heat engines. J. Appl. Phys. 1991, 69, 7465–7469. [Google Scholar] [CrossRef]
- Gong, W.L.; Ma, J.H.; Zhao, J.; Bai, Z.Q. Thermodynamics analysis of a PEM fuel cell stack. Renew. Energy Resour. 2011, 29, 124–128. [Google Scholar]
- Tian, J.; Zeng, Q.K.; Wang, P.; Wang, X.Q. Active steering control based on preview theory for articulated heavy vehicles. PLoS ONE 2021, 16, e0252098. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.M.; Lin, P. Parameter identification of sound absorption model of porous materials based on modified particle swarm optimization algorithm. PLoS ONE 2021, 16, e0250950. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.M.; Zhang, L.; Jiang, Y.P.; Chen, N. Active Control on Path Following and Lateral Stability for Truck-Trailer Combinations. Arabian J. Sci. Eng. 2019, 44, 1365–1377. [Google Scholar] [CrossRef]
- Xu, X.M.; Chen, D.; Zhang, L.; Chen, N. Hopf Bifurcation Characteristics of the Vehicle with Rear Axle Compliance Steering. Shock Vib. 2019, 2019, 3402084. [Google Scholar] [CrossRef] [Green Version]
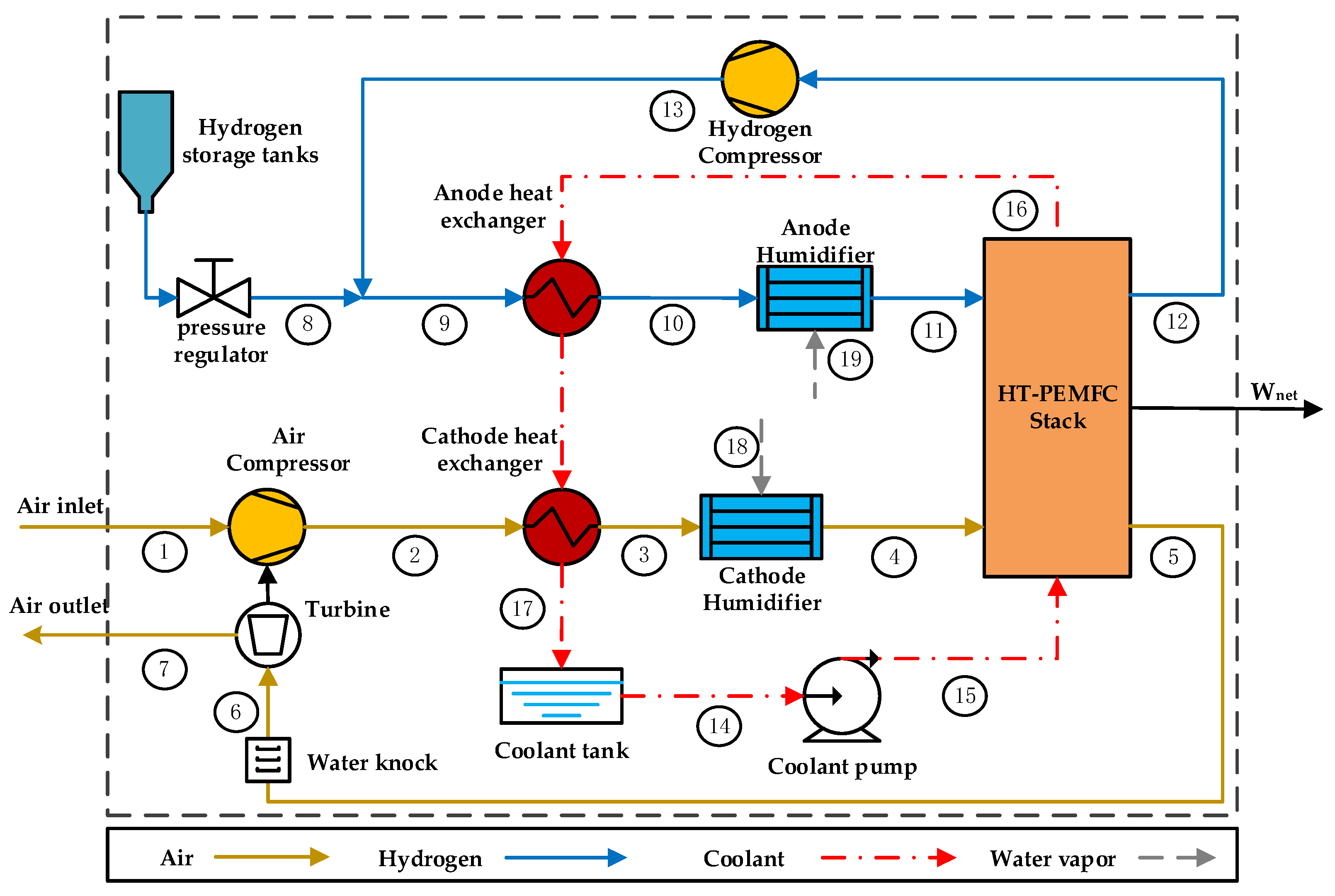
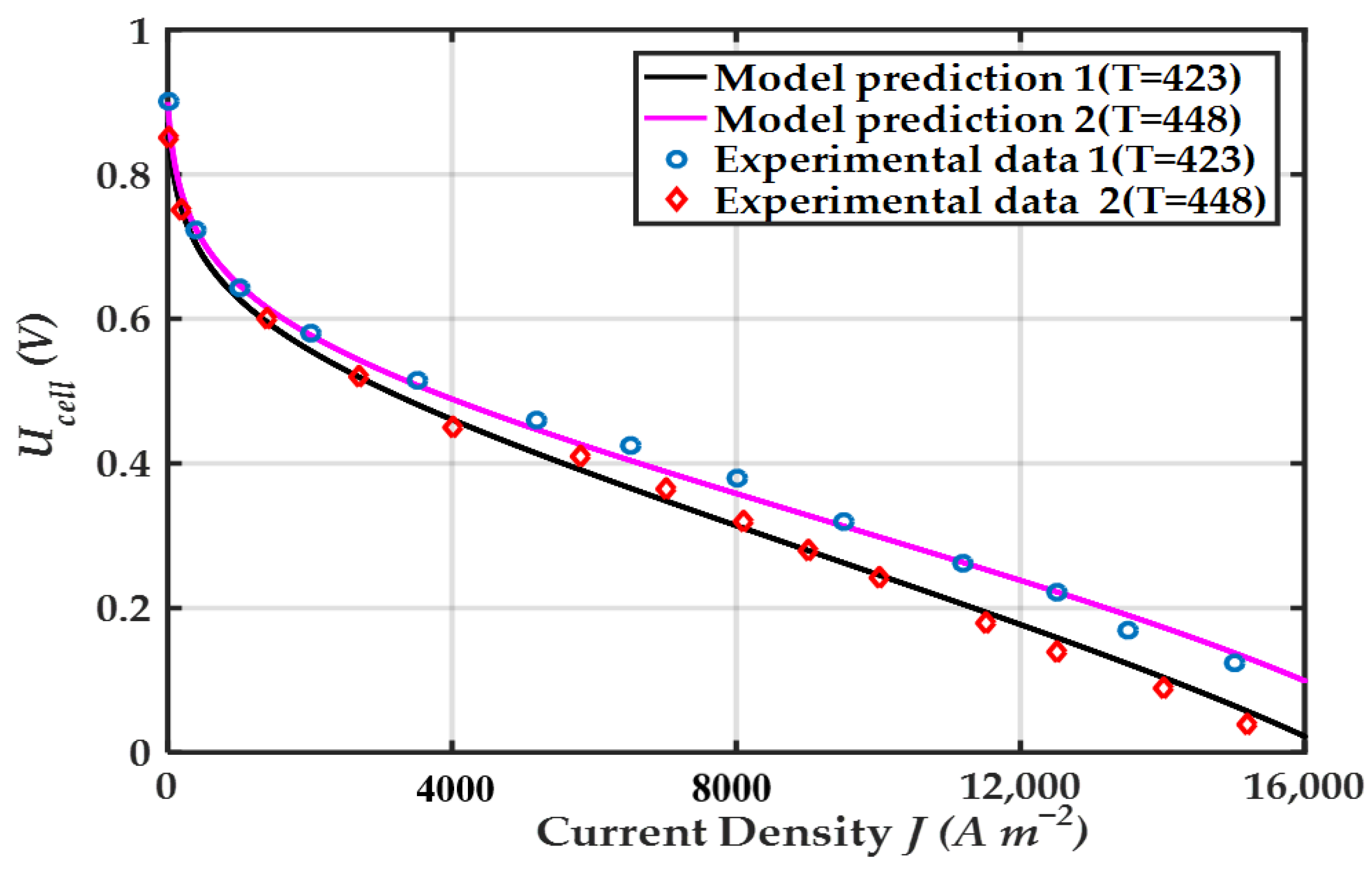
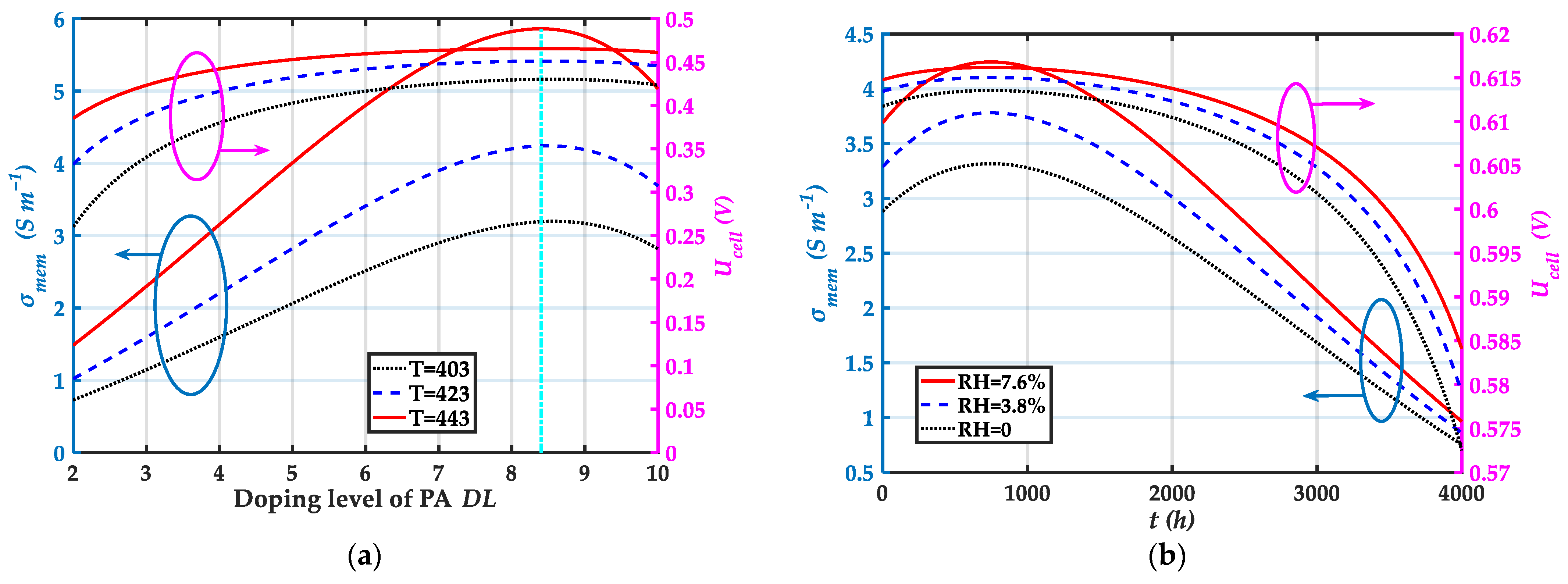


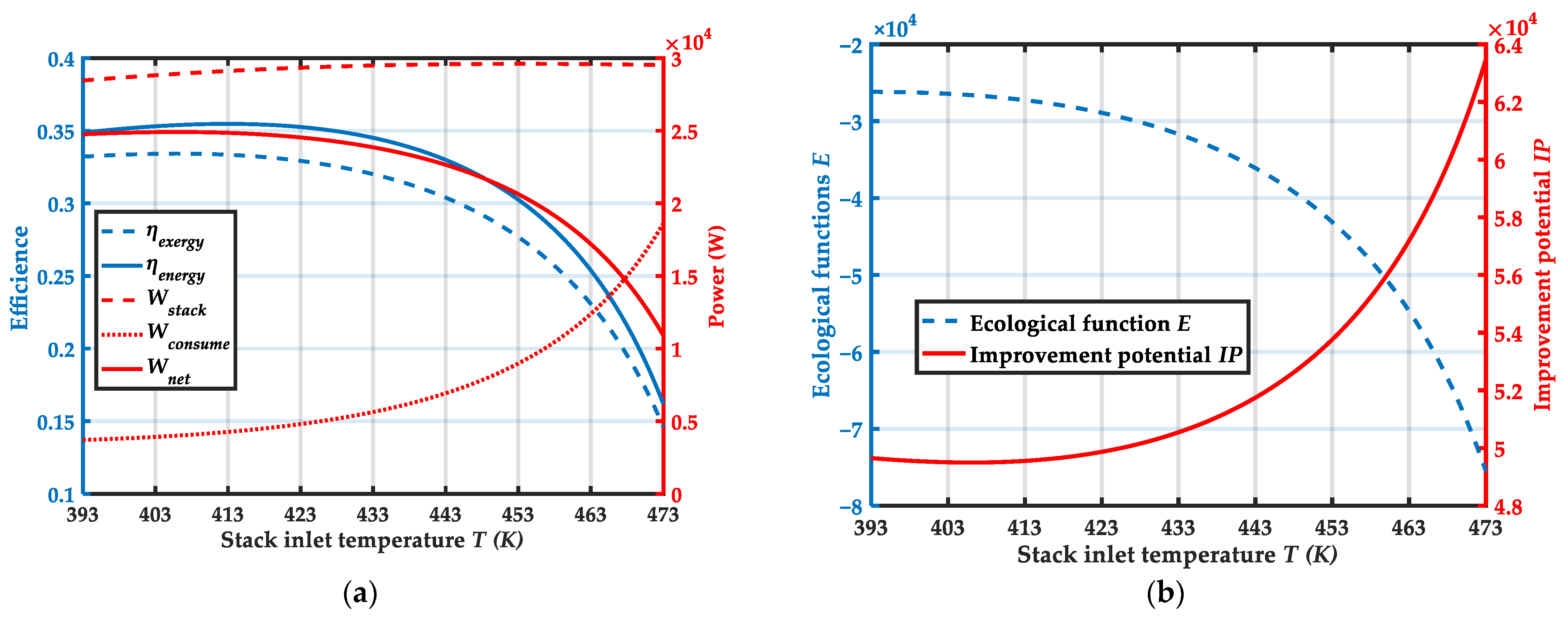

| Component | Parameters | Values |
|---|---|---|
| HT-PEMFC stack | 250 | |
| [59] | ||
| 1.05 [62] | ||
| 2 [62] | ||
| 2 atm | ||
| 2 atm | ||
| 403 K [42] | ||
| 7.6% [42] | ||
| [42] | ||
| Compressors | 55% [62] | |
| Coolant pump | 55% | |
| Turbine | 65% |
| Components (Power: W) | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
|---|---|---|---|---|---|---|---|
| HT-PEMFC stack | 9156.9 | 16,588.3 | 23,106.4 | 28,815.2 | 33,675.9 | 37,532.9 | 40,045.9 |
| AC | −1125.8 | −2251.6 | −3377.4 | −4503.2 | −5629.1 | −6754.9 | −7880.7 |
| HC | −2.4 | −4.9 | −7.3 | −9.7 | −12.2 | −14.6 | −17.0 |
| CHE | −154.1 | −308.1 | −462.2 | −616.3 | −770.3 | −924.4 | −1078.4 |
| AHE | −32.3 | −64.6 | −97.0 | −129.3 | −161.6 | −193.9 | −226.3 |
| CP | −115.3 | −254.1 | −405.3 | −567.6 | −741.3 | −928.7 | −11,345 |
| TUR | 472.0 | 944.0 | 1416.0 | 1887.9 | 2359.9 | 2831.9 | 3303.9 |
| Components (Exergy Loss: W) | Exergy Loss Expressions | Values (J = 0.8) |
|---|---|---|
| HT-PEMFC stack | 35,057.3 | |
| AH | 269.6 | |
| CH | 814.7 | |
| HC | 8.5 | |
| AC | 1709.2 | |
| AHE and CHE | 11,774.3 | |
| CP | 345.2 | |
| TUR | 535.2 | |
| Hydrogen-mixing | 9.5 | |
| Water knock | 772.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Li, D.; Ma, Z.; Zheng, M.; Lu, Z. Thermodynamic Modeling and Performance Analysis of Vehicular High-Temperature Proton Exchange Membrane Fuel Cell System. Membranes 2022, 12, 72. https://doi.org/10.3390/membranes12010072
Li Y, Li D, Ma Z, Zheng M, Lu Z. Thermodynamic Modeling and Performance Analysis of Vehicular High-Temperature Proton Exchange Membrane Fuel Cell System. Membranes. 2022; 12(1):72. https://doi.org/10.3390/membranes12010072
Chicago/Turabian StyleLi, Yanju, Dongxu Li, Zheshu Ma, Meng Zheng, and Zhanghao Lu. 2022. "Thermodynamic Modeling and Performance Analysis of Vehicular High-Temperature Proton Exchange Membrane Fuel Cell System" Membranes 12, no. 1: 72. https://doi.org/10.3390/membranes12010072
APA StyleLi, Y., Li, D., Ma, Z., Zheng, M., & Lu, Z. (2022). Thermodynamic Modeling and Performance Analysis of Vehicular High-Temperature Proton Exchange Membrane Fuel Cell System. Membranes, 12(1), 72. https://doi.org/10.3390/membranes12010072






