Performance Analysis and Optimization of a High-Temperature PEMFC Vehicle Based on Particle Swarm Optimization Algorithm
Abstract
:1. Introduction
2. HT-PEMFC Model
2.1. Reversible Output Voltage
2.2. Irreversible Overpotential
2.3. Power Density and Efficiency of HT-PEMFC
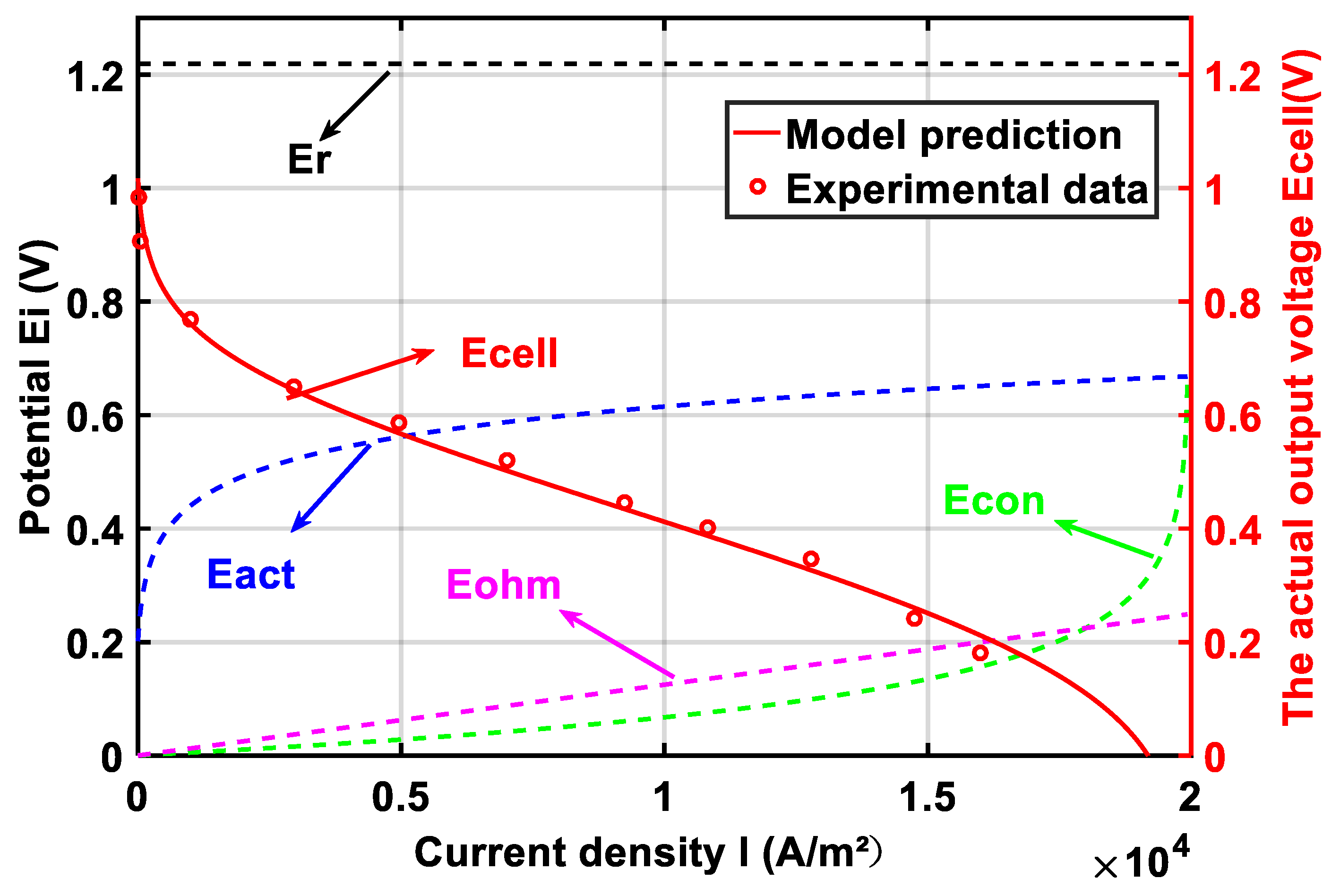
2.4. Model Verification
3. Parametric Studies and Optimization
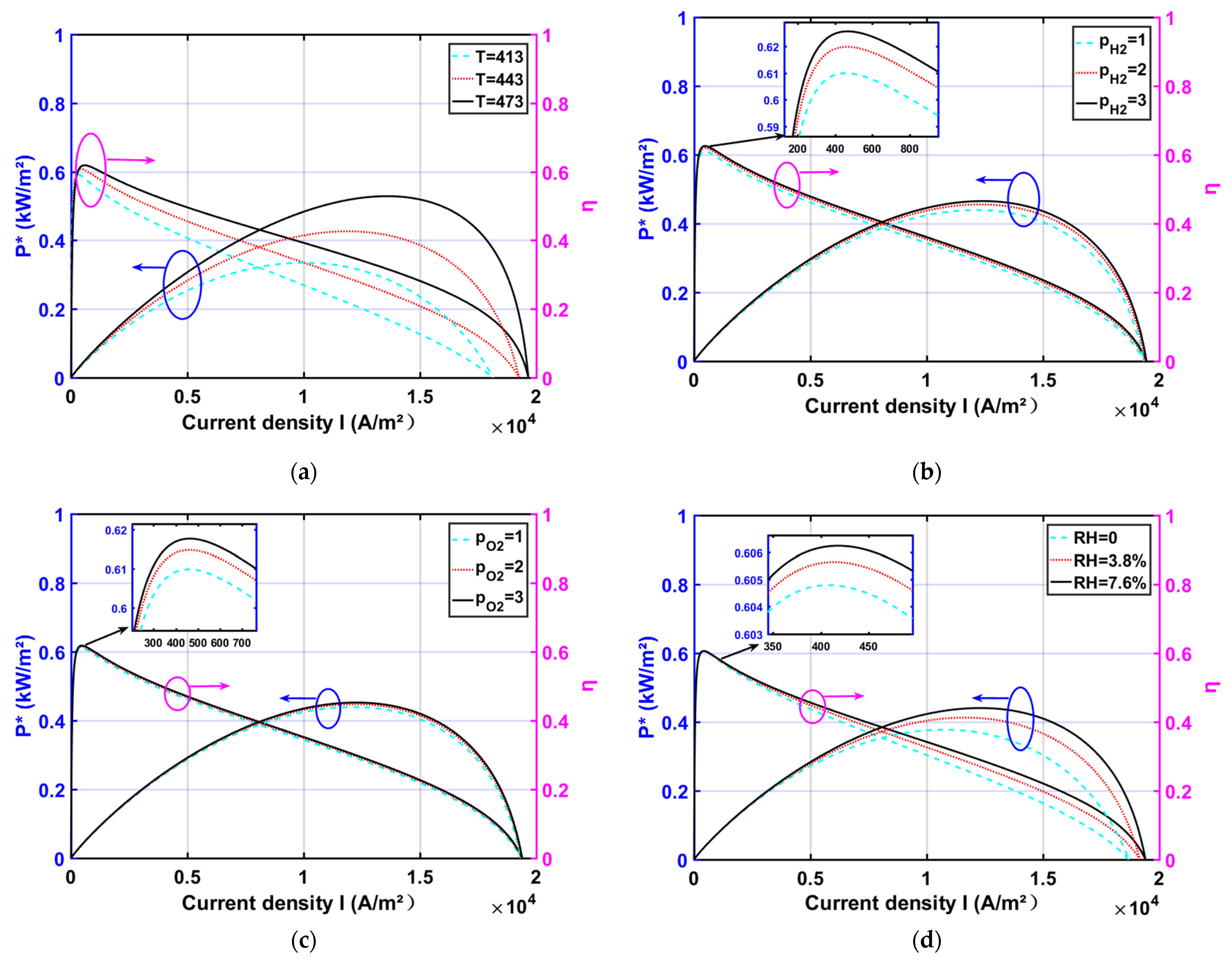
3.1. Effect of Operating Parameters
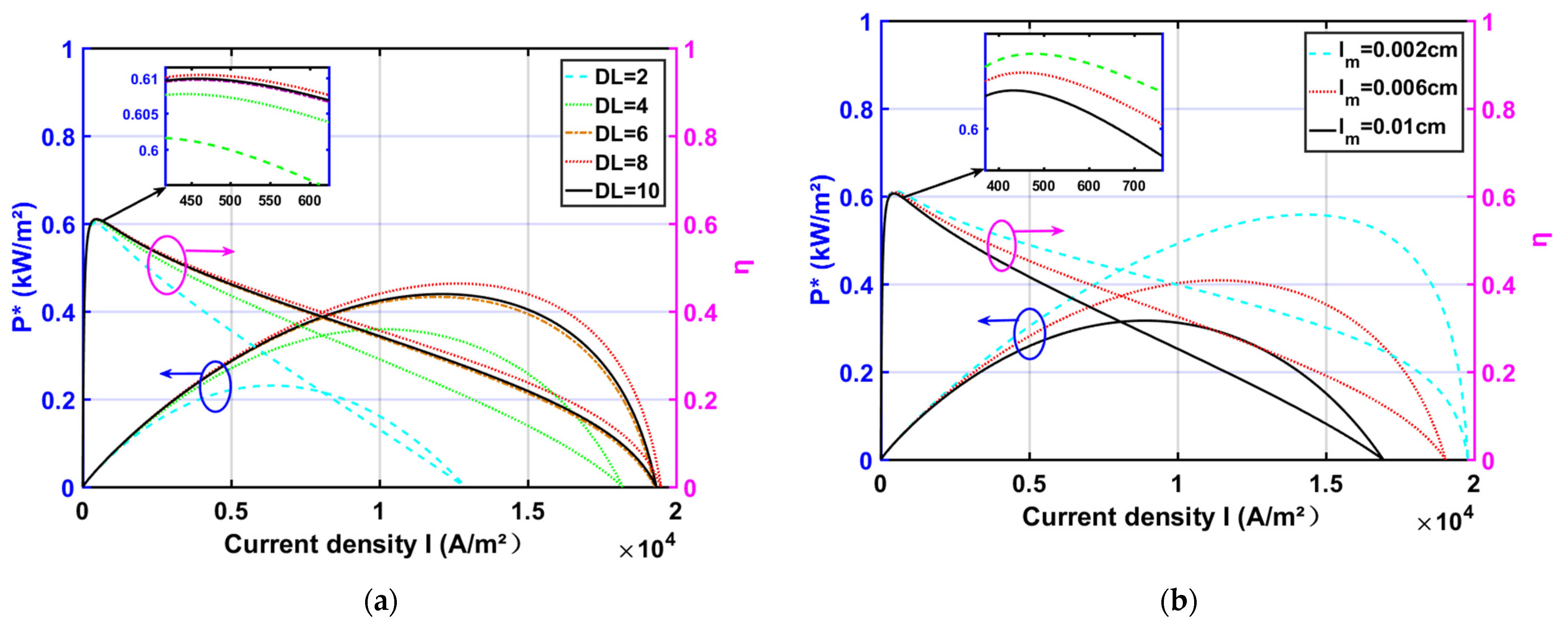
3.2. Effect of Design Parameters
3.3. Finite Time Thermodynamic Optimization
3.3.1. Multi-Objective Optimization Model
- Initialize the population: the particle swarm size is 500 and the maximum number of iterations is 500. The maximum flight speed of the particle is 10% of the optimization variables. Initialize the random position and velocity of each particle.
- Calculate the fitness value: the fitness value of each particle is evaluated by the objective function .
- Update the particle best value () and global best value (): the particle velocity and position update equation are as shown in Equation (17), where and are the velocity and position of the particle after the iteration, respectively. and are random numbers between [0,1]. The learning factor and the inertia weight .
- Judgment: the termination condition selects the maximum number of iterations. If the condition is satisfied, the optimal solution will be output.
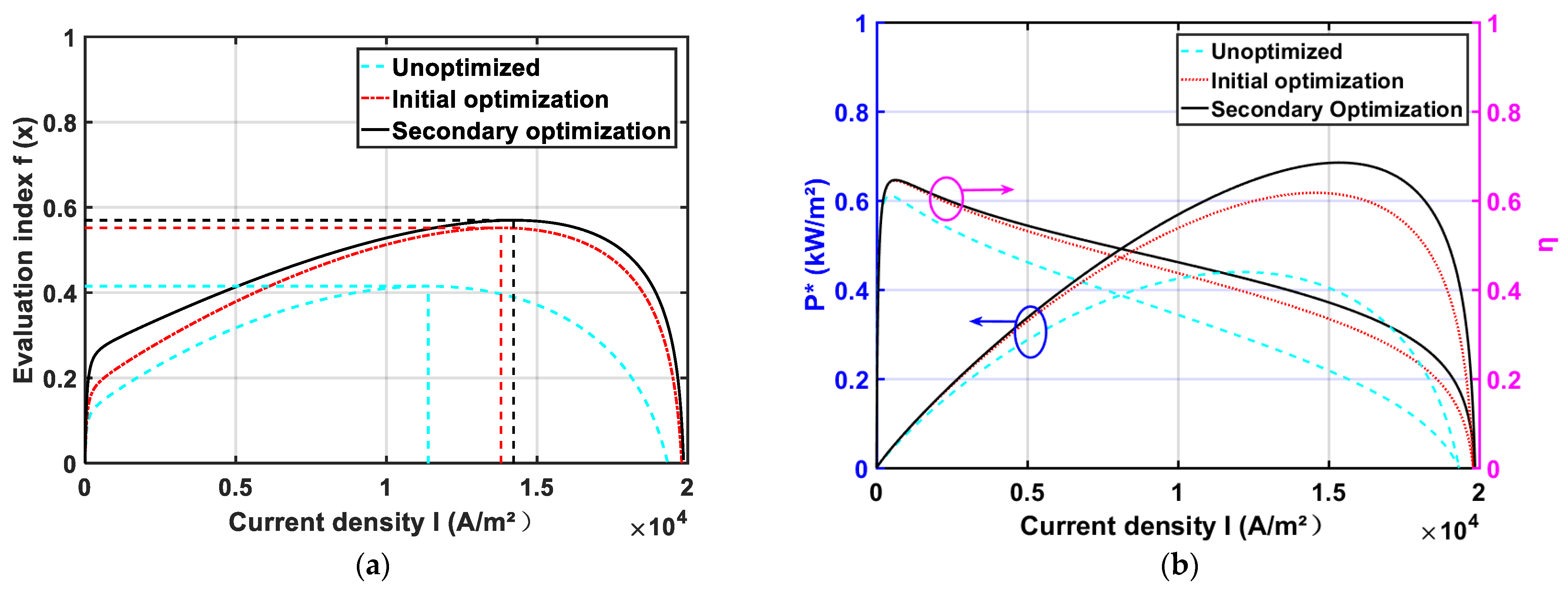
3.3.2. Optimization of Operating and Design Parameters
4. FCV Powertrain Design
4.1. Configuration
4.2. Motor Parameters
4.2.1. Maximum Power and Rated Power
4.2.2. Maximum Speed and Rated Speed
4.2.3. Maximum Torque and Rated Torque
4.3. Fuel Cell Parameters
4.4. Battery Parameters
5. Results and Discussions
6. Conclusions
- The reliability of the model was verified by comparing the HT-PEMFC model with the experimental data. By the parametric studies, the appropriate increase in , , , and is beneficial to the HT-PEMFC output performance improvement. With increasing the doping level , the output performance increases and then decreases. With the decrease in proton film thickness , the output performance is improved;
- The PSO algorithm can optimize the power density and efficiency of the HT-PEMFC single cell based on finite-time thermodynamic theory. The simulation results show that the performance of the optimized HT-PEMFC single cell is improved, the power density can be obtained up to 6.848 kW/m2, and the efficiency can reach up to 64.58%;
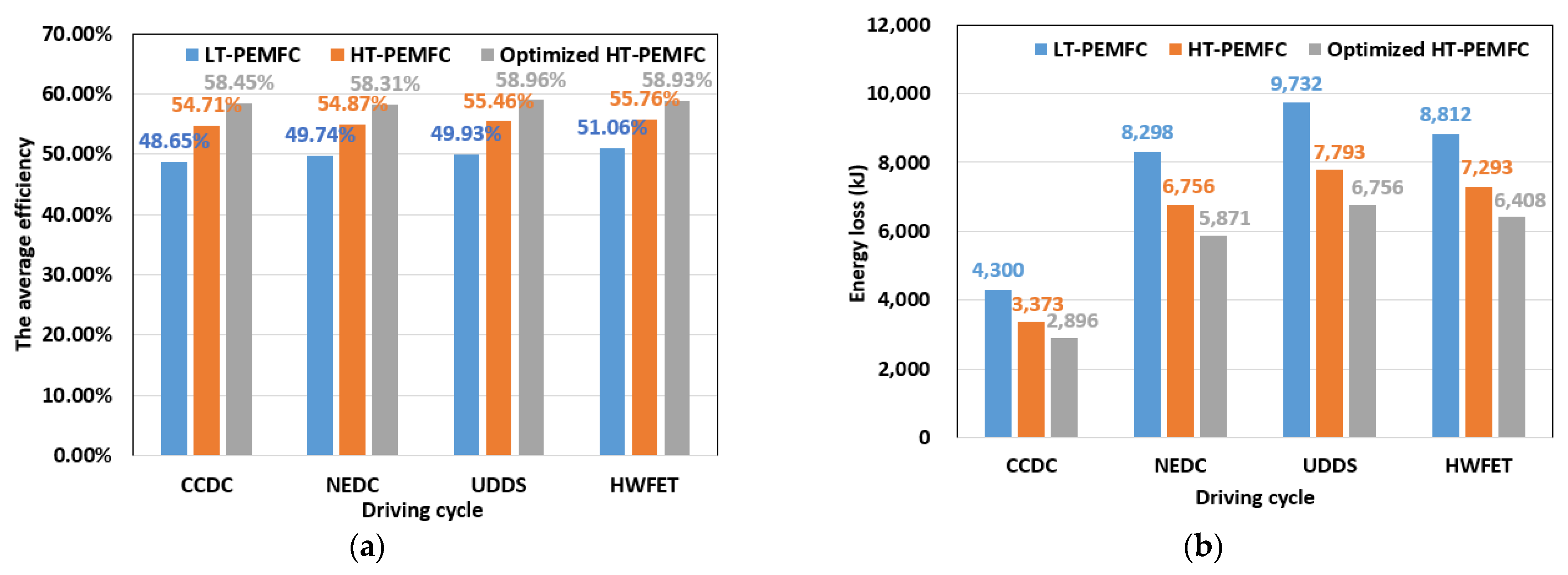
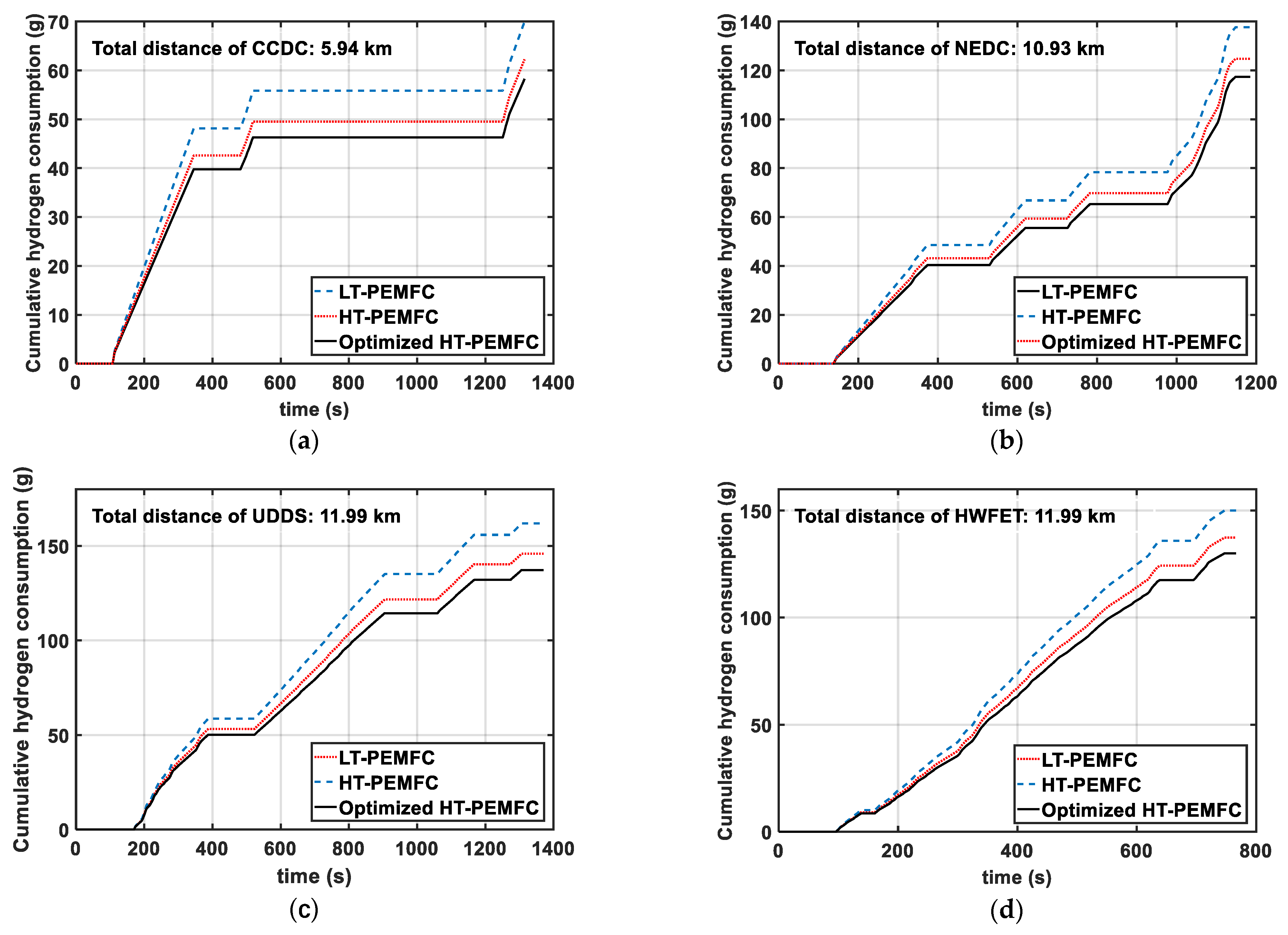
- Three different powertrain solutions are available for FCVs based on the different power density and efficiency curves of the LT-PEMFC, HT-PEMFC, and optimized HT-PEMFC outputs. The simulation comparison shows that the optimized HT-PEMFC stack has the lowest number of single cells, which is conducive to the vehicle’s structural arrangement and light weight. Moreover, the FCV that applied the optimized HT-PEMFC has the highest average efficiency, the lowest energy loss, and the lowest 100 km hydrogen consumption.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Xu, W.; Hu, X. Research on the development of New Energy Vehicle Industry in China. Appl. Mech. Mater. 2013, 291–294, 861–865. [Google Scholar] [CrossRef]
- Zhao, F.Q.; Mu, Z.X.; Hao, H.; Liu, Z.W.; He, X.; Przesmitzki, S.V.; Amer, A.A. Hydrogen fuel cell vehicle development in China: An industry chain perspective. Energy Technol. 2020, 8, 2000179. [Google Scholar] [CrossRef]
- Li, Y.; Kimura, S. Economic competitiveness and environmental implications of hydrogen energy and fuel cell electric vehicles in ASEAN countries: The current and future scenarios. Energy Policy 2021, 148, 111980. [Google Scholar] [CrossRef]
- Liu, S.Q.; Jia, L.M. Review on sustainable development of forest-based biodiesel. J. Nanjing For. Univ. Nat. Sci. Ed. 2020, 44, 216–224. [Google Scholar]
- Wang, J.; Zhang, J.; Yu, Y.; Zhang, Y.; Zhu, X.Y.; Yue, H.Y.; Wang, Z.Q.; Zhou, W.H. Synthesis of Si/C composites derived from directly-carbonized reed plants as high-performance anode for lithium ion batteries. J. For. Eng. 2019, 4, 84–91. [Google Scholar]
- Xia, Z.H.; Zhao, L.Y.; Wu, W.B.; Jing, Y.; Dai, H.Q.; Fang, G.G. Performance of photocatalytic biomass fuel cells based on heteropolyacids. J. For. Eng. 2017, 2, 86–91. [Google Scholar]
- Zhang, Z.G. Researches on green features and category architecture of green strategies of renewable-resource-based enterprises: A case study of forestry enterprise. J. Nanjing For. Univ. Nat. Sci. Ed. 2020, 44, 1–8. [Google Scholar]
- Xie, J.Y.; Cai, B.; Zhang, H.G.; Xu, X. Responses of forest soil labile nitrogen pool and nitrogen cycle to the changes of carbon input. J. Nanjing For. Univ. Nat. Sci. Ed. 2021, 1–16. [Google Scholar] [CrossRef]
- Han, J.; Han, J.; Yu, S. Investigation of FCVs durability under driving cycles using a model-based approach. J. Energy Storage 2020, 27, 101169. [Google Scholar] [CrossRef]
- Dai, F.L.; Luo, J.R.; Zhou, S.H.; Qin, X.Z.; Liu, D.T.; Qi, H.S. Porous hafnium-containing acid/base bifunctional catalysts for efficient upgrading of bio-derived aldehydes. J. Bioresour. Bioprod. 2021, 6, 243–253. [Google Scholar] [CrossRef]
- Alegre, C.; Álvarez-Manuel, L.; Mustata, R.; Valiño, L.; Lozano, A.; Barreras, F. Assessment of the durability of low-cost Al bipolar plates for High Temperature PEM fuel cells. Int. J. Hydrogen Energy 2019, 44, 12748–12759. [Google Scholar] [CrossRef]
- Bandlamudi, V.; Bujlo, P.; Sita, C.; Pasupathi, S. Study on electrode carbon corrosion of high temperature proton exchange membrane fuel cell. Mater. Today Proc. 2018, 5, 10602–10610. [Google Scholar] [CrossRef]
- Nomnqa, M.; Ikhu-Omoregbe, D.; Rabiu, A. Performance evaluation of a HT-PEM fuel cell micro-cogeneration system for domestic application. Energy Syst. 2019, 10, 185–210. [Google Scholar] [CrossRef]
- Reddy, E.H.; Jayanti, S. Thermal management strategies for a 1 kWe stack of a high temperature proton exchange membrane fuel cell. Appl. Therm. Eng. 2012, 48, 465–475. [Google Scholar] [CrossRef]
- Reddy, E.H.; Monder, D.S.; Jayanti, S. Parametric study of an external coolant system for a high temperature polymer electrolyte membrane fuel cell. Appl. Therm. Eng. 2013, 58, 155–164. [Google Scholar] [CrossRef]
- Pohl, E.; Meier, P.; Maximini, M.; vom Schloß, J. Primary energy savings of a modular combined heat and power plant based on high temperature proton exchange membrane fuel cells. Appl. Therm. Eng. 2016, 104, 54–63. [Google Scholar] [CrossRef]
- Lee, D.; Lim, J.W.; Lee, D.G. Cathode/anode integrated composite bipolar plate for high-temperature PEMFC. Compos. Struct. 2017, 167, 144–151. [Google Scholar] [CrossRef]
- Oono, Y.; Sounai, A.; Hori, M. Influence of the phosphoric acid-doping level in a polybenzimidazole membrane on the cell performance of high-temperature proton exchange membrane fuel cells. J. Power Sources 2008, 189, 943–949. [Google Scholar] [CrossRef]
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next generation of proton-exchange membrane fuel cells. Nature 2021, 595, 361–1369. [Google Scholar] [CrossRef]
- Li, Q.F.; Rudbeck, H.C.; Chromik, A.; Jensen, J.O.; Pan, C.; Steenberg, T.; Calverley, M.; Bjerrum, N.J.; Kerres, J. Properties, degradation and high temperature fuel cell test of different types of PBI and PBI blend membranes. J. Membr. Sci. 2010, 347, 260–270. [Google Scholar] [CrossRef]
- Zuo, S.L.; Wang, Y.F.; Zhang, Q.H. Activated carbons for the electrochemical storage of energy and electrochemical catalytic conversion of fuels: A review. J. For. Eng. 2018, 3, 1–11. [Google Scholar]
- Xu, Y.G.; Zhang, H.; Huang, L.L.; Zheng, Q.M.; Cao, S.L.; Chen, L.H. Preparation of acrylic acid modified cellulose acetate ultrafiltration membrane. J. For. Eng. 2017, 2, 90–96. [Google Scholar]
- Zhang, T.Y.; Li, J.; Li, Q.; Yu, M.F.; Sun, H. Combination effects of flow field structure and assembly force on performance of high temperature proton exchange membrane fuel cells. Int. J. Energy Res. 2021, 45, 7903–7917. [Google Scholar] [CrossRef]
- Yan, Q.; Toghiani, H.; Causey, H. Steady state and dynamic performance of proton exchange membrane fuel cells (PEMFCs) under various operating conditions and load changes. J. Power Sources 2006, 161, 492–502. [Google Scholar] [CrossRef]
- Lee, W.Y.; Kim, M.J.; Sohn, Y.J.; Kim, S.G. Power optimization of a combined power system consisting of a high-temperature polymer electrolyte fuel cell and an organic Rankine cycle system. Energy 2016, 113, 1062–1070. [Google Scholar] [CrossRef]
- Yang, C.; Costamagna, P.; Srinivasan, S.; Benziger, J.; Bocarsly, A.B. Approaches and technical challenges to high temperature operation of proton exchange membrane fuel cells. J. Power Sources 2001, 103, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Liu, Z.; Wainright, J.S.; Litt, M.H.; Savinell, R.F. Study of the oxygen reduction reaction (ORR) at Pt interfaced with phosphoric acid doped polybenzimidazole at elevated temperature and low relative humidity. Electrochim. Acta 2005, 51, 3914–3923. [Google Scholar] [CrossRef]
- Krishnan, N.N.; Lee, S.; Ghorpade, R.V.; Konovalova, A.; Jang, J.H.; Kim, H.-J.; Han, J.; Henkensmeier, D.; Han, H. Polybenzimidazole (PBI-OO) based composite membranes using sulfophenylated TiO 2 as both filler and crosslinker, and their use in the HT-PEM fuel cell. J. Membr. Sci. 2018, 560, 11–20. [Google Scholar] [CrossRef]
- Li, Q.; He, R.; Jian, G.; Jensen, J.O.; Bjerrum, N. CO tolerance by the PEMFC operational at temperatures up to 200 °C. In Proceedings of the 2nd European PEFC Forum, Lucerne, Switzerland, 30 June–4 July 2003; pp. 253–262. [Google Scholar]
- Khan, S.S.; Shareef, H.; Wahyudie, A.; Khalid, S.; Sirjani, R. Influences of ambient conditions on the performance of proton exchange membrane fuel cell using various models. Energy Environ. 2019, 30, 1087–1110. [Google Scholar] [CrossRef]
- Li, C.J.; Liu, Y.; Ma, Z.S. Thermodynamic Analysis of the Performance of an Irreversible PEMFC. Defect Diffus. Forum 2018, 380, 350–360. [Google Scholar] [CrossRef]
- Cheddie, D.; Munroe, N. Mathematical model of a PEMFC using a PBI membrane. Energy Convers. Manag. 2005, 47, 1490–1504. [Google Scholar] [CrossRef]
- Lai, H.Y.; Li, Y.T.; Chan, Y.H. Efficiency Enhancement on Hybrid Power System Composed of Irreversible Solid Oxide Fuel Cell and Stirling Engine by Finite Time Thermodynamics. Energies 2021, 14, 1037. [Google Scholar] [CrossRef]
- He, S.; Lin, L.Y.; Wu, Z.X.; Chen, Z.M. Application of finite element analysis in properties test of finger-jointed lumber. J. Bioresour. Bioprod. 2020, 5, 124–133. [Google Scholar] [CrossRef]
- Christopher, N.I.; Egbuna, S.O.; Onoh, M.I.; Christain, A.O.; Onyekwulu, C.S. Optimization and kinetic studies for enzymatic hydrolysis and fermentation of colocynthis vulgaris Shrad seeds shell for bioethanol production. J. Bioresour. Bioprod. 2021, 6, 45–64. [Google Scholar]
- Xia, X.Y.; Wang, F.J.; Fu, Q.; Zhang, N.; Guo, Q.Q. Thermal stability and degradation kinetic model of proanthocyanidins in blueberry (Vaccinium spp.) juice beverage. J. Nanjing For. Univ. Nat. Sci. Ed. 2019, 43, 89–95. [Google Scholar]
- Li, C.J.; Liu, Y.; Xu, B.; Ma, Z. Finite Time thermodynamic optimization of an irreversible proton exchange membrane fuel cell for vehicle use. Processes 2019, 7, 419. [Google Scholar] [CrossRef] [Green Version]
- Li, D.X.; Ma, Z.S.; Xu, B.; Lu, Z.H.; Li, Y.J.; Zheng, M. Ecological performance optimization of a high temperature proton exchange membrane fuel cell. Mathematics 2021, 9, 1332. [Google Scholar] [CrossRef]
- Xu, B.; Li, D.; Ma, Z.; Zheng, M.; Li, Y. Thermodynamic optimization of a high temperature proton exchange membrane fuel cell for fuel cell vehicle applications. Mathematics 2021, 9, 1792. [Google Scholar] [CrossRef]
- Lu, X.H.; Li, B.; Guo, L.; Wang, P.F.; Nasser, Y. Exergy analysis of a polymer fuel cell and identification of its optimum operating conditions using improved Farmland Fertility Optimization. Energy 2020, 216, 119264. [Google Scholar] [CrossRef]
- Li, C.T.; Wu, S.J.; Yu, W.L. Parameter design on the multi-objectives of PEM fuel cell stack using an adaptive neuro-fuzzy inference system and genetic algorithms. Pergamon 2014, 39, 4502–4515. [Google Scholar] [CrossRef]
- Erni, M.; Suhaimi, M.H.N.; Daud, W.R.W.; Majlan, E.H.; Miftah, K. Operating temperature effects on water transport behavior in a single cell PEMFC. Appl. Mech. Mater. 2011, 52–54, 1153–1158. [Google Scholar] [CrossRef]
- Guo, Y.H.; Guo, X.R.; Zhang, H.C.; Hou, S.J. Energetic, exergetic and ecological analyses of a high-temperature proton exchange membrane fuel cell based on a phosphoric-acid-doped polybenzimidazole membrane. Sustain. Energy Technol. Assess. 2019, 38, 100671. [Google Scholar] [CrossRef]
- Olapade, P.O.; Meyers, J.P.; Borup, R.L.; Mukundan, R. Parametric study of the morphological proprieties of HT-PEMFC components for effective membrane hydration. J. Electrochem. Soc. 2011, 158, B639–B649. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, H.; Liu, G. Diffusion—Convection/Electrochemical model studies on polybenzimidazole (PBI) fuel cell based on AC impedance technique. Energy Convers. Manag. 2008, 49, 1019–1027. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Zhao, J.; Wang, F.; Wang, J.; Miao, H.; Yuan, J. Performance evaluation of an integrated high-temperature proton exchange membrane fuel cell and absorption cycle system for power and heating/cooling cogeneration. Energy Convers. Manag. 2019, 181, 292–301. [Google Scholar] [CrossRef]
- Cheddie, D.F.; Munroe, N.D.H. A two-phase model of an intermediate temperature PEM fuel cell. Int. J. Hydrogen Energy 2006, 32, 832–841. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H. Performance analyses of a combined system consisting of high-temperature polymer electrolyte membrane fuel cells and thermally regenerative electrochemical cycles. Energy 2020, 193, 116720. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, L.; Liao, T.J.; Zhou, Y.H.; Zhao, Y.R.; Chen, J.C. Exploiting the waste heat from an alkaline fuel cell via electrochemical cycles. Energy 2018, 142, 983–990. [Google Scholar] [CrossRef]
- Yun, H.M.; Wu, F.; Yin, Y.; Chen, L.G. Multi-Objective optimization of dish stirling engine based on linear weighted evaluation function method. J. Wuhan Inst. Technol. 2020, 42, 218–223. [Google Scholar]
- Scott, K.; Pilditch, S.; Mamlouk, M. Modelling and experimental validation of a high temperature polymer electrolyte fuel cell. J. Appl. Electrochem. 2007, 37, 1245–1259. [Google Scholar] [CrossRef]
- Wang, L.; Hao, R.Y.; Liu, W.; Wen, Z.M. A multi-factor forest fire risk rating prediction model based on particle swarm optimization algorithm and back-propagation neural network. J. For. Eng. 2019, 4, 137–144. [Google Scholar]
- Xu, X.M.; Lin, P. Parameter identification of sound absorption model of porous materials based on modified particle swarm optimization algorithm. PLoS ONE 2021, 16, e0250950. [Google Scholar]
- Wu, S.Y.; Yi, T.T.; Xiao, L. Parametric optimization and performance analysis of subcritical organic Rankine cycle based on multi-objective function. CIESC J. 2014, 65, 4078–4085. [Google Scholar]
- Yang, K.; Wang, J.; Xiao, S.J.; Bai, G.J.; Tian, Z.X.; Li, M. Study on the matching and design of a B-class fuel cell electric vehicle. Chin. J. Automot. Eng. 2018, 8, 399–406. [Google Scholar]
- Liu, J. Study on parameter matching and performance of powertrain of new energy pure electric vehicle. Sci. J. Intell. Syst. Res. 2021, 3, 79–83. [Google Scholar]
- Fu, X.; Zhang, Q.; Tang, J.; Wang, C. Parameter Matching Optimization of a Powertrain System of Hybrid Electric Vehicles Based on Multi-Objective Optimization. Electronics 2019, 8, 875. [Google Scholar] [CrossRef] [Green Version]
- Jiang, K.; Guo, S.; Wu, Q.H. Matching and Optimization of Power System Parameters of Fuel Cell Sightseeing Vehicle. Sci. Technol. Eng. 2019, 19, 351–356. [Google Scholar]
- Tian, J.; Zeng, Q.K.; Wang, P.; Wang, X.Q. Active steering control based on preview theory for articulated heavy vehicles. PLoS ONE 2021, 16, e0252098. [Google Scholar] [CrossRef]
- Li, D.X.; Xu, B.; Tian, J.; Ma, Z.S. Energy management strategy for fuel cell and battery hybrid vehicle based on fuzzy logic. Processes 2020, 8, 882. [Google Scholar] [CrossRef]


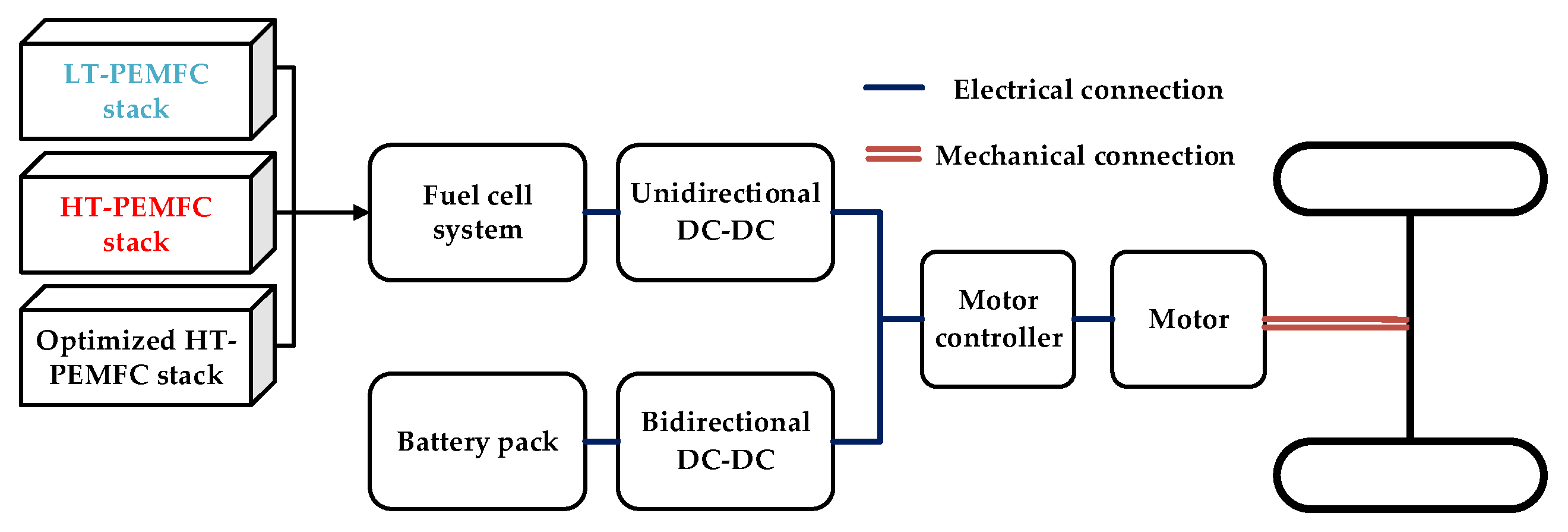
| Vehicle Parameters | Value | Design Requirements | Value |
|---|---|---|---|
| Mass (kg) | 1850 | Maximum speed (km/h) | 150 |
| Rolling resistance coefficient | 0.012 | 0–100 km/h acceleration time (s) | 10 |
| Air resistance coefficient | 0.32 | Maximum climb at 30 km/h (%) | 30 |
| Windward area (m2) | 2.4 | ||
| Wheel rolling radius (m) | 0.33 |
| Powertrain Components | Parameters | Values |
|---|---|---|
| Motor | (kW) | 55 (100) |
| () (r/min) | 4000 (1000) | |
| () (Nm) | 132 (360) | |
| Fuel cell | (kW) | 75 |
| Type | LT-PEMFC; HT-PEMFC; Optimized HT-PEMFC | |
| Battery | /kW | 55 |
| Type | Lithium-ion |
| Driving Cycles | LT-PEMFC | HT-PEMFC | Optimized HT-PEMFC |
|---|---|---|---|
| CCDC | 1178.19 | 1047.78 | 980.65 |
| NEDC | 1259.08 | 1141.45 | 1073.99 |
| UDDS | 1351.05 | 1216.25 | 1144.13 |
| HWFET | 908.91 | 832.23 | 787.53 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Ma, Z.; Zheng, M.; Li, D.; Lu, Z.; Xu, B. Performance Analysis and Optimization of a High-Temperature PEMFC Vehicle Based on Particle Swarm Optimization Algorithm. Membranes 2021, 11, 691. https://doi.org/10.3390/membranes11090691
Li Y, Ma Z, Zheng M, Li D, Lu Z, Xu B. Performance Analysis and Optimization of a High-Temperature PEMFC Vehicle Based on Particle Swarm Optimization Algorithm. Membranes. 2021; 11(9):691. https://doi.org/10.3390/membranes11090691
Chicago/Turabian StyleLi, Yanju, Zheshu Ma, Meng Zheng, Dongxu Li, Zhanghao Lu, and Bing Xu. 2021. "Performance Analysis and Optimization of a High-Temperature PEMFC Vehicle Based on Particle Swarm Optimization Algorithm" Membranes 11, no. 9: 691. https://doi.org/10.3390/membranes11090691
APA StyleLi, Y., Ma, Z., Zheng, M., Li, D., Lu, Z., & Xu, B. (2021). Performance Analysis and Optimization of a High-Temperature PEMFC Vehicle Based on Particle Swarm Optimization Algorithm. Membranes, 11(9), 691. https://doi.org/10.3390/membranes11090691






