Structure-Property Relationship on the Example of Gas Separation Characteristics of Poly(Arylene Ether Ketone)s and Poly(Diphenylene Phtalide)
Abstract
:1. Introduction
2. Materials and Methods
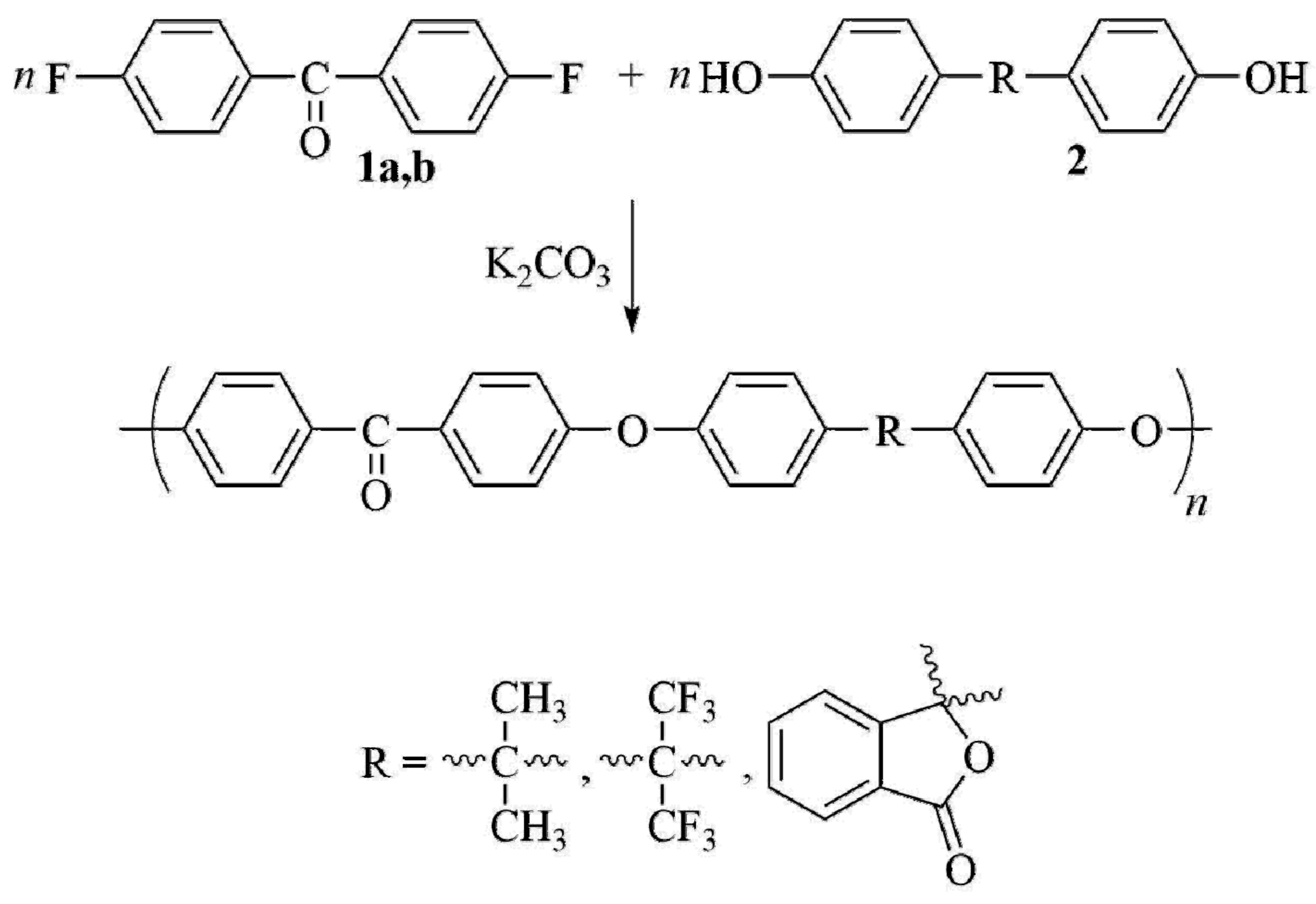
2.1. Polymer Synthesis
2.2. Polymer NMR Characterization
2.3. Investigation Methods
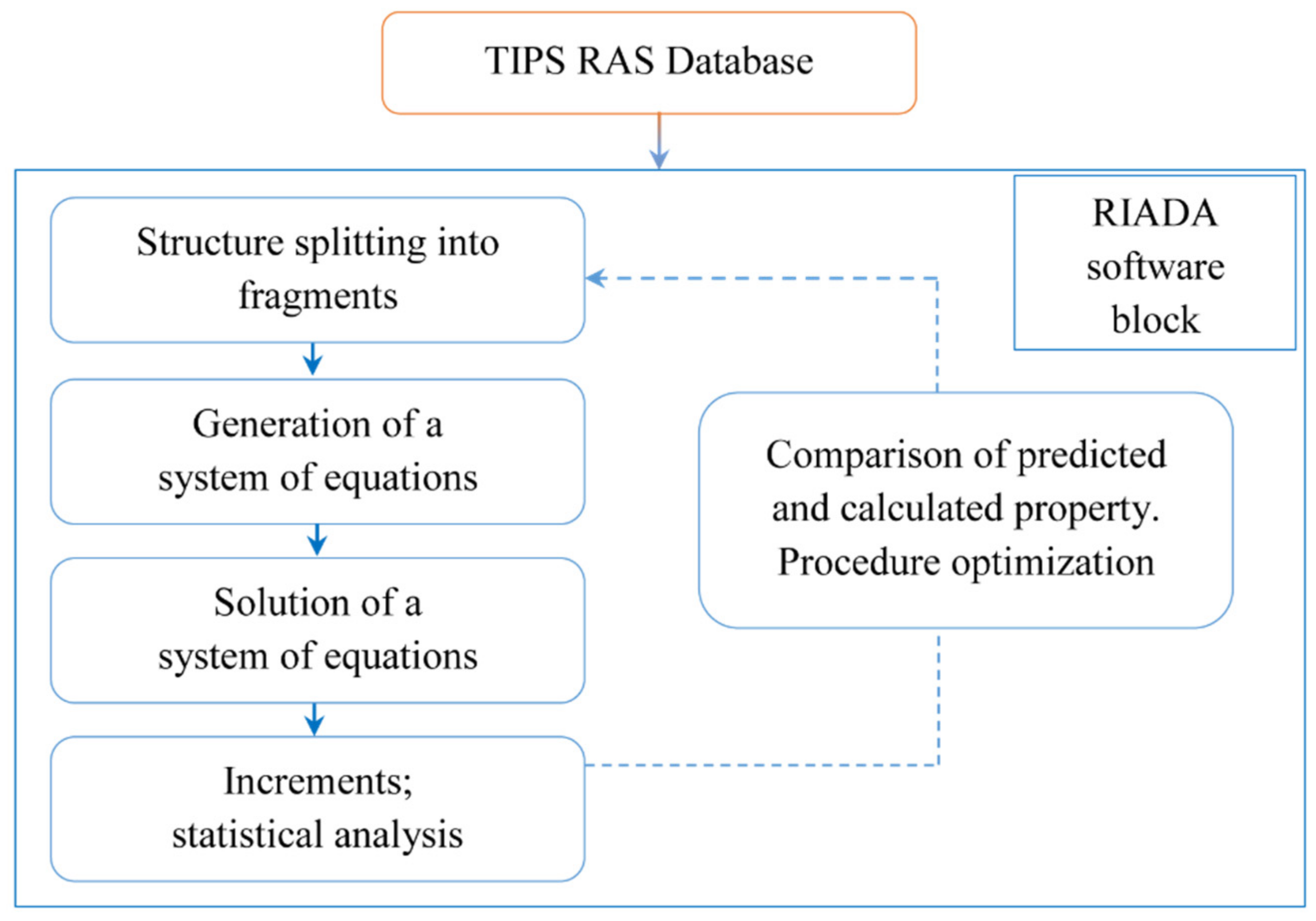
2.4. Prediction Methods
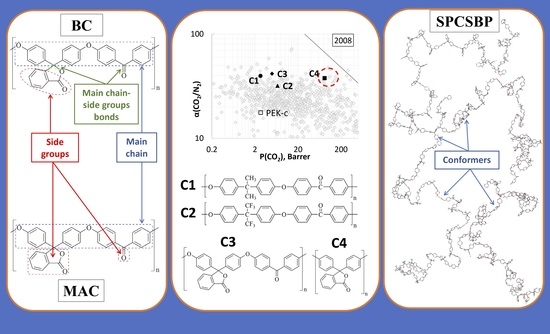
2.4.1. The Method of Modified Atomic Contributions (MAC) and the Method of Bond Contributions (BC)
2.4.2. Short Polymer Chain Surface-Based Prediction
3. Results and Discussion
3.1. Thermal Properties and Free Volume
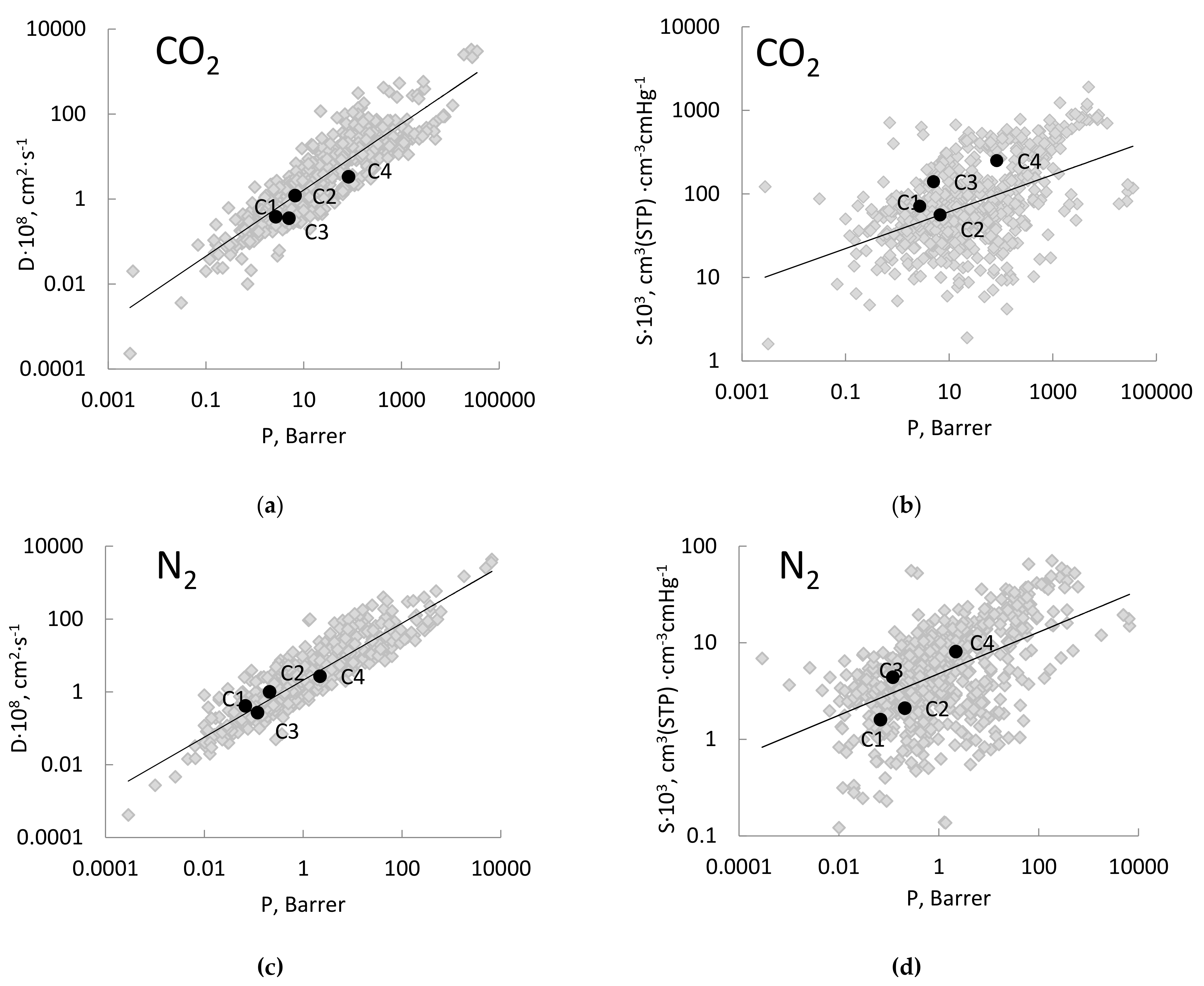
3.2. Experimental Gas Transport Properties
3.3. Predicted Gas Transport Parameters
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yampolskii, Y.; Pinnau, I.; Freeman, B. Materials Science of Membranes for Gas and Vapor Separation; John Wiley Sons, Ltd.: Chichester, UK, 2006. [Google Scholar] [CrossRef]
- Hägg, M.-B.; He, X. Chapter 15. Carbon Molecular Sieve Membranes for Gas Separation. In Membrane Engineering for the Treatment of Gases: Gas-Separation Problems Combined with Membrane Reactors; Royal Society of Chemistry: London, UK, 2011; pp. 162–191. [Google Scholar] [CrossRef]
- Ma, Y.H.; Akis, B.C.; Ayturk, M.E.; Guazzone, F.; Engwall, E.E.; Mardilovich, I.P. Characterization of Intermetallic Diffusion Barrier and Alloy Formation for Pd/Cu and Pd/Ag Porous Stainless Steel Composite Membranes. Ind. Eng. Chem. Res. 2004, 43, 2936–2945. [Google Scholar] [CrossRef]
- Yampolskii, Y.P.; Starannikova, L.E.; Belov, N.A. Hybrid Gas Separation Polymeric Membranes Containing Nanoparticles. Pet. Chem. 2014, 54, 637–651. [Google Scholar] [CrossRef]
- Baker, R.W.; Low, B.T. Gas Separation Membrane Materials: A Perspective. Macromolecules 2014, 47, 6999–7013. [Google Scholar] [CrossRef]
- Matteucci, S.; Yampolskii, Y.; Freeman, B.D.; Pinnau, I. Transport of Gases and Vapors in Glassy and Rubbery Polymers. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley Sons, Ltd.: Chichester, UK, 2006; pp. 1–47. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of Separation Factor versus Permeability for Polymeric Membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Robeson, L.M. The Upper Bound Revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Yampolskii, Y. Polymeric Gas Separation Membranes. Macromolecules 2012, 45, 3298–3311. [Google Scholar] [CrossRef]
- Askadskij, A.A. Computational Materials Science of Polymers; Cambridge International Science Publ.: Cambridge, UK, 2003. [Google Scholar]
- Masuda, T.; Nagai, K. Synthesis and Permeation Properties of Substituted Polyacetylenes for Gas Separation and Pervaporation. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley Sons, Ltd.: Chichester, UK, 2006; pp. 231–250. [Google Scholar] [CrossRef]
- Sanders, D.F.; Smith, Z.P.; Guo, R.; Robeson, L.M.; McGrath, J.E.; Paul, D.R.; Freeman, B.D. Energy-Efficient Polymeric Gas Separation Membranes for a Sustainable Future: A Review. Polymer 2013, 54, 4729–4761. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.H.; Seong, J.G.; Hu, X.; Lee, Y.M. Recent Progress in Microporous Polymers from Thermally Rearranged Polymers and Polymers of Intrinsic Microporosity for Membrane Gas Separation: Pushing Performance Limits and Revisiting Trade-off Lines. J. Polym. Sci. 2020, 58, 2450–2466. [Google Scholar] [CrossRef]
- Wang, S.; Li, X.; Wu, H.; Tian, Z.; Xin, Q.; He, G.; Peng, D.; Chen, S.; Yin, Y.; Jiang, Z.; et al. Advances in High Permeability Polymer-Based Membrane Materials for CO2 Separations. Energy Environ. Sci. 2016, 9, 1863–1890. [Google Scholar] [CrossRef]
- TIPS RAS Database “Gas Separation Parameters of Glassy Polymers”; Informregister of the Russian Federation, 1998; No. 3585.
- Membrane Society of Australasia. Database “Polymer Gas Separation Membranes”. Available online: https://www.membrane-australasia.org/polymer-gas-separation-membranes/ (accessed on 30 July 2021).
- Robeson, L. Polymer membranes for gas separation. Curr. Opin. Solid State Mater. Sci. 1999, 4, 549–552. [Google Scholar] [CrossRef]
- Freeman, B.D. Basis of Permeability/Selectivity Tradeoff Relations in Polymeric Gas Separation Membranes. Macromolecules 1999, 32, 375–380. [Google Scholar] [CrossRef]
- Alentiev, A.Y.; Yampolskii, Y.P. Free Volume Model and Tradeoff Relations of Gas Permeability and Selectivity in Glassy Polymers. J. Membr. Sci. 2000, 165, 201–216. [Google Scholar] [CrossRef]
- Alent’ev, A.Y.; Yampolskii, Y.P.; Vidyakin, M.N.; Lazareva, Y.N. Selection of Membrane Materials for Separation of H2-Containing Mixtures: Database Analysis. Polym. Sci. Ser. A 2006, 48, 1120–1127. [Google Scholar] [CrossRef]
- Robeson, L.M.; Freeman, B.D.; Paul, D.R.; Rowe, B.W. An Empirical Correlation of Gas Permeability and Permselectivity in Polymers and Its Theoretical Basis. J. Membr. Sci. 2009, 341, 178–185. [Google Scholar] [CrossRef]
- Malykh, O.V.; Golub, A.Y.; Teplyakov, V.V. Polymeric Membrane Materials: New Aspects of Empirical Approaches to Prediction of Gas Permeability Parameters in Relation to Permanent Gases, Linear Lower Hydrocarbons and Some Toxic Gases. Adv. Colloid Interface Sci. 2011, 164, 89–99. [Google Scholar] [CrossRef]
- Ryzhikh, V.E.; Alent’ev, A.Y.; Yampol’skii, Y.P. Relation of Gas-Transport Parameters of Amorphous Glassy Polymers to Their Free Volume: Positron Annihilation Study. Polym. Sci. Ser. A 2013, 55, 244–252. [Google Scholar] [CrossRef]
- Alentiev, A.; Yampolskii, Y. Correlation of Gas Permeability and Diffusivity with Selectivity: Orientations of the Clouds of the Data Points and the Effects of Temperature. Ind. Eng. Chem. Res. 2013, 52, 8864–8874. [Google Scholar] [CrossRef]
- Robeson, L.M.; Smith, Z.P.; Freeman, B.D.; Paul, D.R. Contributions of Diffusion and Solubility Selectivity to the Upper Bound Analysis for Glassy Gas Separation Membranes. J. Membr. Sci. 2014, 453, 71–83. [Google Scholar] [CrossRef]
- Swaidan, R.; Ghanem, B.; Pinnau, I. Fine-Tuned Intrinsically Ultramicroporous Polymers Redefine the Permeability/Selectivity Upper Bounds of Membrane-Based Air and Hydrogen Separations. ACS Macro Lett. 2015, 4, 947–951. [Google Scholar] [CrossRef] [Green Version]
- Comesaña-Gándara, B.; Chen, J.; Bezzu, C.G.; Carta, M.; Rose, I.; Ferrari, M.-C.; Esposito, E.; Fuoco, A.; Jansen, J.C.; McKeown, N.B. Redefining the Robeson Upper Bounds for CO2/CH4 and CO2/N2 Separations Using a Series of Ultrapermeable Benzotriptycene-Based Polymers of Intrinsic Microporosity. Energy Environ. Sci. 2019, 12, 2733–2740. [Google Scholar] [CrossRef] [Green Version]
- Alent’ev, A.Y.; Ryzhikh, V.E.; Belov, N.A. Highly Permeable Polyheteroarylenes for Membrane Gas Separation: Recent Trends in Chemical Structure Design. Polym. Sci. Ser. C 2020, 62, 238–258. [Google Scholar] [CrossRef]
- Alentiev, A.; Yampolskii, Y. Prediction of Gas Permeation Parameters of Polymers. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley Sons, Ltd.: Chichester, UK, 2006. [Google Scholar] [CrossRef]
- Robeson, L.A.; Smith, C.D.; Langsam, M. Group Contribution Approach to Predict Permeability and Permselectivity of Aromatic Polymers. J. Membr. Sci. 1997, 132, 33–54. [Google Scholar] [CrossRef]
- Park, J.Y.; Paul, D.R. Correlation and Prediction of Gas Permeability in Glassy Polymer Membrane Materials via a Modified Free Volume Based Group Contribution Method. J. Membr. Sci. 1997, 125, 23–39. [Google Scholar] [CrossRef]
- Yampolskii, Y.; Shishatskii, S.; Alentiev, A.; Loza, K. Group Contribution Method for Transport Property Predictions of Glassy Polymers: Focus on Polyimides and Polynorbornenes. J. Membr. Sci. 1998, 149, 203–220. [Google Scholar] [CrossRef]
- Laciak, D.V.; Robeson, L.M.; Smith, C.D. Group Contribution Modeling of Gas Transport in Polymeric Membranes. In Polymer Membranes for Gas and Vapor Separation: Chemistry and Materials Science; ACS Symposium Series; Freeman, B.D., Pinnau, I., Eds.; American Chemical Society: Washington, DC, USA, 1999; Volume 733. [Google Scholar] [CrossRef] [Green Version]
- Alentiev, A.Y.; Loza, K.A.; Yampolskii, Y.P. Development of the Methods for Prediction of Gas Permeation Parameters of Glassy Polymers: Polyimides as Alternating Co-Polymers. J. Membr. Sci. 2000, 167, 91–106. [Google Scholar] [CrossRef]
- Kubica, P.; Wolinska-Grabczyk, A. Correlation between Cohesive Energy Density, Fractional Free Volume, and Gas Transport Properties of Poly(ethylene-co-vinyl acetate) Materials. Int. J. Polym. Sci. 2015, 2015, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Alentiev, A.; Yampolskii, Y.; Ryzhikh, V.; Tsarev, D. The Database “Gas Separation Properties of Glassy Polymers” (Topchiev Institute): Capabilities and Prospects. Petrol. Chem. 2013, 53, 554–558. [Google Scholar] [CrossRef]
- Velioğlu, S.; Tantekin-Ersolmaz, S.B.; Chew, J.W. Towards the Generalization of Membrane Structure-Property Relationship of Polyimides and Copolyimides: A Group Contribution Study. J. Membr. Sci. 2017, 543, 233–254. [Google Scholar] [CrossRef]
- Ryzhikh, V.; Tsarev, D.; Alentiev, A.; Yampolskii, Y. A Novel Method for Predictions of the Gas Permeation Parameters of Polymers on the Basis of Their Chemical Structure. J. Membr. Sci. 2015, 487, 189–198. [Google Scholar] [CrossRef]
- Velioğlu, S.; Tantekin-Ersolmaz, S.B. Prediction of Gas Permeability Coefficients of Copolyimides by Group Contribution Methods. J. Membr. Sci. 2015, 480, 47–63. [Google Scholar] [CrossRef]
- Surgi, M.R.; Polak, A.J.; Sundahl, R.C. Description of Oxygen Permeability in Various High Polymers Using a Graph Theoretical Approach. J. Polym. Sci. A Polym. Chem. 1989, 27, 2761–2776. [Google Scholar] [CrossRef]
- Bicerano, J. Prediction of Polymer Properties, 3rd ed.; Plastics Engineering, Marcel Dekker: New York, NY, USA, 2002. [Google Scholar]
- Zhong, C.; Yang, C. Approach for the Calculation of High-Order Connectivity Indices of Polymers and Its Application. J. Polym. Sci. B Polym. Phys. 2002, 40, 401–407. [Google Scholar] [CrossRef]
- Goubko, M.; Miloserdov, O.; Yampolskii, Y.; Alentiev, A.; Ryzhikh, V. A Novel Model to Predict Infinite Dilution Solubility Coefficients in Glassy Polymers. J. Polym. Sci. B Polym. Phys. 2017, 55, 228–244. [Google Scholar] [CrossRef]
- Goubko, M.V.; Miloserdov, O.A.; Yampolskii, Y.P.; Ryzhikh, V.Y. Prediction of Solubility Parameters of Light Gases in Glassy Polymers on the Basis of Simulation of a Short Segment of a Polymer Chain. Polym. Sci. Ser. A 2019, 61, 718–732. [Google Scholar] [CrossRef]
- Wessling, M. Relaxation Phenomena in Dense Gas Separation Membranes. Ph.D. Thesis, University of Twente, Twente, The Netherlands, 1993. [Google Scholar]
- Barnett, J.W.; Bilchak, C.R.; Wang, Y.; Benicewicz, B.C.; Murdock, L.A.; Bereau, T.; Kumar, S.K. Designing Exceptional Gas-Separation Polymer Membranes Using Machine Learning. Sci. Adv. 2020, 6, eaaz4301. [Google Scholar] [CrossRef] [PubMed]
- Alentiev, A.; Economou, I.G.; Finkelshtein, E.; Petrou, J.; Raptis, V.E.; Sanopoulou, M.; Soloviev, S.; Ushakov, N.; Yampolskii, Y. Transport Properties of Silmethylene Homo-Polymers and Random Copolymers: Experimental Measurements and Molecular Simulation. Polymer 2004, 45, 6933–6944. [Google Scholar] [CrossRef]
- Heuchel, M.; Hofmann, D.; Pullumbi, P. Molecular Modeling of Small-Molecule Permeation in Polyimides and Its Correlation to Free-Volume Distributions. Macromolecules 2004, 37, 201–214. [Google Scholar] [CrossRef]
- Hofmann, D.; Heuchel, M.; Yampolskii, Y.; Khotimskii, V.; Shantarovich, V. Free Volume Distributions in Ultrahigh and Lower Free Volume Polymers: Comparison between Molecular Modeling and Positron Lifetime Studies. Macromolecules 2002, 35, 2129–2140. [Google Scholar] [CrossRef]
- Theodorou, D.N. Principles of Molecular Simulation of Gas Transport in Polymers. In Materials Science of Membranes for Gas and Vapor Separation; Yampolskii, Y., Pinnau, I., Freeman, B., Eds.; John Wiley Sons, Ltd.: Chichester, UK, 2006; pp. 49–94. [Google Scholar] [CrossRef]
- Neyertz, S.; Douanne, A.; Brown, D. Effect of Interfacial Structure on Permeation Properties of Glassy Polymers. Macromolecules 2005, 38, 10286–10298. [Google Scholar] [CrossRef]
- Neyertz, S. Gas Transport in Dense Polymeric Membranes, Molecular Dynamics Simulations. In Encyclopedia of Membrane Science and Technology; John Wiley Sons, Inc.: Hoboken, NJ, USA, 2013; p. emst101. [Google Scholar] [CrossRef]
- Tocci, E.; De Lorenzo, L.; Bernardo, P.; Clarizia, G.; Bazzarelli, F.; Mckeown, N.B.; Carta, M.; Malpass-Evans, R.; Friess, K.; Pilnáček, K.; et al. Molecular Modeling and Gas Permeation Properties of a Polymer of Intrinsic Microporosity Composed of Ethanoanthracene and Tröger’s Base Units. Macromolecules 2014, 47, 7900–7916. [Google Scholar] [CrossRef]
- Bisoi, S.; Mandal, A.K.; Padmanabhan, V.; Banerjee, S. Aromatic Polyamides Containing Trityl Substituted Triphenylamine: Gas Transport Properties and Molecular Dynamics Simulations. J. Membr. Sci. 2017, 522, 77–90. [Google Scholar] [CrossRef]
- Gartner, T.E.; Jayaraman, A. Modeling and Simulations of Polymers: A Roadmap. Macromolecules 2019, 52, 755–786. [Google Scholar] [CrossRef] [Green Version]
- Gooneie, A.; Schuschnigg, S.; Holzer, C. A Review of Multiscale Computational Methods in Polymeric Materials. Polymers 2017, 9, 16. [Google Scholar] [CrossRef]
- Salazkin, S.N.; Shaposhnikova, V.V. Poly(Arylene Ether Ketones): Thermostable, Heat Resistant, and Chemostable Thermoplastics and Prospects for Designing Various Materials on Their Basis. Polym. Sci. Ser. C 2020, 62, 111–123. [Google Scholar] [CrossRef]
- Shaposhnikova, V.V.; Salazkin, S.N. Synthesis and Properties of Poly(Arylene Ether Ketones). Russ. Chem. Bull. 2014, 63, 2213–2223. [Google Scholar] [CrossRef]
- Shaposhnikova, V.V.; Salazkin, S.N.; Sergeev, V.A.; Blagodatskikh, I.V.; Dubrovina, L.V.; Sakunts, A.A.; Pavlova, S.-S.A. General Features of the Reaction of 4,4′-Difluorobenzophenone with Potassium Diphenoxide of 2,2-Bis (4-Hydroxyphenyl)Propane. Russ. Chem. Bull. 1996, 45, 2397–2401. [Google Scholar] [CrossRef]
- Zolotukhin, M.G.; Kovardakov, V.A.; Salazkin, S.N.; Rafikov, S.R. Some Features of the Synthesis of Polydiphenylene Phthalide by Condensation of P-(3-Chloro-3-Phthalidyl) Diphenyl. Polym. Sci. USSR 1984, 26, 1355–1361. [Google Scholar] [CrossRef]
- Shaposhnikova, V.V.; Salazkin, S.N.; Donetskii, K.I.; Gorshkov, G.V.; Sharapov, D.S.; Mamedova, I.A.; Petrovskii, P.V.; Askadskii, A.A.; Bychko, K.A.; Kazantseva, V.V.; et al. Synthesis and Properties of Cardo Copoly(Arylene Ether Ketones). Polym. Sci. Ser. A 2002, 44, 563–569. [Google Scholar] [CrossRef]
- Fatykhov, A.A.; Sedova, E.A.; Egorov, A.Е.; Salazkin, S.N.; Kraikin, V.A. NMR Study of Phthalide-Type Poly(Phenylene)s. Symmetry and Additivity: NMR Study of Phthalide-Type Poly(Phenylene)s. Symmetry and Additivity. Magn. Reson. Chem. 2017, 55, 958–966. [Google Scholar] [CrossRef]
- Bondi, A.A. Physical Properties of Molecular Crystals, Liquids, and Glasses; Wiley Series on the Science and Technology of Materials; Wiley: New York, NY, USA, 1968. [Google Scholar]
- Yampolskii, Y.; Shishatskii, S.; Alentiev, A.; Loza, K. Correlations with and Prediction of Activation Energies of Gas Permeation and Diffusion in Glassy Polymers. J. Membr. Sci. 1998, 148, 59–69. [Google Scholar] [CrossRef]
- Miloserdov, O. Classifying Amorphous Polymers for Membrane Technology Basing on Accessible Surface Area of Their Conformations. Adv. Syst. Sci. Appl. 2020, 3, 91–104. [Google Scholar] [CrossRef]
- Lee, B.; Richards, F.M. The Interpretation of Protein Structures: Estimation of Static Accessibility. J. Mol. Biol. 1971, 55, 379–400. [Google Scholar] [CrossRef]
- Salazkin, S.N.; Rafikov, S.R.; Zolotukhin, M.G.; Tolstikov, G.A. New Way of Synthesis of Aromatic Polymers. Dokl. Akad. Nauk 1982, 262, 355–359. [Google Scholar] [CrossRef]
- Hirayama, Y.; Yoshinaga, T.; Kusuki, Y.; Ninomiya, K.; Sakakibara, T.; Tamari, T. Relation of Gas Permeability with Structure of Aromatic Polyimides I. J. Membr. Sci. 1996, 111, 169–182. [Google Scholar] [CrossRef]
- Zheng, Y.; Yang, X.; Yuan, M.; Luo, J. Synthesis and gas transport properties of novel poly(ether ether ketone)s containing fluorene group. High Perform. Polym. 2019, 31, 1173–1182. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, T.; Xu, J. Gas Transport Properties of Novel Cardo Poly(Aryl Ether Ketone)s with Pendant Alkyl Groups. Macromolecules 2000, 33, 5672–5679. [Google Scholar] [CrossRef]
- Bondar, V.I.; Freeman, B.D.; Pinnau, I. Gas Sorption and Characterization of Poly(Ether-b-Amide) Segmented Block Copolymers. J. Polym. Sci. B: Polym. Phys. 1999, 37, 2463–2475. [Google Scholar] [CrossRef]
- Ryzhikh, V. Development of Transport Parameters of Polymer Materials Prediction Using Database. Ph.D. Thesis, Topchiev Institute of Petrochemical Synthesis of Russian Academy of Sciences, Moscow, Russia, 2014. [Google Scholar]
- Chatterjee, R.; Kumar, A.G.; Nikiforov, R.; Ryzhikh, V.; Belov, N.; Padmanabhan, V.; Yampolskii, Y.; Banerjee, S. Novel Semi-Fluorinated Poly(Ether Imide)s with Benzyl Ether Side Groups: Synthesis, Physicochemical Characterization, Gas Transport Properties and Simulation. Eur. Polym. J. 2020, 135, 109879. [Google Scholar] [CrossRef]
- Belov, N.; Chatterjee, R.; Nikiforov, R.; Ryzhikh, V.; Bisoi, S.; Kumar, A.G.; Banerjee, S.; Yampolskii, Y. New Poly(Ether Imide)s with Pendant Di-Tert-Butyl Groups: Synthesis, Characterization and Gas Transport Properties. Sep. Purif. Technol. 2019, 217, 183–194. [Google Scholar] [CrossRef]
- Eastmond Geoffrey, C.; Daly John, H.; McKinnon Alexander, S.; Pethrick Richard, A. Poly(Ether Imide)s: Correlation of Positron Annihilation Lifetime Studies with Polymer Structure and Gas Permeability. Polymer 1999, 40, 3605–3610. [Google Scholar] [CrossRef]
- Al-Masri, M.; Fritsch, D.; Kricheldorf, H.R. New Polyimides for Gas Separation. 2. Polyimides Derived from Substituted Catechol Bis(Etherphthalic Anhydride)s. Macromolecules 2000, 33, 7127–7135. [Google Scholar] [CrossRef]
- Finkelshtein, E.S.; Makovetskii, K.L.; Gringolts, M.L.; Rogan, Y.V.; Golenko, T.G.; Starannikova, L.E.; Yampolskii, Y.P.; Shantarovich, V.P.; Suzuki, T. Addition-Type Polynorbornenes with Si(CH3)3 Side Groups: Synthesis, Gas Permeability, and Free Volume. Macromolecules 2006, 39, 7022–7029. [Google Scholar] [CrossRef]
- Dorkenoo, K.D.; Pfromm, P.H.; Rezac, M.E. Gas Transport Properties of a Series of High Tg Polynorbornenes with Aliphatic Pendant Groups. J. Polym. Sci. B Polym. Phys. 1998, 36, 797–803. [Google Scholar] [CrossRef]
- Shida, Y.; Sakaguchi, T.; Shiotsuki, M.; Sanda, F.; Freeman, B.D.; Masuda, T. Synthesis and Properties of Membranes of Poly(Diphenylacetylenes) Having Fluorines and Hydroxyl Groups. Macromolecules 2006, 39, 569–574. [Google Scholar] [CrossRef]
- Hu, Y.; Sakaguchi, T.; Shiotsuki, M.; Sanda, F.; Masuda, T. Synthesis and Characterization of Poly(Diphenylacetylenes) Containing Both Hydroxy and Halogen/Alkyl Groups as Gas Separation Membranes. J. Membr. Sci. 2006, 285, 412–419. [Google Scholar] [CrossRef]
- Puleo, A.C.; Muruganandam, N.; Paul, D.R. Gas Sorption and Transport in Substituted Polystyrenes. J. Polym. Sci. B Polym. Phys. 1989, 27, 2385–2406. [Google Scholar] [CrossRef]
- Salame, M. Transport Properties of Nitrile Polymers: Properties of Nitrile Polymers. J. Polym. Sci. C Polym. Symp. 1973, 41, 1–15. [Google Scholar] [CrossRef]
- Yampolskii, Y.; Wiley, D.; Maher, C. Novel Correlation for Solubility of Gases in Polymers: Effect of Molecular Surface Area of Gases. J. Appl. Polym. Sci. 2000, 76, 552–560. [Google Scholar] [CrossRef]
- Mazo, M.; Balabaev, N.; Alentiev, A.; Yampolskii, Y. Molecular Dynamics Simulation of Nanostructure of High Free Volume Polymers with SiMe3 Side Groups. Macromolecules 2018, 51, 1398–1408. [Google Scholar] [CrossRef]
- Mazo, M.; Balabaev, N.; Alentiev, A.; Strelnikov, I.; Yampolskii, Y. Structure and Properties of High and Low Free Volume Polymers Studied by Molecular Dynamics Simulation. Computation 2019, 7, 27. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Yu, Y.; Gao, G. Non-equilibrium Molecular Dynamics Simulation on Pure Gas Permeability Through Carbon Membranes. Chin. J. Chem. Eng. 2006, 14, 164–170. [Google Scholar] [CrossRef]
- Wang, S.-M.; Yu, Y.-X.; Gao, G.-H. Grand canonical Monte Carlo and non-equilibrium molecular dynamics simulation study on the selective adsorption and fluxes of oxygen/nitrogen gas mixtures through carbon membranes. J. Membr. Sci. 2006, 271, 140–150. [Google Scholar] [CrossRef]


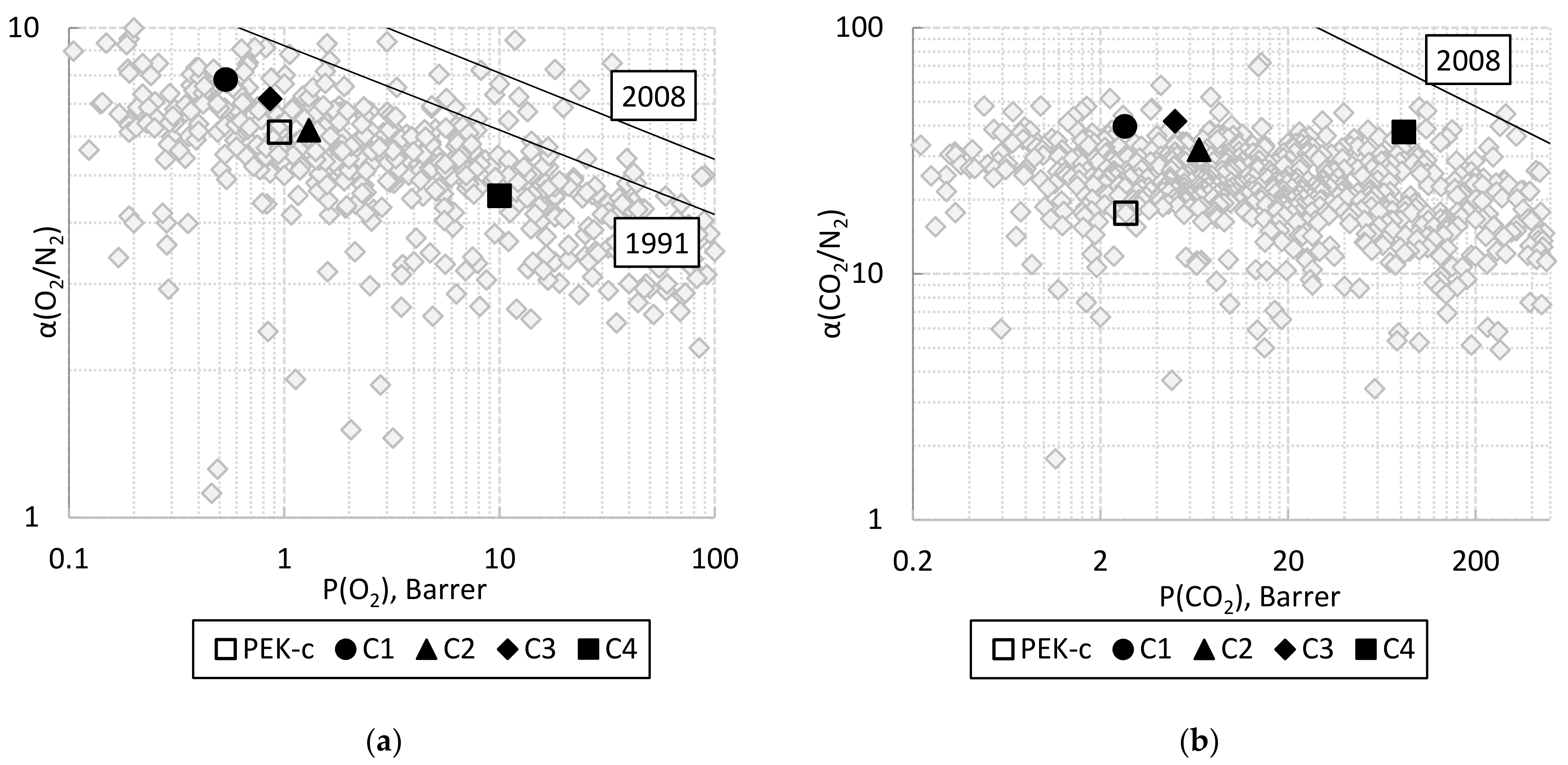
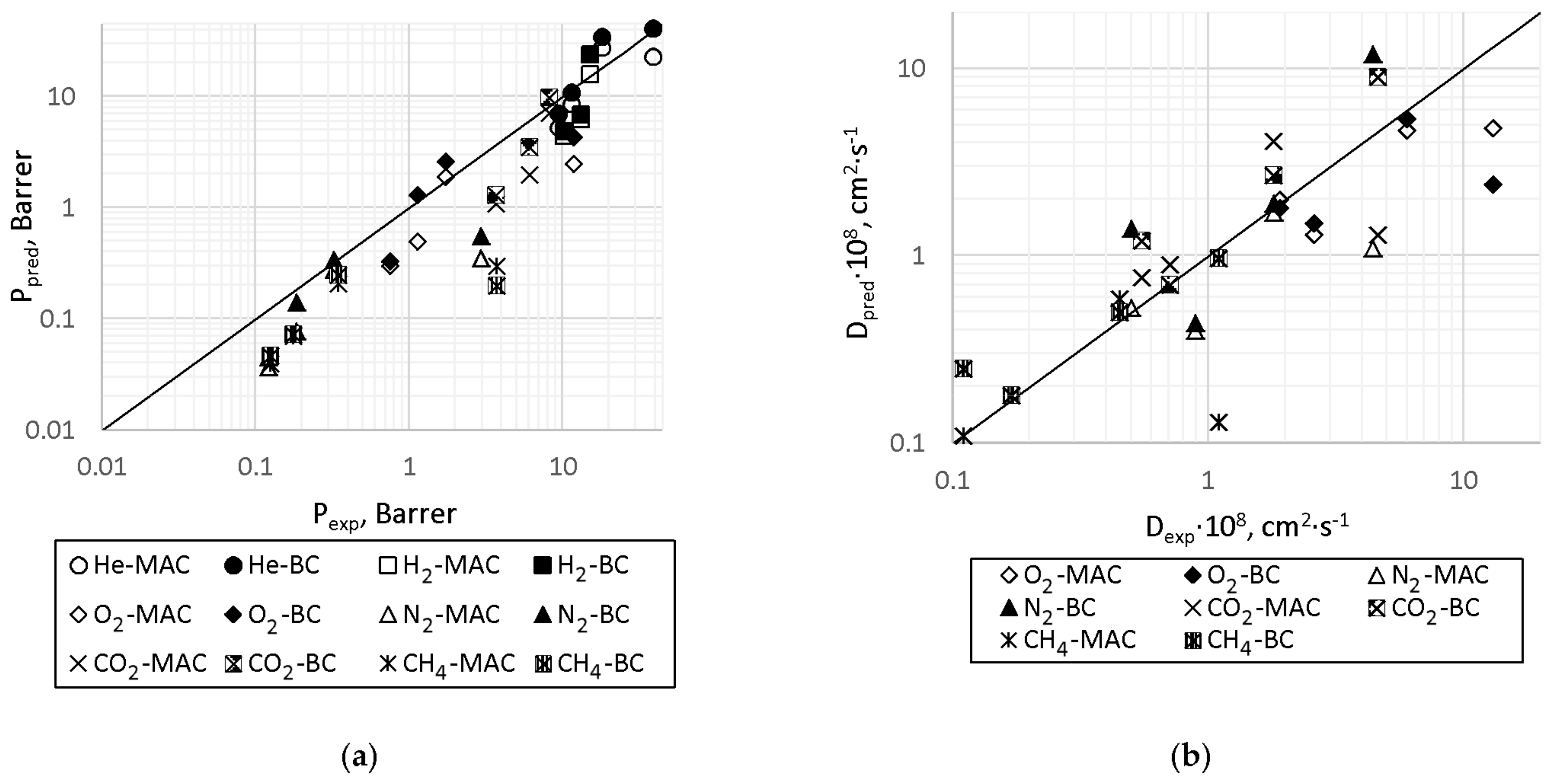
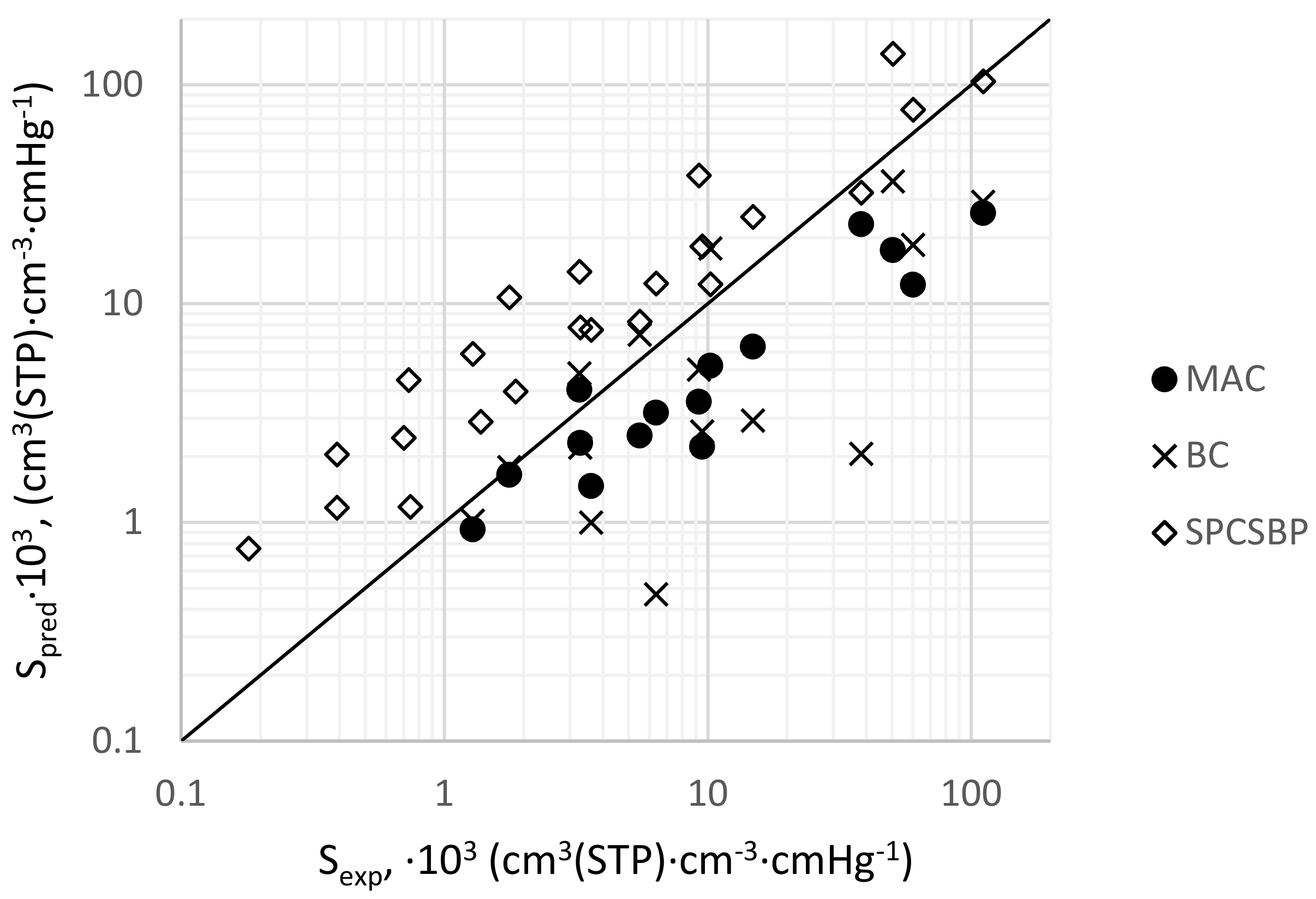
| Class | Number of Polymers |
|---|---|
| Polyimides | 394 |
| Polyacetylenes | 107 |
| Polyesters | 88 |
| Copolymers | 81 |
| Polyethers | 72 |
| Polynorbornenes (metathesis and additive) | 70 |
| Polysulfones | 52 |
| Polyamidoimides | 40 |
| Polyamides | 37 |
| Other nitrogen-containing polymers | 31 |
| Polystyrenes | 22 |
| Polycarbonates | 19 |
| Vinyl polymers | 15 |
| Polyacrylates | 15 |
| Other carbon-chain polymers | 10 |
| Other hetero-chain polymers | 8 |
| Polyphosphazenes | 4 |
| Polymer Designation | Structure | Tg, °C | ρ, g/cm3 | FFV, % |
|---|---|---|---|---|
| C1 |  | 155 | 1.195 | 10.4 |
| C2 |  | 163 | 1.377 | 11.9 |
| C3 |  | 229 218 [69] 249 [70] | 1.259 1.249 [69] - | 11.6 12.3 [69] - |
| C4 | 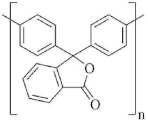 | 440 | 1.215 | 13.3 |
| Polymer | He | H2 | O2 | N2 | CO2 | CH4 |
|---|---|---|---|---|---|---|
| C1 | 6.8 | 7.0 | 0.53 | 0.068 | 2.7 | 0.065 |
| C2 | 14 | 11 | 1.3 | 0.21 | 6.7 | 0.22 |
| C3 | 8.9 | 9.7 | 0.86 | 0.12 | 5.0 | 0.11 |
| C4 | 32 | 52 | 10 | 2.2 | 83 | 2.8 |
| Polymer | He | H2 | O2 | N2 | CO2 | CH4 |
|---|---|---|---|---|---|---|
| C1 | 290 | 76 | 1.5 | 0.41 | 0.38 | 0.067 |
| C2 | 290 | 120 | 3.8 | 1.0 | 1.2 | 0.23 |
| C3 | 230 | 74 | 1.2 | 0.27 | 0.35 | 0.056 |
| C4 | 360 | 230 | 8.9 | 2.7 | 3.3 | 0.68 |
| Polymer | He | H2 | O2 | N2 | CO2 | CH4 |
|---|---|---|---|---|---|---|
| C1 | 0.23 | 0.92 | 3.6 | 1.6 | 71 | 9.7 |
| C2 | 0.48 | 0.94 | 3.4 | 2.1 | 56 | 9.6 |
| C3 | 0.39 | 1.3 | 7.2 | 4.4 | 140 | 20 |
| C4 | 0.89 | 2.3 | 11 | 8.1 | 250 | 41 |
| Polymer | α | ||||||
|---|---|---|---|---|---|---|---|
| O2/N2 | CO2/N2 | CO2/CH4 | He/N2 | H2/CH4 | He/CH4 | H2/N2 | |
| C1 | 7.9 | 40 | 42 | 100 | 110 | 100 | 100 |
| C2 | 6.2 | 32 | 30 | 67 | 50 | 63 | 52 |
| C3 | 7.2 | 42 | 45 | 74 | 88 | 81 | 81 |
| C4 | 4.5 | 38 | 30 | 15 | 19 | 11 | 24 |
| Polymer | Type of Data | He | H2 | O2 | N2 | CO2 | CH4 | MAPE1, % | MPE2, % |
|---|---|---|---|---|---|---|---|---|---|
| C1 | Experimental | 9.33 | 10.1 | 0.753 | 0.120 | 3.67 | 0.124 | - | - |
| MAC | 5.3 | 4.5 | 0.30 | 0.037 | 1.1 | 0.040 | 61 | 61 | |
| BC | 7.1 | 4.9 | 0.33 | 0.045 | 1.3 | 0.047 | 53 | 53 | |
| C2 | Experimental | 17.9 | 15.0 | 1.72 | 0.320 | 8.16 | 0.345 | - | - |
| MAC | 28 | 16 | 1.9 | 0.28 | 7.2 | 0.21 | 23 | −1.7 | |
| BC | 35 | 24 | 2.6 | 0.34 | 9.8 | 0.25 | 43 | −34 | |
| C3 | Experimental | 11.4 | 13.1 | 1.13 | 0.183 | 6.08 | 0.175 | - | - |
| MAC | 8.7 | 6.3 | 0.50 | 0.078 | 2.0 | 0.070 | 53 | 53 | |
| BC | 11 | 6.9 | 1.3 | 0.14 | 3.5 | 0.073 | 32 | 27 | |
| C4 | Experimental | 38.4 | 64.5 | 11.8 | 2.93 | 89.2 | 3.71 | - | - |
| MAC | 23 | 22 | 2.5 | 0.35 | 8.6 | 0.30 | 76 | 76 | |
| BC | 41 | 46 | 4.3 | 0.56 | 10 | 0.20 | 61 | 58 |
| Polymer | Type of Data | O2 | N2 | CO2 | CH4 | MAPE, % | MPE, % |
|---|---|---|---|---|---|---|---|
| C1 | Experimental | 2.6 | 0.89 | 0.71 | 0.17 | - | - |
| MAC | 1.3 | 0.4 | 0.9 | 0.18 | 34 | 12 | |
| BC | 1.5 | 0.44 | 0.7 | 0.18 | 25 | 15 | |
| C2 | Experimental | 6.0 | 1.8 | 1.8 | 0.45 | - | - |
| MAC | 4.7 | 1.7 | 4.1 | 0.59 | 45 | −21 | |
| BC | 5.4 | 1.9 | 2.7 | 0.50 | 18 | −9 | |
| C3 | Experimental | 1.9 | 0.5 | 0.55 | 0.11 | - | - |
| MAC | 2 | 0.53 | 0.77 | 0.11 | 13 | −8 | |
| BC | 1.8 | 1.4 | 1.2 | 0.25 | 107 | −69 | |
| C4 | Experimental | 13 | 4.4 | 4.6 | 1.1 | - | - |
| MAC | 4.8 | 1.1 | 1.3 | 0.13 | 75 | 50 | |
| BC | 2.4 | 12 | 9.0 | 0.97 | 91 | −28 |
| Polymer | Type of Data | He | H2 | O2 | N2 | CO2 | CH4 | MAPE 1, % | MPE2, % |
|---|---|---|---|---|---|---|---|---|---|
| C1 | Experimental | 0.25 | 1.0 | 2.9 | 1.3 | 52 | 7.3 | - | |
| MAC | - | - | 2.3 | 0.93 | 12 | 2.2 | 50 | 33 | |
| BC | - | - | 2.2 | 1.0 | 19 | 2.6 | 44 | 30 | |
| SPCSBP | 0.76 | 2.4 | 7.8 | 5.9 | 77 | 18 | 175 | −175 | |
| C2 | Experimental | 0.49 | 1.0 | 2.9 | 1.8 | 44 | 7.7 | - | |
| MAC | - | - | 4.0 | 1.7 | 18 | 3.6 | 40 | 13 | |
| BC | - | - | 4.8 | 1.8 | 36 | 5.0 | 30 | −3 | |
| SPCSBP | 2.1 | 4.5 | 14 | 11 | 140 | 39 | 362 | −362 | |
| C3 | Experimental | 0.40 | 1.4 | 5.9 | 3.7 | 110 | 15 | - | |
| MAC | - | - | 2.5 | 1.5 | 26 | 6.4 | 63 | 42 | |
| BC | - | - | 7.2 | 1.0 | 29 | 2.9 | 63 | 34 | |
| SPCSBP | 1.2 | 2.9 | 8.3 | 7.6 | 100 | 25 | 86 | −84 | |
| C4 | Experimental | 0.89 | 2.3 | 9.1 | 6.6 | 190 | 33 | - | |
| MAC | - | - | 5.2 | 3.2 | 66 | 23 | 47 | 65 | |
| BC | - | - | 18 | 0.47 | 11 | 2.1 | 94 | 64 | |
| SPCSBP | 1.2 | 4.0 | 12 | 12 | 140 | 32 | 42 | −32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alentiev, A.; Chirkov, S.; Nikiforov, R.; Buzin, M.; Miloserdov, O.; Ryzhikh, V.; Belov, N.; Shaposhnikova, V.; Salazkin, S. Structure-Property Relationship on the Example of Gas Separation Characteristics of Poly(Arylene Ether Ketone)s and Poly(Diphenylene Phtalide). Membranes 2021, 11, 677. https://doi.org/10.3390/membranes11090677
Alentiev A, Chirkov S, Nikiforov R, Buzin M, Miloserdov O, Ryzhikh V, Belov N, Shaposhnikova V, Salazkin S. Structure-Property Relationship on the Example of Gas Separation Characteristics of Poly(Arylene Ether Ketone)s and Poly(Diphenylene Phtalide). Membranes. 2021; 11(9):677. https://doi.org/10.3390/membranes11090677
Chicago/Turabian StyleAlentiev, Alexandre, Sergey Chirkov, Roman Nikiforov, Mikhail Buzin, Oleg Miloserdov, Victoria Ryzhikh, Nikolay Belov, Vera Shaposhnikova, and Sergey Salazkin. 2021. "Structure-Property Relationship on the Example of Gas Separation Characteristics of Poly(Arylene Ether Ketone)s and Poly(Diphenylene Phtalide)" Membranes 11, no. 9: 677. https://doi.org/10.3390/membranes11090677
APA StyleAlentiev, A., Chirkov, S., Nikiforov, R., Buzin, M., Miloserdov, O., Ryzhikh, V., Belov, N., Shaposhnikova, V., & Salazkin, S. (2021). Structure-Property Relationship on the Example of Gas Separation Characteristics of Poly(Arylene Ether Ketone)s and Poly(Diphenylene Phtalide). Membranes, 11(9), 677. https://doi.org/10.3390/membranes11090677