In Silico Study of the Electrically Conductive and Electrochemical Properties of Hybrid Films Formed by Bilayer Graphene and Single-Wall Nanotubes under Axial Stretching
Abstract
:1. Introduction
2. Methods and Approaches
2.1. Calculation Details
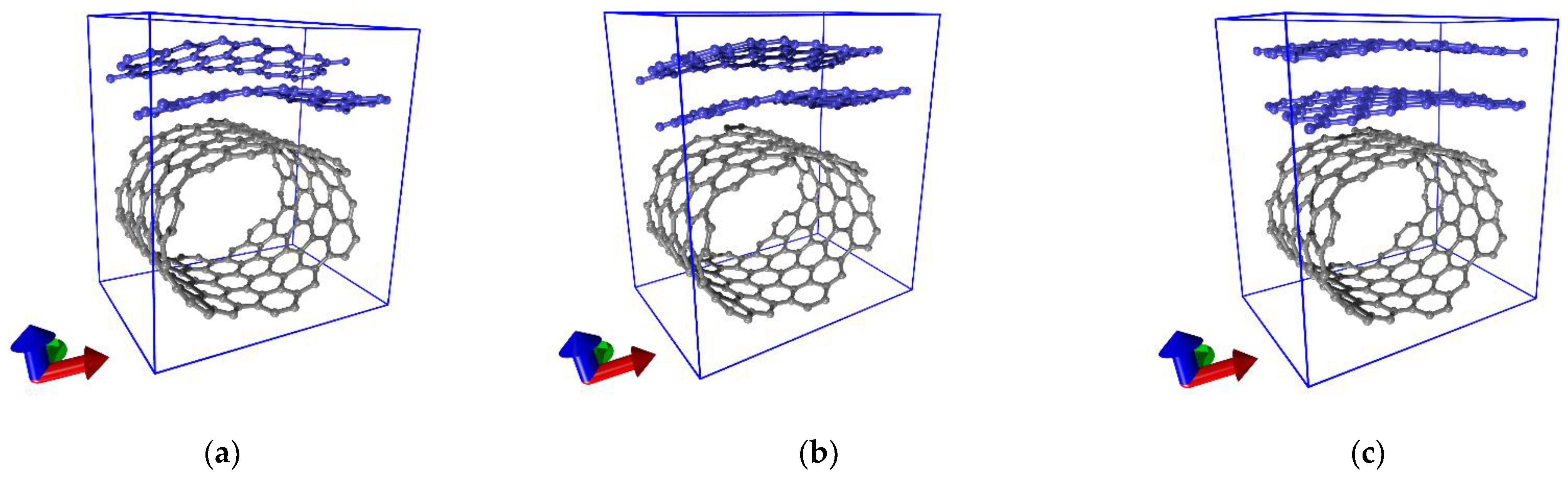
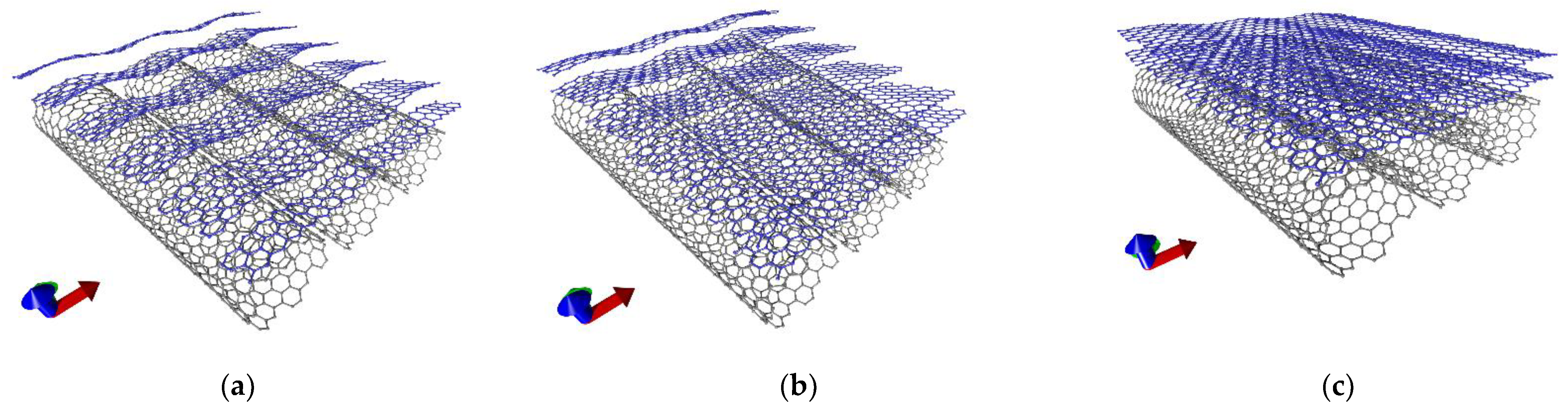
2.2. Topological Models of Hybrid Graphene/SWCNT Films
3. Results and Discussion
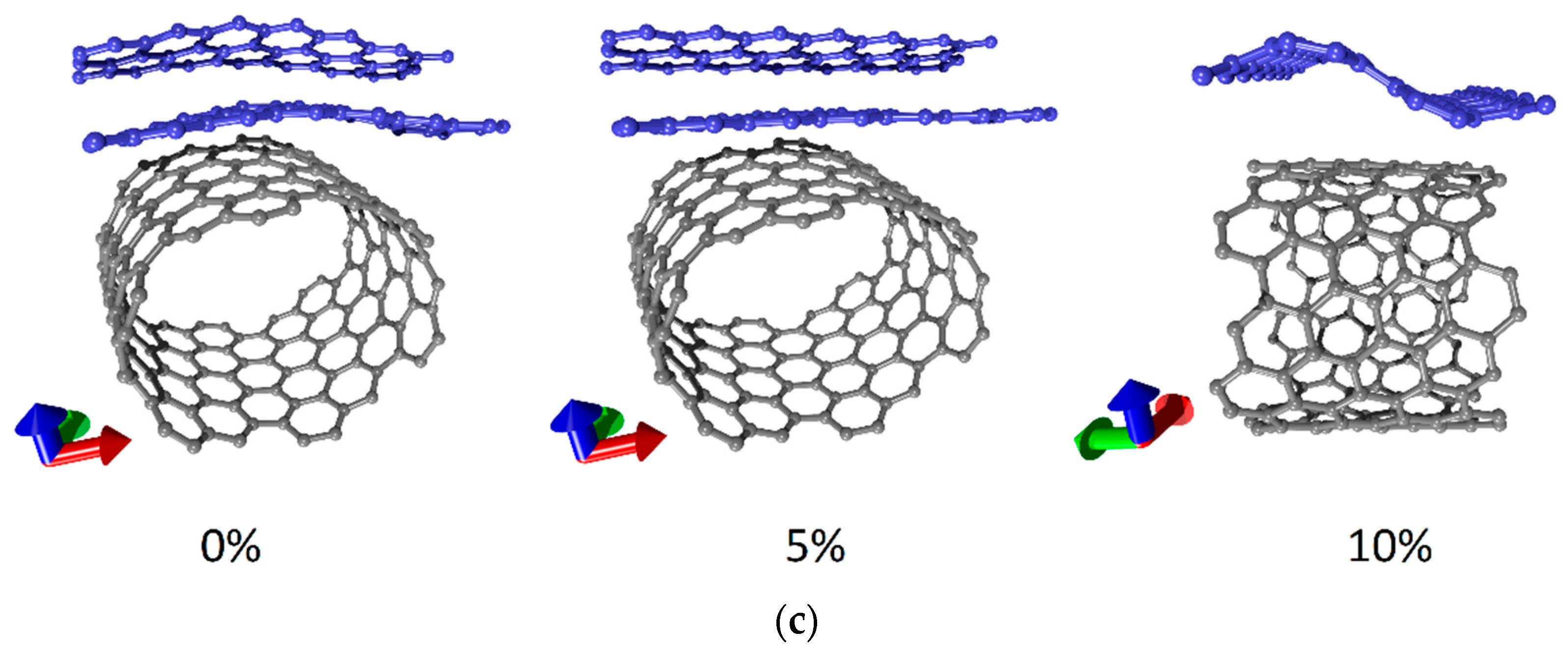
3.1. Axial Stretching of Hybrid Graphene/SWCNT (12, 6) Films
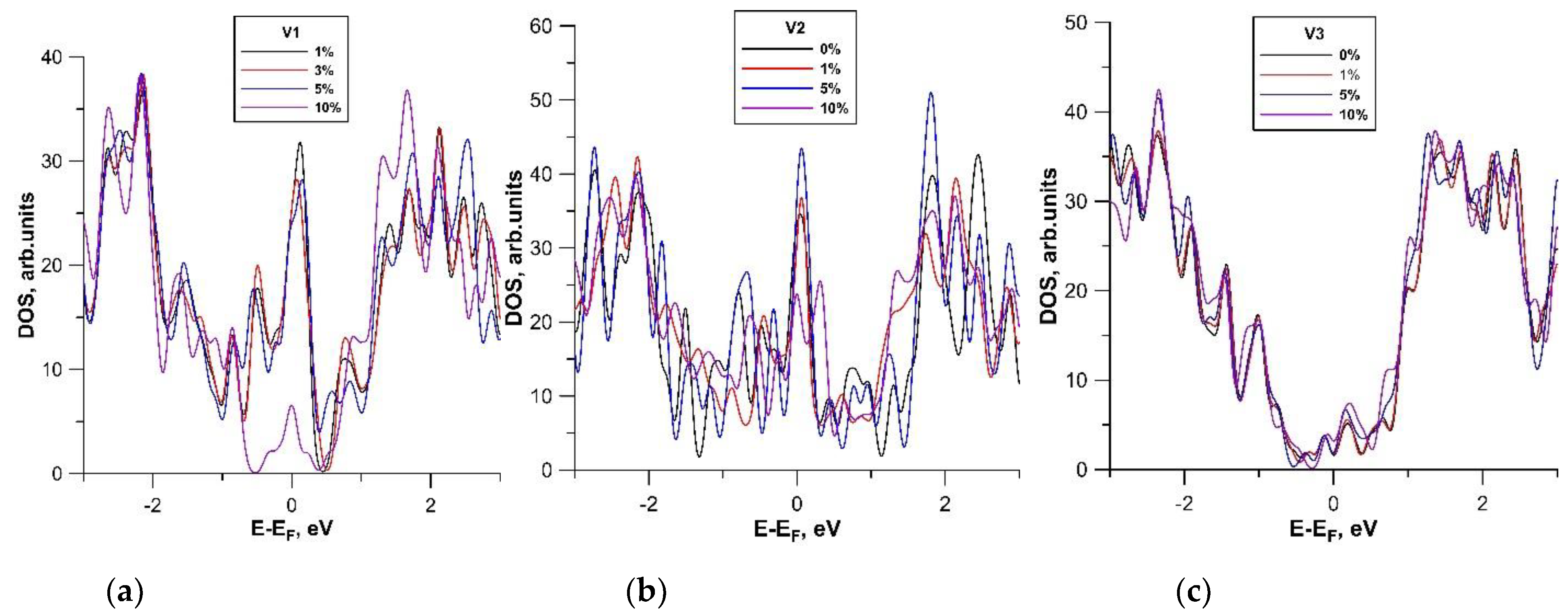
3.2. Effect of Axial Stretching on the Electrically Conductive and Electrochemical Properties of Hybrid Graphene/SWCNT (12, 6) Films
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Wu, W. Stretchable electronics: Functional materials, fabrication strategies and applications. Sci. Technol. Adv. Mater. 2019, 20, 187–224. [Google Scholar] [CrossRef] [Green Version]
- Yin, L.; Lv, J.; Wang, J. Structural innovations in printed, flexible, and stretchable electronics. Adv. Mater. Technol. 2020, 5, 2000694. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Y.; Zhao, Y.; Ren, Z.; Guo, C. Flexible electronics: Stretchable electrodes and their future. Adv. Funct. Mater. 2019, 29, 1805924. [Google Scholar] [CrossRef]
- Cheng, T.; Zhang, Y.; Lai, W.Y.; Huang, W. Stretchable thin-film electrodes for flexible electronics with high deformability and stretchability. Adv. Mater. 2015, 27, 3349–3376. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Xia, K.; Wang, H.; Liang, X.; Yin, Z.; Zhang, Y. Advanced carbon for flexible and wearable electronics. Adv. Mater. 2019, 31, 1801072. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, Y.; Liu, X.; Lv, C.; Li, Y.; Wei, D.; Liu, Z. Carbon-nanomaterial-based flexible batteries for wearable electronics. Adv. Mater. 2019, 31, 1800716. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Gao, W.; Emaminejad, S.; Kiriya, D.; Ota, H.; Nyein, H.Y.; Takei, K.; Javey, A. Printed carbon nanotube electronics and sensor systems. Adv. Mater. 2016, 28, 4397–4414. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Sheng, J.; Chen, Y.; Ni, J.; Li, Y. Carbon nanotubes for flexible batteries: Recent progress and future perspective. Natl. Sci. Rev. 2021, 8, nwaa261. [Google Scholar] [CrossRef]
- Jang, H.; Park, Y.J.; Chen, X.; Das, T.; Kim, M.S.; Ahn, J.H. Graphene-based flexible and stretchable electronics. Adv. Mater. 2016, 28, 4184–4202. [Google Scholar] [CrossRef]
- Shi, Y.; Wen, L.; Zhou, G.; Chen, J.; Pei, S.; Huang, K.; Cheng, H.M.; Li, F. Graphene-based integrated electrodes for flexible lithium ion batteries. 2D Mater. 2015, 2, 024004. [Google Scholar] [CrossRef]
- Du, Y.; Xiao, P.; Yuan, J.; Chen, J. Research progress of graphene-based materials on flexible supercapacitors. Coatings 2020, 10, 892. [Google Scholar] [CrossRef]
- Dai, C.; Sun, G.; Hu, L.; Xiao, Y.; Zhang, Z.; Qu, L. Recent progress in graphene-based electrodes for flexible batteries. InfoMat 2020, 2, 509–526. [Google Scholar] [CrossRef] [Green Version]
- Yoon, S.; Lee, S.; Kim, S.; Park, K.W.; Cho, D.; Jeong, Y. Carbon nanotube film anodes for flexible lithium ion batteries. J. Power Sources 2015, 279, 495–501. [Google Scholar] [CrossRef]
- Sugiawati, V.A.; Vacandio, F.; Yitzhack, N.; Ein-Eli, Y.; Djenizian, T. Direct pre-lithiation of electropolymerized carbon nanotubes for enhanced cycling performance of flexible Li-Ion micro-batteries. Polymers 2020, 12, 406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, P.; Liu, H.; Liao, L.; Fu, J.; Wang, Z.; Lv, G.; Mei, L.; Hao, H.; Xing, J.; Dong, J. Flexible and high capacity lithium-ion battery anode based on a carbon nanotube/electrodeposited nickel sulfide paper-like composite. RSC Adv. 2017, 7, 49739–49744. [Google Scholar] [CrossRef] [Green Version]
- Gilshteyn, E.P.; Amanbayev, D.; Anisimov, A.S.; Kallio, T.; Nasibulin, A.G. All-nanotube stretchable supercapacitor with low equivalent series resistance. Sci. Rep. 2017, 7, 17449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Ma, Y.; Liang, X.; Zhang, D.; Miao, M. Flexible supercapacitors based on carbon nanotube-MnO2 nanocomposite film electrode. Chem. Eng. J. 2019, 371, 145–153. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, W.; Li, X.; Gao, L. Recent progress in flexible energy storage materials for lithium-ion batteries and electrochemical capacitors: A review. J. Mater. Res. 2016, 31, 1648–1664. [Google Scholar] [CrossRef] [Green Version]
- Wang, R.; Xu, C.; Sun, J.; Gao, L.; Lin, C. Flexible free-standing hollow Fe3O4/graphene hybrid films for lithium-ion batteries. J. Mater. Chem. 2013, 1, 1794–1800. [Google Scholar] [CrossRef]
- Qu, Y.D.; Zhang, X.Y.; Lu, W.; Yang, N.J.; Jiang, X. All-solid-state flexible supercapacitor using graphene/g-C3N4 composite capacitor electrodes. J. Mater. Sci. 2020, 55, 16334–16346. [Google Scholar] [CrossRef]
- Cao, H.; Zhou, X.; Deng, W.; Ma, Z.; Liu, Y.; Liu, Z. Layer structured graphene/porous ZnCo2O4 composite film for high performance flexible lithium-ion batteries. Chem. Eng. J. 2018, 343, 654–661. [Google Scholar] [CrossRef]
- Wang, C.; Li, D.; Too, C.O.; Wallace, G.G. Electrochemical properties of graphene paper electrodes used in lithium batteries. Chem. Mater. 2009, 21, 2604–2606. [Google Scholar] [CrossRef]
- Hu, Y.; Li, X.; Wang, J.; Li, R.; Sun, X. Free-standing graphene–carbon nanotube hybrid papers used as current collector and binder free anodes for lithium ion batteries. J. Power Sources 2013, 237, 41–46. [Google Scholar] [CrossRef]
- Sun, H.; You, X.; Deng, J.; Chen, X.; Yang, Z.; Ren, J.; Peng, H. Novel graphene/carbon nanotube composite fibers for efficient wire-shaped miniature energy devices. Adv. Mater. 2014, 26, 2868–2873. [Google Scholar] [CrossRef] [PubMed]
- Du, W.; Ahmed, Z.; Wang, Q.; Yu, C.; Feng, Z.; Li, G.; Zhang, M.; Zhou, C.; Senegor, R.; Yang, C.Y. Structures, properties, and applications of CNT-graphene heterostructures. 2D Mater. 2019, 6, 042005. [Google Scholar] [CrossRef]
- Lv, R.; Cruz-Silva, E.; Terrones, M. Building complex hybrid carbon architectures by covalent interconnections: Graphene-nanotube hybrids and more. ACS Nano 2014, 8, 4061–4069. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Yuan, K. Molecular dynamics simulation of thermal boundary conductance between horizontally aligned carbon nanotube and graphene. Int. J. Therm. Sci. 2018, 132, 589–596. [Google Scholar] [CrossRef]
- Artyukh, A.A.; Chernozatonskii, L.A.; Sorokin, P.B. Mechanical and electronic properties of carbon nanotube-graphene compounds. Phys. Status Solidi B 2010, 247, 2927–2930. [Google Scholar] [CrossRef]
- Cook, B.G.; French, W.R.; Varga, K. Electron transport properties of carbon nanotube–graphene contacts. Appl. Phys. Lett. 2012, 101, 153501. [Google Scholar] [CrossRef]
- Song, L.; Guo, Z.; Chai, G.B.; Wang, Z.; Yongcun, L.; Luan, Y. A finite element method to investigate the elastic properties of pillared graphene sheet under different conditions. Carbon 2018, 140, 210–217. [Google Scholar] [CrossRef]
- Wang, C.H.; Fang, T.H.; Sun, W.L. Mechanical properties of pillared-graphene nanostructures using molecular dynamics simulations. J. Phys. D Appl. Phys. 2014, 47, 405302. [Google Scholar] [CrossRef]
- Kolosov, D.A.; Glukhova, O.E. Boron-decorated pillared graphene as the basic element for supercapacitors: An Ab initio study. Appl. Sci. 2021, 11, 3496. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, T.X. A review on hybridization modification of graphene and its polymer nanocomposites. Chin. Sci. Bull. 2012, 57, 3010–3021. [Google Scholar] [CrossRef] [Green Version]
- Elstner, M.; Seifert, G. Density functional tight binding. Phil. Trans. R. Soc. A 2014, 372, 20120483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- DFTB+ Density Functional Based Tight Binding (and More). Available online: https://dftbplus.org/ (accessed on 10 May 2020).
- Hourahine, B.; Aradi, B.; Blum, V.; Bonafé, F.; Buccheri, A.; Camacho, C.; Cevallos, C.; Deshaye, M.Y.; Dumitrică, T.; Dominguez, A.; et al. DFTB+, a software package for efficient approximate density functional theory based atomistic simulations. J. Chem. Phys. 2020, 152, 124101. [Google Scholar] [CrossRef]
- Zobelli, A.; Ivanovskaya, V.; Wagner, P.; Suarez-Martinez, I.; Yaya, A.; Ewels, C. A comparative study of density functional and density functional tight binding calculations of defects in graphene. Phys. Status Solidi B 2012, 249, 276–282. [Google Scholar] [CrossRef] [Green Version]
- Datta, S. Quantum Transport: Atom to Transistor, 2nd ed.; Cambridge University Press: New York, NY, USA, 2005; pp. 217–251. [Google Scholar]
- Glukhova, O.E.; Shmygin, D.S. The electrical conductivity of CNT/graphene composites: A new method for accelerating transmission function calculations. Beilstein. J. Nanotechnol. 2018, 9, 1254–1262. [Google Scholar] [CrossRef] [PubMed]
- Software Package Mizar. Available online: Nanokvazar.ru/ (accessed on 8 November 2020).
- Mousavi-Khoshdel, S.; Jahanbakhsh-bonab, P.; Targholi, E. Structural, electronic properties, and quantum capacitance of B, N and P-doped armchair carbon nanotubes. Phys. Lett. A 2016, 380, 3378–3383. [Google Scholar] [CrossRef]
- Slepchenkov, M.M.; Barkov, P.V.; Glukhova, O.E. Hybrid films based on bilayer graphene and single-walled carbon nanotubes: Simulation of atomic structure and study of electrically conductive properties. Nanomaterials 2021, 11, 1934. [Google Scholar] [CrossRef]
- Zhang, S.; Kang, L.; Wang, X.; Tong, L.; Yang, L.; Wang, Z.; Qi, K.; Deng, S.; Li, Q.; Bai, X.; et al. Arrays of horizontal carbon nanotubes of controlled chirality grown using designed catalysts. Nature 2017, 543, 234–238. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Wu, F.; Gui, H.; Zheng, M.; Zhou, C. Chirality-controlled synthesis and applications of single-wall carbon nanotubes. ACS Nano 2017, 11, 31–53. [Google Scholar] [CrossRef] [PubMed]
- Wakabayashi, K.; Sasaki, K.I.; Nakanishi, T.; Enoki, T. Electronic states of graphene nanoribbons and analytical solutions. Sci. Technol. Adv. Mater. 2010, 11, 054504. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, P.A.; Chiang, M.H.; Hsu, W.C. All-zigzag graphene nanoribbons for planar interconnect application. J. Appl. Phys. 2017, 122, 034301. [Google Scholar] [CrossRef] [Green Version]



| Model V1 | Model V2 | Model V3 | |
|---|---|---|---|
| Number of atoms | 252 | 280 | 308 |
| Lx (nm) | 1.719 | 1.723 | 1.707 |
| Ly (nm) | 1.135 | 1.134 | 1.110 |
| d (nm) | 0.48 | 0.27 | 0.06 |
| Model V1 | Model V2 | Model V3 | |
|---|---|---|---|
| 0% stretching strain | |||
| Rx (kOhm) | 7.53 | 6.22 | 125.89 |
| Ry (kOhm) | 6.58 | 5.95 | 16.31 |
| 1% stretching strain | |||
| Rx (kOhm) | 8.39 | 6.53 | 128.38 |
| Ry (kOhm) | 6.50 | 5.90 | 15.87 |
| 5% stretching strain | |||
| Rx (kOhm) | 7.68 | 6.00 | 64.19 |
| Rx (kOhm) | 6.42 | 5.85 | 9.20 |
| 10% stretching strain | |||
| Rx (kOhm) | 218.28 | 5.98 | 34.95 |
| Ry (kOhm) | 10.154 | 5.75 | 7.179 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slepchenkov, M.M.; Barkov, P.V.; Glukhova, O.E. In Silico Study of the Electrically Conductive and Electrochemical Properties of Hybrid Films Formed by Bilayer Graphene and Single-Wall Nanotubes under Axial Stretching. Membranes 2021, 11, 658. https://doi.org/10.3390/membranes11090658
Slepchenkov MM, Barkov PV, Glukhova OE. In Silico Study of the Electrically Conductive and Electrochemical Properties of Hybrid Films Formed by Bilayer Graphene and Single-Wall Nanotubes under Axial Stretching. Membranes. 2021; 11(9):658. https://doi.org/10.3390/membranes11090658
Chicago/Turabian StyleSlepchenkov, Michael M., Pavel V. Barkov, and Olga E. Glukhova. 2021. "In Silico Study of the Electrically Conductive and Electrochemical Properties of Hybrid Films Formed by Bilayer Graphene and Single-Wall Nanotubes under Axial Stretching" Membranes 11, no. 9: 658. https://doi.org/10.3390/membranes11090658
APA StyleSlepchenkov, M. M., Barkov, P. V., & Glukhova, O. E. (2021). In Silico Study of the Electrically Conductive and Electrochemical Properties of Hybrid Films Formed by Bilayer Graphene and Single-Wall Nanotubes under Axial Stretching. Membranes, 11(9), 658. https://doi.org/10.3390/membranes11090658







