Theoretical Investigation of Vapor Transport Mechanism Using Tubular Membrane Distillation Module
Abstract
:1. Introduction
1.1. Transport Process
1.2. Heat Transfer
- (I)
- Heat convection is found at the membrane surface from the bulk input to the vapor-liquid.
- (II)
- Evaporation and conductivity through the micro-porous membrane.
- (III)
2. Methods
2.1. Heat Transfer across the Membrane
2.1.1. Heat Transfer Mechanism Along with Boundary Layers
2.1.2. Temperature Polarization Coefficient
2.2. Mass Transfer
2.2.1. Mass Transfer across the Membrane
2.2.2. Mass Transfer within Membrane Pores
- Knudsen diffusion (molecules–wall collision).
- Molecular diffusion (molecules–molecules collision).
- Poiseuille flow (the gas viscosity).
2.2.3. Mass Transfer through the Boundary Layers (Concentration Polarization)
2.2.4. Transport Resistances
2.2.5. DCMD Thermal Efficiency
2.3. Pure and Saltwater Physical Properties
Numerical Model
3. Results and Discussion
3.1. Mechanism of Mass Transport
3.1.1. The Approximated Method for Predicting Permeates Flux Using Average Temperatures of the Inlet, Outlet Membrane Module, and Relative Humidity
3.1.2. The Exact Method for Predicting Permeates Fluxes Using Membrane Interface Temperatures on the Feed and Permeate Side
3.2. Model Validation
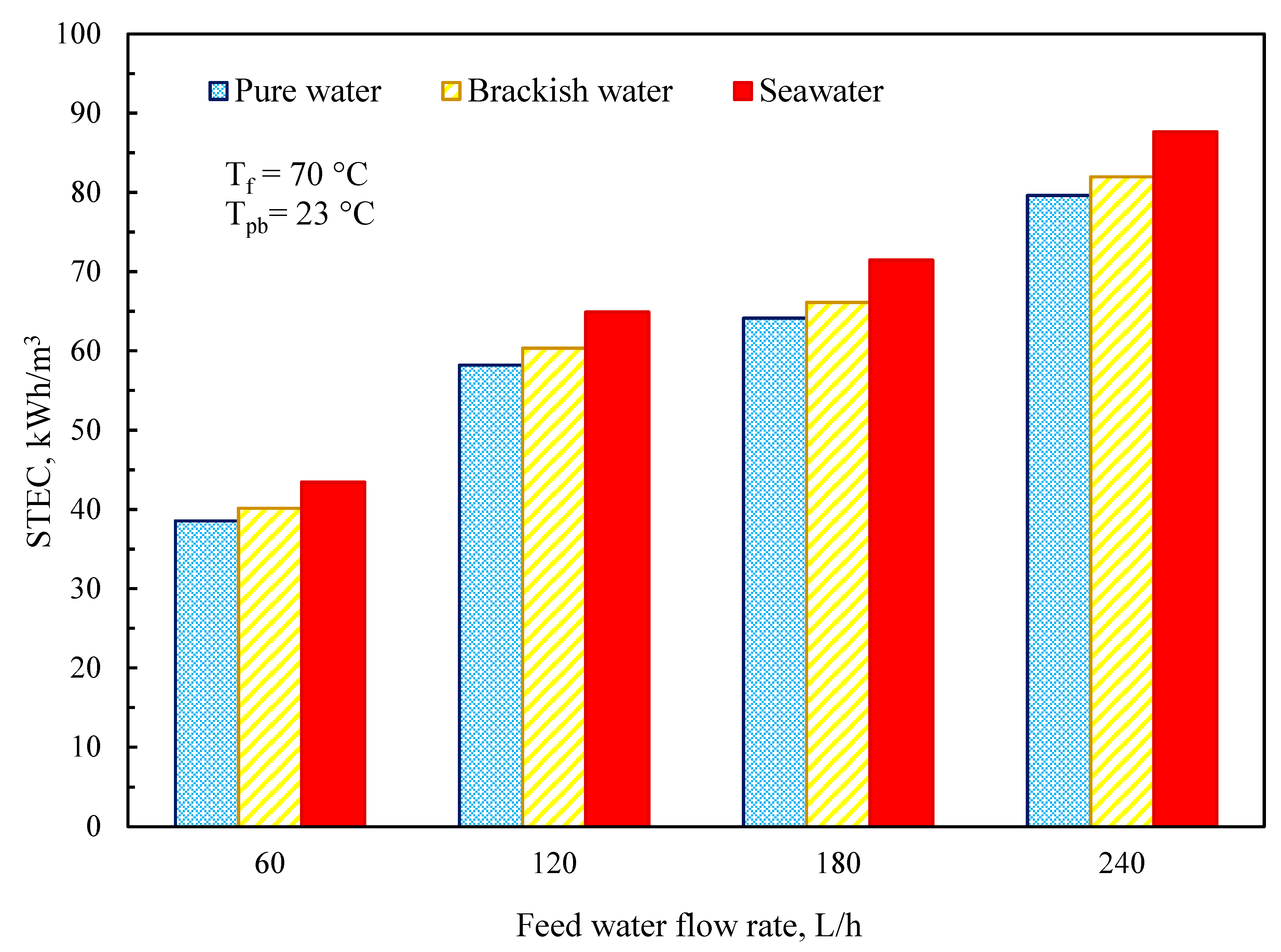
3.3. Effect of Feedwater Flow Rate and Salt Concentration on Permeate Flux
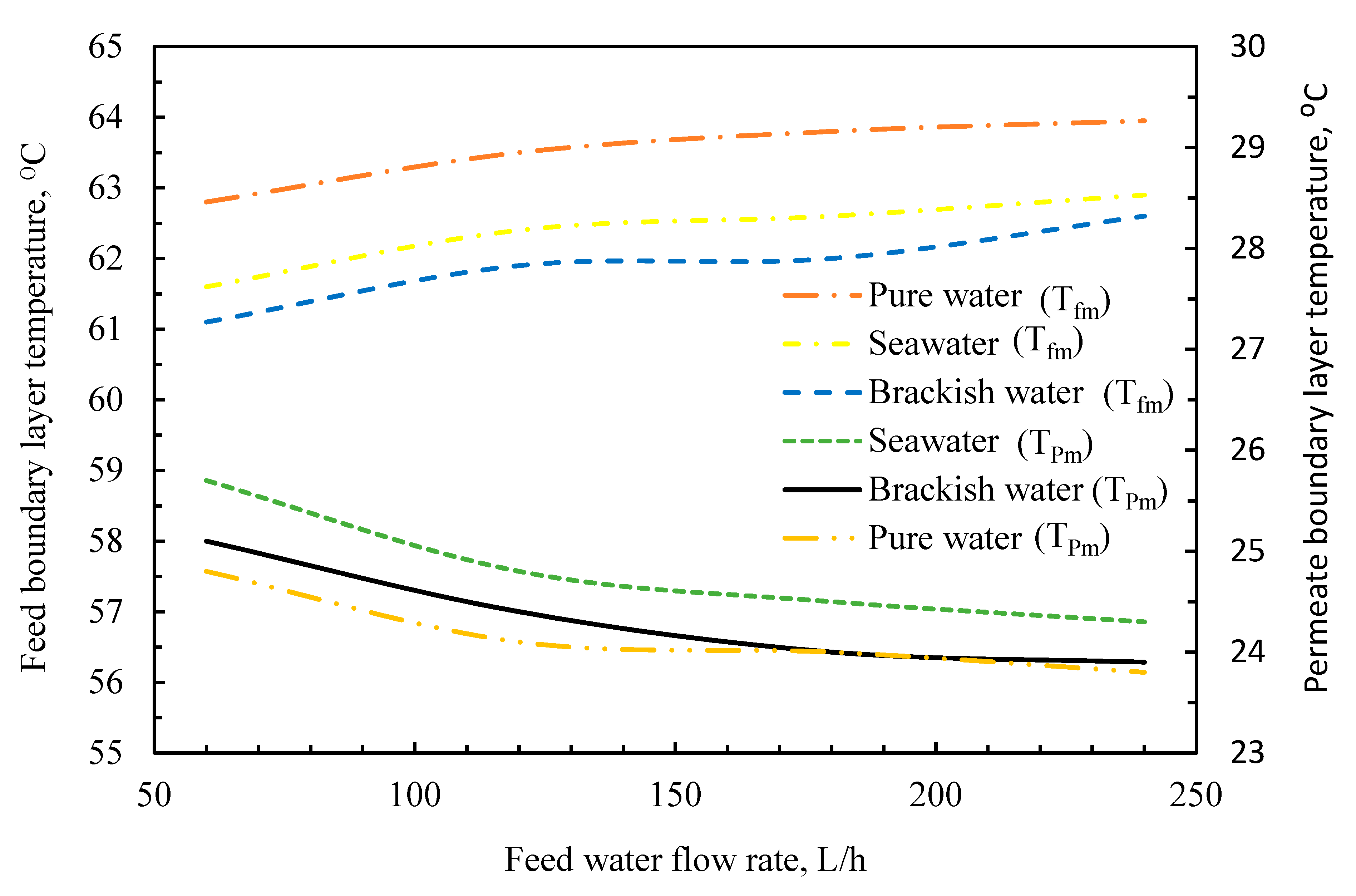
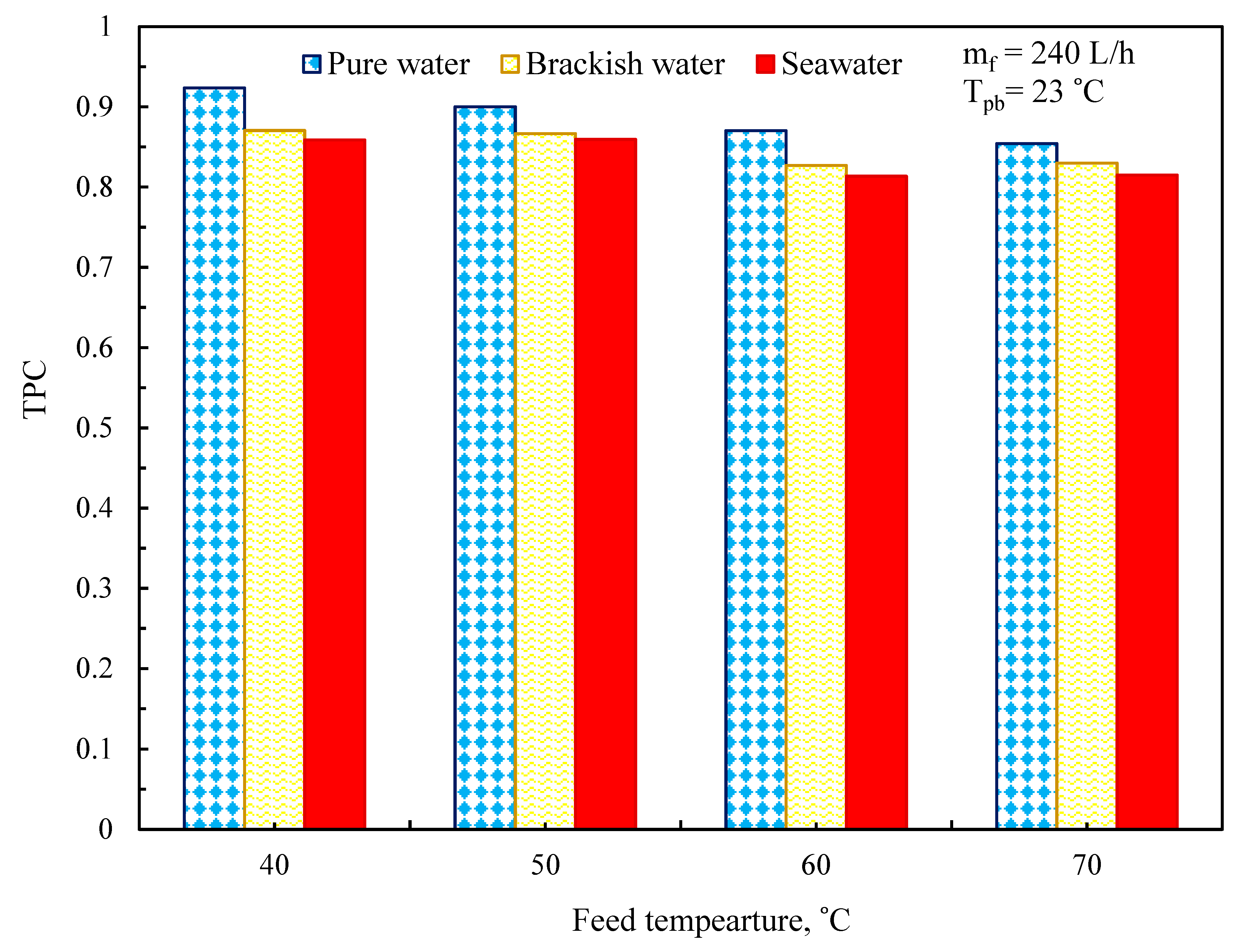
3.4. Temperature Polarization Effect
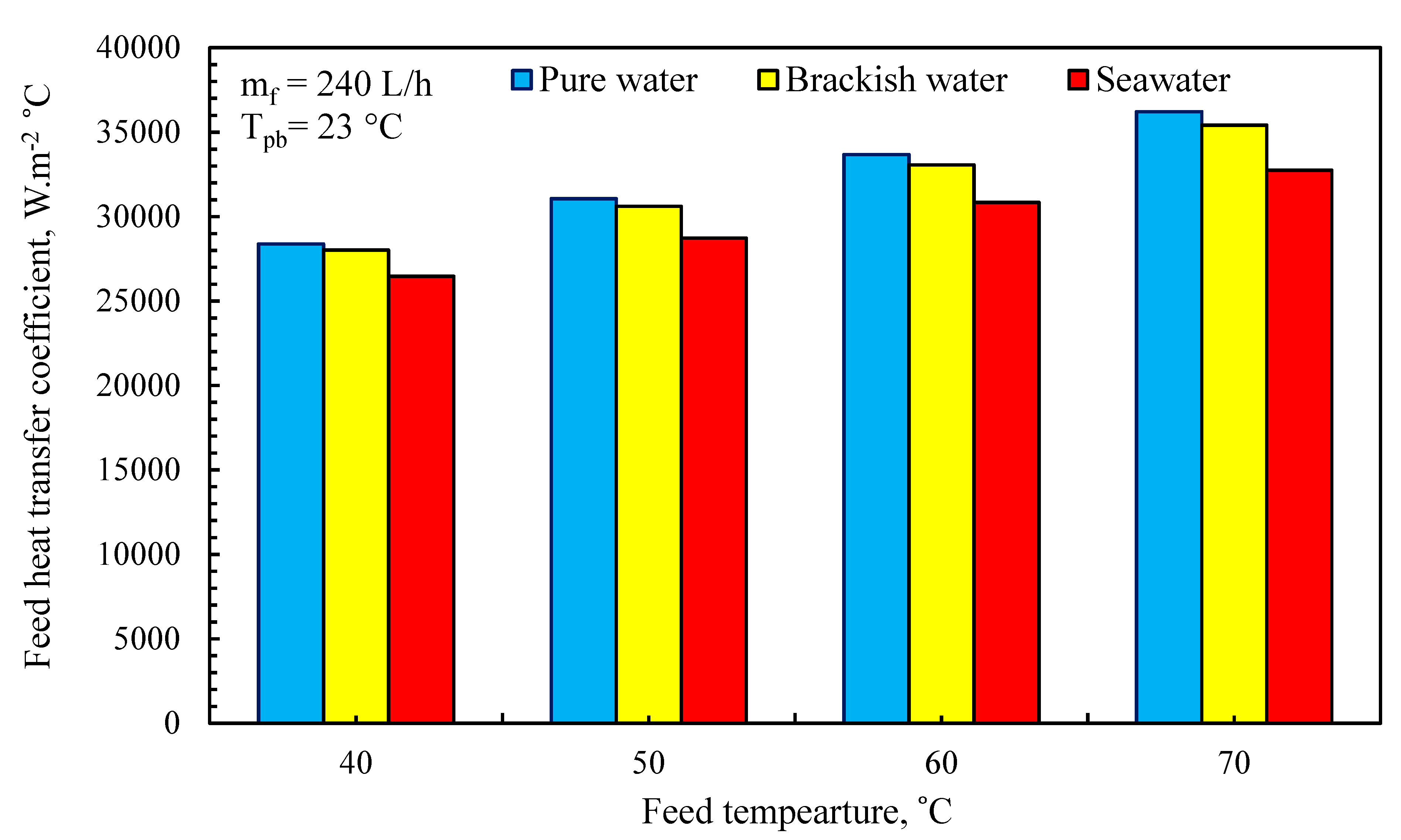
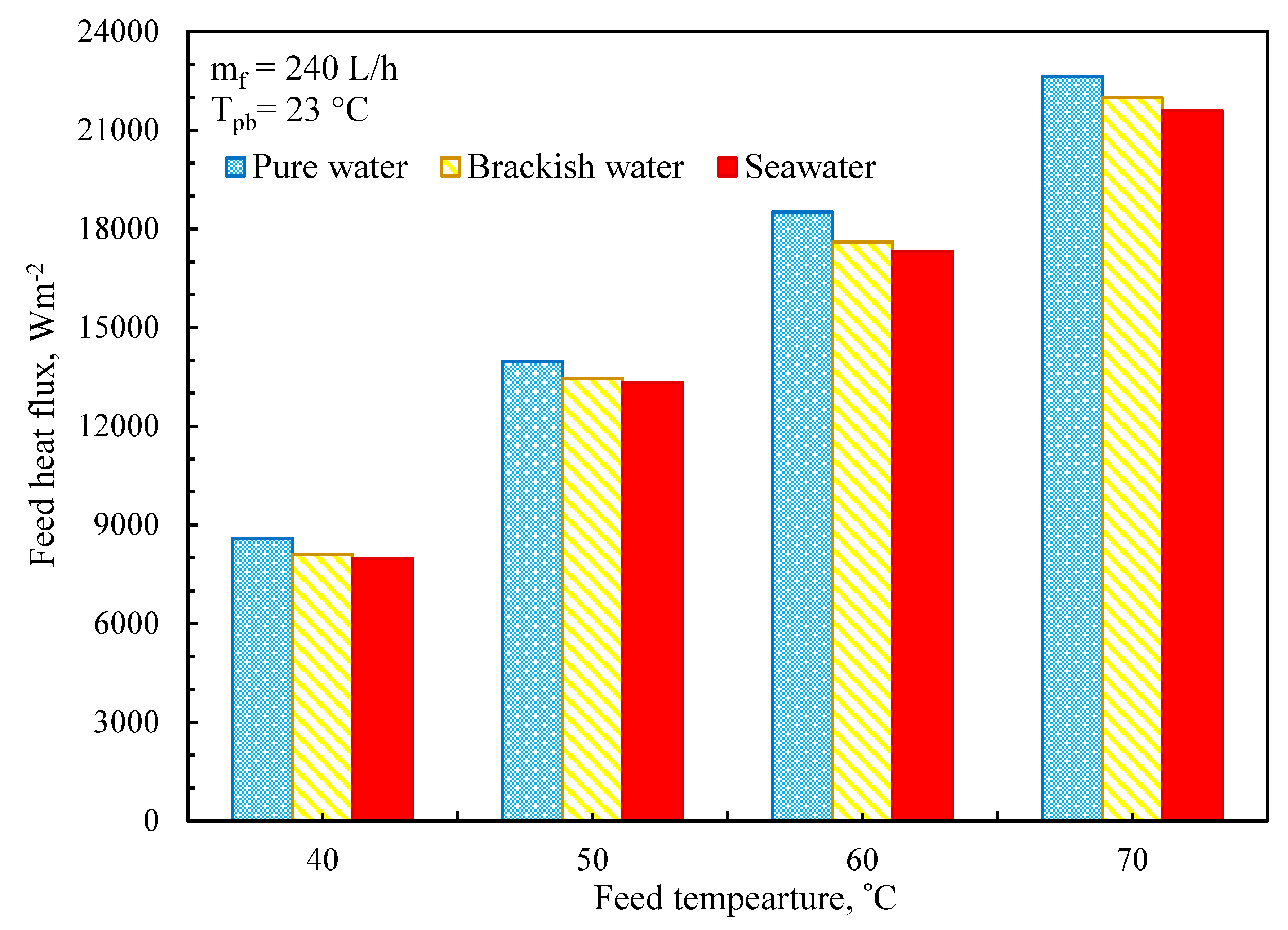
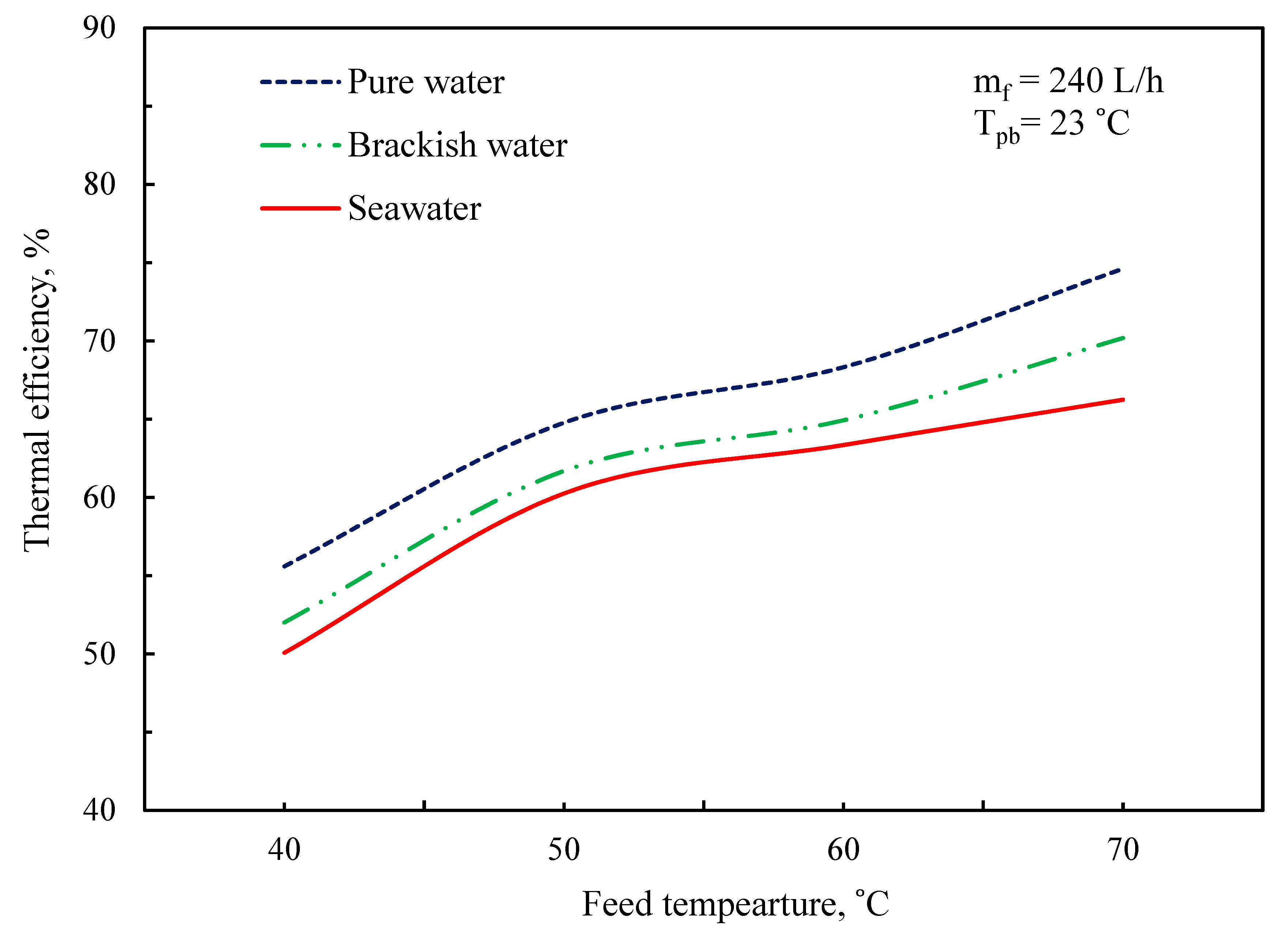
3.5. Thermal Performance of MD System
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Symbols
| Water activity | |
| Area of the membrane | |
| Area of Tank | |
| Heat capacity (J/kg·K) | |
| CFV | Cross flow velocity (m/s) |
| Molar concentration of the solution (mol/L) | |
| Molar concentration at feed temperature | |
| Molar concentration at the membrane surface | |
| Membrane pore size diameter (µm) | |
| Hydraulic diameter (m) | |
| Diffusivity of solute (m2/s) | |
| Diffusivity of water vapor-air mixture (m2/s) | |
| Water feed flow rate (mL/min) | |
| Latent Heat of vaporization | |
| h | Heat transfer coefficient |
| Mass vapor flux (kg/m2·h) | |
| Knudsen diffusion flux (kg/m2·h) | |
| Molecular diffusion flux (kg/m2·h) | |
| Poiseuille flow flux | |
| Thermal conductivity at the polarization layers | |
| Thermal conductivity | |
| Mass transfer coefficient (kg/m2·h·Pa) | |
| Membrane length (mm) | |
| M | Molality of NaCl in NaCl solution (mol/kg) |
| Mass flow rate | |
| Molecular weight of water (kg/kmol) | |
| Pressure (Pa) | |
| Heat flux (W/m2) | |
| RH | Relative humidity |
| R | Resistance at feed boundary layer |
| Mean temperature (°C, K) | |
| T | Temperature (°C, K) |
| Time (s) | |
| Volume of the tank | |
| Fluid velocity (m/s) | |
| Dimensionless numbers | |
| Knudsen number | |
| Re | Reynolds number |
| Sc | Schmidt number |
| Sh | Sherwood number |
| CP | Concentration polarization coefficient (CP) |
| Greek letters | |
| α | Reynolds number exponent |
| β | Schmidt number exponent |
| ρ | Fluid density (kg/m3) |
| μ | Fluid viscosity (Pa·s) |
| Membrane thickness (m) | |
| τ | Membrane tortuosity |
| ε | Membrane porosity |
| Mean free path (m) | |
| Subscripts | |
| b | Bulk |
| c | Conduction |
| g | Gas |
| Exp. | Experimental |
| f | Feed |
| m | Membrane |
| MD | Membrane Distillation |
| M | Molecular diffusion |
| K | Knudsen diffusion |
| K-M | Knudsen-Molecular transition diffusion |
| P | Permeate |
| s | Salt |
| v | Vaporization |
| 1 | Membrane location at feed side |
| 2 | Membrane location at permeate side |
References
- Alhathal Alanezi, A.; Sharif, A.O.; Sanduk, M.; Khan, A.R. Potential of Membrane Distillation-A Comprehensive Review. Int. J. Water 2013, 7, 317–346. [Google Scholar]
- Jamed, M.J.; Alhathal Alanezi, A.; Alsalhy, Q.F. Effects of embedding functionalized multi-walled carbon nanotubes and alumina on the direct contact poly(vinylidene fluoride-co-hexafluoropropylene) membrane distillation performance. Chem. Eng. Commun. 2019, 206, 1035–1057. [Google Scholar] [CrossRef]
- Alhathal Alanezi, A.; Sharif, A.O.; Sanduk, M.; Khan, A.R. Experimental Investigation of Heat and Mass Transfer in Tubular Membrane Distillation Module for Desalination. ISRN Chem. Eng. 2012, 2012, 738731. [Google Scholar]
- Alhathal Alanezi, A.; Safaei, M.R.; Goodarzi, M.; Elhenawy, Y. The effect of inclination angle and Reynolds number on the performance of a direct contact membrane distillation (DCMD) process. Energies 2020, 13, 2824. [Google Scholar] [CrossRef]
- Alhathal Alanezi, A.; Altaee, A.; Sharif, A. The effect of energy recovery device and feed flow rate on the energy efficiency of reverse osmosis process. Chem. Eng. Res. Des. 2020, 158, 12–23. [Google Scholar] [CrossRef]
- Alhathal Alanezi, A. Performance Enhancement of Air Bubbling and Vacuum Membrane Distillation for Water Desalination. Ph.D. Thesis, University of Surrey, Guildford, UK, 2013. Available online: https://ethos.bl.uk/OrderDetails.do?uin=uk.bl.ethos.576164 (accessed on 1 June 2021).
- Alhathal Alanezi, A.; Abdallah, H.; El-Zanati, E.; Ahmad, A.; Sharif, A.O. Performance investigation of O-ring vacuum membrane distillation module for water desalination. J. Chem. 2016, 2016, 9378460. [Google Scholar] [CrossRef] [Green Version]
- Ali, I.; Bamaga, O.A.; Gzara, L.; Bassyouni, M.; Abdel-Aziz, M.H.; Soliman, M.F.; Enrico Drioli, E.; Albeirutty, M. Assessment of blend PVDF membranes, and the effect of polymer concentration and blend composition. Membranes 2018, 8, 13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sztekler, K.; Kalawa, W.; Nowak, W.; Mika, L.; Gradziel, S.; Krzywanski, J.; Radomska, E. Experimental Study of Three-Bed Adsorption Chiller with Desalination Function. Energies 2020, 13, 5827. [Google Scholar] [CrossRef]
- Chang, H.; Ho, C.D.; Chen, Y.H.; Chen, L.; Hsu, T.H.; Lim, J.W.; Chiou, C.P.; Lin, P.H. Enhancing the Permeate Flux of Direct Contact Membrane Distillation Modules with Inserting 3D Printing Turbulence Promoters. Membranes 2021, 11, 266. [Google Scholar] [CrossRef]
- Ni, W.; Li, Y.; Zhao, J.; Zhang, G.; Du, X.; Dong, Y. Simulation Study on Direct Contact Membrane Distillation Modules for High-Concentration NaCl Solution. Membranes 2020, 10, 179. [Google Scholar] [CrossRef]
- Chen, L.; Wu, B. Research Progress in Computational Fluid Dynamics Simulations of Membrane Distillation Processes: A Review. Membranes 2021, 11, 513. [Google Scholar] [CrossRef]
- Gryta, M. The application of submerged modules for membrane distillation. Membranes 2020, 10, 25. [Google Scholar] [CrossRef] [Green Version]
- Curcio, E.; Drioli, E. Membrane distillation and related operations—A review. Sep. Purif. Rev. 2005, 34, 35–86. [Google Scholar] [CrossRef]
- Elrasheedy, A.; Nady, N.; Bassyouni, M.; El-Shazly, A. Metal organic framework based polymer mixed matrix membranes: Review on applications in water purification. Membranes 2019, 9, 88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Babu, B.R.; Rastogi, N.K.; Raghavarao, K.S.M.S. Mass transfer in osmotic membrane distillation of phycocyanin colorant and sweet-lime juice. J. Membr. Sci. 2006, 272, 58–69. [Google Scholar] [CrossRef]
- Babu, B.R.; Rastogi, N.K.; Raghavarao, K.S.M.S. Concentration and temperature polarization effects during osmotic membrane distillation. J. Membr. Sci. 2008, 322, 146–153. [Google Scholar] [CrossRef]
- Yao, M.; Tijing, L.D.; Naidu, G.; Kim, S.H.; Matsuyama, H.; Fane, A.G.; Shon, H.K. A review of membrane wettability for the treatment of saline water deploying membrane distillation. Desalination 2020, 479, 114312. [Google Scholar] [CrossRef]
- Lawson, K.W.; Lloyd, D.R. Membrane distillation. J. Membr. Sci. 1997, 124, 1–25. [Google Scholar] [CrossRef]
- Gryta, M.; Tomaszewska, M.; Morawski, A.W. Membrane distillation with laminar flow. Sep. Purif. Technol. 1997, 11, 93–101. [Google Scholar] [CrossRef]
- McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Bandini, S.; Gostoli, C.; Sarti, G.C. Separation efficiency in vacuum membrane distillation. J. Membr. Sci. 1992, 73, 217–229. [Google Scholar] [CrossRef]
- Sedahmed, G.H.; El-Taweel, Y.A.; Konsowa, A.H.; Abdel-Aziz, M.H. Mass transfer intensification in an annular electrochemical reactor by an inert fixed bed under various hydrodynamic conditions. Chem. Eng. Process. 2011, 50, 1122–1127. [Google Scholar] [CrossRef]
- Burgoyne, A.; Vahdati, M.M. Permeate flux modelling of membrane distillation. Filt. Sep. 1999, 36, 49–53. [Google Scholar]
- Pangarkar, B.L.; Sane, M.G.; Parjane, S.B.; Abhang, R.M.; Guddad, M. The heat and mass transfer phenomena in vacuum membrane distillation for desalination. Int. J. Chem. Biomol. Eng. 2010, 3, 33–38. [Google Scholar]
- Mengual, J.I.; Khayet, M.; Godino, M.P. Heat and mass transfer in vacuum membrane distillation. Int. J. Heat Mass Transfer 2004, 47, 865–875. [Google Scholar] [CrossRef]
- Thanedgunbaworn, R.; Jiraratananon, R.; Nguyen, M.H. Vapour Transpot Mechanism in Osmotic Distillation Process. Int. J. Food Eng. 2009, 5, 1–19. [Google Scholar] [CrossRef]
- Martinez-Diez, L.; Vazquez-Gonzalez, M.I. Effects of polarization on mass transport through hydrophobic porous membranes. Ind. Eng. Chem. Res. 1998, 37, 4128–4135. [Google Scholar] [CrossRef]
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D. Heat and Mass Transfer in Membrane Distillation. J. Membr. Sci. 1987, 33, 299–313. [Google Scholar] [CrossRef]
- Zhigang, L.; Biaohua, C.; Zhongwei, D. “Membrane distillation”. Special Distillation Processes; Elsevier Science: Amsterdam, The Netherlands, 2005; pp. 241–319. [Google Scholar]
- Elhady, S.; Bassyouni, M.; Mansour, R.A.; Elzahar, M.H.; Abdel-Hamid, S.; Elhenawy, Y.; Saleh, M.Y. Oily wastewater treatment using polyamide thin film composite membrane technology. Membranes 2020, 10, 84. [Google Scholar] [CrossRef] [PubMed]
- Srisurichan, S.; Jiraratananon, R.; Fane, A.G. Mass transfer mechanisms and transport resistances in direct contact membrane distillation process. J. Membr. Sci. 2006, 277, 186–194. [Google Scholar] [CrossRef]
- Sandid, A.M.; Bassyouni, M.; Nehari, D.; Elhenawy, Y. Experimental and simulation study of multichannel air gap membrane distillation process with two types of solar collectors. Energ. Conv. Manag. 2021, 243, 114431. [Google Scholar] [CrossRef]
- Thanedgunbaworn, R.; Jiraratananon, R.; Nguyen, M.H. Mass and heat transfer analysis in fructose concentration by osmotic distillation process using hollow fibre module. J. Food Eng. 2007, 78, 126–135. [Google Scholar] [CrossRef]
- Alwatban, A.M.; Alshwairekh, A.M.; Alqsair, U.F.; Alghafis, A.A.; Oztekin, A. Performance improvements by embedded spacer in direct contact membrane distillation–Computational study. Desalination 2019, 470, 114103. [Google Scholar] [CrossRef]
- Mabrouk, A.; Elhenawy, Y.; Abdelkader, M.; Shatat, M. The impact of baffle orientation on the performance of the hollow fiber membrane distillation. Desalin. Water Treat. 2017, 58, 35–45. [Google Scholar] [CrossRef]
- Chen, T.C.; Ho, C.D. Immediate assisted solar direct contact membrane distillation in saline water desalination. J. Membr. Sci. 2010, 358, 122–130. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, V.J.H.; Zubair, S.M. The thermophysical properties of seawater: A review of existing correlations and data accessed thermophysical properties of seawater: A review of existing correlations and data. Desalin. Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Elhenawy, Y.; Elminshawy, N.A.; Bassyouni, M.; Alhathal Alanezi, A.; Drioli, E. Experimental and theoretical investigation of a new air gap membrane distillation module with a corrugated feed channel. J. Membr. Sci. 2020, 594, 117461. [Google Scholar] [CrossRef]
- Alsaadi, A.S.; Ghaffour, N.; Li, J.D.; Gray, S.; Francis, L.; Maab, H.; Amy, G.L. Modeling of air-gap membrane distillation process: A theoretical and experimental study. J. Membr. Sci. 2013, 445, 53–65. [Google Scholar] [CrossRef] [Green Version]
- Geankoplis, C. Transport Processes and Unit Operations; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993; pp. 854–863. [Google Scholar]
- Felder, R.M.; Rousseau, R.W. Elementary Principles of Chemical Processes, 2nd ed.; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 1986; p. 243. [Google Scholar]
- Izquierdo-Gil, M.A.; Garcıa-Payo, M.C.; Fernández-Pineda, C. Air gap membrane distillation of sucrose aqueous solutions. J. Membr. Sci. 1999, 155, 291–307. [Google Scholar] [CrossRef]
- Banat, F.A.; Simandl, J. Theoretical and experimental study in membrane distillation. Desalination 1994, 95, 39–52. [Google Scholar] [CrossRef]
- Abdel-Aziz, M.H.; Nirdosh, I.; Sedahmed, G.H. Liquid–solid mass and heat transfer behavior of a concentric tube airlift reactor. Int. J. Heat Mass Transfer 2013, 58, 735–739. [Google Scholar] [CrossRef]
- Qtaishat, M.; Matsuura, T.; Kruczek, B.; Khayet, M. Heat and mass transfer analysis in direct contact membrane distillation. Desalination 2008, 219, 272–292. [Google Scholar] [CrossRef]
- Zhang, J.; Dow, N.; Duke, M.; Ostarcevic, E.; Li, J.-D.; Gray, S. Identification of material and physical features of membrane distillation membranes for high performance desalination. J. Membr. Sci. 2010, 349, 295–303. [Google Scholar] [CrossRef] [Green Version]
- Khayet, M.; Godino, M.P.; Mengual, J.I. Study of asymmetric polarization in direct contact membrane distillation. Sep. Sci. Technol. 2004, 39, 125–147. [Google Scholar] [CrossRef]
- Khayet, M.; Mengual, J.I.; Matsuura, T. Porous hydrophobic/hydrophilic composite membranes: Application in desalination using direct contact membrane distillation. J. Membr. Sci. 2005, 252, 101–113. [Google Scholar] [CrossRef]
- Laganà, F.; Barbieri, G.; Drioli, E. Direct contact membrane distillation: Modelling and concentration experiments. J. Membr. Sci. 2000, 166, 1–11. [Google Scholar] [CrossRef]
- Godino, P.; Pena, L.; Mengual, J.I. Membrane distillation: Theory and experiments. J. Membr. Sci. 1996, 121, 83–93. [Google Scholar] [CrossRef]
- Gryta, M.; Tomaszewska, M. Heat transport in the membrane distillation process. J. Membr. Sci. 1998, 144, 211–222. [Google Scholar] [CrossRef]
- Tomaszewska, M.; Gryta, M.; Morawski, A.W. Study on the concentration of acids by membrane distillation. J. Membr. Sci. 1995, 102, 113–122. [Google Scholar] [CrossRef]
- Bahmanyar, A.; Asghari, M.; Khoobi, N. Numerical simulation and theoretical study on simultaneously effects of operating parameters in direct contact membrane distillation. Chem. Eng. Process. 2012, 61, 42–50. [Google Scholar] [CrossRef]
- Ruiz-Aguirre, A.; Andrés-Mañas, J.A.; Fernández-Sevilla, J.M.; Zaragoza, G. Experimental characterization and optimization of multi-channel spiral wound air gap membrane distillation modules for seawater desalination. Sep. Purif. Technol. 2018, 205, 212–222. [Google Scholar] [CrossRef]
- El-Ashtoukhy, E.Z.; Abdel-Aziz, M.H. Removal of copper from aqueous solutions by cementation in a bubble column reactor fitted with horizontal screens. Int. J. Min. Process. 2013, 121, 65–69. [Google Scholar] [CrossRef]

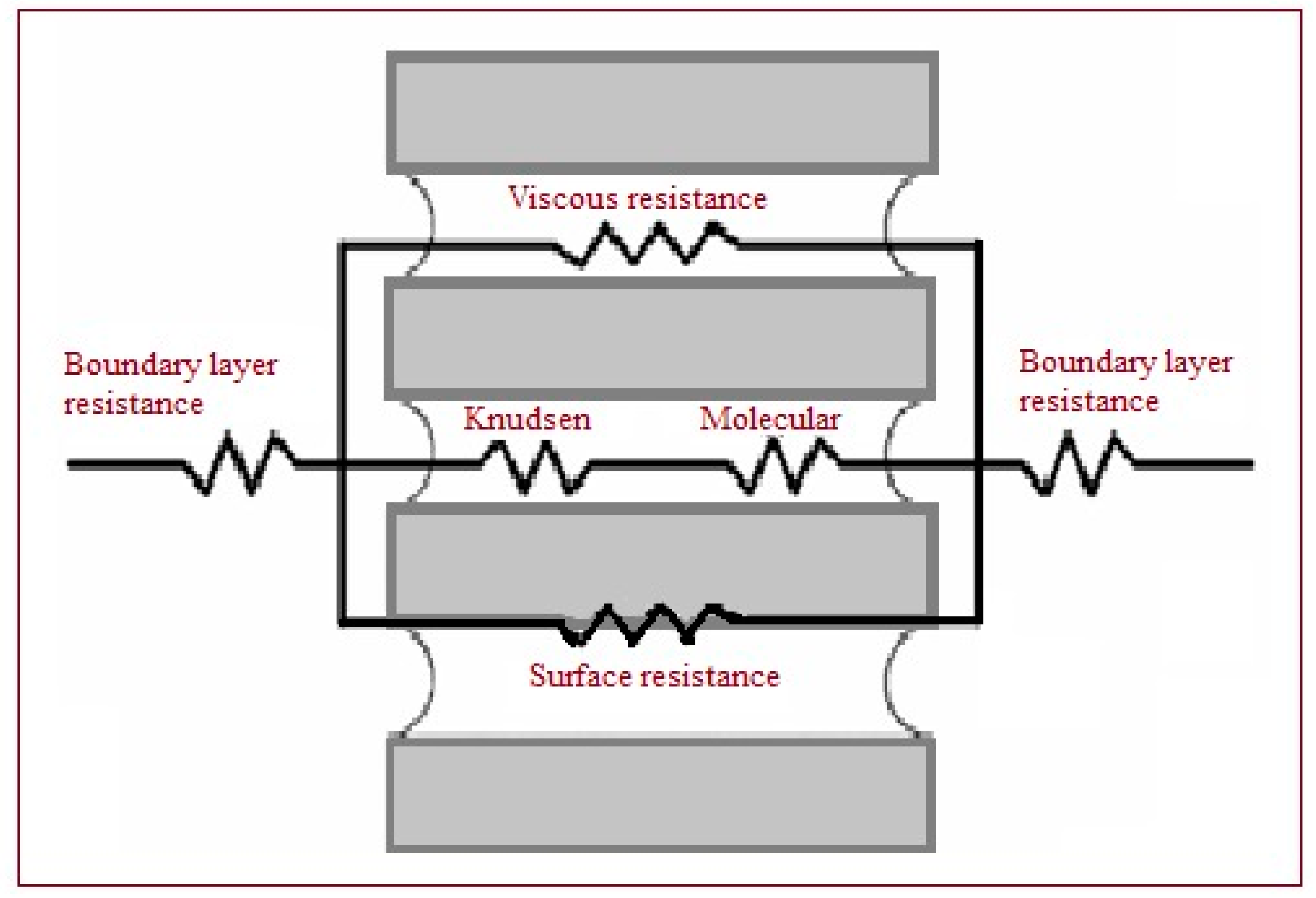


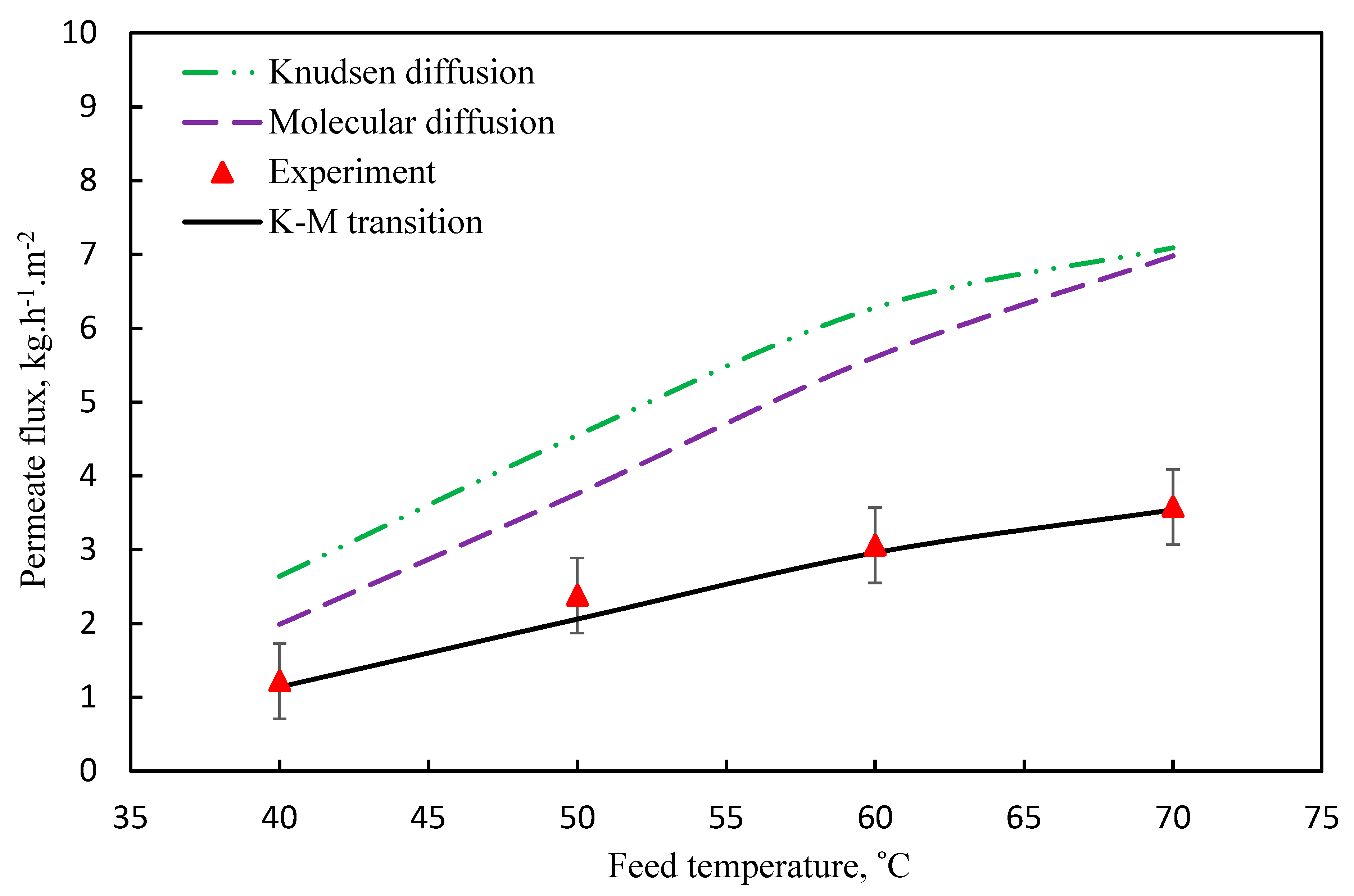
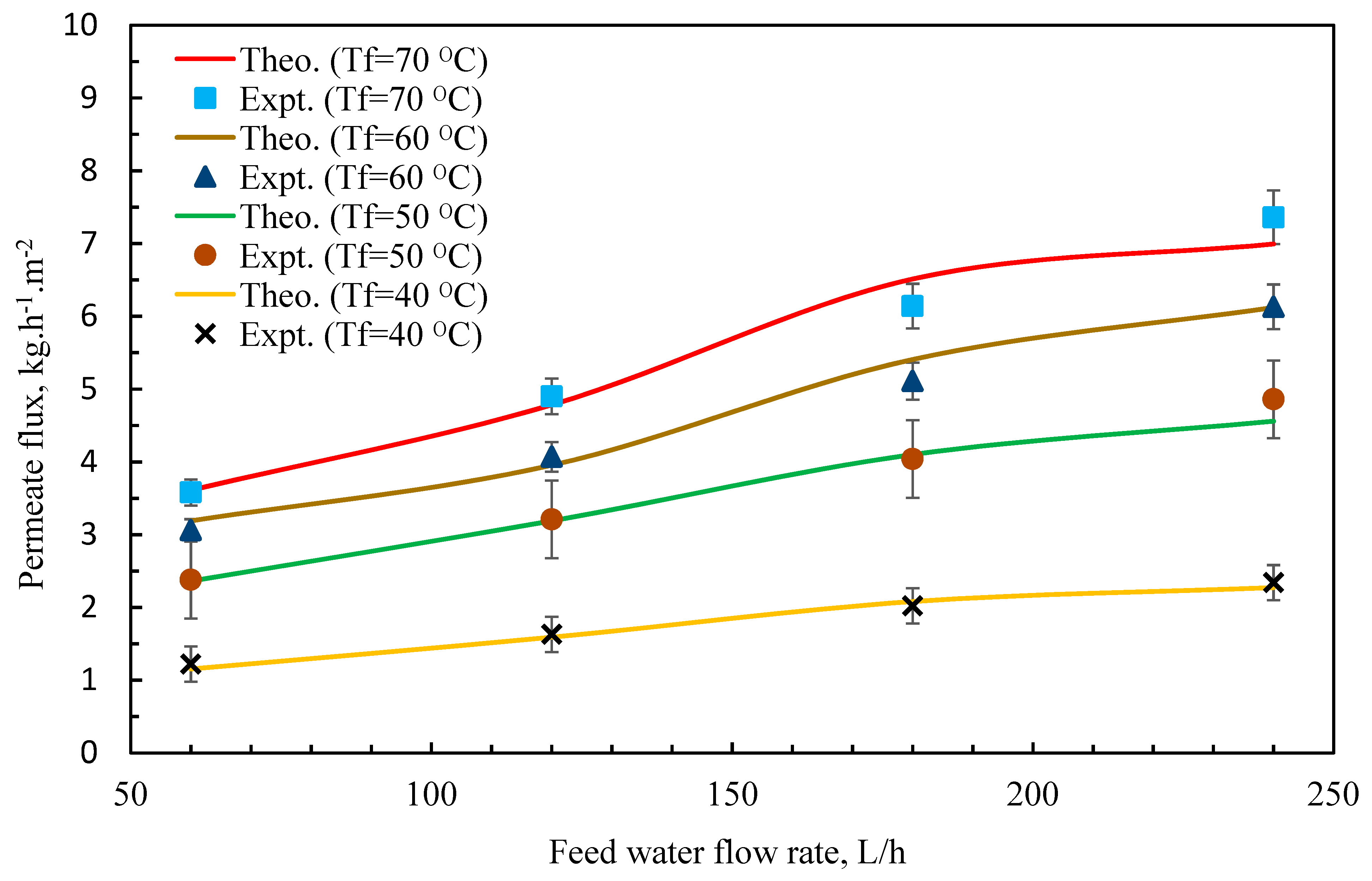
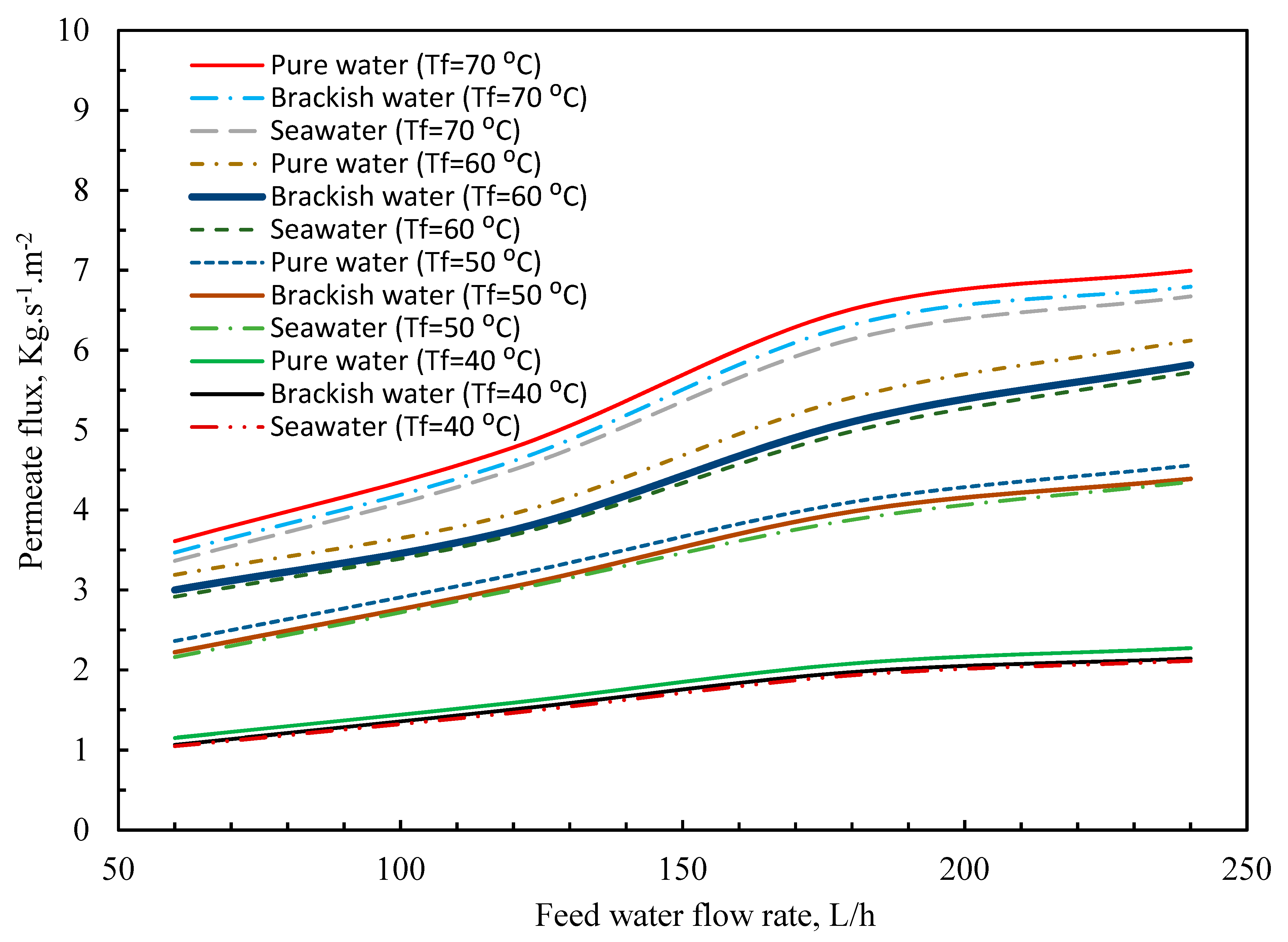


| T | Polyvinylidene Fluoride | Polytetrafluoroethylene | Polypropylene | Air | Water Vapor |
|---|---|---|---|---|---|
| (K) | (W/m⋅K) | ||||
| 296 | 0.17–0.19 | 0.25–0.27 | 0.11–0.16 | 0.026 | 0.022 |
| 348 | 0.21 | 0.29 | 0.20 | 0.03 | 0.022 |
| Characteristic | Correlation | Conditions and Unit |
|---|---|---|
| Heat capacities of water [37] | CP,b = 1000(6.18507 − 0.0159(T + 273.15) + 3.99 × 105(T + 273.15)2 − 3.06 × 10−8(T + 273.15)3) | 16.85 °C < T < 96.85 °C, J/(kg °C) |
| Heat capacities of saline water [28] | Cpsw = 5.328 − 9.76 × 10−2S + 4.04×10−4S2 + (−6.913 × 10−3 + 7.351 × 10−4S 3.15 × 10−6S2)T + (9.6 × 10−6 − 1.927 × 10−6S + 8.23 × 10−9S2)T2 + (2.5 × 10−9 + 1.666 × 10−9S − 7.125 × 10−12S2)T3 | 273.15 K < T < 453.15 K; 0 < S < 180 g/kg, kJ/(kg k) |
| Latent heat of water vaporization [29,30] | ∆Hv = 2024.3 + 1.75535T | 5 °C < T < 200 °C, J/(kg °C) |
| Density of liquid water [37] | ρw = 1000(0.819 + 1.49 × 10−3(T + 273.15) − 2.9975 × 10−6(T + 273.15)2) | 16.85 °C < T < 96.85 °C, kg/(m3) |
| Density of saline water [37] | kg/(m3) | |
| Viscosity of water vapor [37] | 16.85 °C < T < 96.85 °C, kg/(m s) | |
| Viscosity of liquid water [38] | 0 °C ≤ T ≤ 180 °C, kg/(m s) | |
| Viscosity of saline water [38,40] | 10 °C < T < 180 °C; 0 < S < 150 g/kg, kg/(m s) | |
| Thermal conductivity of liquid water [37] | 20 °C < T < 100 °C, W/(m·°C) | |
| Thermal conductivity of saline water [40] | 0 °C < T < 180 °C; 0 < S < 160 g/kg, W/(m·°C) |
| Parameter | Values |
|---|---|
| Thickness of membrane, | 600 [μm] |
| Porosity of membrane, | 51% |
| Pore size of membrane | 0.72 [μm] |
| Tortuosity of membrane, T | 1.96 |
| Thermal conductivity of membrane, Km | 0.27 [W/mK] |
| Feed Reynolds number, Ref | 2500 to 15,000 |
| Permeate Reynolds number, Rep | 332 |
| Concentration at feed inlet, cf, in | 5000 and 35,000 [ppm] |
| Inlet feed temperature, Tf, in | 40, 50, 60 and 70 °C |
| Inlet permeate temperature, Tp, in | 23 °C |
| Device | Accuracy | Range | Standard Uncertainty |
|---|---|---|---|
| Thermocouple | 0.15 °C | 0–150 °C | 0.086 °C |
| Rotameter | 0.1 L/min | 8 L/min | 0.057 L/min |
| TDS meter | 5 ppm | 0–50,000 ppm | 2.89 ppm |
| Balance | 0.5 g | 1 to 25,000 g | 0.289 g |
| Driving Force | |||
|---|---|---|---|
| Gas Mixture , | M | M–K transition | K |
| Method | |
|---|---|
| Knudsen diffusion | 0.75 |
| Molecular diffusion | 0.66 |
| K-M transition | 0.35 |
| Experimental | 0.39 |
| 40 | 210.36 | 225.12 | 2821.54 | 3019.55 | 108.09 | 115.68 |
| 50 | 70.48 | 81.42 | 2534.76 | 2928.51 | 35.03 | 40.48 |
| 60 | 73.89 | 76.39 | 2752.95 | 2845.95 | 37.48 | 38.74 |
| 70 | 690.24 | 698.04 | 2681.88 | 2712.18 | 377.40 | 381.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhathal Alanezi, A.; Bassyouni, M.; Abdel-Hamid, S.M.S.; Ahmed, H.S.; Abdel-Aziz, M.H.; Zoromba, M.S.; Elhenawy, Y. Theoretical Investigation of Vapor Transport Mechanism Using Tubular Membrane Distillation Module. Membranes 2021, 11, 560. https://doi.org/10.3390/membranes11080560
Alhathal Alanezi A, Bassyouni M, Abdel-Hamid SMS, Ahmed HS, Abdel-Aziz MH, Zoromba MS, Elhenawy Y. Theoretical Investigation of Vapor Transport Mechanism Using Tubular Membrane Distillation Module. Membranes. 2021; 11(8):560. https://doi.org/10.3390/membranes11080560
Chicago/Turabian StyleAlhathal Alanezi, Adnan, Mohamed Bassyouni, Shereen M. S. Abdel-Hamid, Hassn Safi Ahmed, Mohamed Helmy Abdel-Aziz, Mohamed Shafick Zoromba, and Yasser Elhenawy. 2021. "Theoretical Investigation of Vapor Transport Mechanism Using Tubular Membrane Distillation Module" Membranes 11, no. 8: 560. https://doi.org/10.3390/membranes11080560
APA StyleAlhathal Alanezi, A., Bassyouni, M., Abdel-Hamid, S. M. S., Ahmed, H. S., Abdel-Aziz, M. H., Zoromba, M. S., & Elhenawy, Y. (2021). Theoretical Investigation of Vapor Transport Mechanism Using Tubular Membrane Distillation Module. Membranes, 11(8), 560. https://doi.org/10.3390/membranes11080560











