Silicon Carbide-Gated Nanofluidic Membrane for Active Control of Electrokinetic Ionic Transport
Abstract
:1. Introduction
2. Materials and Methods
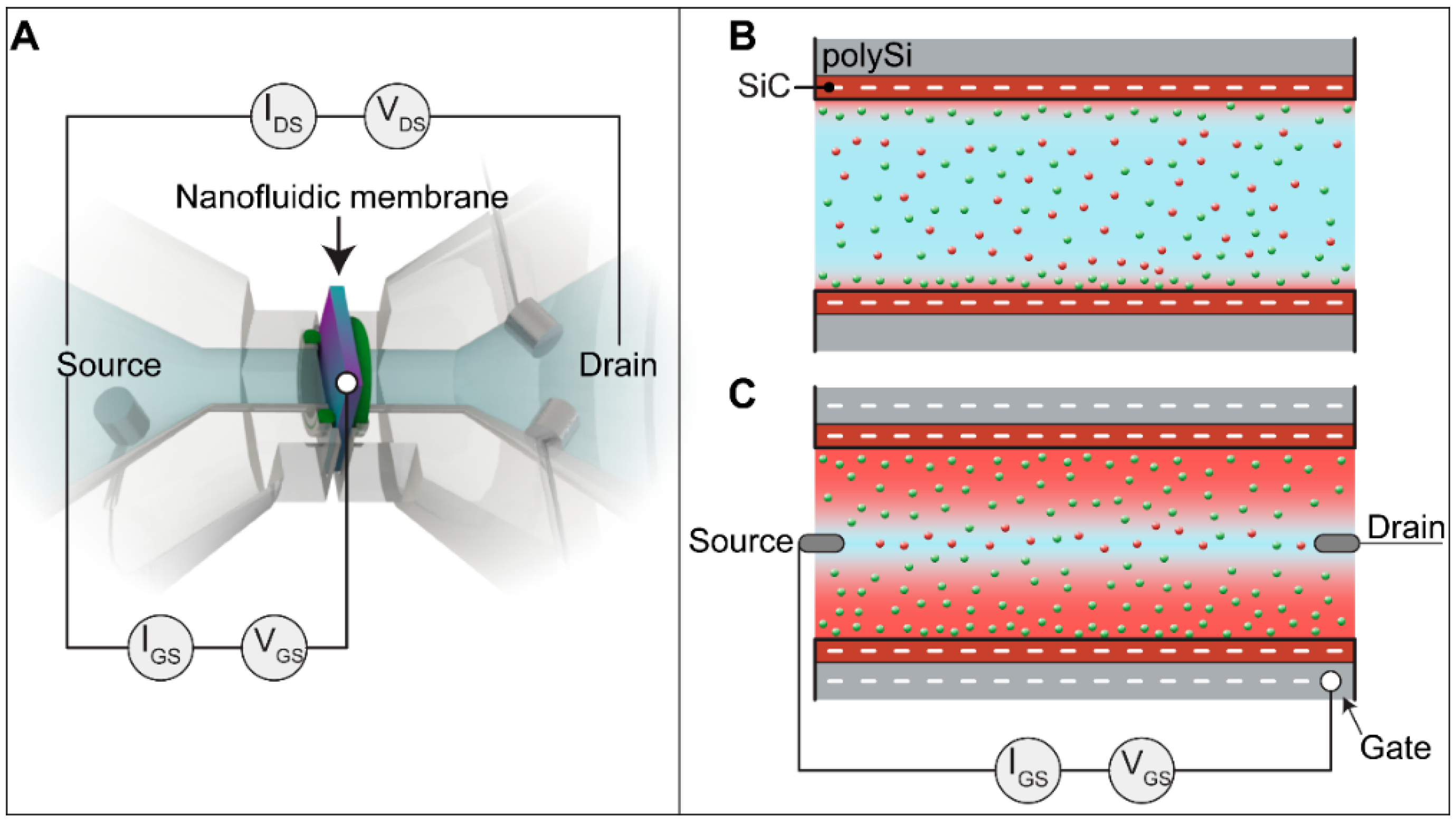
2.1. Nanofluidic Membrane Fabrication
2.2. Blank Fabrication
2.3. Electrode Connection
2.4. Setup for Electrochemical Measurements
2.5. Scanning Electron Microscopy (SEM), Atomic Force Microscopy (AFM), and Ellipsometry
2.6. Conductance, Current-Voltage (I-V) Curves, and Leakage Current
2.7. EIS
3. Results and Discussion
3.1. Nanofluidic Membrane
3.2. Blanks
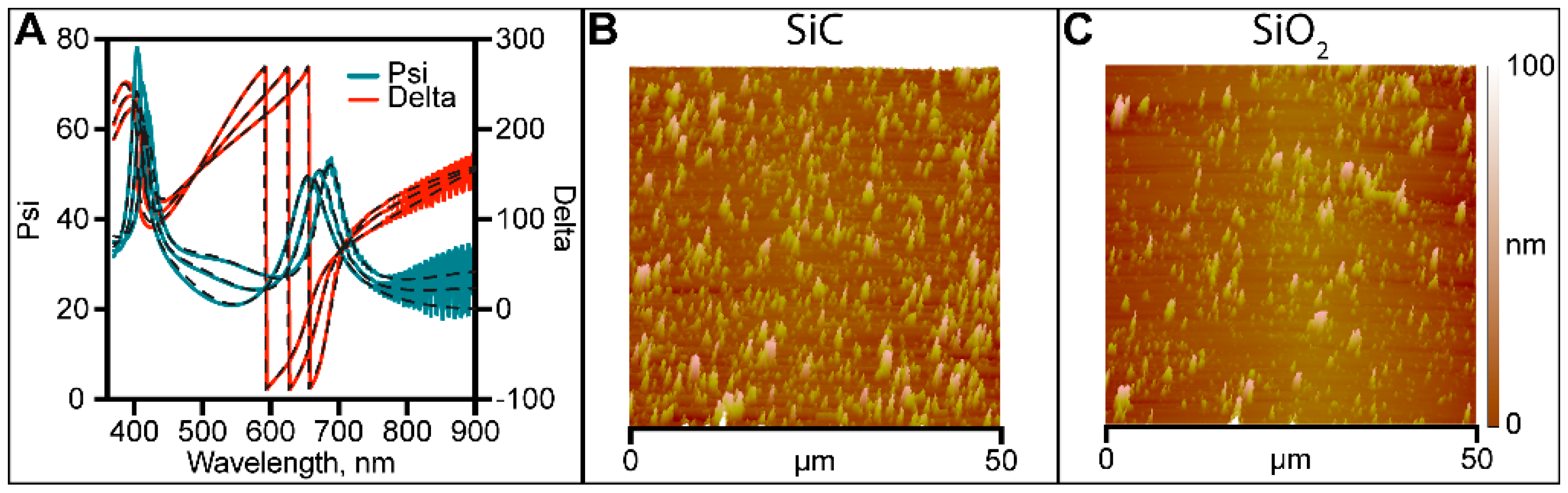
3.2.1. Ellipsometry and AFM
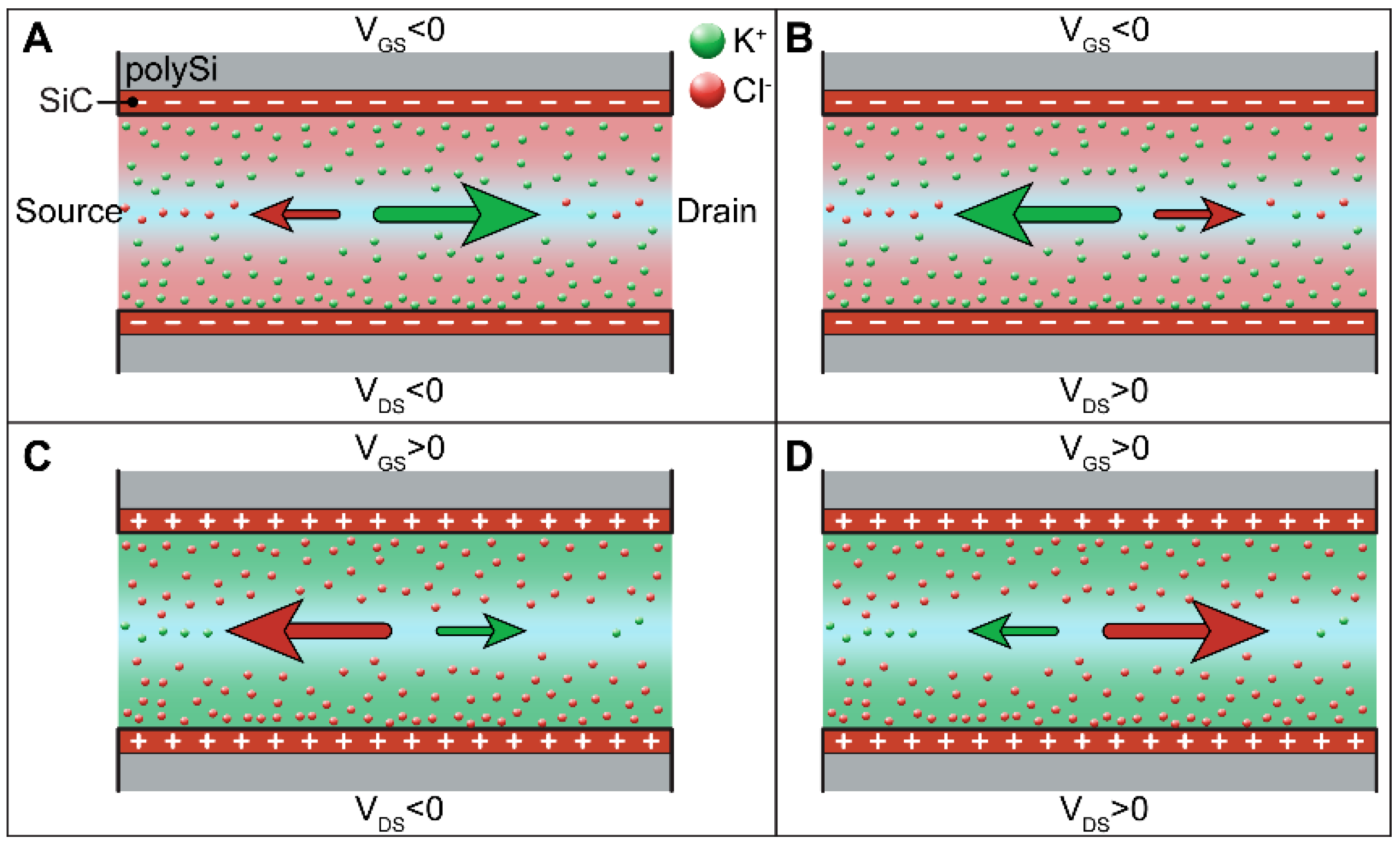
3.3. EDL Modulation: Theoretical Background and Operation Mode
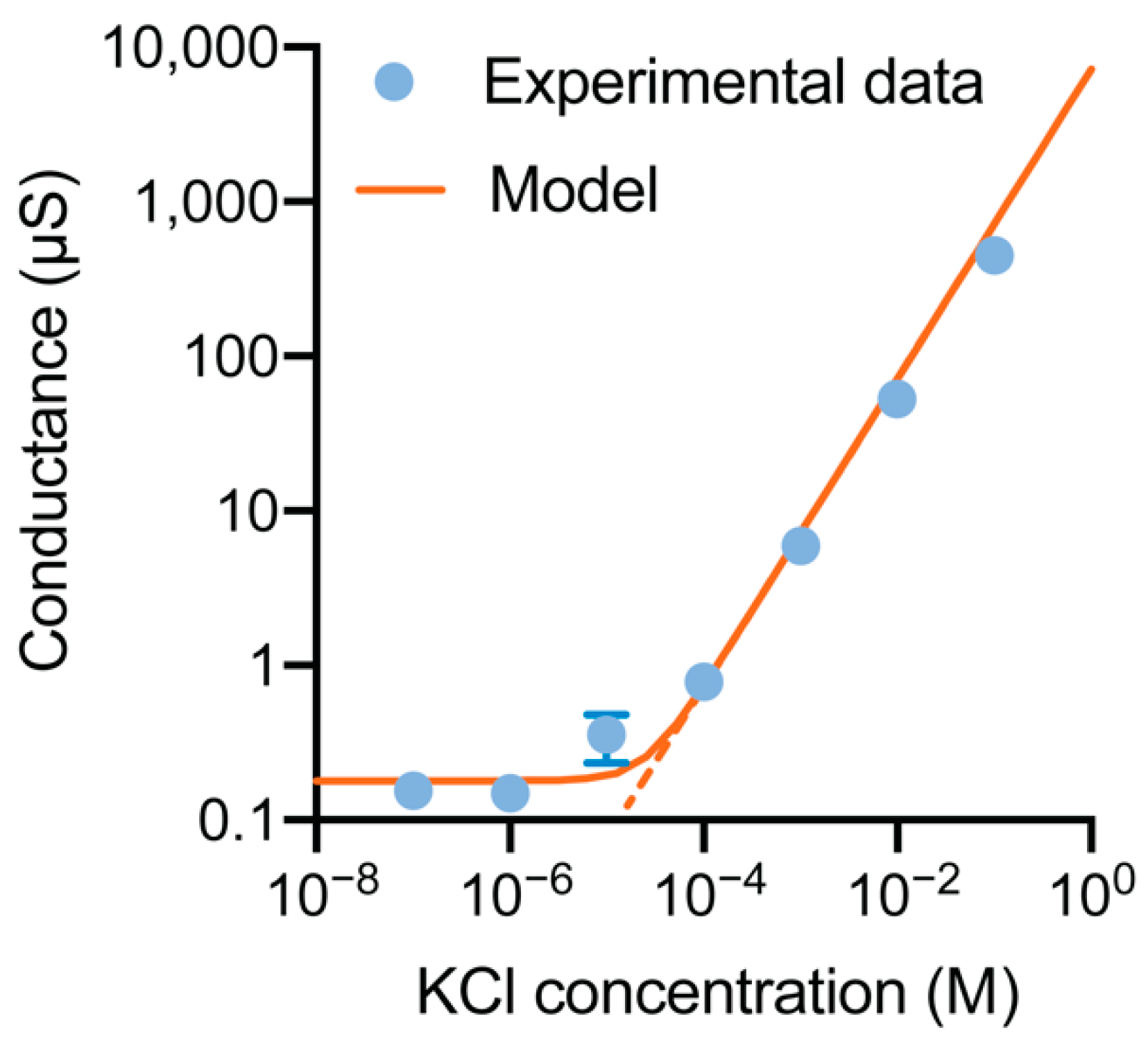
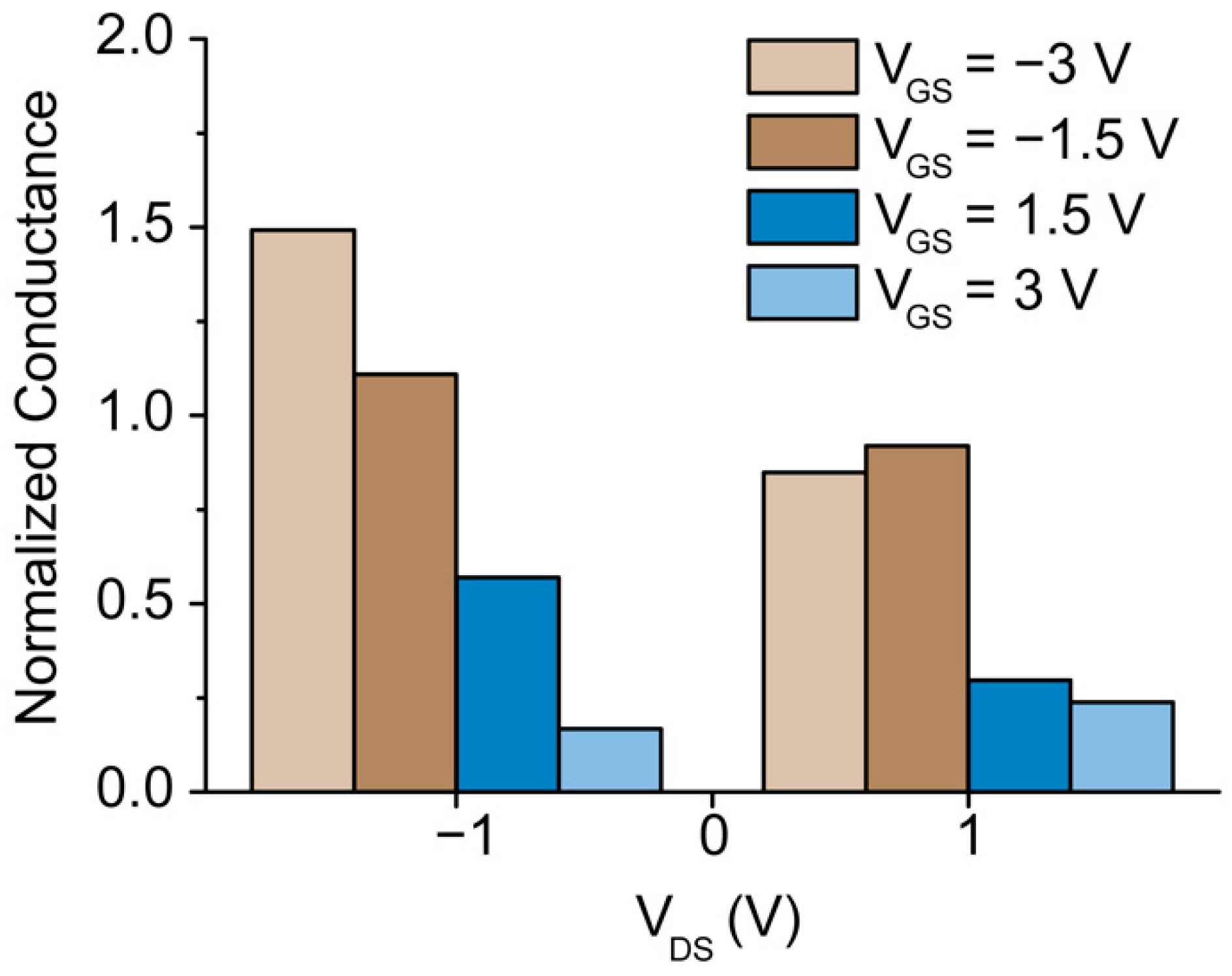
3.4. Ionic Conductance at the Floating Gate
3.5. I-V Characteristics and Leakage Current
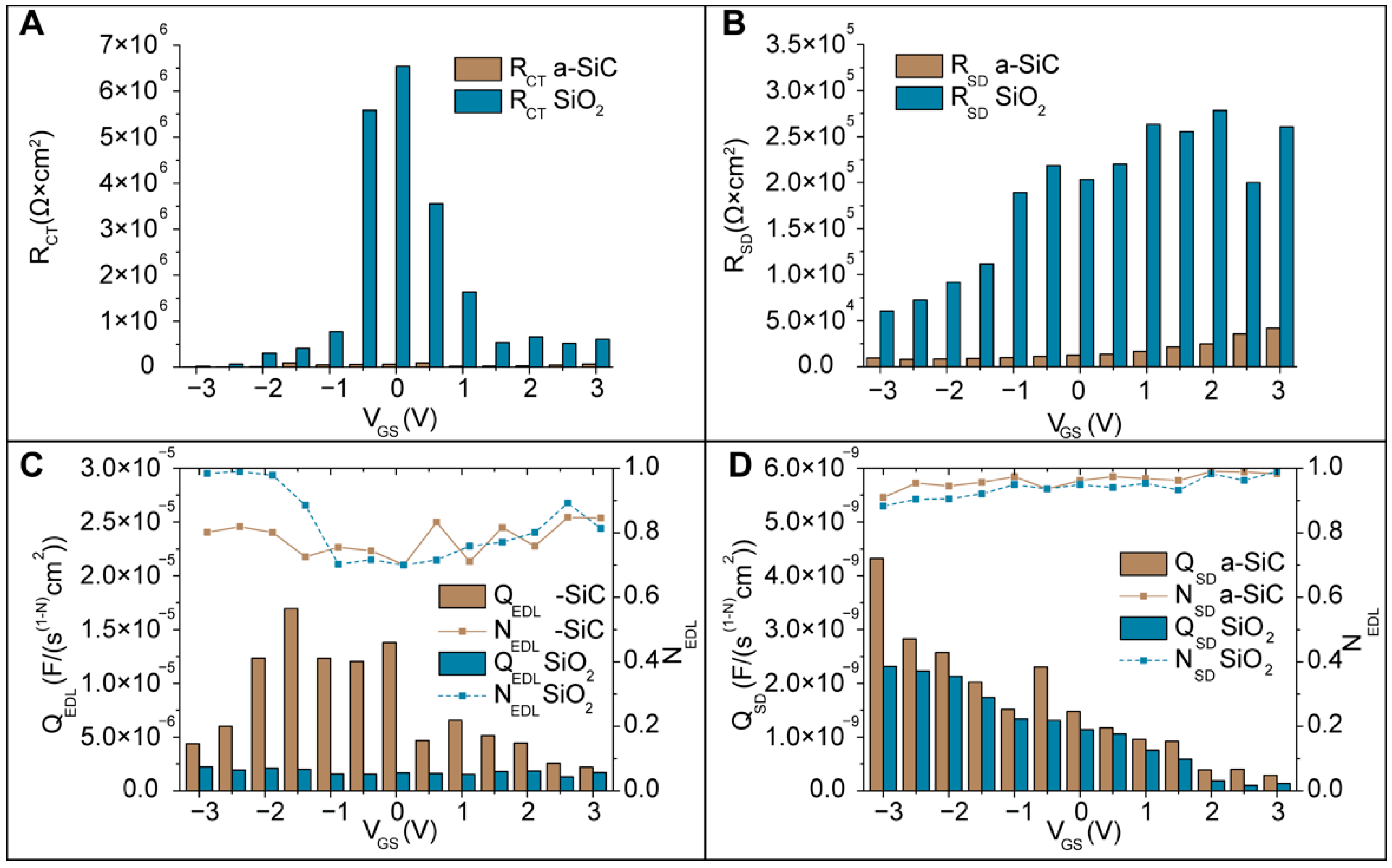
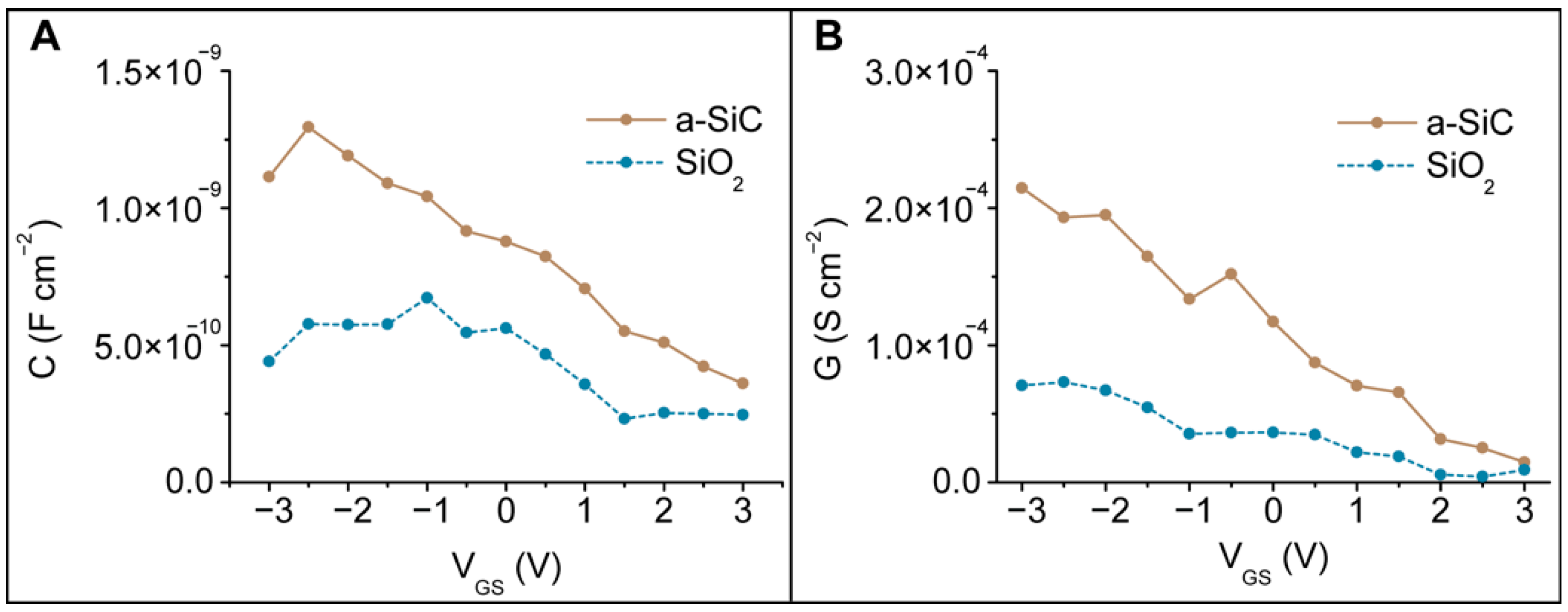
3.6. EIS
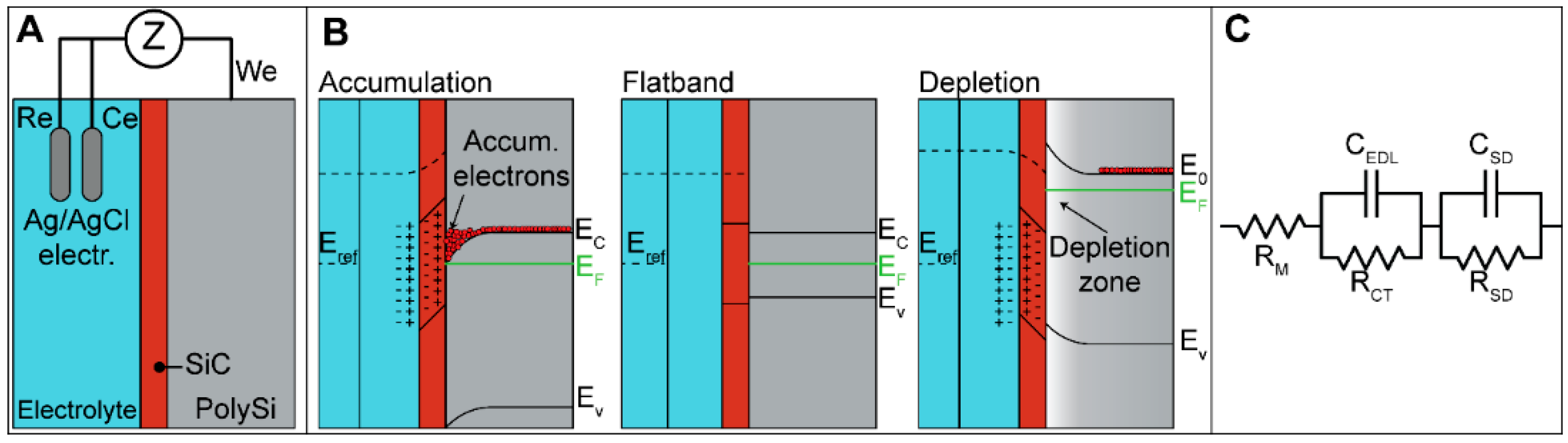
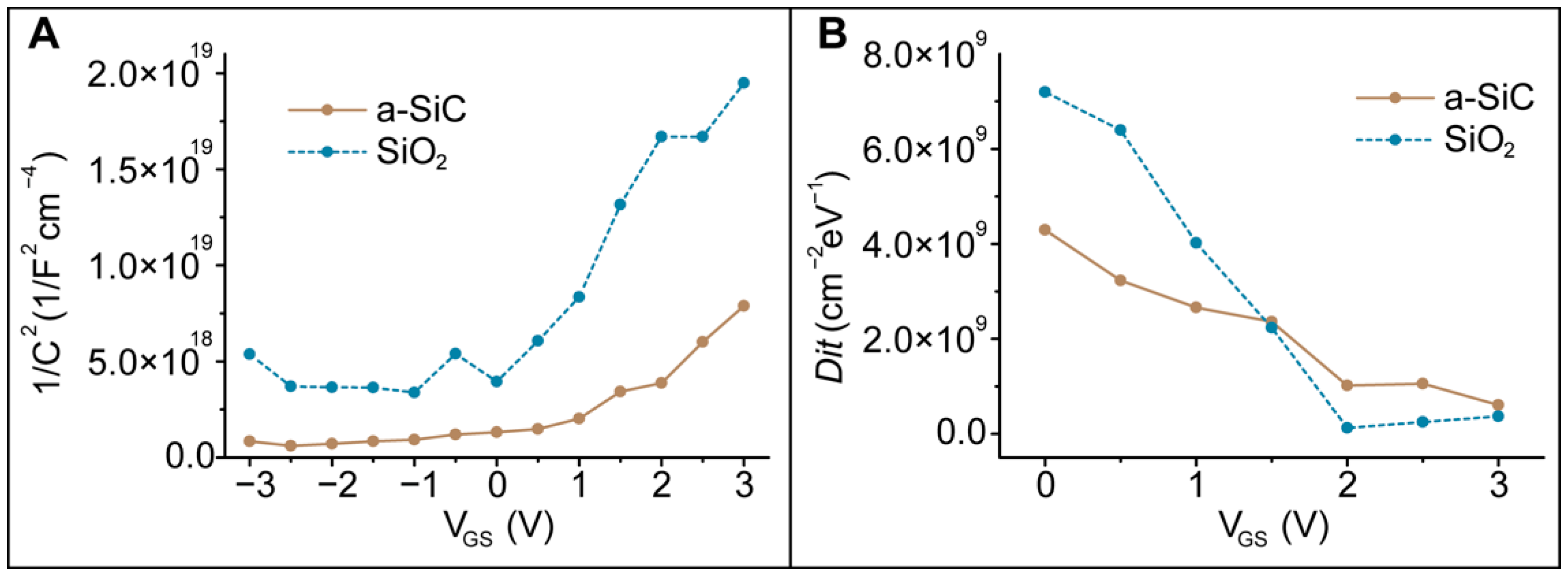
3.6.1. Band Diagram Theory
3.6.2. Schematic Circuit
3.6.3. High Frequency
4. Conclusions and Future Outlook
5. Patents
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prakash, S.; Piruska, A.; Gatimu, E.; Bohn, P.; Sweedler, J.; Shannon, M. Nanofluidics: Systems and Applications. Sens. J. IEEE 2008, 8, 441–450. [Google Scholar] [CrossRef]
- Haywood, D.G.; Saha-Shah, A.; Baker, L.A.; Jacobson, S.C. Fundamental Studies of Nanofluidics: Nanopores, Nanochannels, and Nanopipets. Anal. Chem. 2015, 87, 172–187. [Google Scholar] [CrossRef] [Green Version]
- Yan, Y.; Sheng, Q.; Wang, C.; Xue, J.; Chang, H.-C. Energy Conversion Efficiency of Nanofluidic Batteries: Hydrodynamic Slip and Access Resistance. J. Phys. Chem. C 2013, 117, 8050–8061. [Google Scholar] [CrossRef]
- Daiguji, H.; Yang, P.; Szeri, A.J.; Majumdar, A. Electrochemomechanical Energy Conversion in Nanofluidic Channels. Nano Lett. 2004, 4, 2315–2321. [Google Scholar] [CrossRef]
- van der Heyden, F.H.J.; Bonthuis, D.J.; Stein, D.; Meyer, C.; Dekker, C. Electrokinetic Energy Conversion Efficiency in Nanofluidic Channels. Nano Lett. 2006, 6, 2232–2237. [Google Scholar] [CrossRef] [PubMed]
- van der Heyden, F.H.J.; Bonthuis, D.J.; Stein, D.; Meyer, C.; Dekker, C. Power Generation by Pressure-Driven Transport of Ions in Nanofluidic Channels. Nano Lett. 2007, 7, 1022–1025. [Google Scholar] [CrossRef] [PubMed]
- Karnik, R.; Fan, R.; Yue, M.; Li, D.; Yang, P.; Majumdar, A. Electrostatic Control of Ions and Molecules in Nanofluidic Transistors. Nano Lett. 2005, 5, 943–948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karnik, R.; Castelino, K.; Majumdar, A. Field-Effect Control of Protein Transport in a Nanofluidic Transistor Circuit. Appl. Phys. Lett. 2006, 88, 123114. [Google Scholar] [CrossRef]
- Bruno, G.; Di Trani, N.; Hood, R.L.; Zabre, E.; Filgueira, C.S.; Canavese, G.; Jain, P.; Smith, Z.; Demarchi, D.; Hosali, S.; et al. Unexpected Behaviors in Molecular Transport through Size-Controlled Nanochannels down to the Ultra-Nanoscale. Nat. Commun. 2018, 9, 1682. [Google Scholar] [CrossRef] [Green Version]
- Howorka, S.; Siwy, Z. Nanopore Analytics: Sensing of Single Molecules. Chem. Soc. Rev. 2009, 38, 2360–2384. [Google Scholar] [CrossRef]
- Yeh, L.-H.; Zhang, M.; Joo, S.W.; Qian, S.; Hsu, J.-P. Controlling PH-Regulated Bionanoparticles Translocation through Nanopores with Polyelectrolyte Brushes. Anal. Chem. 2012, 84, 9615–9622. [Google Scholar] [CrossRef]
- Li, W.; Bell, N.A.W.; Hernández-Ainsa, S.; Thacker, V.V.; Thackray, A.M.; Bujdoso, R.; Keyser, U.F. Single Protein Molecule Detection by Glass Nanopores. ACS Nano 2013, 7, 4129–4134. [Google Scholar] [CrossRef] [PubMed]
- Pons-Faudoa, F.P.; Sizovs, A.; Shelton, K.A.; Momin, Z.; Niles, J.A.; Bushman, L.R.; Xu, J.; Chua, C.Y.X.; Nichols, J.E.; Demaria, S.; et al. Preventive Efficacy of a Tenofovir Alafenamide Fumarate Nanofluidic Implant in SHIV-Challenged Nonhuman Primates. Adv. Ther. 2021, 4, 2000163. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.-C.; Viswanath, D.I.; Pesaresi, F.; Xu, Y.; Zhang, L.; Di Trani, N.; Paez-Mayorga, J.; Hernandez, N.; Wang, Y.; Erm, D.R.; et al. Potentiating Antitumor Efficacy through Radiation and Sustained Intratumoral Delivery of Anti-CD40 and Anti-PDL1. Int. J. Radiat. Oncol. Biol. Phys. 2021, 110, 492–506. [Google Scholar] [CrossRef] [PubMed]
- Di Trani, N.; Silvestri, A.; Sizovs, A.; Wang, Y.; Erm, D.R.; Demarchi, D.; Liu, X.; Grattoni, A. Electrostatically Gated Nanofluidic Membrane for Ultra-Low Power Controlled Drug Delivery. Lab. Chip 2020, 20, 1562–1576. [Google Scholar] [CrossRef]
- Trani, N.D.; Silvestri, A.; Bruno, G.; Geninatti, T.; Chua, C.Y.X.; Gilbert, A.; Rizzo, G.; Filgueira, C.S.; Demarchi, D.; Grattoni, A. Remotely Controlled Nanofluidic Implantable Platform for Tunable Drug Delivery. Lab. Chip 2019, 19, 2192–2204. [Google Scholar] [CrossRef] [PubMed]
- Bruno, G.; Canavese, G.; Liu, X.; Filgueira, C.S.; Sacco, A.; Demarchi, D.; Ferrari, M.; Grattoni, A. The Active Modulation of Drug Release by an Ionic Field Effect Transistor for an Ultra-Low Power Implantable Nanofluidic System. Nanoscale 2016, 8, 18718–18725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dekker, C. Solid-State Nanopores. Nat. Nanotechnol. 2007, 2, 209–215. [Google Scholar] [CrossRef]
- Li, J.; Stein, D.; McMullan, C.; Branton, D.; Aziz, M.J.; Golovchenko, J.A. Ion-Beam Sculpting at Nanometre Length Scales. Nature 2001, 412, 166–169. [Google Scholar] [CrossRef] [Green Version]
- Storm, A.J.; Chen, J.H.; Ling, X.S.; Zandbergen, H.W.; Dekker, C. Fabrication of Solid-State Nanopores with Single-Nanometre Precision. Nat. Mater. 2003, 2, 537–540. [Google Scholar] [CrossRef]
- Schoch, R.B.; Renaud, P. Ion Transport through Nanoslits Dominated by the Effective Surface Charge. Appl. Phys. Lett. 2005, 86, 253111. [Google Scholar] [CrossRef]
- Jo, K.; Dhingra, D.M.; Odijk, T.; de Pablo, J.J.; Graham, M.D.; Runnheim, R.; Forrest, D.; Schwartz, D.C. A Single-Molecule Barcoding System Using Nanoslits for DNA Analysis. Proc. Natl. Acad. Sci. USA 2007, 104, 2673–2678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Odijk, T. Scaling Theory of DNA Confined in Nanochannels and Nanoslits. Phys. Rev. E 2008, 77, 060901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tonucci, R.J.; Justus, B.L.; Campillo, A.J.; Ford, C.E. Nanochannel Array Glass. Science 1992, 258, 783–785. [Google Scholar] [CrossRef]
- Pu, Q.; Yun, J.; Temkin, H.; Liu, S. Ion-Enrichment and Ion-Depletion Effect of Nanochannel Structures. Nano Lett. 2004, 4, 1099–1103. [Google Scholar] [CrossRef]
- Boukany, P.E.; Morss, A.; Liao, W.; Henslee, B.; Jung, H.; Zhang, X.; Yu, B.; Wang, X.; Wu, Y.; Li, L.; et al. Nanochannel Electroporation Delivers Precise Amounts of Biomolecules into Living Cells. Nat. Nanotechnol. 2011, 6, 747–754. [Google Scholar] [CrossRef]
- Ballerini, A.; Chua, C.Y.X.; Rhudy, J.; Susnjar, A.; Trani, N.D.; Jain, P.R.; Laue, G.; Lubicka, D.; Shirazi-Fard, Y.; Ferrari, M.; et al. Counteracting Muscle Atrophy on Earth and in Space via Nanofluidics Delivery of Formoterol. Adv. Ther. 2020, 3, 2000014. [Google Scholar] [CrossRef]
- Pons-Faudoa, F.P.; Trani, N.D.; Sizovs, A.; Shelton, K.A.; Momin, Z.; Bushman, L.R.; Xu, J.; Lewis, D.E.; Demaria, S.; Hawkins, T.; et al. Viral Load Reduction in SHIV-Positive Nonhuman Primates via Long-Acting Subcutaneous Tenofovir Alafenamide Fumarate Release from a Nanofluidic Implant. Pharmaceutics 2020, 12, 981. [Google Scholar] [CrossRef]
- Ferrati, S.; Nicolov, E.; Bansal, S.; Zabre, E.; Geninatti, T.; Ziemys, A.; Hudson, L.; Ferrari, M.; Goodall, R.; Khera, M.; et al. Delivering Enhanced Testosterone Replacement Therapy through Nanochannels. Adv. Healthc. Mater. 2015, 4, 446–451. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Xiong, T.; Yu, P.; Fei, J.; Mao, L. Synaptic Iontronic Devices for Brain-Mimicking Functions: Fundamentals and Applications. ACS Appl. Bio Mater. 2021, 4, 71–84. [Google Scholar] [CrossRef]
- Nishizawa, M.; Menon, V.P.; Martin, C.R. Metal Nanotubule Membranes with Electrochemically Switchable Ion-Transport Selectivity. Science 1995, 268, 700–702. [Google Scholar] [CrossRef] [Green Version]
- Gracheva, M.E.; Leburton, J.-P. Simulation of Electrically Tunable Semiconductor Nanopores for Ion Current/Single Bio-Molecule Manipulation. J. Comput. Electron. 2008, 7, 6–9. [Google Scholar] [CrossRef]
- Gracheva, M.E.; Xiong, A.; Aksimentiev, A.; Schulten, K.; Timp, G.; Leburton, J.-P. Simulation of the Electric Response of DNA Translocation through a Semiconductor Nanopore–Capacitor. Nanotechnology 2006, 17, 622–633. [Google Scholar] [CrossRef] [Green Version]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of Biomolecules, Single Cells and Single Nanoparticles in Fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bruno, G.; Geninatti, T.; Hood, R.L.; Fine, D.; Scorrano, G.; Schmulen, J.; Hosali, S.; Ferrari, M.; Grattoni, A. Leveraging Electrokinetics for the Active Control of Dendritic Fullerene-1 Release across a Nanochannel Membrane. Nanoscale 2015, 7, 5240–5248. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Ozalp, E.I.; Darwish, M.; Weldon, J.A. Electrically Gated Nanoporous Membranes for Smart Molecular Flow Control. Nanoscale 2018, 10, 20740–20747. [Google Scholar] [CrossRef]
- Plecis, A.; Schoch, R.B.; Renaud, P. Ionic Transport Phenomena in Nanofluidics: Experimental and Theoretical Study of the Exclusion-Enrichment Effect on a Chip. Nano Lett. 2005, 5, 1147–1155. [Google Scholar] [CrossRef] [PubMed]
- abu-Rjal, R.; Chinaryan, V.; Bazant, M.Z.; Rubinstein, I.; Zaltzman, B. Effect of Concentration Polarization on Permselectivity. Phys. Rev. E 2014, 89, 012302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pal Singh, K.; Kumari, K.; Kumar, M. Field-Effect Control of Electrokinetic Ion Transport in a Nanofluidic Channel. J. Appl. Phys. 2011, 110, 084301. [Google Scholar] [CrossRef]
- Saddow, S.E. Silicon Carbide Biotechnology: A Biocompatible Semiconductor for Advanced Biomedical Devices and Applications; Elsevier: Amsterdam, The Netherlands, 2012; ISBN 978-0-12-385906-8. [Google Scholar]
- Oliveros, A.; Guiseppi-Elie, A.; Saddow, S.E. Silicon Carbide: A Versatile Material for Biosensor Applications. Biomed. Microdevices 2013, 15, 353–368. [Google Scholar] [CrossRef]
- Iliescu, C.; Poenar, D.P. PECVD Amorphous Silicon Carbide (α-SiC) Layers for MEMS Applications. In Physics and Technology of Silicon Carbide Devices; Hijikata, Y., Ed.; InTech: London, UK, 2012; ISBN 978-953-51-0917-4. [Google Scholar]
- Iliescu, C.; Chen, B.; Poenar, D.P.; Lee, Y.Y. PECVD Amorphous Silicon Carbide Membranes for Cell Culturing. Sens. Actuators B Chem. 2008, 129, 404–411. [Google Scholar] [CrossRef]
- Knaack, G.L.; McHail, D.G.; Borda, G.; Koo, B.; Peixoto, N.; Cogan, S.F.; Dumas, T.C.; Pancrazio, J.J. In Vivo Characterization of Amorphous Silicon Carbide as a Biomaterial for Chronic Neural Interfaces. Front. Neurosci. 2016, 10, 301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Trani, N.; Silvestri, A.; Wang, Y.; Demarchi, D.; Liu, X.; Grattoni, A. Silicon Nanofluidic Membrane for Electrostatic Control of Drugs and Analytes Elution. Pharmaceutics 2020, 12, 679. [Google Scholar] [CrossRef]
- Avram, M.; Avram, A.; Bragaru, A.; Chen, B.; Poenar, D.P.; Iliescu, C. Low Stress PECVD Amorphous Silicon Carbide for MEMS Applications. In Proceedings of the CAS 2010 Proceedings (International Semiconductor Conference), Sinaia, Romania, 11–13 October 2010; Volume 01, pp. 239–242. [Google Scholar]
- Scorrano, G.; Bruno, G.; Di Trani, N.; Ferrari, M.; Pimpinelli, A.; Grattoni, A. Gas Flow at the Ultra-Nanoscale: Universal Predictive Model and Validation in Nanochannels of Ångstrom-Level Resolution. ACS Appl. Mater. Interfaces 2018, 10, 32233–32238. [Google Scholar] [CrossRef] [PubMed]
- Ferrati, S.; Fine, D.; You, J.; De Rosa, E.; Hudson, L.; Zabre, E.; Hosali, S.; Zhang, L.; Hickman, C.; Sunder Bansal, S.; et al. Leveraging Nanochannels for Universal, Zero-Order Drug Delivery in Vivo. J. Control. Release Off. J. Control. Release Soc. 2013, 172, 1011–1019. [Google Scholar] [CrossRef]
- Di Trani, N.; Jain, P.; Chua, C.Y.X.; Ho, J.S.; Bruno, G.; Susnjar, A.; Pons-Faudoa, F.P.; Sizovs, A.; Hood, R.L.; Smith, Z.W.; et al. Nanofluidic Microsystem for Sustained Intraocular Delivery of Therapeutics. Nanomed. Nanotechnol. Biol. Med. 2019, 16, 1–9. [Google Scholar] [CrossRef]
- Fine, D.; Grattoni, A.; Hosali, S.; Ziemys, A.; Rosa, E.D.; Gill, J.; Medema, R.; Hudson, L.; Kojic, M.; Milosevic, M.; et al. A Robust Nanofluidic Membrane with Tunable Zero-Order Release for Implantable Dose Specific Drug Delivery. Lab. Chip 2010, 10, 3074–3083. [Google Scholar] [CrossRef]
- Fine, D.; Grattoni, A.; Zabre, E.; Hussein, F.; Ferrari, M.; Liu, X. A Low-Voltage Electrokinetic Nanochannel Drug Delivery System. Lab. Chip 2011, 11, 2526–2534. [Google Scholar] [CrossRef]
- Di Trani, N.; Pimpinelli, A.; Grattoni, A. Finite-Size Charged Species Diffusion and PH Change in Nanochannels. ACS Appl. Mater. Interfaces 2020, 12, 12246–12255. [Google Scholar] [CrossRef] [PubMed]
- Grattoni, A.; Fine, D.; Zabre, E.; Ziemys, A.; Gill, J.; Mackeyev, Y.; Cheney, M.A.; Danila, D.C.; Hosali, S.; Wilson, L.J.; et al. Gated and Near-Surface Diffusion of Charged Fullerenes in Nanochannels. ACS Nano 2011, 5, 9382–9391. [Google Scholar] [CrossRef]
- Jin, X.; Aluru, N.R. Gated Transport in Nanofluidic Devices. Microfluid. Nanofluidics 2011, 11, 297–306. [Google Scholar] [CrossRef]
- Grosjean, A.; Rezrazi, M.; Tachez, M. Study of the Surface Charge of Silicon Carbide (SIC) Particles for Electroless Composite Deposits: Nickel-SiC. Surf. Coat. Technol. 1997, 96, 300–304. [Google Scholar] [CrossRef]
- Jiang, Z.; Stein, D. Electrofluidic Gating of a Chemically Reactive Surface. Langmuir 2010, 26, 8161–8173. [Google Scholar] [CrossRef] [PubMed]
- Fan, R.; Yue, M.; Karnik, R.; Majumdar, A.; Yang, P. Polarity Switching and Transient Responses in Single Nanotube Nanofluidic Transistors. Phys. Rev. Lett. 2005, 95, 086607. [Google Scholar] [CrossRef]
- Fan, R.; Huh, S.; Yan, R.; Arnold, J.; Yang, P. Gated Proton Transport in Aligned Mesoporous Silica Films. Nat. Mater. 2008, 7, 303–307. [Google Scholar] [CrossRef]
- Schoch, R.B.; Han, J.; Renaud, P. Transport Phenomena in Nanofluidics. Rev. Mod. Phys. 2008, 80, 839–883. [Google Scholar] [CrossRef] [Green Version]
- Zhu, F.; Hu, J.; Matulionis, I.; Deutsch, T.; Gaillard, N.; Kunrath, A.; Miller, E.; Madan, A. Amorphous Silicon Carbide Photoelectrode for Hydrogen Production Directly from Water Using Sunlight. Philos. Mag. 2009, 89, 2723–2739. [Google Scholar] [CrossRef]
- Matulionis, I.; Zhu, F.; Hu, J.; Deutsch, T.; Kunrath, A.; Miller, E.; Marsen, B.; Madan, A. Development of a Corrosion-Resistant Amorphous Silicon Carbide Photoelectrode for Solar-to-Hydrogen Photovoltaic/Photoelectrochemical Devices. Proc. SPIE Int. Soc. Opt. Eng. 2008, 7044, 70440D. [Google Scholar] [CrossRef]
- Magafas, L.; Georgoulas, N.; Thanailakis, A. Electrical Properties of A-SiC/c-Si(p) Heterojunctions. Semicond. Sci. Technol. 1992, 7, 1363–1368. [Google Scholar] [CrossRef]
- Meng, A.C.; Tang, K.; Braun, M.R.; Zhang, L.; McIntyre, P.C. Electrochemical Impedance Spectroscopy for Quantitative Interface State Characterization of Planar and Nanostructured Semiconductor-Dielectric Interfaces. Nanotechnology 2017, 28, 415704. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicollian, E.H.; Brews, J.R. MOS (Metal Oxide Semiconductor) Physics and Technology; Wiley–Blackwell: New York, NY, USA, 1982; ISBN 978-0-471-08500-3. [Google Scholar]
- Alexander, C.; Tribollet, B.; Orazem, M. Contribution of Surface Distributions to Constant-Phase-Element (CPE) Behavior: 1. Influence of Roughness. Electrochim. Acta 2015, 173. [Google Scholar] [CrossRef]
- Vieira, D.; Fernandes, P.R. Surface Roughness Influence on CPE Parameters in Electrolytic Cells. Int. J. Electrochem. Sci. 2016, 11, 7775–7784. [Google Scholar] [CrossRef]
- Córdoba-Torres, P.; Mesquita, T.; Devos, O.; Tribollet, B.; Roche, V.; Nogueira, R. On the Intrinsic Coupling between Constant-Phase Element Parameters α and Q in Electrochemical Impedance Spectroscopy. Electrochim. Acta 2012, 72, 172–178. [Google Scholar] [CrossRef]
- Córdoba-Torres, P.; Mesquita, T.; Nogueira, R. Relationship between the Origin of Constant-Phase Element Behavior in Electrochemical Impedance Spectroscopy and Electrode Surface Structure. J. Phys. Chem. C 2015, 119, 150218064838009. [Google Scholar] [CrossRef]
- Ovshinsky, S.R. The Role of Free Radicals in the Formation of Amorphous Thin Films. In Disordered Materials: Science and Technology; Adler, D., Schwartz, B.B., Silver, M., Eds.; Institute for Amorphous Studies Series; Springer: Boston, MA, USA, 1991; pp. 114–119. ISBN 978-1-4684-8745-9. [Google Scholar]
- Viščor, P.; Olsen, N.B. Frequency and Time Response in Relaxation Time Semiconductors. J. Non-Cryst. Solids 1987, 90, 25–28. [Google Scholar] [CrossRef]
- Málek, J.; Shánělová, J. Structural Relaxation in Amorphous Materials. In Properties and Applications of Amorphous Materials; Thorpe, M.F., Tichý, L., Eds.; NATO Science Series; Springer: Dordrecht, The Netherlands, 2001; pp. 35–44. ISBN 978-94-010-0914-0. [Google Scholar]
- Orton, J. Polycrystalline and Amorphous Semiconductors; Oxford University Press: Oxford, UK, 2008; ISBN 978-0-19-171297-5. [Google Scholar]
- Chen, H.; Yuan, Y.; Yu, B.; Ahn, J.; McIntyre, P.C.; Asbeck, P.M.; Rodwell, M.J.W.; Taur, Y. Interface-State Modeling of $\hboxAl_2\hboxO_3$ –InGaAs MOS from Depletion to Inversion. IEEE Trans. Electron Devices 2012, 59, 2383–2389. [Google Scholar] [CrossRef]
- Nicollian, E.H.; Goetzberger, A. The Si-SiO2 Interface—Electrical Properties as Determined by the Metal-Insulator-Silicon Conductance Technique. Bell Syst. Tech. J. 1967, 46, 1055–1133. [Google Scholar] [CrossRef]
- Schroder, D.K. Semiconductor Material and Device Characterization; John Wiley & Sons: Hoboken, NJ, USA, 2015; ISBN 978-0-471-73906-7. [Google Scholar]
- Juan, H.L. Structural and Electrical Characterisations of Amorphous Silicon Carbide Films. Master’s Thesis, National University of Singapore, Singapore, 17 January 2005. [Google Scholar]
- Munakata, C.; Nishimatsu, S. Analysis of ac surface photovoltages in a depleted oxidized p-type silicon wafer. Jpn. J. Appl. Phys. 1986, 25, 807. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silvestri, A.; Di Trani, N.; Canavese, G.; Motto Ros, P.; Iannucci, L.; Grassini, S.; Wang, Y.; Liu, X.; Demarchi, D.; Grattoni, A. Silicon Carbide-Gated Nanofluidic Membrane for Active Control of Electrokinetic Ionic Transport. Membranes 2021, 11, 535. https://doi.org/10.3390/membranes11070535
Silvestri A, Di Trani N, Canavese G, Motto Ros P, Iannucci L, Grassini S, Wang Y, Liu X, Demarchi D, Grattoni A. Silicon Carbide-Gated Nanofluidic Membrane for Active Control of Electrokinetic Ionic Transport. Membranes. 2021; 11(7):535. https://doi.org/10.3390/membranes11070535
Chicago/Turabian StyleSilvestri, Antonia, Nicola Di Trani, Giancarlo Canavese, Paolo Motto Ros, Leonardo Iannucci, Sabrina Grassini, Yu Wang, Xuewu Liu, Danilo Demarchi, and Alessandro Grattoni. 2021. "Silicon Carbide-Gated Nanofluidic Membrane for Active Control of Electrokinetic Ionic Transport" Membranes 11, no. 7: 535. https://doi.org/10.3390/membranes11070535
APA StyleSilvestri, A., Di Trani, N., Canavese, G., Motto Ros, P., Iannucci, L., Grassini, S., Wang, Y., Liu, X., Demarchi, D., & Grattoni, A. (2021). Silicon Carbide-Gated Nanofluidic Membrane for Active Control of Electrokinetic Ionic Transport. Membranes, 11(7), 535. https://doi.org/10.3390/membranes11070535







