Exploring the Conformational Changes Induced by Nanosecond Pulsed Electric Fields on the Voltage Sensing Domain of a Ca2+ Channel
Abstract
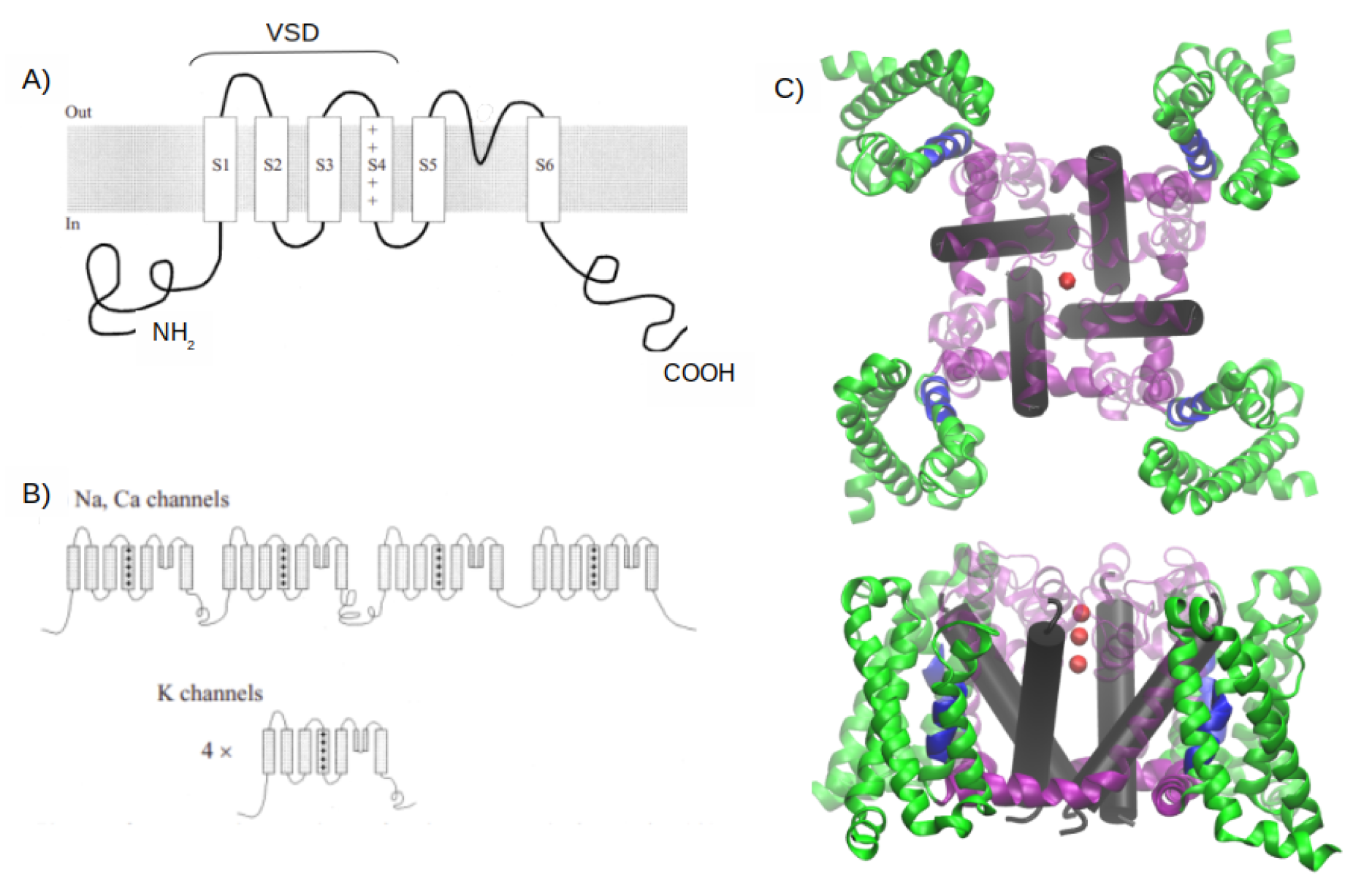
1. Introduction
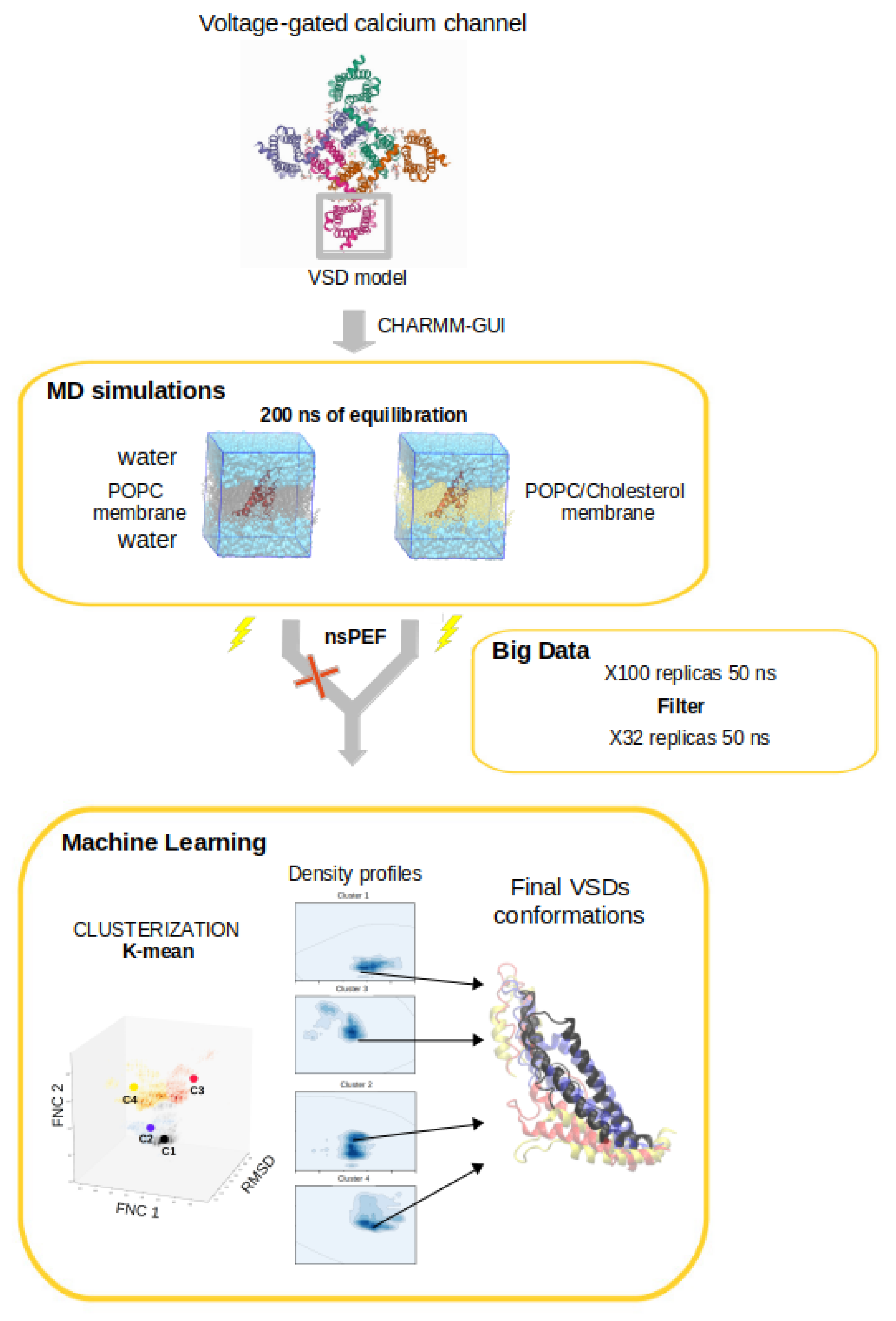
2. MD Simulations Methods
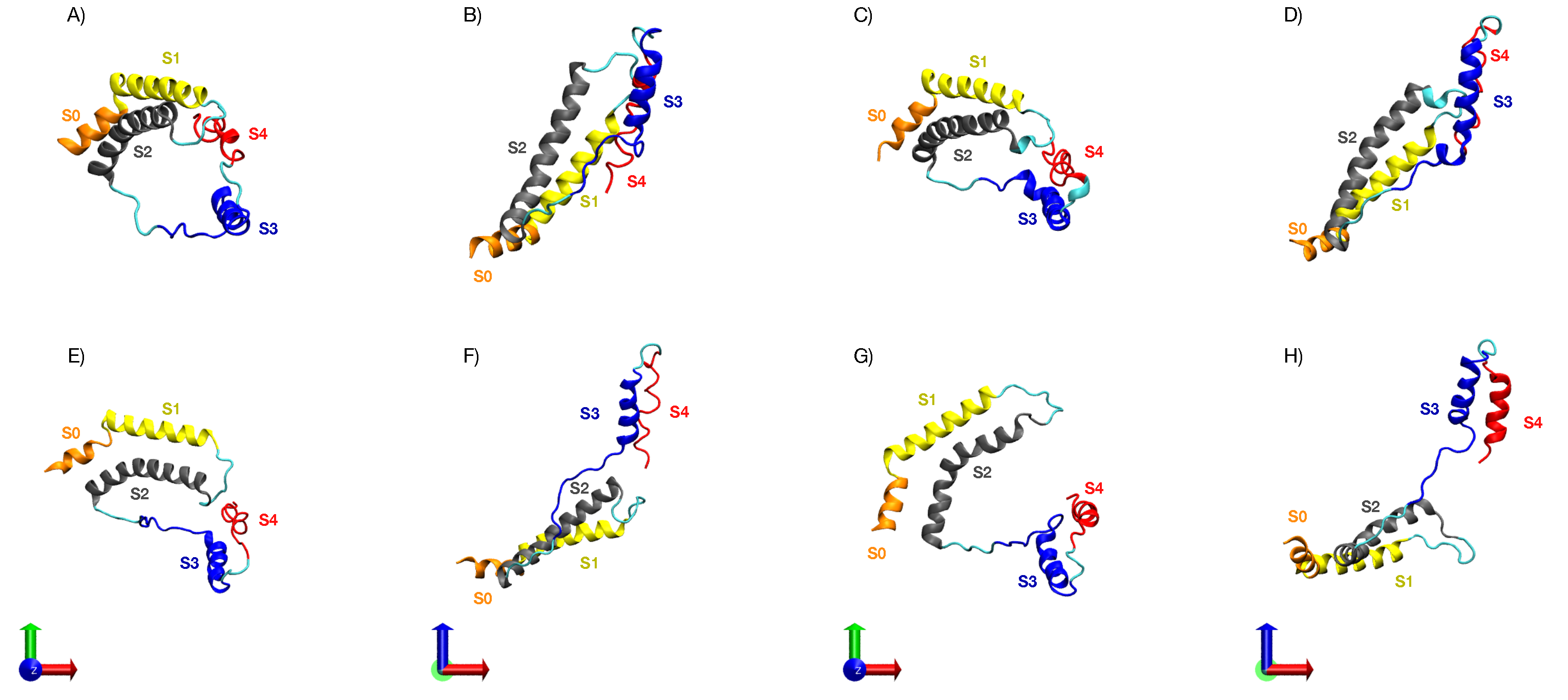
3. Simulation Results
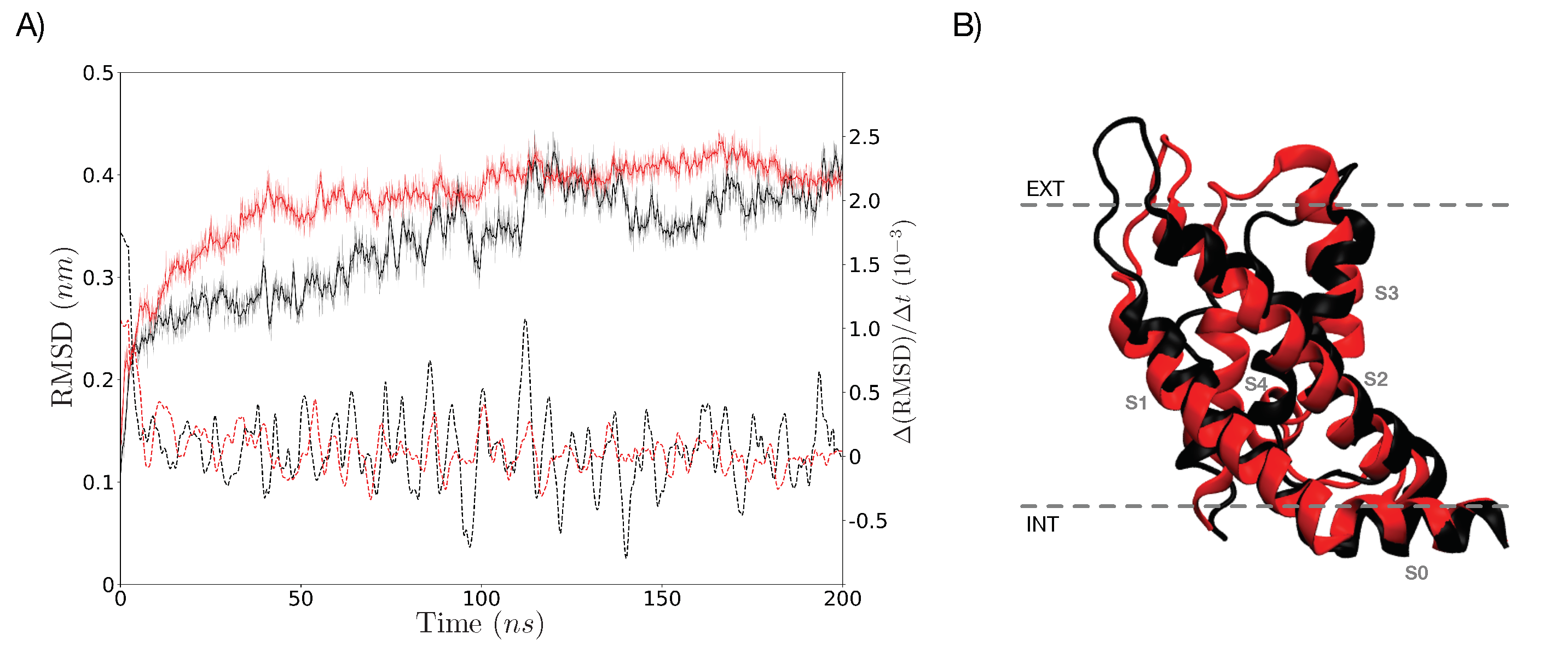
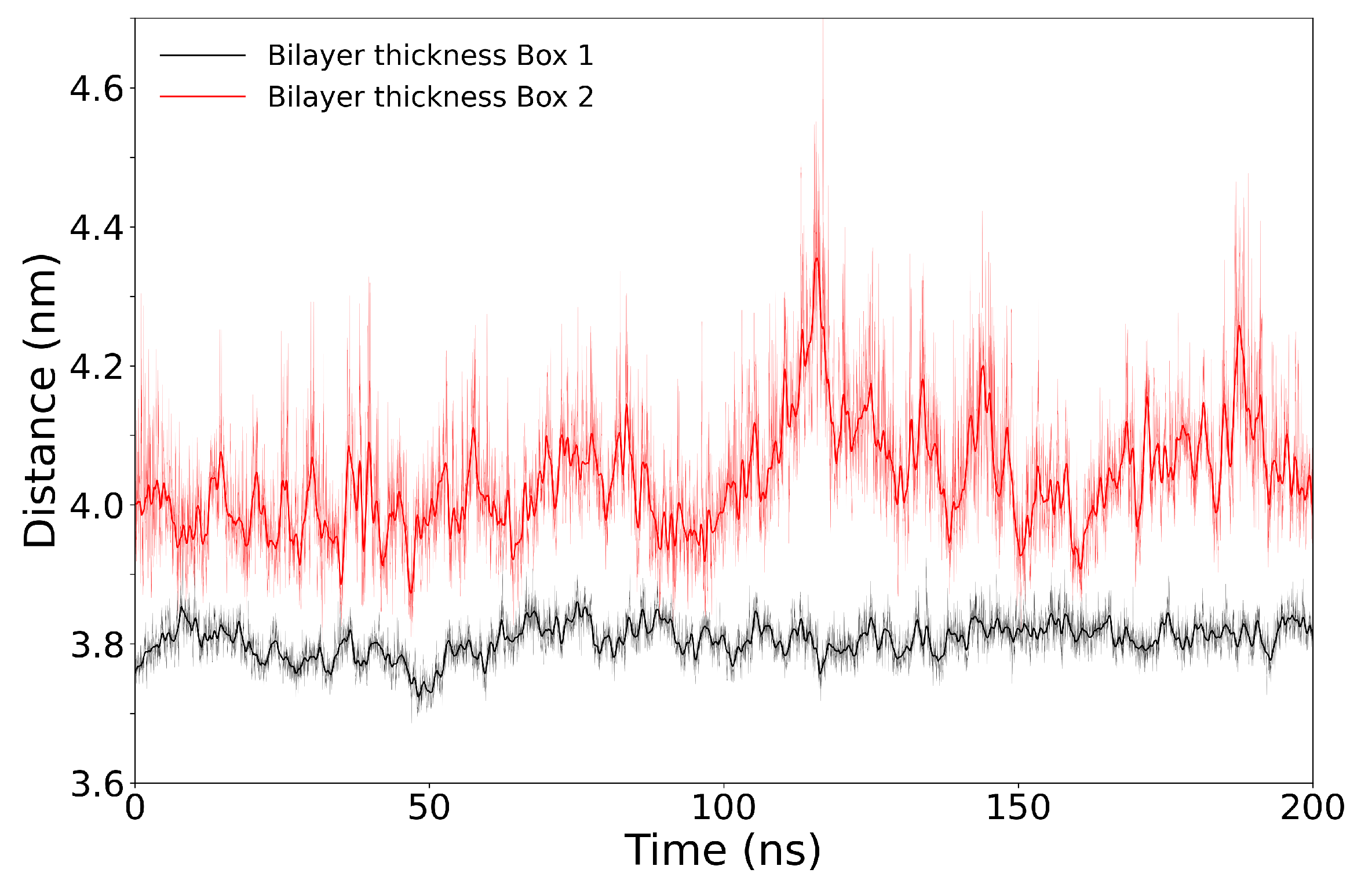
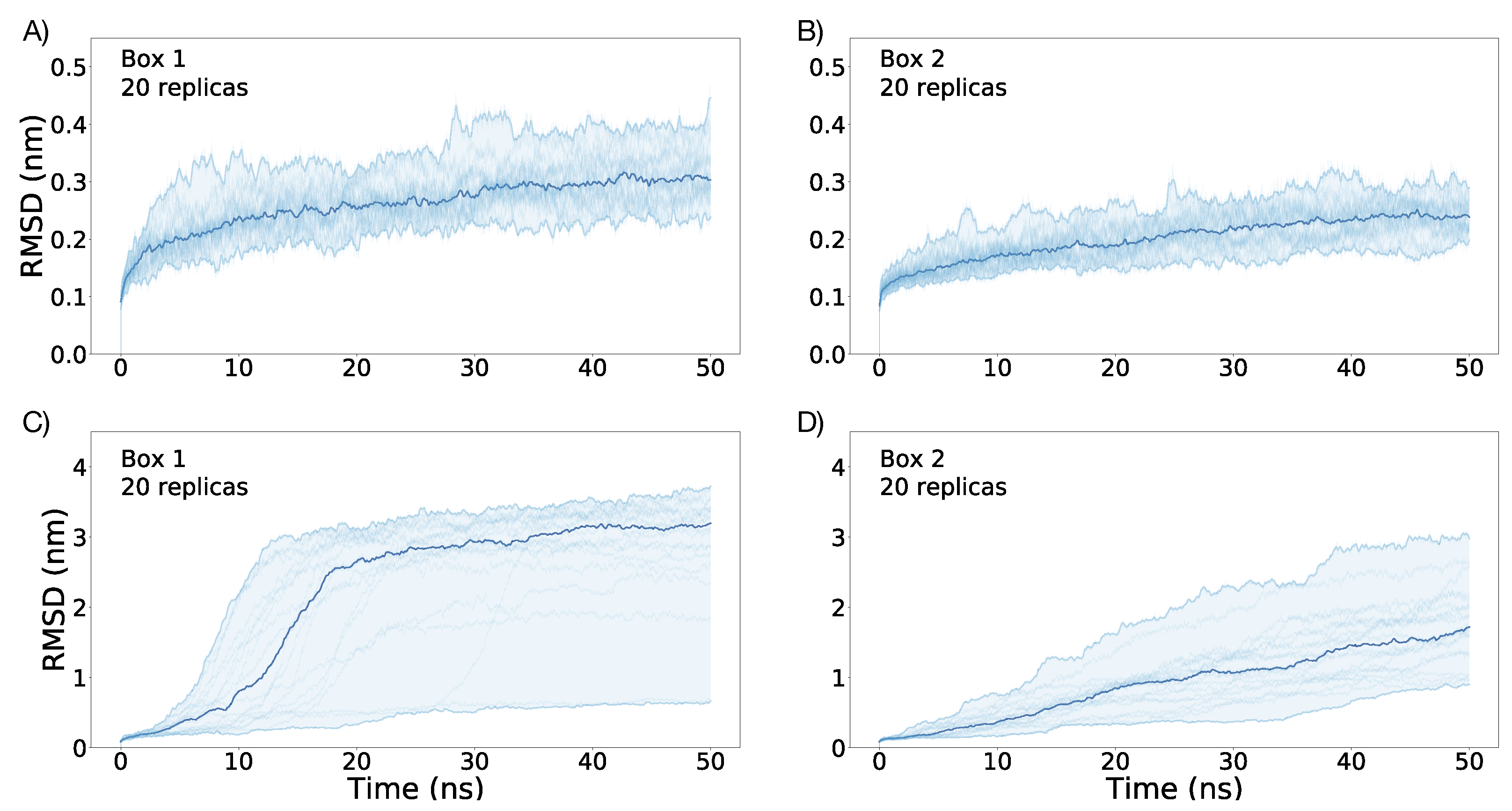
3.1. Simulations under an External Electric Field of 0.1 V/nm
3.2. Simulations under an External Electric Field of 0.2 V/nm
3.3. Simulations of Box 1 and Box 2 without VSD
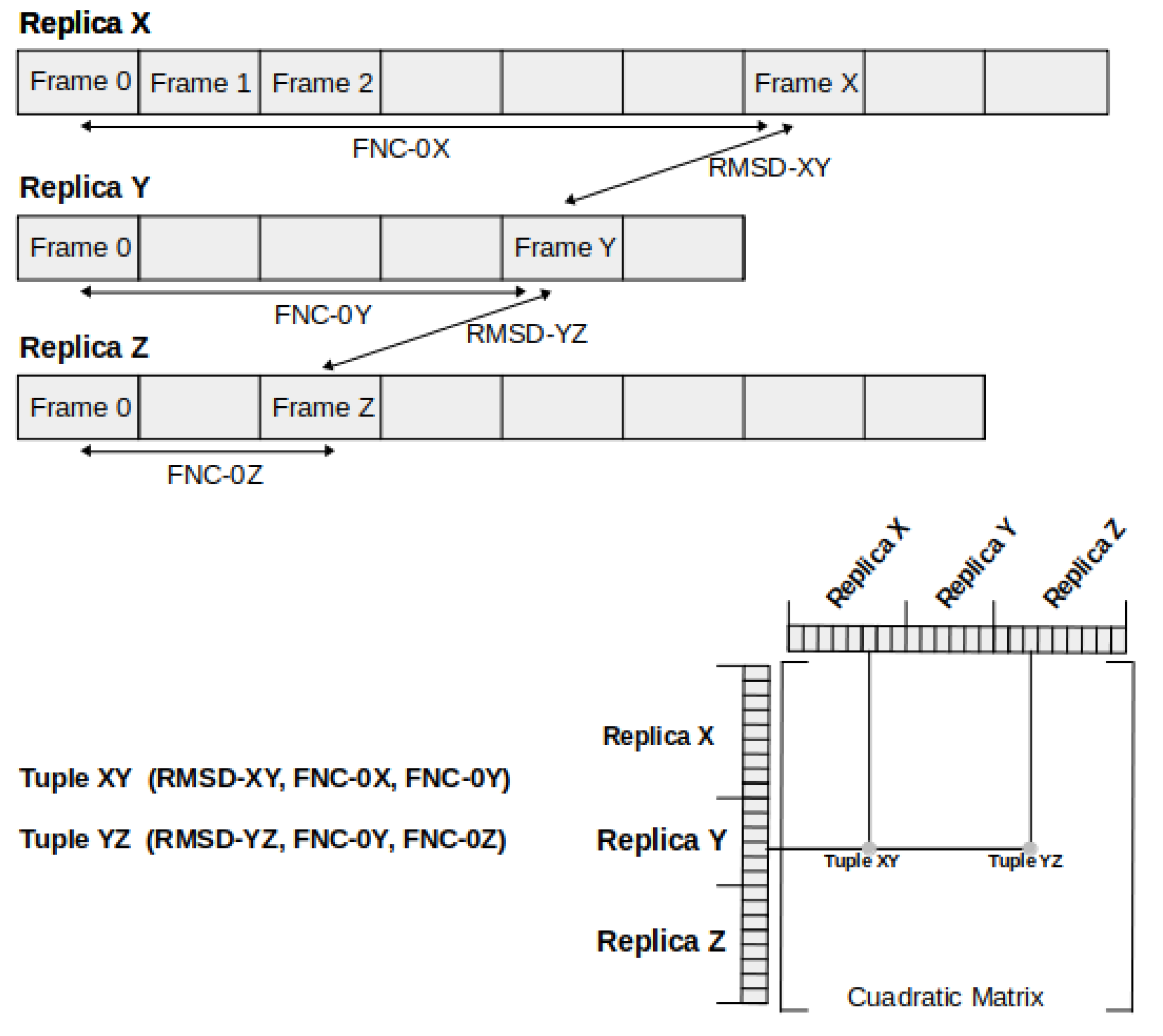
3.4. Clusterization and Calculation of Free Energies
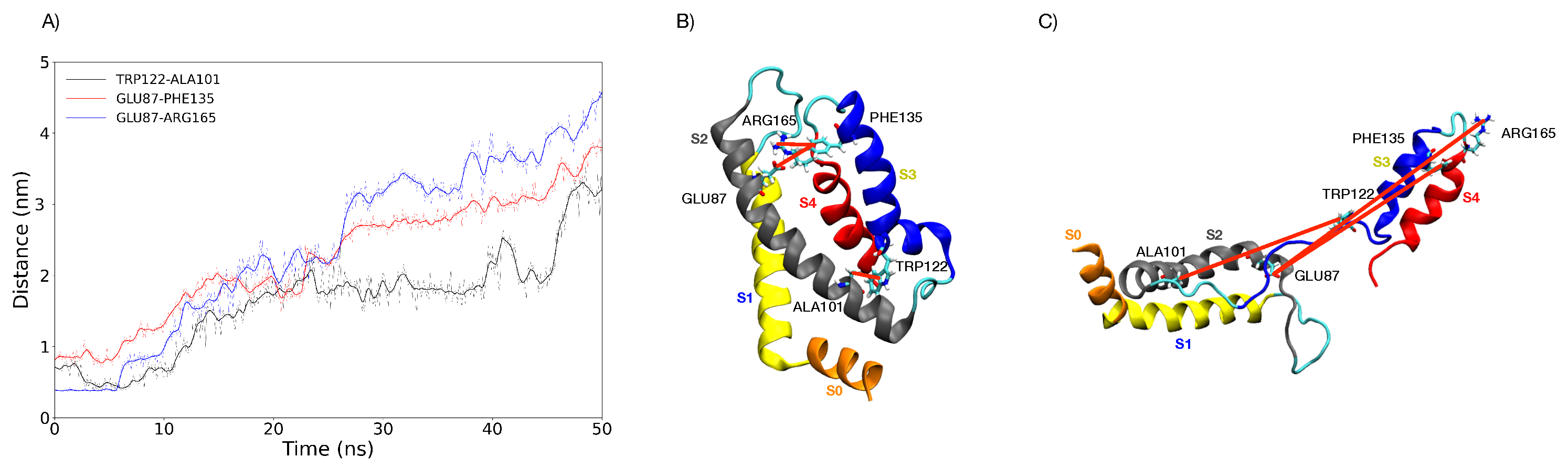
3.5. Characterization of the Representative VSD for Each Cluster
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| nsPEF | Nanosecond Pulsed Electric Field |
| NPS | Nano Pulse Stimulation |
| VSD | Voltage Sensing Domain |
| VGCC | Voltage-Gated Calcium Channel |
| VGC | Voltage-gated ion channels |
| Electric Field | |
| TM | Transmembrane |
| POPC | 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine |
| FNC | Fraction of Native Contacts |
| SASA | Solvent-Accessible Surface Area |
| Free Energy |
References
- Davalos, R.V.; Mir, L.; Rubinsky, B. Tissue ablation with irreversible electroporation. Ann. Biomed. Eng. 2005, 33, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Miklavcic, D.; Davalos, R.V. Electrochemotherapy (ECT) and irreversible electroporation (IRE)-advanced techniques for treating deep-seated tumors based on electroporation. Biomed. Eng. Online 2015, 14, I1. [Google Scholar] [CrossRef] [PubMed]
- Castellví, Q.; Banús, J.; Ivorra, A. 3D assessment of irreversible electroporation treatments in vegetal models. In 1st World Congress on Electroporation and Pulsed Electric Fields in Biology, Medicine and Food & Environmental Technologies; Springer: Singapore, 2016; pp. 294–297. [Google Scholar]
- Meijerink, M.R.; Scheffer, H.J.; Narayanan, G. Irreversible Electroporation in Clinical Practice; Springer: Singapore, 2018. [Google Scholar]
- Neumann, E.; Schaefer-Ridder, M.; Wang, Y.; Hofschneider, P. Gene transfer into mouse lyoma cells by electroporation in high electric fields. EMBO J. 1982, 1, 841–845. [Google Scholar] [CrossRef] [PubMed]
- Tsong, T.Y. On electroporation of cell membranes and some related phenomena. Bioelectrochem. Bioenerg. 1990, 24, 271–295. [Google Scholar] [CrossRef]
- Weaver, J.C.; Chizmadzhev, Y.A. Theory of electroporation: A review. Bioelectrochem. Bioenerg. 1996, 41, 135–160. [Google Scholar] [CrossRef]
- Chen, C.; Smye, S.; Robinson, M.; Evans, J. Membrane electroporation theories: A review. Med. Biol. Eng. Comput. 2006, 44, 5–14. [Google Scholar] [CrossRef]
- Kotnik, T.; Kramar, P.; Pucihar, G.; Miklavcic, D.; Tarek, M. Cell membrane electroporation-Part 1: The phenomenon. IEEE Electr. Insul. Mag. 2012, 28, 14–23. [Google Scholar] [CrossRef]
- Jordan, C.A.; Neumann, E.; Sowers, A.E. Electroporation and Electrofusion in Cell Biology; Springer Science & Business Media: Singapore, 2013. [Google Scholar]
- Orlowski, S.; Belehradek, J., Jr.; Paoletti, C.; Mir, L.M. Transient electropermeabilization of cells in culture. Increase of the cytotoxicity of anticancer drugs. Biochem. Pharmacol. 1988, 37, 4727–4733. [Google Scholar] [CrossRef]
- Miklavčič, D.; Mali, B.; Kos, B.; Heller, R.; Serša, G. Electrochemotherapy: From the drawing board into medical practice. Biomed. Eng. Online 2014, 13, 29. [Google Scholar] [CrossRef]
- Boussetta, N.; Grimi, N.; Lebovka, N.I.; Vorobiev, E. “Cold” electroporation in potato tissue induced by pulsed electric field. J. Food Eng. 2013, 115, 232–236. [Google Scholar] [CrossRef]
- Yarmush, M.L.; Golberg, A.; Serša, G.; Kotnik, T.; Miklavčič, D. Electroporation-based technologies for medicine: Principles, applications, and challenges. Ann. Rev. Biomed. Eng. 2014, 16, 295–320. [Google Scholar] [CrossRef]
- Shi, J.; Ma, Y.; Zhu, J.; Chen, Y.; Sun, Y.; Yao, Y.; Yang, Z.; Xie, J. A review on electroporation-based intracellular delivery. Molecules 2018, 23, 3044. [Google Scholar] [CrossRef]
- Kotnik, T.; Frey, W.; Sack, M.; Meglič, S.H.; Peterka, M.; Miklavčič, D. Electroporation-based applications in biotechnology. Trends Biotechnol. 2015, 33, 480–488. [Google Scholar] [CrossRef] [PubMed]
- Mahnič-Kalamiza, S.; Vorobiev, E.; Miklavčič, D. Electroporation in food processing and biorefinery. J. Membr. Biol. 2014, 247, 1279–1304. [Google Scholar] [CrossRef] [PubMed]
- Toepfl, S.; Heinz, V.; Knorr, D. High intensity pulsed electric fields applied for food preservation. Chem. Eng. Proc. Process Intensif. 2007, 46, 537–546. [Google Scholar] [CrossRef]
- Saldaña, G.; Álvarez, I.; Condón, S.; Raso, J. Microbiological aspects related to the feasibility of PEF technology for food pasteurization. Crit. Rev. Food Sci. Nutr. 2014, 54, 1415–1426. [Google Scholar] [CrossRef] [PubMed]
- Sampedro, F.; Rodrigo, D. Pulsed electric fields (PEF) processing of milk and dairy products. In Emerging Dairy Processing Technologies: Opportunities for the Dairy Industry; John Wiley & Sons: Hoboken, NJ, USA, 2015; pp. 115–148. [Google Scholar]
- Frey, W.; Gusbeth, C.; Sakugawa, T.; Sack, M.; Mueller, G.; Sigler, J.; Vorobiev, E.; Lebovka, N.; Alvarez, I.; Raso, J.; et al. Environmental applications, food and biomass processing by pulsed electric fields. In Bioelectrics; Springer: Tokyo, Japan, 2017; pp. 389–476. [Google Scholar]
- Schoenbach, K.H.; Alden, R.W.; Fox, T.J. Biofouling prevention with pulsed electric fields. In Proceedings of the 1996 International Power Modulator Symposium, Boca Raton, FL, USA, 25–27 June 1996; pp. 75–78. [Google Scholar]
- Napotnik, T.B.; Reberšek, M.; Vernier, P.T.; Mali, B.; Miklavčič, D. Effects of high voltage nanosecond electric pulses on eukaryotic cells (in vitro): A systematic review. Bioelectrochemistry 2016, 110, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Blackmore, P.F.; Hargrave, B.Y.; Xiao, S.; Beebe, S.J.; Schoenbach, K.H. Nanosecond pulse electric field (nanopulse): A novel non-ligand agonist for platelet activation. Arch. Biochem. Biophys. 2008, 471, 240–248. [Google Scholar] [CrossRef]
- Beebe, S.J.; Fox, P.M.; Rec, L.J.; Willis, E.L.K.; Schoenbach, K.H. Nanosecond, high-intensity pulsed electric fields induce apoptosis in human cells. FASEB J. 2003, 17, 1493–1495. [Google Scholar] [CrossRef]
- Semenov, I.; Xiao, S.; Pakhomov, A.G. Primary pathways of intracellular Ca2+ mobilization by nanosecond pulsed electric field. Biochim. Biophys. Acta (BBA) Biomembr. 2013, 1828, 981–989. [Google Scholar] [CrossRef]
- Beebe, S.J.; Fox, P.; Rec, L.; Somers, K.; Stark, R.H.; Schoenbach, K.H. Nanosecond pulsed electric field (nsPEF) effects on cells and tissues: Apoptosis induction and tumor growth inhibition. IEEE Trans. Plasma Sci. 2002, 30, 286–292. [Google Scholar] [CrossRef]
- Craviso, G.L.; Choe, S.; Chatterjee, P.; Chatterjee, I.; Vernier, P.T. Nanosecond electric pulses: A novel stimulus for triggering Ca2+ influx into chromaffin cells via voltage-gated Ca2+ channels. Cell. Mol. Neurobiol. 2010, 30, 1259–1265. [Google Scholar] [CrossRef]
- Bagalkot, T.R.; Terhune, R.C.; Leblanc, N.; Craviso, G.L. Different membrane pathways mediate Ca2+ influx in adrenal chromaffin cells exposed to 150–400 ns electric pulses. BioMed Res. Int. 2018, 2018, 9046891. [Google Scholar] [CrossRef] [PubMed]
- Bagalkot, T.R.; Leblanc, N.; Craviso, G.L. Stimulation or Cancellation of Ca2+ Influx by Bipolar Nanosecond Pulsed Electric Fields in Adrenal Chromaffin Cells Can Be Achieved by Tuning Pulse Waveform. Sci. Rep. 2019, 9, 11545. [Google Scholar] [CrossRef]
- Semenov, I.; Xiao, S.; Kang, D.; Schoenbach, K.H.; Pakhomov, A.G. Cell stimulation and calcium mobilization by picosecond electric pulses. Bioelectrochemistry 2015, 105, 65–71. [Google Scholar] [CrossRef]
- Burke, R.C.; Bardet, S.M.; Carr, L.; Romanenko, S.; Arnaud-Cormos, D.; Leveque, P.; O’Connor, R.P. Nanosecond pulsed electric fields depolarize transmembrane potential via voltage-gated K+, Ca2+ and TRPM8 channels in U87 glioblastoma cells. Biochim. Biophys. Acta (BBA) Biomembr. 2017, 1859, 2040–2050. [Google Scholar] [CrossRef] [PubMed]
- Hristov, K.; Mangalanathan, U.; Casciola, M.; Pakhomova, O.N.; Pakhomov, A.G. Expression of voltage-gated calcium channels augments cell susceptibility to membrane disruption by nanosecond pulsed electric field. Biochim. Biophys. Acta (BBA) Biomembr. 2018, 1860, 2175–2183. [Google Scholar] [CrossRef] [PubMed]
- Rogers, W.R.; Merritt, J.H.; Comeaux, J.A.; Kuhnel, C.T.; Moreland, D.F.; Teltschik, D.G.; Lucas, J.H.; Murphy, M.R. Strength-duration curve for an electrically excitable tissue extended down to near 1 nanosecond. IEEE Trans. Plasma Sci. 2004, 32, 1587–1599. [Google Scholar] [CrossRef]
- Pakhomov, A.G.; Semenov, I.; Casciola, M.; Xiao, S. Neuronal excitation and permeabilization by 200-ns pulsed electric field: An optical membrane potential study with FluoVolt dye. Biochim. Biophys. Acta (BBA) Biomembr. 2017, 1859, 1273–1281. [Google Scholar] [CrossRef]
- White, J.A.; Blackmore, P.F.; Schoenbach, K.H.; Beebe, S.J. Stimulation of capacitative calcium entry in HL-60 cells by nanosecond pulsed electric fields. J. Biol. Chem. 2004, 279, 22964–22972. [Google Scholar] [CrossRef] [PubMed]
- Pakhomova, O.N.; Gregory, B.; Semenov, I.; Pakhomov, A.G. Calcium-mediated pore expansion and cell death following nanoelectroporation. Biochim. Biophys. Acta (BBA) Biomembr. 2014, 1838, 2547–2554. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; He, F.; Han, Y.; Liu, B.; Wei, S. Nanosecond pulsed electric field induces calcium mobilization in osteoblasts. Bioelectrochemistry 2018, 124, 7–12. [Google Scholar] [CrossRef] [PubMed]
- Carr, L.; Bardet, S.M.; Arnaud-Cormos, D.; Leveque, P.; O’Connor, R.P. Visualisation of an nsPEF induced calcium wave using the genetically encoded calcium indicator GCaMP in U87 human glioblastoma cells. Bioelectrochemistry 2018, 119, 68–75. [Google Scholar] [CrossRef]
- Beebe, S.J.; Fox, P.; Rec, L.; Somers, K.; Stark, R.; Schoenbach, K. Nanosecond pulsed electric field (nsPEF) effects on cells and tissues: Apoptosis induction and tumor growth inhibition. PPPS-2001 Pulsed Power Plasma Science 2001. In Proceedings of the 28th IEEE International Conference on Plasma Science and 13th IEEE International Pulsed Power Conference, Las Vegas, NV, USA, 17–22 June 2001; Volume 1, pp. 211–215. [Google Scholar]
- Hall, E.H.; Schoenbach, K.H.; Beebe, S.J. Nanosecond pulsed electric fields induce apoptosis in p53-wildtype and p53-null HCT116 colon carcinoma cells. Apoptosis 2007, 12, 1721–1731. [Google Scholar] [CrossRef]
- Ford, W.E.; Ren, W.; Blackmore, P.F.; Schoenbach, K.H.; Beebe, S.J. Nanosecond pulsed electric fields stimulate apoptosis without release of pro-apoptotic factors from mitochondria in B16f10 melanoma. Arch. Biochem. Biophys. 2010, 497, 82–89. [Google Scholar] [CrossRef]
- Chen, X.; Kolb, J.F.; Swanson, R.J.; Schoenbach, K.H.; Beebe, S.J. Apoptosis initiation and angiogenesis inhibition: Melanoma targets for nanosecond pulsed electric fields. Pigment Cell Melanoma Res. 2010, 23, 554–563. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Beebe, S.J. An apoptosis targeted stimulus with nanosecond pulsed electric fields (nsPEFs) in E4 squamous cell carcinoma. Apoptosis 2011, 16, 382–393. [Google Scholar] [CrossRef]
- Beebe, S.J.; Sain, N.M.; Ren, W. Induction of cell death mechanisms and apoptosis by nanosecond pulsed electric fields (nsPEFs). Cells 2013, 2, 136–162. [Google Scholar] [CrossRef]
- He, L.; Xiao, D.; Feng, J.; Yao, C.; Tang, L. Induction of apoptosis of liver cancer cells by nanosecond pulsed electric fields (nsPEFs). Med. Oncol. 2017, 34, 24. [Google Scholar] [CrossRef]
- Dong, F.; Liu, Z.; Zhang, J.; Fang, J.; Guo, J.; Zhang, Y. Nspefs Promoting the Proliferation of Piec Cells: An in Vitro Study. In Proceedings of the 2017 IEEE International Conference on Plasma Science (ICOPS), Atlantic City, NJ, USA, 21–25 May 2017; p. 1. [Google Scholar]
- Zhang, Y.; Dong, F.; Liu, Z.; Guo, J.; Zhang, J.; Fang, J. Nanosecond pulsed electric fields promoting the proliferation of porcine iliac endothelial cells: An in vitro study. PLoS ONE 2018, 13, e0196688. [Google Scholar] [CrossRef] [PubMed]
- Buchmann, L.; Frey, W.; Gusbeth, C.; Ravaynia, P.S.; Mathys, A. Effect of nanosecond pulsed electric field treatment on cell proliferation of microalgae. Bioresour. Technol. 2019, 271, 402–408. [Google Scholar] [CrossRef]
- Vadlamani, R.A.; Nie, Y.; Detwiler, D.A.; Dhanabal, A.; Kraft, A.M.; Kuang, S.; Gavin, T.P.; Garner, A.L. Nanosecond pulsed electric field induced proliferation and differentiation of osteoblasts and myoblasts. J. R. Soc. Interface 2019, 16, 20190079. [Google Scholar] [CrossRef]
- Schoenbach, K.H.; Abou-Ghazala, A.; Vithoulkas, T.; Alden, R.W.; Turner, R.; Beebe, S. The effect of pulsed electrical fields on biological cells. In Proceedings of the 11th IEEE International Pulsed Power Conference, Baltimore, MD, USA, 29 June–2 July 1997; Volume 1, pp. 73–78. [Google Scholar]
- Müller, K.; Sukhorukov, V.; Zimmermann, U. Reversible electropermeabilization of mammalian cells by high-intensity, ultra-short pulses of submicrosecond duration. J. Membr. Biol. 2001, 184, 161–170. [Google Scholar] [CrossRef]
- Schoenbach, K.H.; Beebe, S.J.; Buescher, E.S. Intracellular effect of ultrashort electrical pulses. Bioelectromagnetics 2001, 22, 440–448. [Google Scholar] [CrossRef]
- Gowrishankar, T.R.; Esser, A.T.; Vasilkoski, Z.; Smith, K.C.; Weaver, J.C. Microdosimetry for conventional and supra-electroporation in cells with organelles. Biochem. Biophys. Res. Commun. 2006, 341, 1266–1276. [Google Scholar] [CrossRef]
- Roth, C.C.; Tolstykh, G.P.; Payne, J.A.; Kuipers, M.A.; Thompson, G.L.; DeSilva, M.N.; Ibey, B.L. Nanosecond pulsed electric field thresholds for nanopore formation in neural cells. J. Biomed. Opt. 2013, 18, 035005. [Google Scholar] [CrossRef]
- Romanenko, S.; Arnaud-Cormos, D.; Leveque, P.; O’Connor, R.P. Ultrashort pulsed electric fields induce action potentials in neurons when applied at axon bundles. In Proceedings of the 2016 9th International Kharkiv Symposium on Physics and Engineering of Microwaves, Millimeter and Submillimeter Waves (MSMW), Kharkiv, Ukraine, 20–24 June 2016; pp. 1–5. [Google Scholar]
- Casciola, M.; Xiao, S.; Pakhomov, A.G. Damage-free peripheral nerve stimulation by 12-ns pulsed electric field. Sci. Rep. 2017, 7, 10453. [Google Scholar] [CrossRef]
- Lamberti, P.; Tucci, V.; Zeni, O.; Romeo, S. Analysis of ionic channel currents under nsPEFs-stimulation by a circuital model of an excitable cell. In Proceedings of the 2020 IEEE 20th Mediterranean Electrotechnical Conference (MELECON), Palermo, Italy, 15–18 June 2020; pp. 411–414. [Google Scholar]
- Wang, S.; Chen, J.; Chen, M.T.; Vernier, P.T.; Gundersen, M.A.; Valderrábano, M. Cardiac myocyte excitation by ultrashort high-field pulses. Biophys. J. 2009, 96, 1640–1648. [Google Scholar] [CrossRef]
- Semenov, I.; Grigoryev, S.; Neuber, J.U.; Zemlin, C.W.; Pakhomova, O.N.; Casciola, M.; Pakhomov, A.G. Excitation and injury of adult ventricular cardiomyocytes by nano-to millisecond electric shocks. Sci. Rep. 2018, 8, 8233. [Google Scholar] [CrossRef]
- Azarov, J.E.; Semenov, I.; Casciola, M.; Pakhomov, A.G. Excitation of murine cardiac myocytes by nanosecond pulsed electric field. J. Cardiovasc. Electrophysiol. 2019, 30, 392–401. [Google Scholar] [CrossRef]
- Pakhomov, A.G.; Xiao, S.; Novickij, V.; Casciola, M.; Semenov, I.; Mangalanathan, U.; Kim, V.; Zemlin, C.; Sozer, E.; Muratori, C.; et al. Excitation and electroporation by MHz bursts of nanosecond stimuli. Biochem. Biophys. Res. Commun. 2019, 518, 759–764. [Google Scholar] [CrossRef]
- Xiao, S.; Kiyan, T.; Blackmore, P.; Schoenbach, K. Pulsed Power for Wound Healing. In Proceedings of the 2008 IEEE International Power Modulators and High-Voltage Conference, Las Vegas, NV, USA, 27–31 May 2008; pp. 69–72. [Google Scholar]
- Hargrave, B.; Li, F. Nanosecond pulse electric field activation of platelet-rich plasma reduces myocardial infarct size and improves left ventricular mechanical function in the rabbit heart. J. Extra-Corpor. Technol. 2012, 44, 198. [Google Scholar]
- Hargrave, B.; Li, F. Nanosecond Pulse Electric Field Activated-Platelet Rich Plasma Enhances the Return of Blood Flow to Large and Ischemic Wounds in a Rabbit Model. Physiol. Rep. 2015, 3, e12461. [Google Scholar] [CrossRef]
- Beebe, S.J.; Blackmore, P.F.; White, J.; Joshi, R.P.; Schoenbach, K.H. Nanosecond pulsed electric fields modulate cell function through intracellular signal transduction mechanisms. Physiol. Meas. 2004, 25, 1077. [Google Scholar] [CrossRef]
- Morotomi-Yano, K.; Uemura, Y.; Katsuki, S.; Akiyama, H.; Yano, K.I. Activation of the JNK pathway by nanosecond pulsed electric fields. Biochem. Biophys. Res. Commun. 2011, 408, 471–476. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Guo, J.; Ge, Z.; Zhang, J. Nanosecond pulsed electric fields (nsPEFs) regulate phenotypes of chondrocytes through Wnt/β-catenin signaling pathway. Sci. Rep. 2014, 4, 5836. [Google Scholar] [CrossRef]
- Guo, S.; Jackson, D.L.; Burcus, N.I.; Chen, Y.J.; Xiao, S.; Heller, R. Gene electrotransfer enhanced by nanosecond pulsed electric fields. Mol. Ther.-Methods Clin. Dev. 2014, 1, 14043. [Google Scholar] [CrossRef]
- Estlack, L.E.; Roth, C.C.; Thompson, G.L.; Lambert, W.A.; Ibey, B.L. Nanosecond pulsed electric fields modulate the expression of Fas/CD95 death receptor pathway regulators in U937 and Jurkat Cells. Apoptosis 2014, 19, 1755–1768. [Google Scholar] [CrossRef] [PubMed]
- Muratori, C.; Pakhomov, A.G.; Gianulis, E.; Meads, J.; Casciola, M.; Mollica, P.A.; Pakhomova, O.N. Activation of the phospholipid scramblase TMEM16F by nanosecond pulsed electric fields (nsPEF) facilitates its diverse cytophysiological effects. J. Biol. Chem. 2017, 292, 19381–19391. [Google Scholar] [CrossRef]
- Zhang, R.; Aji, T.; Shao, Y.; Jiang, T.; Yang, L.; Lv, W.; Chen, Y.; Chen, X.; Wen, H. Nanosecond pulsed electric field (nsPEF) disrupts the structure and metabolism of human Echinococcus granulosus protoscolex in vitro with a dose effect. Parasitol. Res. 2017, 116, 1345–1351. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, R.; Aji, T.; Shao, Y.; Chen, Y.; Wen, H. Novel interventional management of hepatic hydatid cyst with nanosecond pulses on experimental mouse model. Sci. Rep. 2017, 7, 4491. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zhang, R.; Wen, H. Experimental nanopulse ablation of multiple membrane parasite on ex vivo hydatid cyst. BioMed Res. Int. 2018, 2018, 8497283. [Google Scholar] [CrossRef]
- Nuccitelli, R.; Tran, K.; Lui, K.; Huynh, J.; Athos, B.; Kreis, M.; Nuccitelli, P.; De Fabo, E.C. Non-thermal nanoelectroablation of UV-induced murine melanomas stimulates an immune response. Pigment Cell Melanoma Res. 2012, 25, 618–629. [Google Scholar] [CrossRef] [PubMed]
- Chen, R.; Sain, N.M.; Harlow, K.T.; Chen, Y.J.; Shires, P.K.; Heller, R.; Beebe, S.J. A protective effect after clearance of orthotopic rat hepatocellular carcinoma by nanosecond pulsed electric fields. Eur. J. Cancer 2014, 50, 2705–2713. [Google Scholar] [CrossRef]
- Nuccitelli, R.; Berridge, J.C.; Mallon, Z.; Kreis, M.; Athos, B.; Nuccitelli, P. Nanoelectroablation of murine tumors triggers a CD8-dependent inhibition of secondary tumor growth. PLoS ONE 2015, 10, e0134364. [Google Scholar] [CrossRef]
- Nuccitelli, R.; McDaniel, A.; Anand, S.; Cha, J.; Mallon, Z.; Berridge, J.C.; Uecker, D. Nano-Pulse Stimulation is a physical modality that can trigger immunogenic tumor cell death. J. Immunother. Cancer 2017, 5, 32. [Google Scholar] [CrossRef]
- Guo, S.; Jing, Y.; Burcus, N.I.; Lassiter, B.P.; Tanaz, R.; Heller, R.; Beebe, S.J. Nano-pulse stimulation induces potent immune responses, eradicating local breast cancer while reducing distant metastases. Int. J. Cancer 2018, 142, 629–640. [Google Scholar] [CrossRef]
- Skeate, J.G.; Da Silva, D.M.; Chavez-Juan, E.; Anand, S.; Nuccitelli, R.; Kast, W.M. Nano-Pulse Stimulation induces immunogenic cell death in human papillomavirus-transformed tumors and initiates an adaptive immune response. PLoS ONE 2018, 13, e0191311. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Ma, R.; Su, B.; Li, Y.; Zhang, J.; Fang, J. Raising the avermectins production in Streptomyces avermitilis by utilizing nanosecond pulsed electric fields (nsPEFs). Sci. Rep. 2016, 6, 25949. [Google Scholar] [CrossRef]
- Rajabi, F.; Gusbeth, C.; Frey, W.; Maisch, J.; Nick, P. Nanosecond pulsed electrical fields enhance product recovery in plant cell fermentation. Protoplasma 2020, 257, 1585–1594. [Google Scholar] [CrossRef]
- Prorot, A.; Arnaud-Cormos, D.; Lévêque, P.; Leprat, P. Bacterial stress induced by nanosecond pulsed electric fields (nsPEF): Potential applications for food industry and environment. In Proceedings of the IV International Conference on Environmental, Industrial and Applied Microbiology, Torremolinhos, Spain, 14–16 September 2018; p. 194. [Google Scholar]
- Buchmann, L.; Böcker, L.; Frey, W.; Haberkorn, I.; Nyffeler, M.; Mathys, A. Energy input assessment for nanosecond pulsed electric field processing and its application in a case study with Chlorella vulgaris. Innov. Food Sci. Emerg. Technol. 2018, 47, 445–453. [Google Scholar] [CrossRef]
- Haberkorn, I.; Buchmann, L.; Häusermann, I.; Mathys, A. Nanosecond pulsed electric field processing of microalgae based biorefineries governs growth promotion or selective inactivation based on underlying microbial ecosystems. Bioresour. Technol. 2020, 319, 124173. [Google Scholar] [CrossRef]
- Eing, C.J.; Bonnet, S.; Pacher, M.; Puchta, H.; Frey, W. Effects of nanosecond pulsed electric field exposure on Arabidopsis thaliana. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 1322–1328. [Google Scholar] [CrossRef]
- Songnuan, W.; Kirawanich, P. Early growth effects on Arabidopsis thaliana by seed exposure of nanosecond pulsed electric field. J. Electrost. 2012, 70, 445–450. [Google Scholar] [CrossRef]
- Su, B.; Guo, J.; Nian, W.; Feng, H.; Wang, K.; Zhang, J.; Fang, J. Early growth effects of nanosecond pulsed electric field (nsPEFs) exposure on Haloxylon ammodendron. Plasma Process. Polym. 2015, 12, 372–379. [Google Scholar] [CrossRef]
- Molitor, S.C.; Manis, P.B. Voltage-gated Ca2+ conductances in acutely isolated guinea pig dorsal cochlear nucleus neurons. J. Neurophysiol. 1999, 81, 985–998. [Google Scholar] [CrossRef] [PubMed]
- Hille, B. Ion Channels of Excitable Membranes; Sinauer: Sunderland, MA, USA, 2001; Volume 507. [Google Scholar]
- Nishizawa, M.; Nishizawa, K. Molecular dynamics simulation of Kv channel voltage sensor helix in a lipid membrane with applied electric field. Biophys. J. 2008, 95, 1729–1744. [Google Scholar] [CrossRef] [PubMed]
- Delemotte, L.; Tarek, M.; Klein, M.L.; Amaral, C.; Treptow, W. Intermediate states of the Kv1. 2 voltage sensor from atomistic molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2011, 108, 6109–6114. [Google Scholar] [CrossRef]
- Treptow, W.; Tarek, M. Environment of the gating charges in the Kv1. 2 Shaker potassium channel. Biophys. J. 2006, 90, L64–L66. [Google Scholar] [CrossRef]
- Treptow, W.; Tarek, M.; Klein, M.L. Initial response of the potassium channel voltage sensor to a transmembrane potential. J. Am. Chem. Soc. 2009, 131, 2107–2109. [Google Scholar] [CrossRef][Green Version]
- Frey, W.; White, J.; Price, R.; Blackmore, P.; Joshi, R.; Nuccitelli, R.; Beebe, S.; Schoenbach, K.; Kolb, J. Plasma membrane voltage changes during nanosecond pulsed electric field exposure. Biophys. J. 2006, 90, 3608–3615. [Google Scholar] [CrossRef] [PubMed]
- Teissie, J.; Tsong, T.Y. Electric field induced transient pores in phospholipid bilayer vesicles. Biochemistry 1981, 20, 1548–1554. [Google Scholar] [CrossRef]
- Marszalek, P.; Liu, D.; Tsong, T.Y. Schwan equation and transmembrane potential induced by alternating electric field. Biophys. J. 1990, 58, 1053–1058. [Google Scholar] [CrossRef]
- Sugar, I.P.; Neumann, E. Stochastic model for electric field-induced membrane pores electroporation. Biophys. Chem. 1984, 19, 211–225. [Google Scholar] [CrossRef]
- Popescu, D.; Rucǎreanu, C.; Victor, G. A model for the appearance of statistical pores in membranes due to selfoscillations. J. Electroanal. Chem. Interfac. Electrochem. 1991, 320, 91–103. [Google Scholar] [CrossRef]
- Yellen, G. The moving parts of voltage-gated ion channels. Q. Rev. Biophys. 1998, 31, 239–295. [Google Scholar] [CrossRef]
- Terlau, H.; Stühmer, W. Structure and function of voltage-gated ion channels. Die Nat. 1998, 85, 437–444. [Google Scholar] [CrossRef]
- Gonzalez, C.; Contreras, G.F.; Peyser, A.; Larsson, P.; Neely, A.; Latorre, R. Voltage sensor of ion channels and enzymes. Biophys. Rev. 2012, 4, 1–15. [Google Scholar] [CrossRef]
- Zagotta, W.N.; Hoshi, T.; Aldrich, R.W. Shaker potassium channel gating. III: Evaluation of kinetic models for activation. J. Gen. Physiol. 1994, 103, 321–362. [Google Scholar] [CrossRef]
- Baker, O.; Larsson, H.; Mannuzzu, L.; Isacoff, E. Three transmembrane conformations and sequence-dependent displacement of the S4 domain in shaker K+ channel gating. Neuron 1998, 20, 1283–1294. [Google Scholar] [CrossRef]
- Sigg, D.; Bezanilla, F.; Stefani, E. Fast gating in the Shaker K+ channel and the energy landscape of activation. Proc. Natl. Acad. Sci. USA 2003, 100, 7611–7615. [Google Scholar] [CrossRef] [PubMed]
- Blaustein, R.O.; Miller, C. Ion channels: Shake, rattle or roll? Nature 2004, 427, 499. [Google Scholar] [CrossRef] [PubMed]
- Horn, R. Conversation between voltage sensors and gates of ion channels. Biochemistry 2000, 39, 15653–15658. [Google Scholar] [CrossRef]
- Catterall, W.A. Voltage-dependent gating of sodium channels: Correlating structure and function. Trends Neurosci. 1986, 9, 7–10. [Google Scholar] [CrossRef]
- GuY, H.R.; Seetharamulu, P. Molecular model of the action potential sodium channel. Proc. Natl. Acad. Sci. USA 1986, 83, 508–512. [Google Scholar] [CrossRef]
- Bezanilla, F. The voltage sensor in voltage-dependent ion channels. Physiol. Rev. 2000, 80, 555–592. [Google Scholar] [CrossRef]
- Jiang, Y.; Ruta, V.; Chen, J.; Lee, A.; MacKinnon, R. The principle of gating charge movement in a voltage-dependent K+ channel. Nature 2003, 423, 42–48. [Google Scholar] [CrossRef]
- Jiang, Y.; Lee, A.; Chen, J.; Ruta, V.; Cadene, M.; Chait, B.T.; MacKinnon, R. X-ray structure of a voltage-dependent K+ channel. Nature 2003, 423, 33–41. [Google Scholar] [CrossRef]
- Chanda, B.; Asamoah, O.K.; Blunck, R.; Roux, B.; Bezanilla, F. Gating charge displacement in voltage-gated ion channels involves limited transmembrane movement. Nature 2005, 436, 852–856. [Google Scholar] [CrossRef]
- Aggarwal, S.K.; MacKinnon, R. Contribution of the S4 segment to gating charge in the Shaker K+ channel. Neuron 1996, 16, 1169–1177. [Google Scholar] [CrossRef]
- Seoh, S.A.; Sigg, D.; Papazian, D.M.; Bezanilla, F. Voltage-sensing residues in the S2 and S4 segments of the Shaker K+ channel. Neuron 1996, 16, 1159–1167. [Google Scholar] [CrossRef]
- Thomas, S.; Preda-Pais, A.; Casares, S.; Brumeanu, T.D. Analysis of lipid rafts in T cells. Mol. Immunol. 2004, 41, 399–409. [Google Scholar] [CrossRef] [PubMed]
- Alves, A.; Dias, R.A.; Kagami, L.P.; das Neves, G.M.; Torres, F.C.; Eifler-Lima, V.L.; Carvalho, I.; de Miranda Silva, C.; Kawano, D.F. Beyond the “Lock and Key” Paradigm: Targeting Lipid Rafts to Induce the Selective Apoptosis of Cancer Cells. Curr. Med. Chem. 2018, 25, 2082–2104. [Google Scholar] [CrossRef] [PubMed]
- Simons, K.; Ikonen, E. Functional rafts in cell membranes. Nature 1997, 387, 569–572. [Google Scholar] [CrossRef]
- Ramstedt, B.; Slotte, J.P. Interaction of cholesterol with sphingomyelins and acyl-chain-matched phosphatidylcholines: A comparative study of the effect of the chain length. Biophys. J. 1999, 76, 908–915. [Google Scholar] [CrossRef]
- Lozano, M.M.; Hovis, J.S.; Moss, F.R., III; Boxer, S.G. Dynamic reorganization and correlation among lipid raft components. J. Am. Chem. Soc. 2016, 138, 9996–10001. [Google Scholar] [CrossRef]
- Simons, K.; Vaz, W.L. Model systems, lipid rafts, and cell membranes. Annu. Rev. Biophys. Biomol. Struct. 2004, 33, 269–295. [Google Scholar] [CrossRef]
- Simons, K.; Van Meer, G. Lipid sorting in epithelial cells. Biochemistry 1988, 27, 6197–6202. [Google Scholar] [CrossRef]
- Anchisi, L.; Dessì, S.; Pani, A.; Mandas, A. Cholesterol homeostasis: A key to prevent or slow down neurodegeneration. Front. Physiol. 2013, 3, 486. [Google Scholar] [CrossRef]
- Levental, I. Lipid rafts come of age. Nat. Rev. Mol. Cell Biol. 2020, 21, 420. [Google Scholar] [CrossRef]
- Tulodziecka, K.; Diaz-Rohrer, B.B.; Farley, M.M.; Chan, R.B.; Di Paolo, G.; Levental, K.R.; Waxham, M.N.; Levental, I. Remodeling of the postsynaptic plasma membrane during neural development. Mol. Biol. Cell 2016, 27, 3480–3489. [Google Scholar] [CrossRef]
- Phillips, R.; Ursell, T.; Wiggins, P.; Sens, P. Emerging roles for lipids in shaping membrane-protein function. Nature 2009, 459, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Sachs, J.N.; Engelman, D.M. Introduction to the membrane protein reviews: The interplay of structure, dynamics, and environment in membrane protein function. Annu. Rev. Biochem. 2006, 75, 707–712. [Google Scholar] [CrossRef]
- Andersen, O.S.; Koeppe, R.E. Bilayer thickness and membrane protein function: An energetic perspective. Annu. Rev. Biophys. Biomol. Struct. 2007, 36, 107–130. [Google Scholar] [CrossRef] [PubMed]
- Tonnesen, A.; Christensen, S.M.; Tkach, V.; Stamou, D. Geometrical membrane curvature as an allosteric regulator of membrane protein structure and function. Biophys. J. 2014, 106, 201–209. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Huang, J.; MacKerell, A.D., Jr. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. [Google Scholar] [CrossRef]
- Subczynski, W.K.; Pasenkiewicz-Gierula, M.; Widomska, J.; Mainali, L.; Raguz, M. High cholesterol/low cholesterol: Effects in biological membranes: A review. Cell Biochem. Biophys. 2017, 75, 369–385. [Google Scholar] [CrossRef] [PubMed]
- Mainali, L.; Raguz, M.; Subczynski, W.K. Formation of cholesterol bilayer domains precedes formation of cholesterol crystals in cholesterol/dimyristoylphosphatidylcholine membranes: EPR and DSC studies. J. Phys. Chem. B 2013, 117, 8994–9003. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An Nlog (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Evans, D.J.; Holian, B.L. The nose–hoover thermostat. J. Chem. Phys. 1985, 83, 4069–4074. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A web-based graphical user interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef] [PubMed]
- Machado, N.; Callegaro, C.; Christoffolete, M.A.; Martinho, H. Tuning the transdermal transport by application of external continuous electric field: A coarse-grained molecular dynamics study. Phys. Chem. Chem. Phys. 2021, 23, 8273–8281. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global k-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- King, G.J.; Richards, R.R.; Zuckerman, J.D.; Blasier, R.; Dillman, C.; Friedman, R.J.; Gartsman, G.M.; Iannotti, J.P.; Murnahan, J.P.; Mow, V.C.; et al. A standardized method for assessment of elbow function. J. Shoulder Elbow Surg. 1999, 8, 351–354. [Google Scholar]


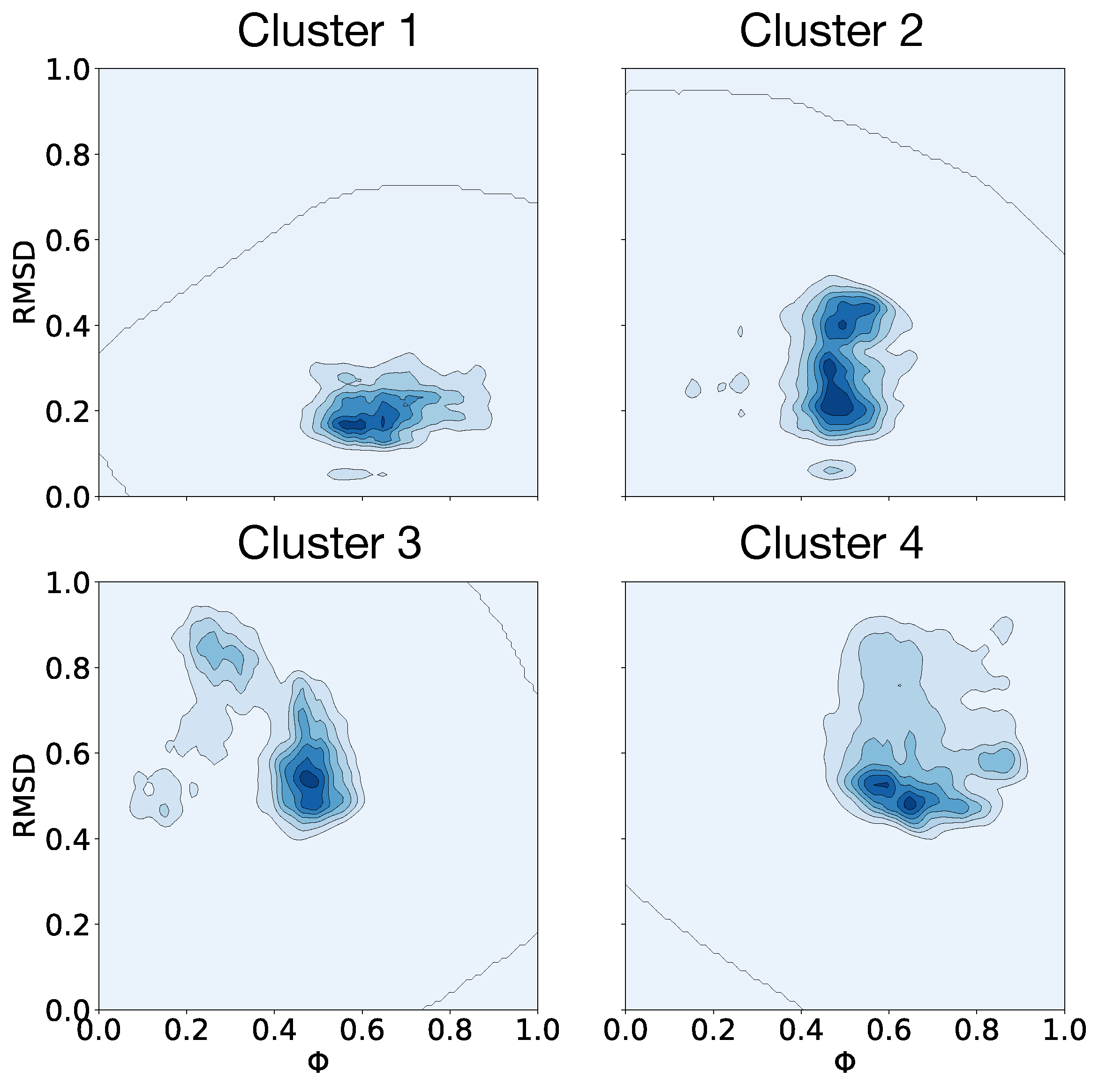
| Clusters | (J/mol) |
|---|---|
| 1–2 | −1225.5 |
| 1–3 | −1753.0 |
| 1–4 | −1796.9 |
| 2–3 | −527.6 |
| 2–4 | −571.5 |
| 3–4 | −43.9 |
| Frames | RGyr (nm) | SASA (Å) | Helix Content (%) | Distance-1 (Å) | Distance-2 (Å) | Distance-3 (Å) |
|---|---|---|---|---|---|---|
| Initial frame | 1.605 | 9106.8 | 76.0 | 7.4 | 7.6 | 3.9 |
| Frame 1 | 2.007 | 10,642.7 | 60.3 | 27.3 | 27.2 | 21.3 |
| Frame 2 | 2.181 | 10,480.4 | 67.8 | 27.9 | 28.3 | 32.7 |
| Frame 3 | 2.795 | 11,745.8 | 65.3 | 40.9 | 48.7 | 46.5 |
| Frame 4 | 2.601 | 11,806.6 | 55.4 | 32.9 | 41.2 | 50.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruiz-Fernández, A.R.; Campos, L.; Villanelo, F.; Gutiérrez-Maldonado, S.E.; Perez-Acle, T. Exploring the Conformational Changes Induced by Nanosecond Pulsed Electric Fields on the Voltage Sensing Domain of a Ca2+ Channel. Membranes 2021, 11, 473. https://doi.org/10.3390/membranes11070473
Ruiz-Fernández AR, Campos L, Villanelo F, Gutiérrez-Maldonado SE, Perez-Acle T. Exploring the Conformational Changes Induced by Nanosecond Pulsed Electric Fields on the Voltage Sensing Domain of a Ca2+ Channel. Membranes. 2021; 11(7):473. https://doi.org/10.3390/membranes11070473
Chicago/Turabian StyleRuiz-Fernández, Alvaro R., Leonardo Campos, Felipe Villanelo, Sebastian E. Gutiérrez-Maldonado, and Tomas Perez-Acle. 2021. "Exploring the Conformational Changes Induced by Nanosecond Pulsed Electric Fields on the Voltage Sensing Domain of a Ca2+ Channel" Membranes 11, no. 7: 473. https://doi.org/10.3390/membranes11070473
APA StyleRuiz-Fernández, A. R., Campos, L., Villanelo, F., Gutiérrez-Maldonado, S. E., & Perez-Acle, T. (2021). Exploring the Conformational Changes Induced by Nanosecond Pulsed Electric Fields on the Voltage Sensing Domain of a Ca2+ Channel. Membranes, 11(7), 473. https://doi.org/10.3390/membranes11070473







