Water as a Blood Model for Determination of CO2 Removal Performance of Membrane Oxygenators
Abstract
1. Introduction
- The use of blood is accompanied by animal suffering.
- The use of blood is not permitted in all technical laboratories.
- Test circuits get contaminated and must be rebuilt due to blood deposits.
- Additional logistical challenges due to limited durability of blood.
- Ethics committee approval must be obtained.
2. Materials and Methods
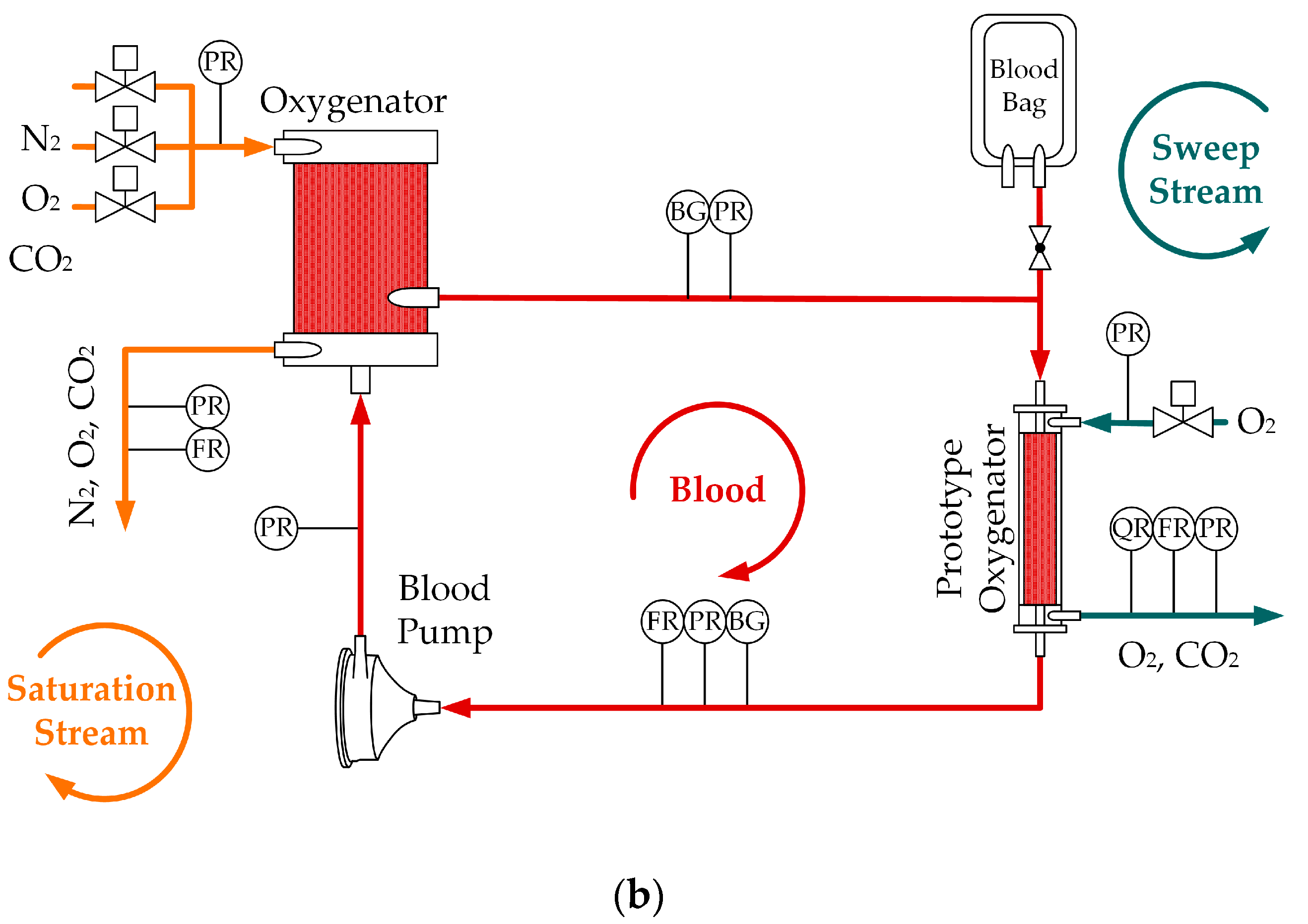
2.1. In Vivo and In Vitro Tests
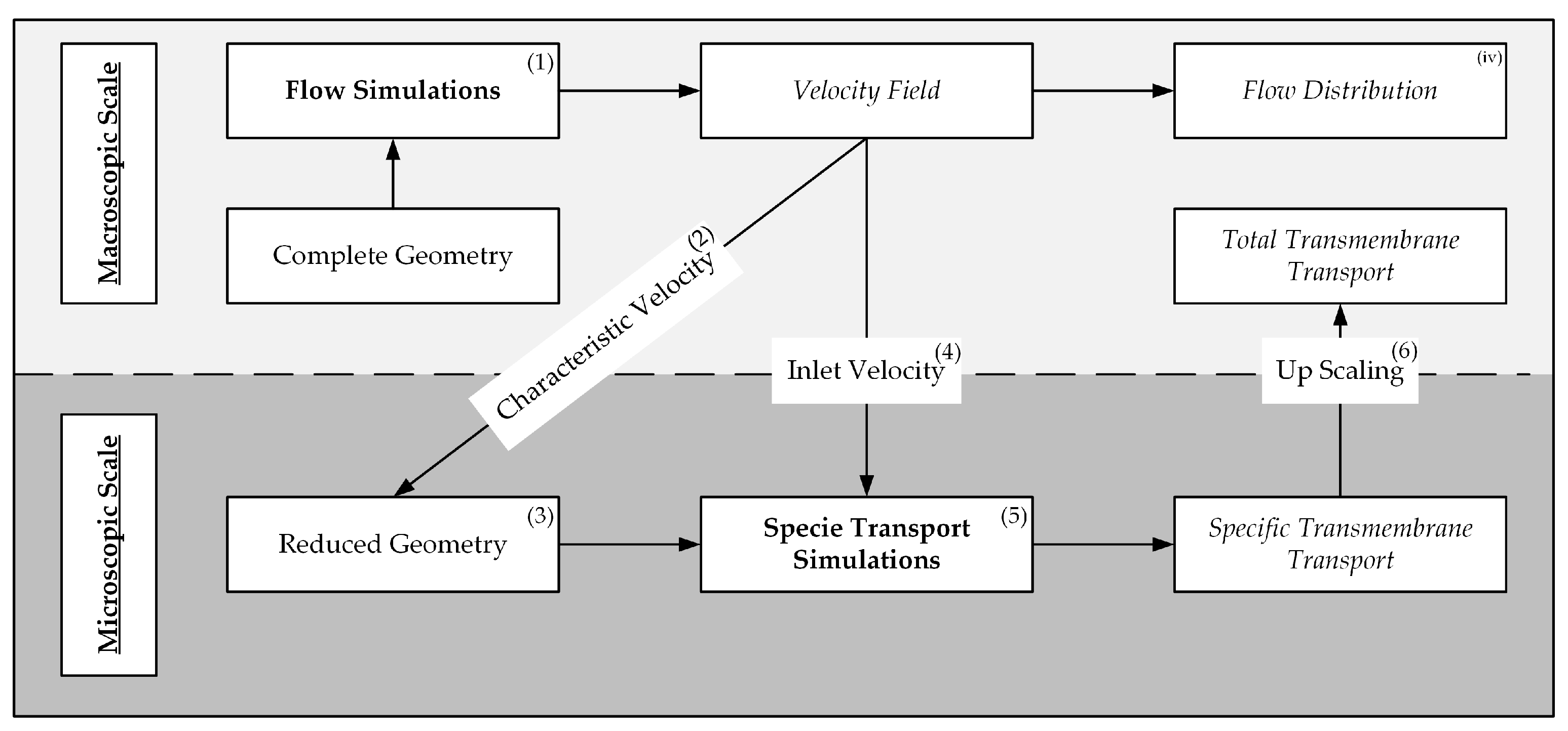
2.2. Computational Fluid Dynamic Simulations
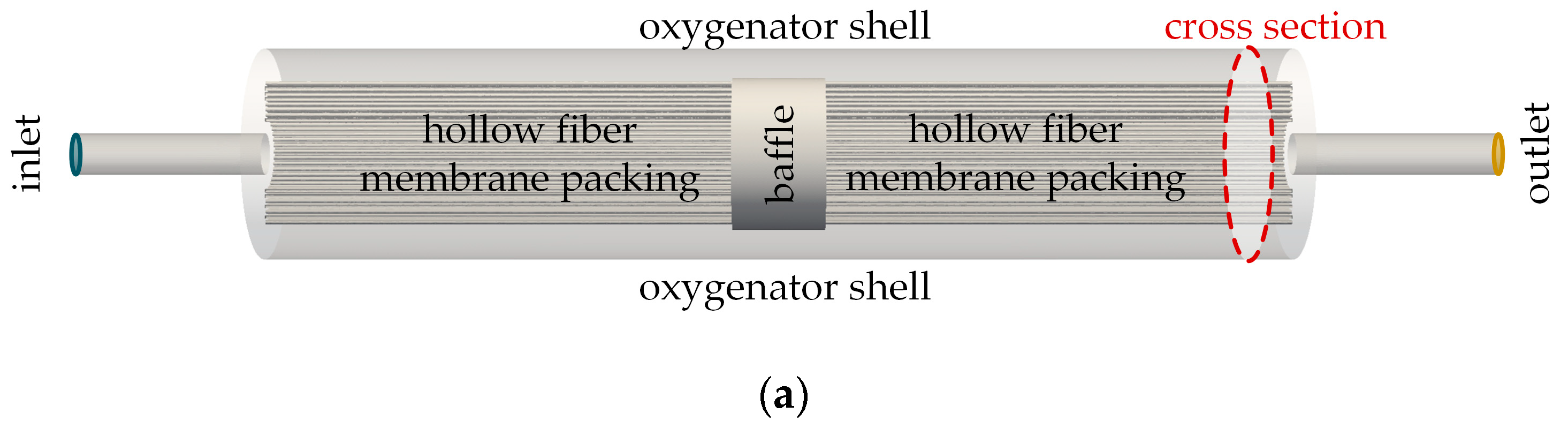
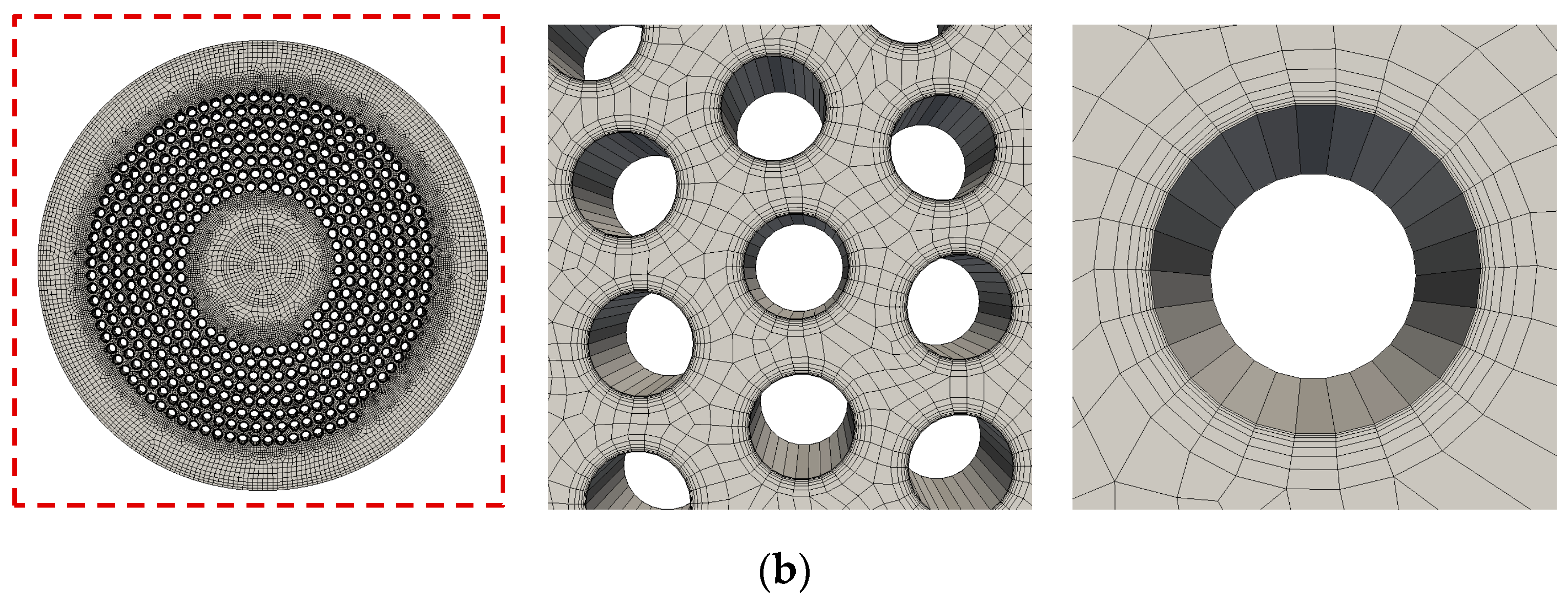
2.2.1. Flow Simulation of the Complete Prototype Oxygenator (Macro Scale)
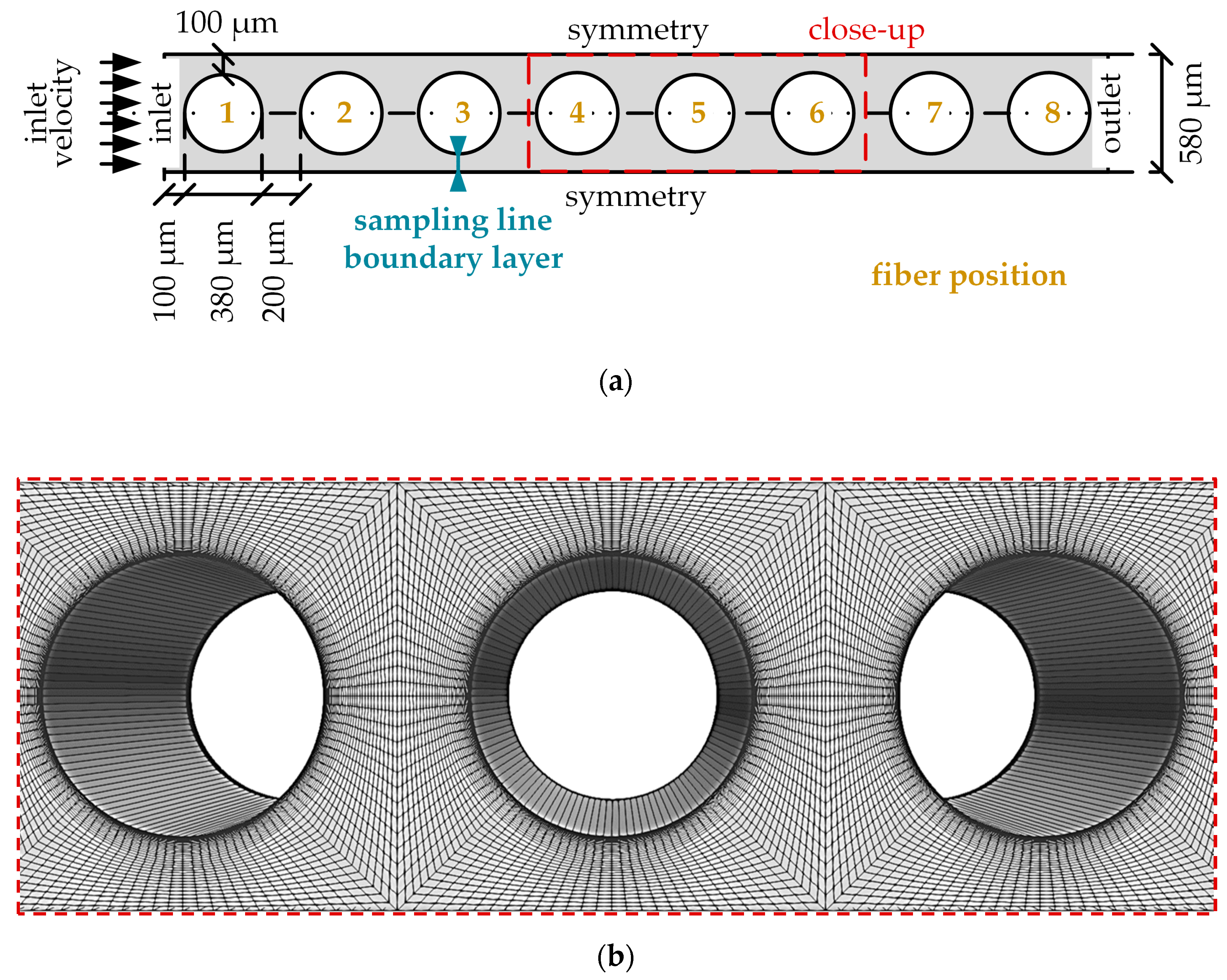
2.2.2. CO2 Transport Simulations of the Simplified Packing (Micro Scale)
3. Results and Discussion
3.1. In Vivo and In Vitro Tests
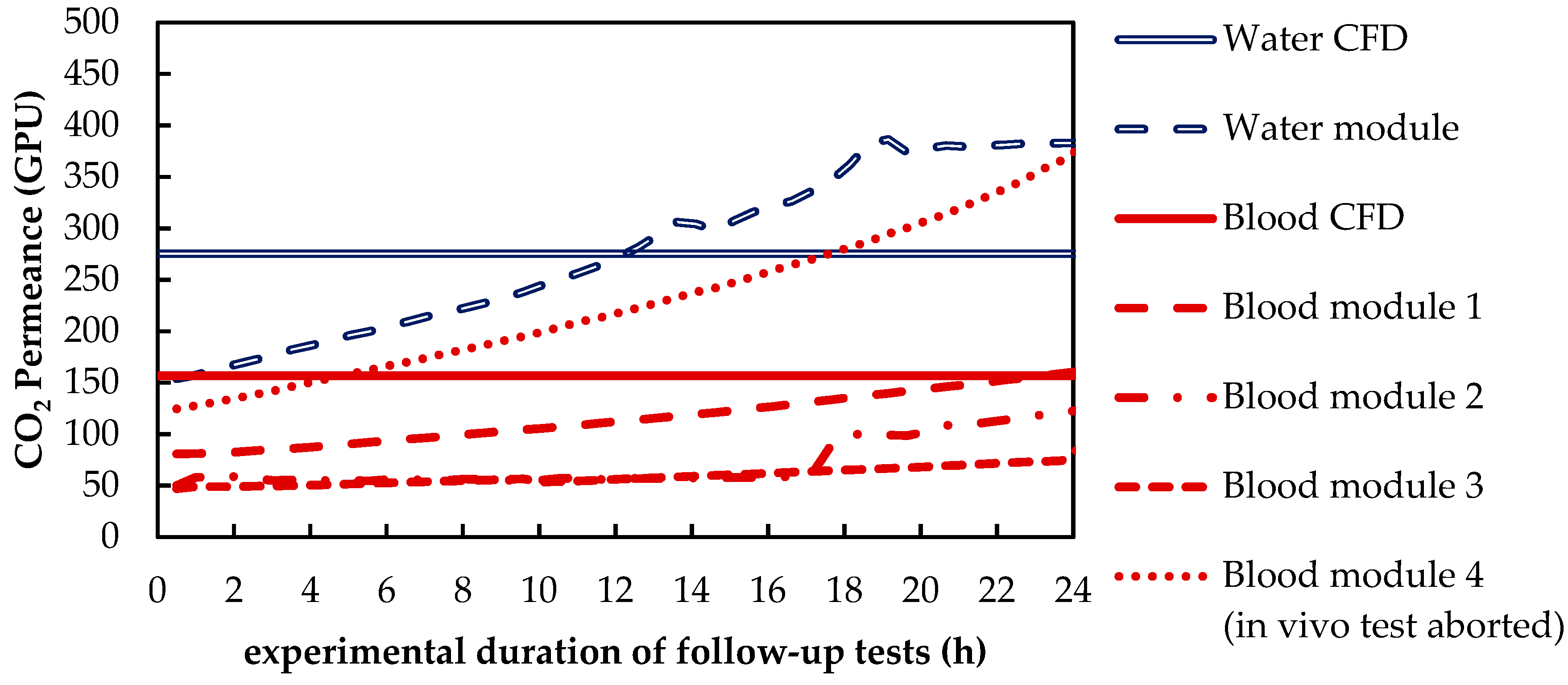
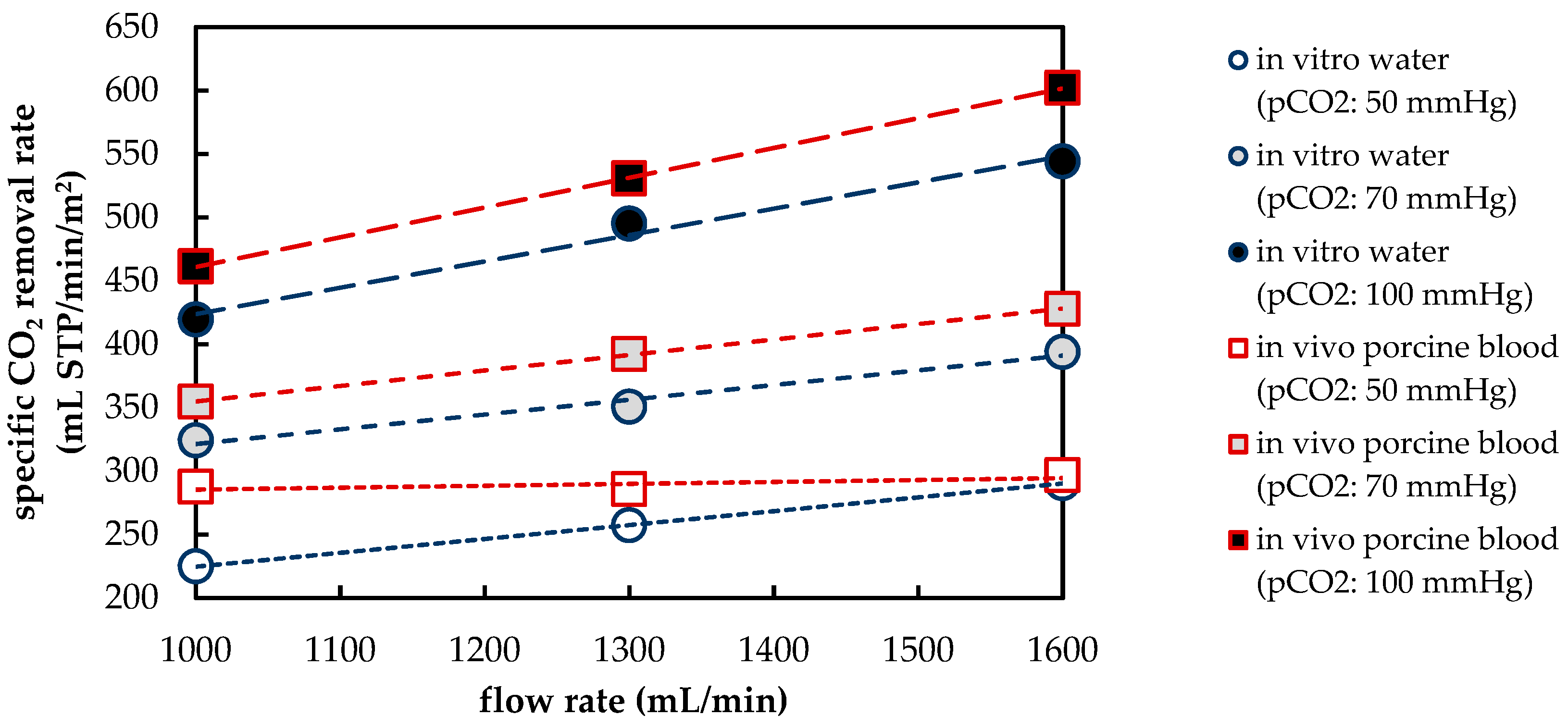
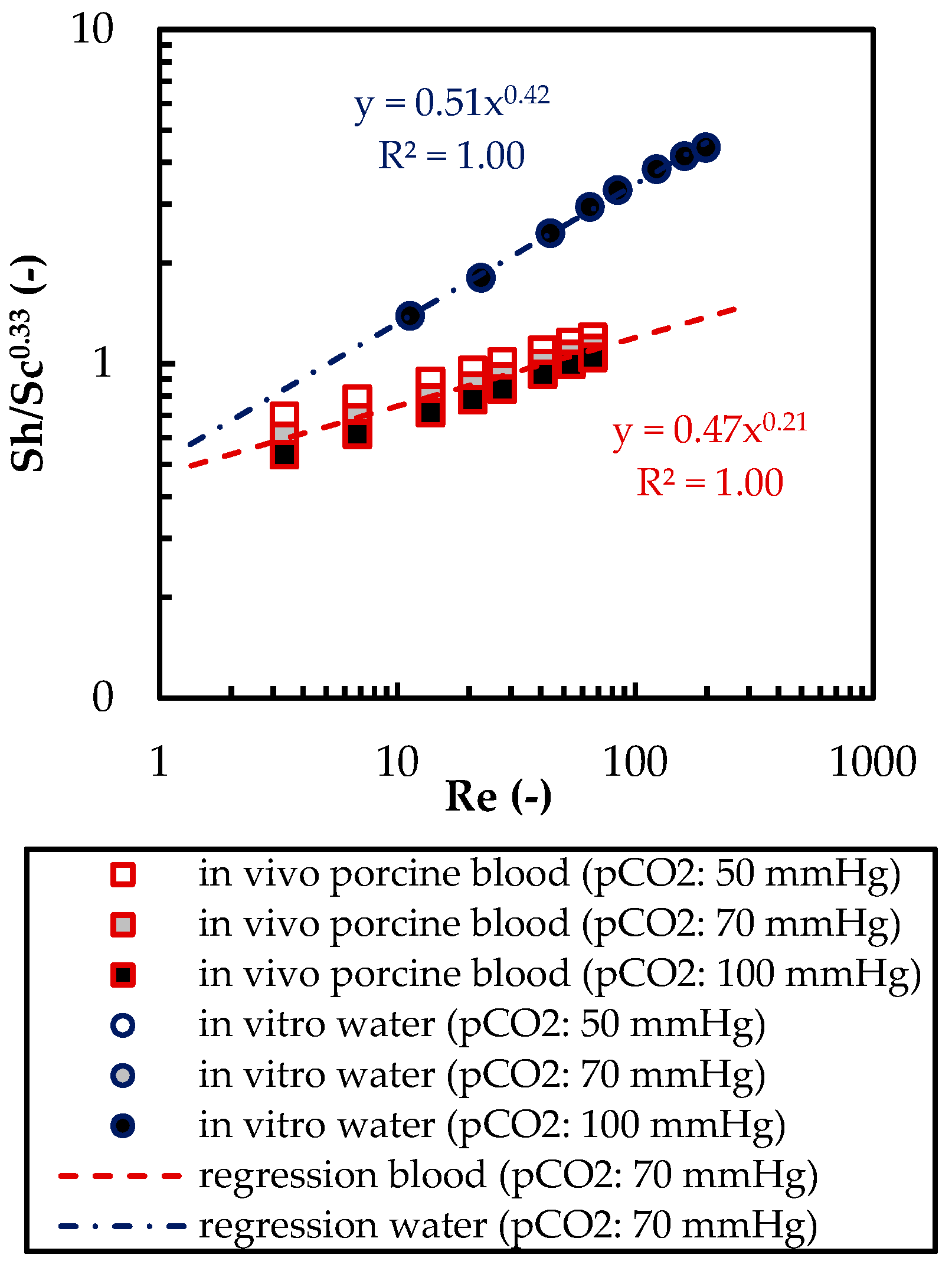
3.1.1. CO2 Removal Rate of In Vivo Porcine Blood and In Vitro Water Tests
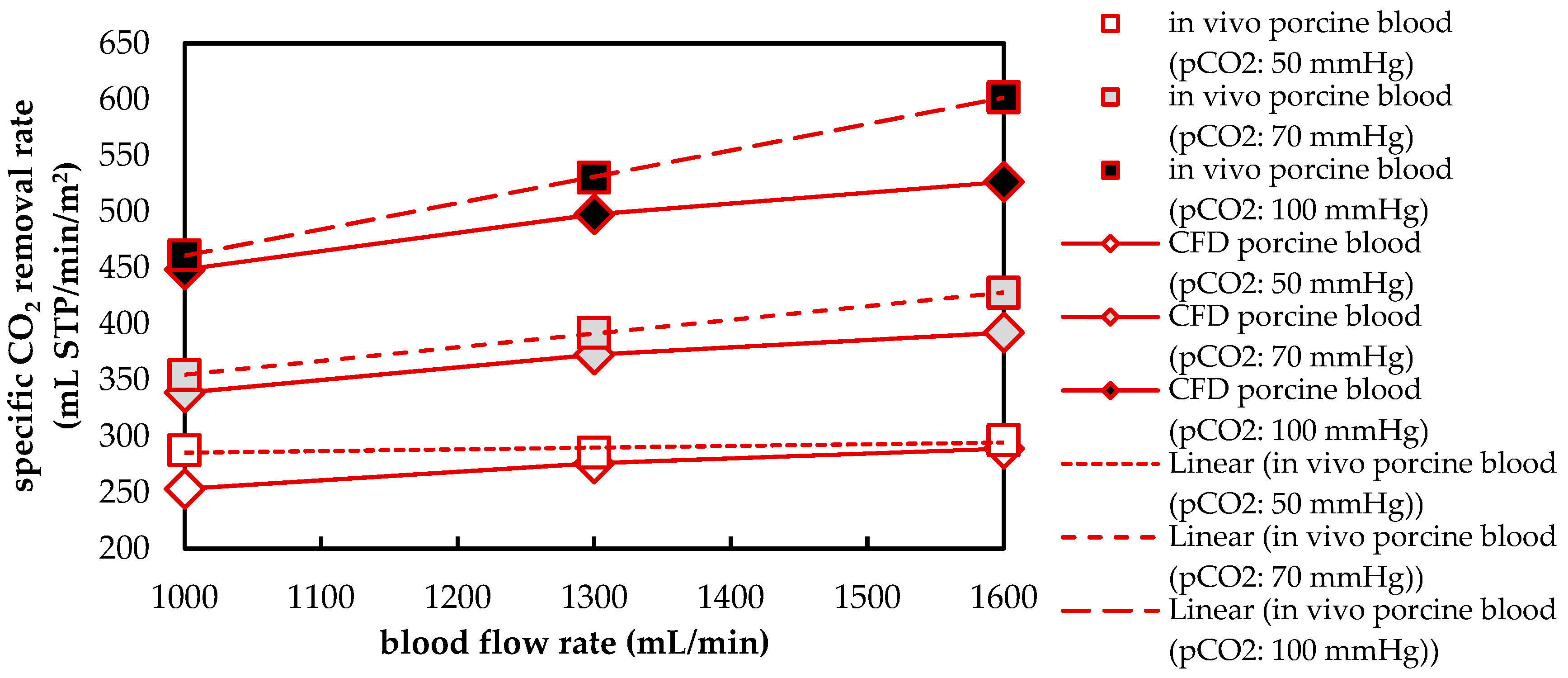
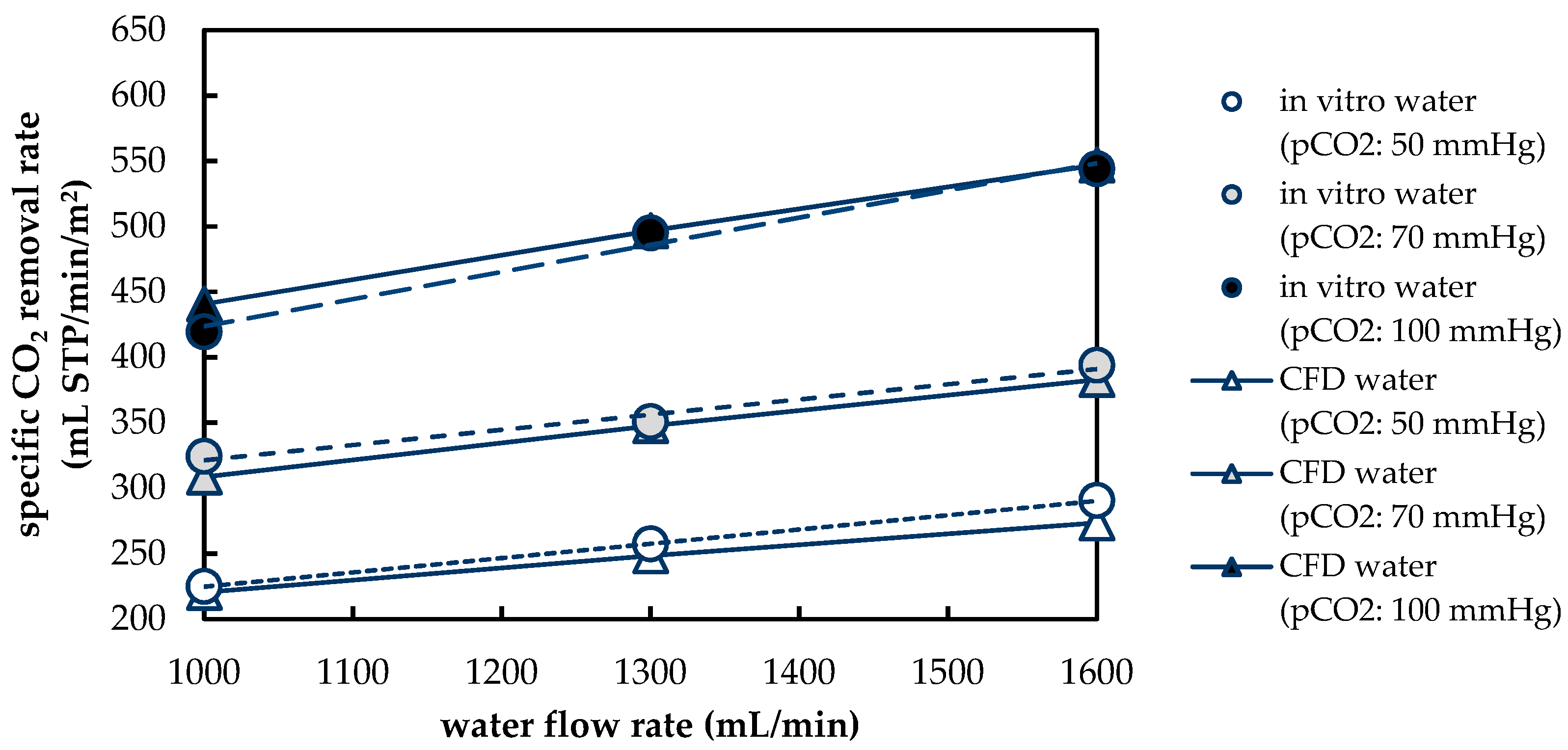
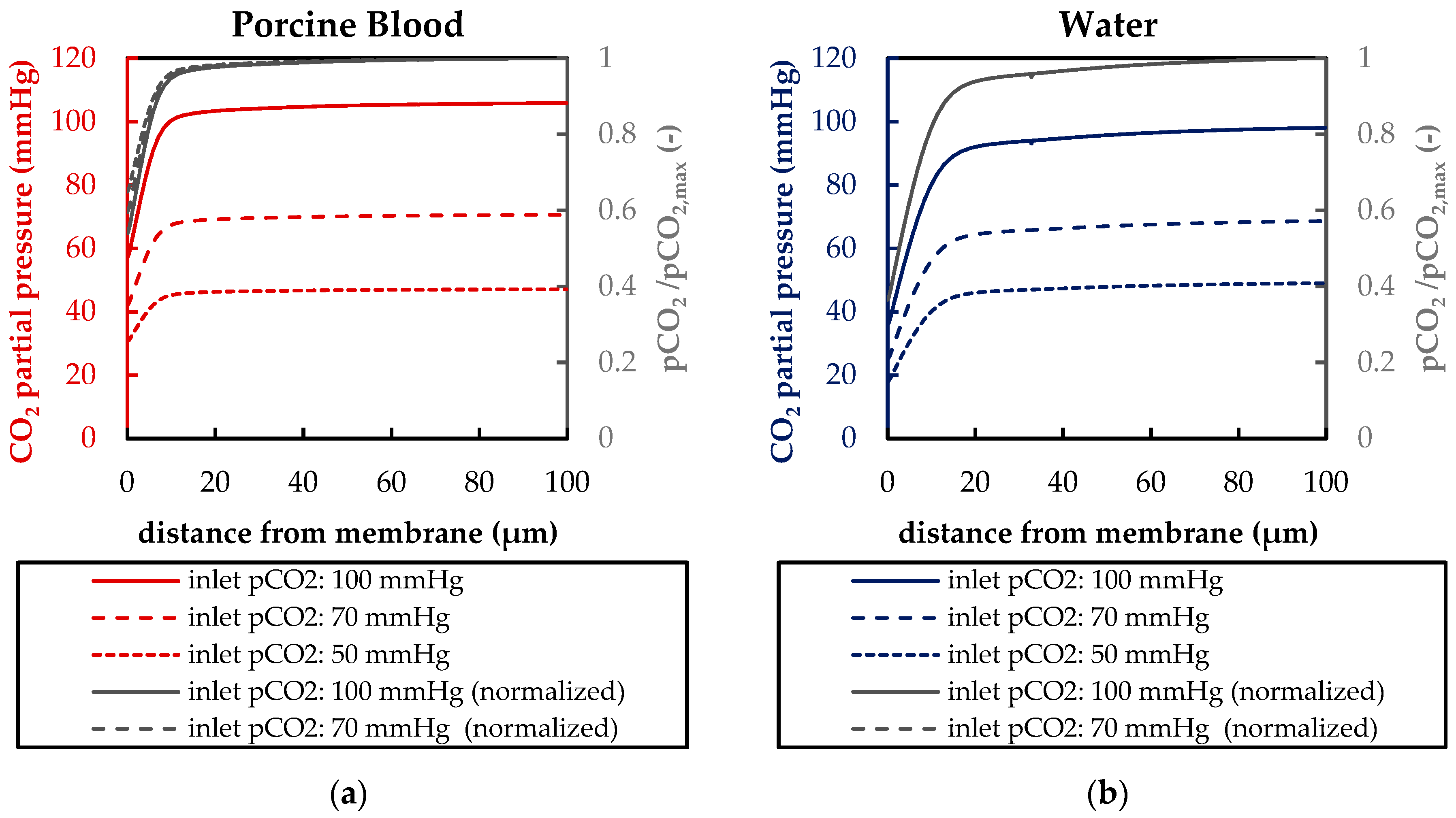
3.1.2. Validation of CFD CO2 Transport Simulations for Porcine Blood and Water
3.2. Computational Fluid Dynamic—CO2 Transport Simulations
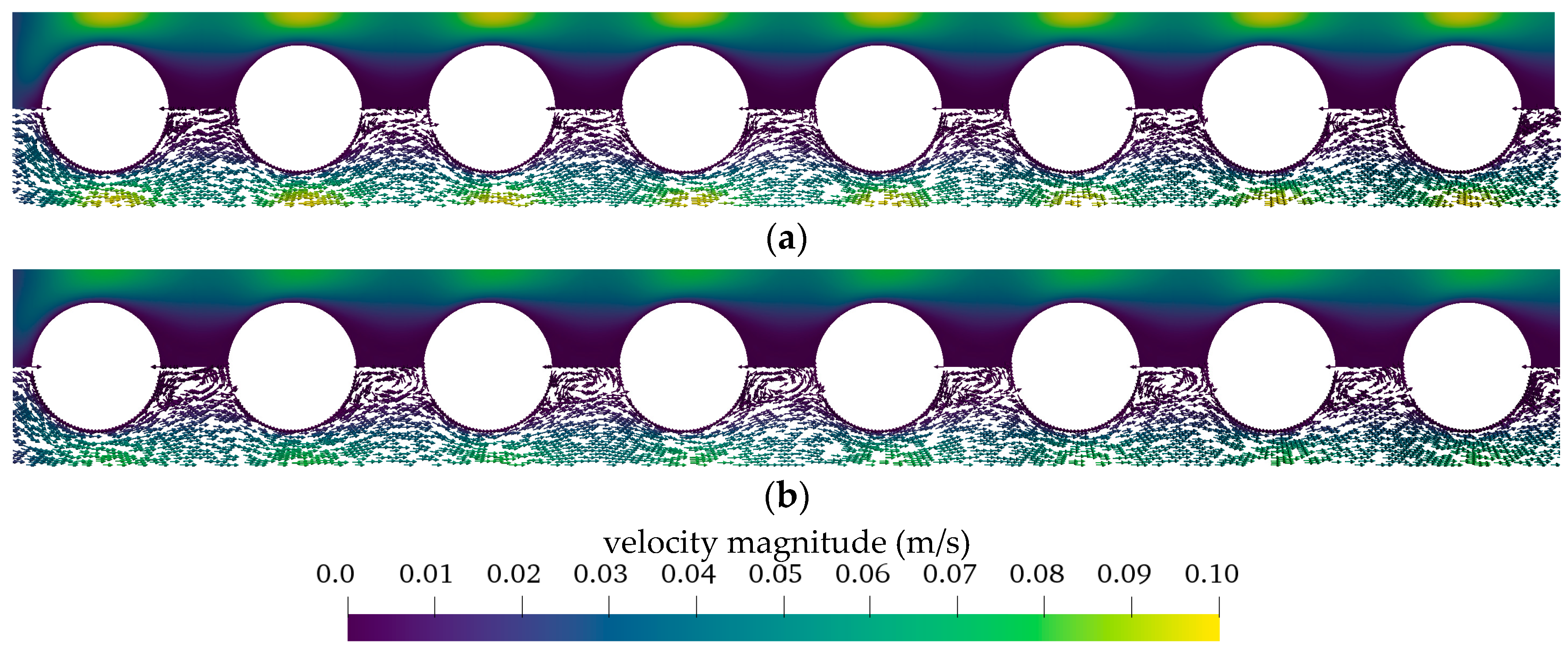
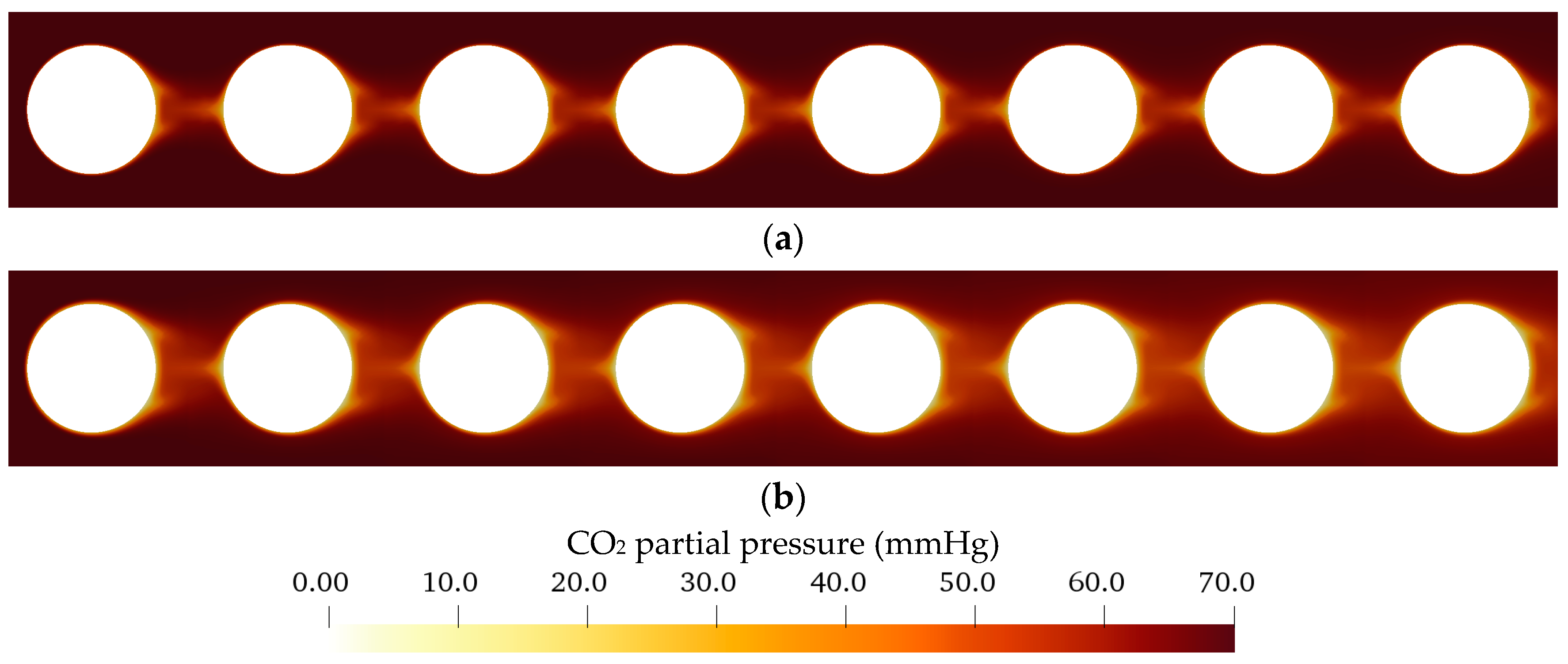
3.2.1. Flow and CO2 Partial Pressure Distribution in the Simplified Packing
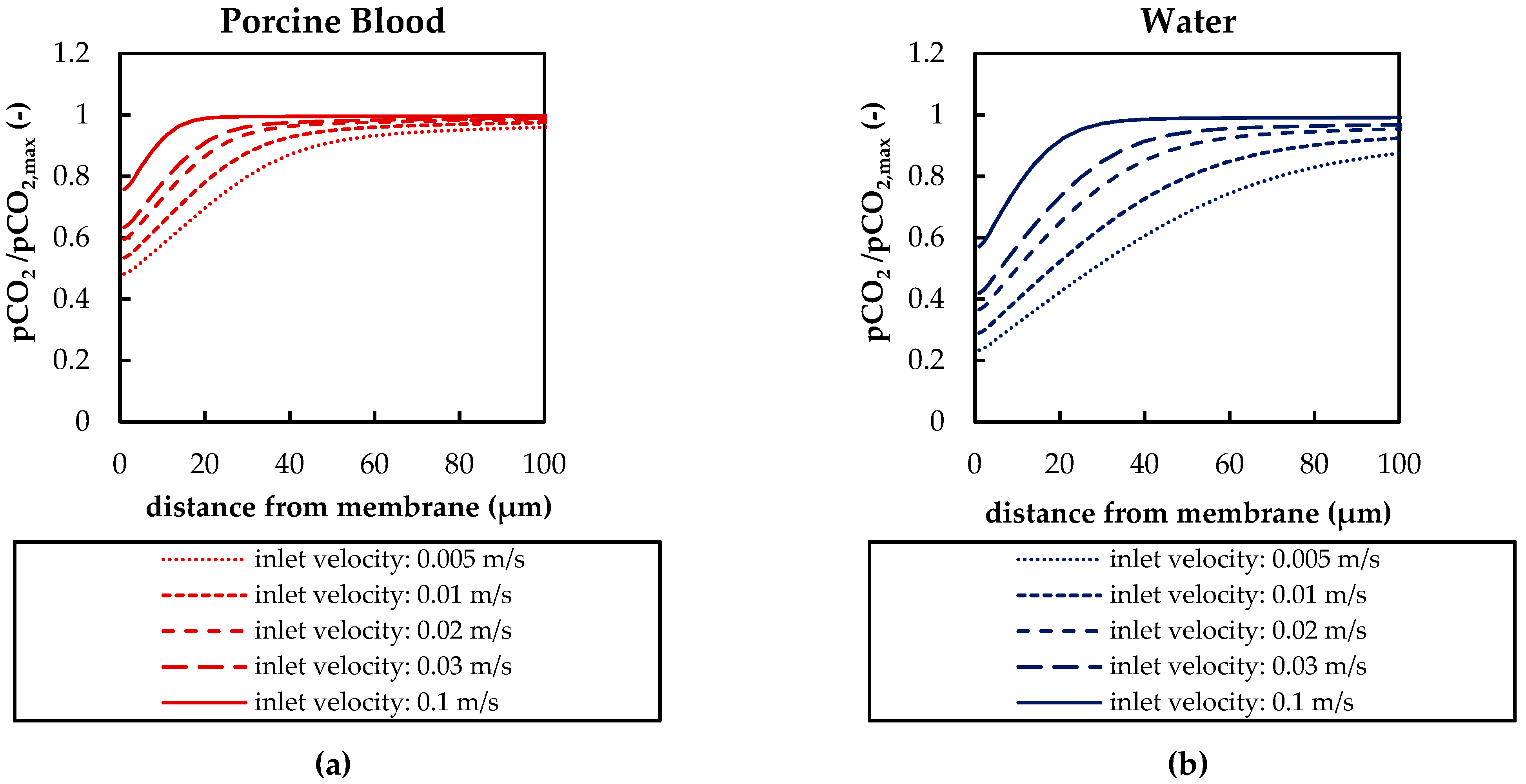
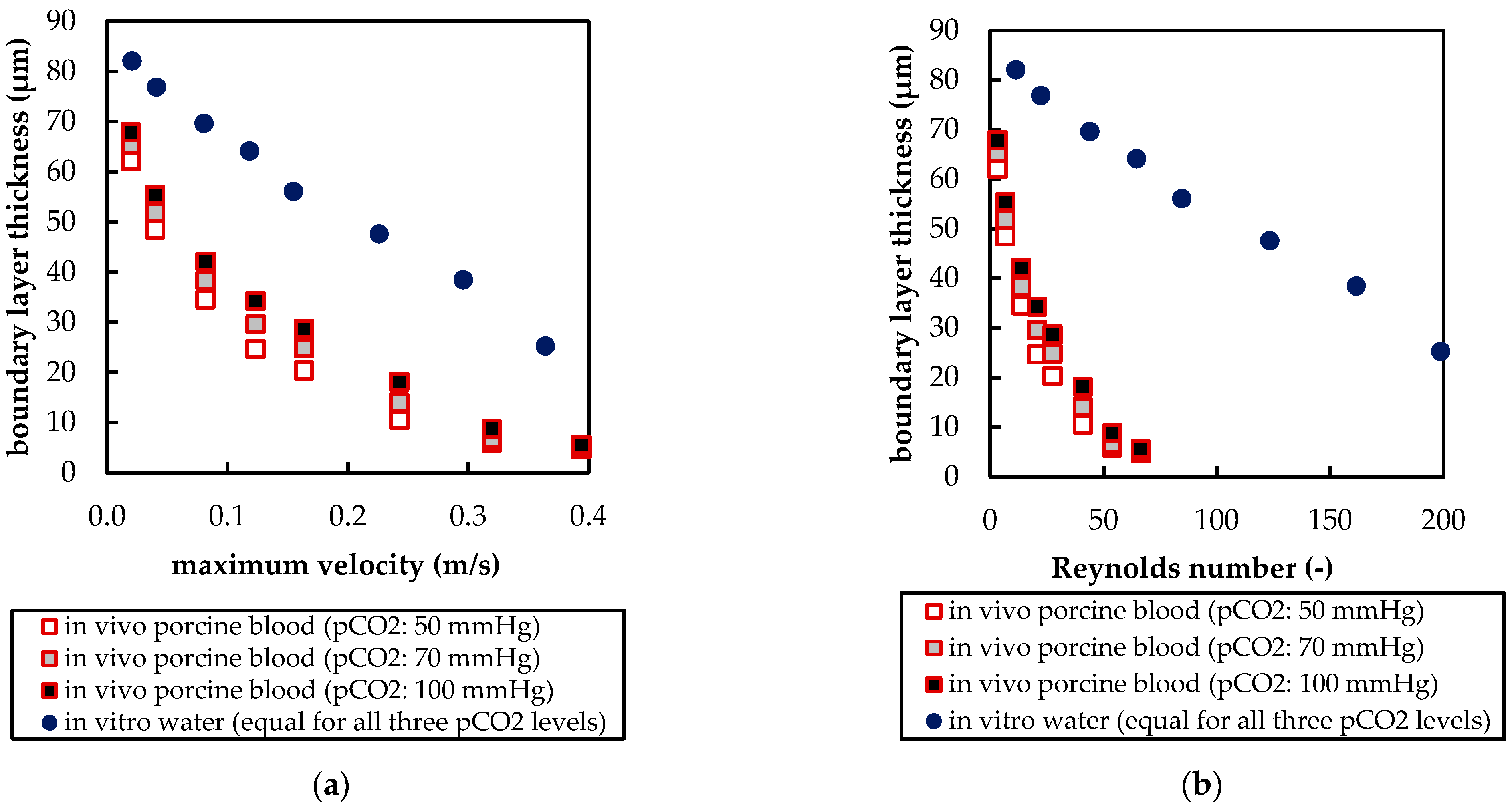
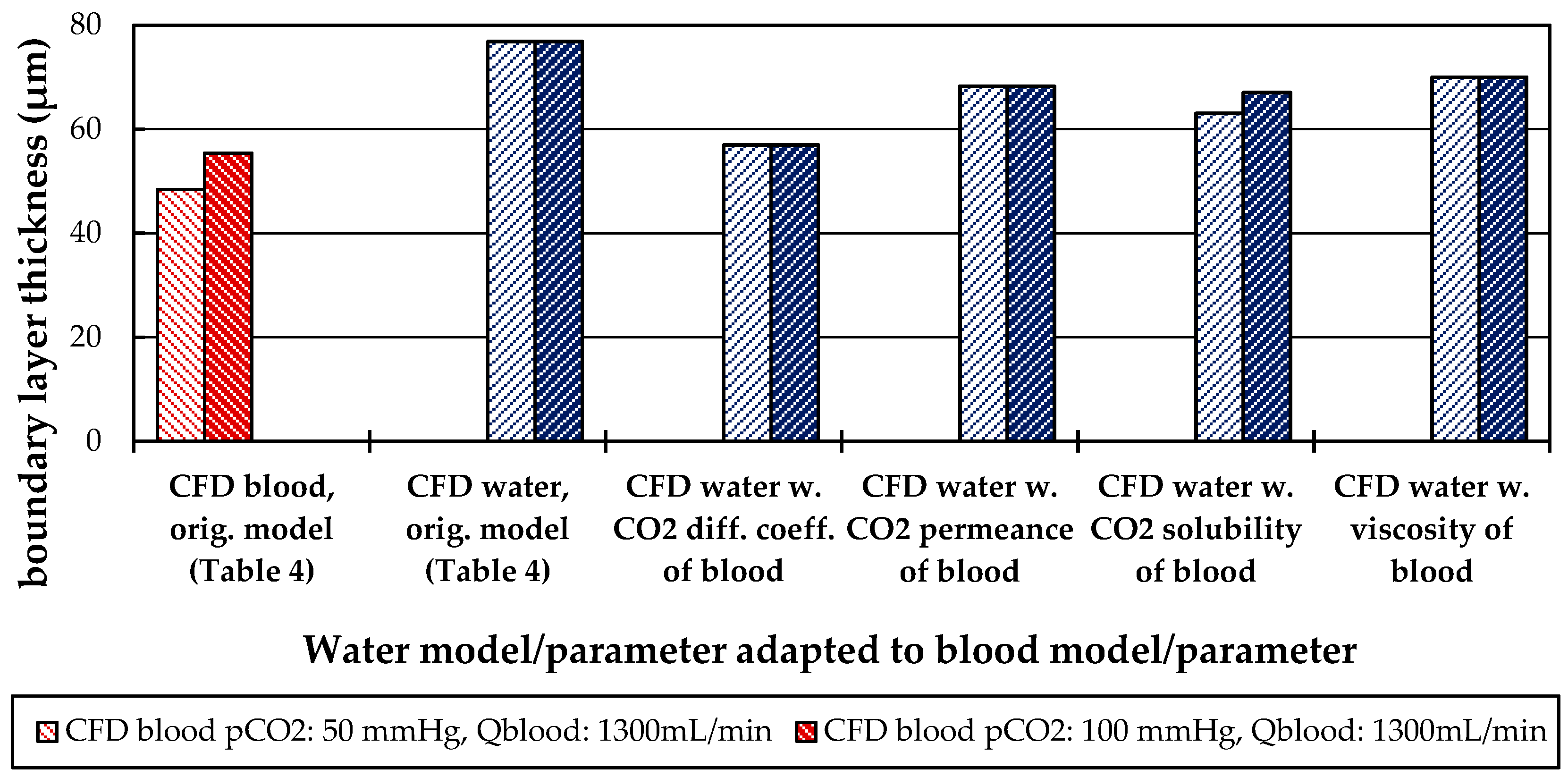
3.2.2. Boundary Layer Study
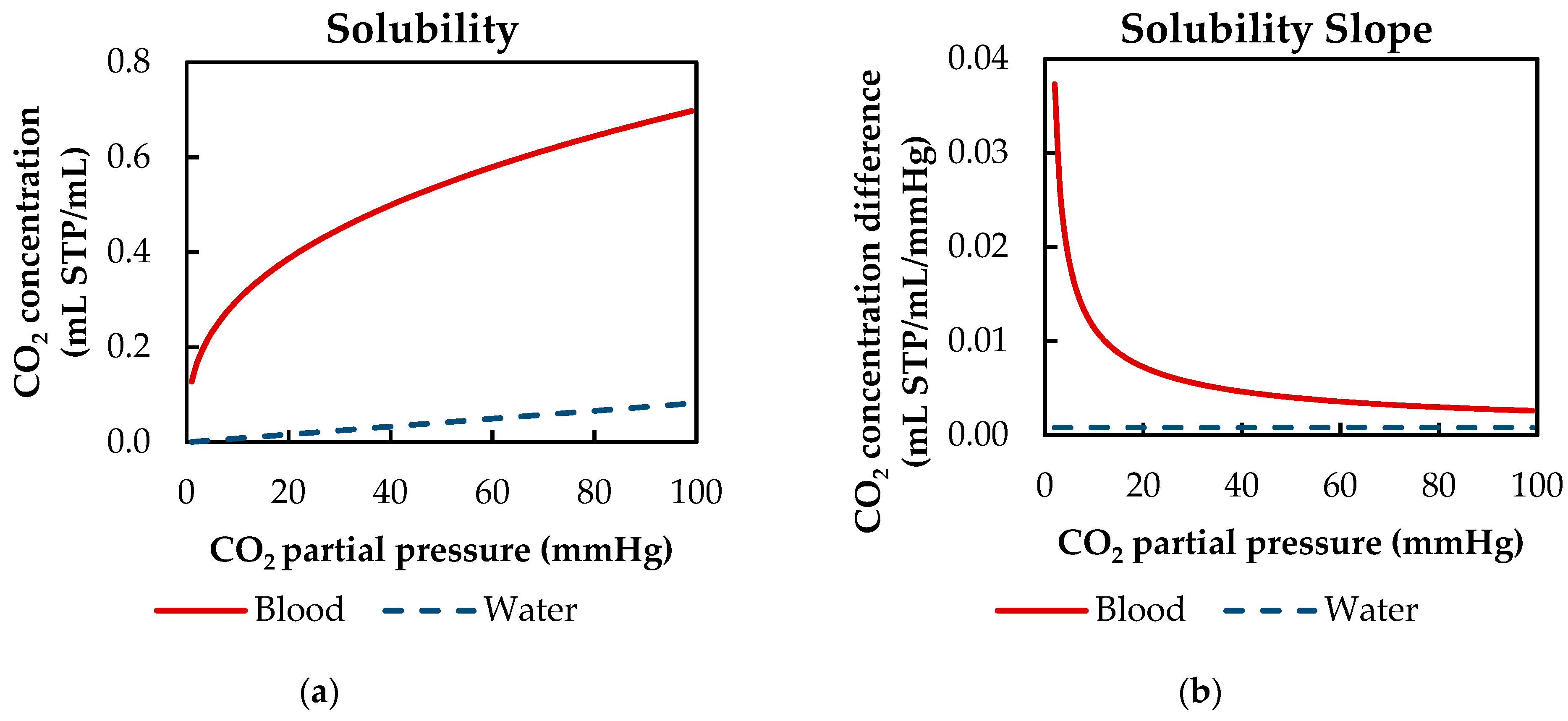
3.2.3. Influences of Fluid Properties on Boundary Layer Thickness
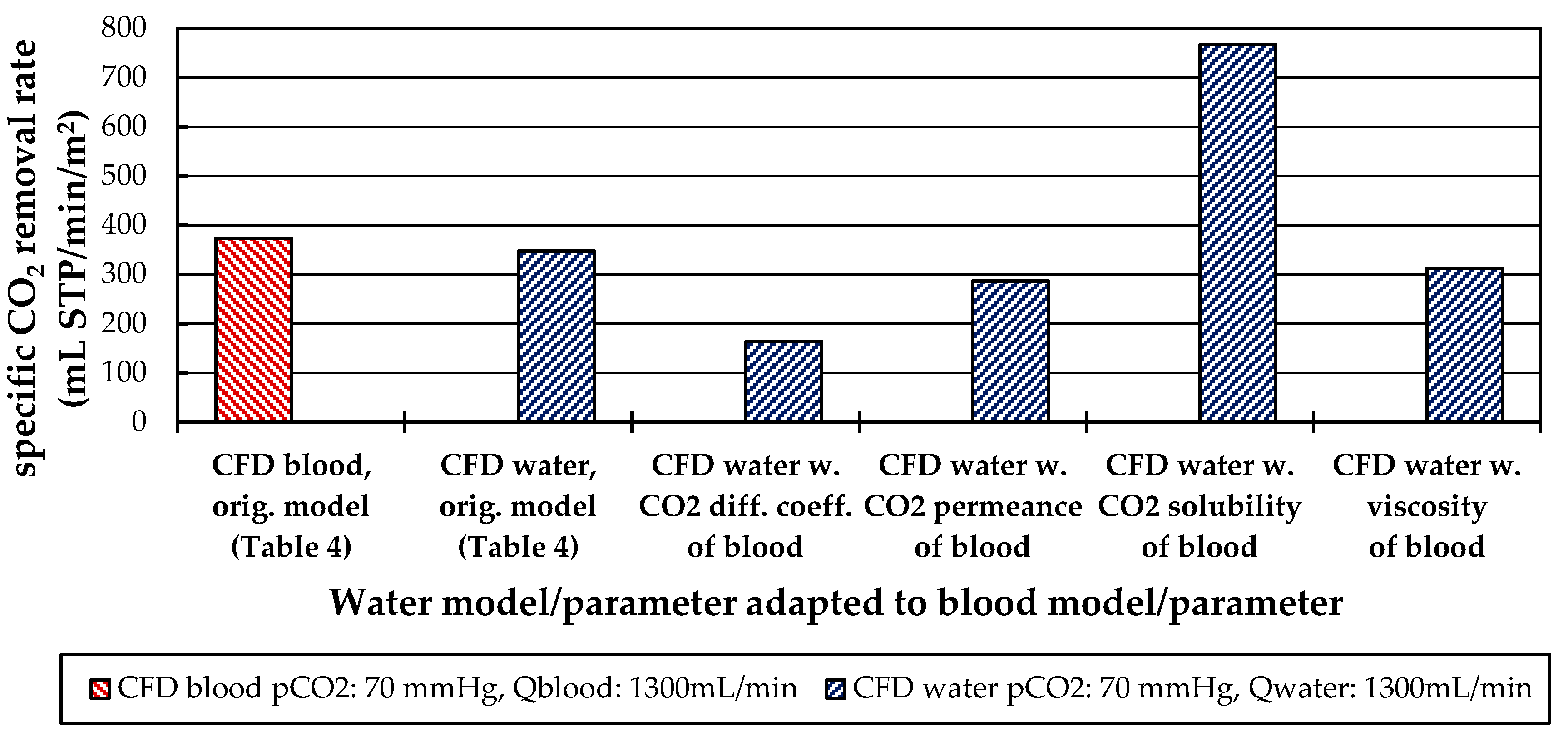
3.2.4. Influences of Fluid Properties on CO2 Removal Rate
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | |
| CFD | Computational fluid dynamics |
| CO2 | Carbon dioxide |
| H+ | Hydronium ion |
| H2CO3 | Carbonic acid |
| HCO3− | Bicarbonate |
| N2 | Nitrogen |
| O2 | Oxygen |
| Latin Symbols | |
| A | Membrane area |
| a | Empirical parameter of Sherwood correlation (multiplier) |
| b | Empirical parameter of Sherwood correlation (exponent) |
| DCO2 | CO2 diffusion coefficient |
| Deff | Coefficient of effective diffusion of CO2 in blood |
| Df | Coefficient of facilitated diffusion of CO2 in blood |
| dfiber | Outer hollow fiber membrane diameter |
| JCO2 | Transmembrane CO2 transport |
| jCO2 | Transmembrane CO2 flux |
| JCO2,blood | Transmembrane CO2 transport in in vivo porcine blood tests |
| JCO2,water | Transmembrane CO2 transport in in vitro water tests |
| kCO2 | CO2 mass transfer coefficient |
| L | Characteristic length of the Reynolds number |
| P | Membrane permeance |
| p | Pressure field |
| PCO2 | CO2 membrane permeance |
| pCO2 | CO2 partial pressure |
| pCO2,inlet | Inlet CO2 partial pressure |
| pCO2,max | Maximum CO2 partial pressure |
| pCO2,water | CO2 partial pressure in water |
| pCO2‘ | Normalized CO2 partial pressure |
| Re | Reynolds number |
| Reinlet | Reynolds number at the inlet pipe of the prototype oxygenator |
| Repacking | Reynolds number in the hollow fiber packing of the prototype oxygenator |
| Sc | Schmidt number |
| Sh | Sherwood number |
| U | Velocity field |
| u | Characteristic velocity of Reynolds number |
| umax | Maximum velocity between two fibers |
| x | Arbitrary point on shell side of prototype oxygenator |
| xinlet | Arbitrary point on shell side at inlet of prototype oxygenator |
| Greek Symbols | |
| αCO2 | CO2 solubility |
| ΔpCO2 | CO2 partial pressure difference between blood bulk flow and gas side |
| δ | CO2 boundary layer thickness |
| ε | Relative deviation of in vivo porcine blood to in vitro water CO2 removal rate |
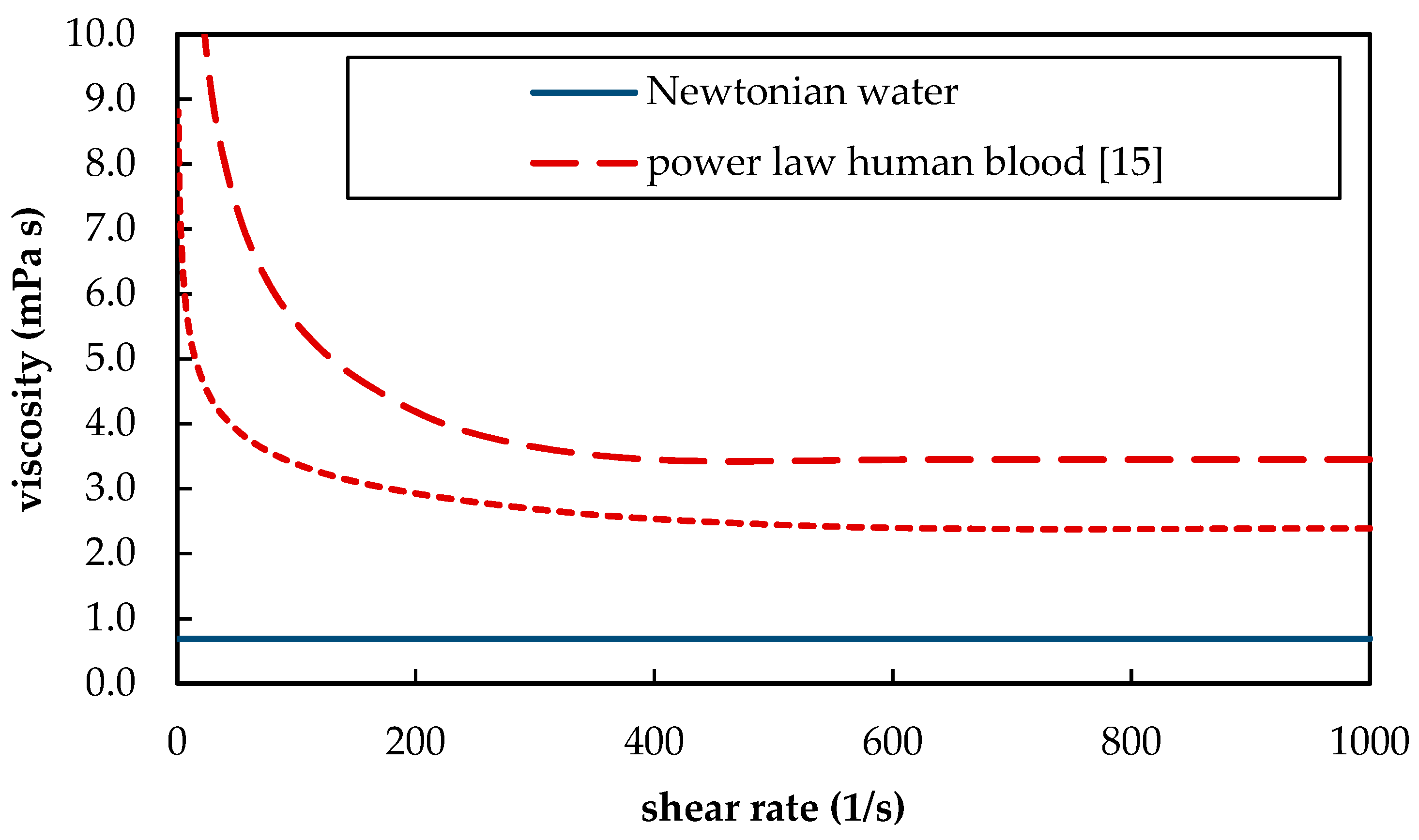
| µ | Dynamic viscosity |
| ν | Kinematic viscosity |
| ρ | Density |
References
- Goerke, A.R.; Leung, J.; Wickramasinghe, S.R. Mass and momentum transfer in blood oxygenators. Chem. Eng. Sci. 2002, 57, 2035–2046. [Google Scholar] [CrossRef]
- Federspiel, W.; Henchir, K. Lung. Artificial: Basic Principles and Current Applications. In Encyclopedia of Biomaterials and Biomedical Engineering, 2nd ed.; Wnek, G., Bowlin, G., Eds.; CRC Press: Danvers, USA, 2008; pp. 1661–1672. ISBN 978-1-4200-7802-2. [Google Scholar]
- Von Segesser, L.K. Coatings for cardiovascular devices: Extracorporeal circuits. In Coatings for Biomedical Applications; Driver, M., Ed.; Woodhead Publishing: Sawston, UK, 2012; pp. 251–263. ISBN 978-1-84569-568-2. [Google Scholar]
- Li, J.; Sly, M.; Chao, R.; Constantinescu, A.; Kulkarn, P.; Wians, F.; Jessen, M.; Eberhart, R. Transient adhesion of platelets in pump-oxygenator systems: Influence of SMA and nitric oxide treatments. J. Biomater. Sci. Polym. Ed. 1999, 10, 235–246. [Google Scholar] [CrossRef]
- Jaffer, I.H.; Reding, M.T.; Key, N.S.; Weitz, J.I. Hematologic Problems in the Surgical Patient. In Hematology; Elsevier BV: Amsterdam, The Netherlands, 2018; pp. 2304–2312.e4. [Google Scholar]
- Popel, A.S. Theory of oxygen transport to tissue. Crit. Rev. Biomed. Eng. 1989, 17, 257–321. [Google Scholar] [PubMed]
- Geers, C.; Gros, G. Carbon Dioxide Transport and Carbonic Anhydrase in Blood and Muscle. Physiol. Rev. 2000, 80, 681–715. [Google Scholar] [CrossRef]
- Lukitsch, B.; Ecker, P.; Elenkov, M.; Janeczek, C.; Jordan, C.; Krenn, C.; Ullrich, R.; Gfoehler, M.; Harasek, M. Suitable CO2 Solubility Models for Determination of the CO2 Removal Performance of Oxygenators. Bioengineering 2021, 8, 33. [Google Scholar] [CrossRef]
- Sander, R. Compilation of Henry’s law constants (version 4.0) for water as solvent. Atmos. Chem. Phys. Discuss. 2015, 15, 4399–4981. [Google Scholar] [CrossRef]
- Loeppky, J.A.L.; Luft, U.; Fletcher, E. Quantitative description of whole blood CO2 dissociation curve and Haldane effect. Respir. Physiol. 1983, 51, 167–181. [Google Scholar] [CrossRef]
- Svitek, R.G.; Federspiel, W.J. A Mathematical Model to Predict CO2 Removal in Hollow Fiber Membrane Oxygenators. Ann. Biomed. Eng. 2008, 36, 992–1003. [Google Scholar] [CrossRef]
- Windberger, U.; Bartholovitsch, A.; Plasenzotti, R.; Korak, K.J.; Heinze, G. Whole blood viscosity, plasma viscosity and erythrocyte aggregation in nine mammalian species: Reference values and comparison of data. Exp. Physiol. 2003, 88, 431–440. [Google Scholar] [CrossRef]
- Mehri, R.; Mavriplis, C.; Fenech, M. Red blood cell aggregates and their effect on non-Newtonian blood viscosity at low hematocrit in a two-fluid low shear rate microfluidic system. PLoS ONE 2018, 13, e0199911. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology Isobaric Properties for Water. Available online: https://webbook.nist.gov/cgi/fluid.cgi?P=1&TLow=20&THigh=40&TInc=1&Applet=on&Digits=5&ID=C7732185&Action=Load&Type=IsoBar&TUnit=C&PUnit=bar&DUnit=kg%2Fm (accessed on 10 December 2020).
- Cho, Y.I.; Kensey, K.R. Effects of the non-Newtonian viscosity of blood on flows in a diseased arterial vessel. Part 1: Steady flows. Biorheology 1991, 28, 241–262. [Google Scholar] [CrossRef]
- Lukitsch, B.; Ecker, P.; Elenkov, M.; Janeczek, C.; Haddadi, B.; Jordan, C.; Krenn, C.; Ullrich, R.; Gfoehler, M.; Harasek, M. Computation of Global and Local Mass Transfer in Hollow Fiber Membrane Modules. Sustainability 2020, 12, 2207. [Google Scholar] [CrossRef]
- Hout, M.S.; Hattler, B.G.; Federspiel, W.J. Validation of a model for flow-dependent carbon dioxide exchange in artificial lungs. Artif. Organs 2000, 24, 114–118. [Google Scholar] [CrossRef]
- Federspiel, W.J.; Haulert, B.G. Sweep Gas Flowrate and C02Exchange in Artificial Lungs. Artif. Organs 1996, 20, 1050–1052. [Google Scholar] [CrossRef]
- Hattler, B.G.; Lund, L.W.; Golob, J.F.; Russian, H.J.; Lann, M.F.; Merrill, T.L.; Frankowski, B.J.; Federspiel, W.J. A respiratory gas exchange catheter: In vitro and in vivo tests in large animals. J. Thorac. Cardiovasc. Surg. 2002, 124, 520–530. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Tabesh, H.; Gholami, M.H.; Torabi, D.; Mottaghy, K. A pH-based experimental method for carbon dioxide exchange evaluation in cylindrical hollow fiber membrane oxygenators. Asia-Pacific J. Chem. Eng. 2019, 14, 2337. [Google Scholar] [CrossRef]
- Mihelc, K.M.; Frankowski, B.J.; Lieber, S.C.; Moore, N.D.; Hattler, B.G.; Federspiel, W.J. Evaluation of a Respiratory Assist Catheter that Uses an Impeller Within a Hollow Fiber Membrane Bundle. ASAIO J. 2009, 55, 569–574. [Google Scholar] [CrossRef] [PubMed]
- Jeffries, R.G.; Frankowski, B.J.; Burgreen, G.W.; Federspiel, W.J. Effect of impeller design and spacing on gas exchange in a percutaneous respiratory assist catheter. Artif. Organs 2014, 38, 1007–1017. [Google Scholar] [CrossRef]
- van Leer, B. Towards the ultimate conservative difference scheme. II. Monotonicity and conservation combined in a second-order scheme. J. Comput. Phys. 1974, 14, 361–370. [Google Scholar] [CrossRef]
- Haddadi, B.; Jordan, C.; Miltner, M.; Harasek, M. Membrane modeling using CFD: Combined evaluation of mass transfer and geometrical influences in 1D and 3D. J. Membr. Sci. 2018, 563, 199–209. [Google Scholar] [CrossRef]
- Harasek, M.; Haddadi, B.; Miltner, M.; Schretter, P.; Jordan, C. Fully Resolved CFD Simulation of a Hollow Fibre Membrane Module. Chem. Eng. Trans. 2016, 52, 433–438. [Google Scholar] [CrossRef]
- Himmelblau, D.M. Diffusion of Dissolved Gases in Liquids. Chem. Rev. 1964, 64, 527–550. [Google Scholar] [CrossRef]
- Low, K.W.Q.; Van Loon, R.; Rolland, S.A.; Sienz, J. Formulation of Generalized Mass Transfer Correlations for Blood Oxygenator Design. J. Biomech. Eng. 2017, 139, 031007. [Google Scholar] [CrossRef] [PubMed]
- Baehr, H.D.; Karl, S. Wärme- und Stoffübertragung; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-87688-5. (In German) [Google Scholar]
- Schetz, J.A.; Bowersox, R.D.W. Boundary Layer Analysis, 2nd ed.; American Institute of Aeronautics and Astronautics (AIAA): Reston, VA, USA, 2011. [Google Scholar]




| Boundary | Velocity | Pressure |
|---|---|---|
| Inlet | uniform constant value | zero gradient 1 |
| Outlet | zero gradient 1 | uniform constant value |
| Membrane | no-slip | zero gradient 1 |
| Walls | no-slip | zero gradient1 |
| Total Flow Rate (mL/min) | Inlet Velocity Blood (m/s) 1 | Inlet Velocity Water (m/s) 1 |
|---|---|---|
| 1000 | 0.015 | 0.0148 |
| 1300 | 0.024 | 0.0192 |
| 1600 | 0.031 | 0.0237 |
| Boundary | Velocity | Pressure | CO2 |
|---|---|---|---|
| Inlet | uniform constant value | zero gradient 1 | uniform constant value |
| Outlet | zero gradient 1 | uniform constant value | zero gradient 1 |
| Membrane | uniform constant value | zero gradient 1 | zero gradient 1,2 |
| Sides | symmetry | symmetry | symmetry |
| Symbol | Description | Value Blood [8] | Value Water | Unit |
|---|---|---|---|---|
| αCO2 | CO2 solubility | 8.77 × 10−3 (1) | 8.27 × 10−4 | mL CO2/mL/mmHg |
| DCO2 | CO2 diffusion coefficient | 5.05 × 10−10 (2) | 2.38 × 10−9 | m2/s |
| µ | dynamic viscosity | 2.38 × 10−3 (3) | 6.91 × 10−4 | Pa s |
| ρ | density at 37 °C | 1.05 × 103 | 9.93 × 102 | kg/m3 |
| PCO2 | CO2 permeance of used fibers | 157 | 275 | GPU |
| Flow Rate 1 | Deviation (ε) of In Vitro CO2 Removal (Water) to In Vivo CO2 Removal (Blood) | ||
|---|---|---|---|
| (mL/min) | pCO2: 50 mmHg | pCO2: 70 mmHg | pCO2: 100 mmHg |
| 1000 | 21.8% | 8.6% | 9.7% |
| 1300 | 9.9% | 10.6% | 6.7% |
| 1600 | 2.1% | 7.9% | 9.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukitsch, B.; Koller, R.; Ecker, P.; Elenkov, M.; Janeczek, C.; Pekovits, M.; Haddadi, B.; Jordan, C.; Gfoehler, M.; Harasek, M. Water as a Blood Model for Determination of CO2 Removal Performance of Membrane Oxygenators. Membranes 2021, 11, 356. https://doi.org/10.3390/membranes11050356
Lukitsch B, Koller R, Ecker P, Elenkov M, Janeczek C, Pekovits M, Haddadi B, Jordan C, Gfoehler M, Harasek M. Water as a Blood Model for Determination of CO2 Removal Performance of Membrane Oxygenators. Membranes. 2021; 11(5):356. https://doi.org/10.3390/membranes11050356
Chicago/Turabian StyleLukitsch, Benjamin, Raffael Koller, Paul Ecker, Martin Elenkov, Christoph Janeczek, Markus Pekovits, Bahram Haddadi, Christian Jordan, Margit Gfoehler, and Michael Harasek. 2021. "Water as a Blood Model for Determination of CO2 Removal Performance of Membrane Oxygenators" Membranes 11, no. 5: 356. https://doi.org/10.3390/membranes11050356
APA StyleLukitsch, B., Koller, R., Ecker, P., Elenkov, M., Janeczek, C., Pekovits, M., Haddadi, B., Jordan, C., Gfoehler, M., & Harasek, M. (2021). Water as a Blood Model for Determination of CO2 Removal Performance of Membrane Oxygenators. Membranes, 11(5), 356. https://doi.org/10.3390/membranes11050356







