Effect of the Agglomerate Geometry on the Effective Electrical Conductivity of a Porous Electrode
Abstract
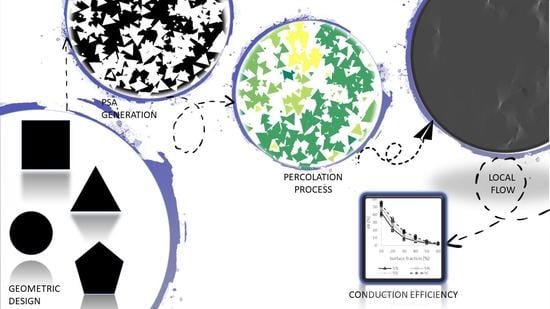
1. Introduction
2. Materials and Methods
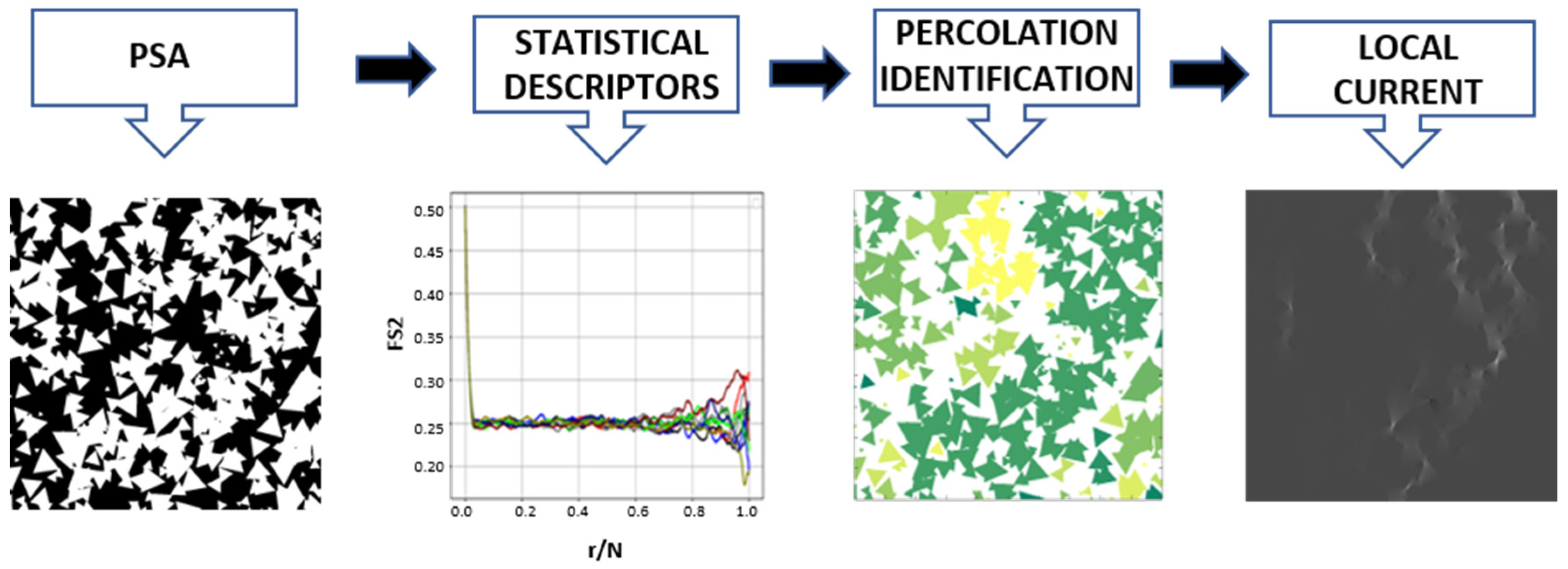
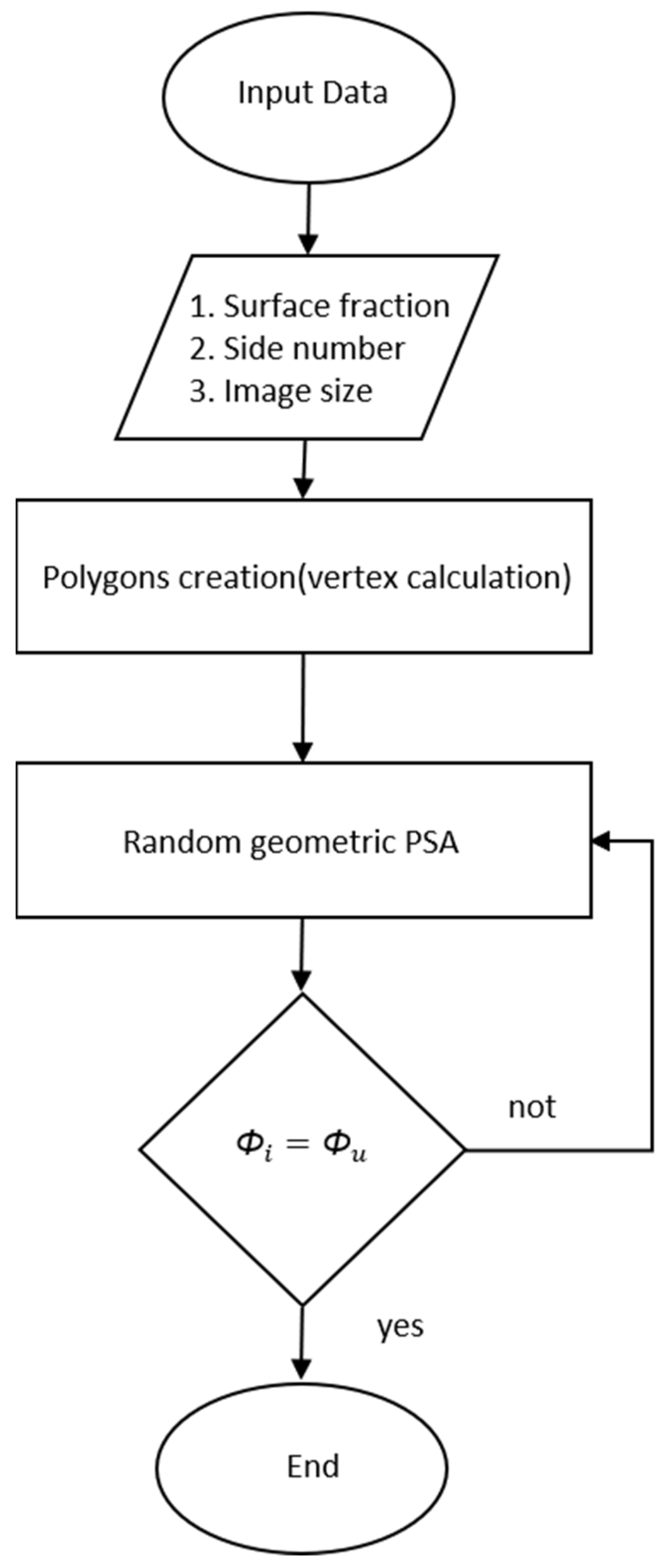
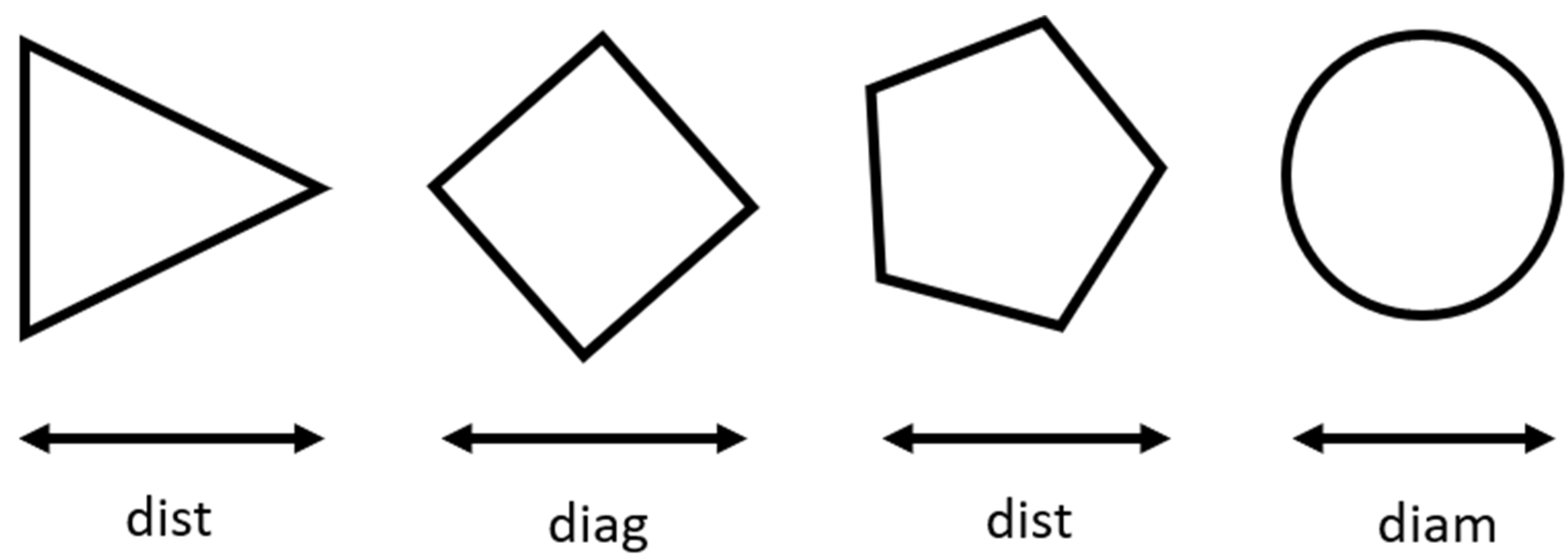
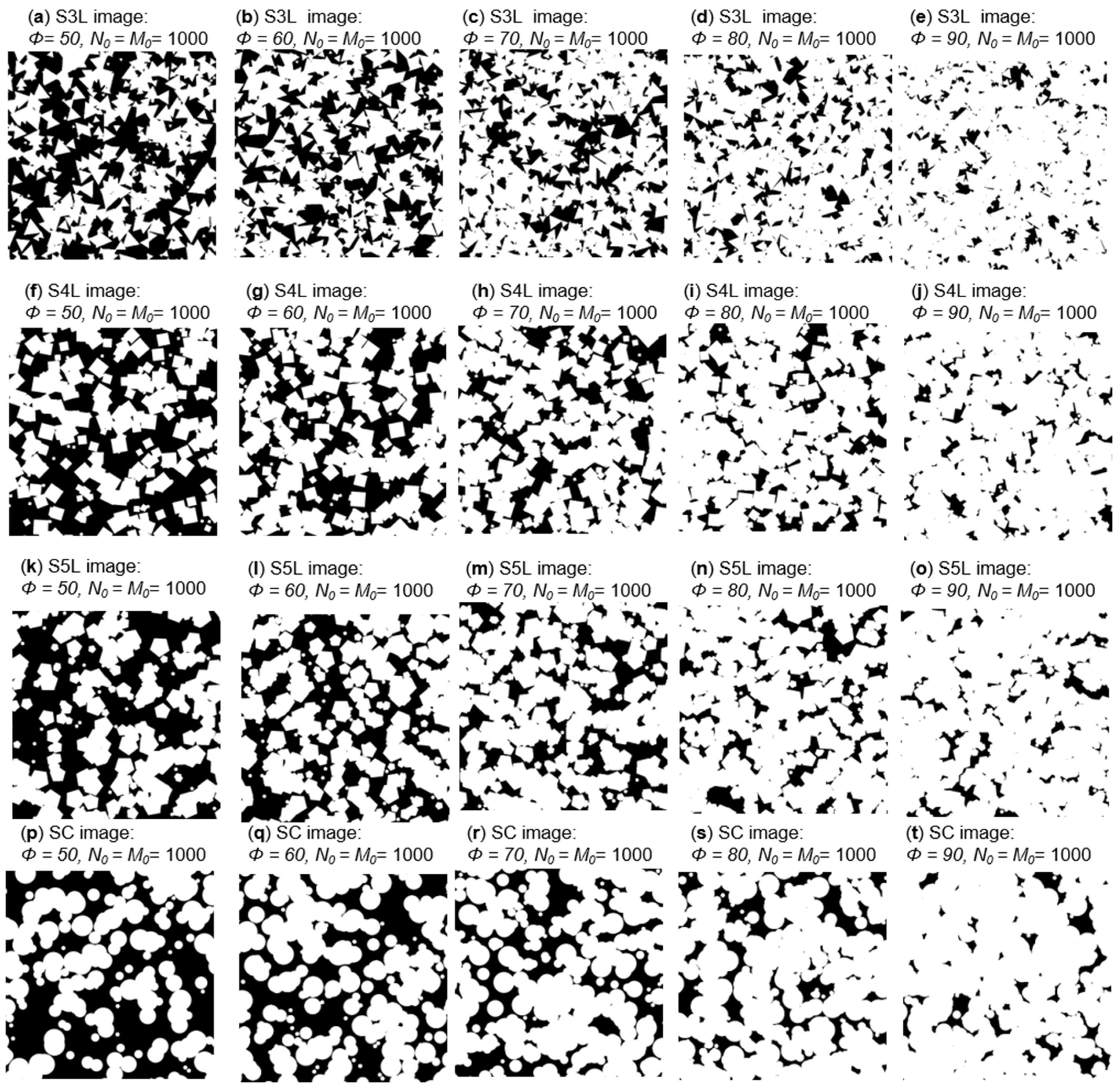
2.1. PSA Generation Process
2.2. Statistical Descriptors
2.2.1. Two-Point Correlation Function
2.2.2. Line-Path Correlation Function
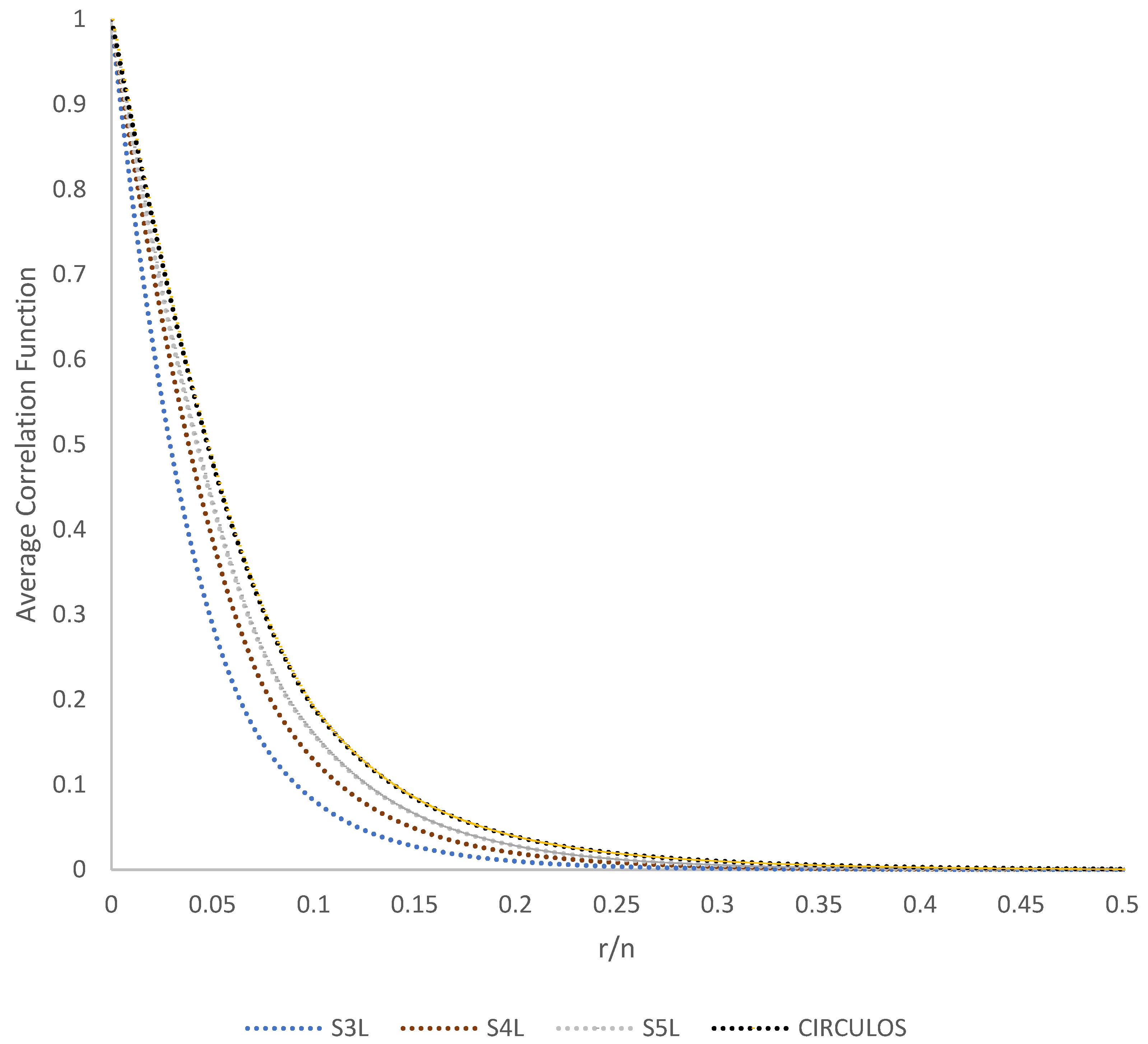
2.2.3. Average Correlation Function
2.3. Conduction Efficiency
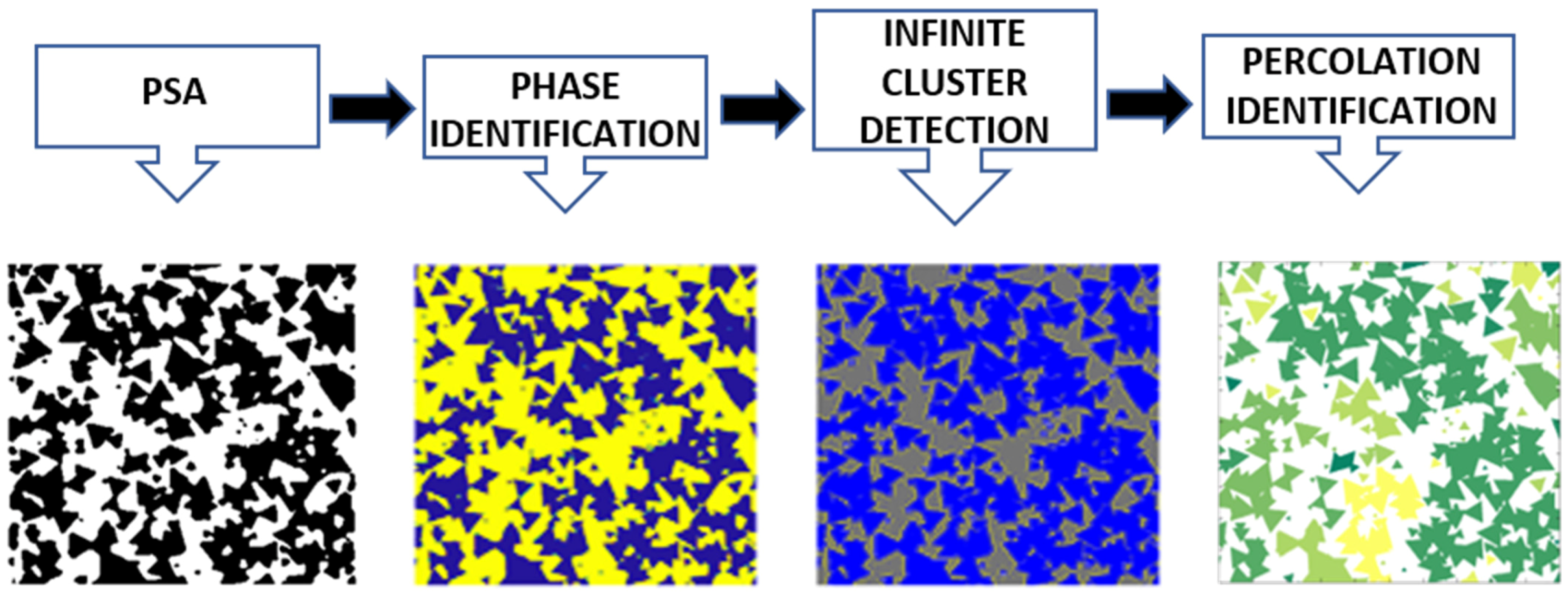
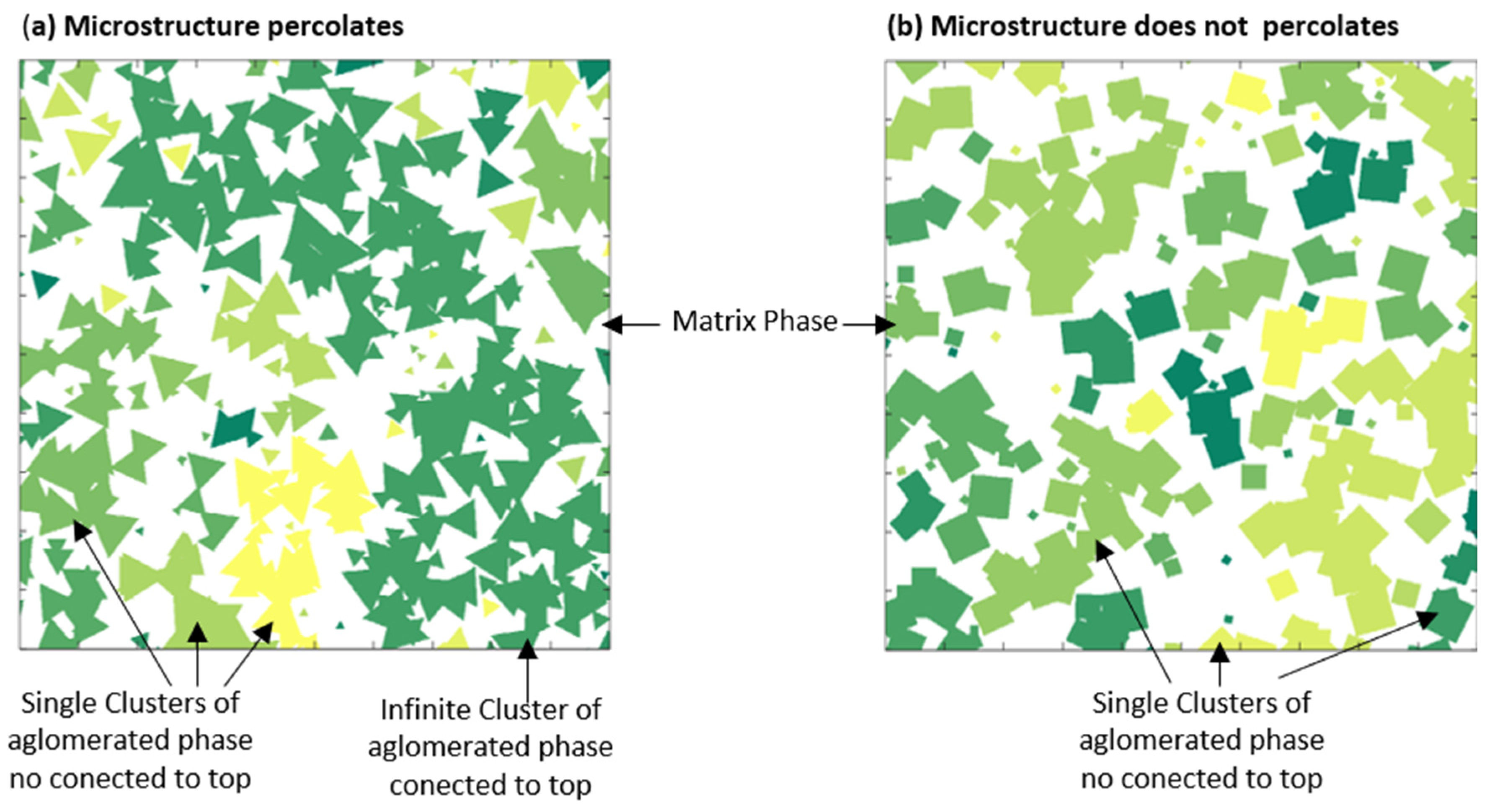
2.4. Percolation
3. Results and Discussions
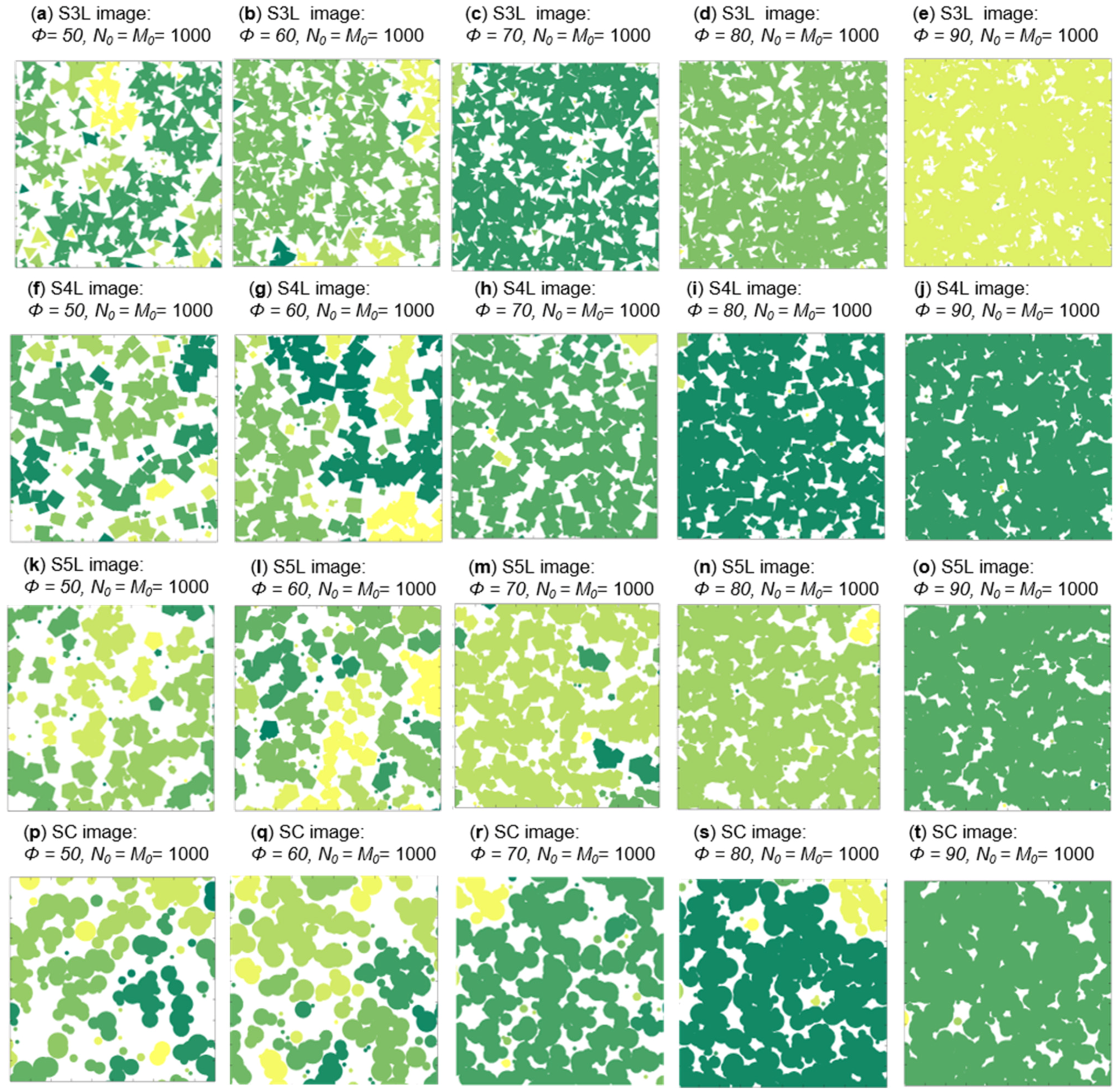
3.1. PSA Generation Process
3.2. Statistical Analysis of Microstructures
3.3. Percolation Process
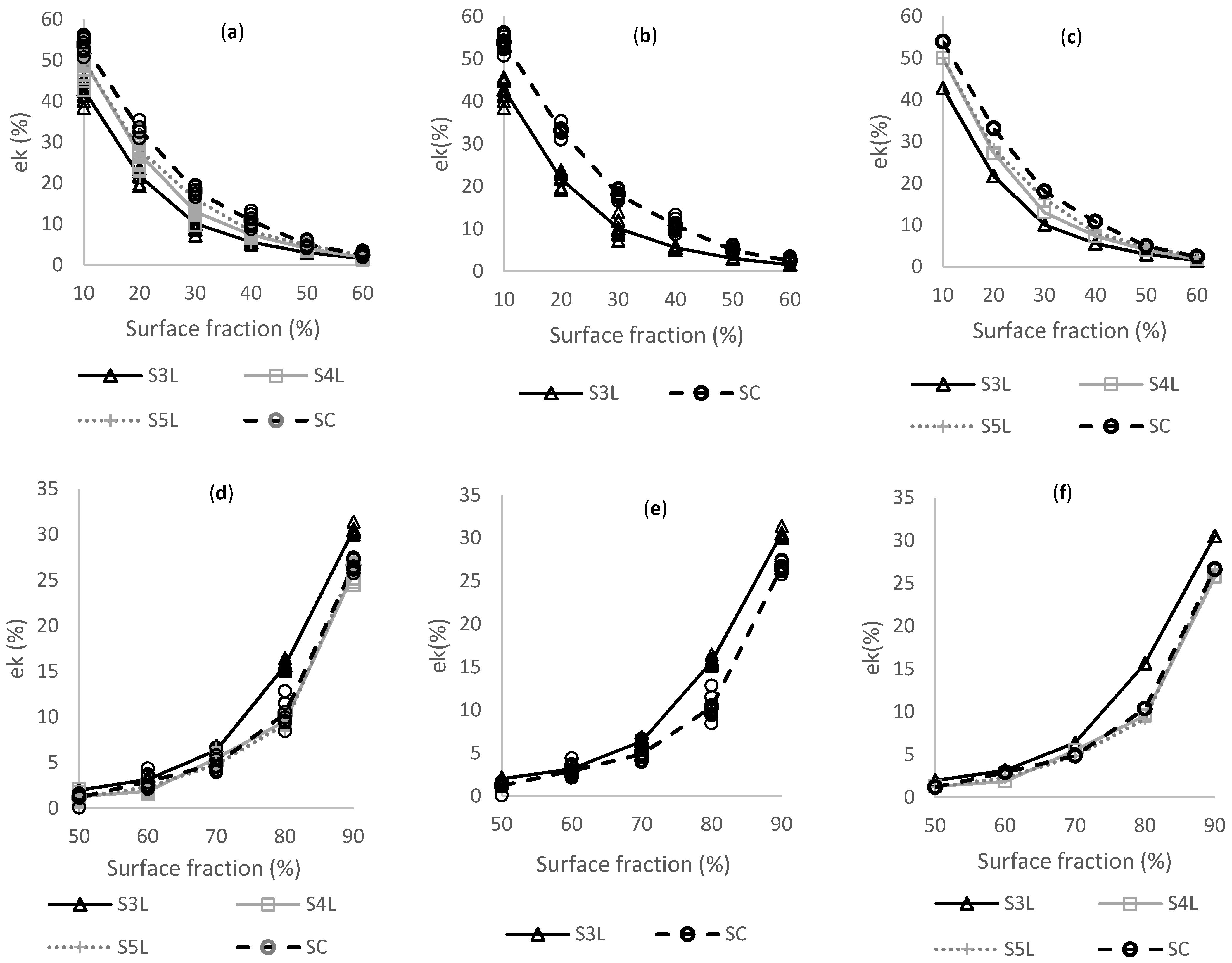
3.4. Conduction Efficiency
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Description |
| ETC | Effective Transport Coefficient |
| MEA | Membrane Electrode Assembly |
| H2 | Hydrogen |
| FC | Fuel Cells |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| CL | Catalytic Layer |
| RHM | Random Heterogeneous Materials |
| GDL | Gas Diffuser Layer |
| PSA | Polygonal Synthetic Agglomerate |
| FVM | Finite Volume Method |
| ω | Number of configurations |
| Ω | Microstructure assembly |
| W | Number of random series |
| X | Position of an arbitrary point |
| r | length of an arbitrary line segment |
| Phase function of the phase Π | |
| Surface Fraction of the phase Π | |
| Two-point correlation function | |
| Line-path correlation function | |
| Average correlation function | |
| Autocovariance function | |
| Normalized autocovariance function | |
| Normalized line-path correlation function | |
| Effective conductivity | |
| Nominal conductivity | |
| Electric current | |
| J | Generalized flux |
| Effective electric flux | |
| E | Applied potential |
| R | Electrical resistance |
| Conduction efficiency | |
| θ | Angle of the vertex position |
| L | Number of sides of the polygon |
| e | Vertex index |
| SC | Circular geometry |
| S3L | 3 Sides geometry |
| S4L | 4 Sides geometry |
| S5L | 5 Sides geometry |
References
- Gahleitner, G. Hydrogen from renewable electricity: An international review of power-to-gas pilot plants for stationary applications. Int. J. Hydrog. Energy 2013, 38, 2039–2061. [Google Scholar] [CrossRef]
- Cabezas, M.D.; Frak, A.E.; Sanguinetti, A.; Franco, J.I.; Fasoli, H.J. Hydrogen energy vector: Demonstration pilot plant with minimal peripheral equipment. Int. J. Hydrog. Energy 2014, 39, 18165–18172. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Zhang, J. Review of characterization and modeling of polymer electrolyte fuel cell catalyst layer: The blessing and curse of ionomer. Front. Energy 2017, 11, 334–364. [Google Scholar] [CrossRef]
- Falcão, D.; Gomes, P.; Oliveira, V.; Pinho, C.; Pinto, A. 1D and 3D numerical simulations in PEM fuel cells. Int. J. Hydrog. Energy 2011, 36, 12486–12498. [Google Scholar] [CrossRef]
- Simari, C.; Enotiadis, A.; Nicotera, I. Transport Properties and Mechanical Features of Sulfonated Polyether Ether Ketone/Organosilica Layered Materials Nanocomposite Membranes for Fuel Cell Applications. Membranes 2020, 10, 87. [Google Scholar] [CrossRef]
- Barbosa, R.; Andaverde, J.; Escobar, B.; Cano, U. Stochastic reconstruction and a scaling method to determine effective transport coefficients of a proton exchange membrane fuel cell catalyst layer. J. Power Sources 2011, 196, 1248–1257. [Google Scholar] [CrossRef]
- Wang, W.; Qu, Z.; Wang, X.; Zhang, J. A Molecular Model of PEMFC Catalyst Layer: Simulation on Reactant Transport and Thermal Conduction. Membranes 2021, 11, 148. [Google Scholar] [CrossRef] [PubMed]
- Vel, S.S.; Goupee, A.J. Multiscale thermoelastic analysis of random heterogeneous materials: Part I: Microstructure characterization and homogenization of material properties. Comput. Mater. Sci. 2010, 48, 22–38. [Google Scholar] [CrossRef]
- Rodriguez, A.; Barbosa, R.; Rios, A.; Ortegon, J.; Escobar, B.; Gayosso, B.; Couder, C. Effect of An Image Resolution Change on the Effective Transport Coefficient of Heterogeneous Materials. Materials 2019, 12, 3757. [Google Scholar] [CrossRef]
- Wilberforce, T.; Ijaodola, O.; Emmanuel, O.; Thompson, J.; Olabi, A.; Abdelkareem, M.; Sayed, E.; Elsaid, K.; Maghrabie, H. Optimization of Fuel Cell Performance Using Computational Fluid Dynamics. Membranes 2021, 11, 146. [Google Scholar] [CrossRef]
- Nakagomi, K.; Shimizu, A.; Kobatake, H.; Yakami, M.; Fujimoto, K.; Togashi, K. Multi-shape graph cuts with neighbor prior constraints and its application to lung segmentation from a chest CT volume. Med. Image Anal. 2013, 17, 62–77. [Google Scholar] [CrossRef]
- Spadea, M.F.; Pileggi, G.; Zaffino, P.; Salome, P.; Catana, C.; Izquierdo-Garcia, D.; Amato, F.; Seco, J. Deep Convolution Neural Network (DCNN) Multiplane Approach to Synthetic CT Generation from MR Images—Application in Brain Proton Therapy. Int. J. Radiat. Oncol. 2019, 105, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Sánchez, A.; Couder-Castañeda, C.; Hernández-Gómez, J.J.; Medina, I.; Pena-Ruiz, S.; Sosa-Pedroza, J.; Enciso-Aguilar, M.A. Analysis of Electromagnetic Propagation from MHz to THz with a Memory-Optimised CPML-FDTD Algorithm. Int. J. Antennas Propag. 2018, 2018, 5710943. [Google Scholar] [CrossRef]
- Diaz-Albarran, L.; Lugo-Hernandez, E.; Ramirez-Garcia, E.; Enciso-Aguilar, M.; Valdez-Perez, D.; Cereceda-Company, P.; Granados, D.; Costa-Krämer, J. Development and characterization of cyclic olefin copolymer thin films and their dielectric characteristics as CPW substrate by means of Terahertz Time Domain Spectroscopy. Microelectron. Eng. 2018, 191, 84–90. [Google Scholar] [CrossRef]
- Jiang, B.; Ma, X.; Lu, Y.; Li, Y.; Feng, L.; Shi, Z. Ship detection in spaceborne infrared images based on Convolutional Neural Networks and synthetic targets. Infrared Phys. Technol. 2019, 97, 229–234. [Google Scholar] [CrossRef]
- Sánchez, J.G.; Balderrama, V.S.; Garduño, S.I.; Osorio, E.; Viterisi, A.; Estrada, M.; Ferre-Borrull, J.; Pallares, J.; Marsal, L.F. Impact of inkjet printed ZnO electron transport layer on the characteristics of polymer solar cells. RSC Adv. 2018, 8, 13094–13102. [Google Scholar] [CrossRef]
- Moussaoui, H.; Laurencin, J.; Gavet, Y.; Delette, G.; Hubert, M.; Cloetens, P.; Le Bihan, T.; Debayle, J. Stochastic geometrical modeling of solid oxide cells electrodes validated on 3D reconstructions. Comput. Mater. Sci. 2018, 143, 262–276. [Google Scholar] [CrossRef]
- An, J.; Tang, B.; Ning, X.; Zhou, J.; Zhao, B.; Xu, W.; Corredor, A.C.; Lombardi, J.R. Photoinduced Shape Evolution: From Triangular to Hexagonal Silver Nanoplates. J. Phys. Chem. C 2007, 111, 18055–18059. [Google Scholar] [CrossRef]
- Vinayan, B.; Sethupathi, K.; Ramaprabhu, S. Facile synthesis of triangular shaped palladium nanoparticles decorated nitrogen doped graphene and their catalytic study for renewable energy applications. Int. J. Hydrog. Energy 2013, 38, 2240–2250. [Google Scholar] [CrossRef]
- Kim, Y.; Yun, G.J. Effects of microstructure morphology on stress in mechanoluminescent particles: Micro CT image-based 3D finite element analyses. Compos. Part A Appl. Sci. Manuf. 2018, 114, 338–351. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, W. A numerical study of air–vapor–heat transport through textile materials with a moving interface. J. Comput. Appl. Math. 2011, 236, 819–833. [Google Scholar] [CrossRef]
- El Moumen, A.; Kanit, T.; Imad, A.; El Minor, H. Computational thermal conductivity in porous materials using homogenization techniques: Numerical and statistical approaches. Comput. Mater. Sci. 2015, 97, 148–158. [Google Scholar] [CrossRef]
- Kanani, D.M.; Fissell, W.H.; Roy, S.; Dubnisheva, A.; Fleischman, A.; Zydney, A.L. Permeability–selectivity analysis for ultrafiltration: Effect of pore geometry. J. Membr. Sci. 2010, 349, 405–410. [Google Scholar] [CrossRef]
- Siddiqui, M.U.; Arif, A.F.M.; Bashmal, S. Permeability-Selectivity Analysis of Microfiltration and Ultrafiltration Membranes: Effect of Pore Size and Shape Distribution and Membrane Stretching. Membranes 2016, 6, 40. [Google Scholar] [CrossRef] [PubMed]
- Aizawa, T.; Wakui, Y. Correlation between the Porosity and Permeability of a Polymer Filter Fabricated via CO2-Assisted Polymer Compression. Membranes 2020, 10, 391. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.-H.; Le, T.T.M.; Hsu, K.-C. Application of PolyHIPE Membrane with Tricaprylmethylammonium Chloride for Cr(VI) Ion Separation: Parameters and Mechanism of Transport Relating to the Pore Structure. Membranes 2018, 8, 11. [Google Scholar] [CrossRef]
- O’Rourke, M.; Duffy, N.; De Marco, R.; Potter, I. Electrochemical Impedance Spectroscopy—A Simple Method for the Characterization of Polymer Inclusion Membranes Containing Aliquat 336. Membranes 2011, 1, 132–148. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, W.; Zhang, J.; Yin, B.; Liu, X. 3D shape segmentation using multiple random walkers. J. Comput. Appl. Math. 2018, 329, 353–363. [Google Scholar] [CrossRef]
- Deng, D.; Wu, H.; Sun, P.; Wang, R.; Shi, Z.; Luo, X. A new geometric modeling approach for woven fabric based on Frenet frame and Spiral Equation. J. Comput. Appl. Math. 2018, 329, 84–94. [Google Scholar] [CrossRef]
- Grabowski, G. Modelling of thermal expansion of single- and two-phase ceramic polycrystals utilising synthetic 3D microstructures. Comput. Mater. Sci. 2019, 156, 7–16. [Google Scholar] [CrossRef]
- Wu, Y.; Zhou, W.; Wang, B.; Yang, F. Modeling and characterization of two-phase composites by Voronoi diagram in the Laguerre geometry based on random close packing of spheres. Comput. Mater. Sci. 2010, 47, 951–961. [Google Scholar] [CrossRef]
- Alveen, P.; Carolan, D.; McNamara, D.; Murphy, N.; Ivankovic, A. Micromechanical modelling of ceramic based composites with statistically representative synthetic microstructures. Comput. Mater. Sci. 2013, 79, 960–970. [Google Scholar] [CrossRef]
- Zheng, Y.; Colón, L.I.; Hassan, N.U.; Williams, E.; Stefik, M.; LaManna, J.; Hussey, D.; Mustain, W. Effect of Membrane Properties on the Carbonation of Anion Exchange Membrane Fuel Cells. Membranes 2021, 11, 102. [Google Scholar] [CrossRef]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Gao, M.; Li, X.; Xu, Y.; Wu, T.; Wang, J. Reconstruction of three-dimensional anisotropic media based on analysis of morphological completeness. Comput. Mater. Sci. 2019, 167, 123–135. [Google Scholar] [CrossRef]
- Palenichka, R.M.; Zaremba, M.B.; Missaoui, R. Multiscale model-based feature extraction in structural texture images. J. Electron. Imaging 2006, 15, 023013. [Google Scholar] [CrossRef]
- Torquato, S. Theory of Random Heterogeneous Materials. In Handbook of Materials Modeling; J.B. Metzler: Stuttgart, Germany, 2005; pp. 1333–1357. [Google Scholar]
- Ledesma-Alonso, R.; Barbosa, R.; Ortegón, J. Effect of the image resolution on the statistical descriptors of heterogeneous media. Phys. Rev. E 2018, 97, 023304. [Google Scholar] [CrossRef] [PubMed]
- Papamichael, N. Numerical conformal mapping onto a rectangle with applications to the solution of Laplacian problems. J. Comput. Appl. Math. 1989, 28, 63–83. [Google Scholar] [CrossRef]
- Torquato, S. Statistical Description of Microstructures. Annu. Rev. Mater. Res. 2002, 32, 77–111. [Google Scholar] [CrossRef]
- Snarskii, A.A.; Bezsudnov, I.V.; Sevryukov, V.A.; Morozovskiy, A.; Malinsky, J. Transport Processes in Macroscopically Disordered Media; J.B. Metzler: Stuttgart, Germany, 2016. [Google Scholar]
- Torquato, S.; Haslach, H. Random Heterogeneous Materials: Microstructure and Macroscopic Properties. Appl. Mech. Rev. 2002, 55, B62–B63. [Google Scholar] [CrossRef]
- Broadbent, S.R.; Hammersley, J.M. Percolation processes. Math. Proc. Camb. Philos. Soc. 1957, 53, 629–641. [Google Scholar] [CrossRef]




| Percolation (Matrix Phase) | Percolation (Agglomerate Phase) | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSA | SURFACE FRACTION (%) | |||||||||||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
| S3L | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| S4L | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| S5L | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| SC | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodriguez, A.; Pool, R.; Ortegon, J.; Escobar, B.; Barbosa, R. Effect of the Agglomerate Geometry on the Effective Electrical Conductivity of a Porous Electrode. Membranes 2021, 11, 357. https://doi.org/10.3390/membranes11050357
Rodriguez A, Pool R, Ortegon J, Escobar B, Barbosa R. Effect of the Agglomerate Geometry on the Effective Electrical Conductivity of a Porous Electrode. Membranes. 2021; 11(5):357. https://doi.org/10.3390/membranes11050357
Chicago/Turabian StyleRodriguez, Abimael, Roger Pool, Jaime Ortegon, Beatriz Escobar, and Romeli Barbosa. 2021. "Effect of the Agglomerate Geometry on the Effective Electrical Conductivity of a Porous Electrode" Membranes 11, no. 5: 357. https://doi.org/10.3390/membranes11050357
APA StyleRodriguez, A., Pool, R., Ortegon, J., Escobar, B., & Barbosa, R. (2021). Effect of the Agglomerate Geometry on the Effective Electrical Conductivity of a Porous Electrode. Membranes, 11(5), 357. https://doi.org/10.3390/membranes11050357