Competition between Cations via Classical Poisson–Nernst–Planck Models with Nonzero but Small Permanent Charges
Abstract
1. Introduction
1.1. Poisson–Nernst–Planck Models for Ionic Flows
1.2. Electrochemical Potential
1.3. Permanent Charge
1.4. Comparison with Some Existing Works
1.5. Main Results
- (i)
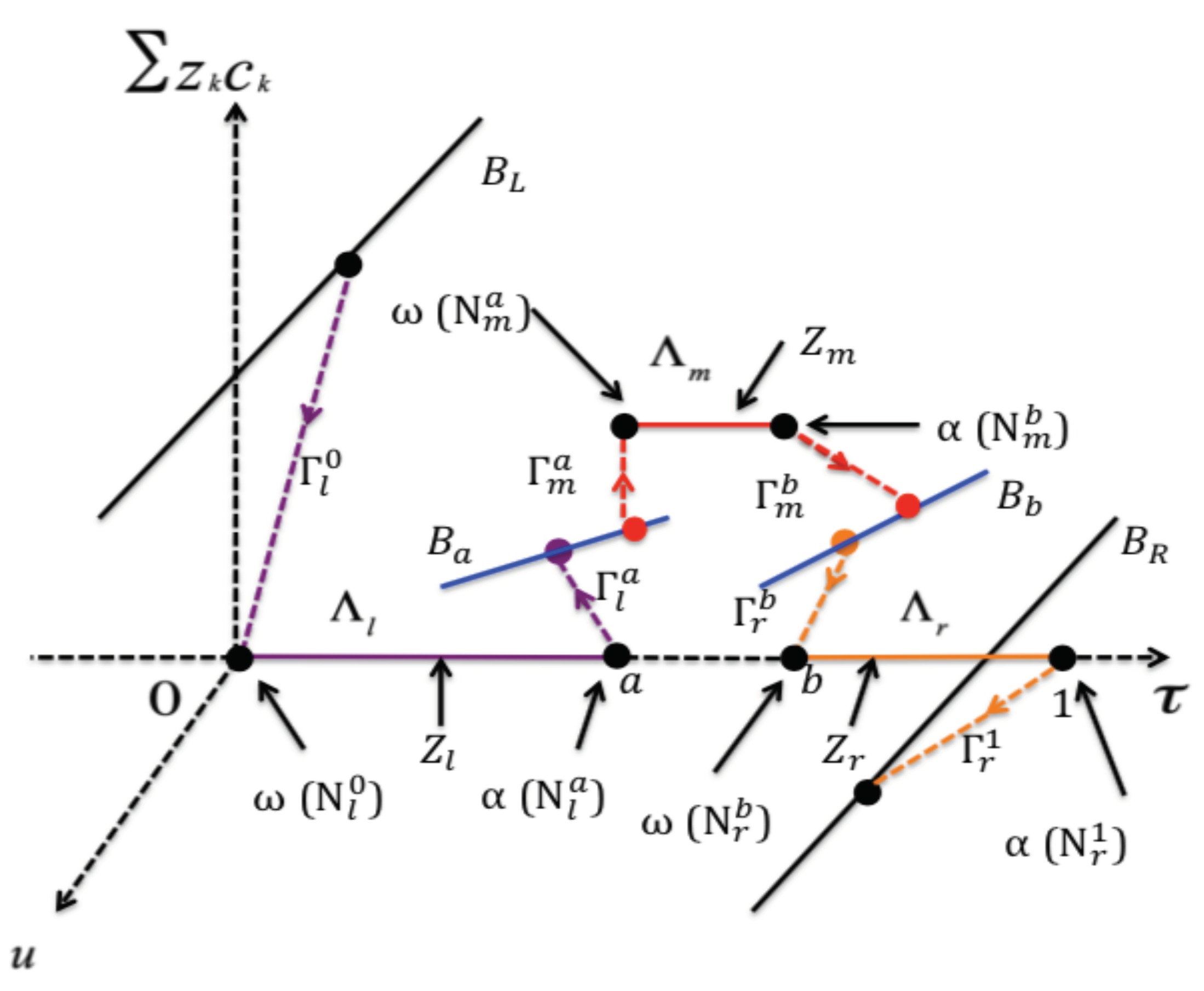
- Constructing a singular orbit of the limiting PNP system () over the whole interval , which is a union of singular orbits over the subintervals and . Over each subinterval, the singular orbit consists of two boundary/internal layers and a regular layer; see Proposition 2 and Lemma 2 in Section 2.1.1 for the singular over , in Proposition 4 and Lemma 3 for the one over in Section 2.1.2, and Proposition 5 and Lemma 4 for the one over in Section 2.1.3.
- (ii)
- Establishing the existence and local uniqueness result of the underlying PNP system ( but small); see Theorem 1 in Section 2.1.5.
- (iii)
- Obtaining the zeroth order and first order (in ) solutions of system (40) and (41), crucial to derive explicit expressions of the individual fluxes up to the first order in ; see Propositions 6 and 7 in Section 2.2.
- (iv)
- (v)
- Study on competition between cations in terms of from two directions: the sign of and the monotonicity of in the electric potential V, based on distinct interplays among and consisting of three cases
- (v1)
- Case study with ; see Theorems 2–4 in Section 3.1.1.
- (v2)
- Case study with ; see Theorems 5–7 in Section 3.1.2.
- (v3)
- Case study with ; see Theorems 8 and 9 in Section 3.1.3.
- (vi)
- Analysis on the magnitude of , equivalent to examine the sign of , where ; see Theorems 10 and 11 in Section 3.1.4.
1.6. Problem Set-Up
2. Methods
2.1. Geometric Singular Perturbation Theory for (8) and (9)
- (i)
- The singular orbit on consists of two boundary layers and and one regular layer with beingIn particular, given the flux densities and the value are uniquely determined (see Section 2.1.1).
- (ii)
- The singular orbit on consists of two boundary layers and and one regular layer with beingIn particular, given and , the flux densities and the value and are uniquely determined (see Section 2.1.2).
- (iii)
- The singular orbit on consists of two boundary layers and and one regular layer with beingIn particular, given , the flux densities and the value are uniquely determined (see Section 2.1.3).
2.1.1. Singular Orbit on with
- (i)
- The stable manifold intersects transversally at points and the ω-limit set of iswhere for are arbitrary, and
- (ii)
- The unstable manifold intersects transversally at points and the α-limit set of iswhere for are arbitrary, and forand
- (iii)
- The boundary layer at is determined up to as follows: the ϕ-component satisfies the Hamiltonian systemtogether with and as andSimilarly, the boundary layer at is determined in the following way: the ϕ-component satisfies the Hamiltonian systemtogether with and as and
2.1.2. Singular Orbit on with
- (i)
- System (26) has the following eight integrals,
- (ii)
- The stable manifold intersects transversally at points and the ω-limit set of iswhere for are arbitrary, and is the unique solution ofwhere andwhere
- (iii)
- The unstable manifold intersects transversally at points and the α-limit set of iswhere for are arbitrary, and is the unique solution ofwhere andwhere
- (iv)
- The boundary layer at is determined up to as follows: the ϕ-component satisfies the Hamiltonian systemtogether with and as andSimilarly, the boundary layer at is determined in the following way: the ϕ-component satisfies the Hamiltonian systemtogether with and as and
2.1.3. Singular Orbit on with
- (i)
- System (36) has the following integrals:
- (ii)
- The stable manifold intersects transversally at points and the ω-limit set of iswhere for are arbitrary, andand
- (iii)
- The unstable manifold intersects transversally at points and the α-limit set of iswhere for are arbitrary, and
- (iv)
- The boundary layer at is determined up to as follows: the ϕ-component satisfies the Hamiltonian systemtogether with and as andSimilarly, the boundary layer at is determined in the following way: the ϕ-component satisfies the Hamiltonian systemtogether with and as and
2.1.4. Matching and Singular Orbits on the Whole Interval
2.1.5. Existence of Solutions near the Singular Orbit
- The boundary layer connects the point to the point
- The regular layer connects the point to the point
- The internal layer connects the point to the point
- The internal layer connects the point to the point
- The regular layer connects the point to the point
- The internal layer connects the point to the point
- The internal layer connects the point to the point
- The regular layer connects the point to the point
- The boundary layer connects the point to the point
- (i)
- is transversal along , which is established in Proposition 2;
- (ii)
- the vector field on is not tangent to at , which follows from in (21).
2.2. Regular Perturbation Analysis: Expansions along Small
- (i)
- if , then ;
- (ii)
- if , then .
- (i)
- if , then and ;
- (ii)
- if , then, there exists a unique such that
- (ii1)
- and , for ;
- (ii2)
- , for ;
- (ii3)
- and , for .
- (iii)
- if , then, there exists a unique such that
- (iii1)
- and , for ;
- (iii2)
- and , for ;
- (iii3)
- and , for ;
- (iii4)
- , for ;
- (iii5)
- and , for .
- if , then, , which implies ; this completes the proof of statement (i).
- For the case with , we first claim that there exists a unique such that for . In fact, based on the facts that and is strictly increasing on , it suffices to show that for , which follows from . For convenience, for , we setDirect calculations give for all , and hence, is concave downward for . Further, is implied by , since . To prove , setIt is easy to check that and . Further one arrive at the conclusion that based on the facts that and for .
- -
- If , then one can easily obtain for all , and more specifically, , which implies , for , , for , , which indicates , for ; this completes the proof of statement (ii).
- -
- if , then, the straight line and have the unique intersection , which means that there exists a unique such that , which suggests , for , and further , for , , which yields , for , , for , , which hints , for ; this completes the proof of statement (iii).
3. Results
3.1. Competitions between Cations
3.1.1. Case Study with
- (i)
- if , then, (resp. ), for (resp. ), that is, the (small) positive reduces (resp. enhances) ;
- (ii)
- if , then, (resp. ), for (resp. ), that is, the (small) positive enhances (resp. reduces) .
- (i)
- if , then, there exists a critical potential with such that increases on and decreases on .
- (ii)
- if , then, there exists a critical potential with such that decreases on and increases on .
3.1.2. Case Study with
- (i)
- and ;
- (ii)
- and and ;
- (iii)
- and and .
- (i)
- , and ;
- (ii)
- , and ;
- (iii)
- , and ;
- (iv)
- , and .
- (i)
- For and one has, (resp. ) if or (resp. ), that is, the (small) positive enhances (resp. reduces) ;
- (ii)
- For and , one has, (resp. ) if or (resp. ), that is, the (small) positive reduces (resp. enhances) ;
- (iii)
- For and , one has, (resp. ) if or (resp. ), that is, the (small) positive enhances (resp. reduces) .
- (i)
- If , then, there exists a critical between and such that decreases on and increases on ;
- (ii)
- If , then, there exists a critical between and such that increases on and decreases on .
3.1.3. Case Study with
- (i)
- For ,
- (i1)
- (resp. ) if (resp. ), that is, the (small) positive reduces (resp. enhances) ;
- (i2)
- either always increases or there exist two critical and with such that increases on , decreases on and increases on ;
- (ii)
- For ,
- (ii1)
- (resp. ) if (resp. ), that is, the (small) positive enhances (resp. reduces) .
- (ii2)
- either always decreases or there exist two critical and with such that decreases on , increases on and decreases on .
3.1.4. Studies on the Magnitude of
- (i)
- the sign of , which characterizes the small positive permanent charge effects on the competition between two cations. To be specific, if (resp. ), then, the small positive permanent charge enhances (resp. reduces) , and in either way, it affects the preference of the ion channel over different cation, which is closely related to the selectivity phenomena of the ion channel.
- (ii)
- the monotonicity of in the electric potential V, which further reduces or strengthens the preference by adjusting/controlling the boundary membrane potential. Taking the case for example, if , then, one can increase the boundary electric potential to further strengthen the individual flux , which indicates that more cation will go through the ion channel; while if , one then need to decrease the boundary electric potential for more cation to go through the ion channels.
- (i)
- if either , or and , then and
- (i1)
- for , , equivalently, (small) positive enhances ;
- (i2)
- for , , equivalently, (small) positive reduces ;
- (ii)
- if and , then and
- (ii1)
- for , , equivalently, (small) positive enhances ;
- (ii2)
- for , , equivalently, (small) positive reduces ;
- (i)
- if and , then, the ion channel prefers the cation over the cation , and the small positive permanent charge further enhances this preference;
- (ii)
- if and , then, the ion channel prefers the cation over the cation , and the small positive permanent charge further enhances this preference.
3.2. Numerical Simulations
- (i)
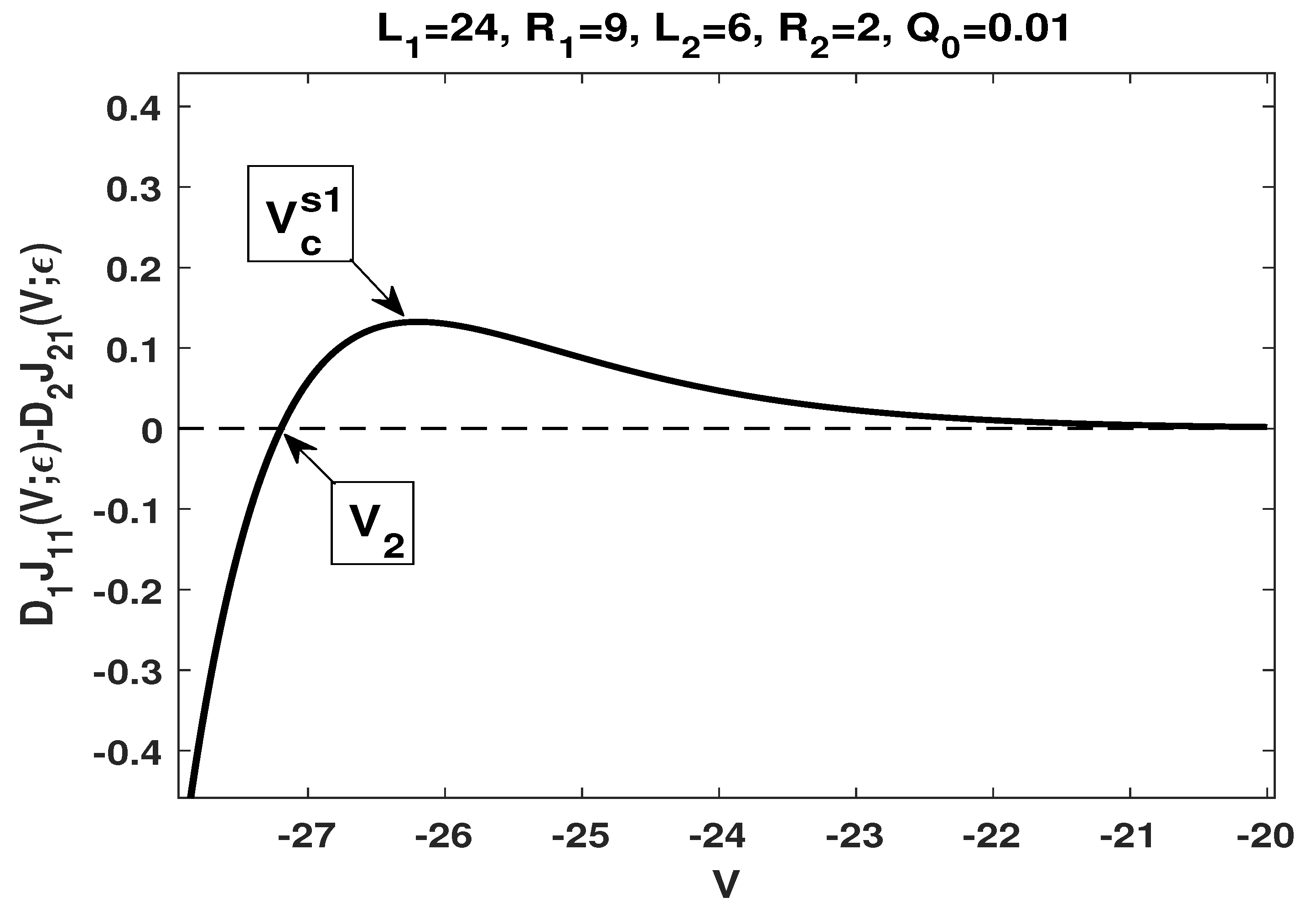
- By choosing and , one hasIt follows thatwhich is consistent with the conditions stated in (ii) of Lemma 8, and indicates that . Together with Lemma 7, we have . Therefore, , which is consistent with the condition (i) stated in Theorems 3 and 4, respectively.Our numerical results show that (see Figure 2) , approximation of defined in (48), which is given byhas a unique zero , and a critical point such that if and if ; furthermore, increases in the potential V if , and decreases in the potential V if .We remark that the numerical result is consistent with our analytical result, more precisely, statement (i) of both Theorems 3 and 4.
- (ii)
- By choosing and , one hasIt follows thatwhich is consistent with the conditions stated in (ii) of Corollary 4.Our numerical results show that (see Figure 3) , approximation of defined in (48), which is given byhas two zeros and with , and a critical point between and such that if or , and if ; furthermore, decreases in the potential V if , and increases in the potential V if .We remark that the numerical result is consistent with our analytical result, more precisely, statement (iii) of Theorem 6 and statement (i) of Theorem 7.
- (iii)
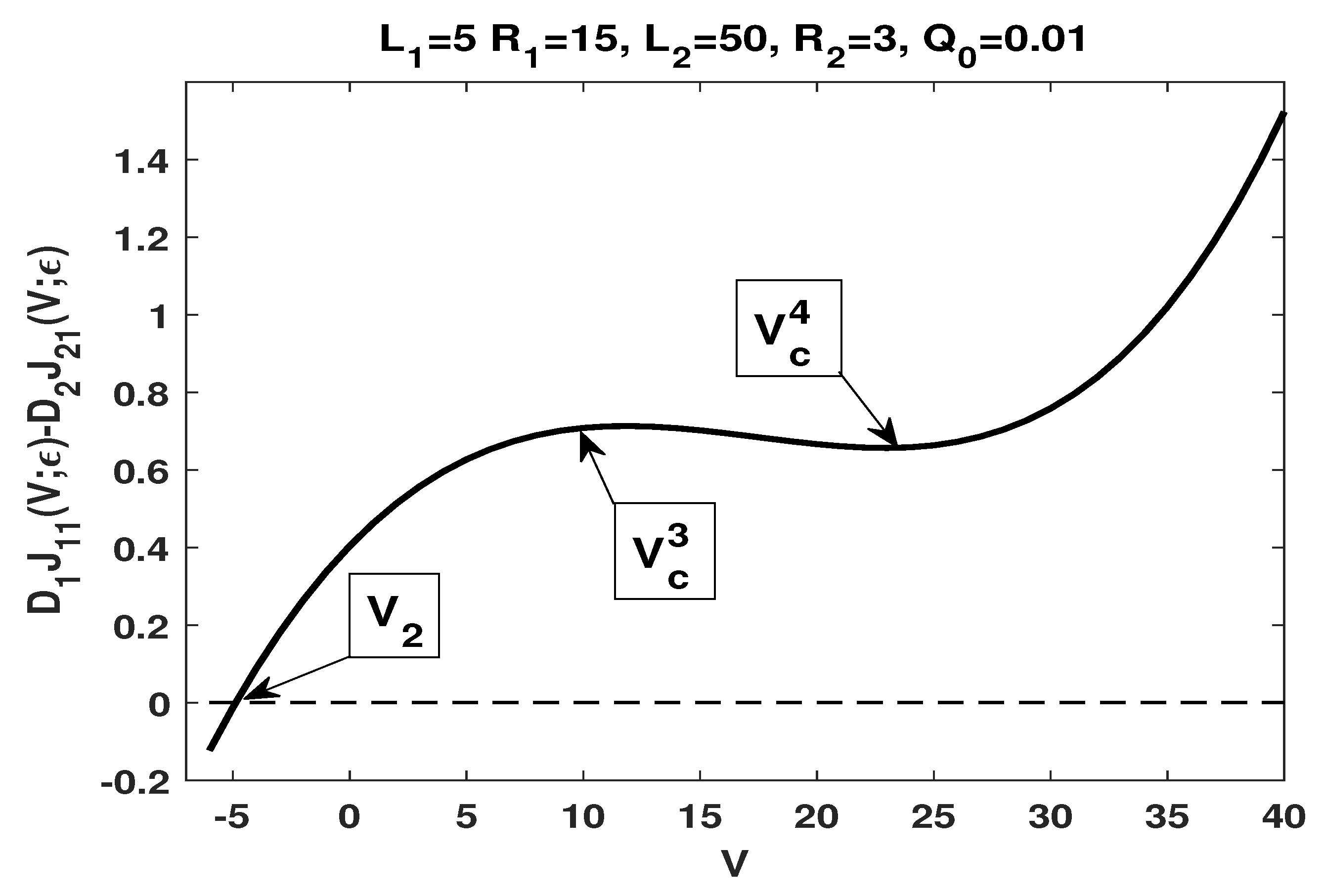
- By choosing and , one hasIt follows thatFrom Lemma 7, one has and from Lemma 8 (statement (ii1)), one has , and hence, , which satisfies the condition required in the statement (i) of Theorem 9.Our numerical results show that (see Figure 4) has one zero and two critical points and with such that if and if ; furthermore, increases in the potential V if , decreases in the potential V if , and increases in the potential V if .We remark that the numerical result is consistent with our analytical result stated in (i) of Theorem 9.
4. Concluding Remarks
- (i)
- the existence of a complete set of first integrals (Proposition 1, first statement (i) in Proposition 4 and Proposition 5, respectively);
- (ii)
- the observation made in Section 2.1.2 allows one to transform the limit slow system (32) to a linear system (33) with constant coefficients;
- (i)
- it includes almost all relevant physical parameters;
- (ii)
- once a solution of the governing system is obtained, the singular orbit (the zeroth order approximation (in ) solution of the boundary value problem) can be readily determined.
- (i)
- As functions of the membrane potential V (fixing other system parameters),
- (i1)
- and can be positive (resp. negative), which further depends on the nonlinear interaction among boundary concentrations and diffusion coefficients. The sign of provides critical information related to the selectivity phenomena of ion channels, while the sign of provides efficient ways to further adjust/control the preference of the ion channel over distinct cation (Characterized in Theorems 2–9);
- (i2)
- , the magnitude of , which is equivalent to for small positive , is analyzed, which provides further information of the ion channel over distinct cations (Theorems 10 and 11).
- (ii)
- Critical potentials that balance the small permanent charge effects on (such as and ) are identified (Definition 1). Those critical potentials can be experimentally estimated. Taking for example, one can take an experimental curve as and numerically (or analytically) compute for ideal case that allows one to get an estimate of by considering the zeros of . The critical potentials play critical roles in characterizing permanent charge effects on ionic flows through membrane channels.
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Eisenberg, B. Ions in Fluctuating Channels: Transistors Alive. Fluct. Noise Lett. 2012, 11, 76–96. [Google Scholar] [CrossRef]
- Eisenberg, B. Crowded charges in ion channels. In Advances in Chemical Physics; Rice, S.A., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 77–223. [Google Scholar]
- Gillespie, D. A Singular Perturbation Analysis of the Poisson–Nernst–Planck System: Applications to Ionic Channels. Ph.D. Thesis, Rush University at Chicago, Chicago, IL, USA, 1999. [Google Scholar]
- Mofidi, H.; Eisenberg, B.; Liu, W. Effects of Diffusion Coefficients and Permanent Charge on Reversal Potentials in Ionic Channels. Entropy 2020, 22, 325. [Google Scholar] [CrossRef]
- Bates, P.W.; Chen, J.; Zhang, M. Dynamics of ionic flows via Poisson–Nernst–Planck systems with local hard-sphere potentials: Competition between cations. Math. Biosci. Eng. 2020, 17, 3736–3766. [Google Scholar] [CrossRef]
- Bates, P.W.; Jia, Y.; Lin, G.; Lu, H.; Zhang, M. Individual flux study via steady-state Poisson–Nernst–Planck systems: Effects from boundary conditions. SIAM J. Appl. Dyn. Syst. 2017, 16, 410–430. [Google Scholar] [CrossRef]
- Eisenberg, B.; Liu, W. Poisson–Nernst–Planck systems for ion channels with permanent charges. SIAM J. Math. Anal. 2007, 38, 1932–1966. [Google Scholar] [CrossRef]
- Ji, S.; Eisenberg, B.; Liu, W. Flux ratios and channel structures. J. Dyn. Differ. Equ. 2019, 31, 1141–1183. [Google Scholar] [CrossRef]
- Ji, S.; Liu, W.; Zhang, M. Effects of (small) permanent charges and channel geometry on ionic flows via classical Poisson–Nernst–Planck models. SIAM J. Appl. Math. 2015, 75, 114–135. [Google Scholar] [CrossRef]
- Liu, W. Geometric singular perturbation approach to steady-state Poisson–Nernst–Planck systems. SIAM J. Appl. Math. 2005, 65, 754–766. [Google Scholar] [CrossRef]
- Liu, W. One-dimensional steady-state Poisson–Nernst–Planck systems for ion channels with multiple ion species. J. Differ. Equ. 2009, 246, 428–451. [Google Scholar] [CrossRef]
- Liu, W.; Xu, H. A complete analysis of a classical Poisson–Nernst–Planck model for ionic flow. J. Differ. Equ. 2015, 258, 1192–1228. [Google Scholar] [CrossRef]
- Park, J.-K.; Jerome, J.W. Qualitative properties of steady-state Poisson–Nernst–Planck systems: Mathematical study. SIAM J. Appl. Math. 1997, 57, 609–630. [Google Scholar] [CrossRef]
- Wen, Z.; Zhang, L.; Zhang, M. Dynamics of classical Poisson–Nernst–Planck systems with multiple cations and boundary layers. J. Dyn. Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Eisenberg, B. Ion Channels as Devices. J. Comput. Electr. 2003, 2, 245–249. [Google Scholar] [CrossRef]
- Eisenberg, B. Proteins, channels, and crowded ions. Biophys. Chem. 2003, 100, 507–517. [Google Scholar] [CrossRef]
- Im, W.; Roux, B. Ion permeation and selectivity of OmpF porin: A theoretical study based on molecular dynamics, Brownian dynamics, and continuum electrodiffusion theory. J. Mol. Biol. 2002, 322, 851–869. [Google Scholar] [CrossRef]
- Roux, B.; Allen, T.W.; Berneche, S.; Im, W. Theoretical and computational models of biological ion channels. Q. Rev. Biophys. 2004, 37, 15–103. [Google Scholar] [CrossRef]
- Schuss, Z.; Nadler, B.; Eisenberg, R.S. Derivation of Poisson and Nernst-Planck equations in a bath and channel from a molecular model. Phys. Rev. E 2001, 64, 036116. [Google Scholar] [CrossRef]
- Barcilon, V. Ion flow through narrow membrane channels: Part I. SIAM J. Appl. Math. 1992, 52, 1391–1404. [Google Scholar] [CrossRef]
- Hyon, Y.; Eisenberg, B.; Liu, C. A mathematical model for the hard sphere repulsion in ionic solutions. Commun. Math. Sci. 2010, 9, 459–475. [Google Scholar]
- Hyon, Y.; Fonseca, J.; Eisenberg, B.; Liu, C. A new Poisson–Nernst–Planck Equation (PNP-FS-IF) for charge inversion near walls. Biophys. J. 2011, 100, 578a. [Google Scholar] [CrossRef][Green Version]
- Hyon, Y.; Liu, C.; Eisenberg, B. PNP equations with steric effects: A model of ion flow through channels. J. Phys. Chem. B 2012, 116, 11422–11441. [Google Scholar]
- Biesheuvel, P.M. Two-fluid model for the simultaneous flow of colloids and fluids in porous media. J. Colloid Interface Sci. 2011, 355, 389–395. [Google Scholar] [CrossRef]
- Chen, D.; Eisenberg, R.; Jerome, J.; Shu, C. Hydrodynamic model of temperature change in open ionic channels. Biophys. J. 1995, 69, 2304–2322. [Google Scholar] [CrossRef]
- Eisenberg, B.; Hyon, Y.; Liu, C. Energy variational analysis of ions in water and channels: Field theory for primitive models of complex ionic fluids. J. Chem. Phys. 2010, 133, 104104. [Google Scholar] [CrossRef] [PubMed]
- Fair, J.C.; Osterle, J.F. Reverse Electrodialysis in charged capillary membranes. J. Chem. Phys. 1971, 54, 3307–3316. [Google Scholar] [CrossRef]
- Gross, R.J.; Osterle, J.F. Membrane transport characteristics of ultra fine capillary. J. Chem. Phys. 1968, 49, 228–234. [Google Scholar] [CrossRef]
- Sasidhar, V.; Ruckenstein, E. Electrolyte osmosis through capillaries. J. Colloid Interface Sci. 1981, 82, 439–457. [Google Scholar] [CrossRef]
- Wei, G.W. Differential geometry based multiscale models. Bull. Math. Biol. 2010, 72, 1562–1622. [Google Scholar] [CrossRef]
- Wei, G.W.; Zheng, Q.; Chen, Z.; Xia, K. Variational multiscale models for charge transport. SIAM Rev. 2012, 54, 699–754. [Google Scholar] [CrossRef] [PubMed]
- Barcilon, V.; Chen, D.-P.; Eisenberg, R.S. Ion flow through narrow membrane channels: Part II. SIAM J. Appl. Math. 1992, 52, 1405–1425. [Google Scholar] [CrossRef]
- Abaid, N.; Eisenberg, R.S.; Liu, W. Asymptotic expansions of I-V relations via a Poisson–Nernst–Planck system. SIAM J. Appl. Dyn. Syst. 2008, 7, 1507–1526. [Google Scholar] [CrossRef][Green Version]
- Barcilon, V.; Chen, D.-P.; Eisenberg, R.S.; Jerome, J.W. Qualitative properties of steady-state Poisson–Nernst–Planck systems: Perturbation and simulation study. SIAM J. Appl. Math. 1997, 57, 631–648. [Google Scholar]
- Lee, C.-C.; Lee, H.; Hyon, Y.; Lin, T.-C.; Liu, C. New Poisson-Boltzmann type equations: One-dimensional solutions. Nonlinearity 2011, 24, 431–458. [Google Scholar] [CrossRef]
- Liu, W.; Wang, B. Poisson–Nernst–Planck systems for narrow tubular-like membrane channels. J. Dyn. Differ. Equ. 2010, 22, 413–437. [Google Scholar] [CrossRef]
- Singer, A.; Gillespie, D.; Norbury, J.; Eisenberg, R.S. Singular perturbation analysis of the steady-state Poisson–Nernst–Planck system: Applications to ion channels. Eur. J. Appl. Math. 2008, 19, 541–560. [Google Scholar] [CrossRef] [PubMed]
- Singer, A.; Norbury, J. A Poisson–Nernst–Planck model for biological ion channels–an asymptotic analysis in a three-dimensional narrow funnel. SIAM J. Appl. Math. 2009, 70, 949–968. [Google Scholar] [CrossRef]
- Wang, X.-S.; He, D.; Wylie, J.; Huang, H. Singular perturbation solutions of steady-state Poisson–Nernst–Planck systems. Phys. Rev. E 2014, 89, 022722. [Google Scholar] [CrossRef] [PubMed]
- Nooner, W.; Eisenberg, R.S. Ion permeation and glutamate residues linked by Poisson–Nernst–Planck theory in L-type Calcium channels. Biophys. J. 1998, 75, 1287–1305. [Google Scholar] [CrossRef]
- Gillespie, D.; Nonner, W.; Eisenberg, R.S. Coupling Poisson–Nernst–Planck and density functional theory to calculate ion flux. J. Phys. Condens. Matter 2002, 14, 12129–12145. [Google Scholar] [CrossRef]
- Kilic, M.S.; Bazant, M.Z.; Ajdari, A. Steric effects in the dynamics of electrolytes at large applied voltages. II. Modified Poisson–Nernst–Planck equations. Phys. Rev. E 2007, 75, 021503. [Google Scholar] [CrossRef]
- Lin, G.; Liu, W.; Yi, Y.; Zhang, M. Poisson–Nernst–Planck systems for ion flow with density functional theory for local hard-sphere potential. SIAM J. Appl. Dyn. Syst. 2013, 12, 1613–1648. [Google Scholar] [CrossRef]
- Liu, W.; Tu, X.; Zhang, M. Poisson–Nernst–Planck systems for ion flow with density functional theory for hard-sphere potential: I-V relations and critical potentials. Part II: Numerics. J. Dyn. Differ. Equ. 2012, 24, 985–1004. [Google Scholar] [CrossRef]
- Rouston, D.J. Bipolar Semiconductor Devices; McGraw-Hill: New York, NY, USA, 1990. [Google Scholar]
- Warner, R.M., Jr. Microelectronics: Its unusual origin and personality. IEEE Trans. Electron. Devices 2001, 48, 2457–2467. [Google Scholar] [CrossRef]
- Eisenberg, B.; Liu, W. Relative dielectric constants and selectivity ratios in open ionic channels. Mol. Based Math. Biol. 2017, 5, 125–137. [Google Scholar] [CrossRef]
- Jones, C. Geometric singular perturbation theory. In Dynamical Systems (Montecatini Terme, 1994); Lect. Notes in Math.; Springer: Berlin/Heidelberg, Germany, 1995; Volume 1609, pp. 44–118. [Google Scholar]
- Fenichel, N. Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 1979, 31, 53–98. [Google Scholar] [CrossRef]
- Tin, S.-K.; Kopell, N.; Jones, C. Invariant manifolds and singularly perturbed boundary value problems. SIAM J. Numer. Anal. 1994, 31, 1558–1576. [Google Scholar] [CrossRef]
- Jones, C.; Kopell, N. Tracking invariant manifolds with differential forms in singularly perturbed systems. J. Differ. Equ. 1994, 108, 64–88. [Google Scholar] [CrossRef]
- Mohammad, M.M.; Prakash, S.; Matouschek, A.; Movileanu, L. Controlling a single protein in a nanopore through electrostatic teaps. J. Am. Chem. Soc. 2008, 130, 4081–4088. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M. Competition between Cations via Classical Poisson–Nernst–Planck Models with Nonzero but Small Permanent Charges. Membranes 2021, 11, 236. https://doi.org/10.3390/membranes11040236
Zhang M. Competition between Cations via Classical Poisson–Nernst–Planck Models with Nonzero but Small Permanent Charges. Membranes. 2021; 11(4):236. https://doi.org/10.3390/membranes11040236
Chicago/Turabian StyleZhang, Mingji. 2021. "Competition between Cations via Classical Poisson–Nernst–Planck Models with Nonzero but Small Permanent Charges" Membranes 11, no. 4: 236. https://doi.org/10.3390/membranes11040236
APA StyleZhang, M. (2021). Competition between Cations via Classical Poisson–Nernst–Planck Models with Nonzero but Small Permanent Charges. Membranes, 11(4), 236. https://doi.org/10.3390/membranes11040236





