A Molecular Model of PEMFC Catalyst Layer: Simulation on Reactant Transport and Thermal Conduction
Abstract
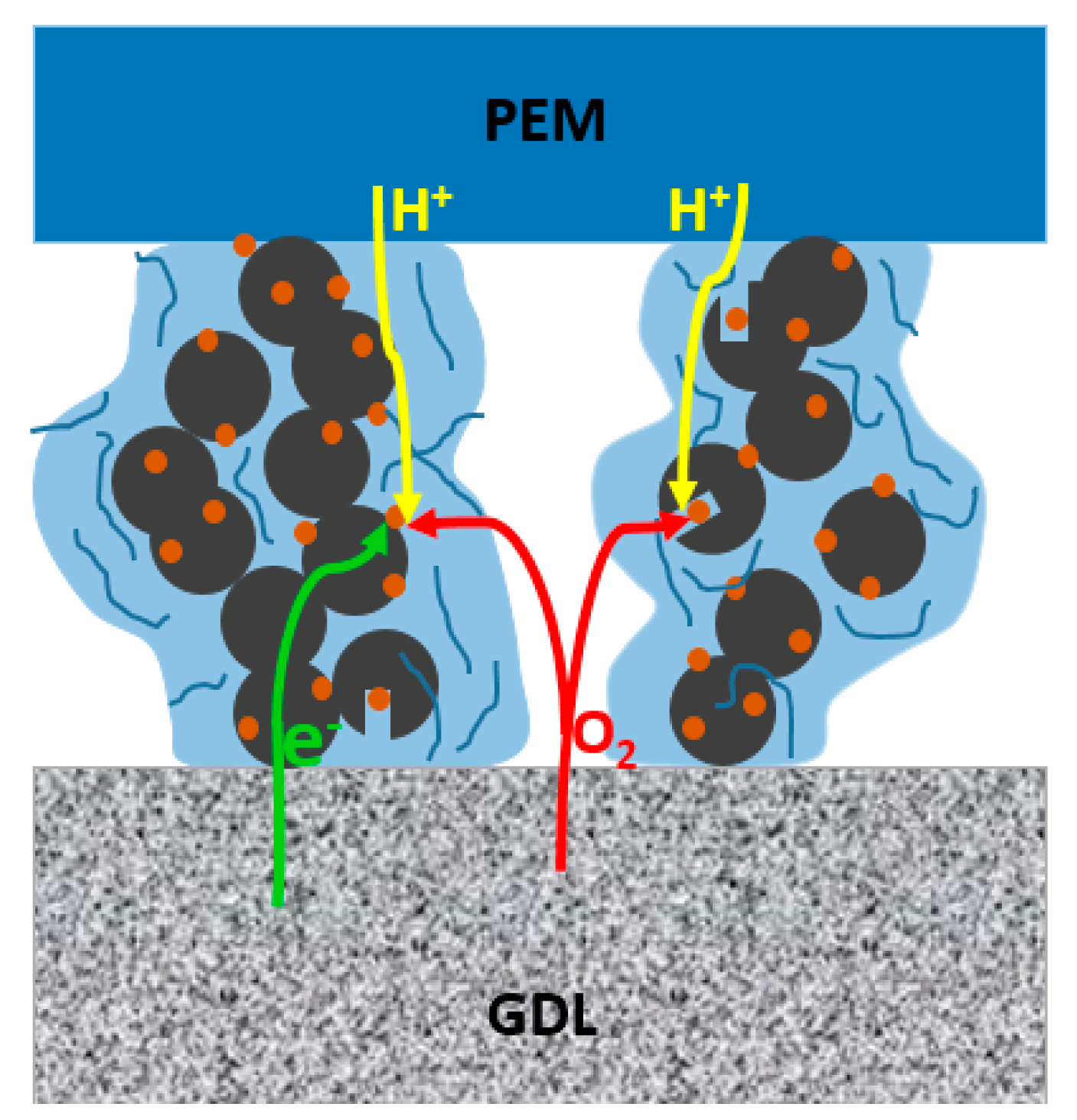
1. Introduction
2. Materials and Methods
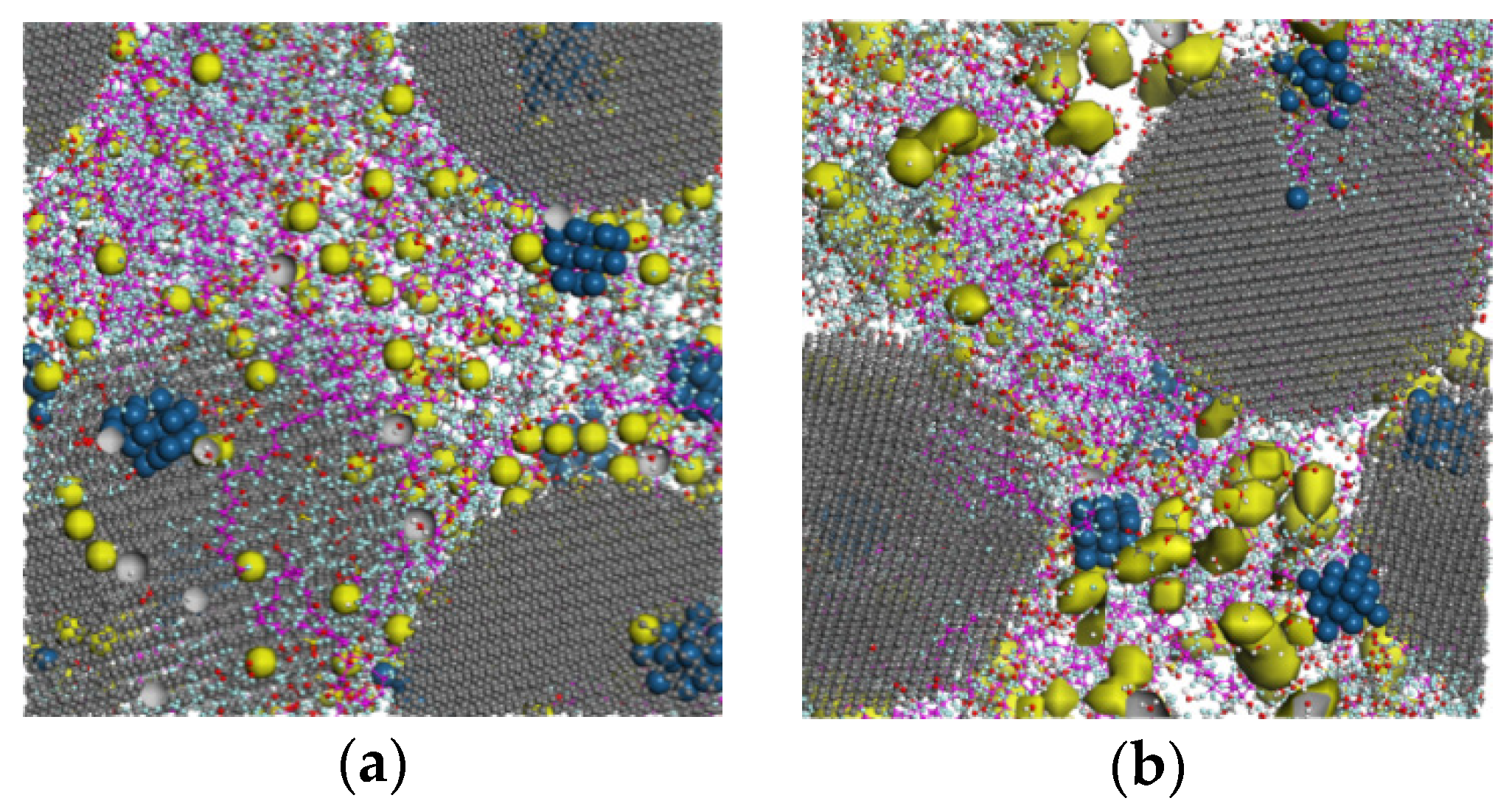
2.1. Model and Dynamics Simulation Details
2.2. Analysis Theory
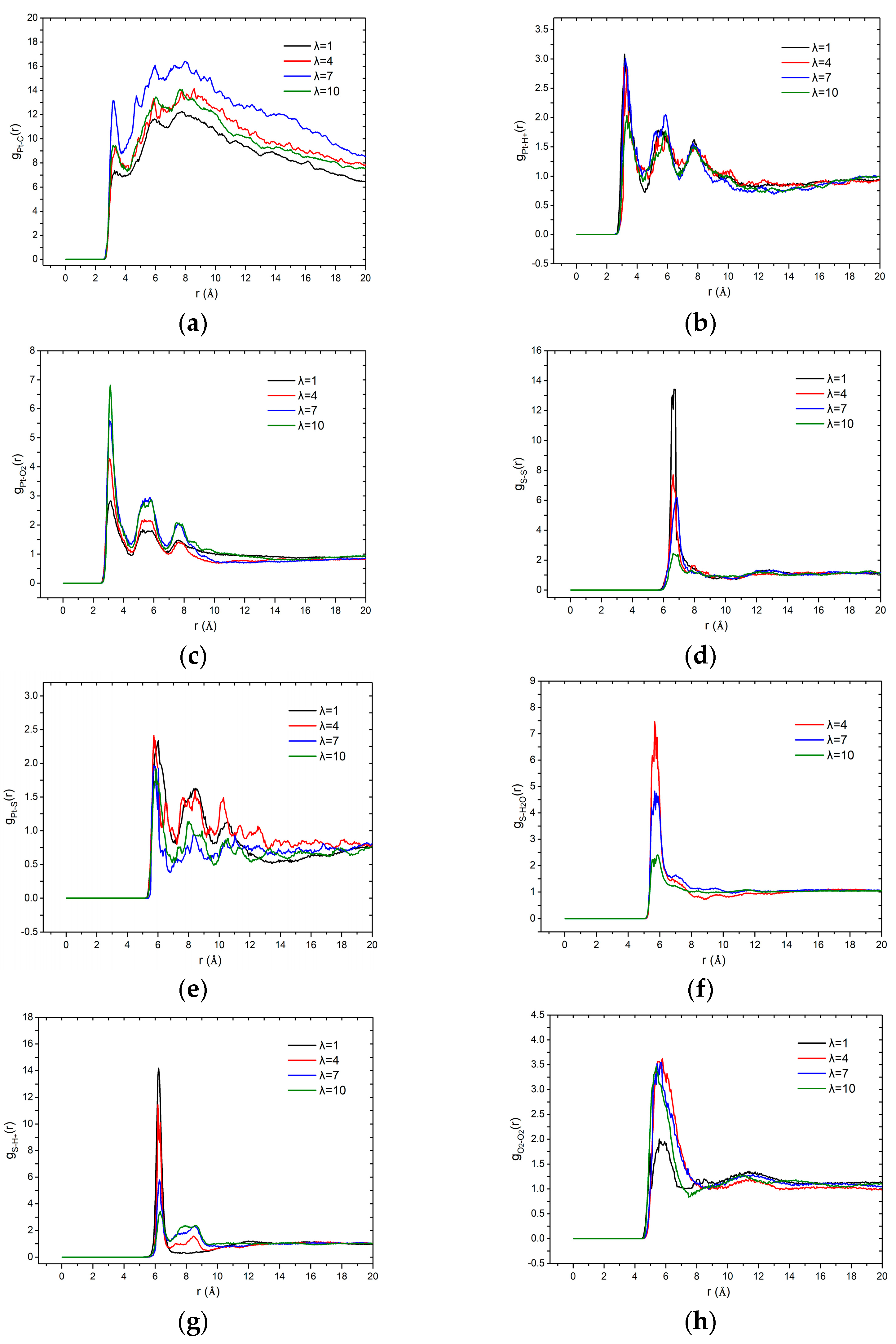
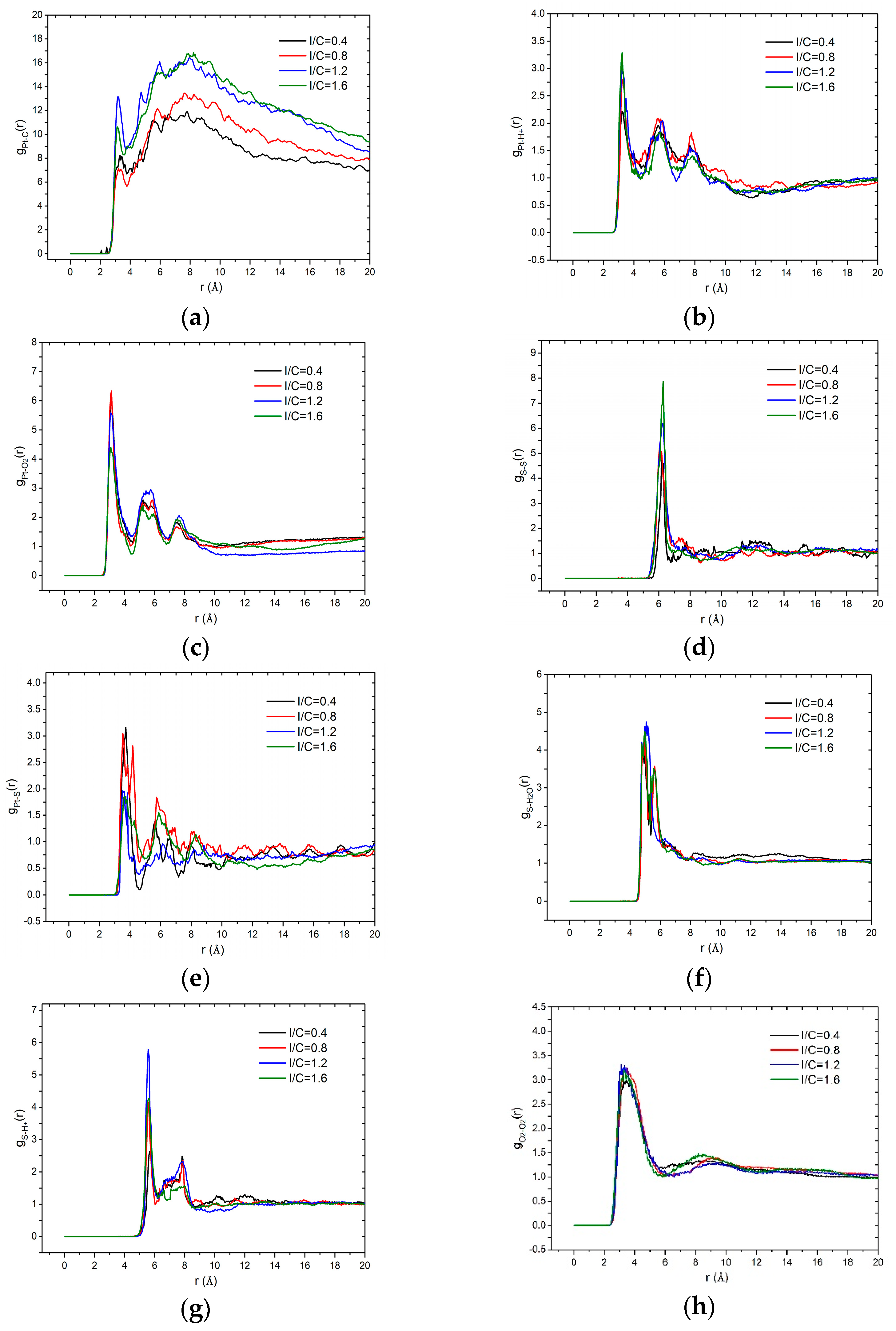
2.2.1. Radial Distribution Function
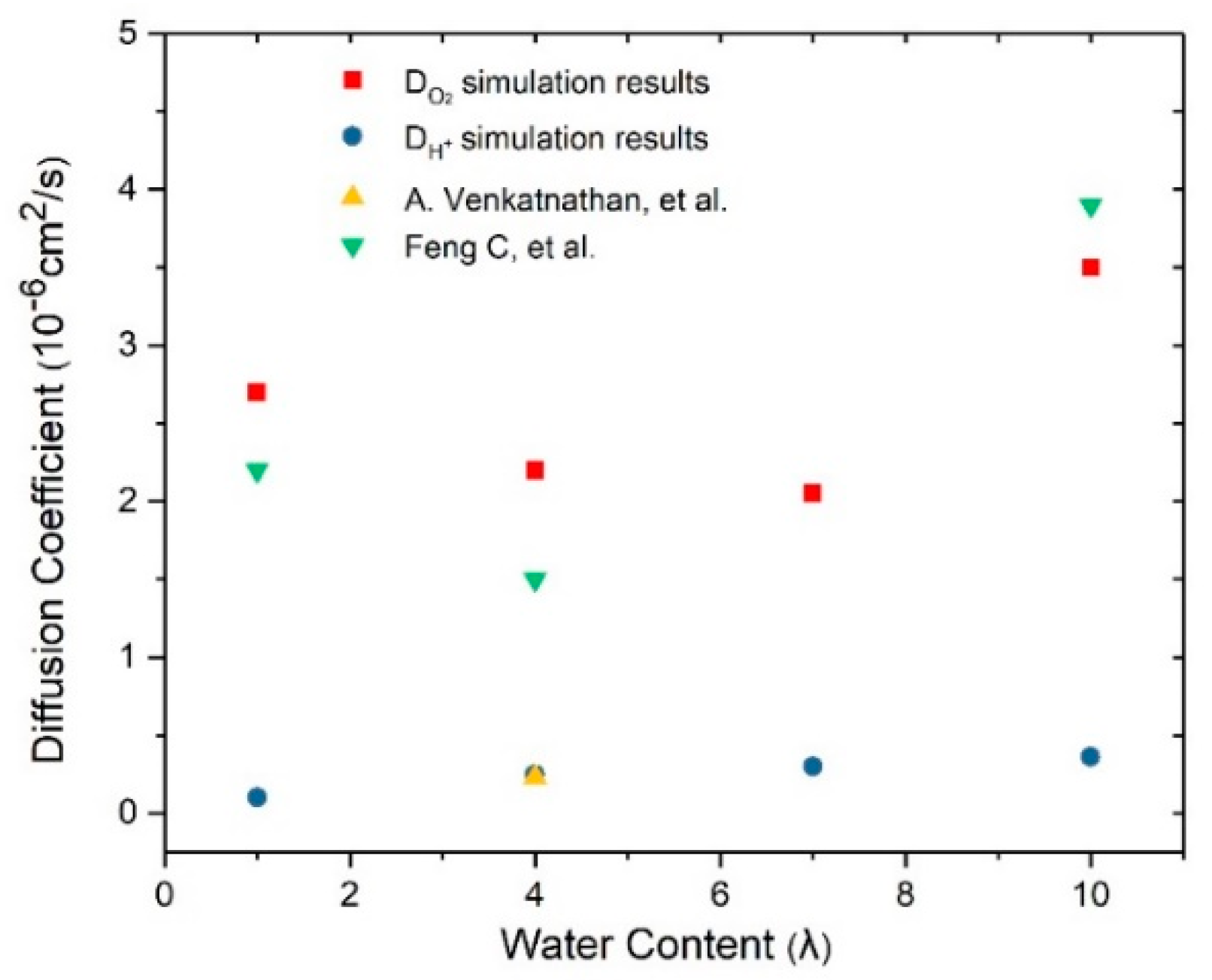
2.2.2. Mean Square Displacement and Diffusion Coefficient
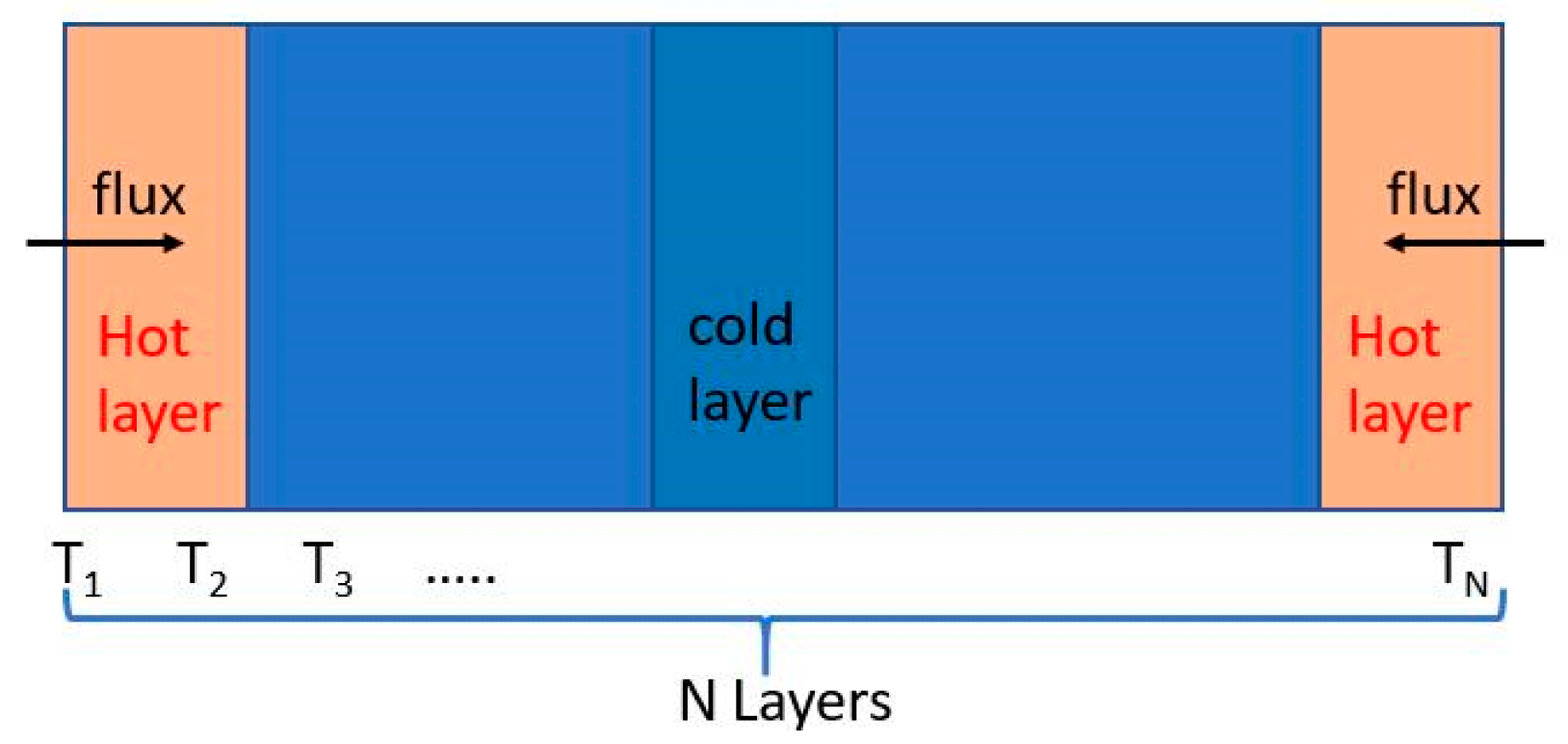
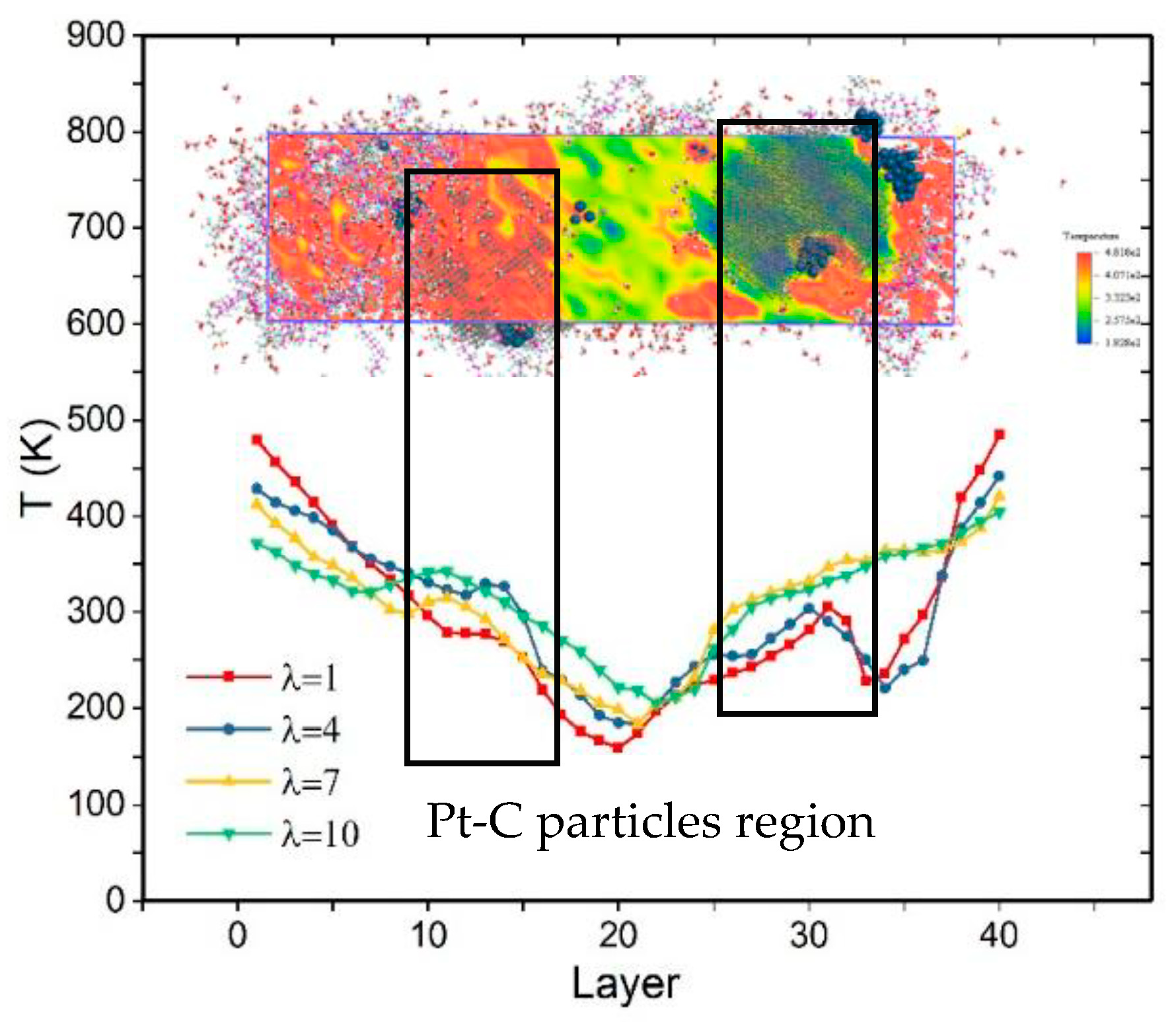
2.2.3. Thermal Conductivity
3. Results and Discussion
3.1. Effects of Water Content and Ionomer-to-Carbon Ratio on RDFs
3.2. Effects of Water Content and Ionomer-to-Carbon Ratio on Diffusion Coefficients
3.3. Effects of Water Content and Ionomer-to-Carbon Ratio on Thermal Conductivity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Debe, M.K. Electrocatalyst approaches and challenges for automotive fuel cells. Nature 2012, 486, 43–51. [Google Scholar] [CrossRef] [PubMed]
- Jiao, K.; Ni, M. Challenges and opportunities in modelling of proton exchange membrane fuel cells (PEMFC). Int. J. Energy Res. 2017, 41, 1793–1797. [Google Scholar] [CrossRef]
- Dickinson, E.J.F.; Smith, G. Modelling the proton-conductive membrane in practical polymer electrolyte membrane fuel cell (PEMFC) simulation: A review. Membranes 2020, 10, 310. [Google Scholar] [CrossRef]
- German, N.; Ramanaviciene, A.; Ramanavicius, A. Formation and electrochemical evaluation of polyaniline and polypyrrole nanocomposites based on glucose oxidase and gold nanostructures. Polymers 2020, 12, 3026. [Google Scholar] [CrossRef] [PubMed]
- Kongkanand, A.; Mathias, M.F. The priority and challenge of high-power performance of low-platinum proton-exchange membrane fuel cells. J. Phys. Chem. Lett. 2016, 7, 1127–1137. [Google Scholar] [CrossRef]
- Gasteiger, H.A.; Kocha, S.S.; Sompalli, B.; Wagner, F.T. Activity benchmarks and requirements for Pt, Pt-alloy, and non-Pt oxygen reduction catalysts for PEMFCs. J. Appl. Catal. B Environ. 2005, 56, 9–35. [Google Scholar] [CrossRef]
- Yoon, W.; Weber, A.Z. Modeling low-platinum-loading effects in fuel cell catalyst layers. J. Electrochem. Soc. 2011, 158, B1007. [Google Scholar] [CrossRef]
- Weber, A.Z.; Borup, R.L.; Darling, R.M.; Das, P.K.; Dursch, T.J.; Gu, W.; Harvey, D.; Kusoglu, A.; Litster, S.; Mench, M.M.; et al. A Critical review of modeling transport phenomena in polymer-electrolyte fuel cells. J. Electrochem. Soc. 2014, 161, F1254. [Google Scholar] [CrossRef]
- Iden, H.; Sato, K.; Ohma, A.; Shinohara, K. Relationship among microstructure, ionomer property and proton transport in pseudo catalyst layers. J. Electrochem. Soc. 2011, 158, B987. [Google Scholar] [CrossRef]
- Liu, H.; Epting, W.K.; Litster, S. Gas transport resistance in polymer electrolyte thin films on oxygen reduction reaction catalysts. Langmuir ACS J. Surf. 2015, 31, 9853–9858. [Google Scholar] [CrossRef] [PubMed]
- Page, K.A.; Kusoglu, A.; Stafford, C.M.; Kim, S.; Kline, R.J.; Weber, A.Z. Confinement-driven increase in ionomer thin-film modulus. Nano Lett. 2014, 14, 2299–2304. [Google Scholar] [CrossRef]
- Eastman, S.A.; Kim, S.; Page, K.A.; Rowe, B.W.; Yager, K.G. Effect of confinement on structure, water solubility, and water transport in nafion thin films. Macromolecules 2013, 46, 571. [Google Scholar] [CrossRef]
- Liang, M.; Liu, L.; Xiao, B.; Yang, S.; Wang, Z.; Han, H. An analytical model for the transverse permeability of gas diffusion layer with electrical double layer effects in proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2018, 43, 17880–17888. [Google Scholar] [CrossRef]
- Liang, M.; Fu, K.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transf. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Fang, W.Z.; Tang, Y.Q.; Chen, L.; Kang, Q.J.; Tao, W.Q. Influences of the perforation on effective transport properties of gas diffusion layers. Int. J. Heat Mass Transf. 2018, 126, 243–255. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Tao, W. Pore-scale study of reactive transport processes in catalyst layer agglomerates of proton exchange membrane fuel cells. Electrochim. Acta 2019, 306, 454–465. [Google Scholar] [CrossRef]
- Kudo, K.; Kitano, N.; Morimoto, Y. Molecular dynamics simulations on O2 permeation through nafion ionomer on platinum surface. Electrochim. Acta 2016, 188, 767–776. [Google Scholar] [CrossRef]
- Zheng, C.; Geng, F.; Rao, Z. Proton mobility and thermal conductivities of fuel cell polymer membranes: Molecular dynamics simulation. Comput. Mater. Sci. 2017, 132, 55–61. [Google Scholar] [CrossRef]
- Rao, Z.; Zheng, C.; Geng, F. Proton conduction of fuel cell polymer membranes: Molecular dynamics simulation. Comput. Mater. Sci. 2018, 142, 122–128. [Google Scholar] [CrossRef]
- Qu, K.; Feng, C. The thermal-mechanical properties of functionally graded membrane electrode assembly of PEMFC. J. Mol. Modeling 2019, 25, 353. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Li, Y.; Song, K.; He, P.F. Structural characteristics, diffusion mechanism and mechanical behaviour of cathode catalyst layer. Comput. Mater. Sci. 2020, 177, 109572. [Google Scholar] [CrossRef]
- Fan, L.; Wang, Y.; Jiao, K. Oxygen transport routes in ionomer film on polyhedral platinum nanoparticles. ACS Nano 2020, 14. [Google Scholar] [CrossRef]
- Kurihara, Y.; Mabuchi, T.; Tokumasu, T. Molecular dynamics study of oxygen transport resistance through ionomer thin film on Pt surface. J. Power Sources 2019, 414, 263–271. [Google Scholar] [CrossRef]
- Kang, H.; Kwon, S.H.; Lawler, R.; Lee, J.H.; Doo, G.; Kim, H.-T.; Yim, S.-D.; Jang, S.S.; Lee, S.G. Nanostructures of nafion film at platinum/carbon surface in catalyst layer of PEMFC: Molecular dynamics simulation approach. J. Phys. Chem. C 2020, 124, 21386–21395. [Google Scholar] [CrossRef]
- Fan, L.; Wu, K.; Tongsh, C.; Zhu, M.; Xie, X.; Jiao, K. Mechanism of water content on the electrochemical surface area of the catalyst layer in the proton exchange membrane fuel cell. J. Phys. Chem. Lett. 2019, 10, 6409–6413. [Google Scholar] [CrossRef]
- Fan, L.; Xi, F.; Wang, X.; Xuan, J.; Jiao, K. Effects of side chain length on the structure, oxygen transport and thermal conductivity for perfluorosulfonic acid membrane: Molecular dynamics simulation. J. Electrochem. Soc. 2019, 166, F511–F518. [Google Scholar] [CrossRef]
- Zhao, Z.; Hossain, M.D.; Xu, C.; Lu, Z.; Liu, Y.S.; Hsieh, S.H.; Lee, I.; Gao, W.; Yang, J.; Merinov, B.V. Tailoring a three-phase microenvironment for high-performance oxygen reduction reaction in proton exchange membrane fuel cells. Matter 2020, 3, 1774–1790. [Google Scholar] [CrossRef]
- Kuzmin, A.E.; Kulikova, M.V.; Maximov, A.L. Mechanism of Fischer–Tropsch synthesis over nanosized catalyst particles: Approaches and problems of ab initio calculations. Pet. Chem. 2019, 59, 485–497. [Google Scholar] [CrossRef]
- Kim, T.; Kwon, Y.; Kwon, S.; Gil, J. Substrate effect of platinum-decorated carbon on enhanced hydrogen oxidation in PEMFC. ACS Omega 2020, 5. [Google Scholar] [CrossRef] [PubMed]
- Dhali, S.; Karakoti, M.; Pandey, S.; Santhibhushan, B.; Sahoo, N.G. Graphene oxide supported Pd-Fe nanohybrid as an efficient electrocatalyst for proton exchange membrane fuel cells. Int. J. Hydrog. Energy 2019, 45, 18704–18715. [Google Scholar] [CrossRef]
- Li, F.; Qin, Y.; Chalgin, A.; Gu, X.; Chen, W.; Ma, Y.; Xiang, Q.; Wu, Y.; Shi, F.; Zong, Y. A non-Pt electronically coupled semiconductor heterojunction for enhanced oxygen reduction electrocatalytic property. ChemistrySelect 2019, 4. [Google Scholar] [CrossRef]
- Yang, J.; Ren, Y.; Tian, A.M.; Sun, H. COMPASS force field for 14 inorganic molecules, He, Ne, Ar, Kr, Xe, H2, O2, N2, NO, CO, CO2, NO2, CS2, and SO2, in liquid phases. J. Phys. Chem. B 2000, 104, 4951–4957. [Google Scholar] [CrossRef]
- Terao, T.; Muller-Plathe, F. A nonequilibrium molecular dynamics method for thermal conductivities based on thermal noise. J. Chem. Phys. 2005, 122, 81103. [Google Scholar] [CrossRef]
- Jund, P.; Jullien, R. Molecular-dynamics calculation of the thermal conductivity of vitreous silica. Phys. Rev. B 2007, 59, 13707–13711. [Google Scholar] [CrossRef]
- Carcadea, E.; Varlam, M.; Marinoiu, A.; Raceanu, M.; Ismail, M.S.; Ingham, D.B. Influence of catalyst structure on PEM fuel cell performance—A numerical investigation. Int. J. Hydrog. Energy 2019, 44, 12829–12841. [Google Scholar] [CrossRef]
- Huang, J.; Li, Z.; Zhang, J. Review of characterization and modeling of polymer electrolyte fuel cell catalyst layer: The blessing and curse of ionomer. Front. Energy 2017, 11, 334–364. [Google Scholar] [CrossRef]
- Mabuchi, T.; Tokumasu, T. Relationship between proton transport and morphology of perfluorosulfonic acid membranes: A reactive molecular dynamics approach. J. Phys. Chem. B 2018, 122, 5922–5932. [Google Scholar] [CrossRef]
- Venkatnathan, A.; Devanathan, R.; Dupuis, M. Atomistic simulations of hydrated nafion and temperature effects on hydronium ion mobility. J. Phys. Chem. B 2007, 111, 7234–7244. [Google Scholar] [CrossRef]
- Wu, K.; Xie, X.; Wang, B.; Yang, Z.; Du, Q.; Xuan, J.; Zu, B.; Liu, Z.; Jiao, K. Two-dimensional simulation of cold start processes for proton exchange membrane fuel cell with different hydrogen flow arrangements. Int. J. Hydrog. Energy 2020, 45, 17795–17812. [Google Scholar] [CrossRef]
- Yang, J.; Zirong, Y.; Kui, J.; Qing, D. Sensitivity analysis of uncertain parameters based on an improved proton exchange membrane fuel cell analytical model. Energy Convers. Manag. 2018, 164, 639–654. [Google Scholar]

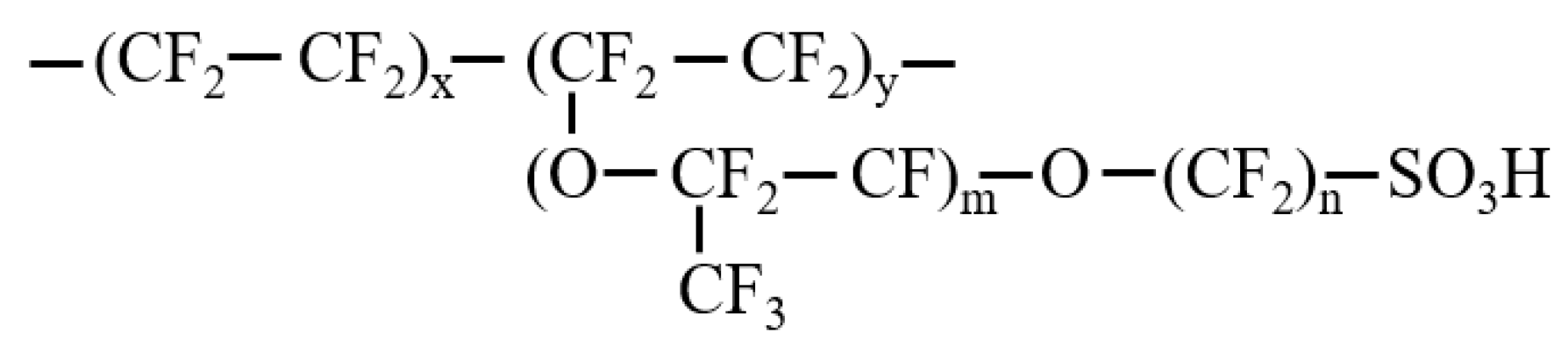




| λ = 1 | λ = 4 | λ = 7 | λ = 10 | |
|---|---|---|---|---|
| NIonomer | 30 | 30 | 30 | 30 |
| NPt-C | 3 | 3 | 3 | 3 |
| NO2 | 200 | 200 | 200 | 200 |
| NH2O | 0 | 600 | 1200 | 1800 |
| NH3O+ | 200 | 200 | 200 | 200 |
| I/C = 0.4 | I/C = 0.8 | I/C = 1.2 | I/C = 1.6 | |
|---|---|---|---|---|
| NIonomer | 10 | 20 | 30 | 40 |
| NPt-C | 3 | 3 | 3 | 3 |
| NO2 | 200 | 200 | 200 | 200 |
| NH2O | 1200 | 1200 | 1200 | 1200 |
| NH3O+ | 200 | 200 | 200 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Qu, Z.; Wang, X.; Zhang, J. A Molecular Model of PEMFC Catalyst Layer: Simulation on Reactant Transport and Thermal Conduction. Membranes 2021, 11, 148. https://doi.org/10.3390/membranes11020148
Wang W, Qu Z, Wang X, Zhang J. A Molecular Model of PEMFC Catalyst Layer: Simulation on Reactant Transport and Thermal Conduction. Membranes. 2021; 11(2):148. https://doi.org/10.3390/membranes11020148
Chicago/Turabian StyleWang, Wenkai, Zhiguo Qu, Xueliang Wang, and Jianfei Zhang. 2021. "A Molecular Model of PEMFC Catalyst Layer: Simulation on Reactant Transport and Thermal Conduction" Membranes 11, no. 2: 148. https://doi.org/10.3390/membranes11020148
APA StyleWang, W., Qu, Z., Wang, X., & Zhang, J. (2021). A Molecular Model of PEMFC Catalyst Layer: Simulation on Reactant Transport and Thermal Conduction. Membranes, 11(2), 148. https://doi.org/10.3390/membranes11020148








