Runge–Kutta Numerical Method Followed by Richardson’s Extrapolation for Efficient Ion Rejection Reassessment of a Novel Defect-Free Synthesized Nanofiltration Membrane
Abstract
1. Introduction
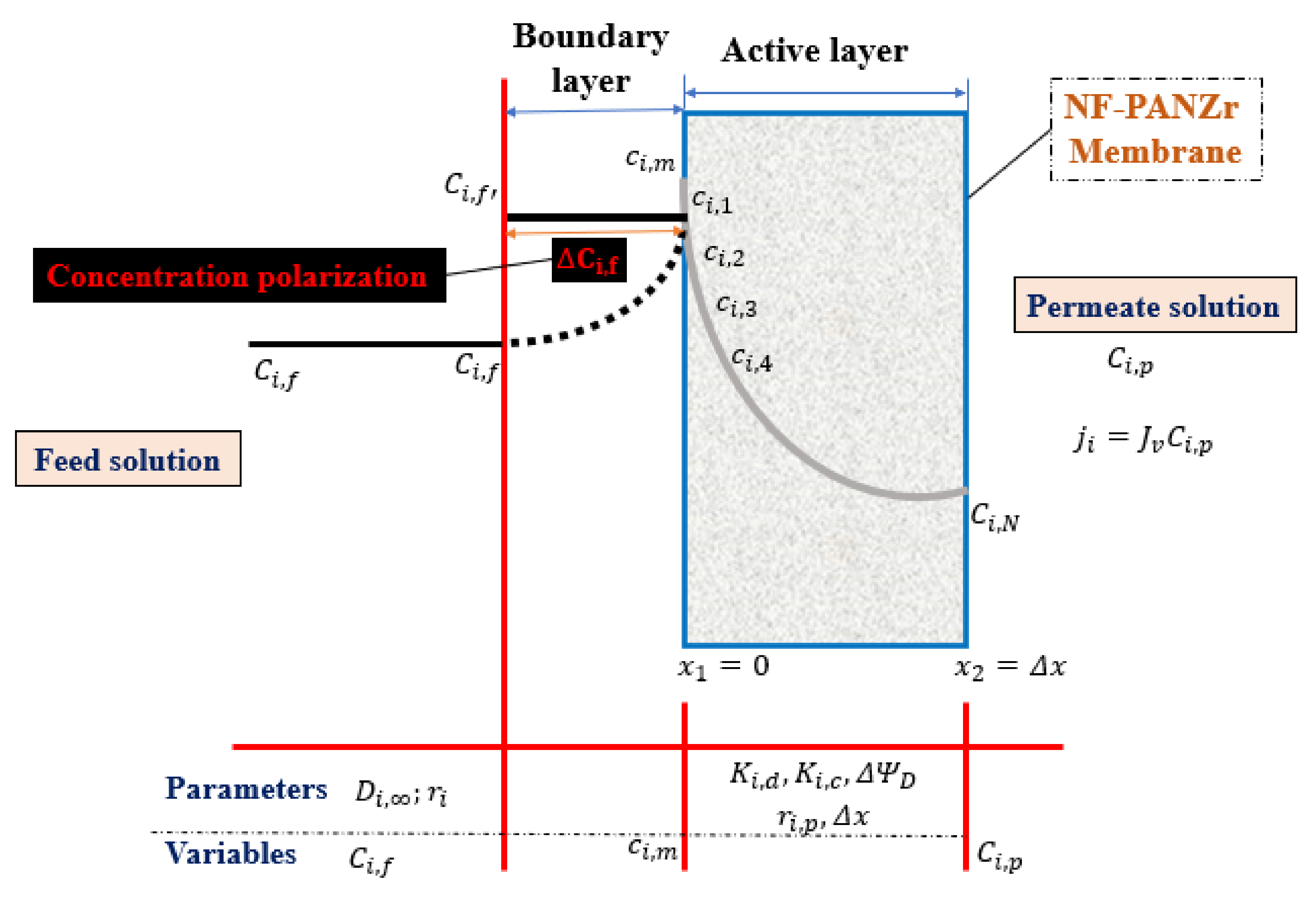
2. Mathematical Modeling
2.1. Model Assumptions
- (i)
- Boundary conditions:It is assumed that Equations (5) and (9) can be solved over the following conditions:At x = 0,At x = Δx,
- (ii)
- The solution understudy is ideal.
- (iii)
- Each solute particle is subjected to an extended Nernst–Planck equation and could therefore be transportable.
- (iv)
- The effective charge density of NF-PANZr membranes does not change from one point to another on its surface.
- (v)
- The layer thickness of nanoparticles is assumed to be negligible toward the platform thickness.
- (vi)
- The NF membrane consists of an identical bundle of straight cylindrical pores, with each pore displaying a uniform depth and radius .
- (vii)
- The electric potentials inside the membrane and the solutions are all defined in terms of averaged quantities.
- (viii)
- The Donnan equilibrium is applied at both the interface of feed solution—membrane and the interface of membrane—permeate solution.
2.2. Focus on Model Equations
2.3. Description of the Computation Procedure
- (i)
- Based on Equation (12), the knowledge of the value of , makes possible the integration of both Equations (5) and (9) after the determination of the initial concentration inside the NF-PANZr membrane .
- (ii)
- Based on the Runge–Kutta numerical method, k1, k2, k3 and k4 and then , , , , …, could be well estimated (Equations (24)–(28); Equations (5) and (9)).
- (iii)
- Since the value is obtained, the permeate concentration, , was then computed.
- (iv)
- Lastly, Equation (13) was used to evaluate the ion [i] rejection.
2.4. Ion Transport across NF-PANZr Membrane
3. Experimental Section
3.1. Materials
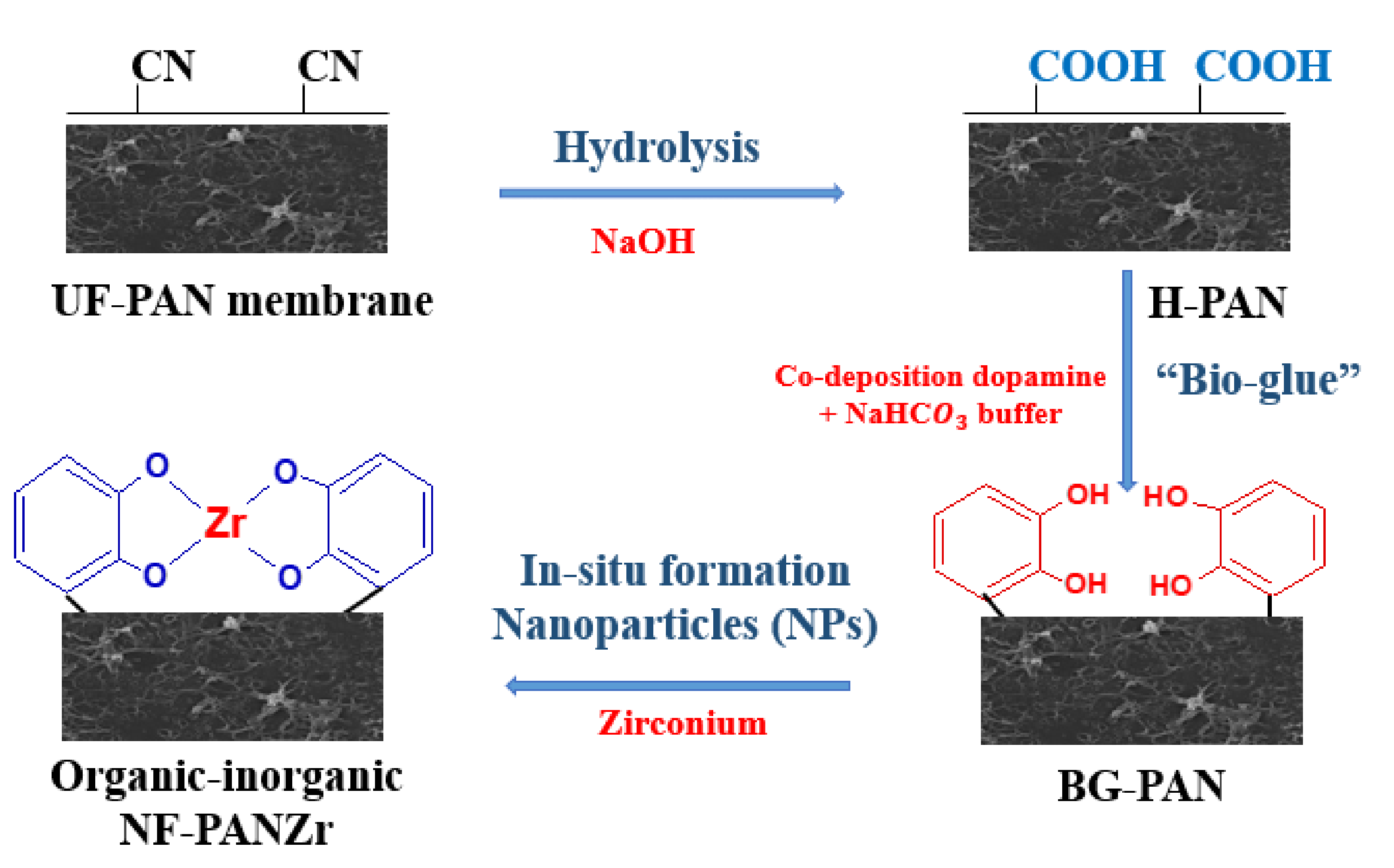
3.2. Novel Organic–Inorganic Nanofiltration Membrane NF-PANZr Preparation
- Step-1: Hydrolysis of polyacrylonitrile (PAN) membrane
- Step-2: Co-deposition of dopamine hydrochloride (DA) and sodium bicarbonate buffer (Buffer)
- Step-3: Deposition of zirconium (Zr) nanoparticles
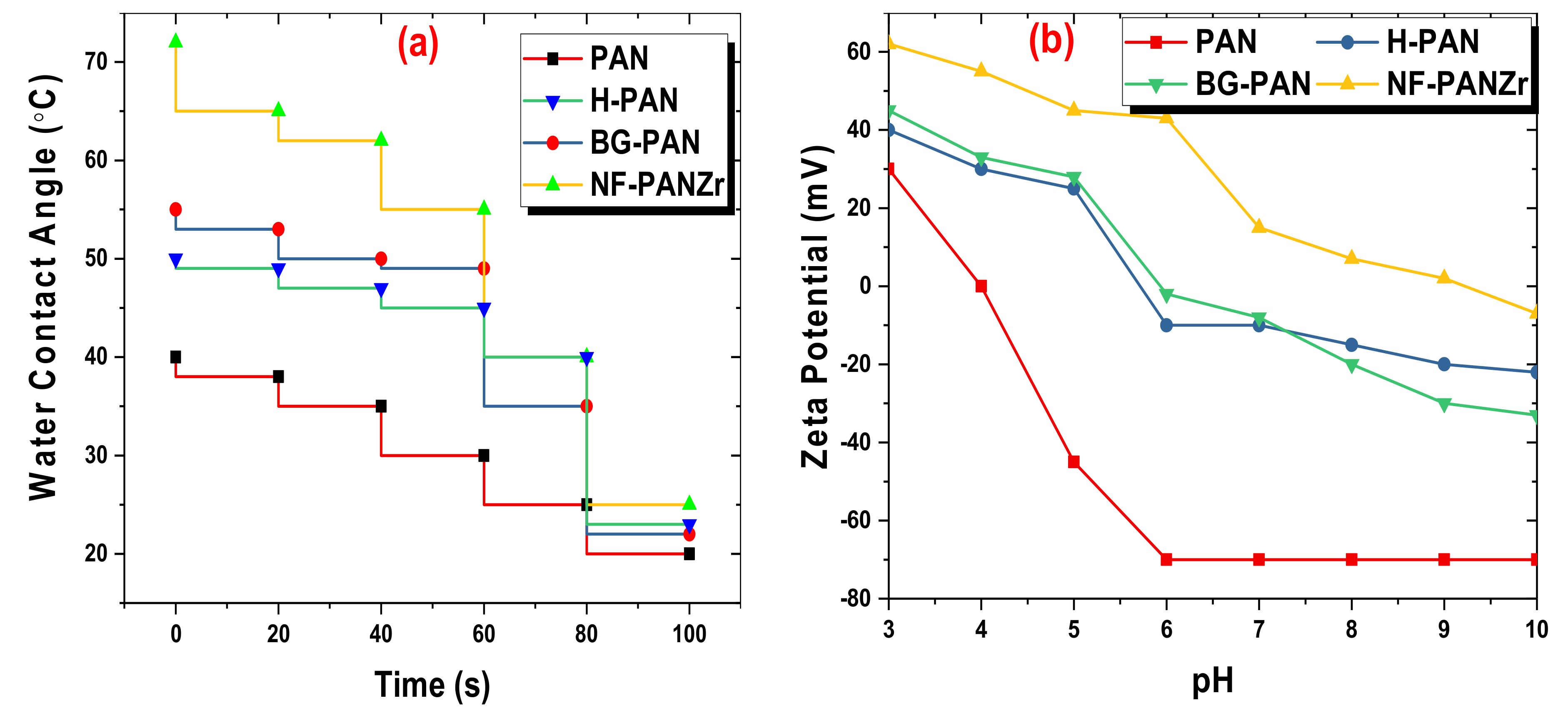
3.3. NF-PANZr Membrane Properties’ Characterization
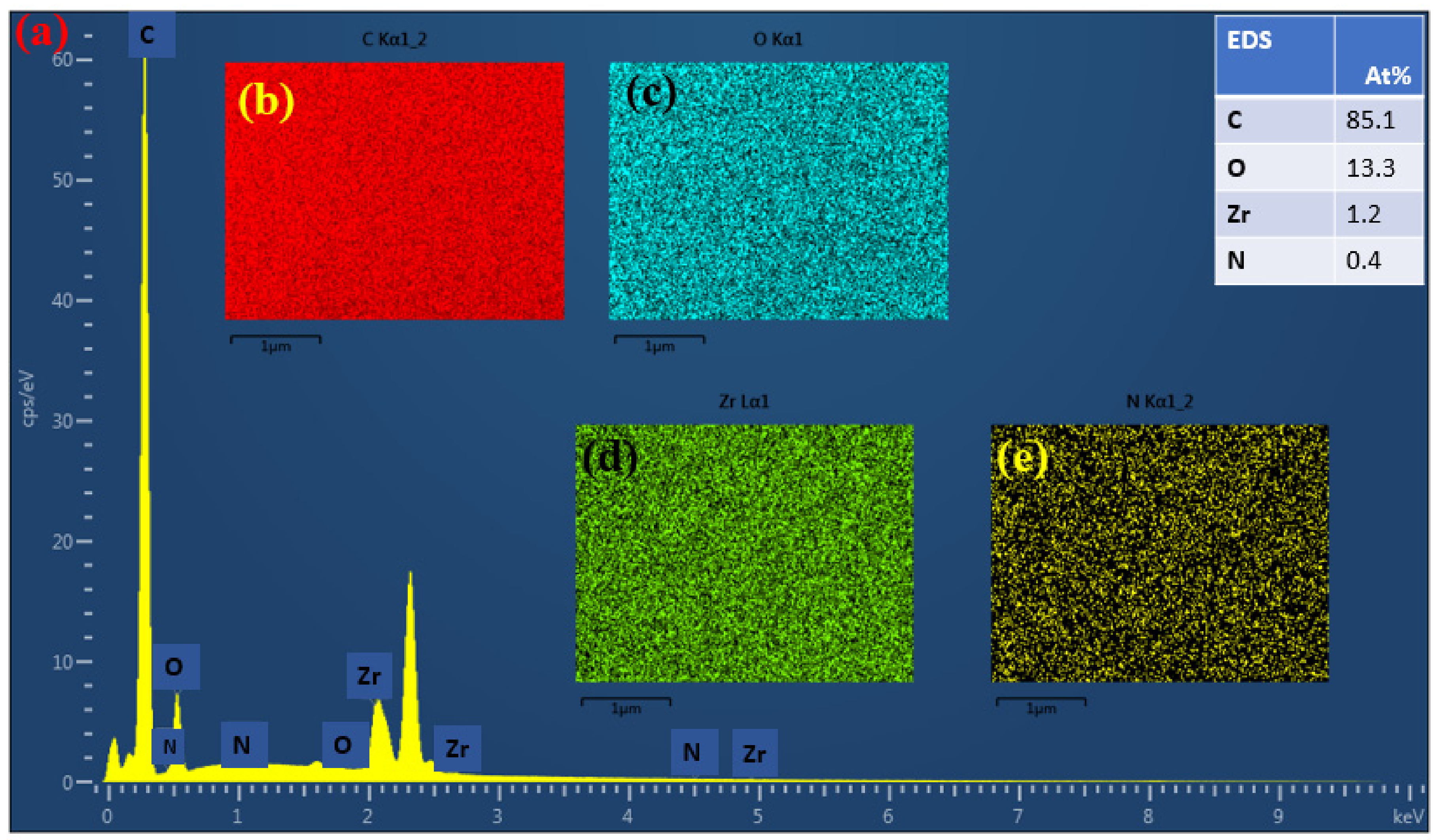
3.4. NF-PANZr Membrane Structure Characterization
3.5. Filtration Performance of Organic–Inorganic NF-PANZr Membrane
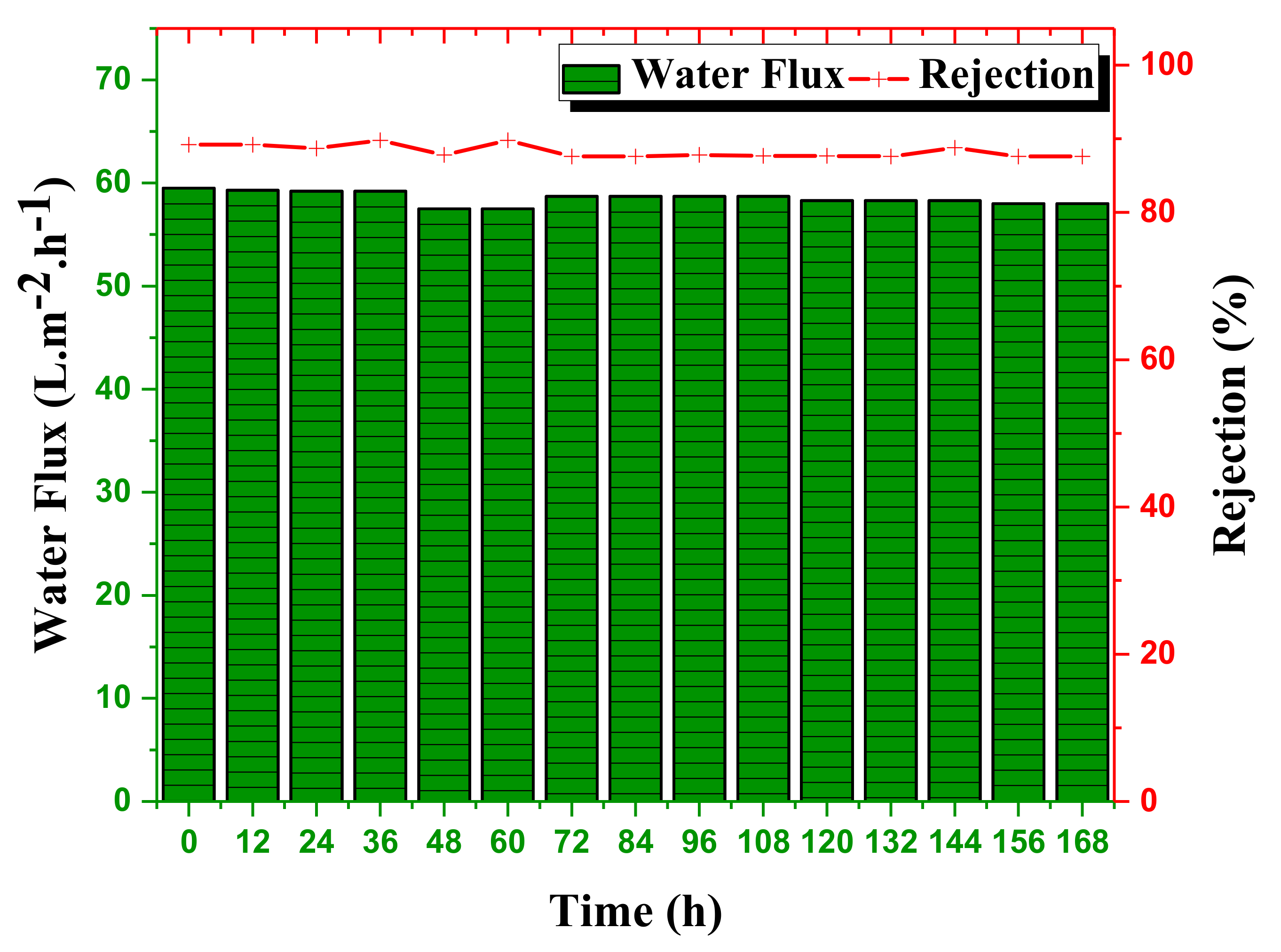
3.6. Long-Term Stability of NF-PANZr Membrane
3.7. Richardson Extrapolation
3.8. Statistical Error Analysis
4. Results and Discussion
4.1. NF-PANZr Properties’ Characterization
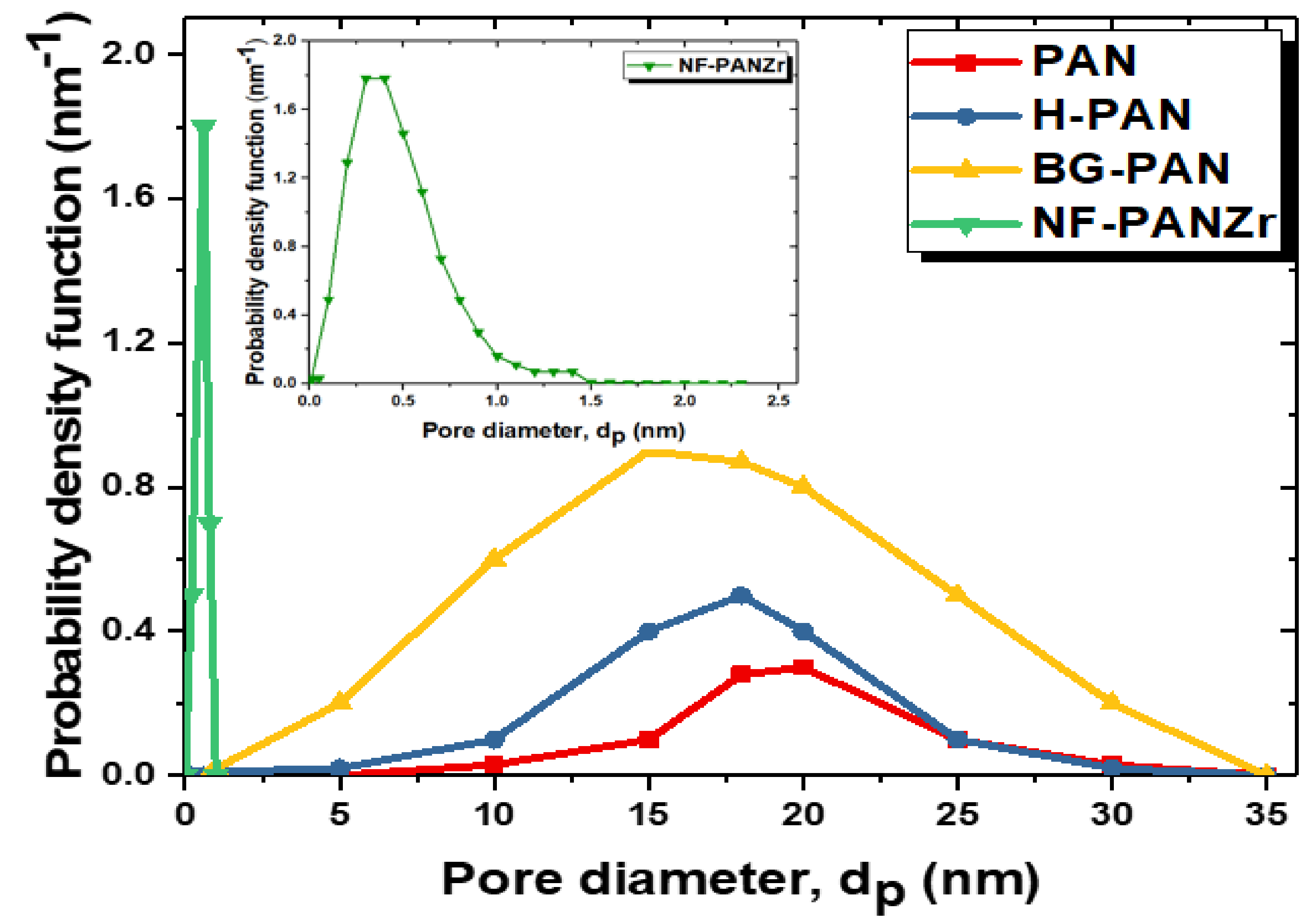
4.2. NF-PANZr Structures’ Characterization
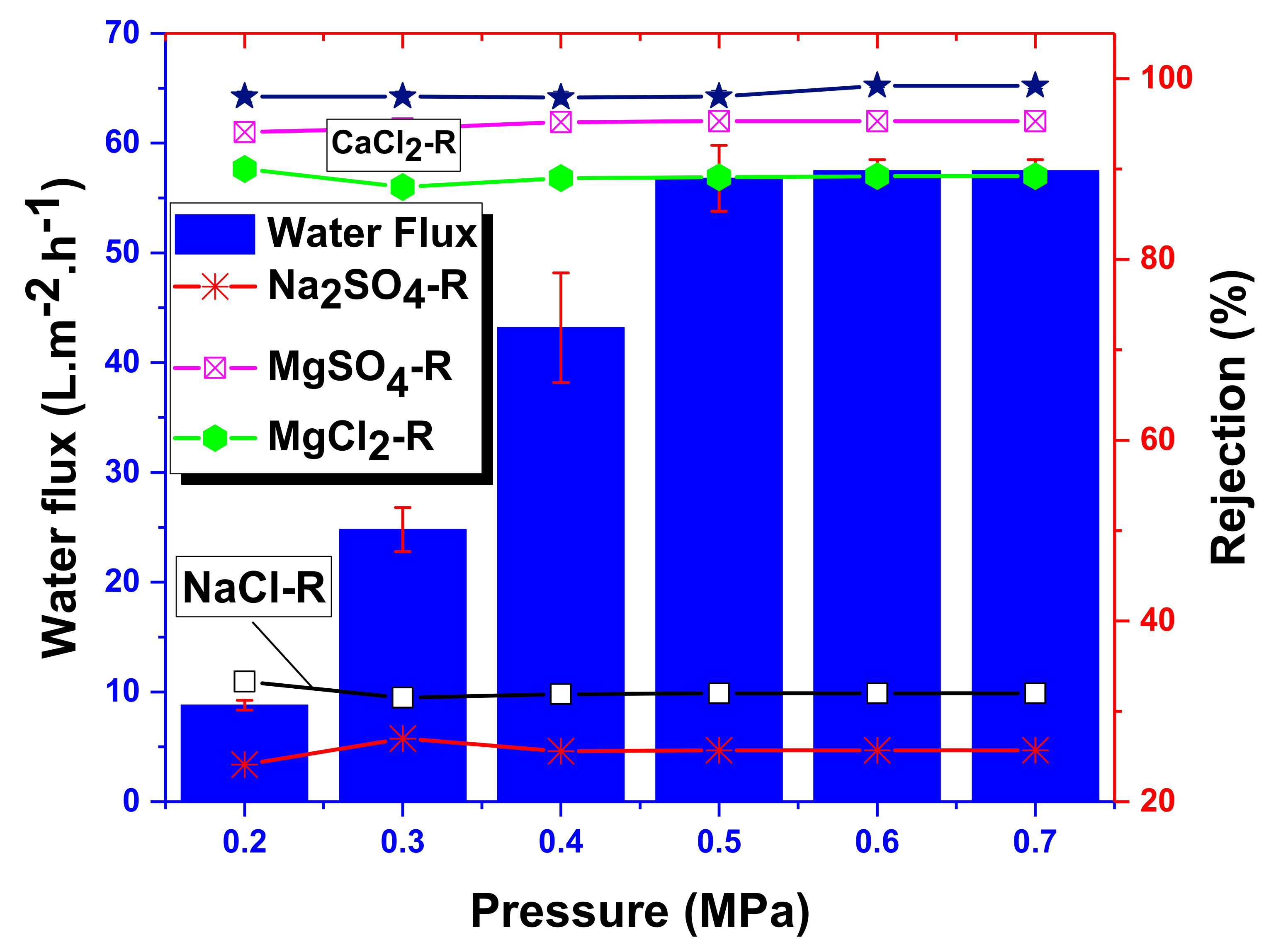
4.3. Experimental Salt Rejection
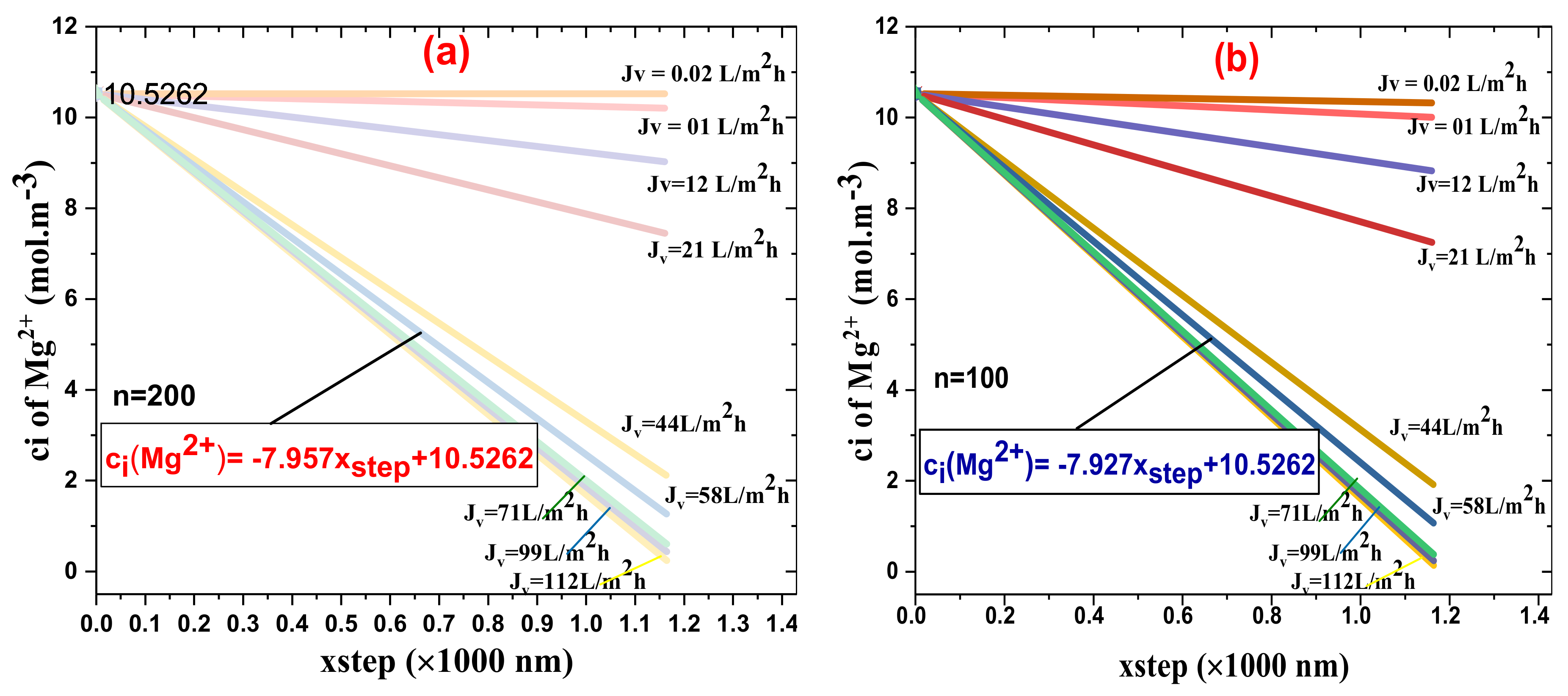
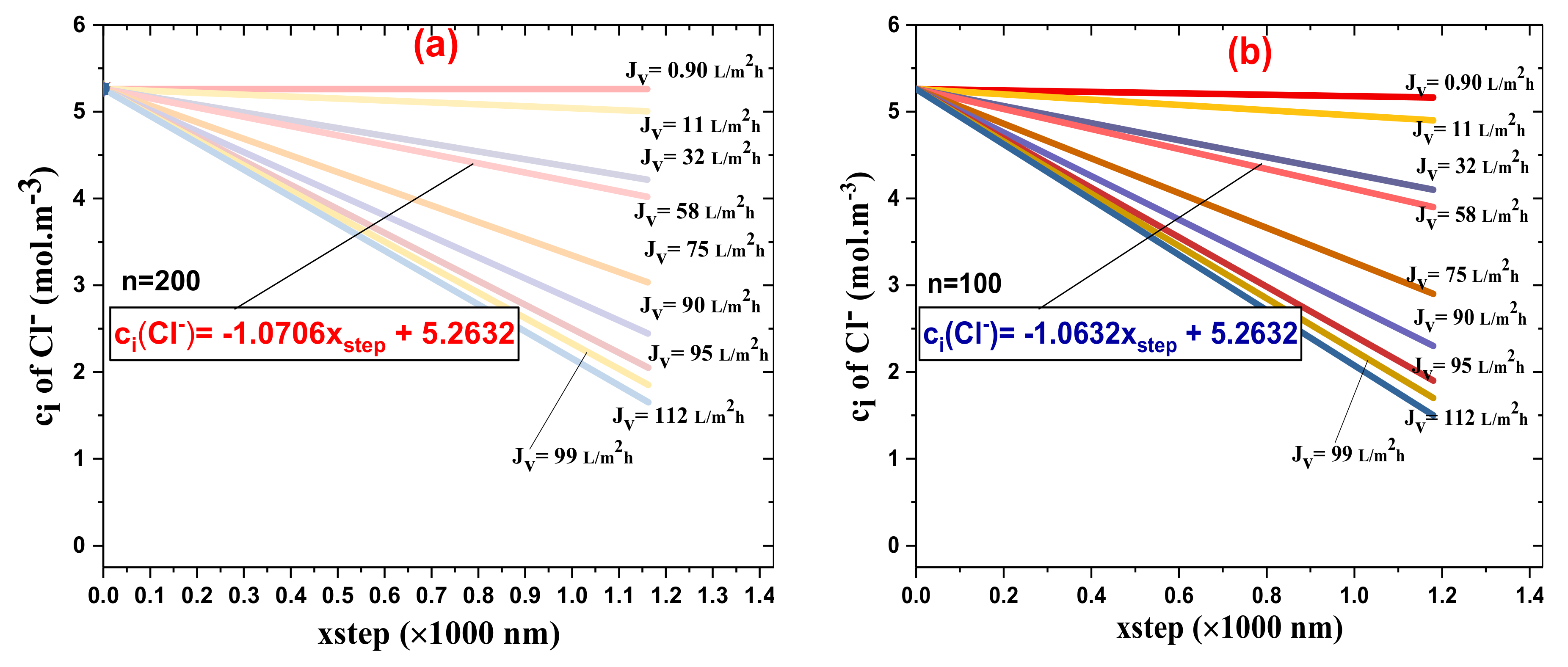
4.4. Runge–Kutta Model Reevaluation of Cl− and Mg2+ Rejection
4.5. NF-PANZr Long-Term Stability
4.6. Richardson Extrapolation and Statistical Error Analysis
4.7. Comparison of the Model Implemented in This Study with Other Previous Membrane Models
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| ion [i] concentration within pore, mol·m−3 | |
| feed-solution concentration, mol·m−3 | |
| ion [i] in feed-solution concentration, mol·m−3 | |
| uncharged solute bulk permeate concentration, mol·m−3 | |
| / | uncharged solute/charged solute pore diffusion coefficient, |
| solute bulk diffusion coefficient, m2.s−1 | |
| e | electronic charge, |
| I | ionic strength, mol·m−3 |
| j | number of data points per solute in fitting, dimensionless |
| ionic flux of ion [i] (pore area basis), mol·m−2·s−1 | |
| uncharged solute flux (pore area basis), mol·m−2·s−1 | |
| k | feed-side mass transfer coefficient, m/s |
| k | Boltzmann constant, |
| hindrance factor for convection of ion I, dimensionless | |
| ionic hindrance factor for diffusion, dimensionless | |
| P | pressure N/m2 |
| effective pore radius, m | |
| R | rejection (%) |
| R | universal gas constant, |
| V | solvent velocity, m/s |
| effective charge density, mol/m3 | |
| T | absolute temperature in K |
| ion [i] valence, dimensionless | |
| x | axial position within the pore, m |
| the activity coefficient of ion [i] within the pore, dimensionless | |
| applied pressure, N·m−2 | |
| the bulk activity coefficient of ion [i], dimensionless | |
| effective pressure driving force, N·m−2 | |
| membrane thickness, m | |
| the osmotic pressure difference, N·m−2 | |
| λ | the ratio of ionic or uncharged solute radius to pore radius, dimensionless |
| Donnan potential, V | |
| η | solvent viscosity within pores, N·s·m−2 |
| bulk/pore dielectric constant, dimensionless | |
| the ratio of effective membrane charge density to bulk feed concentration, dimensionless | |
| the ratio of ionic radius to pore radius, dimensionless | |
| the steric partition coefficient of ion [i], dimensionless | |
| the potential within the pore, V |
References
- Akhmouch, A.; Clavreul, D.J.W. Stakeholder engagement for inclusive water governance: “Practicing what we preach” with the OECD water governance initiative. Water 2016, 8, 204. [Google Scholar] [CrossRef]
- Ziolkowska, J.R. Desalination leaders in the global market–current trends and future perspectives. Water Sci. Technol. Water Supply 2016, 16, 563–578. [Google Scholar] [CrossRef]
- Telzhensky, M.; Birnhack, L.; Lehmann, O.; Windler, E.; Lahav, O. Selective separation of seawater Mg2+ ions for use in downstream water treatment processes. Chem. Eng. J. 2011, 175, 136–143. [Google Scholar] [CrossRef]
- Nativ, P.; Birnhack, L.; Lahav, O.J.S.; Technology, P. DiaNanofiltration-based method for inexpensive and selective separation of Mg2+ and Ca2+ ions from seawater, for improving the quality of soft and desalinated waters. Sep. Purif. Technol. 2016, 166, 83–91. [Google Scholar] [CrossRef]
- Alsayed, A.F.; Ashraf, M.A. Modified nanofiltration membrane treatment of saline water: A review. Desalin. Water Treat. 2020, 187, 93–105. [Google Scholar] [CrossRef]
- Li, X.; Liu, C.; Yin, W.; Chong, T.H.; Wang, R. Design and development of layer-by-layer based low-pressure antifouling nanofiltration membrane used for water reclamation. J. Membr. Sci. 2019, 584, 309–323. [Google Scholar] [CrossRef]
- Li, Q.; Liao, Z.; Fang, X.; Wang, D.; Xie, J.; Sun, X.; Wang, L.; Li, J. Tannic acid-polyethyleneimine crosslinked loose nanofiltration membrane for dye/salt mixture separation. J. Membr. Sci. 2019, 584, 324–332. [Google Scholar] [CrossRef]
- Peydayesh, M.; Mohammadi, T.; Nikouzad, S.K. A positively charged composite loose nanofiltration membrane for water purification from heavy metals. J. Membr. Sci. 2020, 118205. [Google Scholar] [CrossRef]
- Hedayatipour, M.; Jaafarzadeh, N.; Ahmadmoazzam, M. Removal optimization of heavy metals from effluent of sludge dewatering process in oil and gas well drilling by nanofiltration. J. Environ. Manag. 2017, 203, 151–156. [Google Scholar] [CrossRef]
- Qin, H.; Guo, W.; Huang, X.; Gao, P.; Xiao, H. Preparation of yttria-stabilized ZrO2 nanofiltration membrane by reverse micelles-mediated sol-gel process and its application in pesticide wastewater treatment. J. Eur. Ceram. Soc. 2020, 40, 145–154. [Google Scholar] [CrossRef]
- You, M.; Li, W.; Pan, Y.; Fei, P.; Wang, H.; Zhang, W.; Zhi, L.; Meng, J. Preparation and characterization of antibacterial polyamine-based cyclophosphazene nanofiltration membranes. J. Membr. Sci. 2019, 592, 117371. [Google Scholar] [CrossRef]
- Fahimirad, S.; Fahimirad, Z.; Sillanpää, M. Efficient removal of water bacteria and viruses using electrospun nanofibers. Sci. Total Environ. 2020, 751, 141673. [Google Scholar] [CrossRef]
- Conidi, C.; Castro-Muñoz, R.; Cassano, A. Nanofiltration in beverage industry. In Nanotechnology in the Beverage Industry; Elsevier: Amsterdam, The Netherlands, 2020; pp. 525–548. [Google Scholar]
- Yu, W.; Liu, T.; Crawshaw, J.; Liu, T.; Graham, N.J. Ultrafiltration and nanofiltration membrane fouling by natural organic matter: Mechanisms and mitigation by pre-ozonation and pH. Water Res. 2018, 139, 353–362. [Google Scholar] [CrossRef]
- Nath, K.; Dave, H.K.; Patel, T.M. Technology. Revisiting the recent applications of nanofiltration in food processing industries: Progress and prognosis. Trends Food Sci. Technol. 2018, 73, 12–24. [Google Scholar] [CrossRef]
- Chen, G.; Gras, S.; Kentish, S.J.S.; Technology, P. The application of forward osmosis to dairy processing. Sep. Purif. Technol. 2020, 246, 116900. [Google Scholar] [CrossRef]
- Igouzal, M.; El-Azhar, F.; Hafsi, M.; Taky, M.; Elmidaoui, A.J.D.; Treatment, W. Removal of hardness from groundwater using two nanofiltration membranes: Experimental study and modeling. Desalin. Water Treat. 2017, 93, 30–39. [Google Scholar] [CrossRef]
- Dixon, M.B.; Boerlage, S.F.; Churman, H.; Henthorne, L.; Anderson, D.M. Removal of Algal Toxins and Taste and Odor Compounds during Desalination. In Harmful Algal Blooms (HABs) and Desalination: A Guide to Impacts, Monitoring and Management; Intergovernmental Oceanographic Commission of UNESCO: Paris, France, 2017. [Google Scholar]
- Zarei, F.; Moattari, R.M.; Rajabzadeh, S.; Bagheri, M.; Taghizadeh, A.; Mohammadi, T.; Matsuyama, H. Preparation of thin film composite nano-filtration membranes for brackish water softening based on the reaction between functionalized UF membranes and polyethyleneimine. J. Membr. Sci. 2019, 588, 117207. [Google Scholar] [CrossRef]
- Donnan, F.G. Theory of membrane equilibria and membrane potentials in the presence of non-dialysing electrolytes. A contribution to physical-chemical physiology. J. Membr. Sci. 1995, 100, 45–55. [Google Scholar] [CrossRef]
- Lu, S.; Ding, Y.; Guo, J. Kinetics of fine particle aggregation in turbulence. Adv. Colloid Interface Sci. 1998, 78, 197–235. [Google Scholar] [CrossRef]
- Bowen, W.R.; Welfoot, J.S. Modelling the performance of membrane nanofiltration—critical assessment and model development. Chem. Eng. Sci. 2002, 57, 1121–1137. [Google Scholar] [CrossRef]
- Oatley, D.L.; Llenas, L.; Pérez, R.; Williams, P.M.; Martínez-Lladó, X.; Rovira, M. Review of the dielectric properties of nanofiltration membranes and verification of the single oriented layer approximation. Adv. Colloid Interface Sci. 2012, 173, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ahmadian, A.; Salahshour, S.; Chan, C.S.; Baleanu, D. Numerical solutions of fuzzy differential equations by an efficient Runge–Kutta method with generalized differentiability. Fuzzy Sets Syst. 2018, 331, 47–67. [Google Scholar] [CrossRef]
- Van Gestel, T.; Vandecasteele, C.; Buekenhoudt, A.; Dotremont, C.; Luyten, J.; Leysen, R.; Van der Bruggen, B.; Maes, G. Salt retention in nanofiltration with multilayer ceramic TiO2 membranes. J. Membr. Sci. 2002, 209, 379–389. [Google Scholar] [CrossRef]
- Yaldız, S. Application of Tubular Ceramic Nanofiltration Membranes for Textile Waste Water Desalination. Master’s Thesis, Izmir Institute of Technology, Urla, Turkey, 2017. [Google Scholar]
- He, Y.; Liu, J.; Han, G.; Chung, T.-S. Novel thin-film composite nanofiltration membranes consisting of a zwitterionic co-polymer for selenium and arsenic removal. J. Membr. Sci. 2018, 555, 299–306. [Google Scholar] [CrossRef]
- Cheng, S.; Oatley, D.L.; Williams, P.M.; Wright, C. Positively charged nanofiltration membranes: Review of current fabrication methods and introduction of a novel approach. Adv. Colloid Interface Sci. 2011, 164, 12–20. [Google Scholar] [CrossRef]
- Déon, S.; Fievet, P.; Doubad, C.O. Tangential streaming potential/current measurements for the characterization of composite membranes. J. Membr. Sci. 2012, 423, 413–421. [Google Scholar] [CrossRef]
- Bauman, M.; Košak, A.; Lobnik, A.; Petrinić, I.; Luxbacher, T. Nanofiltration membranes modified with alkoxysilanes: Surface characterization using zeta-potential. Colloids and Surfaces A Physicochem. Eng. Asp. 2013, 422, 110–117. [Google Scholar] [CrossRef]
- Tofighy, M.A.; Mohammadi, T.J.C.E.J. Divalent heavy metal ions removal from contaminated water using positively charged membrane prepared from a new carbon nanomaterial and HPEI. Chem. Eng. J. 2020, 388, 124192. [Google Scholar] [CrossRef]
- Zhao, Z.; Liu, B.; Ilyas, A.; Vanierschot, M.; Muylaert, K.; Vankelecom, I.F. Harvesting microalgae using vibrating, negatively charged, patterned polysulfone membranes. J. Membr. Sci. 2021, 618, 118617. [Google Scholar] [CrossRef]
- Ding, J.; Pu, L.; Zou, D.; Cao, M.; Shan, C.; Zhang, Q.; Gao, G.; Pan, B.J.C. Removal of model dyes on charged UF membranes: Experiment and simulation. Chemosphere 2020, 240, 124940. [Google Scholar] [CrossRef]
- Yang, C.; Xu, W.; Nan, Y.; Wang, Y.; Chen, X.J.S. Novel negatively charged nanofiltration membrane based on 4, 4′-diaminodiphenylmethane for dye removal. Sep. Purif. Technol. 2020, 117089. [Google Scholar] [CrossRef]
- Lv, Y.; Yang, H.-C.; Liang, H.-Q.; Wan, L.-S.; Xu, Z.-K. Novel nanofiltration membrane with ultrathin zirconia film as selective layer. J. Membr. Sci. 2016, 500, 265–271. [Google Scholar] [CrossRef]
- Nicomel, N.; Leus, K.; Folens, K.; Van Der Voort, P.; Du Laing, G. Technologies for arsenic removal from water: Current status and future perspectives. Int. J. Environ. Res. Public Health 2016, 13, 62. [Google Scholar] [CrossRef]
- Song, Z.; Fathizadeh, M.; Huang, Y.; Chu, K.H.; Yoon, Y.; Wang, L.; Xu, W.L.; Yu, M. TiO2 nanofiltration membranes prepared by molecular layer deposition for water purification. J. Membr. Sci. 2016, 510, 72–78. [Google Scholar] [CrossRef]
- Gholami, S.; López, J.; Rezvani, A.; Vatanpour, V.; Cortina, J.L. Fabrication of thin-film nanocomposite nanofiltration membranes incorporated with aromatic amine-functionalized multiwalled carbon nanotubes. Rejection performance of inorganic pollutants from groundwater with improved acid and chlorine resistance. Chem. Eng. J. 2020, 384, 123348. [Google Scholar] [CrossRef]
- Farsi, A.; Boffa, V.; Qureshi, H.F.; Nijmeijer, A.; Winnubst, L.; Christensen, M.L. Modeling water flux and salt rejection of mesoporous γ-alumina and microporous organosilica membranes. J. Membr. Sci. 2014, 470, 307–315. [Google Scholar] [CrossRef]
- Jadhav, S.V.; Marathe, K.V.; Rathod, V.K. A pilot scale concurrent removal of fluoride, arsenic, sulfate and nitrate by using nanofiltration: Competing ion interaction and modelling approach. J. Water Process. Eng. 2016, 13, 153–167. [Google Scholar] [CrossRef]
- Chakrabortty, S.; Roy, M.; Pal, P. Removal of fluoride from contaminated groundwater by cross flow nanofiltration: Transport modeling and economic evaluation. Desalination 2013, 313, 115–124. [Google Scholar] [CrossRef]
- Okhovat, A.; Mousavi, S.M. Modeling of arsenic, chromium and cadmium removal by nanofiltration process using genetic programming. Appl. Soft Comput. 2012, 12, 793–799. [Google Scholar] [CrossRef]


| Parameters | Abbreviation | Value |
|---|---|---|
| Faraday’s constant (F) | F | 96,487 C·mol−1 |
| Universal gas constant | R | 8.314 |
| Boltzmann constant (k) | K | 1.38066 × 10−23 J·K−1 |
| Permittivity of free space ( | 8.85419 | |
| Operating temperature (T) | T | 303.15 K |
| Operating pressure () | P | 0.60 MPa |
| Hydrogen potential | pH | 6.0 |
| Crossflow velocity | CFV |
| Membrane | MWCO (kDa) | ||
|---|---|---|---|
| PAN Platform | 21 | 1.13 | 100 |
| H-PAN | 18 | 1.32 | 13 |
| BG-PAN | 15 | 1.36 | 17 |
| NF-PANZr | 0.4 | 1.45 | 8.8 |
| Parameters | Units | Value | References |
|---|---|---|---|
| Rejection_NaCl | % | 32.0 | This study |
| Rejection_MgSO4 | % | 95.3 | |
| Permeate_flux | 58 | ||
| Membrane_geometry | Flat − Sheet | 1 m × 1 m | |
| Membrane_surface area | cm2 | 29.22 | |
| Membrane_thickness | nm | 1180 ± 5.17 | |
| Pore_size | nm | 0.4 | Equation (31) |
| NF-PANZr Membrane | |||||
|---|---|---|---|---|---|
| Experimental | Predicted | Error (%) RE | |||
| 31.9 | 32.2 | 36.2 | 31.93 | 0.09 | |
| 95.3 | 95.1 | 92.3 | 95.29 | 0.01 | |
| Ion | Ion Diffusivity | Stokes Radii | Partial Molar Volume | References |
|---|---|---|---|---|
| 133 | 0.184 | −1.20 | [22] | |
| 203 | 0.121 | 17.82 | ||
| 106 | 0.231 | 14.18 | ||
| 72 | 0.348 | −21.57 |
| Membrane Type | Designation | Model | Error (%) | References |
|---|---|---|---|---|
| Synthesized | NF-PANZr | Runge–Kutta + Richardson Extrapolation | 0.01–0.09 | This study |
| alumina mesoporous | model | 0.05 | [39] | |
| Organosilica microporous | model | <0.05 | ||
| NF_PAN_TI | Euler numerical method | 0.09 | ||
| Commercial | NF 90 | Gauss–Newton | 1.91 | [40] |
| NF 270 | Gauss–Newton | 3.34 | ||
| NF-1 | DSPM modified | 1.2 | [41] | |
| NF-2 | DSPM modified | 5.2 | ||
| NF-20 | DSPM modified | 3.4 | ||
| UTC-70UB | GP model | 0.20 | [42] | |
| Desal-DK | 2P model + dielectric | 0.30 | [22] | |
| Desal-DK | DSPM | 0.13 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Worou, C.N.; Kang, J.; Shen, J.; Yan, P.; Wang, W.; Gong, Y.; Chen, Z. Runge–Kutta Numerical Method Followed by Richardson’s Extrapolation for Efficient Ion Rejection Reassessment of a Novel Defect-Free Synthesized Nanofiltration Membrane. Membranes 2021, 11, 130. https://doi.org/10.3390/membranes11020130
Worou CN, Kang J, Shen J, Yan P, Wang W, Gong Y, Chen Z. Runge–Kutta Numerical Method Followed by Richardson’s Extrapolation for Efficient Ion Rejection Reassessment of a Novel Defect-Free Synthesized Nanofiltration Membrane. Membranes. 2021; 11(2):130. https://doi.org/10.3390/membranes11020130
Chicago/Turabian StyleWorou, Chabi Noël, Jing Kang, Jimin Shen, Pengwei Yan, Weiqiang Wang, Yingxu Gong, and Zhonglin Chen. 2021. "Runge–Kutta Numerical Method Followed by Richardson’s Extrapolation for Efficient Ion Rejection Reassessment of a Novel Defect-Free Synthesized Nanofiltration Membrane" Membranes 11, no. 2: 130. https://doi.org/10.3390/membranes11020130
APA StyleWorou, C. N., Kang, J., Shen, J., Yan, P., Wang, W., Gong, Y., & Chen, Z. (2021). Runge–Kutta Numerical Method Followed by Richardson’s Extrapolation for Efficient Ion Rejection Reassessment of a Novel Defect-Free Synthesized Nanofiltration Membrane. Membranes, 11(2), 130. https://doi.org/10.3390/membranes11020130








