Review of Transport Phenomena and Popular Modelling Approaches in Membrane Distillation
Abstract
1. Introduction
- (A)
- (B)
- Air gap MD (AGMD), in which a low-temperature air gap is on the permeate side and interposed between the membrane and a condensation surface cooled normally by a cooling flow [9].
- (C)
- (D)
- Conventional modelling approaches [21], which are based on the foundation of mass transfer and heat transfer through porous materials. Characterisation of the membrane and flow dynamics are critical to providing acceptable modelling results. Some membrane properties obtained prior to the tests could be varied during the experiment under different pressures and temperatures and need to be fitted with the operation conditions in the modelling accordingly [22].
- Computer simulation approaches, such as computational fluid dynamics (CFD). CFD models were developed in the early 1950s, initially for solving aeronautic problems [23]. They have been widely used as an analysis tool to study transport phenomena in MD [24]. Membrane characteristics and flow dynamic information are still required for the simulation. However, CFD can be used to study the hydrodynamic conditions, heat and mass transfers in MD modules for optimisation purpose [25,26].
- Mathematical statics approaches, such as response surface methodology (RSM) [27,28,29]. RSM is a collection of mathematical and statistical methods based on fitting a polynomial equation to the experimental data and is able to predict the behaviour of a data set with the objective of making statistical previsions [30].
2. Mechanism of Heat Transfer and Mass Transfer through Porous MD Membranes
2.1. Heat Transfer from the Feed Stream to the Permeate Side
- Firstly, heat transfers from the feed side to the permeate side across the porous membrane as sensible heat and latent heat, which incur the temperature difference between the boundary layer and bulk flow;
- Secondly, the temperature difference between the bulk flow and membrane surface leads to heat transfers from the bulk flow to the boundary layer via heat convection.
2.2. Mass Transfer through the Porous Membrane
- Firstly, vaporisation of feed at the liquid/gas interface or the interface between the membrane and the feed;
- secondly, transportation of vapour from the interface between the feed and the membrane to the interface between the membrane and permeate side, which is driven by the vapour pressure difference across the membrane pores; and
- thirdly, transportation of the vapour from the interface between the membrane and permeate side into the permeate side [44].
2.3. Interaction of Heat and Mass Transfers
2.4. Mass Transfer and Heat Transfer in Four Major Configurations
2.4.1. Direct Contact Membrane Distillation
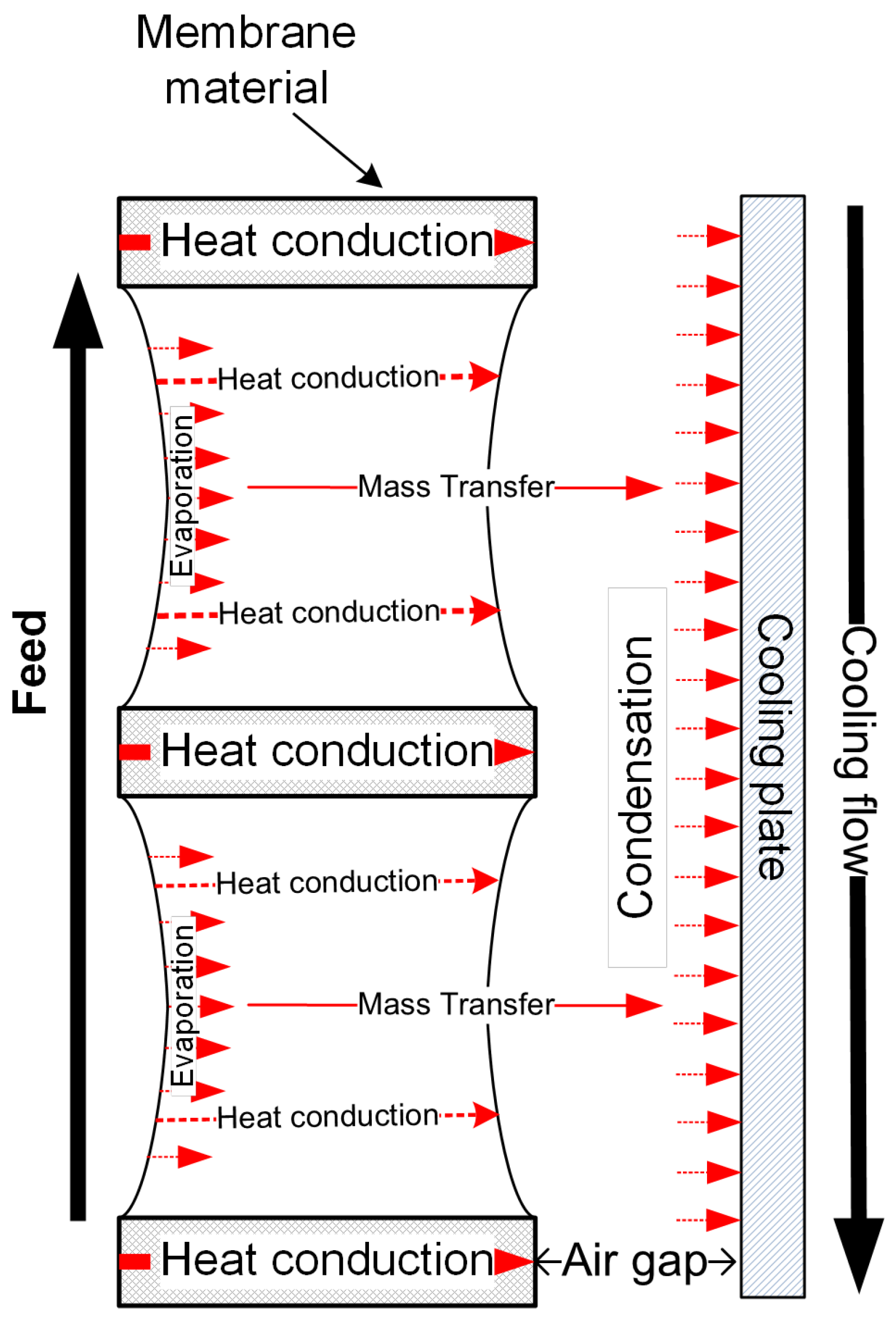
2.4.2. Air Gap Membrane Distillation
- Heat transfer (Qgap) through the air gap can be described by:
- Heat transfer (Qc) through the condensate layer, where the temperature decreases from Tc to Tpl:
- Heat transfer (Qpl) through the cooling plate:
- Heat transfer (Qcl) through the cooling flow:
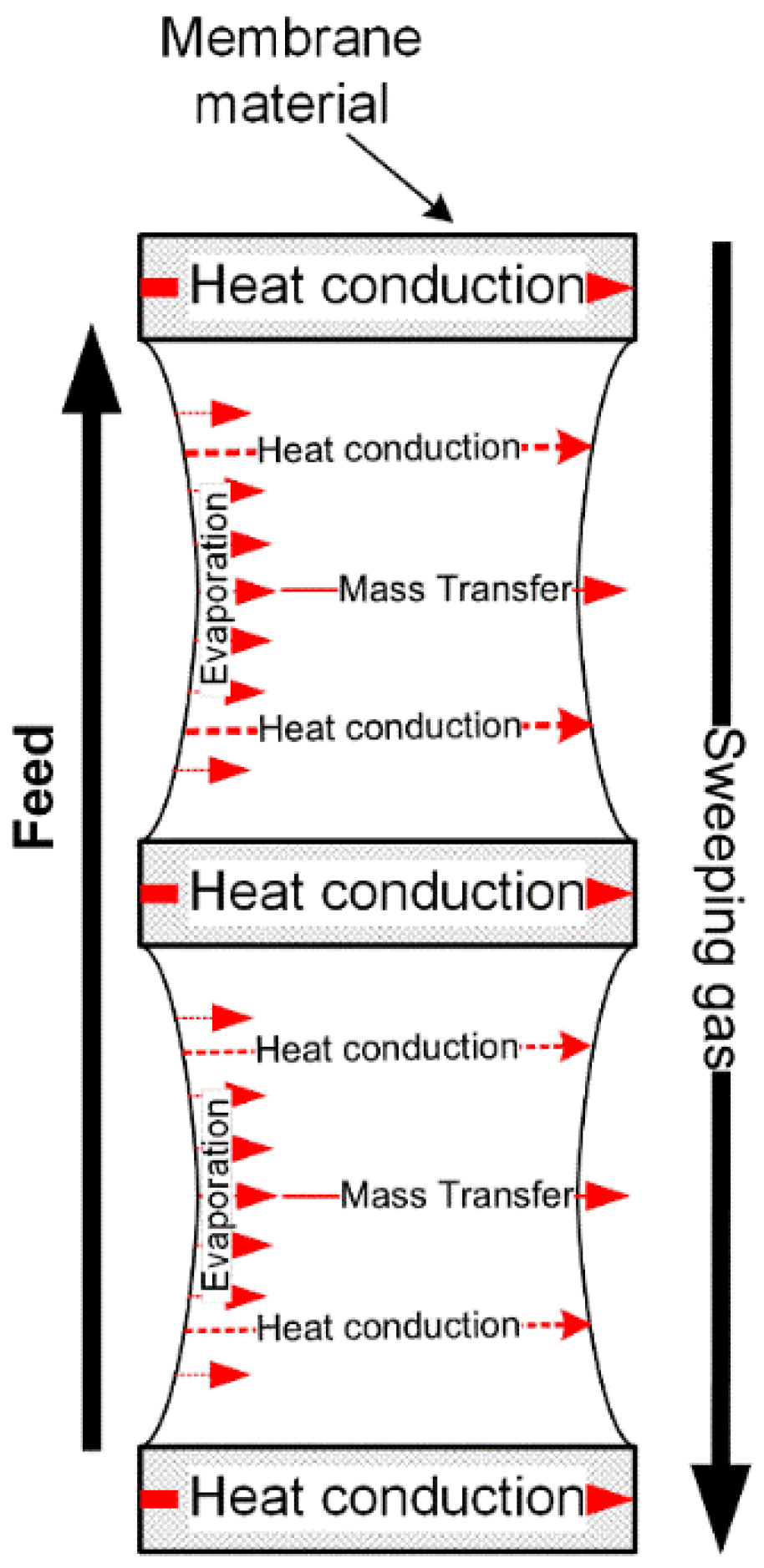
2.4.3. Sweeping Gas Membrane Distillation
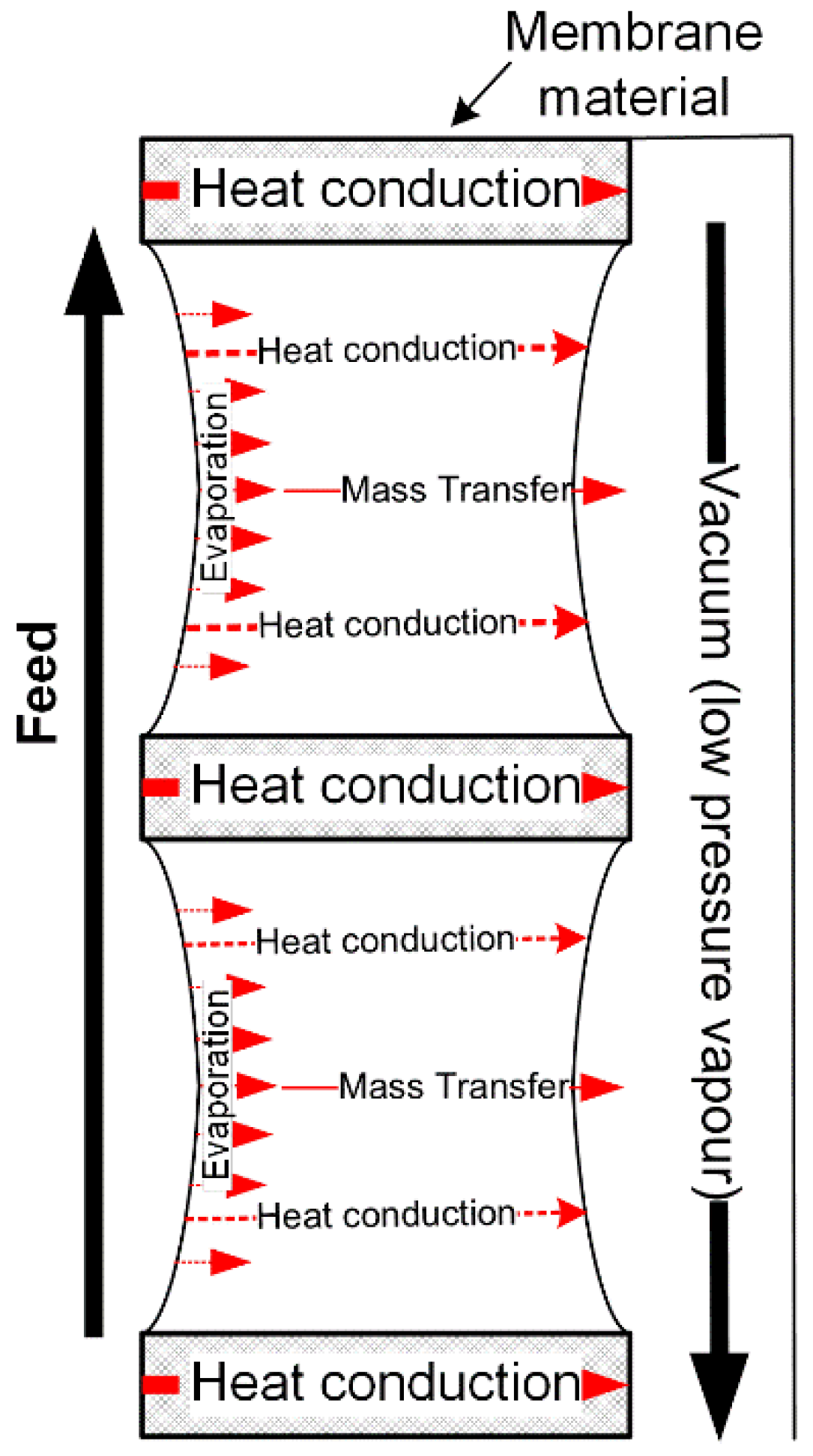
2.4.4. Vacuum Membrane Distillation
2.4.5. Comparison of Thermal Energy Efficiency in Four Configurations
2.4.6. Separation Organics and Water Mixtures by Hybrid Membrane
3. Modelling Approaches
3.1. Conventional Modelling Approaches
- membrane characteristics, based on Equations (14) and (15), including porosity, pore size, pore tortuosity, membrane thickness and thermal conductivity [22,96]. Furthermore, as the properties of some membranes will be changed under the operation conditions, such as being compressed under pressure, the correlations between the membrane properties and the operation conditions need to be set up [22,58,97];
- the configurations of the module, including the length and width of the flow channel, hydraulic diameter and spacer structure (Equations (8)–(11)); and
- parameters of the feed stream, including thermal conductivity, viscosity, linear velocity, salt concentration and temperatures.
- For DCMD, the information required is the same as the feed side.
- For AGMD, based on Equations (20) and (21), the information required is the air gap width, thermal conductivities of the air and condensate, the thickness of the condensate layer (which could be calculated based on the theoretical model), thickness and thermal conductivity of the cooling plate, and parameters of the cooling stream.
- In SGMD, the required seeping gas properties include thermal conductivity, viscosity, linear velocity, water content and temperatures.
- The permeate side of VMD is under reduced pressure. Therefore, pressure in the vacuum chamber is commonly the only parameter that needs to be known.
- One direction of flow;
- No heat loss from the module;
- No property variation along the whole piece of membrane;
- Only vapour phase in the pores;
- No convective heat transfer in the membrane pores;
- No influence of pore size distribution on mass transfer;
- Vapour pressure, velocity profile and temperature profile not being affected by the dissolved salt at low concentration; and
- Membrane pores being cylindrical and not interconnected.
- No total pressure variation inside the air gap;
- Condensate in form of film, whose thickness is much thinner than that of the air gap; and
- Mass transfer mechanism dominated by diffusion.
3.2. Computational Fluid Dynamics (CFD)
3.3. Response Surface Methodology (RSM)
- complicated characterizations of membrane properties and module parameters exist, such as measuring pore size, porosity, thickness and thermal conductivity of the membrane and determining the geometric structure of MD module, which are not as essential in conventional and CFD methods;
- variation of membrane properties do not affect the modelling results, since the recorded experimental data have contained the variations, which will be involved in the fitting process;
- control parameters can be predicted from the required output such as flux or energy requirement; and
- synergic effects of two variables on one function can be conducted for process optimisation.
- However, there are also some limitations of RSM:
- The modelling results from RSM may not be able to apply to other systems. The experimental data are foundational for RSM. The data used in the RSM normally include solute concentration, stream velocity, temperature, flux, GOR, vapour pressure and energy input [27,29,31,121,122]. However, all these data should be from the identical systems, and the predicted results should be strictly applicable to these identical systems. For example, if the spacer in the channel is replaced or a different type of membrane is used, the response of the modelling might be altered.
- A comprehensive amount of experimental work/variables is required to achieve the representative data and minimise the error. The results predicted by RSM would be more accurate if the increased data and parameters acquired from the experiment are used for the fitting process.
- It is not possible to simulate the data that can be measured or calculated based on the measurement data. For example, TPC cannot be calculated by the measurable data and cannot be predicted by the RSM. However, Cheng et al. overcame this limitation by combining conventional modelling with RSM [31].
3.4. Critical Assessment and Comparison of the Different Approaches
3.5. Modelling of Operational Cost of MD
4. Research Gaps and Future Study
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | membrane area |
| ∆Qf | heat loss from the feed flow |
| Across | cross sectional area of empty channel |
| b | membrane thickness |
| bair | thickness of the air gap |
| Cf | specific heat of the feed |
| d | pore diameter |
| DAB | relative diffusivity of the vapour (A) to air (B) |
| df | diameter of spacer filaments |
| dh | hydraulic diameter of the spacer filled channel |
| E | thermal efficiency |
| Hlatent | latent heat of vaporization |
| hsg | convective heat transfer coefficient |
| J | flux |
| Jm and Jk | vapour fluxes contributed, respectively, by molecular and Knudsen diffusions |
| kB | Boltzman constant |
| Kn | Knudsen number |
| l | mean free path |
| lm | mesh size |
| ṁf | mass flow rate of the feed |
| mw and ma | molecular weights of vapour and air |
| P0i, and P0j | saturated vapour pressures of volatiles and water |
| Pg and Tg | mean pressure and temperature in the air gap |
| Ppore | pressure in the pore |
| PT1 and PT2 | vapour pressures on feed and permeate sides at membrane interfaces |
| Q1,Q2 | total heat transferred across the membrane |
| Qf | volumetric flow rate of feed |
| Qsg | heat transfer from the membrane surface on the permeate side to the bulk gas stream |
| Qvacuum | heat transfer on permeate side in VMD |
| R | universal gas constant |
| Rm and Rk | mass transfer resistances to molecular and Knudsen diffusions |
| Sspacer | specific surface of the spacer |
| t | pore tortuosity |
| T | mean temperature in the pores, |
| T1 and T2 | temperatures at the membrane surfaces of the feed and permeate sides |
| Tc | surface temperature of the condensate |
| Tcl | temperature of interface between the cooling plate and the cooling flow |
| Tcl,b | temperature of the bulky cooling flow |
| Tf,i and Tf,o | inlet and outlet temperatures of feed |
| Tpl | temperature of interface between the condensate and the cooling plate |
| Tsg | temperature of the bulk gas flow |
| vs | velocity in the spacer filled channel |
| x2 and xc | molar fractions of the water vapour at surfaces of membrane and condensate |
| yi and xi | molar ratios of the volatile component in gas phase and liquid phase |
| yj and xj | molar ratios of water in gas phase and liquid phase |
| α | convective heat transfer coefficient |
| αf | the convective heat transfer coefficient |
| αi,j | relative volatility |
| ε | porosity of membrane |
| εspacer | porosity of spacer |
| λ, λair, λf and λsolid | thermal conductivities of membrane, air, feed and the membrane material |
| λc and bc | thermal conductivity and thickness of the condensate layer |
| λpl and bpl | thermal conductivity and thickness of the cooling plate |
| μ µg | viscosities of liquid and gas |
| ρ | density of the liquid steam |
| σ1 and σa | collision diameters of vapour and air |
| τ | temperature polarisation coefficient |
References
- Weyl, P.K. Recovery of Demineralized Water from Saline Waters. U.S. Patent 3340186, 5 September 1967. [Google Scholar]
- Carlsson, L. The new generation in sea water desalination SU membrane distillation system. Desalination 1983, 45, 221–222. [Google Scholar] [CrossRef]
- Smolders, K.; Franken, A.C.M. Terminology for Membrane Distillation. Desalination 1989, 72, 249–262. [Google Scholar] [CrossRef]
- Nthunya, L.N.; Gutierrez, L.; Derese, S.; Nxumalo, E.N.; Verliefde, A.R.; Mamba, B.B.; Mhlanga, S.D. A review of nanoparticle-enhanced membrane distillation membranes: Membrane synthesis and applications in water treatment. J. Chem. Technol. Biotechnol. 2019, 94, 2757–2771. [Google Scholar] [CrossRef]
- Gryta, M. Effectiveness of water desalination by membrane distillation process. Membranes 2012, 2, 415–429. [Google Scholar] [CrossRef]
- Alklaibi, A.M.; Lior, N. Membrane-distillation desalination: Status and potential. Desalination 2005, 171, 111–131. [Google Scholar] [CrossRef]
- Martinez-Diez, L.; Florido-Diaz, F.J. Theoretical and experimental studies on desalination using membrane distillation. Desalination 2001, 139, 373–379. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R. Direct contact membrane distillation: Effect of mass transfer on heat transfer. J. Membr. Sci. 2001, 188, 137–143. [Google Scholar] [CrossRef]
- Josson, A.S.; Wimmerstedt, R.; Harrysson, A.C. Membrane distillation—A theoretical study of evaporation through microporous membranes. Desalination 1985, 56, 237–249. [Google Scholar] [CrossRef]
- Bandini, S.; Gostoli, C.; Sarti, G.C. Separation efficiency in vacuum membrane distillation. J. Membr. Sci. 1992, 73, 217–229. [Google Scholar] [CrossRef]
- Sarti, G.C.; Gostoli, C.; Bandini, S. Extraction of organic components from aqueous streams by vacuum membrane distillation. J. Membr. Sci. 1993, 80, 21–33. [Google Scholar] [CrossRef]
- Rivier, C.A.; García-Payo, M.C.; Marison, I.W.; von Stockar, U. Separation of binary mixtures by thermostatic sweeping gas membrane distillation: I. Theory and simulations. J. Membr. Sci. 2002, 201, 1–16. [Google Scholar] [CrossRef]
- Khayet, M.; Godino, P.; Mengual, J.I. Theory and experiments on sweeping gas membrane distillation. J. Membr. Sci. 2000, 165, 261–272. [Google Scholar] [CrossRef]
- Khayet, M.; Godino, P.; Mengual, J.I. Nature of flow on sweeping gas membrane distillation. J. Membr. Sci. 2000, 170, 243–255. [Google Scholar] [CrossRef]
- Garcia-Payo, M.C.; Rivier, C.A.; Marison, I.W.; von Stockar, U. Separation of binary mixtures by thermostatic sweeping gas membrane distillation: II. Experimental results with aqueous formic acid solutions. J. Membr. Sci. 2002, 198, 197–210. [Google Scholar] [CrossRef]
- Curcio, E.; Drioli, E. Membrane Distillation and Related Operations: A Review. Sep. Purif. Rev. 2005, 34, 35–86. [Google Scholar] [CrossRef]
- Al-Obaidani, S.; Curcio, E.; Macedonio, F.; Di Profio, G.; Al-Hinai, H.; Drioli, E. Potential of membrane distillation in seawater desalination: Thermal efficiency, sensitivity study and cost estimation. J. Membr. Sci. 2008, 323, 85–98. [Google Scholar] [CrossRef]
- Tomaszewska, M. Membrane Distillation-Examples of Applications in Technology and Environmental Protection. Environ. Stud. 2000, 9, 27–36. [Google Scholar]
- Hanemaaijer, J.H.; van Medevoort, J.; Jansen, A.E.; Dotremont, C.; van Sonsbeek, E.; Yuan, T.; De Ryck, L. Memstill membrane distillation—A future desalination technology. Desalination 2006, 199, 175–176. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Z.; Gao, Y.; Shi, Z.; Gray, S. Chapter 8—Achievements in membrane distillation processes for wastewater and water treatment. In Current Trends and Future Developments on (Bio-) Membranes; Basile, A., Ghasemzadeh, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 221–238. [Google Scholar] [CrossRef]
- Hitsov, I.; Maere, T.; De Sitter, K.; Dotremont, C.; Nopens, I. Modelling approaches in membrane distillation: A critical review. Sep. Purif. Technol. 2015, 142, 48–64. [Google Scholar] [CrossRef]
- Zhang, J.; Gray, S.; Li, J.-D. Modelling heat and mass transfers in DCMD using compressible membranes. J. Membr. Sci. 2012, 387, 7–16. [Google Scholar] [CrossRef]
- Katsandri, A. A theoretical analysis of a spacer filled flat plate membrane distillation modules using CFD: Part I: Velocity and shear stress analysis. Desalination 2017, 408, 145–165. [Google Scholar] [CrossRef]
- Shirazi, M.M.A.; Kargari, A.; Ismail, A.F.; Matsuura, T. Computational fluid dynamic (CFD) opportunities applied to the membrane distillation process: State-of-the-art and perspectives. Desalination 2016, 377, 73–90. [Google Scholar] [CrossRef]
- Cai, J.; Liu, Z.; Guo, F. Transport Analysis of Anti-Wetting Composite Fibrous Membranes for Membrane Distillation. Membranes 2021, 11, 14. [Google Scholar] [CrossRef] [PubMed]
- La Cerva, M.; Cipollina, A.; Ciofalo, M.; Albeirutty, M.; Turkmen, N.; Bouguecha, S.; Micale, G. CFD Investigation of Spacer-Filled Channels for Membrane Distillation. Membranes 2019, 9, 91. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Li, N.; Zhang, J. Modeling and multi-objective optimization of vacuum membrane distillation for enhancement of water productivity and thermal efficiency in desalination. Chem. Eng. Res. Des. 2018, 132, 697–713. [Google Scholar] [CrossRef]
- Khayet, M.; Cojocaru, C.; García-Payo, C. Application of response surface methodology and experimental design in direct contact membrane distillation. Ind. Eng. Chem. Res. 2007, 46, 5673–5685. [Google Scholar] [CrossRef]
- Kim, B.; Choi, Y.; Choi, J.; Shin, Y.; Lee, S. Effect of surfactant on wetting due to fouling in membrane distillation membrane: Application of response surface methodology (RSM) and artificial neural networks (ANN). Korean J. Chem. Eng. 2020, 37, 1–10. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Cheng, D.; Li, N.; Bai, H.; Zhang, J.; Wang, Z.; Zeng, F.; Sun, J.; Xie, Z. Simulation and multi-objective optimization of heat and mass transfer in direct contact membrane distillation by response surface methodology integrated modeling. Chem. Eng. Res. Des. 2020, 159, 565–581. [Google Scholar] [CrossRef]
- Martínez, L.; Florido-Díaz, F.J.; Hernández, A.; Prádanos, P. Characterisation of three hydrophobic porous membranes used in membrane distillation: Modelling and evaluation of their water vapour permeabilities. J. Membr. Sci. 2002, 203, 15–27. [Google Scholar] [CrossRef]
- Olatunji, S.O.; Camacho, L.M. Heat and Mass Transport in Modeling Membrane Distillation Configurations: A Review. Front. Energy Res. 2018, 6. [Google Scholar] [CrossRef]
- Qtaishat, M.; Matsuura, T.; Kruczek, B.; Khayet, M. Heat and mass transfer analysis in direct contact membrane distillation. Desalination 2008, 219, 272–292. [Google Scholar] [CrossRef]
- Lei, Z.; Chen, B.; Ding, Z. (Eds.) Membrane distillation. In Special Distillation Processes; Elsevier Science: Amsterdam, The Netherlands, 2005; pp. 241–319. [Google Scholar]
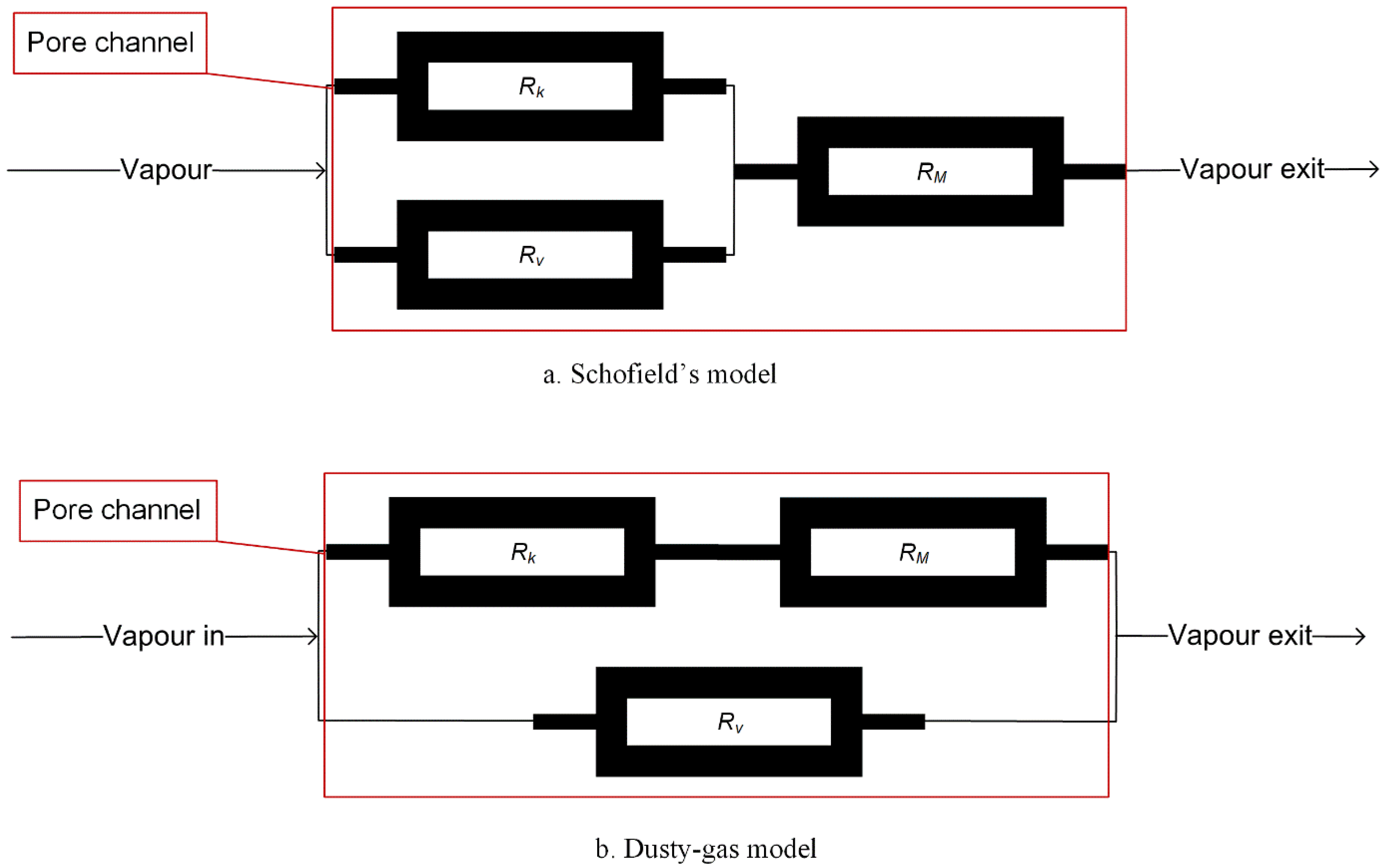
- Schofield, R.W.; Fane, A.G.; Fell, C.J.D. Gas and vapour transport through microporous membranes. II. Membrane distillation. J. Membr. Sci. 1990, 53, 173–185. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G.; Halim, C. Mass flux enhancement using spacer filled channels in direct contact membrane distillation. J. Membr. Sci. 2001, 187, 193–201. [Google Scholar] [CrossRef]
- Martinez-Diez, L.; Vazquez-Gonzalez, M.I.; Florido-Diaz, F.J. Study of membrane distillation using channel spacers. J. Membr. Sci. 1998, 144, 45–56. [Google Scholar] [CrossRef]
- Yao, Y. (Ed.) Principle of Chemical Engineering, 1st ed.; Tianjin Science Technology Press: Tianjin, China, 1992; p. 225. [Google Scholar]
- Schwinge, J.; Wiley, D.E.; Fane, A.G.; Guenther, R. Characterization of a zigzag spacer for ultrafiltration. J. Membr. Sci. 2000, 172, 19–31. [Google Scholar] [CrossRef]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Effects of net-type spacers on heat and mass transfer in direct contact membrane distillation and comparison with ultrafiltration studies. J. Membr. Sci. 2003, 217, 193–206. [Google Scholar] [CrossRef]
- Chernyshov, M.N.; Meindersma, G.W.; de Haan, A.B. Comparison of spacers for temperature polarization reduction in air gap membrane distillation. Desalination 2005, 183, 363–374. [Google Scholar] [CrossRef]
- Da Costa, A.R.; Fane, A.G.; Wiley, D.E. Spacer characterization and pressure drop modelling in spacer-filled channels for ultrafiltration. J. Membr. Sci. 1994, 87, 79–98. [Google Scholar] [CrossRef]
- Zhang, J.; Dow, N.; Duke, M.; Ostarcevic, E.; Li, J.-D.; Gray, S. Identification of material and physical features of membrane distillation membranes for high performance desalination. J. Membr. Sci. 2010, 349, 295–303. [Google Scholar] [CrossRef]
- Penman, H.L. Estimating evaporation. Eos Trans. Am. Geophys. Union 1956, 37, 43–50. [Google Scholar] [CrossRef]
- Ding, Z.; Ma, R.; Fane, A.G. A new model for mass transfer in direct contact membrane distillation. Desalination 2003, 151, 217–227. [Google Scholar] [CrossRef]
- Kast, W.; Hohenthanner, C.R. Mass transfer within the gas-phase of porous media. Int. J. Heat Mass Transf. 2000, 43, 807–823. [Google Scholar] [CrossRef]
- Kuhn, H.; Forstering, H.-D. Principles of Physical Chemistry; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Albert, R.A.; Silbey, R.J. Physical Chemistry, 2nd ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Cussler, E.L. Diffusion: Mass Transfer in Fluid System, 2nd ed.; Cambridge University Press: New York, NY, USA, 1997. [Google Scholar]
- Lei, Z.; Chen, B.; Ding, Z. Special Distillation Processes; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Phattaranawik, J.; Jiraratananon, R.; Fane, A.G. Effect of pore size distribution and air flux on mass transport in direct contact membrane distillation. J. Membr. Sci. 2003, 215, 75–85. [Google Scholar] [CrossRef]
- Mason, E.A.; Malinauskas, A.P. Gas Transport in Porous Media: The Dusty-Gas Model; Elsevier Scientific Pub. Co.: Amsterdam, The Netherlands; New York, NY, USA, 1983. [Google Scholar]
- Fernandez-Pineda, C.; Izquierdo-Gil, M.A.; Garcia-Payo, M.C. Gas permeation and direct contact membrane distillation experiments and their analysis using different models. J. Membr. Sci. 2002, 198, 33–49. [Google Scholar] [CrossRef]
- Khayet, M.; Velázquez, A.; Mengual, J.I. Modelling mass transport through a porous partition: Effect of pore size distribution. J. Non-Equilib. Thermodyn. 2004, 29, 279–299. [Google Scholar] [CrossRef]
- Woods, J.; Pellegrino, J.; Burch, J. Generalized guidance for considering pore-size distribution in membrane distillation. J. Membr. Sci. 2011, 368, 124–133. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.-D.; Duke, M.; Xie, Z.; Gray, S. Performance of asymmetric hollow fibre membranes in membrane distillation under various configurations and vacuum enhancement. J. Membr. Sci. 2010, 362, 517–528. [Google Scholar] [CrossRef]
- Zhang, J.; Gray, S.; Li, J.-D. Predicting the influence of operating conditions on DCMD flux and thermal efficiency for incompressible and compressible membrane systems. Desalination 2013, 323, 142–149. [Google Scholar] [CrossRef]
- Alklaibi, A.M.; Lior, N. Transport analysis of air-gap membrane distillation. J. Membr. Sci. 2005, 255, 239–253. [Google Scholar] [CrossRef]
- Loussif, N.; Orfi, J. Comparative study of air gap, direct contact and sweeping gas membrane distillation configurations. Membr. Water Treat 2016, 7, 71–86. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.-D.; Duke, M.; Hoang, M.; Xie, Z.; Groth, A.; Tun, C.; Gray, S. Modelling of vacuum membrane distillation. J. Membr. Sci. 2013, 434, 1–9. [Google Scholar] [CrossRef]
- Cengel, Y.A.; Boles, M.A. Thermodynamics: An Engineering Approach, 6th ed.; SI Units; The McGraw-Hill Companies, Inc.: New York, NY, USA, 2007. [Google Scholar]
- Avlonitis, S.; Kouroumbas, K.; Vlachakis, N. Energy consumption and membrane replacement cost for seawater RO desalination plants. Desalination 2003, 157, 151–158. [Google Scholar] [CrossRef]
- Raluy, G.; Serra, L.; Uche, J. Life cycle assessment of MSF, MED and RO desalination technologies. Energy 2006, 31, 2361–2372. [Google Scholar] [CrossRef]
- Dow, N.; Gray, S.; Zhang, J.; Ostarcevic, E.; Liubinas, A.; Atherton, P.; Roeszler, G.; Gibbs, A.; Duke, M. Pilot trial of membrane distillation driven by low grade waste heat: Membrane fouling and energy assessment. Desalination 2016, 391, 30–42. [Google Scholar] [CrossRef]
- Zaragoza, G.; Ruiz-Aguirre, A.; Guillén-Burrieza, E. Efficiency in the use of solar thermal energy of small membrane desalination systems for decentralized water production. Appl. Energy 2014, 130, 491–499. [Google Scholar] [CrossRef]
- Hamed, O.A.; Al-Sofi, M.A.; Imam, M.; Mustafa, G.M.; Mardouf, K.B.; Al-Washmi, H. Thermal performance of multi-stage flash distillation plants in Saudi Arabia. Desalination 2000, 128, 281–292. [Google Scholar] [CrossRef]
- Schneider, K.; van Gassel, T.J. Membrandestillation. Chem. Ing. Tech. 1984, 56, 514–521. [Google Scholar] [CrossRef]
- Mills, A.F. Mass Transfer; Prentice-Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Carrero-Parreño, A.; Onishi, V.C.; Ruiz-Femenia, R.; Salcedo-Díaz, R.; Caballero, J.A.; Reyes-Labarta, J.A. Optimization of multistage membrane distillation system for treating shale gas produced water. Desalination 2019, 460, 15–27. [Google Scholar] [CrossRef]
- Dutta, N.; Singh, B.; Subbiah, S.; Muthukumar, P. Performance analysis of a single and multi-staged direct contact membrane distillation module integrated with heat recovery units. Chem. Eng. J. Adv. 2020, 4, 100055. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Attia, H.; Osman, M.S.; Johnson, D.J.; Wright, C.; Hilal, N. Modelling of air gap membrane distillation and its application in heavy metals removal. Desalination 2017, 424, 27–36. [Google Scholar] [CrossRef]
- Boukhriss, M.; Khemili, S.; Hamida, M.B.B.; Bacha, H.B. Simulation and experimental study of an AGMD membrane distillation pilot for the desalination of seawater or brackish water with zero liquid discharged. Heat Mass Transf. 2018, 54, 3521–3531. [Google Scholar] [CrossRef]
- Karanikola, V.; Corral, A.F.; Jiang, H.; Eduardo Sáez, A.; Ela, W.P.; Arnold, R.G. Sweeping gas membrane distillation: Numerical simulation of mass and heat transfer in a hollow fiber membrane module. J. Membr. Sci. 2015, 483, 15–24. [Google Scholar] [CrossRef]
- Zhao, S.; Wardhaugh, L.; Zhang, J.; Feron, P.H. Condensation, re-evaporation and associated heat transfer in membrane evaporation and sweeping gas membrane distillation. J. Membr. Sci. 2015, 475, 445–454. [Google Scholar] [CrossRef]
- Zhao, S.; Feron, P.H.; Xie, Z.; Zhang, J.; Hoang, M. Condensation studies in membrane evaporation and sweeping gas membrane distillation. J. Membr. Sci. 2014, 462, 9–16. [Google Scholar] [CrossRef]
- Safi, N.N.; Ibrahim, S.; Zouli, N.; Majdi, H.S.; Alsalhy, Q.F.; Drioli, E.; Figoli, A. A Systematic Framework for Optimizing a Sweeping Gas Membrane Distillation (SGMD). Membranes 2020, 10, 254. [Google Scholar] [CrossRef]
- Swaminathan, J. Numerical and Experimental Investigation of Membrane Distillation Flux and Energy Efficiency. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2014. [Google Scholar]
- Schofield, R.; Fane, A.; Fell, C.; Macoun, R. Factors affecting flux in membrane distillation. Desalination 1990, 77, 279–294. [Google Scholar] [CrossRef]
- Hsu, S.; Cheng, K.; Chiou, J.-S. Seawater desalination by direct contact membrane distillation. Desalination 2002, 143, 279–287. [Google Scholar] [CrossRef]
- Naidu, G.; Choi, Y.; Jeong, S.; Hwang, T.M.; Vigneswaran, S. Experiments and modeling of a vacuum membrane distillation for high saline water. J. Ind. Eng. Chem. 2014, 20, 2174–2183. [Google Scholar] [CrossRef]
- Criscuoli, A.; Carnevale, M.C.; Drioli, E. Evaluation of energy requirements in membrane distillation. Chem. Eng. Process. Process Intensif. 2008, 47, 1098–1105. [Google Scholar] [CrossRef]
- Zhang, Y.; Peng, Y.; Ji, S.; Li, Z.; Chen, P. Review of thermal efficiency and heat recycling in membrane distillation processes. Desalination 2015, 367, 223–239. [Google Scholar] [CrossRef]
- Liu, G.; Zhu, C.; Cheung, C.; Leung, C. Theoretical and experimental studies on air gap membrane distillation. Heat Mass Transf. 1998, 34, 329–335. [Google Scholar] [CrossRef]
- Gao, L.; Zhang, J.; Gray, S.; Li, J.-D. Experimental study of hollow fiber permeate gap membrane distillation and its performance comparison with DCMD and SGMD. Sep. Purif. Technol. 2017, 188, 11–23. [Google Scholar] [CrossRef]
- Li, B.; Sirkar, K.K. Novel membrane and device for vacuum membrane distillation-based desalination process. J. Membr. Sci. 2005, 257, 60–75. [Google Scholar] [CrossRef]
- Fan, H.; Peng, Y. Application of PVDF membranes in desalination and comparison of the VMD and DCMD processes. Chem. Eng. Sci. 2012, 79, 94–102. [Google Scholar] [CrossRef]
- Zhang, J.; Li, J.-D.; Duke, M.; Hoang, M.; Xie, Z.; Groth, A.; Tun, C.; Gray, S. Influence of module design and membrane compressibility on VMD performance. J. Membr. Sci. 2013, 442, 31–38. [Google Scholar] [CrossRef]
- Zhang, J.; Li, N.; Ng, D.; Ike, I.A.; Xie, Z.; Gray, S. Depletion of VOC in wastewater by vacuum membrane distillation using a dual-layer membrane: Mechanism of mass transfer and selectivity. Environ. Sci. Water Res. Technol. 2019, 5, 119–130. [Google Scholar] [CrossRef]
- Villalobos García, J.; Dow, N.; Milne, N.; Zhang, J.; Naidoo, L.; Gray, S.; Duke, M. Membrane distillation trial on textile wastewater containing surfactants using hydrophobic and hydrophilic-coated polytetrafluoroethylene (PTFE) membranes. Membranes 2018, 8, 31. [Google Scholar] [CrossRef] [PubMed]
- Halvorsen, I.J.; Skogestad, S. Distillation theory. Encycl. Sep. Sci. 2000, 1117–1134. [Google Scholar]
- Kujawski, W.; Kujawa, J.; Wierzbowska, E.; Cerneaux, S.; Bryjak, M.; Kujawski, J. Influence of hydrophobization conditions and ceramic membranes pore size on their properties in vacuum membrane distillation of water–organic solvent mixtures. J. Membr. Sci. 2016, 499, 442–451. [Google Scholar] [CrossRef]
- Koter, S.; Kujawska, A.; Kujawski, W. Modeling of transport and separation in a thermopervaporation process. J. Membr. Sci. 2015, 480, 129–138. [Google Scholar] [CrossRef]
- Lovasz, A.; Farkas, T.; Mizsey, P. Methodology for modelling of pervaporation: Step from binary to ternary mixtures. Desalination 2009, 241, 188–196. [Google Scholar] [CrossRef]
- Yang, X.; Duke, M.; Zhang, J.; Li, J.-D. Modeling of heat and mass transfer in vacuum membrane distillation for ammonia separation. Sep. Purif. Technol. 2019, 224, 121–131. [Google Scholar] [CrossRef]
- Gao, F.; Chen, X.; Yu, G.; Asumana, C. Compressible gases transport through porous membrane: A modified dusty gas model. J. Membr. Sci. 2011, 379, 200–206. [Google Scholar] [CrossRef]
- Chernyshov, M.N.; Meindersma, G.W.; de Haan, A.B. Modelling temperature and salt concentration distribution in membrane distillation feed channel. Desalination 2003, 157, 315–324. [Google Scholar] [CrossRef]
- Charfi, K.; Khayet, M.; Safi, M.J. Numerical simulation and experimental studies on heat and mass transfer using sweeping gas membrane distillation. Desalination 2010, 259, 84–96. [Google Scholar] [CrossRef]
- Bui, V.A.; Vu, L.T.T.; Nguyen, M.H. Modelling the simultaneous heat and mass transfer of direct contact membrane distillation in hollow fibre modules. J. Membr. Sci. 2010, 353, 85–93. [Google Scholar] [CrossRef]
- Alsaadi, A.S.; Ghaffour, N.; Li, J.-D.; Gray, S.; Francis, L.; Maab, H.; Amy, G.L. Modeling of air-gap membrane distillation process: A theoretical and experimental study. J. Membr. Sci. 2013, 445, 53–65. [Google Scholar] [CrossRef]
- Guijt, C.M.; Meindersma, G.W.; Reith, T.; de Haan, A.B. Air gap membrane distillation: 1. Modelling and mass transport properties for hollow fibre membranes. Sep. Purif. Technol. 2005, 43, 233–244. [Google Scholar] [CrossRef]
- Hitsov, I.; De Sitter, K.; Dotremont, C.; Cauwenberg, P.; Nopens, I. Full-scale validated Air Gap Membrane Distillation (AGMD) model without calibration parameters. J. Membr. Sci. 2017, 533, 309–320. [Google Scholar] [CrossRef]
- Perfilov, V.; Fila, V.; Sanchez Marcano, J. A general predictive model for sweeping gas membrane distillation. Desalination 2018, 443, 285–306. [Google Scholar] [CrossRef]
- Lee, J.-G.; Lee, E.-J.; Jeong, S.; Guo, J.; An, A.K.; Guo, H.; Kim, J.; Leiknes, T.; Ghaffour, N. Theoretical modeling and experimental validation of transport and separation properties of carbon nanotube electrospun membrane distillation. J. Membr. Sci. 2017, 526, 395–408. [Google Scholar] [CrossRef]
- Madalosso, H.B.; de Sousa Silva, R.; Merlini, A.; Battisti, R.; Machado, R.A.F.; Marangoni, C. Modeling and experimental validation of direct contact membrane distillation applied to synthetic dye solutions. J. Chem. Technol. Biotechnol. 2020. [Google Scholar] [CrossRef]
- Swaminathan, J.; Chung, H.W.; Warsinger, D.M.; AlMarzooqi, F.A.; Arafat, H.A.; Lienhard, V.J.H. Energy efficiency of permeate gap and novel conductive gap membrane distillation. J. Membr. Sci. 2016, 502, 171–178. [Google Scholar] [CrossRef]
- Hwang, H.J.; He, K.; Gray, S.; Zhang, J.; Moon, I.S. Direct contact membrane distillation (DCMD): Experimental study on the commercial PTFE membrane and modeling. J. Membr. Sci. 2011, 371, 90–98. [Google Scholar] [CrossRef]
- Dow, N.; Villalobos García, J.; Niadoo, L.; Milne, N.; Zhang, J.; Gray, S.; Duke, M. Demonstration of membrane distillation on textile waste water: Assessment of long term performance, membrane cleaning and waste heat integration. Environ. Sci. Water Res. Technol. 2017, 3, 433–449. [Google Scholar] [CrossRef]
- Al-Sharif, S.; Albeirutty, M.; Cipollina, A.; Micale, G. Modelling flow and heat transfer in spacer-filled membrane distillation channels using open source CFD code. Desalination 2013, 311, 103–112. [Google Scholar] [CrossRef]
- Cipollina, A.; Micale, G.; Rizzuti, L. Membrane distillation heat transfer enhancement by CFD analysis of internal module geometry. Desalination Water Treat. 2011, 25, 195–209. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.; Wiley, D. Review of 3D CFD modeling of flow and mass transfer in narrow spacer-filled channels in membrane modules. Chem. Eng. Process. Process Intensif. 2010, 49, 759–781. [Google Scholar] [CrossRef]
- Yu, H.; Yang, X.; Wang, R.; Fane, A.G. Numerical simulation of heat and mass transfer in direct membrane distillation in a hollow fiber module with laminar flow. J. Membr. Sci. 2011, 384, 107–116. [Google Scholar] [CrossRef]
- Yang, X.; Yu, H.; Wang, R.; Fane, A.G. Optimization of microstructured hollow fiber design for membrane distillation applications using CFD modeling. J. Membr. Sci. 2012, 421, 258–270. [Google Scholar] [CrossRef]
- Eleiwi, F.; Ghaffour, N.; Alsaadi, A.S.; Francis, L.; Laleg-Kirati, T.M. Dynamic modeling and experimental validation for direct contact membrane distillation (DCMD) process. Desalination 2016, 384, 1–11. [Google Scholar] [CrossRef]
- Lou, J.; Vanneste, J.; DeCaluwe, S.C.; Cath, T.Y.; Tilton, N. Computational fluid dynamics simulations of polarization phenomena in direct contact membrane distillation. J. Membr. Sci. 2019, 591, 117150. [Google Scholar] [CrossRef]
- Shakaib, M.; Hasani, S.; Ahmed, I.; Yunus, R.M. A CFD study on the effect of spacer orientation on temperature polarization in membrane distillation modules. Desalination 2012, 284, 332–340. [Google Scholar] [CrossRef]
- Cipollina, A.; Di Miceli, A.; Koschikowski, J.; Micale, G.; Rizzuti, L. CFD simulation of a membrane distillation module channel. Desalination Water Treat. 2009, 6, 177–183. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; John wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Gil, J.D.; Ruiz-Aguirre, A.; Roca, L.; Zaragoza, G.; Berenguel, M. Prediction models to analyse the performance of a commercial-scale membrane distillation unit for desalting brines from RO plants. Desalination 2018, 445, 15–28. [Google Scholar] [CrossRef]
- Boubakri, A.; Hafiane, A.; Bouguecha, S.A.T. Application of response surface methodology for modeling and optimization of membrane distillation desalination process. J. Ind. Eng. Chem. 2014, 20, 3163–3169. [Google Scholar] [CrossRef]
- Deng, H.; Yang, X.; Tian, R.; Hu, J.; Zhang, B.; Cui, F.; Guo, G. Modeling and optimization of solar thermal-photovoltaic vacuum membrane distillation system by response surface methodology. Sol. Energy 2020, 195, 230–238. [Google Scholar] [CrossRef]
- Qtaishat, M.R.; Matsuura, T. 13—Modelling of pore wetting in membrane distillation compared with pervaporation. In Pervaporation, Vapour Permeation and Membrane Distillation; Basile, A., Figoli, A., Khayet, M., Eds.; Woodhead Publishing: Oxford, UK, 2015; pp. 385–413. [Google Scholar] [CrossRef]
- Damtie, M.M.; Woo, Y.C.; Kim, B.; Park, K.-D.; Hailemariam, R.H.; Shon, H.K.; Choi, J.-S. Analysis of mass transfer behavior in membrane distillation: Mathematical modeling under various conditions. Chemosphere 2019, 236, 124289. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Zhang, J.; Gray, S. Modelling mass and heat transfers of Permeate Gap Membrane Distillation using hollow fibre membrane. Desalination 2019, 467, 196–209. [Google Scholar] [CrossRef]
- Eykens, L.; Hitsov, I.; De Sitter, K.; Dotremont, C.; Pinoy, L.; Nopens, I.; Van der Bruggen, B. Influence of membrane thickness and process conditions on direct contact membrane distillation at different salinities. J. Membr. Sci. 2016, 498, 353–364. [Google Scholar] [CrossRef]
- Upadhyaya, S.; Singh, K.; Chaurasia, S.; Dohare, R.K.; Agarwal, M. Mathematical and CFD modeling of vacuum membrane distillation for desalination. Desalination Water Treat. 2016, 57, 11956–11971. [Google Scholar] [CrossRef]
- Amigo, J.; Urtubia, R.; Suárez, F. Exploring the interactions between hydrodynamics and fouling in membrane distillation systems—A multiscale approach using CFD. Desalination 2018, 444, 63–74. [Google Scholar] [CrossRef]
- Kezia, K.; Lee, J.; Weeks, M.; Kentish, S. Direct contact membrane distillation for the concentration of saline dairy effluent. Water Res. 2015, 81, 167–177. [Google Scholar] [CrossRef]
- Khalifa, A.E.; Lawal, D.U. Application of response surface and Taguchi optimization techniques to air gap membrane distillation for water desalination—A comparative study. Desalination Water Treat. 2016, 57, 28513–28530. [Google Scholar] [CrossRef]
- Li, J.; Xu, S.; Hassan, M.; Shao, J.; Ren, L.F.; He, Y. Effective modeling and optimization of PVDF–PTFE electrospinning parameters and membrane distillation process by response surface methodology. J. Appl. Polym. Sci. 2019, 136, 47125. [Google Scholar] [CrossRef]
- Ghaemi, N.; Madaeni, S.S.; Daraei, P.; Rajabi, H.; Shojaeimehr, T.; Rahimpour, F.; Shirvani, B. PES mixed matrix nanofiltration membrane embedded with polymer wrapped MWCNT: Fabrication and performance optimization in dye removal by RSM. J. Hazard. Mater. 2015, 298, 111–121. [Google Scholar] [CrossRef]
- Khayet, M.; Matsuura, T. Membrane Distillation: Principles and Applications; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Alkhudhiri, A.; Darwish, N.; Hilal, N. Membrane distillation: A comprehensive review. Desalination 2012, 287, 2–18. [Google Scholar] [CrossRef]
- Khayet, M. Solar desalination by membrane distillation: Dispersion in energy consumption analysis and water production costs (a review). Desalination 2013, 308, 89–101. [Google Scholar] [CrossRef]
- Kesieme, U.K.; Milne, N.; Aral, H.; Cheng, C.Y.; Duke, M. Economic analysis of desalination technologies in the context of carbon pricing, and opportunities for membrane distillation. Desalination 2013, 323, 66–74. [Google Scholar] [CrossRef]
- Cheng, D.; Zhao, L.; Li, N.; Smith, S.J.; Wu, D.; Zhang, J.; Ng, D.; Wu, C.; Martinez, M.R.; Batten, M.P. Aluminum fumarate MOF/PVDF hollow fiber membrane for enhancement of water flux and thermal efficiency in direct contact membrane distillation. J. Membr. Sci. 2019, 588, 117204. [Google Scholar] [CrossRef]
- Elmarghany, M.R.; El-Shazly, A.H.; Rajabzadeh, S.; Salem, M.S.; Shouman, M.A.; Sabry, M.N.; Matsuyama, H.; Nady, N. Triple-layer nanocomposite membrane prepared by electrospinning based on modified PES with carbon nanotubes for membrane distillation applications. Membranes 2020, 10, 15. [Google Scholar] [CrossRef] [PubMed]
- Al-Furaiji, M.; Arena, J.T.; Ren, J.; Benes, N.; Nijmeijer, A.; McCutcheon, J.R. Triple-layer nanofiber membranes for treating high salinity brines using direct contact membrane distillation. Membranes 2019, 9, 60. [Google Scholar] [CrossRef]
- Korolkov, I.V.; Kuandykova, A.; Yeszhanov, A.B.; Güven, O.; Gorin, Y.G.; Zdorovets, M.V. Modification of pet ion-track membranes by silica nanoparticles for direct contact membrane distillation of salt solutions. Membranes 2020, 10, 322. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Zhang, J.; Li, N.; Ng, D.; Gray, S.R.; Xie, Z. Antiwettability and performance stability of a composite hydrophobic/hydrophilic dual-layer membrane in wastewater treatment by membrane distillation. Ind. Eng. Chem. Res. 2018, 57, 9313–9322. [Google Scholar] [CrossRef]
- Chiao, Y.-H.; Yap Ang, M.B.M.; Huang, Y.-X.; DePaz, S.S.; Chang, Y.; Almodovar, J.; Wickramasinghe, S.R. A “Graft to” Electrospun Zwitterionic Bilayer Membrane for the Separation of Hydraulic Fracturing-Produced Water via Membrane Distillation. Membranes 2020, 10, 402. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Wu, C.; Lu, X.; Ng, D.; Truong, Y.B.; Zhang, J.; Xie, Z. Theoretical guidance for fabricating higher flux hydrophobic/hydrophilic dual-layer membranes for direct contact membrane distillation. J. Membr. Sci. 2020, 596, 117608. [Google Scholar] [CrossRef]


| State in the Pore | Kn < 0.01 | 0.01 < Kn < 1 | Kn > 1 | ||
|---|---|---|---|---|---|
| Composition | Total Pressure Difference | Partial Pressure Difference | |||
| Gas mixture | 0 | ≠0 | M | K-M | K |
| Single gas | ≠0 | N/A | P | P-K | K |
| Gas mixture | ≠0 | ≠0 | P-M | P-M-K | K |
| DCMD | AGMD | SGMD | VMD | |
|---|---|---|---|---|
| Water Flux (Lm−2h−1) | 7–55 [80] | 0.5–7 [81] | 4.3–23 [14] | 13.9–56.2 [82,83] |
| Thermal efficiency (%) | 20–70 [17,84] | 90–98 [85] | 30–95 [60,86] | 90–98 [87,88,89] |
| Approaches | Published Articles | Classification Based on Approach Method | Applications | Merits | Disadvantages/Limitations |
|---|---|---|---|---|---|
| Conventional modelling | ~8000 | Conventional heat and mass transfers | Prediction of performance influenced by feed properties, operation conditions, membrane characteristics, configurations [73,123,124,125,126] |
|
|
| CFD | ~1000 | Computer science | Prediction of performance influenced by geometric structure of turbulence promoters (spacer baffle plate), modules structure [23,26,110,111,127,128] |
|
|
| RSM | ~700 | Data acquisition from the overall system | Prediction of performance influenced by fouling and wetting, membrane characteristics, operation conditions, module geometric dimensions, feed properties [120,129,130,131,132] |
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Y.; Dai, X.; Zhao, L.; Gao, L.; Xie, Z.; Zhang, J. Review of Transport Phenomena and Popular Modelling Approaches in Membrane Distillation. Membranes 2021, 11, 122. https://doi.org/10.3390/membranes11020122
Dong Y, Dai X, Zhao L, Gao L, Xie Z, Zhang J. Review of Transport Phenomena and Popular Modelling Approaches in Membrane Distillation. Membranes. 2021; 11(2):122. https://doi.org/10.3390/membranes11020122
Chicago/Turabian StyleDong, Yan, Xiaodong Dai, Lianyu Zhao, Li Gao, Zongli Xie, and Jianhua Zhang. 2021. "Review of Transport Phenomena and Popular Modelling Approaches in Membrane Distillation" Membranes 11, no. 2: 122. https://doi.org/10.3390/membranes11020122
APA StyleDong, Y., Dai, X., Zhao, L., Gao, L., Xie, Z., & Zhang, J. (2021). Review of Transport Phenomena and Popular Modelling Approaches in Membrane Distillation. Membranes, 11(2), 122. https://doi.org/10.3390/membranes11020122










