Dynamic Modeling of a Proton-Exchange Membrane Fuel Cell Using a Gaussian Approach
Abstract
:1. Introduction
- Provides a novel FC model to estimate the output voltage behavior from the operating current of a fuel cell for steady-state and dynamic responses.
- The training complexity of the algorithm is medium, which makes it easily adaptable to different profiles for testing.
- The proposed FC model can be used in computer simulations and hardware emulators due to its simple implementation using an approximation to the exponential function.
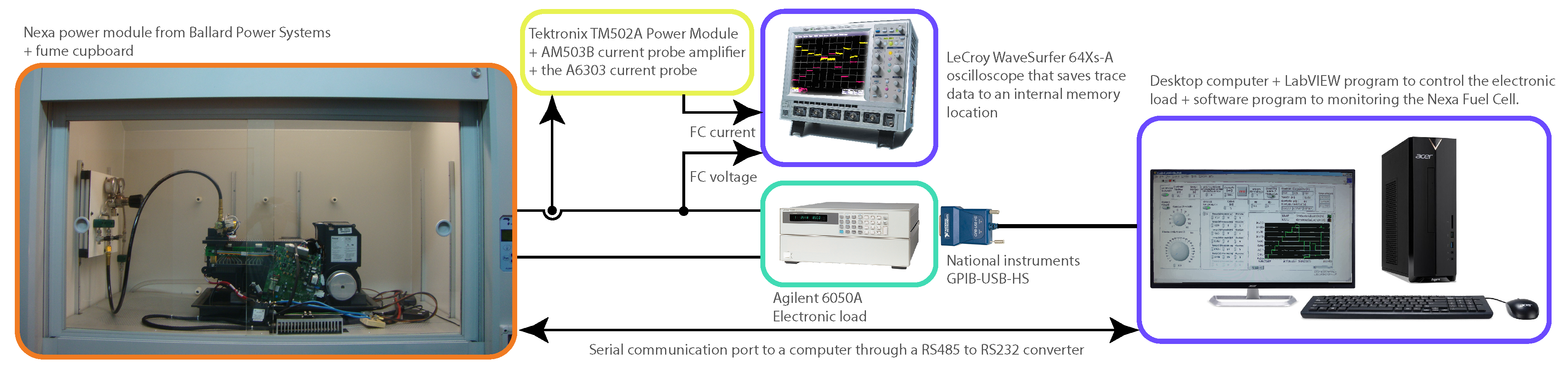
- A commercial Nexa Fuel Cell Power Module is used to validate the proposed FC model.
- The results are compared using analytical and numerical techniques under the same data acquisition parameter to ensure a fair comparison between the models.
2. Gaussian Model
3. Unconstrained Nonlinear Optimization
- The electric current I is x,
- while the voltage v can be either or the approximation .
| Algorithm 1: Unconstrained nonlinear optimization procedure. |
| Input: Measured dataset |
| 1: Use the mathematical model defined by Equation (2) |
| 2: Determine the specific objective function to be minimized through Equation (3) |
| 3: Calculate the residual vector |
| 4: Determine the Jacobian matrix |
| 5: Use a Non-linear Least Squares algorithm to estimate the optimal parameters as described in Equation (5) |
| Output: The vector parameter |
4. Experimental Results
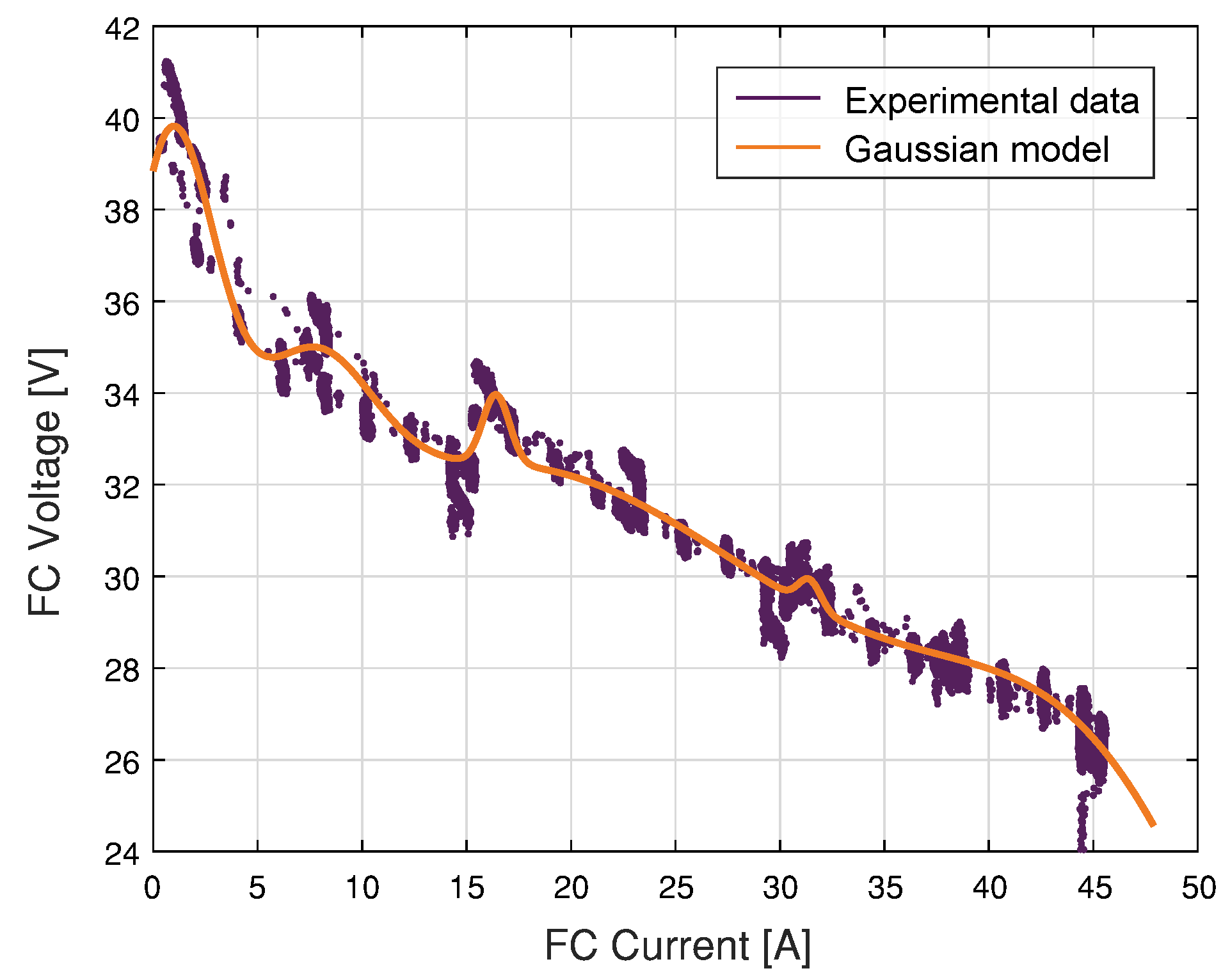
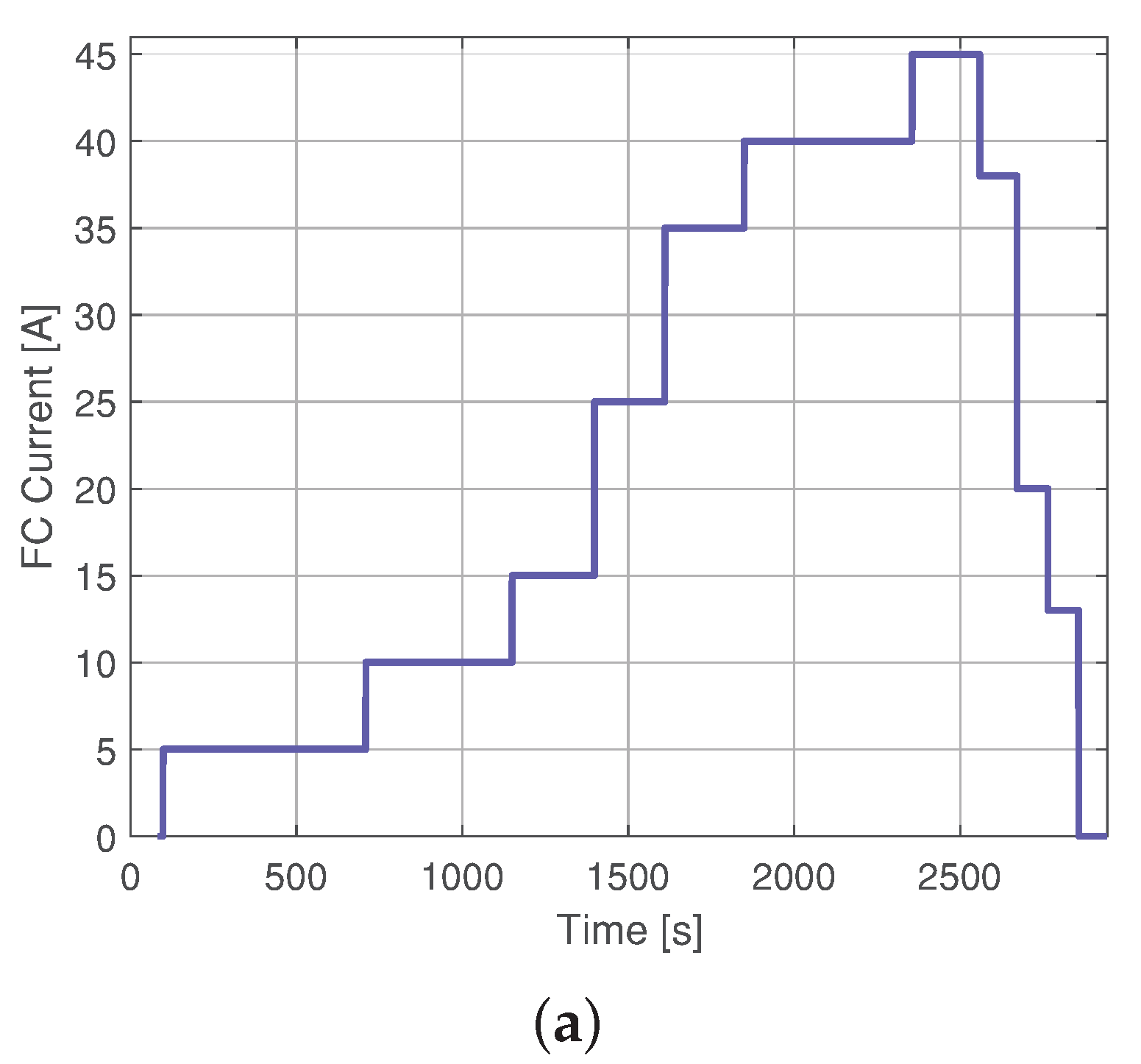
4.1. Training Models
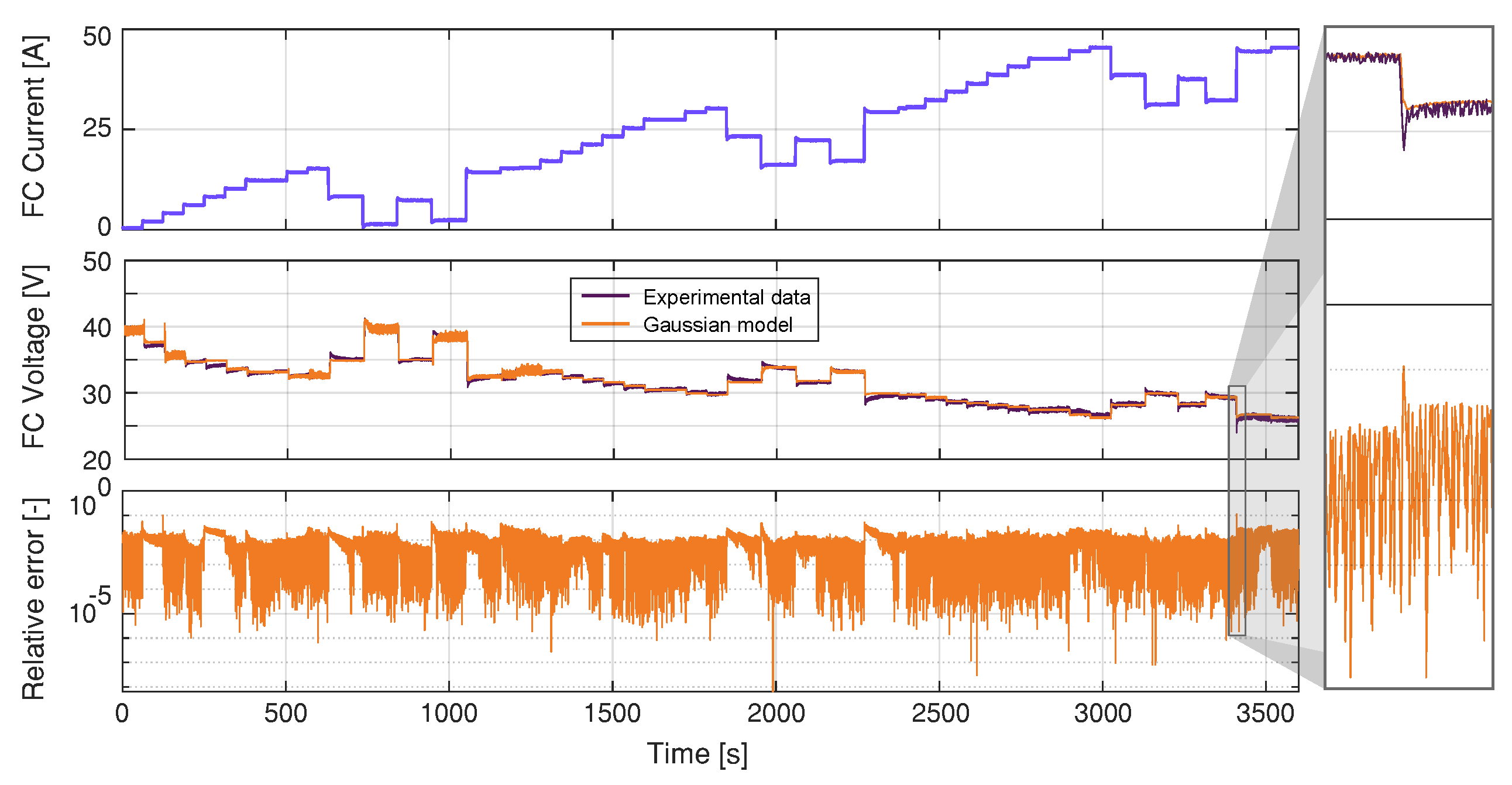
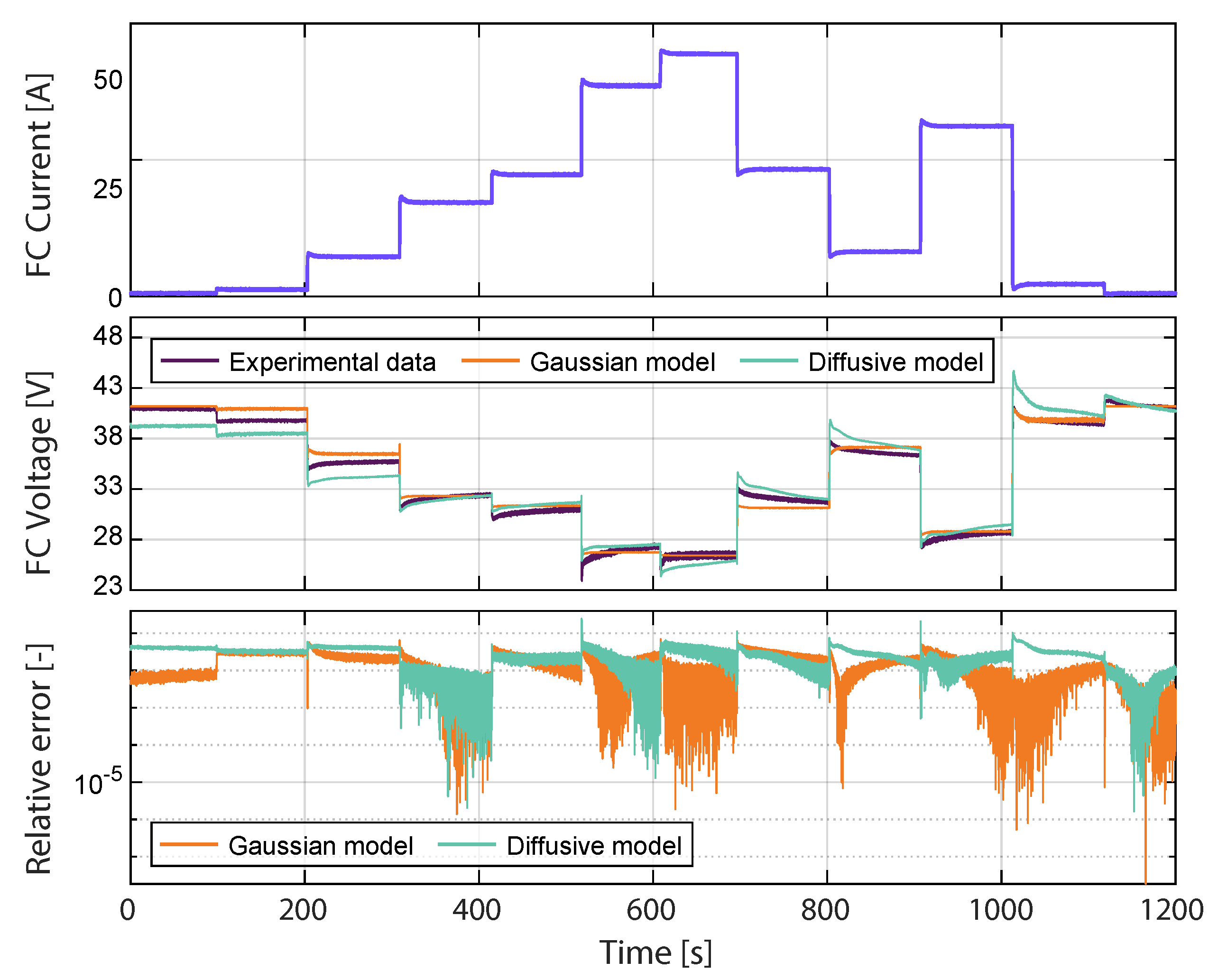
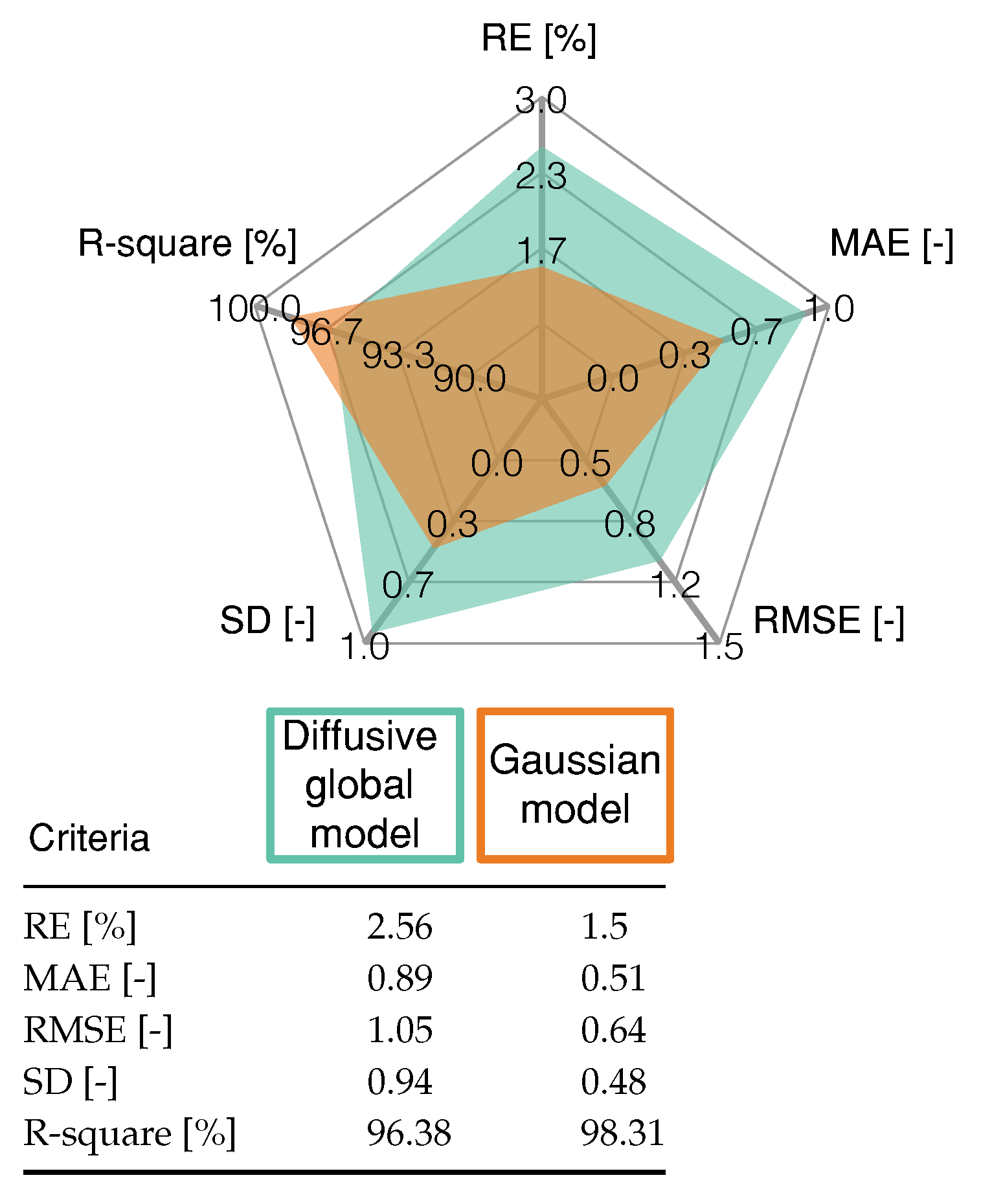
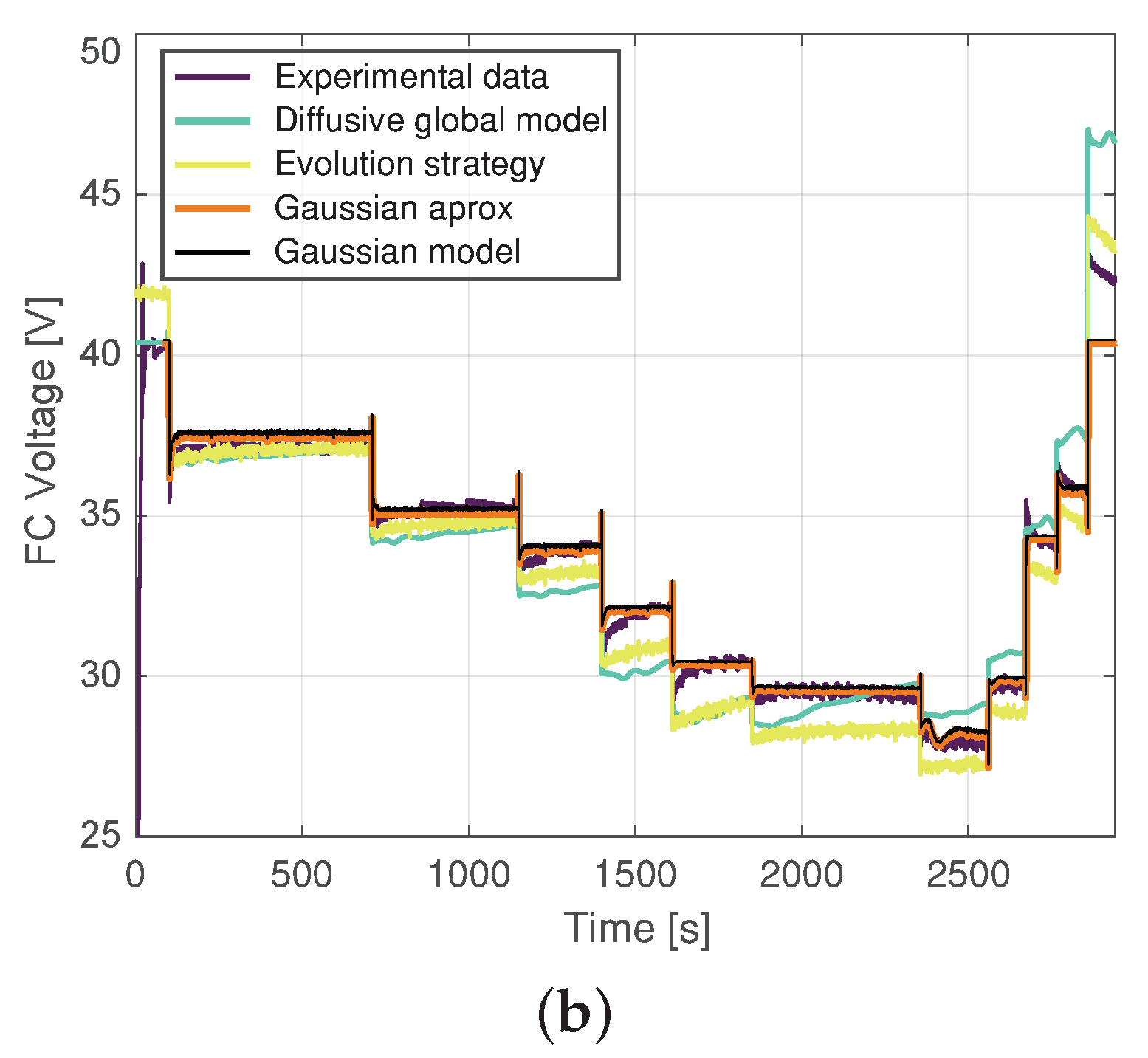
4.2. Validating Model
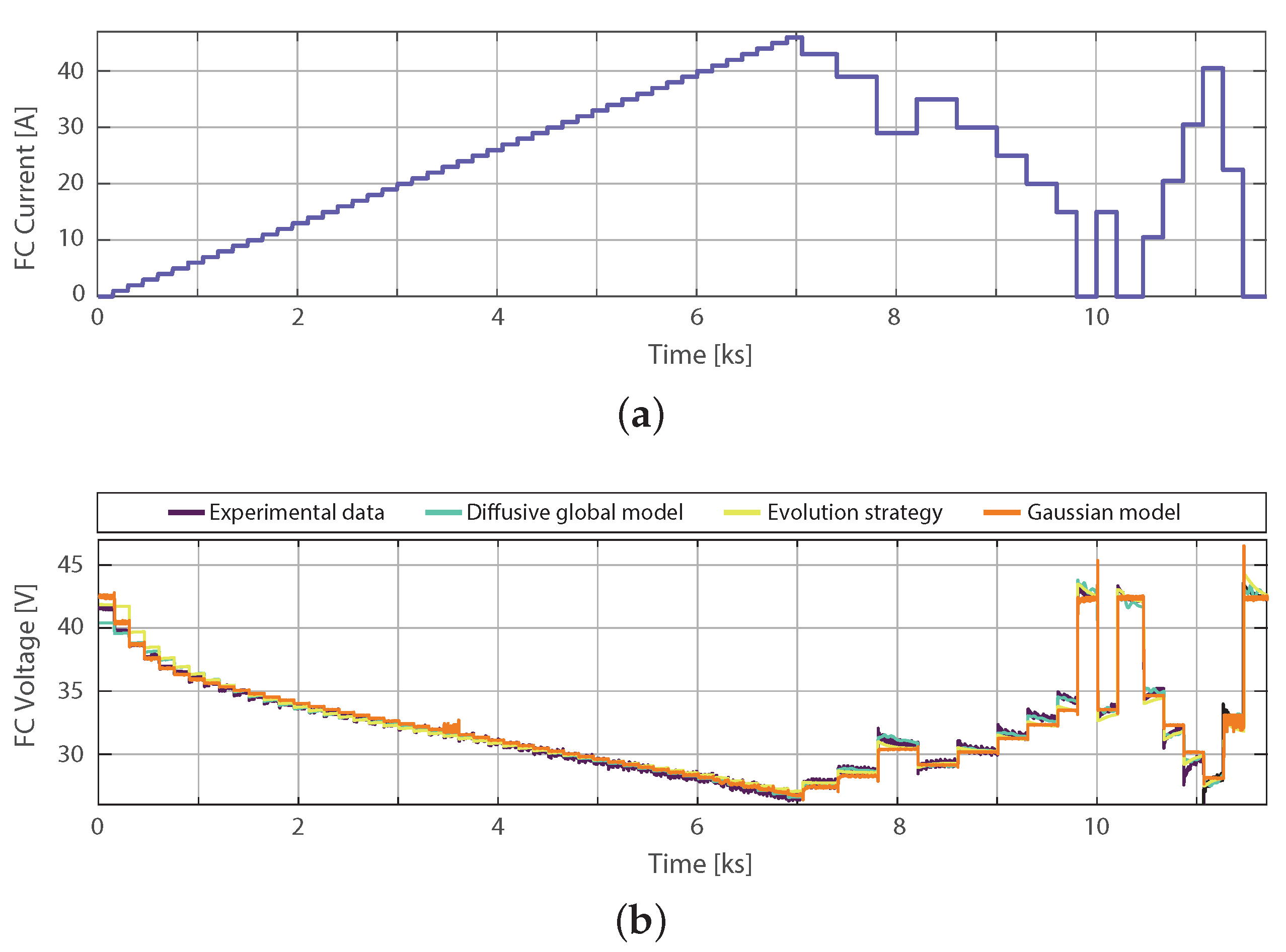
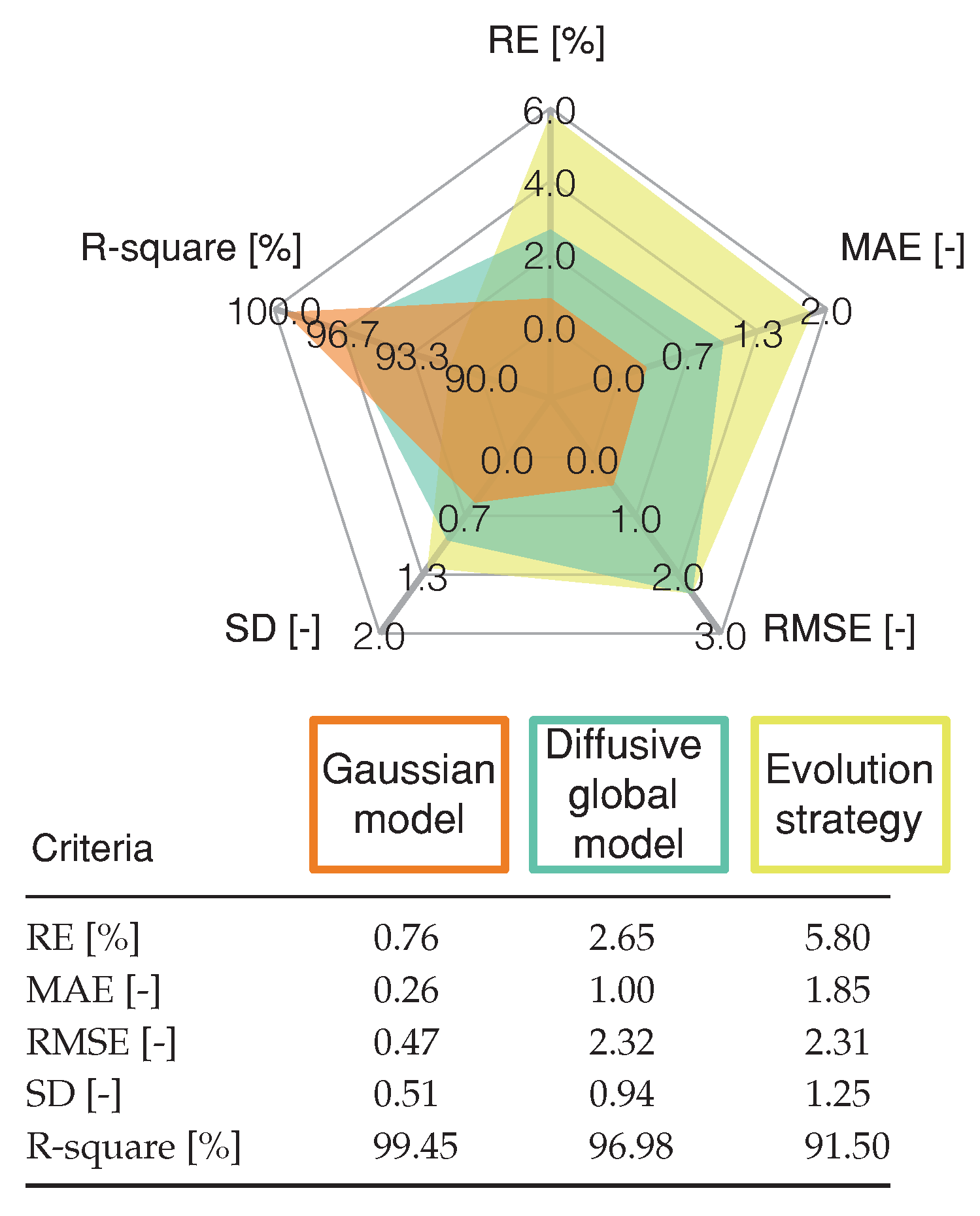
4.3. Comparison of Gaussian Model with the Parameter Identification by Means of Evolution Strategy
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ARX | Auto regressive eXogenous |
| ASO | Atom search optimization |
| CHHO | Chaotic Harris Hawks optimization. |
| ES | Evolution strategy. |
| FC | Fuel cell. |
| GOA | Grasshopper optimisation algorithm. |
| GWO | Grey wolf optimizer. |
| HGA | Hybrid genetic algorithm. |
| KF | Kalman filter. |
| MAE | Mean absolute error. |
| MAEO | Modified Artificial Ecosystem Optimization. |
| MPA | Marine Predators Algorithm. |
| PEMFC | Proton exchange membrane fuel cell. |
| PO | Political Optimizer. |
| RE | Relative error. |
| RLS | Recursive least square. |
| SD | Standard deviation. |
| VSDE | Vortex search differential evolution. |
References
- Pellow, M.A.; Emmott, C.J.; Barnhart, C.J.; Benson, S.M. Hydrogen or batteries for grid storage? A net energy analysis. Energy Environ. Sci. 2015, 8, 1938–1952. [Google Scholar] [CrossRef] [Green Version]
- Staffell, I.; Scamman, D.; Abad, A.V.; Balcombe, P.; Dodds, P.E.; Ekins, P.; Shah, N.; Ward, K.R. The role of hydrogen and fuel cells in the global energy system. Energy Environ. Sci. 2019, 12, 463–491. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.Y.; Cha, K.H.; Lim, T.W.; Hur, T. Eco efficiency of H2 and fuel cell buses. Int. J. Hydrogen Energy 2011, 36, 1754–1765. [Google Scholar] [CrossRef]
- González-Castaño, C.; Restrepo, C.; Revelo-Fuelagán, J.; Lorente-Leyva, L.L.; Peluffo-Ordóñez, D.H. A Fast-Tracking Hybrid MPPT Based on Surface-Based Polynomial Fitting and P&O Methods for Solar PV under Partial Shaded Conditions. Mathematics 2021, 9, 2732. [Google Scholar]
- González-Castaño, C.; Lorente-Leyva, L.L.; Muñoz, J.; Restrepo, C.; Peluffo-Ordóñez, D.H. An MPPT strategy based on a surface-based polynomial fitting for solar photovoltaic systems using real-time hardware. Electronics 2021, 10, 206. [Google Scholar] [CrossRef]
- San Martín, I.; Ursúa, A.; Sanchis, P. Modelling of PEM fuel cell performance: Steady-state and dynamic experimental validation. Energies 2014, 7, 670–700. [Google Scholar] [CrossRef] [Green Version]
- Menesy, A.S.; Sultan, H.M.; Selim, A.; Ashmawy, M.G.; Kamel, S. Developing and applying chaotic harris hawks optimization technique for extracting parameters of several proton exchange membrane fuel cell stacks. IEEE Access 2019, 8, 1146–1159. [Google Scholar] [CrossRef]
- Restrepo, C.; Konjedic, T.; Garces, A.; Calvente, J.; Giral, R. Identification of a proton-exchange membrane fuel cell’s model parameters by means of an evolution strategy. IEEE Trans. Ind. Inform. 2014, 11, 548–559. [Google Scholar] [CrossRef]
- Sazali, N.; Wan Salleh, W.N.; Jamaludin, A.S.; Mhd Razali, M.N. New perspectives on fuel cell technology: A brief review. Membranes 2020, 10, 99. [Google Scholar] [CrossRef] [PubMed]
- Pinagapani, A.K.; Mani, G.; Chandran, K.; Pandian, K.; Sawantmorye, E.; Vaghela, P. Dynamic Modeling and Validation of PEM Fuel Cell via System Identification Approach. J. Electr. Eng. Technol. 2021, 16, 2211–2220. [Google Scholar] [CrossRef]
- Gebregergis, A.; Pillay, P. Implementation of fuel cell emulation on dspand dspace controllers in the design of power electronic converters. In Proceedings of the 2008 IEEE Industry Applications Society Annual Meeting, Edmonton, AB, Canada, 5–9 October 2008; pp. 1–8. [Google Scholar]
- Kwan, T.H.; Yao, Q. A cost effective experimental emulator for fuel cell based combined heat and power systems. Energy Procedia 2019, 158, 1437–1448. [Google Scholar] [CrossRef]
- Voottipruex, K.; Sangswang, A.; Naetiladdanon, S.; Mujjalinvimut, E.; Wongyoa, N. Pem fuel cell emulator based on dynamic model with relative humidity calculation. In Proceedings of the 2017 14th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 27–30 June 2017; pp. 529–532. [Google Scholar]
- Premkumar, K.; Vishnupriya, M.; Thamizhselvan, T.; Sanjeevikumar, P.; Manikandan, B. PSO optimized PI controlled DC-DC buck converter-based proton-exchange membrane fuel cell emulator for testing of MPPT algorithm and battery charger controller. Int. Trans. Electr. Energy Syst. 2021, 31, e12754. [Google Scholar] [CrossRef]
- Yodwong, B.; Guilbert, D.; Hinaje, M.; Phattanasak, M.; Kaewmanee, W.; Vitale, G. Proton Exchange Membrane Electrolyzer Emulator for Power Electronics Testing Applications. Processes 2021, 9, 498. [Google Scholar] [CrossRef]
- Ali, M.; El-Hameed, M.; Farahat, M. Effective parameters’ identification for polymer electrolyte membrane fuel cell models using grey wolf optimizer. Renew. Energy 2017, 111, 455–462. [Google Scholar] [CrossRef]
- Turgut, O.E.; Coban, M.T. Optimal proton exchange membrane fuel cell modelling based on hybrid Teaching Learning Based Optimization–Differential Evolution algorithm. Ain Shams Eng. J. 2016, 7, 347–360. [Google Scholar] [CrossRef]
- Mo, Z.J.; Zhu, X.J.; Wei, L.Y.; Cao, G.Y. Parameter optimization for a PEMFC model with a hybrid genetic algorithm. Int. J. Energy Res. 2006, 30, 585–597. [Google Scholar] [CrossRef]
- Menesy, A.S.; Sultan, H.M.; Korashy, A.; Banakhr, F.A.; Ashmawy, M.G.; Kamel, S. Effective parameter extraction of different polymer electrolyte membrane fuel cell stack models using a modified artificial ecosystem optimization algorithm. IEEE Access 2020, 8, 31892–31909. [Google Scholar] [CrossRef]
- Fathy, A.; Abd Elaziz, M.; Alharbi, A.G. A novel approach based on hybrid vortex search algorithm and differential evolution for identifying the optimal parameters of PEM fuel cell. Renew. Energy 2020, 146, 1833–1845. [Google Scholar] [CrossRef]
- Agwa, A.M.; El-Fergany, A.A.; Sarhan, G.M. Steady-state modeling of fuel cells based on atom search optimizer. Energies 2019, 12, 1884. [Google Scholar] [CrossRef] [Green Version]
- Louzazni, M.; Al-Dahidi, S.; Mussetta, M. Fuel Cell Characteristic Curve Approximation Using the Bézier Curve Technique. Sustainability 2020, 12, 8127. [Google Scholar] [CrossRef]
- Yao, L.; Ge, Z. Nonlinear Gaussian Mixture Regression for Multimode Quality Prediction With Partially Labeled Data. IEEE Trans. Ind. Inform. 2019, 15, 4044–4053. [Google Scholar] [CrossRef]
- Restrepo, C.; Garcia, G.; Calvente, J.; Giral, R.; Martínez-Salamero, L. Static and dynamic current–voltage modeling of a proton exchange membrane fuel cell using an input–output diffusive approach. IEEE Trans. Ind. Electron. 2015, 63, 1003–1015. [Google Scholar] [CrossRef]
- El-Fergany, A.A. Electrical characterisation of proton exchange membrane fuel cells stack using grasshopper optimiser. IET Renew. Power Gener. 2018, 12, 9–17. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H.; Shaw, S.R. Dynamic models and model validation for PEM fuel cells using electrical circuits. IEEE Trans. Energy Convers. 2005, 20, 442–451. [Google Scholar] [CrossRef]
- Diab, A.A.Z.; Tolba, M.A.; El-Magd, A.G.A.; Zaky, M.M.; El-Rifaie, A.M. Fuel cell parameters estimation via marine predators and political optimizers. IEEE Access 2020, 8, 166998–167018. [Google Scholar] [CrossRef]
- Barragán, A.J.; Enrique, J.M.; Segura, F.; Andújar, J.M. Iterative fuzzy modeling of hydrogen fuel cells by the extended Kalman filter. IEEE Access 2020, 8, 180280–180294. [Google Scholar] [CrossRef]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1824–1832. [Google Scholar] [CrossRef]
- Li, B.; Long, Y.; Song, H. Detection of green apples in natural scenes based on saliency theory and Gaussian curve fitting. Int. J. Agric. Biol. Eng. 2018, 11, 192–198. [Google Scholar] [CrossRef] [Green Version]
- Bertsekas, D.P. Nonlinear programming. J. Oper. Res. Soc. 1997, 48, 334. [Google Scholar] [CrossRef]
- Yuan, Y.X. A review of trust region algorithms for optimization. Iciam 2000, 99, 271–282. [Google Scholar]
- Villacorta, K.D.; Oliveira, P.R.; Soubeyran, A. A trust-region method for unconstrained multiobjective problems with applications in satisficing processes. J. Optim. Theory Appl. 2014, 160, 865–889. [Google Scholar] [CrossRef]
- Bonhoff, K. The NEXA {sup T} M 1200 Watt Compact Power Supply. In Proceedings of the The Fuel Cell World, Lucerne, Switzerland, 1–5 July 2002. [Google Scholar]
- Kim, H.I.; Cho, C.Y.; Nam, J.H.; Shin, D.; Chung, T.Y. A simple dynamic model for polymer electrolyte membrane fuel cell (PEMFC) power modules: Parameter estimation and model prediction. Int. J. Hydrogen Energy 2010, 35, 3656–3663. [Google Scholar] [CrossRef]
- Ramos Paja, C.A.; Romero Nevado, A.; Giral Castillon, R.; Martinez-Salamero, L.; Sanchez Saenz, C.I. Switching and linear power stages evaluation for PEM fuel cell emulation. Int. J. Circuit Theory Appl. 2011, 39, 475–499. [Google Scholar] [CrossRef]
- Guo, H. A Simple Algorithm for Fitting a Gaussian Function [DSP Tips and Tricks]. IEEE Signal Process. Mag. 2011, 28, 134–137. [Google Scholar] [CrossRef]
- Exponential Taylor methods: Analysis and implementation. Comput. Math. Appl. 2013, 65, 487–499. [CrossRef]
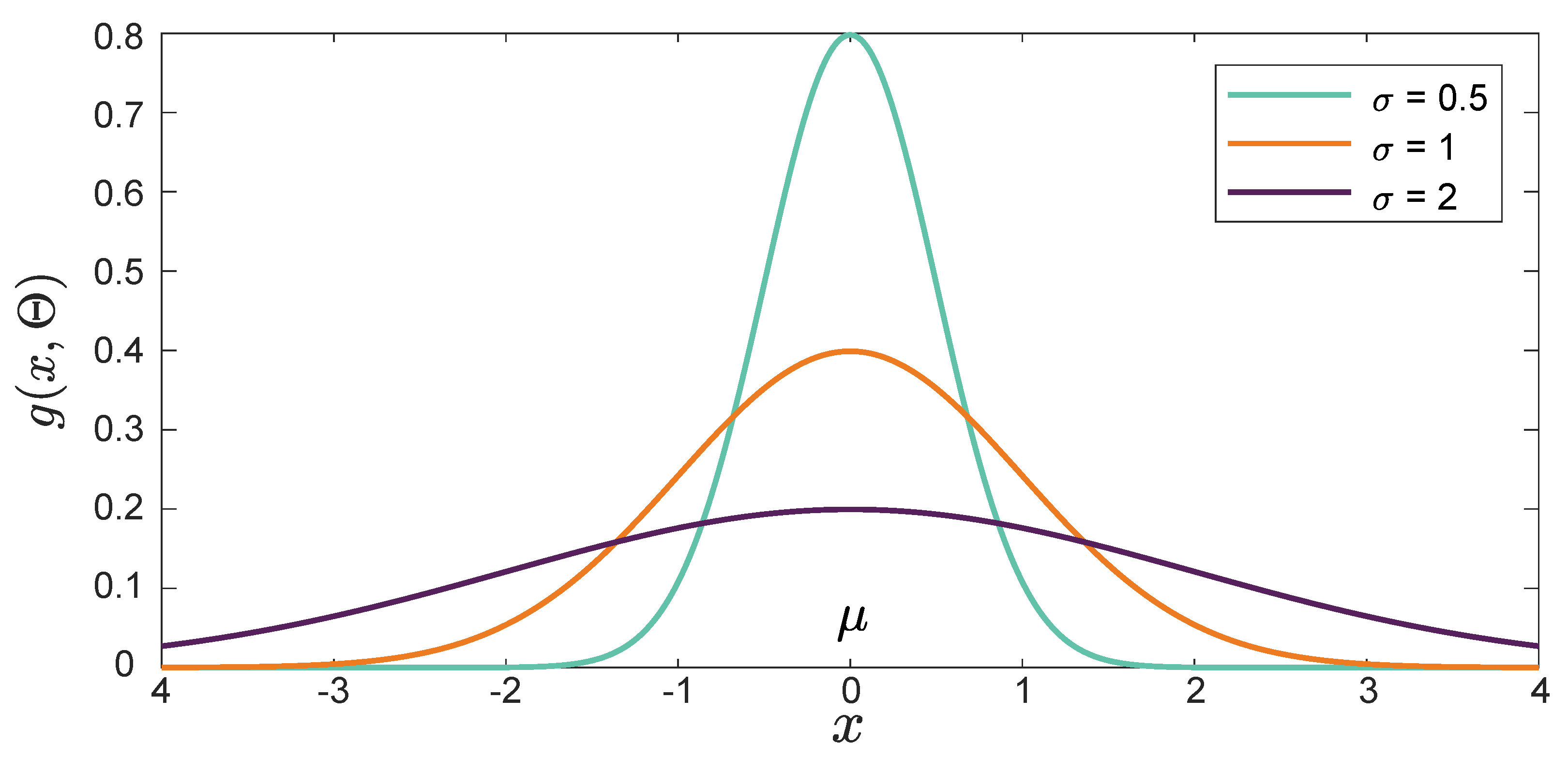
| FC Model Strategy | Ref. | Static Model | V-I Dynamic Model | Variables Used to Evaluate the Model | Training Complexity | Implemen-Tation Cost | Tested with a Real FC |
|---|---|---|---|---|---|---|---|
| CHHO | [7] |  |  | , , , , | M | H |  |
| GOA | [25] |  |  | , , , , | L | H |  |
| GWO | [16] |  |  | , , , , | L | H |  |
| HGA | [18] |  |  | , , , , | L | H |  |
| Electrical circuit | [26] |  |  | , , , , |  | H |  |
| MAEO | [19] |  |  | , , , , | L | H |  |
| VSDE | [20] |  |  | , , , , | M | H |  |
| ASO | [21] |  |  | , , , , | H | H |  |
| Electrical model | [6] |  |  | , , , , |  | H |  |
| MPA-PO | [27] |  |  | , , , , | M | H |  |
| TS-KF | [28] |  |  | , | H | H |  |
| ARX-RLS | [10] |  |  | , , , , | L | H |  |
| Bézier Curve | [22] |  |  | M | H |  | |
| ES | [8] |  |  | , , , , |  | H |  |
| Diffusive model | [24] |  |  | H | M |  | |
| This work | [-] |  |  | M | L |  |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Castaño, C.; Lorente-Leyva, L.L.; Alpala, J.; Revelo-Fuelagán, J.; Peluffo-Ordóñez, D.H.; Restrepo, C. Dynamic Modeling of a Proton-Exchange Membrane Fuel Cell Using a Gaussian Approach. Membranes 2021, 11, 953. https://doi.org/10.3390/membranes11120953
González-Castaño C, Lorente-Leyva LL, Alpala J, Revelo-Fuelagán J, Peluffo-Ordóñez DH, Restrepo C. Dynamic Modeling of a Proton-Exchange Membrane Fuel Cell Using a Gaussian Approach. Membranes. 2021; 11(12):953. https://doi.org/10.3390/membranes11120953
Chicago/Turabian StyleGonzález-Castaño, Catalina, Leandro L. Lorente-Leyva, Janeth Alpala, Javier Revelo-Fuelagán, Diego H. Peluffo-Ordóñez, and Carlos Restrepo. 2021. "Dynamic Modeling of a Proton-Exchange Membrane Fuel Cell Using a Gaussian Approach" Membranes 11, no. 12: 953. https://doi.org/10.3390/membranes11120953
APA StyleGonzález-Castaño, C., Lorente-Leyva, L. L., Alpala, J., Revelo-Fuelagán, J., Peluffo-Ordóñez, D. H., & Restrepo, C. (2021). Dynamic Modeling of a Proton-Exchange Membrane Fuel Cell Using a Gaussian Approach. Membranes, 11(12), 953. https://doi.org/10.3390/membranes11120953









