Mass Transport in Osmotically Driven Membrane Processes
Abstract
1. Introduction
2. Materials and Methods
2.1. Membrane Characteristics
2.2. Equations for Fluid Flow and Mass Transfer
2.3. Model Verification with Empty Flow Channels
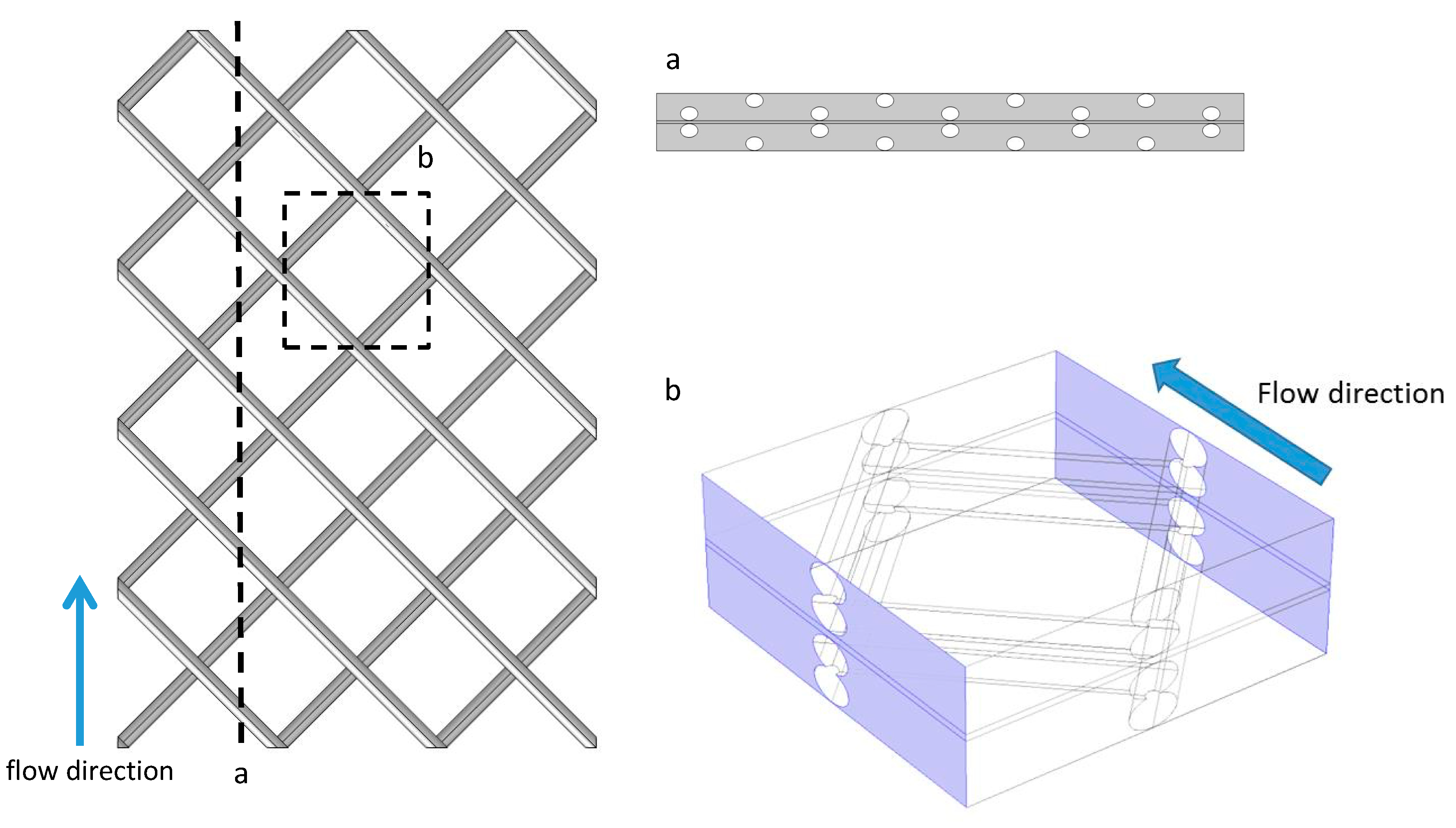
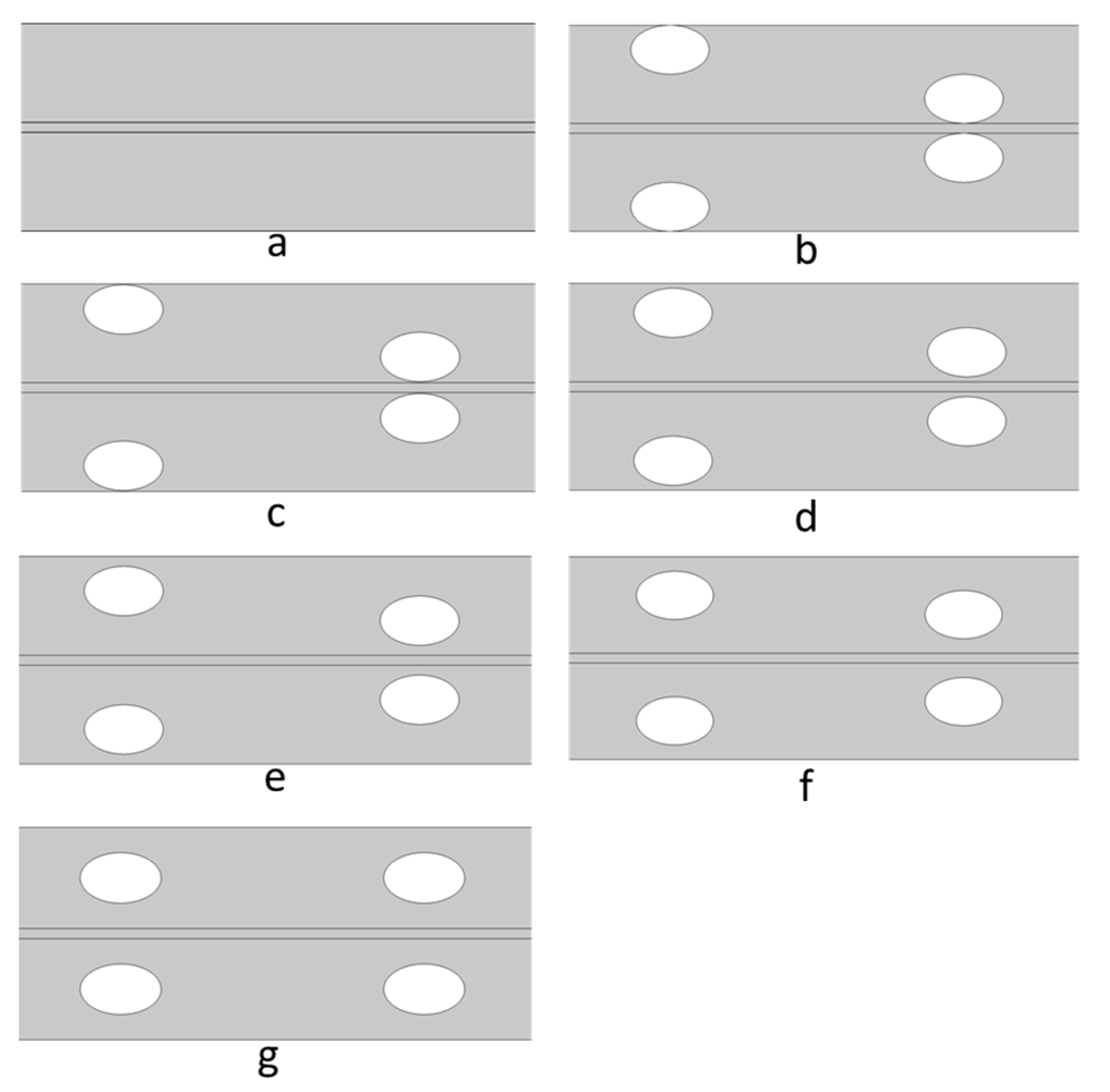
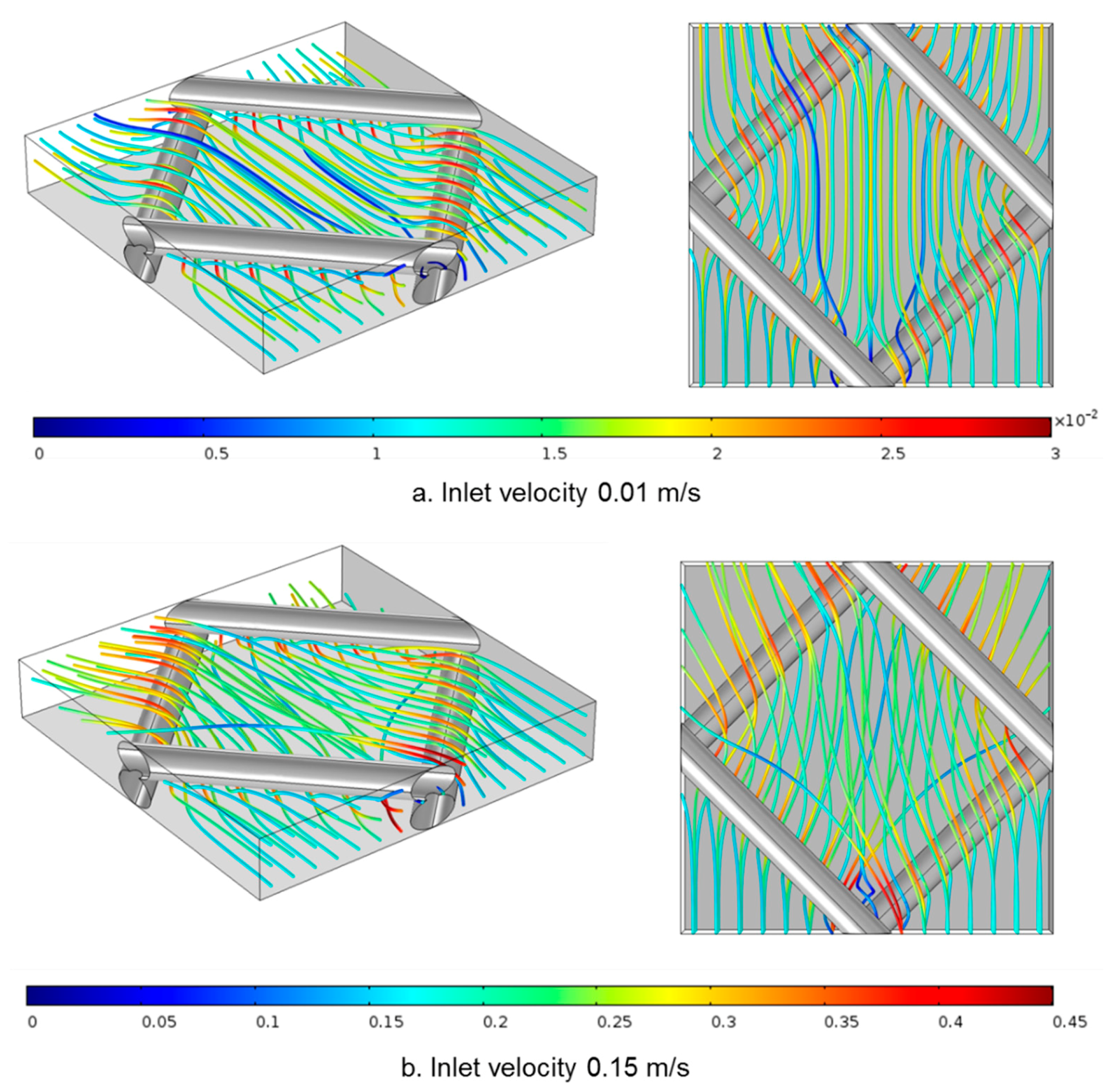
2.4. Spacer Filled 2D and 3D Flow Channels
3. Results and Discussion
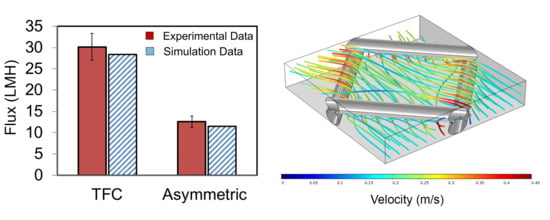
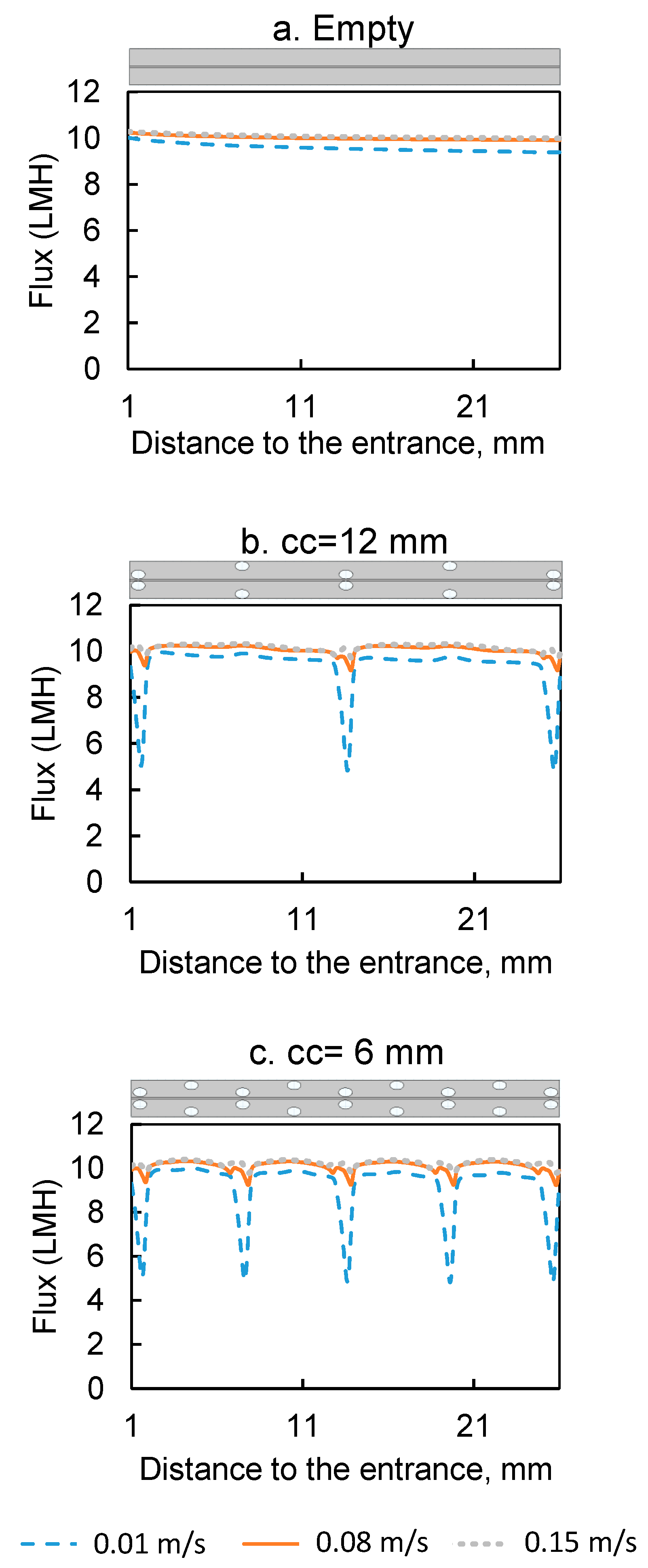
3.1. Modeling Verification
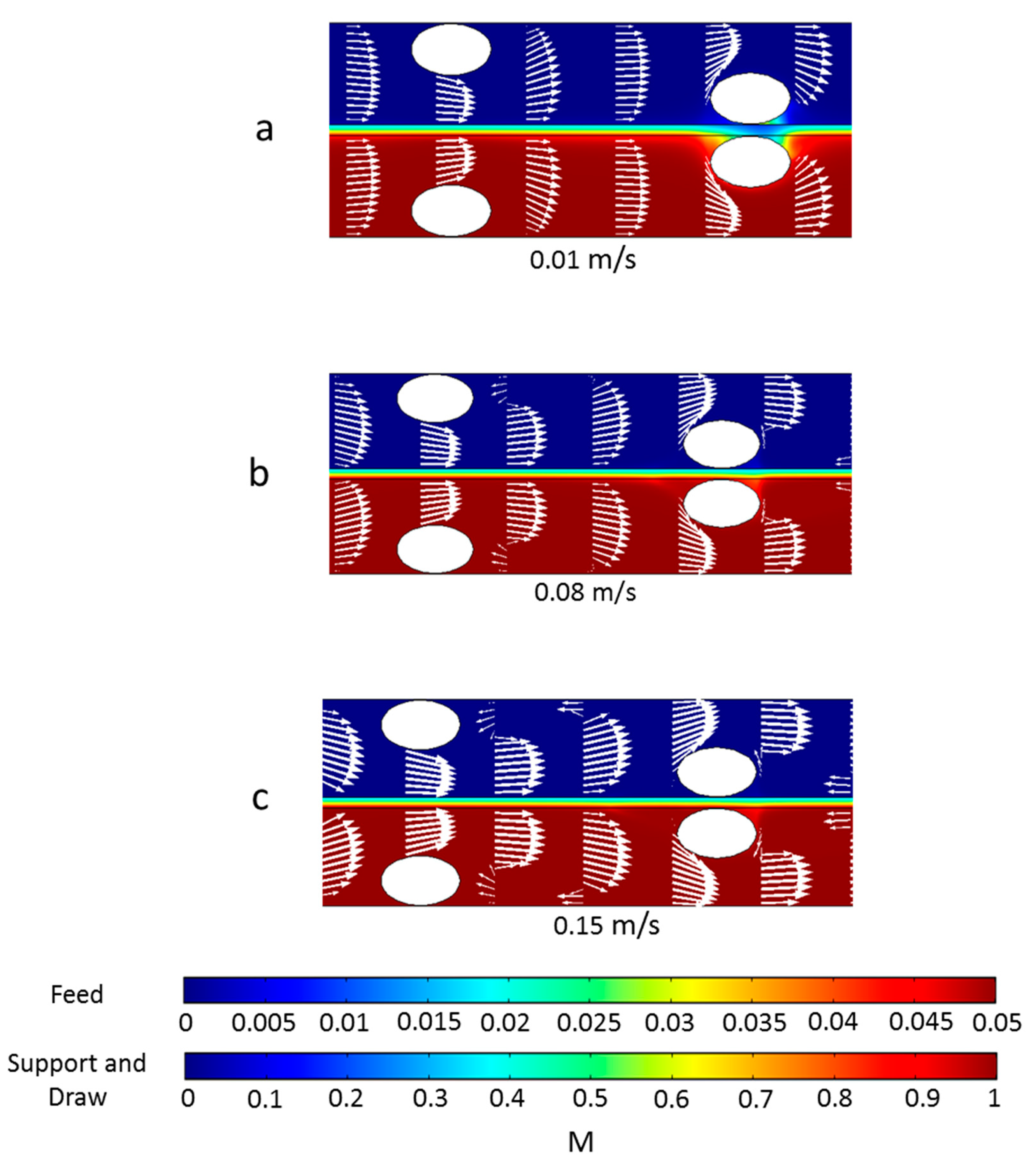
3.2. D Simulations with Feed Spacer-Filled Flow Channels
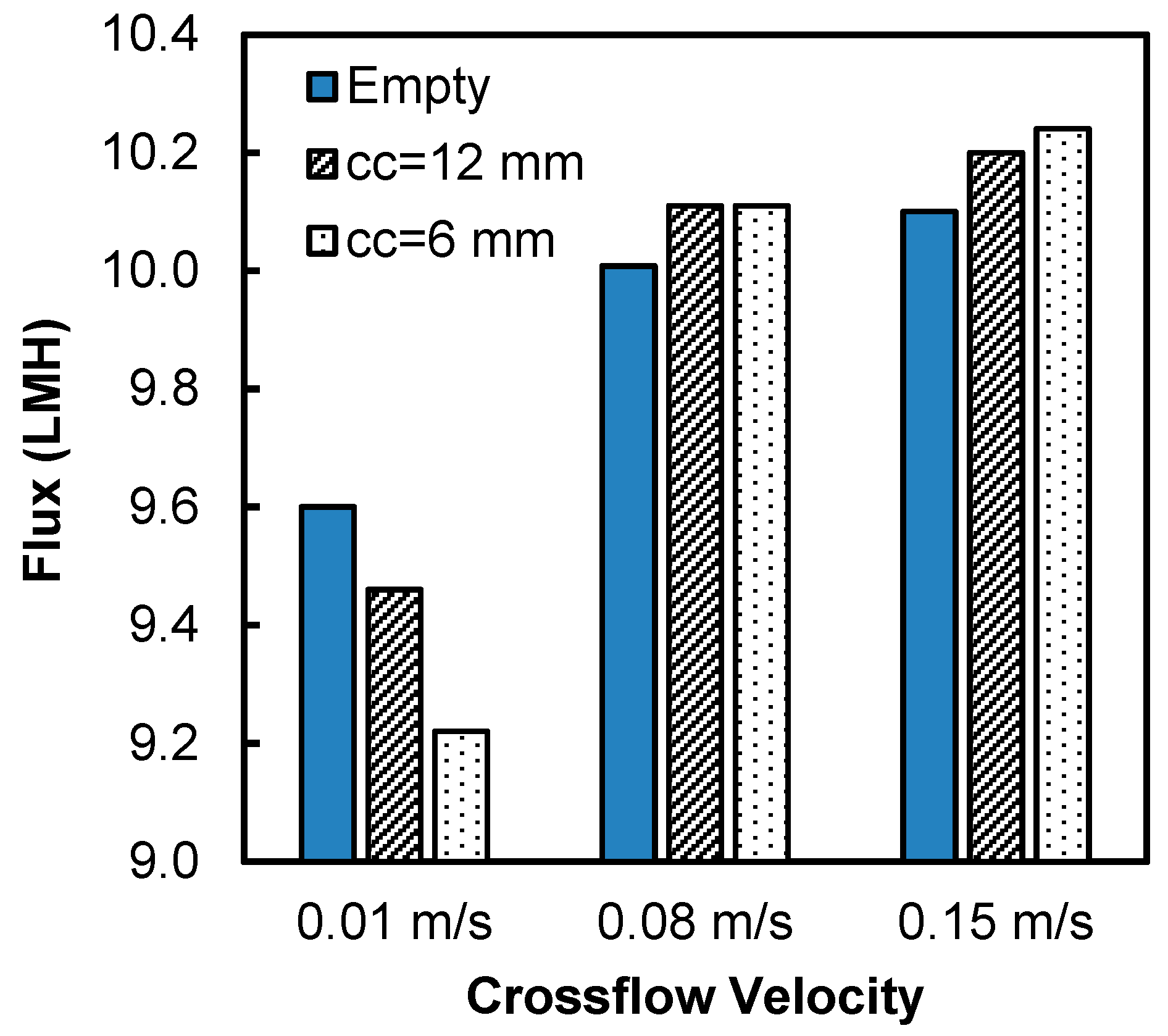
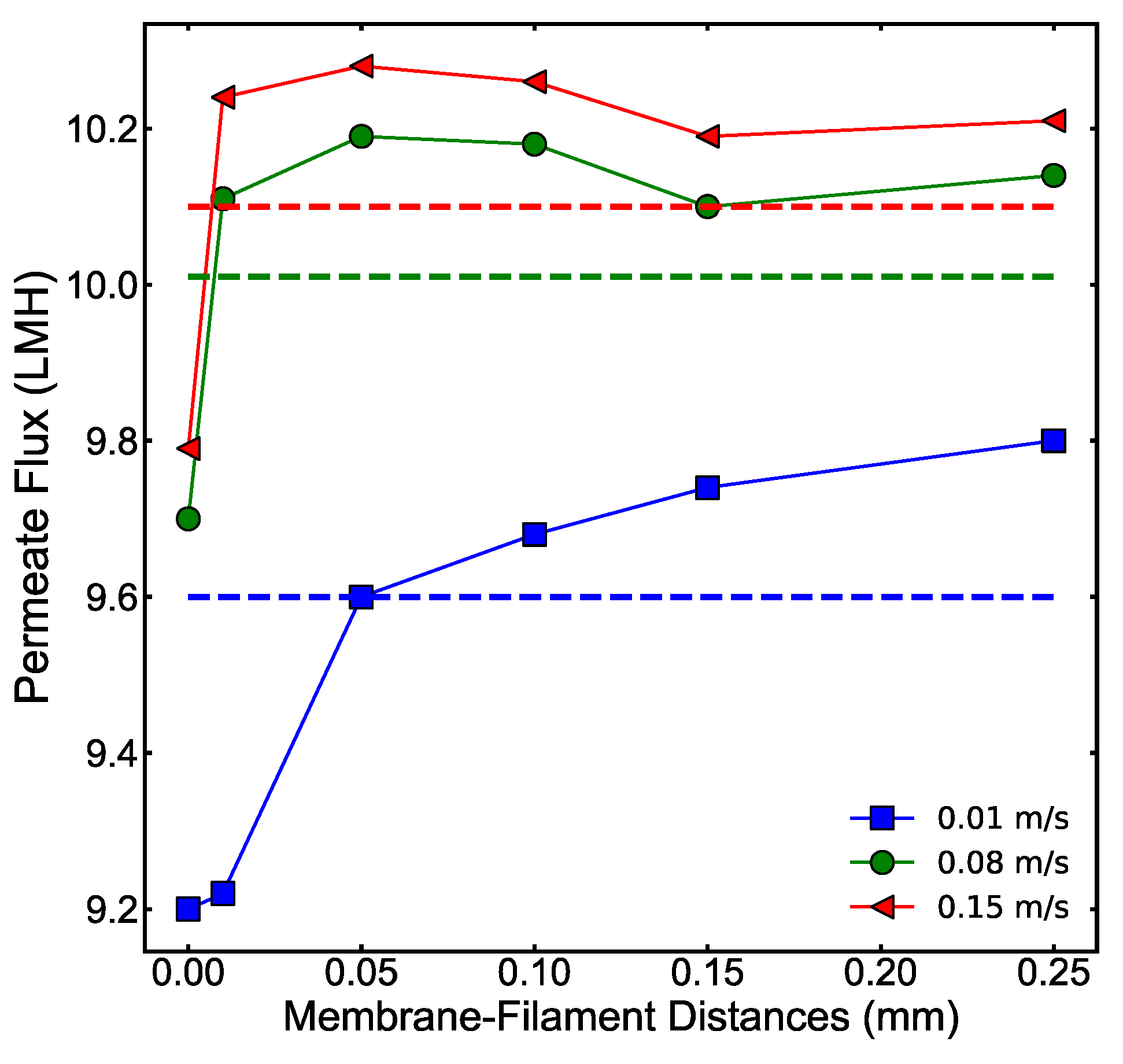
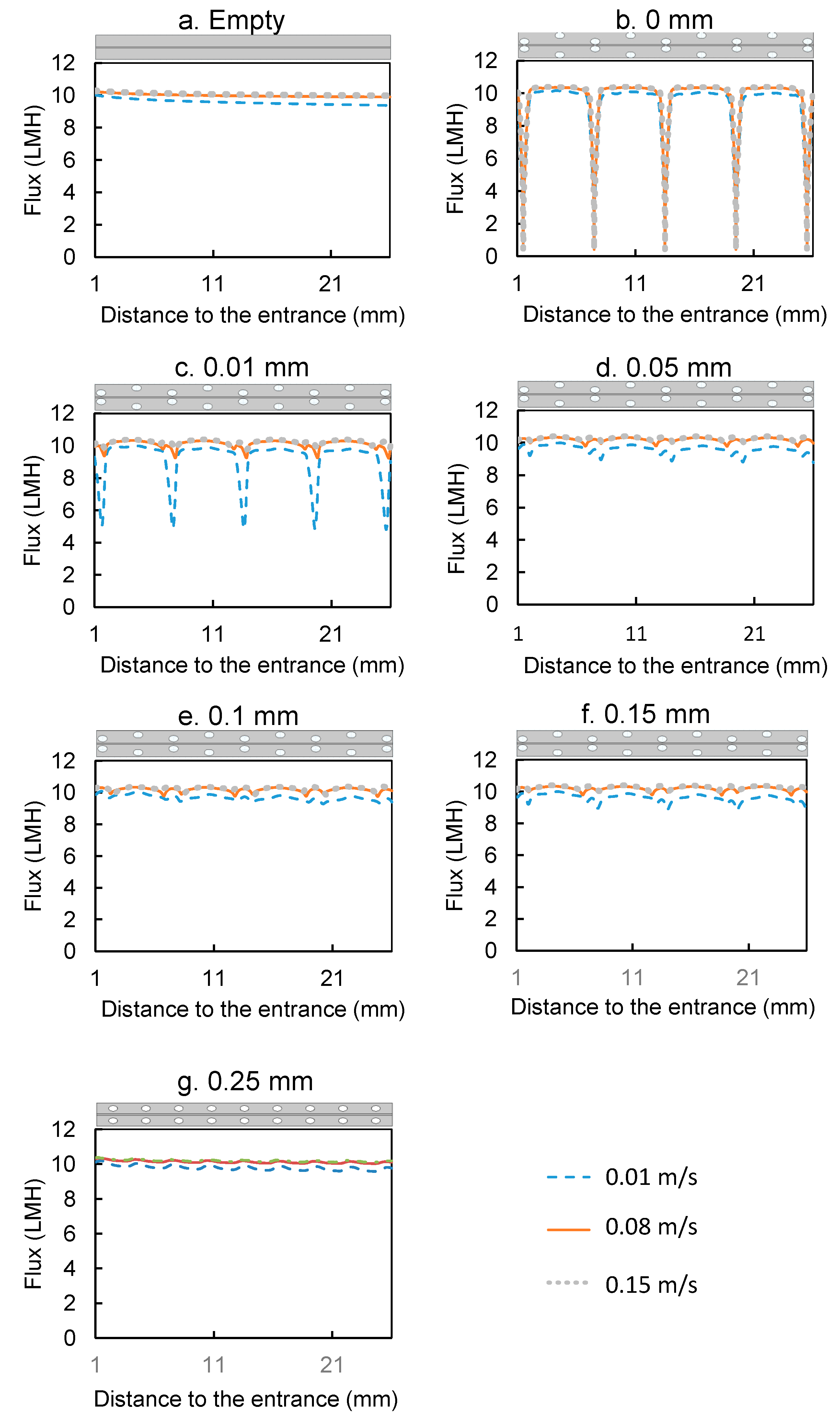
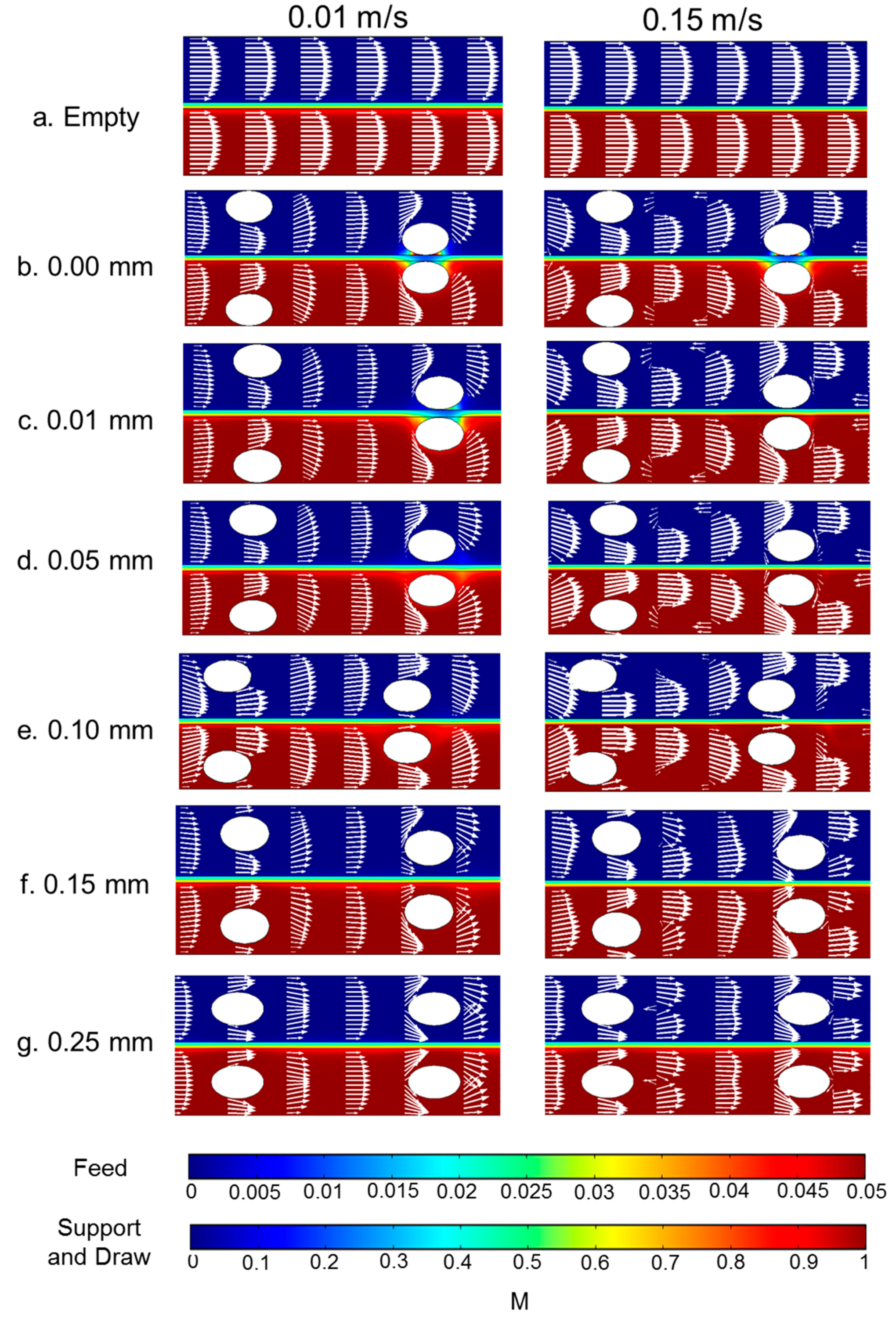
3.3. The Impact of Spacer Membrane–Filament Distance
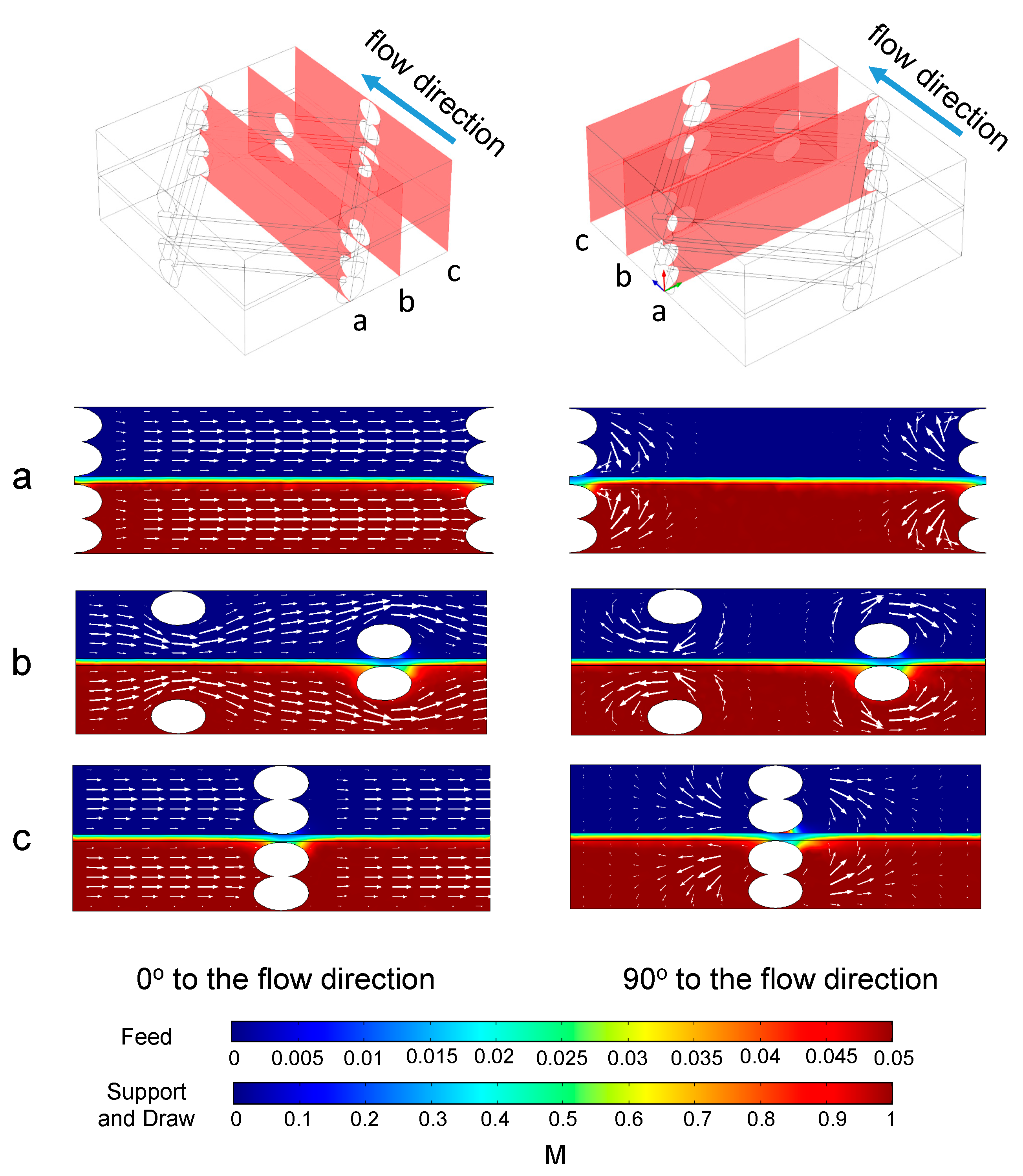
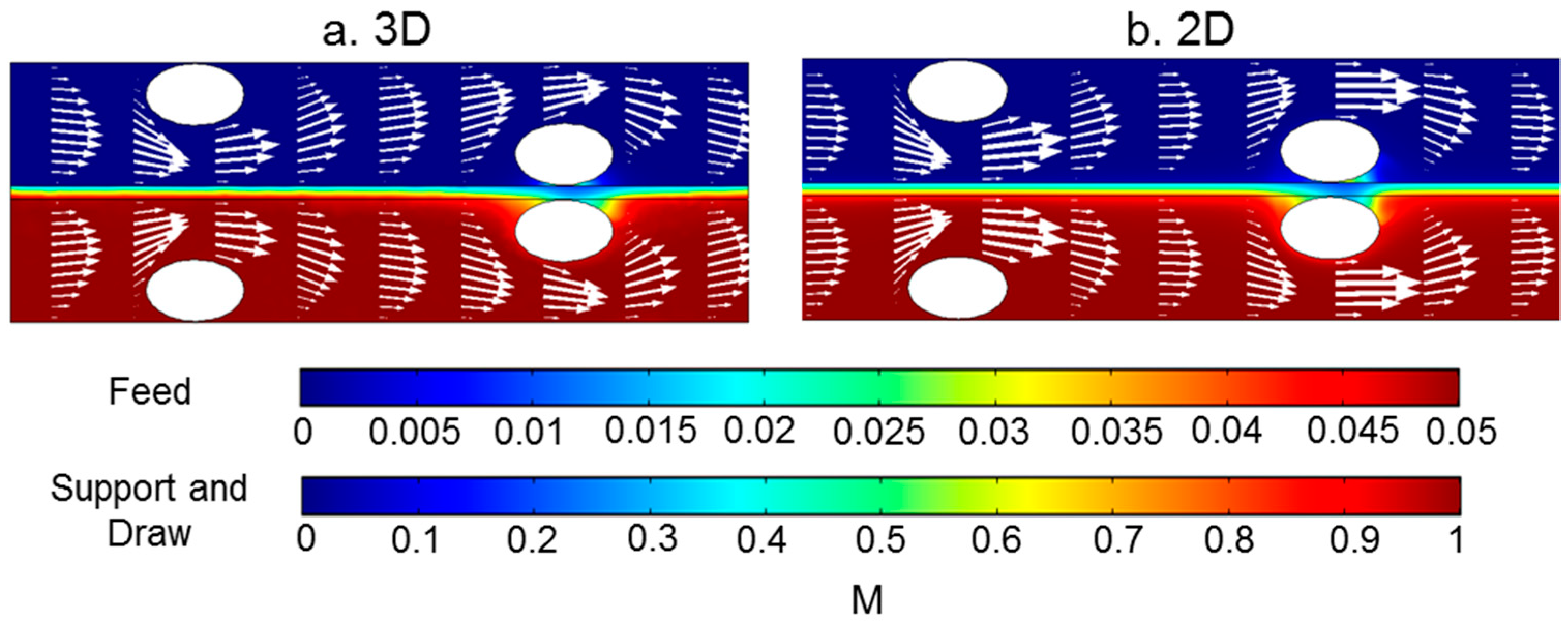
3.4. 3D Simulations with Spacer Filled Flow Channels
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
List of Symbols
| Water permeability of the membrane at 293 K, m/(s·Pa) | |
| Salt permeability of the membrane, 1/s | |
| c | Salt concentration, M |
| Inflow salt concentration at the draw solution side, M | |
| Inflow salt concentration at the feed solution side, M | |
| Diffusion coefficient in the membrane channel, m2/s | |
| Effective diffusion coefficient in the membrane support layer, m2/s | |
| Flux of water, m/s | |
| Flux of salt through the membrane, M·m/s | |
| L | Length of the channel, mm |
| P | Pressure, Pa |
| R | Salt rejection ratio |
| velocity, m/s | |
| Inflow velocity at the draw solution side, m/s | |
| Inflow velocity at the feed side, m/s |
Greek Letters
| ε | Porosity of the membrane support layer |
| τ | Tortuosity of the membrane support layer |
| κ | Hydraulic conductivity, m/s |
| Density, kg/m3 | |
| Dynamics viscosity, Pa·s | |
| Forchheimer coefficient | |
| Osmotic pressure, draw solution side nearest the membrane, Pa | |
| Osmotic pressure, feed solution side nearest the membrane, Pa | |
| Shear rate, 1/s |
References
- Cath, T.Y.; Childress, A.; Elimelech, M. Forward osmosis: Principles, applications, and recent developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- Klaysom, C.; Cath, T.Y.; Depuydt, T.; Vankelecom, I.F. Forward and pressure retarded osmosis: Potential solutions for global challenges in energy and water supply. Chem. Soc. Rev. 2013, 42, 6959–6989. [Google Scholar] [CrossRef]
- Achilli, A.; Childress, A.E. Pressure retarded osmosis: From the vision of Sidney Loeb to the first prototype installation — Review. Desalination 2010, 261, 205–211. [Google Scholar] [CrossRef]
- Cath, T.Y.; Elimelech, M.; McCutcheon, J.R.; McGinnis, R.L.; Achilli, A.; Anastasio, D.; Brady, A.R.; E Childress, A.; Farr, I.V.; Hancock, N.T.; et al. Standard Methodology for Evaluating Membrane Performance in Osmotically Driven Membrane Processes. Desalination 2013, 312, 31–38. [Google Scholar] [CrossRef]
- Zhou, Z.; Lee, J.Y.; Chung, T.-S. Thin film composite forward-osmosis membranes with enhanced internal osmotic pressure for internal concentration polarization reduction. Chem. Eng. J. 2014, 249, 236–245. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; McGinnis, R.L.; Elimelech, M. A novel ammonia—Carbon dioxide forward (direct) osmosis desalination process. Desalination 2005, 174, 1–11. [Google Scholar] [CrossRef]
- Shaffer, D.L.; Yip, N.Y.; Gilron, J.; Elimelech, M. Seawater desalination for agriculture by integrated forward and reverse osmosis: Improved product water quality for potentially less energy. J. Membr. Sci. 2012, 415–416, 1–8. [Google Scholar] [CrossRef]
- Alturki, A.; A McDonald, J.; Khan, S.J.; Hai, F.I.; E Price, W.; Nghiem, L.D. Performance of a novel osmotic membrane bioreactor (OMBR) system: Flux stability and removal of trace organics. Bioresour. Technol. 2012, 113, 201–206. [Google Scholar] [CrossRef]
- Hickenbottom, K.L.; Vanneste, J.; Elimelech, M.; Cath, T.Y. Assessing the current state of commercially available membranes and spacers for energy production with pressure retarded osmosis. Desalination 2016, 389, 108–118. [Google Scholar] [CrossRef]
- Liberman, B.; Greenberg, G.; Levitin, V.; Oz-Ari, T. Three Pressure Retarded (PRO) Process. In Proceedings of the International Desalination Association World Congress on Desalination and Water Reuse, Tianjin, China, 20–25 October 2013. [Google Scholar]
- Goosen, M.F.A.; Sablani, S.S.; Al-Hinai, H.; Al-Obeidani, S.; Al-Belushi, R.; Jackson, D. Fouling of Reverse Osmosis and Ultrafiltration Membranes: A Critical Review. Sep. Sci. Technol. 2005, 39, 2261–2297. [Google Scholar] [CrossRef]
- Elimelech, M.; Bhattacharjee, S. A novel approach for modeling concentration polarization in crossflow membrane filtration based on the equivalence of osmotic pressure model and filtration theory. J. Membr. Sci. 1998, 145, 223–241. [Google Scholar] [CrossRef]
- Sagiv, A.; Zhu, A.; Christofides, P.D.; Cohen, Y.; Semiat, R. Analysis of forward osmosis desalination via two-dimensional FEM model. J. Membr. Sci. 2014, 464, 161–172. [Google Scholar] [CrossRef]
- Zhao, S.; Zou, L.; Tang, C.Y.; Mulcahy, D. Recent developments in forward osmosis: Opportunities and challenges. J. Membr. Sci. 2012, 396, 1–21. [Google Scholar] [CrossRef]
- McCutcheon, J.R.; Elimelech, M. Influence of concentrative and dilutive internal concentration polarization on flux behavior in forward osmosis. J. Membr. Sci. 2006, 284, 237–247. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, S.; Yang, F. Use of a spacer to mitigate concentration polarization during forward osmosis process. Desalination 2014, 347, 112–119. [Google Scholar] [CrossRef]
- Tan, C.H.; Ng, H.Y. Revised external and internal concentration polarization models to improve flux prediction in forward osmosis process. Desalination 2013, 309, 125–140. [Google Scholar] [CrossRef]
- Li, W.; Gao, Y.; Tang, C.Y. Network modeling for studying the effect of support structure on internal concentration polarization during forward osmosis: Model development and theoretical analysis with FEM. J. Membr. Sci. 2011, 379, 307–321. [Google Scholar] [CrossRef]
- Gray, G.T.; McCutcheon, J.R.; Elimelech, M. Internal concentration polarization in forward osmosis: Role of membrane orientation. Desalination 2006, 197, 1–8. [Google Scholar] [CrossRef]
- Tan, C.H.; Ng, H.Y. Modified models to predict flux behavior in forward osmosis in consideration of external and internal concentration polarizations. J. Membr. Sci. 2008, 324, 209–219. [Google Scholar] [CrossRef]
- Park, M.; Kim, J.H. Numerical analysis of spacer impacts on forward osmosis membrane process using concentration polarization index. J. Membr. Sci. 2013, 427, 10–20. [Google Scholar] [CrossRef]
- Linares, R.V.; Bucs, S.; Li, Z.; AbuGhdeeb, M.; Amy, G.L.; Vrouwenvelder, J.S. Impact of spacer thickness on biofouling in forward osmosis. Water Res. 2014, 57, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Zou, S.; Wang, Y.-N.; Wicaksana, F.; Aung, T.; Wong, P.C.Y.; Fane, A.G.; Tang, C.Y. Direct microscopic observation of forward osmosis membrane fouling by microalgae: Critical flux and the role of operational conditions. J. Membr. Sci. 2013, 436, 174–185. [Google Scholar] [CrossRef]
- Coday, B.D.; Almaraz, N.; Cath, T.Y. Forward osmosis desalination of oil and gas wastewater: Impacts of membrane selection and operating conditions on process performance. J. Membr. Sci. 2015, 488, 40–55. [Google Scholar] [CrossRef]
- Liang, Y.; Chapman, M.; Weihs, G.F.; Wiley, D.E. CFD modelling of electro-osmotic permeate flux enhancement on the feed side of a membrane module. J. Membr. Sci. 2014, 470, 378–388. [Google Scholar] [CrossRef]
- Li, F.; Meindersma, G.; De Haan, A.; Reith, T. Optimization of non-woven spacers by CFD and validation by experiments. Desalination 2002, 146, 209–212. [Google Scholar] [CrossRef]
- Fimbres-Weihs, G.; Wiley, D.E. Review of 3D CFD modeling of flow and mass transfer in narrow spacer-filled channels in membrane modules. Chem. Eng. Process. Process Intensif. 2010, 49, 759–781. [Google Scholar] [CrossRef]
- Alexiadis, A.; Wiley, D.E.; Vishnoi, A.; Lee, R.; Fletcher, D.F.; Bao, J. CFD modelling of reverse osmosis membrane flow and validation with experimental results. Desalination 2007, 217, 242–250. [Google Scholar] [CrossRef]
- Karode, S.K.; Kumar, A. Flow visualization through spacer filled channels by computational fluid dynamics I.: Pressure drop and shear rate calculations for flat sheet geometry. J. Membr. Sci. 2001, 193, 69–84. [Google Scholar] [CrossRef]
- Lian, B.; Blandin, G.; Leslie, G.; Le-Clech, P. Impact of module design in forward osmosis and pressure assisted osmosis: An experimental and numerical study. Desalination 2018, 426, 108–117. [Google Scholar] [CrossRef]
- Gruber, M.; Johnson, C.J.; Tang, C.; Jensen, M.H.; Yde, L.; Nielsen, C. Validation and Analysis of Forward Osmosis CFD Model in Complex 3D Geometries. Membr. 2012, 2, 764–782. [Google Scholar] [CrossRef]
- Xie, P.; Murdoch, L.C.; Ladner, D.A. Hydrodynamics of sinusoidal spacers for improved reverse osmosis performance. J. Membr. Sci. 2014, 453, 92–99. [Google Scholar] [CrossRef]
- Toh, K.Y.; Liang, Y.Y.; Lau, W.J.; Weihs, G.A.F. A Review of CFD Modelling and Performance Metrics for Osmotic Membrane Processes. Membr. 2020, 10, 285. [Google Scholar] [CrossRef] [PubMed]
- McGinnis, R.; McGurgan, G. Forward osmosis membranes, Oasys Water, Inc. U.S. Patent US8181794B2, 22 May 2012. [Google Scholar]
- Tiraferri, A.; Yip, N.Y.; Phillip, W.A.; Schiffman, J.D.; Elimelech, M. Relating performance of thin-film composite forward osmosis membranes to support layer formation and structure. J. Membr. Sci. 2011, 367, 340–352. [Google Scholar] [CrossRef]
- Phillip, W.A.; Schiffman, J.D.; Elimelech, M. High performance thin-film membrane. Environ. Sci. Technol. 2010, 44, 3812–3818. [Google Scholar]
- Jambhekar, V. Forchheimer Porous-Media Flow Models—Numerical Investigation and Comparison with Experimental Data. Master’s Thesis, Universität Stuttgart-Institut für Wasserund Umweltsystemmodellierung, Stuttgart, Germany, December 2011. [Google Scholar]
- Xie, P. Simulation of Reverse Osmosis and Osmotically Driven Membrane Processes, Dissertation, Clemson University Department of Environmental Engineering and Earth Sciences. Ph.D. Thesis, Clemson University, Clemson, SC, USA, 2016. [Google Scholar]
- Fimbres-Weihs, G.; Wiley, D.E. Numerical study of mass transfer in three-dimensional spacer-filled narrow channels with steady flow. J. Membr. Sci. 2007, 306, 228–243. [Google Scholar] [CrossRef]
- Siddiqui, A.S.S.; Farhat, N.; Bucs, S.S.; Linares, R.V.; Picioreanu, C.; Kruithof, J.C.; Van Loosdrecht, M.C.; Kidwell, J.; Vrouwenvelder, J.S. Development and characterization of 3D-printed feed spacers for spiral wound membrane systems. Water Res. 2016, 91, 55–67. [Google Scholar] [CrossRef]
- Shirazi, M.M.A.; Kargari, A.; Ismail, A.F.; Matsuura, T. Computational Fluid Dynamic (CFD) opportunities applied to the membrane distillation process: State-of-the-art and perspectives. Desalination 2016, 377, 73–90. [Google Scholar] [CrossRef]
- Guillen, G.; Hoek, E. Modeling the impacts of feed spacer geometry on reverse osmosis and nanofiltration processes. Chem. Eng. J. 2009, 149, 221–231. [Google Scholar] [CrossRef]
- Sousa, P.; Soares, A.A.; Monteiro, E.; Rouboa, A. A CFD study of the hydrodynamics in a desalination membrane filled with spacers. Desalination 2014, 349, 22–30. [Google Scholar] [CrossRef]
- Vrouwenvelder, J.S.; Von Der Schulenburg, D.G.; Kruithof, J.C.; Johns, M.L.; Van Loosdrecht, M.C. M Biofouling of spiral-wound nanofiltration and reverse osmosis membranes: A feed spacer problem. Water Res. 2009, 43, 583–594. [Google Scholar] [CrossRef]
- Vrouwenvelder, J.S.; Picioreanu, C.; Kruithof, J.C.; Van Loosdrecht, M.C. Biofouling in spiral wound membrane systems: Three-dimensional CFD model based evaluation of experimental data. J. Membr. Sci. 2010, 346, 71–85. [Google Scholar] [CrossRef]
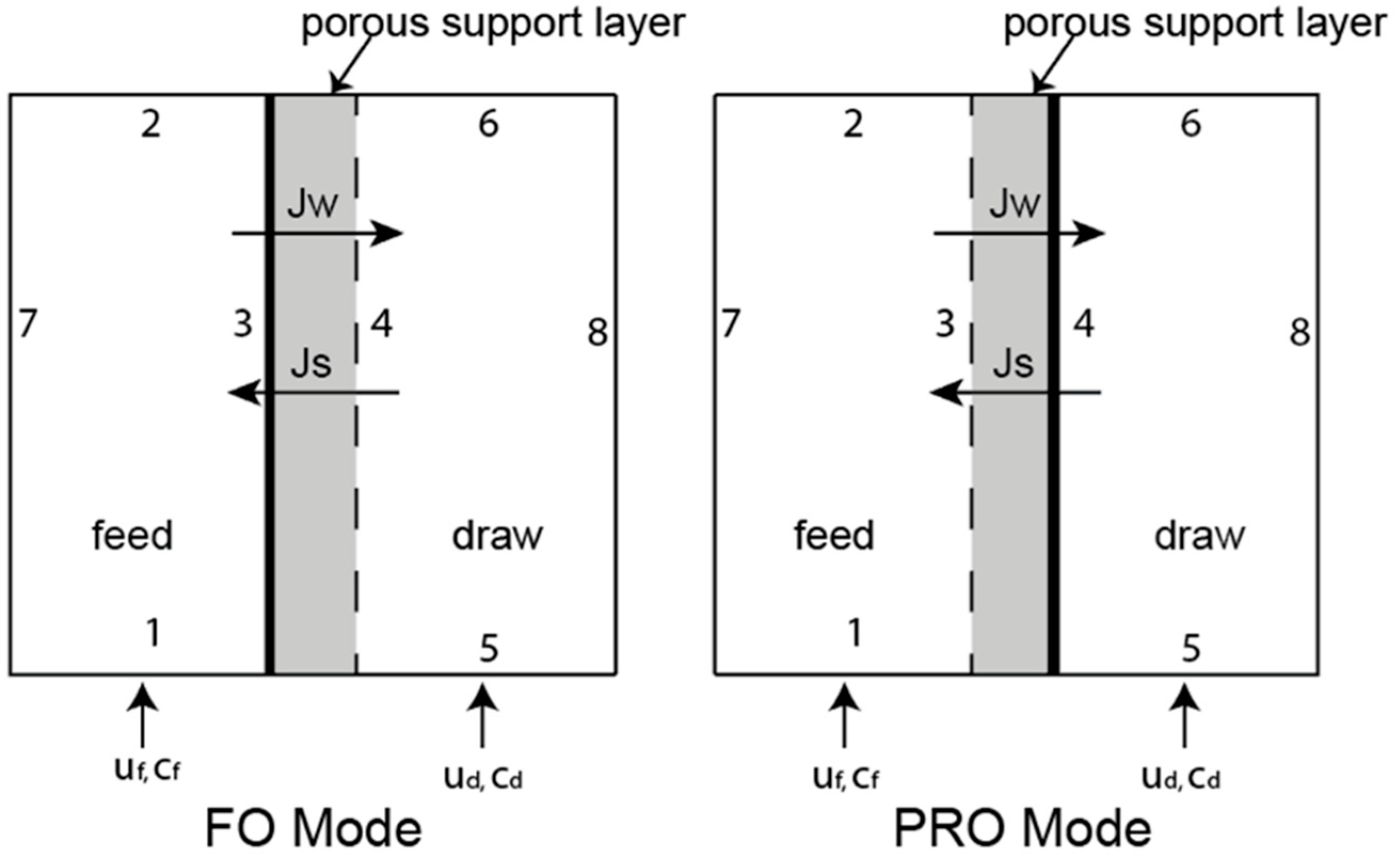

| Boundary Number | Fluid Flow | Solute Mass Transport | ||||
|---|---|---|---|---|---|---|
| Feed Channel | Porous Support | Draw Channel | Feed Channel | Porous Support | Draw Channel | |
| 1 | Inlet (uf) | Inlet (cf) | ||||
| 2 | Outlet Atm. Pressure | Outlet Atm. Pressure | ||||
| 3 | Outlet (Jw) No-slip parallel to membrane | Inlet (Jw) | Inlet (Js) | Outlet (Js) | ||
| 4 | Outlet (Jw) | Inlet (Jw) No-slip parallel to membrane | Inlet (Js) | Outlet (Js) | ||
| 5 | Inlet () | Inlet (cd) | ||||
| 6 | Outlet Atm. Pressure | Outlet Atm. Pressure | ||||
| 7 | Impermeable No-slip | Impermeable No-slip | ||||
| 8 | Impermeable No-slip | Impermeable No-slip | ||||
| FO #1 | FO #2 | PRO #1 | PRO #2 | |||||
|---|---|---|---|---|---|---|---|---|
| TFC | Asymmetric | TFC | Asymmetric | TFC | Asymmetric | TFC | Asymmetric | |
| Lab A | 3.13 | 1.32 | 2.66 | 1.96 | 3.67 | 1.50 | 3.21 | 1.34 |
| Lab B | 0.14 | 0.97 | 0.43 | 0.16 | 1.83 | 0.10 | 1.16 | 0.04 |
| Lab C | 1.35 | 0.35 | 3.24 | 1.15 | 4.37 | 0.76 | 0.68 | 0.07 |
| Average | 1.54 | 0.88 | 2.11 | 1.09 | 3.29 | 0.79 | 1.69 | 0.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, P.; Cath, T.Y.; Ladner, D.A. Mass Transport in Osmotically Driven Membrane Processes. Membranes 2021, 11, 29. https://doi.org/10.3390/membranes11010029
Xie P, Cath TY, Ladner DA. Mass Transport in Osmotically Driven Membrane Processes. Membranes. 2021; 11(1):29. https://doi.org/10.3390/membranes11010029
Chicago/Turabian StyleXie, Peng, Tzahi Y. Cath, and David A. Ladner. 2021. "Mass Transport in Osmotically Driven Membrane Processes" Membranes 11, no. 1: 29. https://doi.org/10.3390/membranes11010029
APA StyleXie, P., Cath, T. Y., & Ladner, D. A. (2021). Mass Transport in Osmotically Driven Membrane Processes. Membranes, 11(1), 29. https://doi.org/10.3390/membranes11010029