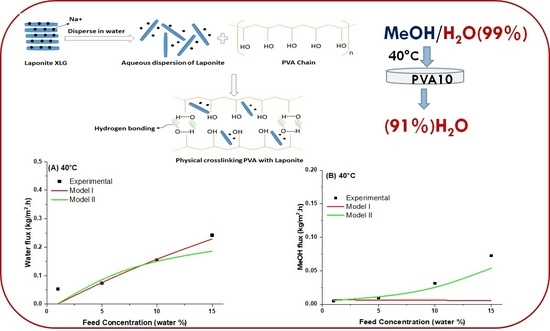
Pervaporative Dehydration of Methanol Using PVA/Nanoclay Mixed Matrix Membranes: Experiments and Modeling
Abstract
1. Introduction
2. Experimental
2.1. Material
2.2. Membrane Fabrication
2.3. Swelling Measurements
2.4. Pervaporation Tests
3. Modeling of Pervaporation
4. Results and Discussion
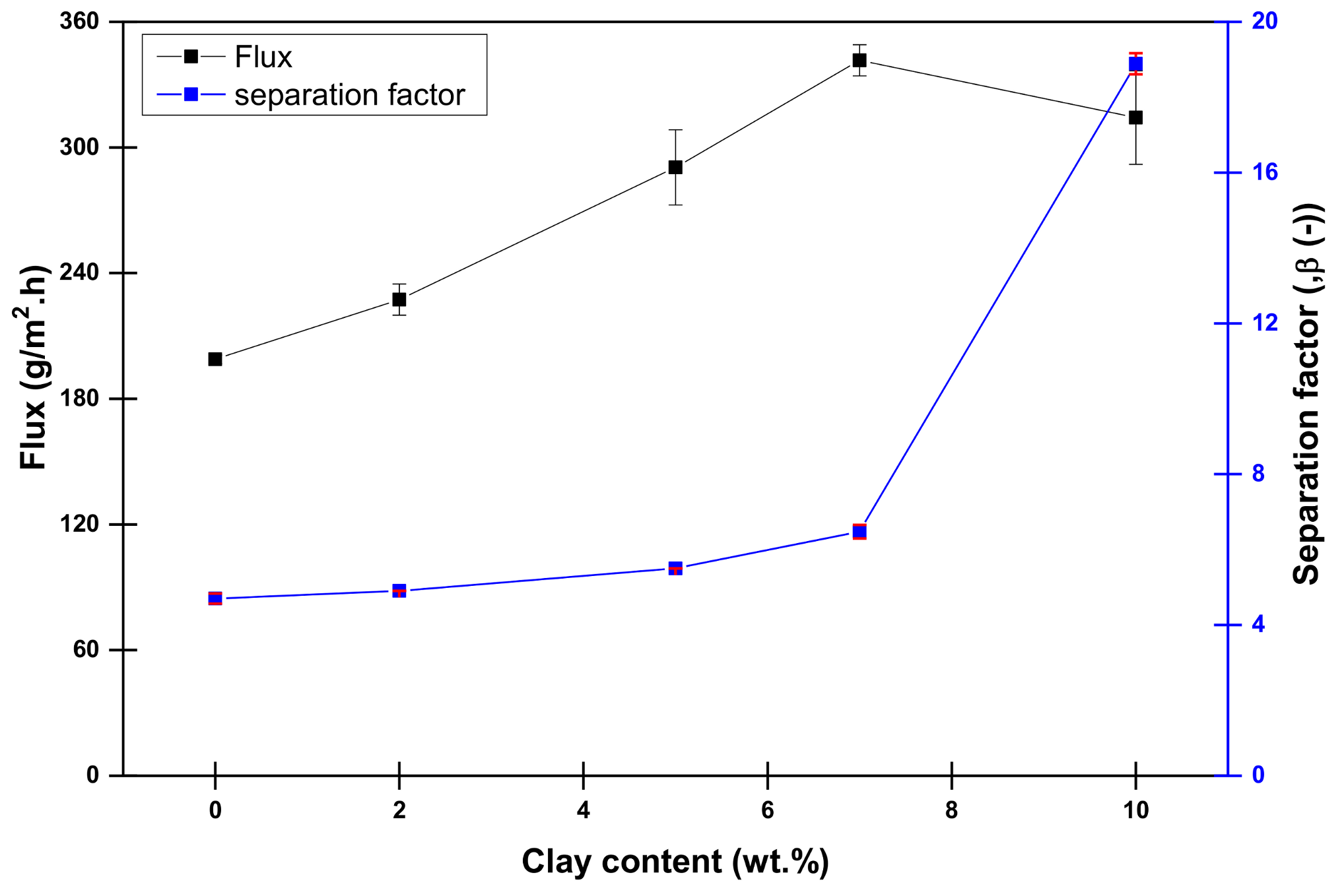
4.1. Influence of Laponite Content on the Dehydration of Methanol Aqueous Solution
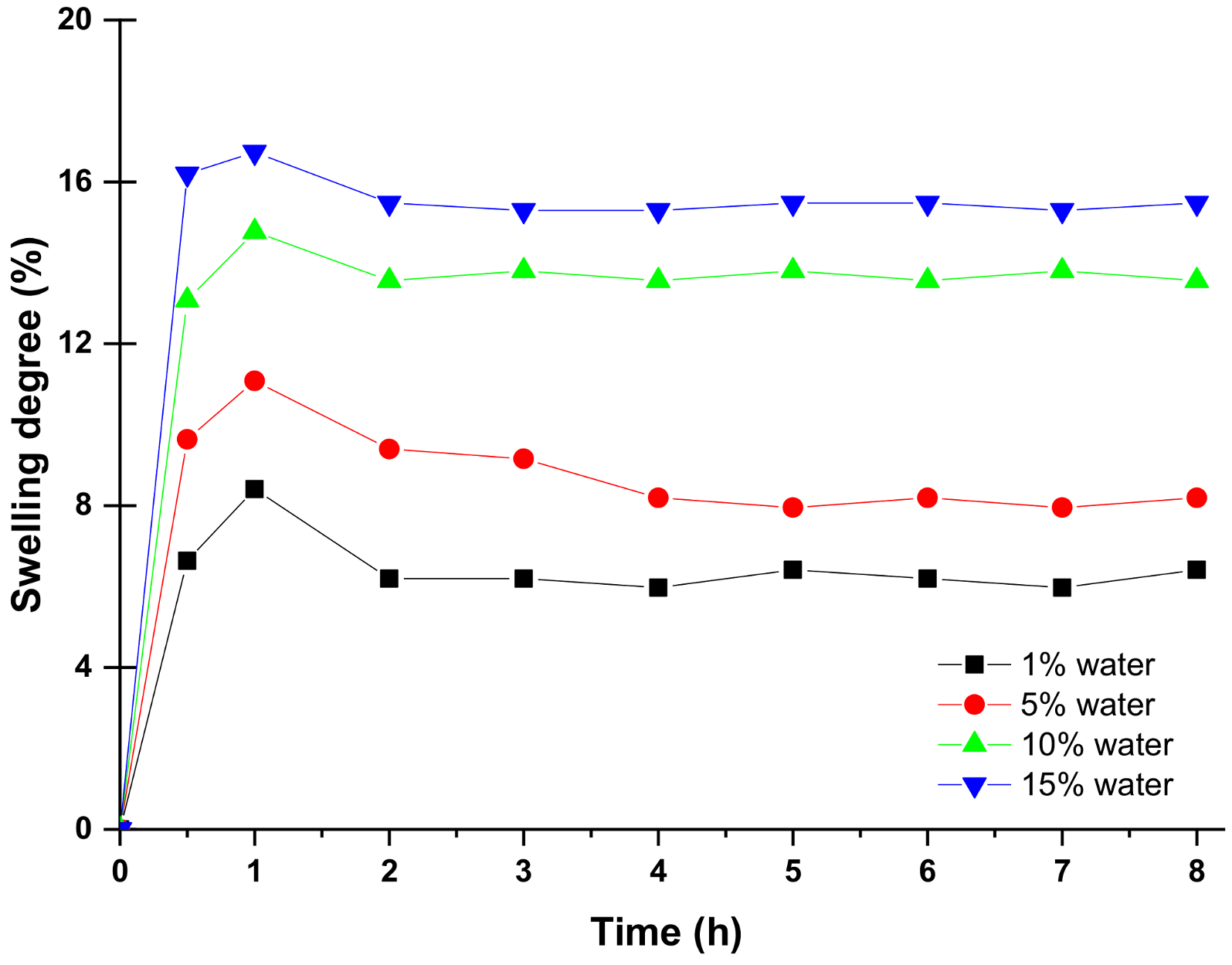
4.2. Swelling of PVA 10 Mixed Matrix Membranes in Methanol/Water Mixtures
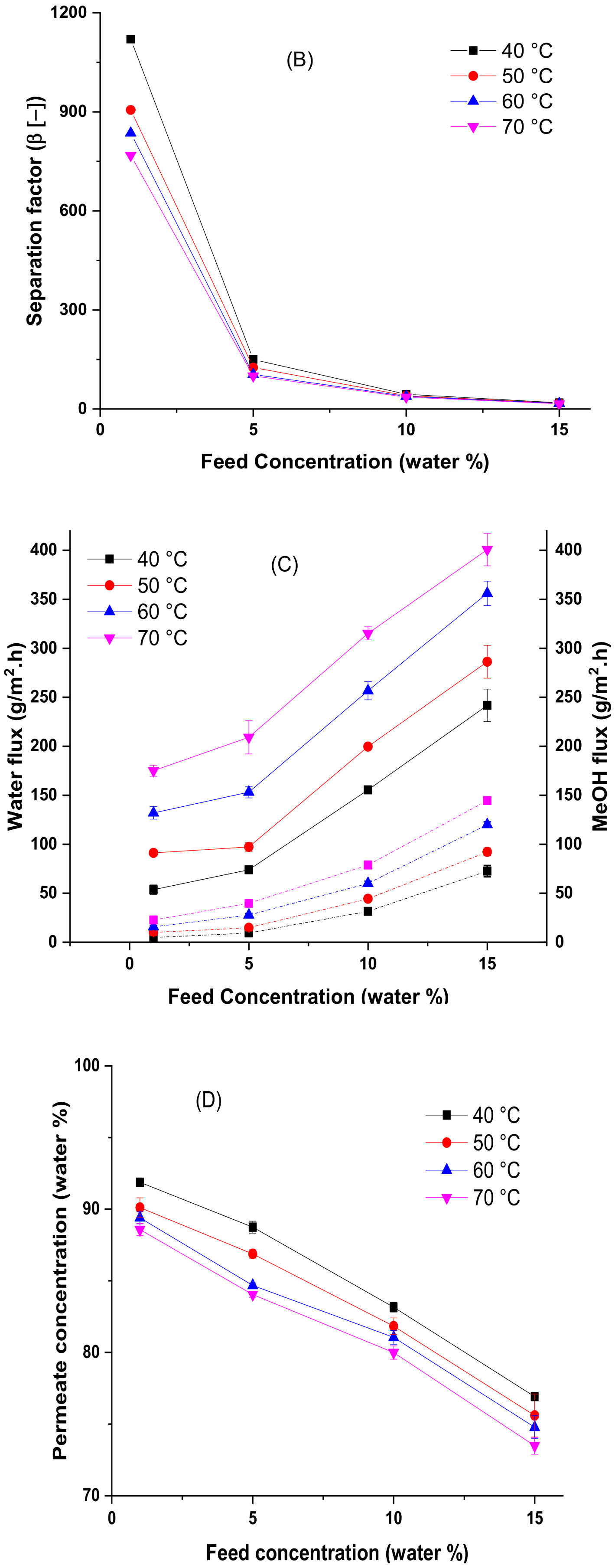
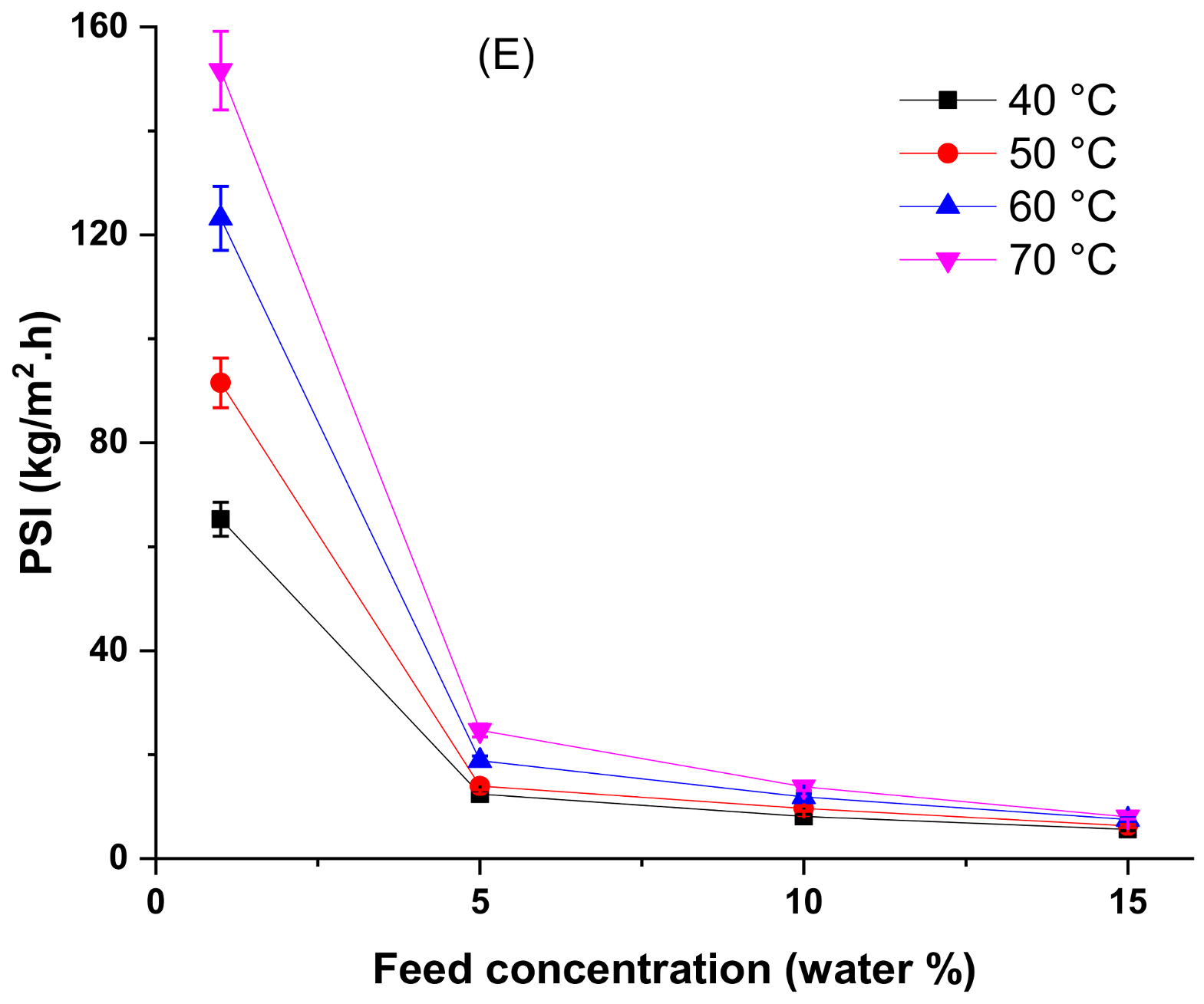
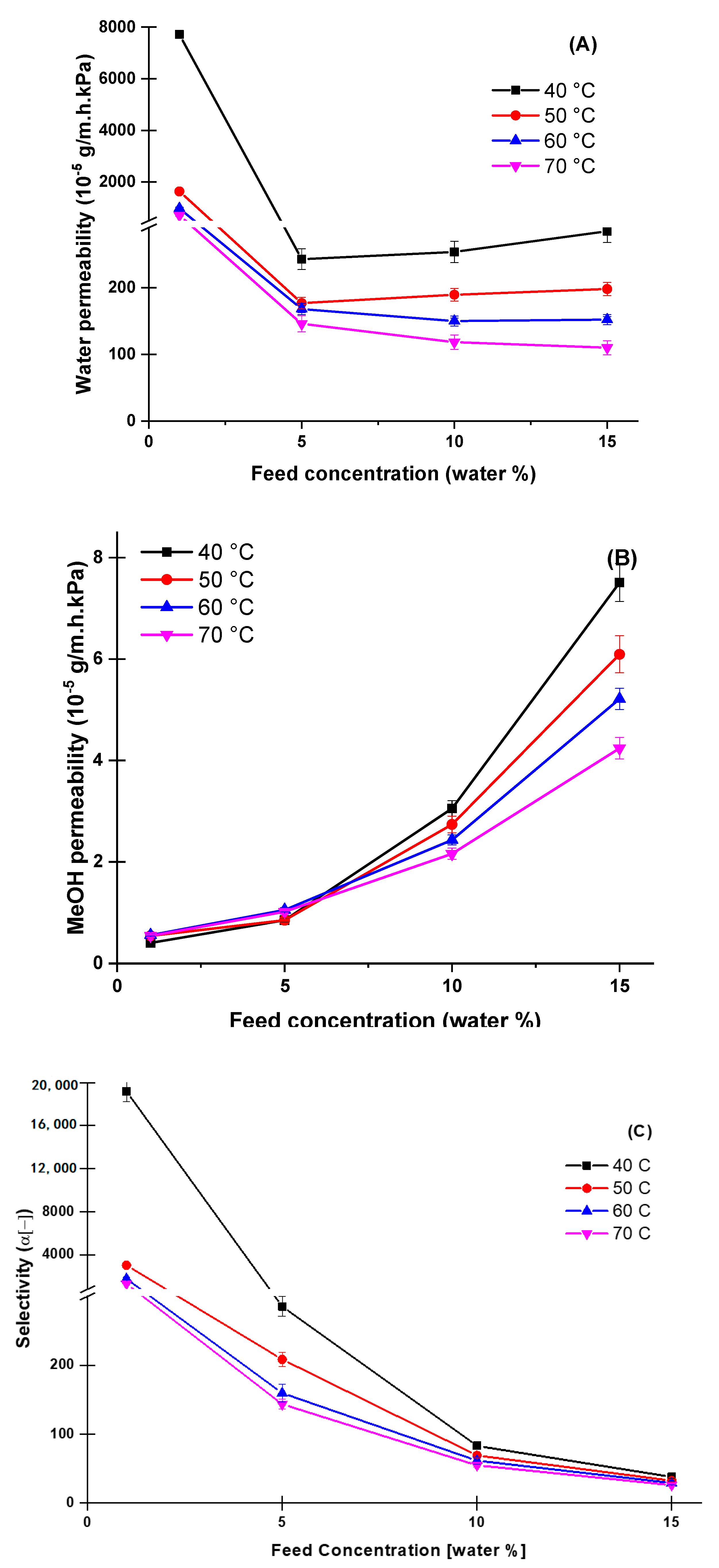
4.3. Effect of Temperature and Feed Concentration at the Pervaporation Performance
4.4. Comparison of Pervaporation Dehydration Performance of Aqueous Methanol Solutions
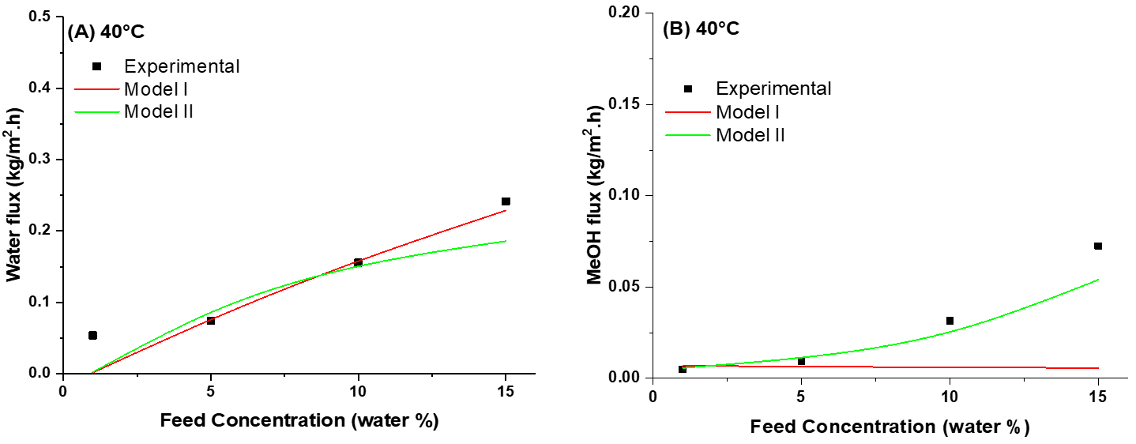
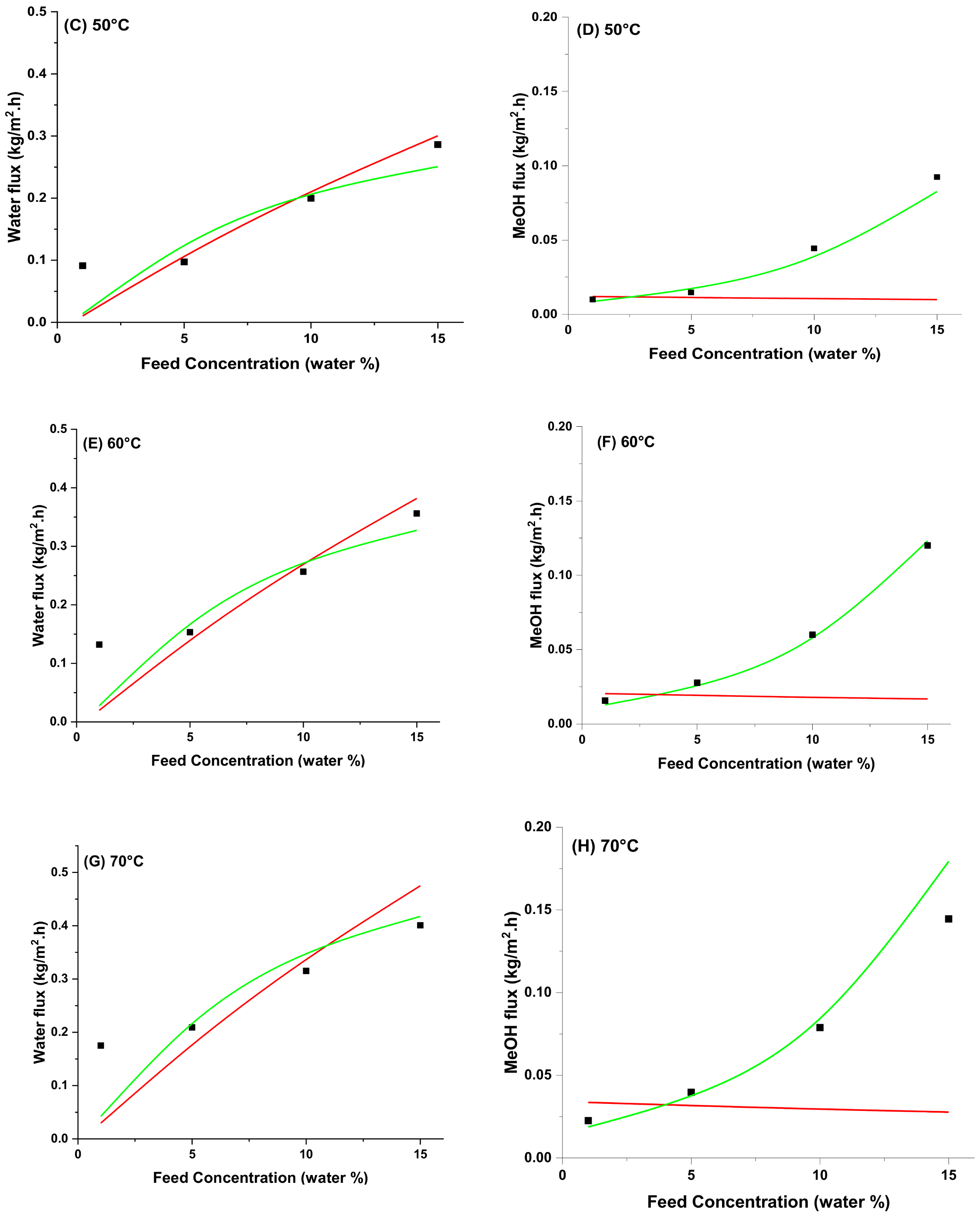
4.5. Modeling of Pervaporation Using PVA/Laponite Nanoclay MMM
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Membrane transfer area | |
| Constant in Model II | |
| Transport coefficient of component | |
| Relative transport coefficient of component | |
| Activation energy of component | |
| F | Feed |
| Component number | |
| Component number | |
| Total flux | |
| Partial flux | |
| Permeate | |
| Pure component vapour pressure | |
| Partial pressure of component on the liquid phase membrane side | |
| Partial pressure of component on the vapour phase membrane side | |
| Pressure on the permeate side | |
| Retentate | |
| Ʀ | Gas constant |
| Time | |
| Temperature | |
| Reference temperature: 293 | |
| Concentration of component in the feed |
Abbreviations
| OF | Objective function |
| PSI | Pervaporation Separation Index |
| PVA | Polyvinyl alcohol |
| PV | Pervaporation |
| Greek letters | |
| Selectivity | |
| Separation factor | |
| Average activity coefficient of component | |
| Activity coefficient of component in the feed | |
| Membrane thickness | |
References
- Toth, A.J.; Szanyi, A.; Koczka, K.; Mizsey, P. Enhanced separation of highly non-ideal mixtures with extractive heterogeneous-azeotropic distillation. Sep. Sci. Technol. 2016, 51, 1238–1247. [Google Scholar] [CrossRef]
- Toth, A.J.; Szanyi, A.; Haaz, E.; Mizsey, P. Separation of process wastewater with extractive heterogeneous-azeotropic distillation. Hung. J. Ind. Chem. 2016, 44, 29–32. [Google Scholar] [CrossRef]
- Shao, P.; Huang, R.Y.M. Polymeric membrane pervaporation. J. Membr. Sci. 2007, 287, 162–179. [Google Scholar] [CrossRef]
- Jonquières, A.; Clément, R.; Lochon, P.; Néel, J.; Dresch, M.; Chrétien, B. Industrial state-of-the-art of pervaporation and vapour permeation in the western countries. J. Membr. Sci. 2002, 206, 87–117. [Google Scholar] [CrossRef]
- Kanse, N.G.; Dawande, S.D. A Review of Pervaporation Membrane System for the Separation of Ethanol/Water (Azeotropic Mixture). Int. J. Eng. Sci. Res. Technol. 2015, 4, 472–479. [Google Scholar]
- Brüschke, H.E.A.; Wynn, N.P. Pervaporation. In Encyclopedia of Separation Science/Level II—Methods and Instrumentation/MEMBRANE SEPARATIONS; Membrane Technology and Research: Menlo Park, CA, USA, 2000. [Google Scholar]
- Abels, C.; Carstensen, F.; Wessling, M. Membrane processes in biorefinery applications. J. Membr. Sci. 2013, 444, 285–317. [Google Scholar] [CrossRef]
- Balat, M.; Balat, H. Recent trends in global production and utilization of bio-ethanol fuel. Appl. Energy 2009, 86, 2273–2282. [Google Scholar] [CrossRef]
- Suhas, D.P.; Aminabhavi, T.M.; Jeong, H.M.; Raghu, A.V. Hydrogen peroxide treated graphene as an effective nanosheet filler for separation application. RSC Adv. 2015, 5, 100984–100995. [Google Scholar] [CrossRef]
- Dharupaneedi, S.P.; Anjanapura, R.V.; Han, J.M.; Aminabhavi, T.M. Functionalized Graphene Sheets Embedded in Chitosan Nanocomposite Membranes for Ethanol and Isopropanol Dehydration via Pervaporation. Ind. Eng. Chem. Res. 2014, 53, 14474–14484. [Google Scholar] [CrossRef]
- Jiang, L.Y.; Wang, Y.; Chung, T.-S.; Qiao, X.Y.; Lai, J.-Y. Polyimides membranes for pervaporation and biofuels separation. Prog. Polym. Sci. 2009, 34, 1135–1160. [Google Scholar] [CrossRef]
- Feng, X.; Huang, R.Y.M. Liquid separation by membrane pervaporation. Ind. Eng. Chem. Res. 1997, 36, 1048–1066. [Google Scholar] [CrossRef]
- Vane, L.M. Separation technologies for recovery and dehydration of alcohols from fermentation broths. Biofuels Bioprod. Biorefin. 2008, 2, 553–588. [Google Scholar] [CrossRef]
- Toth, A.J.; Mizsey, P. Methanol removal from aqueous mixture with organophilic pervaporation: Experiments and modelling. Chem. Eng. Res. Des. 2015, 98, 123–135. [Google Scholar] [CrossRef]
- Selim, A.; Toth, A.J.; Fozer, D.; Haaz, E.; Valentínyi, N.; Nagy, T.; Keri, O.; Bakos, L.P.; Szilágyi, I.M.; Mizsey, P. Effect of silver-nanoparticles generated in poly (vinyl alcohol) membranes on ethanol dehydration via pervaporation. Chin. J. Chem. Eng. 2019, 27, 1595–1607. [Google Scholar] [CrossRef]
- Rautenbach, R.; Herion, C.; Meyer-Blumentoth, U. Pervaporation membrane separation processes. In Membrane Science and Technology Series; Elsevier: Amsterdam, The Netherlands, 1990; Volume 1, pp. 181–191. [Google Scholar]
- Le, N.L.; Wang, Y.; Chung, T.-S. Synthesis, cross-linking modifications of 6FDA-NDA/DABA polyimide membranes for ethanol dehydration via pervaporation. J. Membr. Sci. 2012, 415, 109–121. [Google Scholar] [CrossRef]
- Bolto, B.; Hoang, M.; Xie, Z. A review of membrane selection for the dehydration of aqueous ethanol by pervaporation. Chem. Eng. Process. 2011, 50, 227–235. [Google Scholar] [CrossRef]
- Bolto, B.; Tran, T.; Hoang, M.; Xie, Z. Crosslinked poly(vinyl alcohol) membranes. Prog. Polym. Sci. 2009, 24, 969–981. [Google Scholar] [CrossRef]
- Chapman, P.D.; Oliveira, T.; Livingston, A.G.; Li, K. Membranes for the dehydration of solvents by pervaporation. J. Membr. Sci. 2008, 318, 5–37. [Google Scholar] [CrossRef]
- Hua, D.; Ong, Y.K.; Wang, Y.; Yang, T.; Chung, T.-S. ZIF-90/P84 mixed matrix membranes for pervaporation dehydration of isopropanol. J. Membr. Sci. 2014, 453, 155–167. [Google Scholar] [CrossRef]
- Kulprathipanja, S.; Neuzil, R.W.; Li, N.N. Separation of Fluids by Means of Mixed Matrix Membranes. U.S. Patent No. 4,740,219, 26 April 1988. [Google Scholar]
- Castro-Muñoz, R.; Galiano, F.; Fíla, V.; Drioli, E.; Figoli, A. Mixed matrix membranes (MMMs) for ethanol purification through pervaporation: Current state of the art. Rev. Chem. Eng. 2018, 35, 565–590. [Google Scholar] [CrossRef]
- Jose, T.; George, S.C. Induced Hydrophilicity of the Nanoclay on the Pervaporation Performance of Crosslinked Poly (Vinyl Alcohol) Nanocomposite Membranes. Polym. Plast. Technol. Eng. 2016, 55, 1266–1281. [Google Scholar] [CrossRef]
- Adoor, S.G.; Sairam, M.; Manjeshwar, L.S.; Raju, K.V.S.N.; Aminabhavi, T.M. Sodium montmorillonite clay loaded novel mixed matrix membranes of poly(vinyl alcohol) for pervaporation dehydration of aqueous mixtures of isopropanol and 1,4-dioxane. J. Membr. Sci. 2006, 285, 182–195. [Google Scholar] [CrossRef]
- Ravindra, S.; Rajinikanth, V.; Mulaba-Bafubiandi, A.F.; Vallabhapurapu, V.S. Performance enhancement of the poly (vinyl alcohol) (PVA) by activated natural clay clinoptilolite for pervaporation separation of aqueous–organic mixtures. Desal. Water Treat. 2016, 57, 4920–4934. [Google Scholar] [CrossRef]
- Wassel, E.; Es-Souni, M.; Berger, N.; Schopf, D.; Dietze, M.; Solterbeck, C.-H.; Es-Souni, M. Nanocomposite Films of Laponite/PEG-Grafted Polymers and Polymer Brushes with Nonfouling Properties. Langmuir 2017, 33, 6739–6750. [Google Scholar] [CrossRef] [PubMed]
- Daniel, L.M.; Frost, R.L.; Zhu, H.Y. Edge-modification of laponite with dimethyl-octylmethoxysilane. J. Colloid Interface Sci. 2008, 321, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Morariu, S.; Bercea, M.; Brunchi, C.-E. Influence of Laponite RD on the properties of poly(vinyl alcohol) hydrogels. J. Appl. Polym. Sci. 2018, 135, 46661–46672. [Google Scholar] [CrossRef]
- Liu, W.; Yee, S.; Adanur, S. Properties of electrospun PVA/nanoclay composites. J. Text. Inst. 2013, 105, 423–429. [Google Scholar] [CrossRef]
- Golafshan, N.; Rezahasani, R.; Esfahani, M.T.; Kharaziha, M.; Khorasani, S.N. Nanohybrid hydrogels of laponite: PVA-Alginate as a potential wound healing material. Carbohydr. Polym. 2017, 176, 392–401. [Google Scholar] [CrossRef]
- Wang, S.; Zheng, F.; Huang, Y.; Fang, Y.; Shen, M.; Zhu, M.; Shi, X. Encapsulation of amoxicillin within laponite-doped poly (lactic-co-glycolic acid) nanofibers: Preparation, characterization, and antibacterial activity. ACS Appl. Mater. Interfaces 2012, 4, 6393–6401. [Google Scholar] [CrossRef]
- Perotti, G.F.; Barud, H.S.; Messaddeq, Y.; Ribeiro, S.J.L.; Constantino, V.R.L. Bacterial cellulose-laponite clay nanocomposites. Polymer 2011, 52, 157–163. [Google Scholar] [CrossRef]
- Hansen, C.M. Hansen Solubility Parameters: A User’s Handbook, 2nd ed.; Taylor & Francis Group: Boca Raton, FL, USA, 2007. [Google Scholar]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107. [Google Scholar] [CrossRef]
- Heintz, A.; Stephan, W. A generalized solution–diffusion model of the pervaporation process through composite membranes. Part I. Prediction of mixture solubilities in the dense active layer using the UNIQUAC model. J. Membr. Sci. 1994, 89, 143–151. [Google Scholar] [CrossRef]
- Lipnizki, F.; Hausmanns, S.; Ten, P.-K.; Field, R.W.; Laufenberg, G. Organophilic pervaporation: Prospects and performance. Chem. Eng. J 1997, 3, 113–129. [Google Scholar] [CrossRef]
- Schaetzel, P.; Vauclair, C.; Nguyen, Q.T.; Bouzerar, R. A simplified solution–diffusion theory in pervaporation: The total solvent volume fraction model. J. Membr. Sci. 2004, 244, 117–127. [Google Scholar] [CrossRef]
- Selim, A.; Valentínyi, N.; Mizsey, P. Influence of double-network interpenetration on ethanol dehydration performance of PVA-based pervaporation membranes. Chem. Pap. 2019, 73, 1069–1081. [Google Scholar] [CrossRef]
- Valentínyi, N.; Cséfalvay, E.; Mizsey, P. Modelling of pervaporation: Parameter estimation and model development. Chem. Eng. Res. Des. 2013, 91, 174–183. [Google Scholar] [CrossRef]
- Toth, A.J. Liquid Waste Treatment with Physicochemical Tools for Environmental Protection. Ph.D. Thesis, Budapest University of Technology and Economics, Budapest, Hungary, 2015. [Google Scholar]
- Ashraf, M.T.; Schmidt, J.E.; Kujawa, J.; Kujawski, W.; Arafat, H.A. One-dimensional modeling of pervaporation systems using a semi-empirical flux model. Sep. Purif. Technol. 2017, 174, 502–512. [Google Scholar] [CrossRef]
- Selim, A.; Toth, A.J.; Haaz, E.; Fozer, D.; Szanyi, A.; Hegyesi, N.; Mizsey, P. Preparation and characterization of PVA/GA/Laponite membranes to enhance pervaporation desalination performance. Sep. Purif. Technol. 2019, 221, 201–210. [Google Scholar] [CrossRef]
- Du, J.; Zhu, J.; Wu, R.; Xu, S.; Tan, Y.; Wang, J. A facile approach to prepare strong poly(acrylic acid)/LAPONITE® ionic nanocomposite hydrogels at high clay concentrations. RSC Adv. 2015, 5, 60152–60160. [Google Scholar] [CrossRef]
- Ueda, Y.; Tanaka, T.; Iizuka, A.; Sakai, Y.; Kojima, T.; Satokawa, S.; Yamasaki, A. Membrane Separation of Ethanol from Mixtures of Gasoline and Bioethanol with Heat-Treated PVA membranes. Ind. Eng. Chem. Res. 2011, 50, 1023–1027. [Google Scholar] [CrossRef]
- Hasimi, A.; Stavropoulou, A.; Papadokostaki, K.G.; Sanopoulou, M. Transport of water in polyvinyl alcohol films: Effect of thermal treatment and chemical cross-linking. Eur. Polym. J. 2008, 44, 4098–4107. [Google Scholar] [CrossRef]
- Liang, B.; Zhan, W.; Qi, G.; Lin, S.; Nan, Q.; Liu, Y.; Cao, B.; Pan, K. High performance graphene oxide/polyacrylonitrile composite pervaporation membranes for desalination applications. J. Mater. Chem. A 2015, 3, 5140–5147. [Google Scholar] [CrossRef]
- Tang, Y.; Widjojo, N.; Shi, G.M.; Chung, T.-S.; Weber, M.; Maletzko, C. Development of flat-sheet membranes for C1–C4 alcohols dehydration via pervaporation from sulfonated polyphenylsulfone(sPPSU). J. Membr. Sci. 2012, 415, 686–695. [Google Scholar] [CrossRef]
- Xu, Y.M.; Tang, Y.P.; Chung, T.-S.; Weber, M.; Maletzko, C. Polyarylether membranes for dehydration of ethanol and methanol via pervaporation. Sep. Purif. Technol. 2018, 193, 165–174. [Google Scholar] [CrossRef]
- Xu, Y.M.; Japip, S.; Chung, T.-S. Mixed matrix membranes with nano-sized functional UiO-66-type MOFs embedded in 6FDA-HAB/DABA polyimide for dehydration of C1-C3 alcohols via pervaporation. J. Membr. Sci. 2018, 549, 217–226. [Google Scholar] [CrossRef]
- Wang, Y.; HongGoh, S.; Chung, T.S.; Na, P. Polyamide-imide/polyetherimide dual-layer hollow fiber membranes for pervaporation dehydration of C1–C4 alcohols. J. Membr. Sci. 2009, 326, 222–233. [Google Scholar] [CrossRef]
- Bano, S.; Mahmood, A.; Lee, K.-H. Vapor permeation separation of methanol-water mixtures: Effect of experimental conditions. Ind. Eng. Chem. Res. 2013, 52, 10450–10459. [Google Scholar] [CrossRef]
- Baelen, D.V.; Bruggen, B.V.d.; Dungen, K.V.d.; Degreve, J.; Vandecasteele, C. Pervaporation of water/alcohol mixtures and acetic acid/ water mixtures. Chem. Eng. Sci. 2005, 60, 1583–1590. [Google Scholar] [CrossRef]
- Shelden, R.A.; Thompson, E.V. Dependence of diffusive permeation rates and selectivities on upstream and downstream pressures. IV. Computer simulation of non-ideal systems. J. Membr. Sci. 1984, 19, 39–49. [Google Scholar] [CrossRef]


| Solvent/Polymer | δd [MPa0.5] | δp [MPa0.5] | δh [MPa0.5] | δt [MPa0.5] |
|---|---|---|---|---|
| Methanol | 15.10 | 12.30 | 22.30 | 29.61 |
| Ethanol | 15.80 | 8.80 | 19.40 | 26.52 |
| IPA | 15.80 | 6.10 | 16.40 | 23.58 |
| Water | 15.50 | 16.00 | 42.40 | 47.90 |
| Membranes | T | Fwater | Jtotal | β | Reference |
|---|---|---|---|---|---|
| [°C] | [wt%] | [kg/m2·h] | [–] | ||
| 5% SPPSU | 60 | ~15 | 0.03 | 11.1 | [48] |
| PPSU | 60 | 15 | 0.05 | 28.7 | [49] |
| H-PESU | 60 | 15 | 0.06 | 31.3 | |
| PAI-PEI HOLLOW FIBER | 60 | 15 | 1.03 | 4.71 | [51] |
| SODIUM ALGINATE/PVA | 60 | 10 | 0.03 | 135 | [52] |
| SULZER PERVAP-2201 | 60 | 10 | 0.50 | 3 | [53] |
| POLYIMIDE/UIO66-NH2 (10%) | 60 | 15 | 0.17 | 13.22 | [50] |
| PVA10 | 60 | 10 | 0.32 | 38.52 | This study |
| 15 | 0.48 | 16.8 | |||
| 70 | 10 | 0.4 | 36 | ||
| 15 | 0.55 | 15.72 |
| Function | Model I | Model II | ||
|---|---|---|---|---|
| Water | MeOH | Water | MeOH | |
| D [kmol/m2·h] | 2.63 × 10−2 | 6.90 × 10−5 | 3.38 × 10−2 | 4.10 |
| Ev [KJ/Kmol] | 21,068.62 | 49,344.13 | 23,435.44 | 37,481.79 |
| B [-] | −2.18 | −11.06 | ||
| OF-Water | 3.24 | 3.04 | ||
| OF-MeOH | 6.01 | 0.39 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Selim, A.; Toth, A.J.; Fozer, D.; Szanyi, A.; Mizsey, P. Pervaporative Dehydration of Methanol Using PVA/Nanoclay Mixed Matrix Membranes: Experiments and Modeling. Membranes 2020, 10, 435. https://doi.org/10.3390/membranes10120435
Selim A, Toth AJ, Fozer D, Szanyi A, Mizsey P. Pervaporative Dehydration of Methanol Using PVA/Nanoclay Mixed Matrix Membranes: Experiments and Modeling. Membranes. 2020; 10(12):435. https://doi.org/10.3390/membranes10120435
Chicago/Turabian StyleSelim, Asmaa, András Jozsef Toth, Daniel Fozer, Agnes Szanyi, and Péter Mizsey. 2020. "Pervaporative Dehydration of Methanol Using PVA/Nanoclay Mixed Matrix Membranes: Experiments and Modeling" Membranes 10, no. 12: 435. https://doi.org/10.3390/membranes10120435
APA StyleSelim, A., Toth, A. J., Fozer, D., Szanyi, A., & Mizsey, P. (2020). Pervaporative Dehydration of Methanol Using PVA/Nanoclay Mixed Matrix Membranes: Experiments and Modeling. Membranes, 10(12), 435. https://doi.org/10.3390/membranes10120435