Discriminative Cut-Offs, Concurrent Criterion Validity, and Test–Retest Reliability of the Oxford Vaccine Hesitancy Scale
Abstract
1. Introduction
2. Methods
2.1. Samples
2.2. Measures
2.3. ROC Curves
2.4. Cut-Off Derivation Algorithms
2.5. Test–Retest Reliability
3. Results
3.1. Sample Population
3.2. ROC Curves and AUC Values
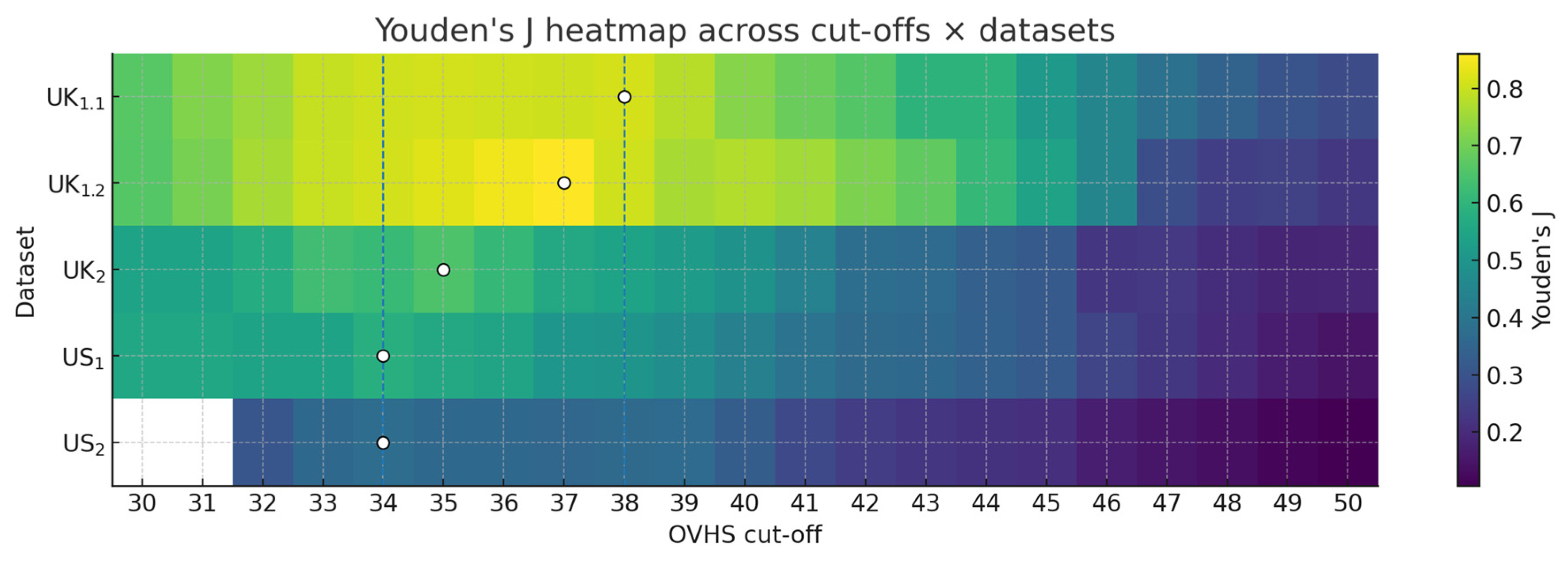
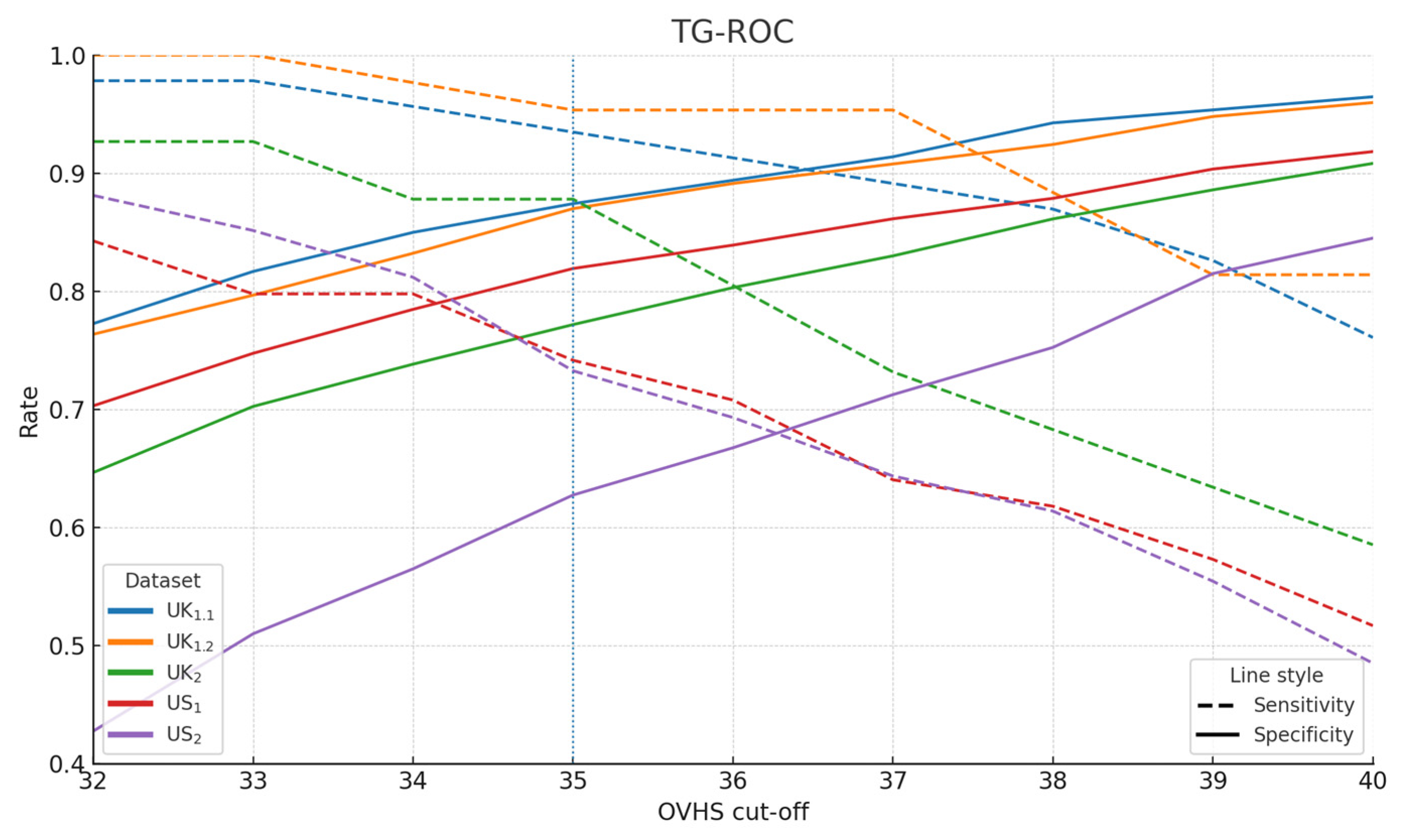
3.3. Cut-Off Derivation
3.4. Test–Retest Reliability
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shapiro, G.K.; Tatar, O.; Dube, E.; Amsel, R.; Knauper, B.; Naz, A.; Perez, S.; Rosberger, Z. The vaccine hesitancy scale: Psychometric properties and validation. Vaccine 2018, 36, 660–667. [Google Scholar] [CrossRef]
- Kantor, J.; Carlisle, R.C.; Morrison, M.; Pollard, A.J.; Vanderslott, S. Oxford Vaccine Hesitancy Scale (OVHS): A UK-based and US-based online mixed-methods psychometric development and validation study of an instrument to assess vaccine hesitancy. BMJ Open 2024, 14, e084669. [Google Scholar] [CrossRef]
- Opel, D.J.; Taylor, J.A.; Zhou, C.; Catz, S.; Myaing, M.; Mangione-Smith, R. The relationship between parent attitudes about childhood vaccines survey scores and future child immunization status: A validation study. JAMA Pediatr. 2013, 167, 1065–1071. [Google Scholar] [CrossRef]
- Martin, L.R.; Petrie, K.J. Understanding the Dimensions of Anti-Vaccination Attitudes: The Vaccination Attitudes Examination (VAX) Scale. Ann. Behav. Med. 2017, 51, 652–660. [Google Scholar] [CrossRef]
- Betsch, C.; Schmid, P.; Heinemeier, D.; Korn, L.; Holtmann, C.; Böhm, R. Beyond confidence: Development of a measure assessing the 5C psychological antecedents of vaccination. PLoS ONE 2018, 13, e0208601. [Google Scholar] [CrossRef]
- Ghazy, R.M.; ElHafeez, S.A.; Shaaban, R.; Elbarazi, I.; Abdou, M.S.; Ramadan, A.; Kheirallah, K.A. Determining the Cutoff Points of the 5C Scale for Assessment of COVID-19 Vaccines Psychological Antecedents among the Arab Population: A Multinational Study. J. Prim. Care Community Health 2021, 12, 21501327211018568. [Google Scholar] [CrossRef]
- Machida, M.; Takamiya, T.; Odagiri, Y.; Fukushima, N.; Kikuchi, H.; Inoue, S. Estimation of cutoff score for the 7C of vaccination readiness scale. Vaccine X 2023, 15, 100394. [Google Scholar] [CrossRef] [PubMed]
- Masters, N.B.; Tefera, Y.A.; Wagner, A.L.; Boulton, M.L. Vaccine hesitancy among caregivers and association with childhood vaccination timeliness in Addis Ababa, Ethiopia. Hum. Vaccines Immunother. 2018, 14, 2340–2347. [Google Scholar] [CrossRef]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [CrossRef] [PubMed]
- Hassanzad, M.; Hajian-Tilaki, K. Methods of determining optimal cut-point of diagnostic biomarkers with application of clinical data in ROC analysis: An update review. BMC Med. Res. Methodol. 2024, 24, 84. [Google Scholar] [CrossRef]
- Ghazy, R.M.; Elkhadry, S.W.; Abdel-Rahman, S.; Taha, S.H.N.; Youssef, N.; Elshabrawy, A.; Ibrahim, S.A.; Al Awaidy, S.; Al-Ahdal, T.; Padhi, B.K.; et al. External validation of the parental attitude about childhood vaccination scale. Front. Public Health 2023, 11, 1146792. [Google Scholar] [CrossRef]
- Bussink-Voorend, D.; Hautvast, J.L.A.; Wiersma, T.; Akkermans, R.; Hulscher, M. Developing a practical tool for measuring parental vaccine hesitancy: A people-centered validation approach in Dutch. Hum. Vaccin Immunother. 2025, 21, 2466303. [Google Scholar] [CrossRef] [PubMed]
- Terwee, C.B.; Bot, S.D.M.; de Boer, M.R.; van der Windt, D.A.W.M.; Knol, D.L.; Dekker, J.; Bouter, L.M.; de Vet, H.C.W. Quality criteria were proposed for measurement properties of health status questionnaires. J. Clin. Epidemiol. 2007, 60, 34–42. [Google Scholar] [CrossRef]
- Opel, D.J.; Robinson, J.D.; Heritage, J.; Korfiatis, C.; Taylor, J.A.; Mangione-Smith, R. Characterizing providers’ immunization communication practices during health supervision visits with vaccine-hesitant parents: A pilot study. Vaccine 2012, 30, 1269–1275. [Google Scholar] [CrossRef]
- Opel, D.J.; Taylor, J.A.; Mangione-Smith, R.; Solomon, C.; Zhao, C.; Catz, S.; Martin, D. Validity and reliability of a survey to identify vaccine-hesitant parents. Vaccine 2011, 29, 6598–6605. [Google Scholar] [CrossRef]
- Abd Halim, H.; Abdul-Razak, S.; Md Yasin, M.; Isa, M.R. Validation study of the Parent Attitudes About Childhood Vaccines (PACV) questionnaire: The Malay version. Hum. Vaccin Immunother. 2020, 16, 1040–1049. [Google Scholar] [CrossRef] [PubMed]
- Mutlu, M.; Cayir, Y.; Kasali, K. Validity and reliability of the Turkish version of the Parent Attitudes About Childhood Vaccines (PACV) scale. J. Healthc. Qual. Res. 2023, 38, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Eisenblaetter, M.; Madiouni, C.; Laraki, Y.; Capdevielle, D.; Raffard, S. Adaptation and Validation of a French Version of the Vaccination Attitudes Examination (VAX) Scale. Vaccines 2023, 11, 1001. [Google Scholar] [CrossRef]
- Wilhelm, M.; Bender, F.L.; Euteneuer, F.; Salzmann, S.; Ewen, A.-C.I.; Rief, W. Psychometric validation of the Vaccination Attitudes Examination (VAX) scale in German pre-pandemic and mid-pandemic samples. Sci. Rep. 2024, 14, 30543. [Google Scholar] [CrossRef]
- Duplaga, M.; Zwierczyk, U.; Kowalska-Duplaga, K. The Assessment of the Reliability and Validity of the Polish Version of the Adult Vaccine Hesitancy Scale (PL-aVHS) in the Context of Attitudes toward COVID-19 Vaccination. Vaccines 2022, 10, 1666. [Google Scholar] [CrossRef] [PubMed]
- Karabulut, N.; Gurcayir, D.; Yaman Aktas, Y.; Abi, O. The Turkish version of the Oxford Covid-19 Vaccine Hesitancy Scale. Cent. Eur. J. Nurs. Midwifery 2022, 13, 691–698. [Google Scholar] [CrossRef]
- Bae, S.; Kim, H. The Reliability and Validity of the Korean Version of the 5C Psychological Antecedents of Vaccination Scale. J. Korean Acad. Nurs. 2023, 53, 324–339. [Google Scholar] [CrossRef]
- Shapiro, G.K.; Kaufman, J.; Brewer, N.T.; Wiley, K.; Menning, L.; Leask, J.; Abad, N.; Betsch, C.; Bura, V.; Correa, G.; et al. A critical review of measures of childhood vaccine confidence. Curr. Opin. Immunol. 2021, 71, 34–45. [Google Scholar] [CrossRef]
- Kantor, J.; Vanderslott, S.; Morrison, M.; Pollard, A.J.; Carlisle, R.C. The Oxford Needle Experience (ONE) scale: A UK-based and US-based online mixed-methods psychometric development and validation study of an instrument to assess needle fear, attitudes and expectations in the general public. BMJ Open 2023, 13, e074466. [Google Scholar] [CrossRef]
- Kantor, B.N.; Kantor, J. Development and validation of the Oxford Pandemic Attitude Scale-COVID-19 (OPAS-C): An internet-based cross-sectional study in the UK and USA. BMJ Open 2021, 11, e043758. [Google Scholar] [CrossRef]
- Kantor, J.; Carlisle, R.C.; Vanderslott, S.; Pollard, A.J.; Morrison, M. Development and validation of the Oxford Benchmark Scale for Rating Vaccine Technologies (OBSRVT), a scale for assessing public attitudes to next-generation vaccine delivery technologies. Hum. Vaccines Immunother. 2025, 21, 2469994. [Google Scholar] [CrossRef]
- Kantor, J.; Aasi, S.Z.; Alam, M.; Paoli, J.; Ratner, D. Development and Validation of the Oxford Skin Cancer Treatment Scale, a Patient-Reported Outcome Measure for Health-Related Quality of Life and Treatment Satisfaction After Skin Cancer Treatment. Dermatol. Surg 2024, 50, 991–996. [Google Scholar] [CrossRef]
- Schisterman, E.F.; Perkins, N.J.; Liu, A.; Bondell, H. Optimal Cut-Point and Its Corresponding Youden Index to Discriminate Individuals Using Pooled Blood Samples. Epidemiology 2005, 16, 73–81. [Google Scholar] [CrossRef]
- Fluss, R.; Faraggi, D.; Reiser, B. Estimation of the Youden Index and its Associated Cutoff Point. Biom. J 2005, 47, 458–472. [Google Scholar] [CrossRef] [PubMed]
- Perkins, N.J.; Schisterman, E.F. The Inconsistency of “Optimal” Cutpoints Obtained using Two Criteria based on the Receiver Operating Characteristic Curve. Am. J. Epidemiol. 2006, 163, 670–675. [Google Scholar] [CrossRef] [PubMed]
- Bunce, C. Correlation, Agreement, and Bland–Altman Analysis: Statistical Analysis of Method Comparison Studies. Am. J. Ophthalmol. 2009, 148, 4–6. [Google Scholar] [CrossRef]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Silveira, P.S.P.; Rocha, F.T.; Vieira, J.E.; Siqueira, J.O. From blue November to broader diagnosis: The Youden index to evaluate the performance of any diagnostic tests. Clinics 2025, 80, 100804. [Google Scholar] [CrossRef]
- Ünal, İ.; Ünal, E.; Sertdemir, Y.; Kobaner, M. Defining optimal cut-off points for multiple class ROC analysis: Generalization of the Index of Union method. J. Biopharm. Stat. 2025, 1–19. [Google Scholar] [CrossRef]
- Greiner, M. Two-graph receiver operating characteristic (TG-ROC): Update version supports optimisation of cut-off values that minimise overall misclassification costs. J. Immunol. Methods 1996, 191, 93–94. [Google Scholar] [CrossRef] [PubMed]
- Kantor, J.; Morrison, M.; Vanderslott, S.; Pollard, A.J.; Carlisle, R.C. Public attitudes towards intranasal and ultrasound mediated vaccine delivery: A cross-sectional study in the United Kingdom and United States. Vaccine 2025, 69, 127950. [Google Scholar] [CrossRef] [PubMed]
- Shrout, P.E.; Fleiss, J.L. Intraclass correlations: Uses in assessing rater reliability. Psychol. Bull. 1979, 86, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Liljequist, D.; Elfving, B.; Skavberg Roaldsen, K. Intraclass correlation-A discussion and demonstration of basic features. PLoS ONE 2019, 14, e0219854. [Google Scholar] [CrossRef]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef]
- de Vet, H.C.W.; Mokkink, L.B.; Mosmuller, D.G.; Terwee, C.B. Spearman-Brown prophecy formula and Cronbach’s alpha: Different faces of reliability and opportunities for new applications. J. Clin. Epidemiol. 2017, 85, 45–49. [Google Scholar] [CrossRef] [PubMed]
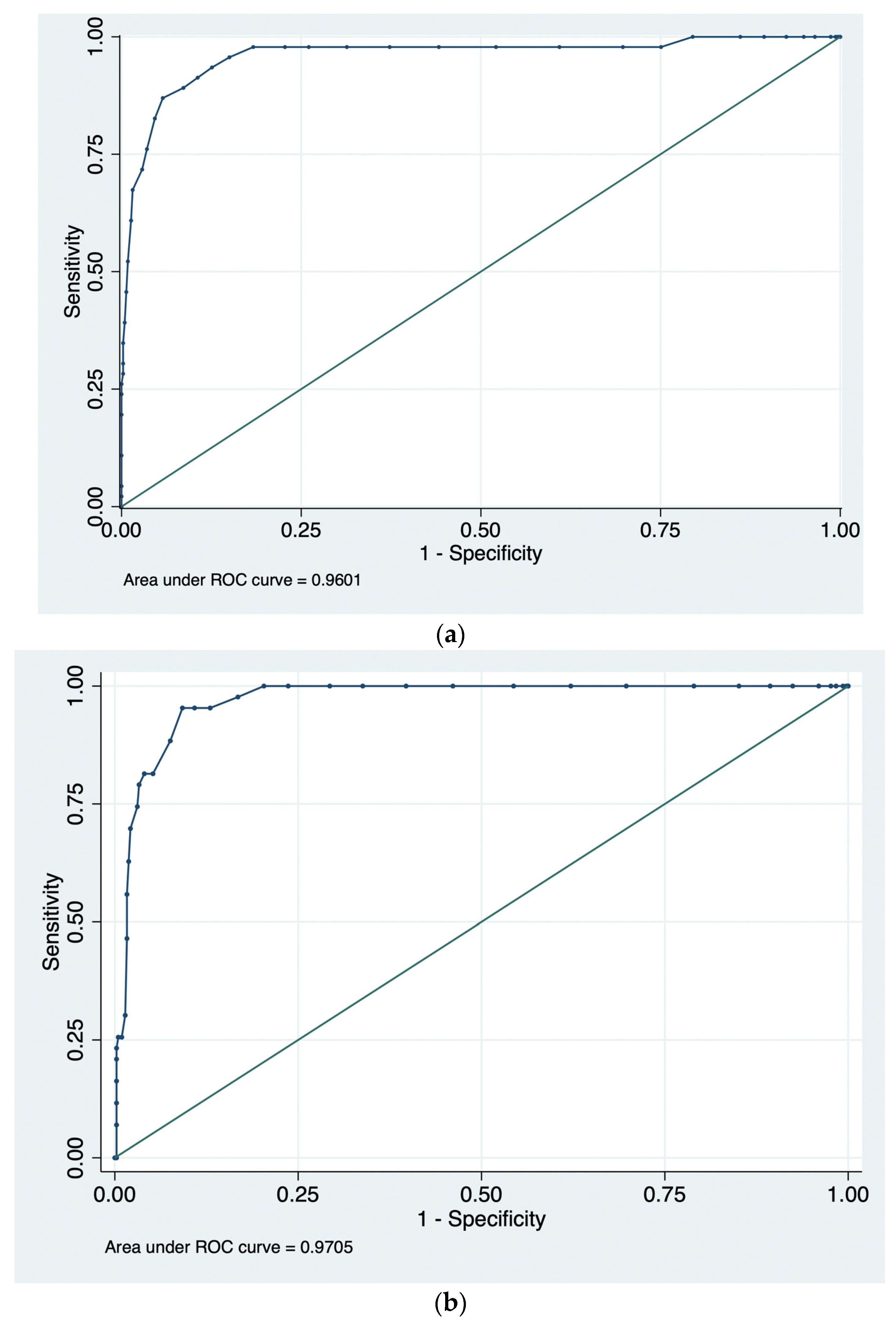
| Sample | n | AUC | 95% CI (BCa) | 95% CI (Percentile) |
|---|---|---|---|---|
| UK1.1 | 504 | 0.960 | 0.890–0.981 | 0.920–0.986 |
| UK1.2 | 462 | 0.971 | 0.951–0.983 | 0.954–0.984 |
| UK2 | 491 | 0.891 | 0.844–0.926 | 0.848–0.929 |
| US1 | 500 | 0.851 | 0.799–0.891 | 0.803–0.894 |
| US2 | 500 | 0.760 | 0.704–0.807 | 0.706–0.809 |
| Metric | UK1.1 | UK1.2 | UK2 | US1 | US2 |
|---|---|---|---|---|---|
| Prevalence | 0.092 | 0.092 | 0.084 | 0.181 | 0.202 |
| Sensitivity | 0.935 | 0.954 | 0.878 | 0.742 | 0.733 |
| Specificity | 0.874 | 0.870 | 0.772 | 0.819 | 0.628 |
| Youden J | 0.809 | 0.824 | 0.650 | 0.561 | 0.360 |
| Balanced accuracy | 0.905 | 0.912 | 0.825 | 0.780 | 0.680 |
| LR + | 7.400 | 7.333 | 3.848 | 4.104 | 1.967 |
| LR − | 0.075 | 0.054 | 0.158 | 0.315 | 0.426 |
| PPV | 0.430 | 0.427 | 0.261 | 0.475 | 0.332 |
| NPV | 0.993 | 0.995 | 0.986 | 0.935 | 0.903 |
| Metric | UK1.1 | UK1.2 | UK2 | US1 | US2 |
|---|---|---|---|---|---|
| Optimal OVHS Cut-off (≥) | 38 | 37 | 35 | 34 | 34 |
| Prevalence | 0.092 | 0.092 | 0.084 | 0.181 | 0.202 |
| Sensitivity | 0.870 | 0.954 | 0.878 | 0.798 | 0.812 |
| Specificity | 0.943 | 0.908 | 0.772 | 0.785 | 0.565 |
| Youden J | 0.812 | 0.861 | 0.650 | 0.583 | 0.377 |
| ΔJ to ≥35 | 0.003 | 0.038 | 0.000 | 0.022 | 0.017 |
| Balanced accuracy | 0.906 | 0.931 | 0.825 | 0.791 | 0.689 |
| LR + | 15.150 | 10.342 | 3.851 | 3.706 | 1.866 |
| LR − | 0.138 | 0.051 | 0.158 | 0.258 | 0.333 |
| PPV | 0.606 | 0.513 | 0.261 | 0.449 | 0.320 |
| NPV | 0.986 | 0.995 | 0.986 | 0.946 | 0.923 |
| Scale | ICC | 95% CI | |
|---|---|---|---|
| OVHS overall (13 items) | Single measure | 0.884 | 0.863–0.903 |
| Average measure | 0.939 | 0.926–0.949 | |
| Beliefs (7 items) | Single measure | 0.901 | 0.882–0.916 |
| Average measure | 0.948 | 0.937–0.956 | |
| Deliberation (3 items) | Single measure | 0.649 | 0.593–0.699 |
| Average measure | 0.787 | 0.745–0.823 | |
| Pain (3 items) | Single measure | 0.677 | 0.624–0.724 |
| Average measure | 0.807 | 0.768–0.840 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kantor, J.; Vanderslott, S.; Morrison, M.; Carlisle, R.C. Discriminative Cut-Offs, Concurrent Criterion Validity, and Test–Retest Reliability of the Oxford Vaccine Hesitancy Scale. Vaccines 2025, 13, 1200. https://doi.org/10.3390/vaccines13121200
Kantor J, Vanderslott S, Morrison M, Carlisle RC. Discriminative Cut-Offs, Concurrent Criterion Validity, and Test–Retest Reliability of the Oxford Vaccine Hesitancy Scale. Vaccines. 2025; 13(12):1200. https://doi.org/10.3390/vaccines13121200
Chicago/Turabian StyleKantor, Jonathan, Samantha Vanderslott, Michael Morrison, and Robert C. Carlisle. 2025. "Discriminative Cut-Offs, Concurrent Criterion Validity, and Test–Retest Reliability of the Oxford Vaccine Hesitancy Scale" Vaccines 13, no. 12: 1200. https://doi.org/10.3390/vaccines13121200
APA StyleKantor, J., Vanderslott, S., Morrison, M., & Carlisle, R. C. (2025). Discriminative Cut-Offs, Concurrent Criterion Validity, and Test–Retest Reliability of the Oxford Vaccine Hesitancy Scale. Vaccines, 13(12), 1200. https://doi.org/10.3390/vaccines13121200





