Modelling of the Innate and Adaptive Immune Response to SARS Viral Infection, Cytokine Storm and Vaccination
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Model of Innate Immune Response
Innate Immune Response Model Reduction for the Study of Stationary Solutions
2.2. Mathematical Model of Innate and Adaptive Immune Response
2.3. Mathematical Model of Cytokine Storm
Model Reduction for the Study of Stationary Solutions
2.4. Vaccination Model
2.5. Parameter Indentification
3. Results
3.1. Innate Immune Response
3.1.1. Stationary Solutions and Dynamical Behaviour
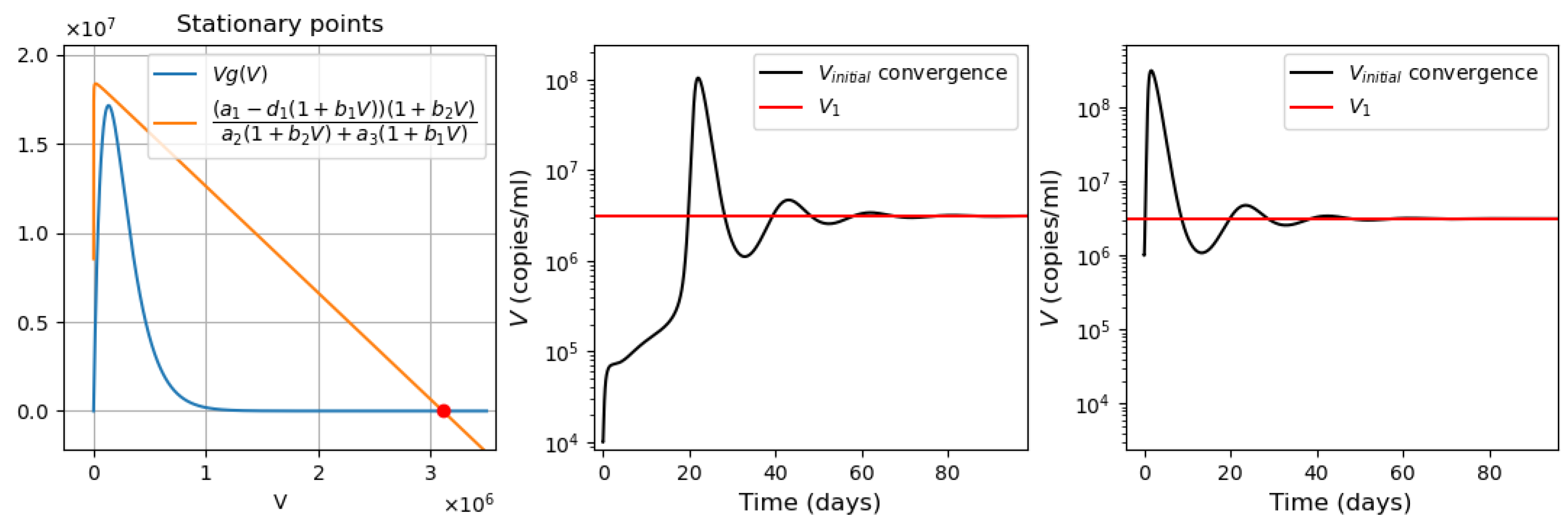
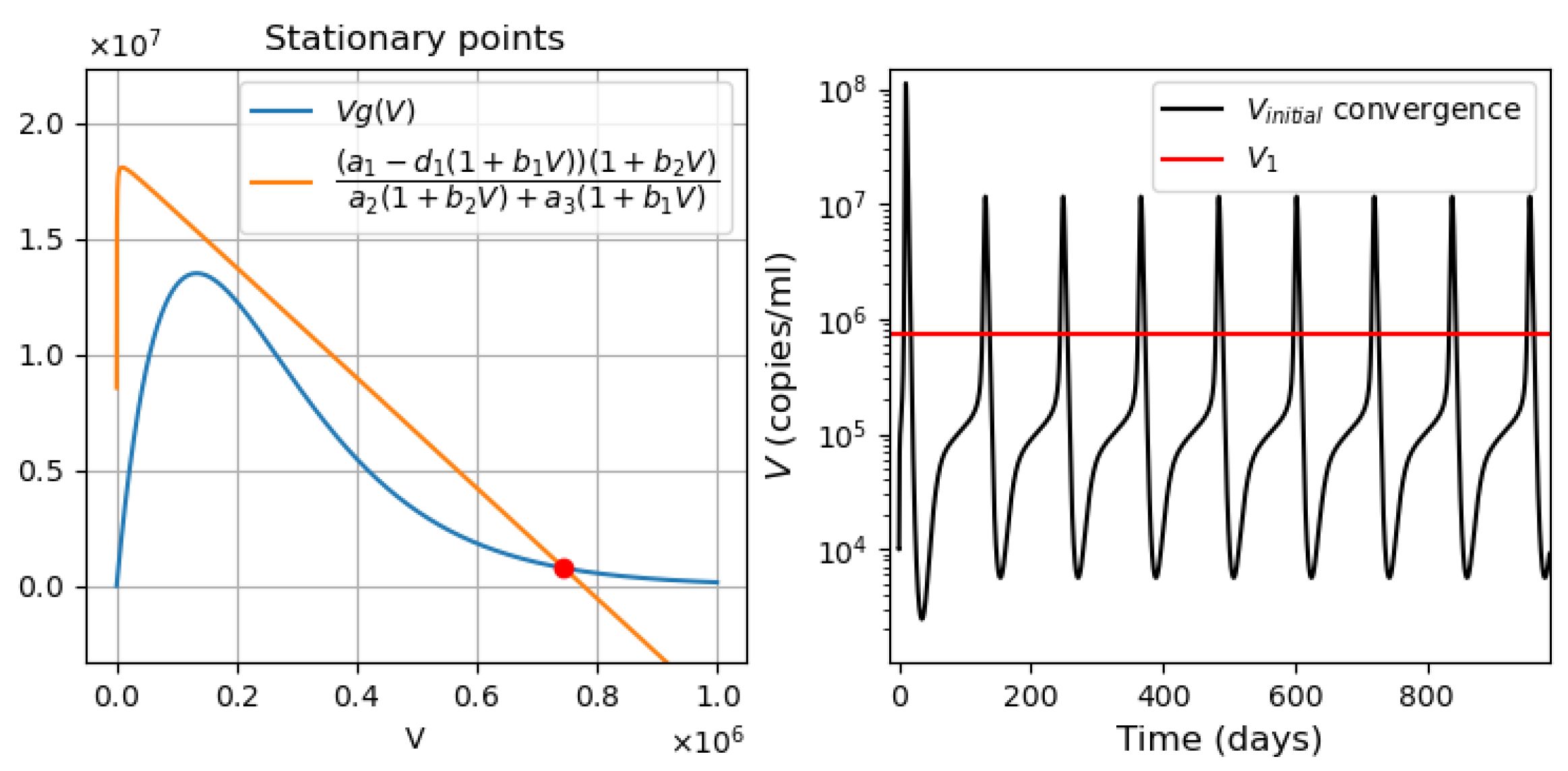
- Virus bi-stability. Applying the estimated values from Appendix A Table A1 in Equation (9), we determine the presence of three positive stationary points. This corresponds to the case of system bistability, where the first and third stationary points are stable. The virus concentration is essentially larger in the second point compared with the first one. The system bistability implies different dynamics depending on the initial viral loads (Figure 1).
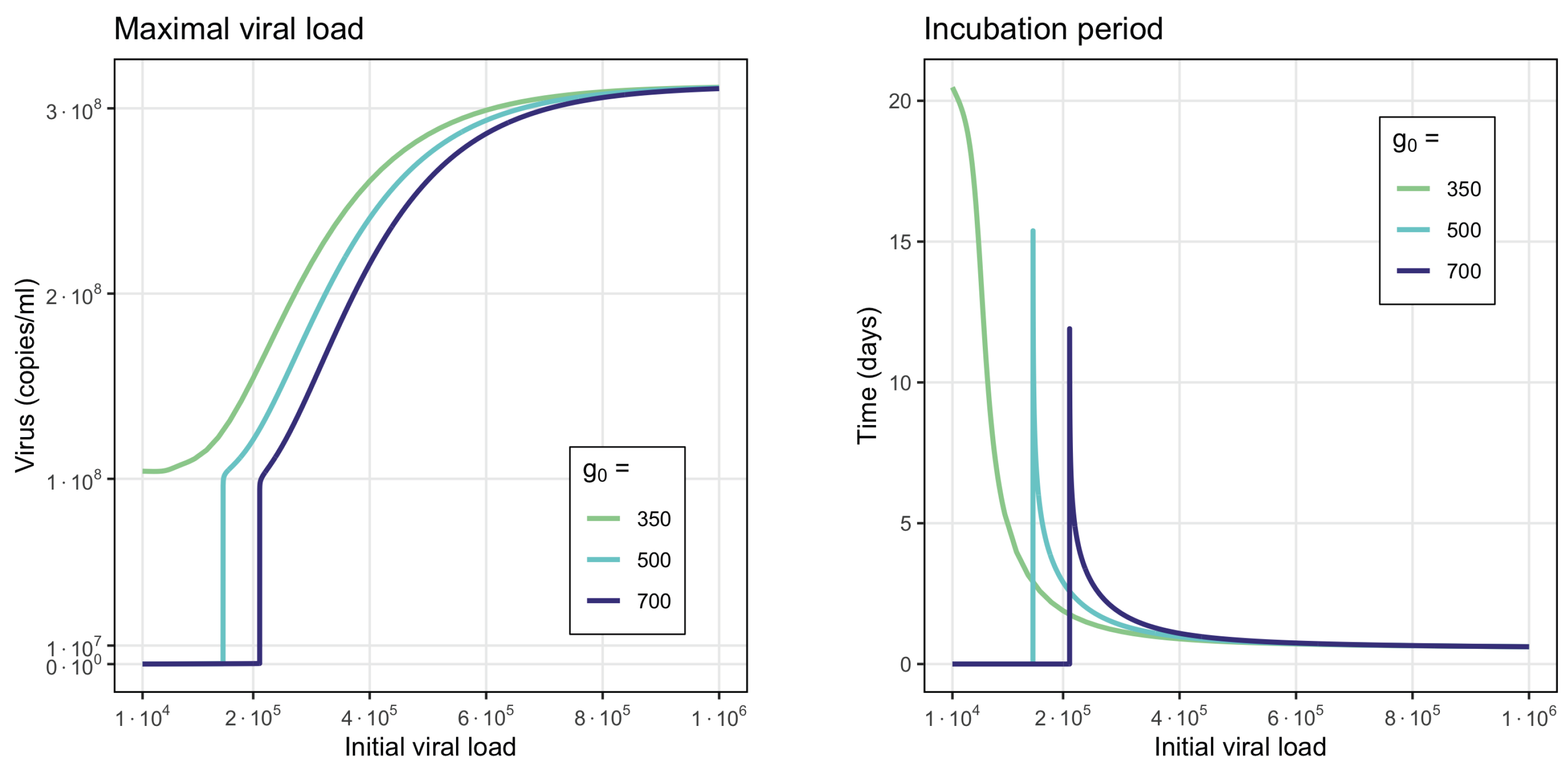
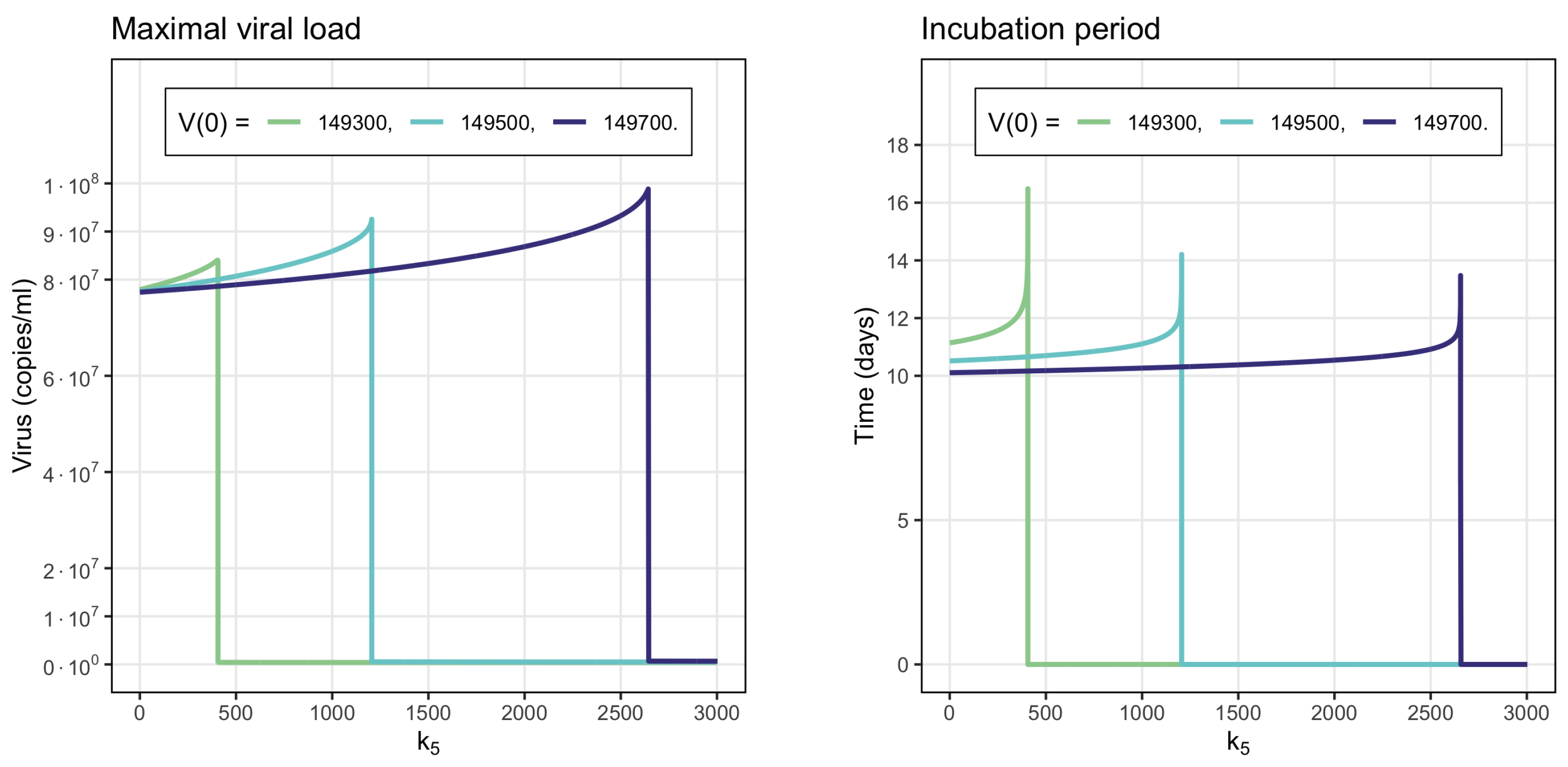
- Virus monostability with a large stability value. The case with a single stable point and large virus concentration is realized for a sufficiently small interferon production rate (, here and further, the dimensions of the parameters are indicated in Table A1, Table A2, Table A3 and Table A4 in Appendix A) or for a small virus clearance rate (). Decreasing the value of increases the stationary virus concentration. As might be expected, the increase in interferon clearance rate () or in turn the increase in the virus production rate () also lead the system to this type of stability. Characteristic of this stability case is the appearance of a large virus peak with either a low or high initial viral load. For higher initial viral load, the peak is larger, and it is reached faster (Figure 2).
- Virus monostability with a small stability value. For a small virus production rate ( or ), the system becomes monostable with a small stability value. Low virus influence on interferon production () or high interferon influence on virus production () can also induce this effect.
- Periodic oscillations. If we decrease at the same time the values of and , the system manifests periodic dynamics. As can be seen in Figure 3, the position of the stationary point coincides with that of Figure 2, which corresponds to monostability. However, because the value of the stationary point is not large enough, the kinetics of the system becomes characterized by a periodic behavior. The simulations in this case lead us to deduce that the period of oscillations decreases for smaller interferon production rate .
3.1.2. Infection Dynamics with the Innate Immune Response
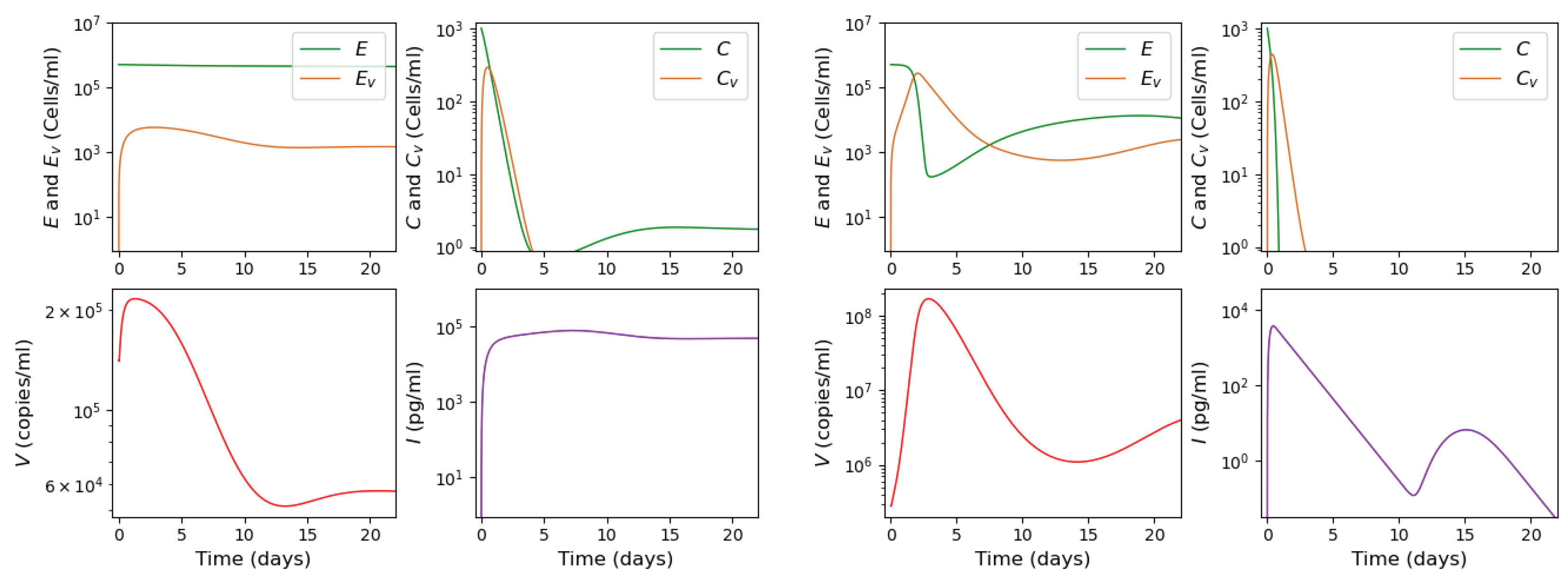
3.2. Innate and Adaptive Immune Response
3.3. Cytokine Storm
3.3.1. Stationary solutions
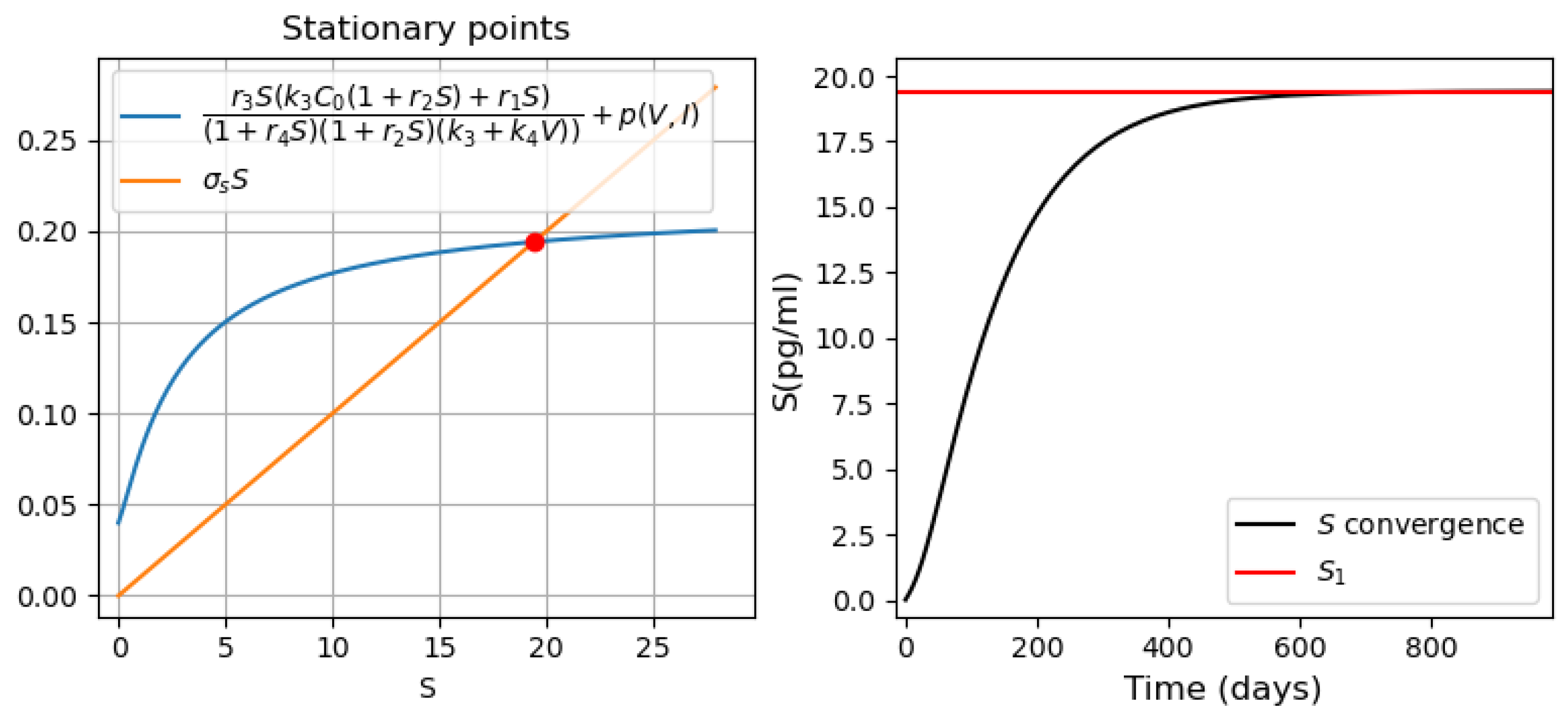
- Three stationary points (Figure 9a). The convergence of the solution to the first or third stationary points depends on the initial value of . If the initial condition is less than the value of the second stationary point (green line ), then the solution converges to the first stationary point . For all other initial conditions, the solution converges to the third stationary point (Figure 9d).
3.3.2. Different Regimes of Inflammatory Response
- Monostability of the system with pro-inflammatory cytokines. For the parameter values used in Figure 10 (on the left), there is a single positive stationary point. The solution of Equation (28) corresponding to pro-inflammatory cytokines converges to this stationary value (Figure 10, right). The choice of the initial viral load affects only the time of convergence of the solution to a stationary value.
- Bistability of the system with pro-inflammatory cytokines. For the parameter values used in Figure 11, there are three positive stationary points. The initial condition corresponds to the zero concentration of uninfected dendritic cells and macrophages. Under this initial condition, the concentration of converges to the first stationary value of (Figure 11, middle). When the initial concentration changes , the concentration of pro-inflammatory cytokines S converges to the third stationary value (Figure 11, right). It should be noted that is the initial value used in the study of the innate immune response.
3.3.3. Systemic Inflammation
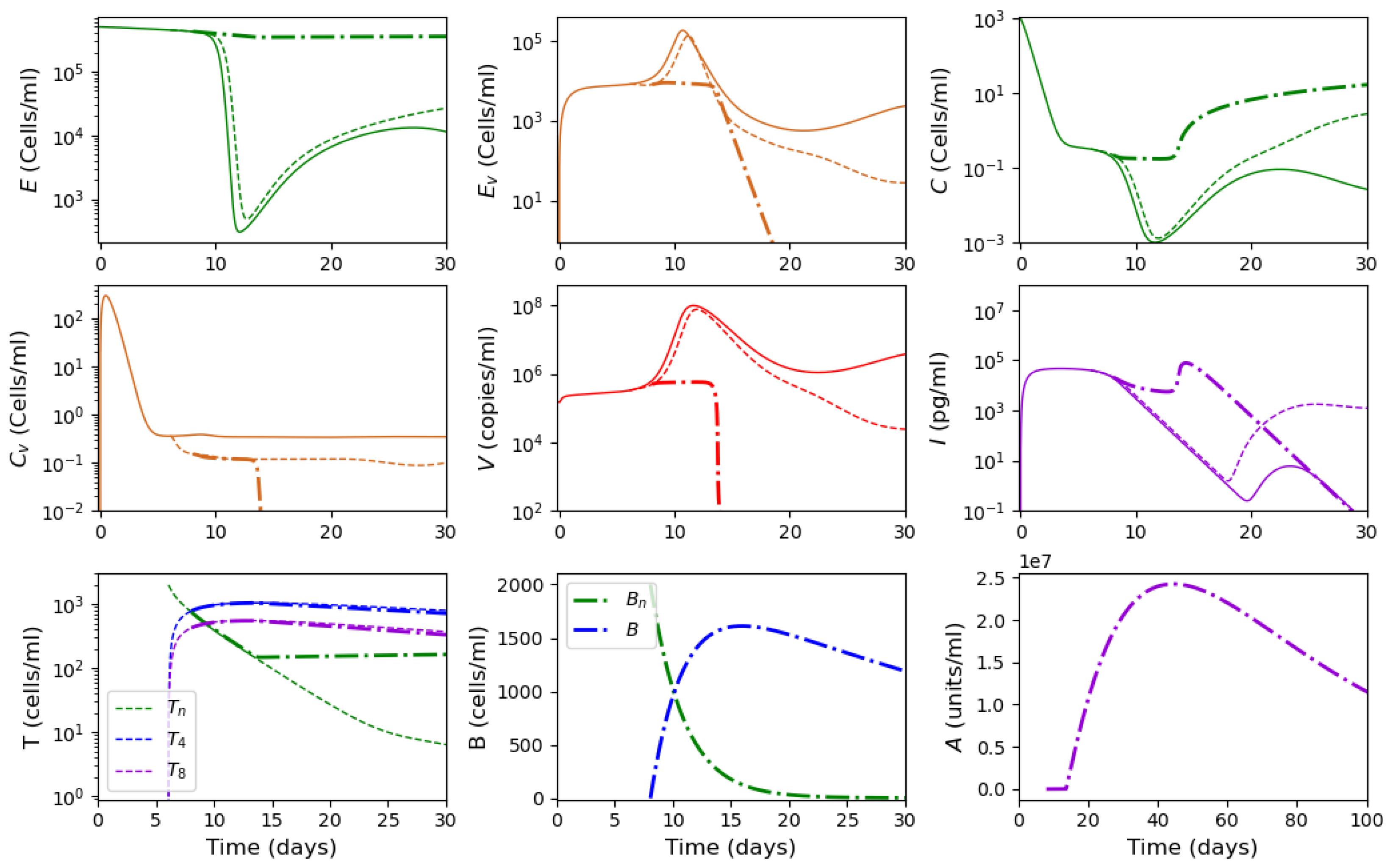
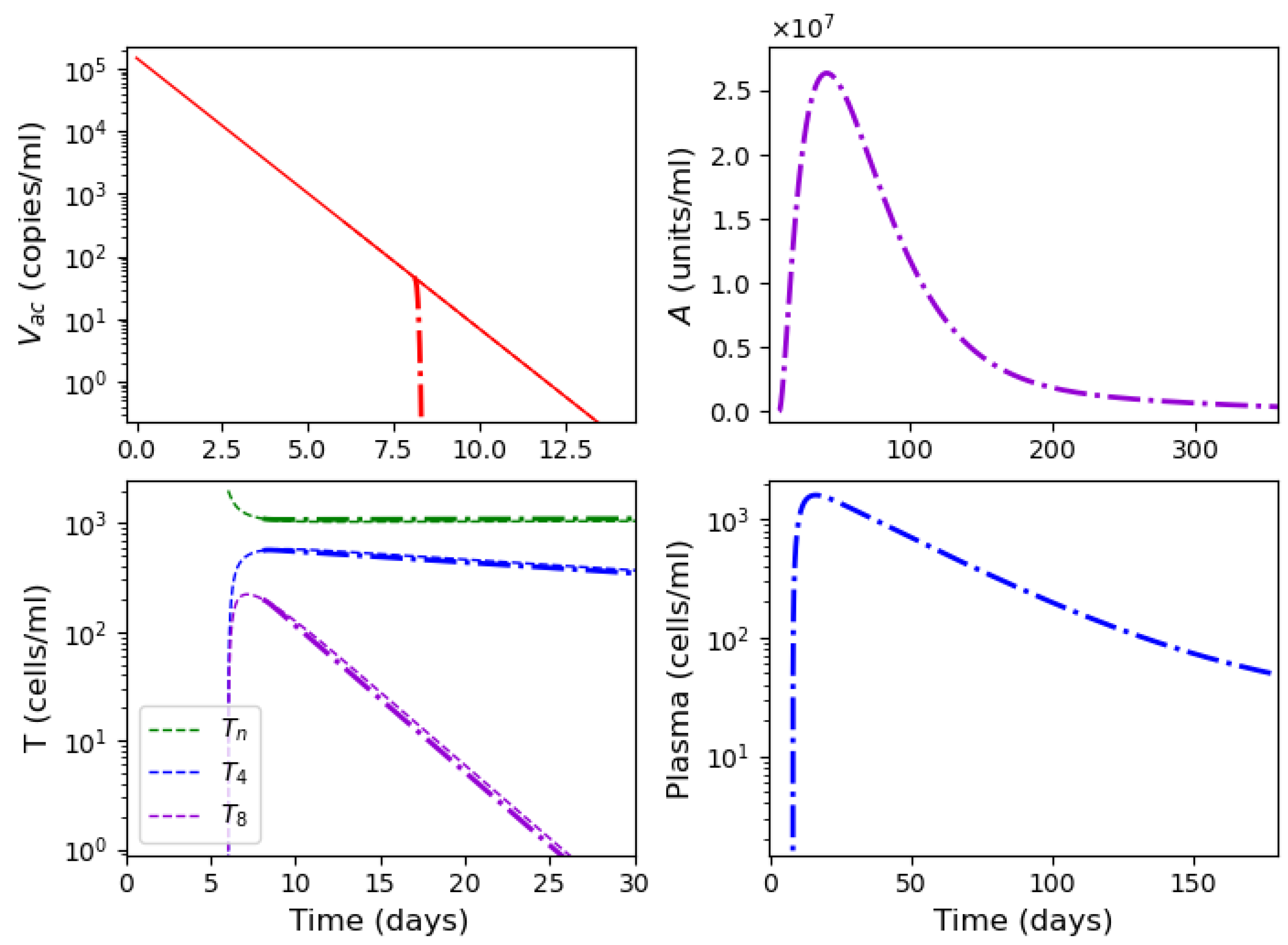
3.4. Vaccination
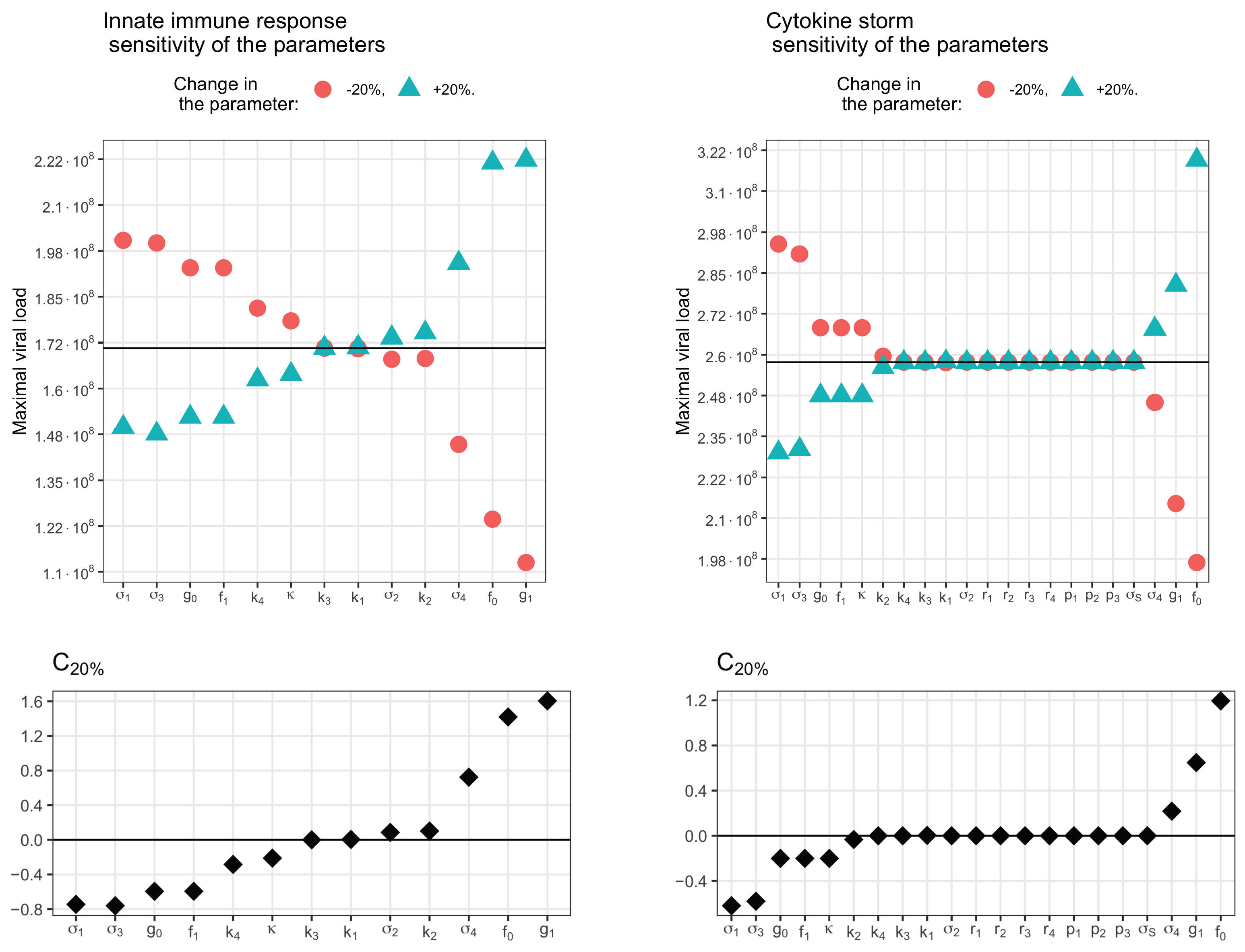
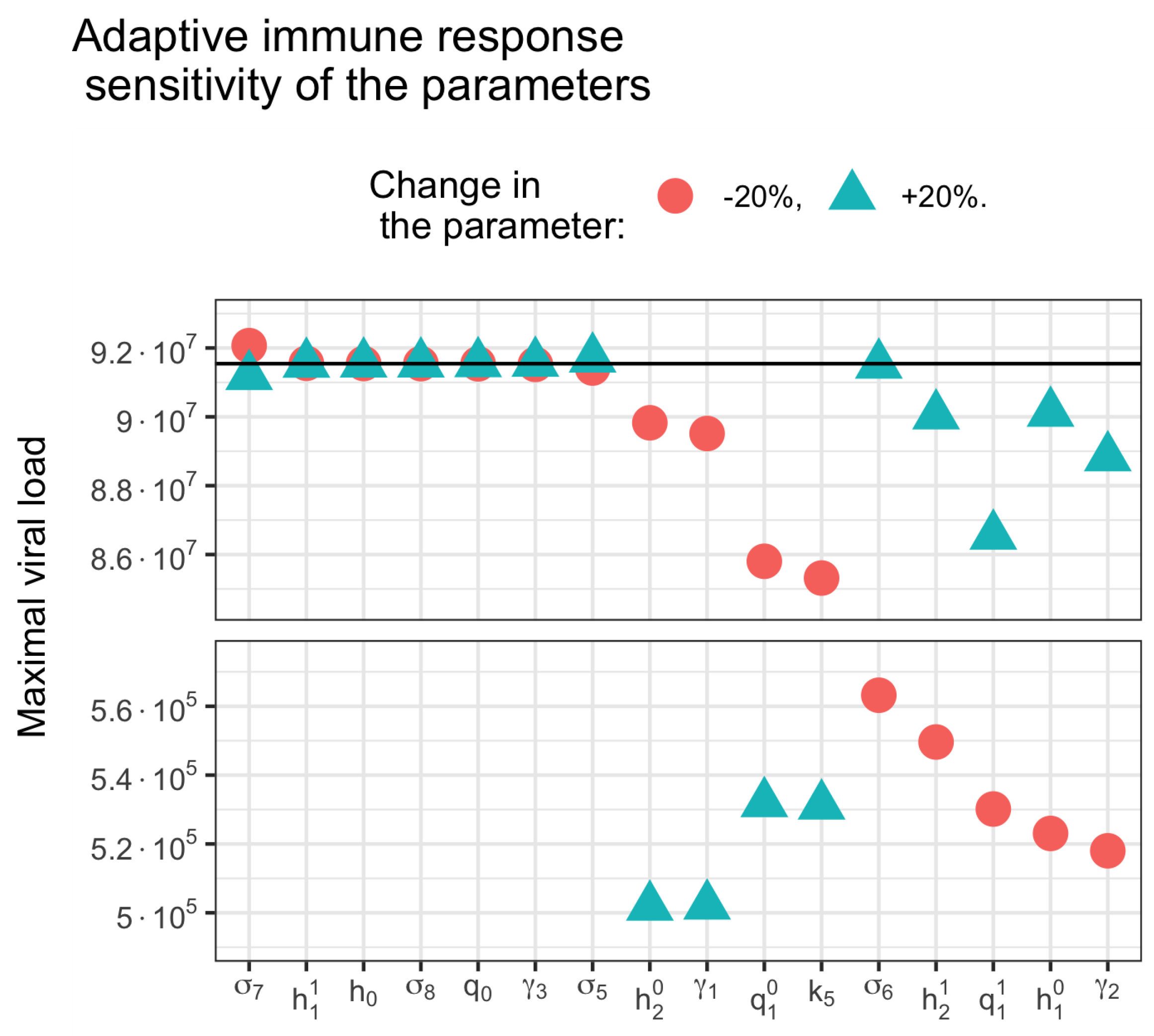
3.5. Sensitivity Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Models Schemes, Parameters and Stationary Solutions Figures
Appendix A.1. Models Schemes
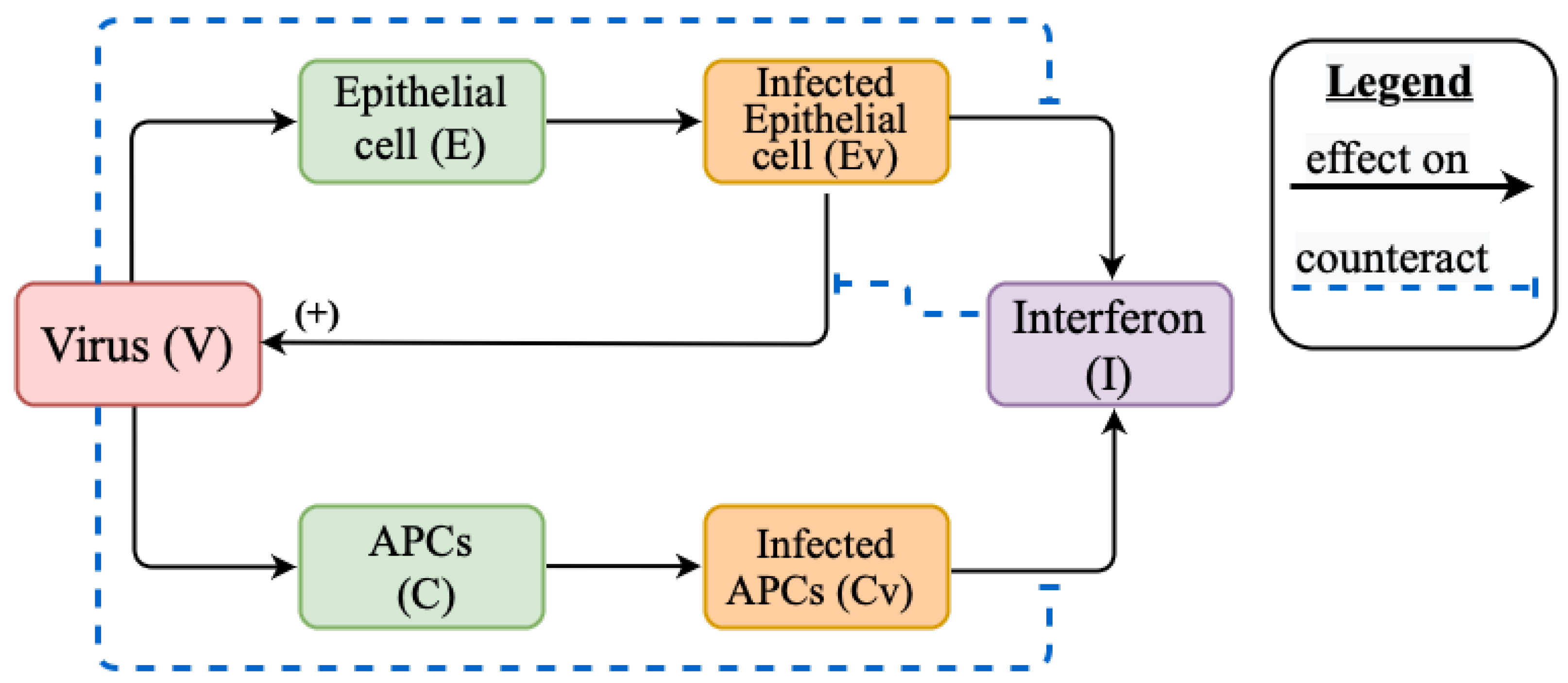
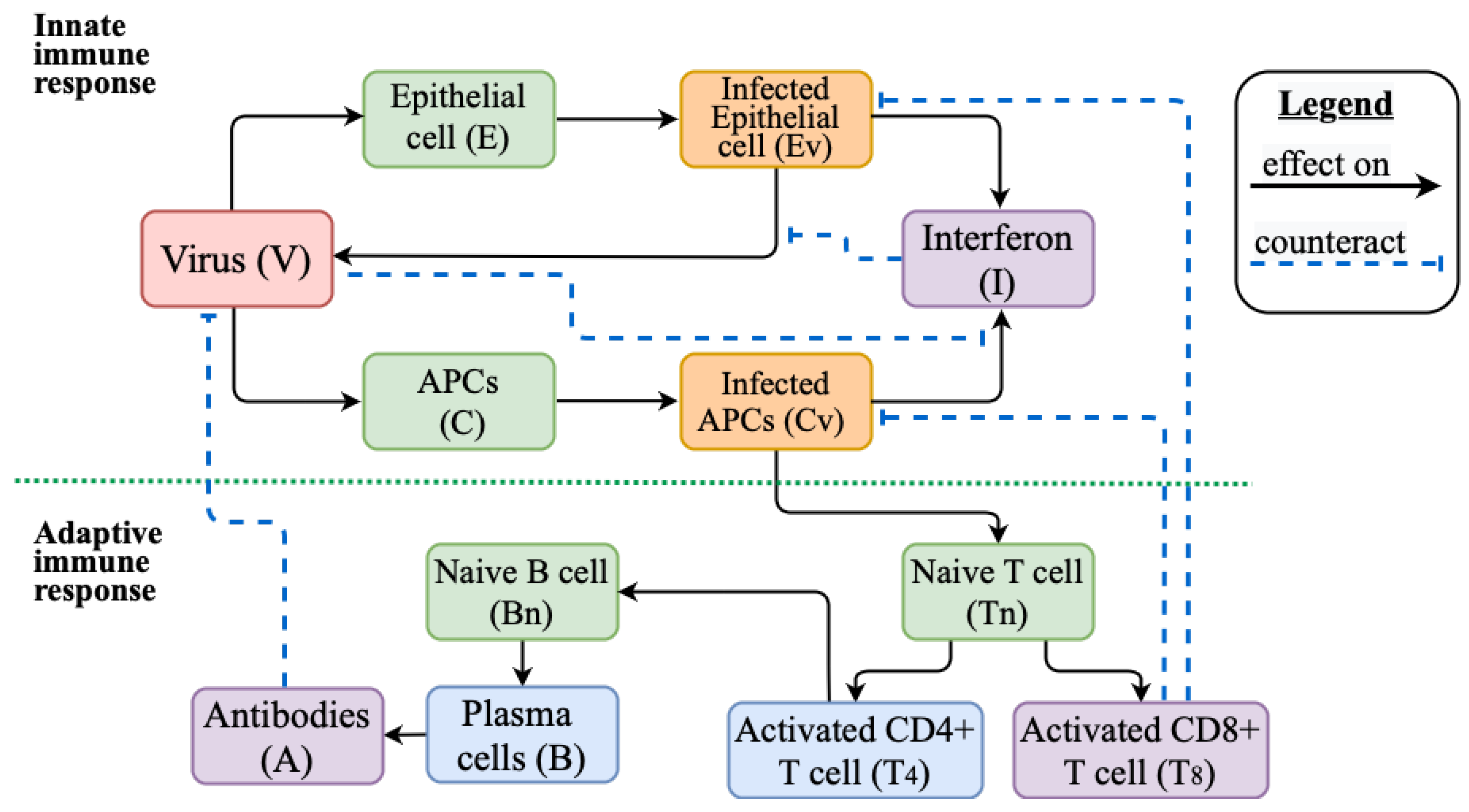
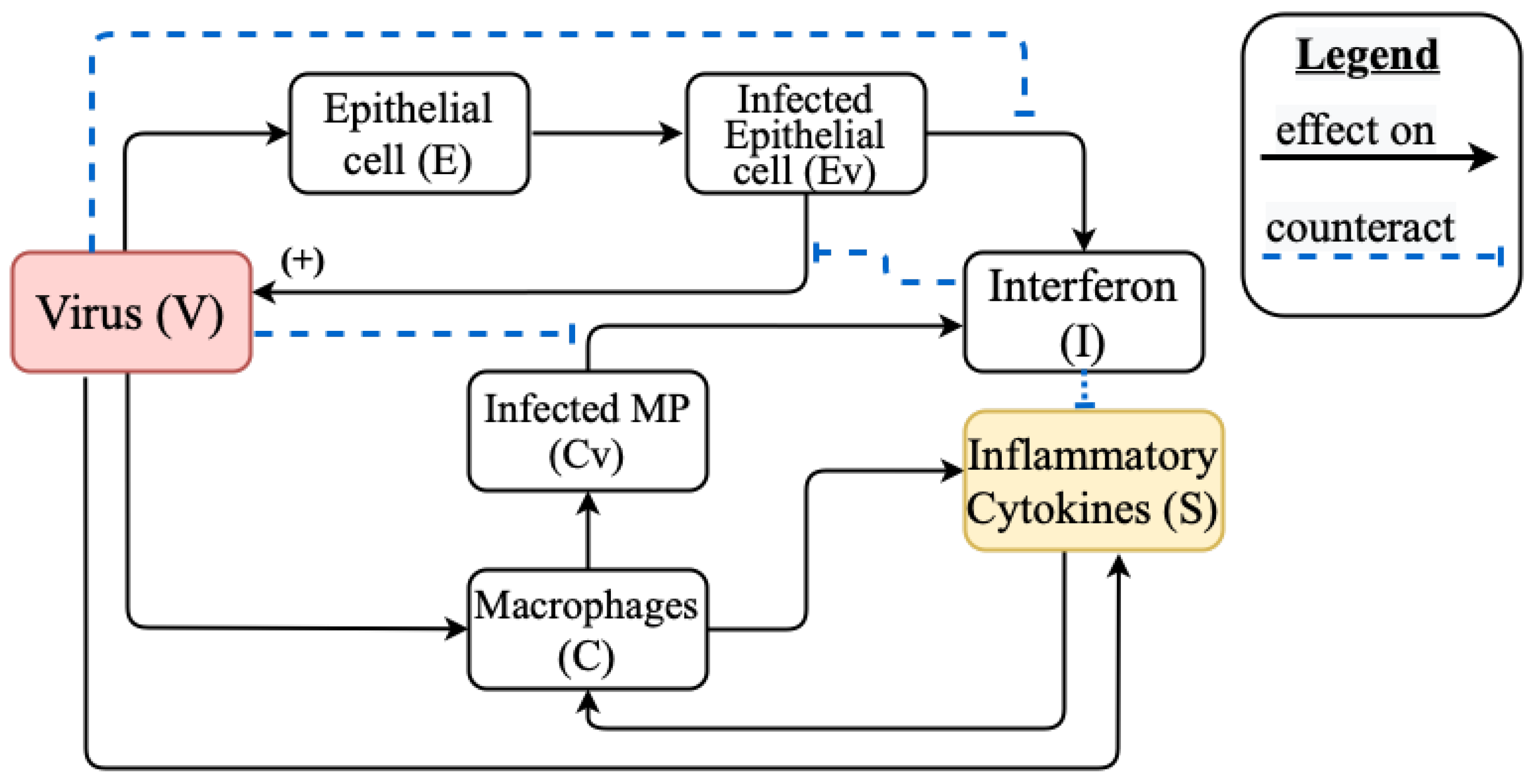
Appendix A.2. Model Variable Definitions and Initial Values
| Parameter | Value | Definition |
|---|---|---|
| [37] | Initial number of epithelial cells (cells/mL) | |
| [37] | Initial number of dendritic cells | |
| and macrophages (cells/mL) | ||
| [37] | Death rate of uninfected epithelial cells (day−1) | |
| Infection rate of epithelial cells | ||
| by virus [day−1 (copies/mL)−1] | ||
| 0.001 [37] | Death rate of uninfected APCs (day−1) | |
| Infection rate of APCs | ||
| by virus [day−1 (copies/mL)−1] | ||
| 1.2 [29,37] | Death rate of infected epithelial cells (day−1) | |
| 2.9 [37] | Death rate of infected APCs (day−1) | |
| 1 [27,37] | Virus decay rate (day−1) | |
| 1 [80,81] | Interferon clearance rate (day−1) | |
| 1900 [35] | Virus production | |
| rate [(cells· day)−1 (copies/mL)] | ||
| 0.001 | Rate of interferon influence in virus | |
| production [(pg/mL)−1] | ||
| 0.1 | Coefficient of infected ECs that | |
| stimulates the Interferon secretion | ||
| 500 [35] | Interferon secretion rate [(pg/mL) (cells · day)−1] | |
| Rate of virus influence in interferon | ||
| production [(copies/mL)−1] |
| Parameter | Value | Definition |
|---|---|---|
| 1 | Naive T-lymphocytes production | |
| rate cells/day | ||
| 1.51 [37,78] | T-helper cells (CD4+) differentiation | |
| rate [(cells · day)−1] | ||
| 0.001 | T-helper cells (CD4+) differentiation | |
| rate (cells−1) | ||
| 0.85 | Cytotoxic T cells (CD8+) differentiation | |
| rate [(cells · day)−1] | ||
| 0.1 | Cytotoxic T cells (CD8+) differentiation | |
| rate (cells−1) | ||
| 1 | Naive B-lymphocytes production | |
| rate cells/day | ||
| Effector B-cells differentiation | ||
| rate [(cells · day)−1] | ||
| Effector B-cells differentiation | ||
| rate (cells−1) | ||
| 0.023 [82] | T-helper cells (CD4+) elimination | |
| rate (day−1) | ||
| 0.031 [82] | Cytotoxic T cells (CD8+) elimination | |
| rate (day−1) | ||
| 0.028 [83] | Effector B-cells elimination | |
| rate (day−1) | ||
| 0.04 [35,37,79] | Antibodies decay | |
| rate (day−1) | ||
| 1205.63 | Antibodies secretion | |
| rate [(cells·day)−1 (units/mL)] | ||
| [37,77] | Killing rate of infected epithelial cells | |
| by [(cells · day)−1] | ||
| 0.01 | Killing rate of infected APCs | |
| by [(cells · day)−1] | ||
| 0.004 [37] | Rate constant of virus neutralization by | |
| unit antivirus antibody | ||
| [(day)−1 (copies or units/mL)] |
| Parameter | Value | Definition |
|---|---|---|
| 3 | Antigen presenting cells production rate by | |
| cytokines [(cells/day) (pg/mL)−1] | ||
| 0.1 | Antigen presenting cells production rate by | |
| cytokines [(pg/mL)−1] | ||
| 1 | Pro-inflammatory cytokines | |
| secretion rate [(cells · day)−1] | ||
| 0.1 | Pro-inflammatory cytokines | |
| secretion rate [(pg/mL)−1] | ||
| 0.4 | Pro-inflammatory cytokines secretion rate by | |
| virus [(pg) (copies · day)−1] | ||
| 10 | Rate of virus influence in cytokines | |
| secretion [(copies/mL)−1] | ||
| 0.2 | Rate of interferon influence in cytokines | |
| secretion [(pg/mL)−1] | ||
| 0.25 [84] | Pro-inflammatory cytokines elimination rate (day−1) |
| Variable | Definition | Initial Condition |
|---|---|---|
| E | Uninfected epithelial cells (cells/mL) | 5 · 10 [37] |
| Infected epithelial cells (cells/mL) | 0 | |
| C | Uninfected dendritic cells | 0 and 10 [37] |
| and macrophages (cells/mL) | ||
| Infected dendritic cells | 0 | |
| and macrophages (cells/mL) | ||
| V | Virus load (copies/mL) | it varies |
| I | Interferon (pg/mL) | 0 |
| Naive T-lymphocytes cells | 2 · 10 | |
| T-helper cells | 0 | |
| T-killer cells | 0 | |
| Naive B-lymphocytes cells | 1 · 10 [37] | |
| B | Plasma cells | 0 |
| A | Antiviral antibody titer | 0 |
| S | Pro-inflammatory cytokines (pg/mL) | 0 |
References
- WHO. The Top 10 Causes of Death. Available online: https://www.who.int/news-room/fact-sheets/detail/the-top-10-causes-of-death (accessed on 20 December 2022).
- Pinner, R.W.; Teutsch, S.M.; Simonsen, L.; Klug, L.A.; Graber, J.M.; Clarke, M.J.; Berkelman, R.L. Trends in infectious diseases mortality in the United States. JAMA 1996, 275, 189–193. [Google Scholar] [CrossRef]
- Armstrong, G.L. Trends in Infectious Disease Mortality in the United States During the 20th Century. J. Am. Med. Assoc. 1999, 281, 61. [Google Scholar] [CrossRef]
- Burrell, C.J.; Howard, C.R.; Murphy, F.A. Fenner and White’s Medical Virology, 5th ed.; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Chaplin, D.D. Overview of the immune response. J. Allergy Clin. Immunol. 2010, 125, S3–S23. [Google Scholar] [CrossRef]
- Medzhitov, R. Recognition of microorganisms and activation of the immune response. Nature 2007, 449, 819–826. [Google Scholar] [CrossRef] [PubMed]
- Tosi, M.F. Innate immune responses to infection. J. Allergy Clin. Immunol. 2005, 116, 241–249. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.W.; Barry, P.A.; Szubin, R.; Wang, D.; Baumgarth, N. Human cytomegalovirus suppresses type I interferon secretion by plasmacytoid dendritic cells through its interleukin 10 homolog. Virology 2009, 390, 330–337. [Google Scholar] [CrossRef] [PubMed]
- Britannica. The Editors of Encyclopaedia. “Interferon”. Encyclopedia Britannica, 28 September 2022. Available online: https://www.britannica.com/science/interferon (accessed on 1 November 2022).
- Sen, G.C. Viruses and Interferons. Annu. Rev. Microbiol. 2001, 55, 255–281. [Google Scholar] [CrossRef]
- Kotenko, S.V.; Durbin, J.E. Contribution of type III interferons to antiviral immunity: Location, location, location. J. Biol. Chem. 2017, 292, 7295–7303. [Google Scholar] [CrossRef]
- Parkin, J.; Cohen, B. An overview of the immune system. Lancet 2001, 357, 1777–1789. [Google Scholar] [CrossRef]
- Thimme, R.; Lohmann, V.; Weber, F. A target on the move: Innate and adaptive immune escape strategies of hepatitis C virus. Antivir. Res. 2006, 69, 129–141. [Google Scholar] [CrossRef]
- Medzhitov, R.; Janeway, C.A. Innate immunity: Impact on the adaptive immune response. Curr. Opin. Immunol. 1997, 9, 4–9. [Google Scholar] [CrossRef] [PubMed]
- Gautret, P.; Gray, G.C.; Charrel, R.N.; Odezulu, N.G.; Al-Tawfiq, J.A.; Zumla, A.; Memish, Z.A. Emerging viral respiratory tract infections—Environmental risk factors and transmission. Lancet Infect. Dis. 2014, 14, 1113–1122. [Google Scholar] [CrossRef] [PubMed]
- Jakubzick, C.V.; Randolph, G.J.; Henson, P.M. Monocyte differentiation and antigen-presenting functions. Nat. Rev. Immunol. 2017, 17, 349–362. [Google Scholar] [CrossRef] [PubMed]
- Subbarao, K.; Mahanty, S. Respiratory Virus Infections: Understanding COVID-19. Immunity 2020, 52, 905–909. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.; Zhou, J.; Wong, B.H.; Li, C.; Chan, J.F.-W.; Cheng, Z.-S.; Yang, D.; Wang, D.; Lee, A.C.-Y.; Li, C.; et al. Middle East respiratory syndrome coronavirus efficiently infects human primary T lymphocytes and activates the extrinsic and intrinsic apoptosis pathways. J. Infect. Dis. 2015, 213, 904–914. [Google Scholar] [CrossRef] [PubMed]
- Channappanavar, R.; Perlman, S. Pathogenic human coronavirus infections: Causes and consequences of cytokine storm and immunopathology. Semin. Immunopathol. 2017, 39, 529–539. [Google Scholar] [CrossRef] [PubMed]
- Jafarzadeh, A.; Chauhan, P.; Saha, B.; Jafarzadeh, S.; Nemati, M. Contribution of monocytes and macrophages to the local tissue inflammation and cytokine storm in COVID-19: Lessons from SARS and MERS, and potential therapeutic interventions. Life Sci. 2020, 257, 118102. [Google Scholar] [CrossRef]
- Cohn, L.; Hawrylowicz, C.; Ray, A. Biology of Lymphocytes. Middleton’s Allergy 2014, 1, 203–214. [Google Scholar]
- Marshall, J.S.; Warrington, R.; Watson, W.; Kim, H.L. An introduction to immunology and immunopathology. Allergy Asthma Clin. Immunol. 2018, 14, 49. [Google Scholar] [CrossRef]
- Robert, P.A.; Kunze-Schumacher, H.; Greiff, V.; Krueger, A. Modeling the Dynamics of T-Cell Development in the Thymus. Entropy 2021, 23, 437. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 4th ed.; W.W. Norton & Company: New York, NY, USA, 2002. [Google Scholar]
- Allen, H.C.; Sharma, P. Histology, Plasma Cells. In StatPearls [Internet]. Treasure Island (FL); StatPearls Publishing: Tampa, FL, USA, 2020. [Google Scholar]
- Eftimie, R.; Gillard, J.J.; Cantrell, D.A. Mathematical Models for Immunology: Current State of the Art and Future Research Directions. Bull. Math. Biol. 2016, 78, 2091–2134. [Google Scholar] [CrossRef] [PubMed]
- Bocharov, G.; Volpert, V.; Ludewig, B.; Meyerhans, A. Editorial: Mathematical Modeling of the Immune System in Homeostasis, Infection and Disease. Front. Immunol. 2020, 10, 2944. [Google Scholar] [CrossRef] [PubMed]
- Kirschner, D.E.; Chang, S.T.; Riggs, T.W.; Perry, N.; Linderman, J.J. Toward a multiscale model of antigen presentation in immunity. Immunol. Rev. 2007, 216, 93–118. [Google Scholar] [CrossRef] [PubMed]
- Baccam, P.; Beauchemin, C.; Macken, C.A.; Hayden, F.G.; Perelson, A.S. Kinetics of Influenza A Virus Infection in Humans. J. Virol. 2006, 80, 7590–7599. [Google Scholar] [CrossRef]
- Canini, L.; Carrat, F. Population Modeling of Influenza A/H1N1 Virus Kinetics and Symptom Dynamics. J. Virol. 2010, 85, 2764–2770. [Google Scholar] [CrossRef]
- Saenz, R.A.; Quinlivan, M.; Elton, D.; MacRae, S.; Blunden, A.S.; Mumford, J.A.; Daly, J.M.; Digard, P.; Cullinane, A.; Grenfell, B.T.; et al. Dynamics of Influenza Virus Infection and Pathology. J. Virol. 2010, 84, 3974–3983. [Google Scholar] [CrossRef]
- Miao, H.; Hollenbaugh, J.A.; Zand, M.S.; Holden-Wiltse, J.; Mosmann, T.R.; Perelson, A.S.; Wu, H.; Topham, D.J. Quantifying the Early Immune Response and Adaptive Immune Response Kinetics in Mice Infected with Influenza A Virus. J. Virol. 2010, 84, 6687–6698. [Google Scholar] [CrossRef]
- Crauste, F.; Terry, E.; Mercier, I.L.; Mafille, J.; Djebali, S.; Andrieu, T.; Mercier, B.; Kaneko, G.; Arpin, C.; Marvel, J.; et al. Predicting pathogen-specific CD8 T cell immune responses from a modeling approach. J. Theor. Biol. 2015, 374, 66–82. [Google Scholar] [CrossRef]
- Luo, S.; Reed, M.; Mattingly, J.C.; Koelle, K. The impact of host immune status on the within-host and population dynamics of antigenic immune escape. J. R. Soc. Interface 2012, 9, 2603–2613. [Google Scholar] [CrossRef]
- Hancioglu, B.; Swigon, D.; Clermont, G. A dynamical model of human immune response to influenza A virus infection. J. Theor. Biol. 2007, 246, 70–86. [Google Scholar] [CrossRef]
- Bocharov, G.; Romanyukha, A. Mathematical Model of Antiviral Immune Response III. Influenza A Virus Infection. J. Theor. Biol. 1994, 167, 323–360. [Google Scholar] [CrossRef]
- Lee, H.Y.; Topham, D.J.; Park, S.Y.; Hollenbaugh, J.; Treanor, J.; Mosmann, T.R.; Jin, X.; Ward, B.M.; Miao, H.; Holden-Wiltse, J.; et al. Simulation and Prediction of the Adaptive Immune Response to Influenza A Virus Infection. J. Virol. 2009, 83, 7151–7165. [Google Scholar] [CrossRef] [PubMed]
- Du, S.Q.; Yuan, W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID-19 and implications for viral pathogenesis. J. Med. Virol. 2020, 92, 1615–1628. [Google Scholar] [CrossRef] [PubMed]
- Chimal-Eguia, J.C. Mathematical Model of Antiviral Immune Response against the COVID-19 Virus. Mathematics 2021, 9, 1356. [Google Scholar] [CrossRef]
- Ghostine, R.; Gharamti, M.; Hassrouny, S.; Hoteit, I. Mathematical Modeling of Immune Responses against SARS-CoV-2 Using an Ensemble Kalman Filter. Mathematics 2021, 9, 2427. [Google Scholar] [CrossRef]
- Ghosh, I. Within Host Dynamics of SARS-CoV-2 in Humans: Modeling Immune Responses and Antiviral Treatments. SN Comput. Sci. 2021, 2, 482. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Hao, M.; Pan, Z.; Lei, J.; Zou, X. Data-driven multi-scale mathematical modeling of SARS-CoV-2 infection reveals heterogeneity among COVID-19 patients. PLoS Comput. Biol. 2021, 17, e1009587. [Google Scholar] [CrossRef]
- Garcia-Martinez, K.; Luaces-Alvarez, P.L.; Sanchez-Valdes, L.; Leon-Monzon, K.; Crombet-Ramos, T.; Perez-Rodrıguez, R. Understanding the Impact of Cuban Immunotherapy Protocols during COVID-19 Disease: Contributions from Mathematical Modeling and Statistical Approaches. Mov. COVID-19 Math. Model. Vaccine Des. Theory Pract. Exp. 2022, 1, 435–467. [Google Scholar]
- Reis, R.F.; Pigozzo, A.B.; Bonin, C.R.B.; Quintela, B.D.M.; Pompei, L.T.; Vieira, A.C.; Silva, L.D.L.E.; Xavier, M.P.; Weber dos Santos, R.; Lobosco, M. A Validated Mathematical Model of the Cytokine Release Syndrome in Severe COVID-19. Front. Mol. Biosci. 2021, 8, 639423. [Google Scholar] [CrossRef]
- Yu, Z.; Ellahi, R.; Nutini, A.; Sohail, A.; Sait, S.M. Modeling and simulations of CoViD-19 molecular mechanism induced by cytokines storm during SARS-CoV2 infection. J. Mol. Liq. 2021, 327, 114863. [Google Scholar] [CrossRef]
- Sasidharakurup, H.; Kumar, G.; Nair, B.; Diwakar, S. Mathematical Modeling of Severe Acute Respiratory Syndrome Coronavirus 2 Infection Network with Cytokine Storm, Oxidative Stress, Thrombosis, Insulin Resistance, and Nitric Oxide Pathways. OMICS A J. Integr. Biol. 2021, 25, 770–781. [Google Scholar] [CrossRef] [PubMed]
- Kareva, I.; Berezovskaya, F.; Karev, G. Mathematical model of a cytokine storm. bioRxiv 2022. [Google Scholar] [CrossRef]
- Leon, C.; Tokarev, A.A.; Volpert, V.A. Modelling of cytokine storm in respiratory viral infections. Comput. Res. Model. 2022, 14, 619–645. [Google Scholar] [CrossRef]
- Compans, R.W.; Herrler, G. Virus Infection of Epithelial Cells. Mucosal Immunol. 2005, 769–782. [Google Scholar] [CrossRef]
- Katze, M.G.; He, Y.; Gale, M. Viruses and interferon: A fight for supremacy. Nat. Rev. Immunol. 2002, 2, 675–687. [Google Scholar] [CrossRef]
- Hadjadj, J.; Yatim, N.; Barnabei, L.; Corneau, A.; Boussier, J.; Smith, N.; Péré, H.; Charbit, B.; Bondet, V.; Chenevier-Gobeaux, C.; et al. Impaired type I interferon activity and inflammatory responses in severe COVID-19 patients. Science 2020, 369, 718–724. [Google Scholar] [CrossRef]
- Samuel, C.E. Antiviral Actions of Interferons. Clin. Microbiol. Rev. 2001, 4, 778–809. [Google Scholar] [CrossRef]
- WHO. What We Know about the COVID-19 Immune Response. Available online: https://www.who.int/docs/default-source/coronaviruse/risk-comms-updates/update-34-immunity-2nd.pdf (accessed on 20 December 2022).
- den Haan, J.M.; Arens, R.; van Zelm, M.C. The activation of the adaptive immune system: Cross-talk between antigen-presenting cells, T cells and B cells. Immunol. Lett. 2014, 162, 103–112. [Google Scholar] [CrossRef]
- Rossi, M.; Young, J.W. Human Dendritic Cells: Potent Antigen-Presenting Cells at the Crossroads of Innate and Adaptive Immunity. J. Immunol. 2005, 175, 1373–1381. [Google Scholar] [CrossRef]
- Davis, C.B. Evidence for a stochastic mechanism in the differentiation of mature subsets of T lymphocytes. Cell 1993, 73, 237–247. [Google Scholar] [CrossRef]
- Borgulya, P.; Kishi, H.; Muller, U.; Kirberg, J.; von Boehmer, H. Development of the CD4 and CD8 lineage of T cells: Instruction versus selection. EMBO J. 1991, 10, 913–918. [Google Scholar] [CrossRef] [PubMed]
- Bendelac, A.; Schwartz, R.H. CD4+ and CD8+ T cells acquire specific lymphokine secretion potentials during thymic maturation. Nature 1991, 353, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Gigante, M.; Ranieri, E. Cytotoxic T-Cells: Methods and Protocols (Methods in Molecular Biology), 2nd ed.; Humana: Louisville, KY, USA, 2021; Volume 2325. [Google Scholar]
- Liu, Z.-X. Fas-Mediated Apoptosis Causes Elimination of Virus-Specific Cytotoxic T Cells in the Virus-Infected Liver. J. Immunol. 2001, 166, 3035–3041. [Google Scholar] [CrossRef] [PubMed]
- Lannunziato, F.; Maggi, L.; Mazzoni, A. T-Helper Cells: Methods and Protocols (Methods in Molecular Biology), 1st ed.; Humana: Louisville, KY, USA, 2021; Volume 2285. [Google Scholar]
- Noelle, R.J.; Snow, E.C. T helper cell-dependent B cell activation. FASEB J. 1991, 5, 2770–2776. [Google Scholar] [CrossRef]
- Singh, H.; Grosschedl, R. Molecular Analysis of B Lymphocyte Development and Activation (Current Topics in Microbiology and Immunology Book 290); Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Agematsu, K. Plasma Cell Generation from B-Lymphocytes via CD27/CD70 Interaction. Leuk. Lymphoma 1999, 35, 219–225. [Google Scholar] [CrossRef]
- Nutt, S.L. The generation of antibody-secreting plasma cells. Nat. Rev. Immunol. 2015, 15, 160–171. [Google Scholar] [CrossRef]
- Fagraeus, A. Plasma Cellular Reaction and its Relation to the Formation of Antibodies in vitro. Nature 1947, 159, 499. [Google Scholar] [CrossRef]
- Dixon, F. Advances in Immunology; Academic Press: Cambridge, MA, USA, 2014; Volume 25. [Google Scholar]
- Ilinykh, P.; Huang, K. Characterization of Antibody Responses to Virus Infections in Humans; Mdpi AG: Basel, Switzerland, 2022. [Google Scholar]
- Mazanec, M.B. Intracellular neutralization of virus by immunoglobulin A antibodies. Proc. Natl. Acad. Sci. USA 1992, 89, 6901–6905. [Google Scholar] [CrossRef]
- COVID-19 and the Cytokine Storm: The Crucial Role of IL-6. Available online: https://www.enzolifesciences.com/science-center/technotes/2020/april/covid-19-and-the-cytokine-storm-the-crucial-role-of-il-6/10.1007/s11606-020-06067-8 (accessed on 31 May 2021).
- Huang, C.; Wang, Y.; Li, X.; Ren, L.; Zhao, J.; Hu, Y.; Zhang, L.; Fan, G.; Xu, J.; Gu, X.; et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet 2020, 395, 497–506. [Google Scholar] [CrossRef]
- Tay, M.Z.; Poh, C.M.; Rénia, L.; MacAry, P.A.; Ng, L.F.P. The trinity of COVID-19: Immunity, inflammation and intervention. Nat. Rev. Immunol. 2020, 20, 363–374. [Google Scholar] [CrossRef]
- Otsuka, R.; Seino, K.I. Macrophage activation syndrome and COVID-19. Inflamm. Regen. 2020, 40, 19. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.-D.; Ding, M.; Dong, X.; Zhang, J.-J.; Azkur, A.K.; Azkur, D.; Gan, H.; Sun, Y.-L.; Fu, W.; Li, W.; et al. Risk factors for severe and critically ill COVID-19 patients: A review. Allergy 2020, 76, 428–455. [Google Scholar] [CrossRef] [PubMed]
- Karki, R.; Kanneganti, T.-D. The ‘cytokine storm’: Molecular mechanisms and therapeutic prospects. Trends Immunol. 2021, 42, 681–705. [Google Scholar] [CrossRef] [PubMed]
- Diamond, M.S.; Kanneganti, T.-D. Innate immunity: The first line of defense against SARS-CoV-2. Nat. Immunol. 2022, 23, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Barchet, W.; Oehen, S.; Klenerman, P.; Wodarz, D.; Bocharov, G.; Lloyd, A.L.; Nowak, M.A.; Hengartner, H.; Zinkernagel, R.M.; Ehl, S. Direct quantitation of rapid elimination of viral antigen-positive lymphocytes by antiviral CD8+ T cellsin vivo. Eur. J. Immunol. 2000, 30, 1356–1363. [Google Scholar] [CrossRef]
- de Boer, R.J.; Oprea, M.; Antia, R.; Murali-Krishna, K.; Ahmed, R.; Perelson, A.S. Recruitment Times, Proliferation, and Apoptosis Rates during the CD8+ T-Cell Response to Lymphocytic Choriomeningitis Virus. J. Virol. 2001, 75, 10663–10669. [Google Scholar] [CrossRef]
- Marchuk, G.; Petrov, R.; Romanyukha, A.; Bocharov, G. Mathematical model of antiviral immune response. I. Data analysis, generalized picture construction and parameters evaluation for hepatitis B. J. Theor. Biol. 1991, 151, 1–40. [Google Scholar] [CrossRef]
- Wills, R.J. Clinical Pharmacokinetics of Interferons. Clin. Pharmacokinet. 1990, 19, 390–399. [Google Scholar] [CrossRef]
- Arnaud, P. Les différents interférons: Pharmacologie, mécanismes d’action, tolérance et effets secondaires. Rev. MéDecine Interne 2002, 23, 449S–458S. [Google Scholar] [CrossRef]
- Baliu-Piqué, M.; Verheij, M.W.; Drylewicz, J.; Ravesloot, L.; de Boer, R.J.; Koets, A.; Tesselaar, K.; Borghans, J.A.M. Short Lifespans of Memory T-cells in Bone Marrow, Blood, and Lymph Nodes Suggest That T-cell Memory Is Maintained by Continuous Self-Renewal of Recirculating Cells. Front. Immunol. 2018, 9, 2054. [Google Scholar] [CrossRef]
- Milo, R.; Jorgensen, P.; Moran, U.; Weber, G.; Springer, M. BioNumbers—The database of key numbers in molecular and cell biology. Nucleic Acids Res. 2009, 38 (Suppl. 1), D750–D753. [Google Scholar] [CrossRef] [PubMed]
- Kuribayashi, T. Elimination half-lives of interleukin-6 and cytokine-induced neutrophil chemoattractant-1 synthesized in response to inflammatory stimulation in rats. Lab. Anim. Res. 2018, 34, 80. [Google Scholar] [CrossRef] [PubMed]
- Fajnzylber, J.; Regan, J.; Coxen, K.; Corry, H.; Wong, C.; Rosenthal, A.; Worrall, D.; Giguel, F.; Piechocka-Trocha, A.; Atyeo, C.; et al. SARS-CoV-2 viral load is associated with increased disease severity and mortality. Nat. Commun. 2020, 11, 5493. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Zhang, D.; Yang, P.; Poon, L.L.M.; Wang, Q. Viral load of SARS-CoV-2 in clinical samples. Lancet Infect. Dis. 2020, 20, 411–412. [Google Scholar] [CrossRef]
- Rhodes, S.J.; Knight, G.M.; Kirschner, D.E.; White, R.G.; Evans, T.G. Dose finding for new vaccines: The role for immunostimulation/immunodynamic modelling. J. Theor. Biol. 2019, 465, 51–55. [Google Scholar] [CrossRef]
- Baldi, E.; Bucherelli, C. The Inverted “U-Shaped” Dose-Effect Relationships in Learning and Memory: Modulation of Arousal and Consolidation. Onlinearity Biol. Toxicol. Med. 2005, 3, nonlin.003.01.0. [Google Scholar] [CrossRef]
- Wu, Y.; Kang, L.; Guo, Z.; Liu, J.; Liu, M.; Liang, W. Incubation Period of COVID-19 Caused by Unique SARS-CoV-2 Strains. JAMA Netw. Open 2022, 5, e2228008. [Google Scholar] [CrossRef]
- Marois, I.; Cloutier, A.; Garneau, M.; Richter, M.V. Initial infectious dose dictates the innate, adaptive, and memory responses to influenza in the respiratory tract. J. Leukoc. Biol. 2012, 92, 107–121. [Google Scholar] [CrossRef]
- Gandhi, M.; Beyrer, C.; Goosby, E. Masks Do More Than Protect Others During COVID-19: Reducing the Inoculum of SARS-CoV-2 to Protect the Wearer. J. Gen. Intern. Med. 2020, 35, 3063–3066. [Google Scholar] [CrossRef]
- Bhaskar, S.; Sinha, A.; Banach, M.; Mittoo, S.; Weissert, R.; Kass, J.S.; Rajagopal, S.; Pai, A.R.; Kutty, S. Cytokine Storm in COVID-19—Immunopathological Mechanisms, Clinical Considerations, and Therapeutic Approaches: The REPROGRAM Consortium Position Paper. Front. Immunol. 2020, 11, 1648. [Google Scholar] [CrossRef]
- Schulert, G.S.; Grom, A.A. Macrophage activation syndrome and cytokine-directed therapies. Best Pract. Res. Clin. Rheumatol. 2014, 28, 277–292. [Google Scholar] [CrossRef] [PubMed]
- Avau, A.; Matthys, P. Therapeutic potential of interferon-γ and its antagonists in autoinflammation: Lessons from murine models of systemic juvenile idiopathic arthritis and macrophage activation syndrome. Pharmaceuticals 2015, 8, 793–815. [Google Scholar] [CrossRef] [PubMed]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leon, C.; Tokarev, A.; Bouchnita, A.; Volpert, V. Modelling of the Innate and Adaptive Immune Response to SARS Viral Infection, Cytokine Storm and Vaccination. Vaccines 2023, 11, 127. https://doi.org/10.3390/vaccines11010127
Leon C, Tokarev A, Bouchnita A, Volpert V. Modelling of the Innate and Adaptive Immune Response to SARS Viral Infection, Cytokine Storm and Vaccination. Vaccines. 2023; 11(1):127. https://doi.org/10.3390/vaccines11010127
Chicago/Turabian StyleLeon, Cristina, Alexey Tokarev, Anass Bouchnita, and Vitaly Volpert. 2023. "Modelling of the Innate and Adaptive Immune Response to SARS Viral Infection, Cytokine Storm and Vaccination" Vaccines 11, no. 1: 127. https://doi.org/10.3390/vaccines11010127
APA StyleLeon, C., Tokarev, A., Bouchnita, A., & Volpert, V. (2023). Modelling of the Innate and Adaptive Immune Response to SARS Viral Infection, Cytokine Storm and Vaccination. Vaccines, 11(1), 127. https://doi.org/10.3390/vaccines11010127






