Global Dynamics of SARS-CoV-2 Infection with Antibody Response and the Impact of Impulsive Drug Therapy
Abstract
1. Introduction
2. Derivation of the Mathematical Model
- : the uninfected susceptible target cells, which are surface epithelial cells with ACE-2 receptors located in the respiratory tract, including the lungs and nasal and trachea/ bronchial tissues;
- : the SARS-CoV-2-infected virus-producing cells;
- : the virus particles.
3. Dynamics of the Model without Impulses
3.1. Non-Negativity and Boundedness
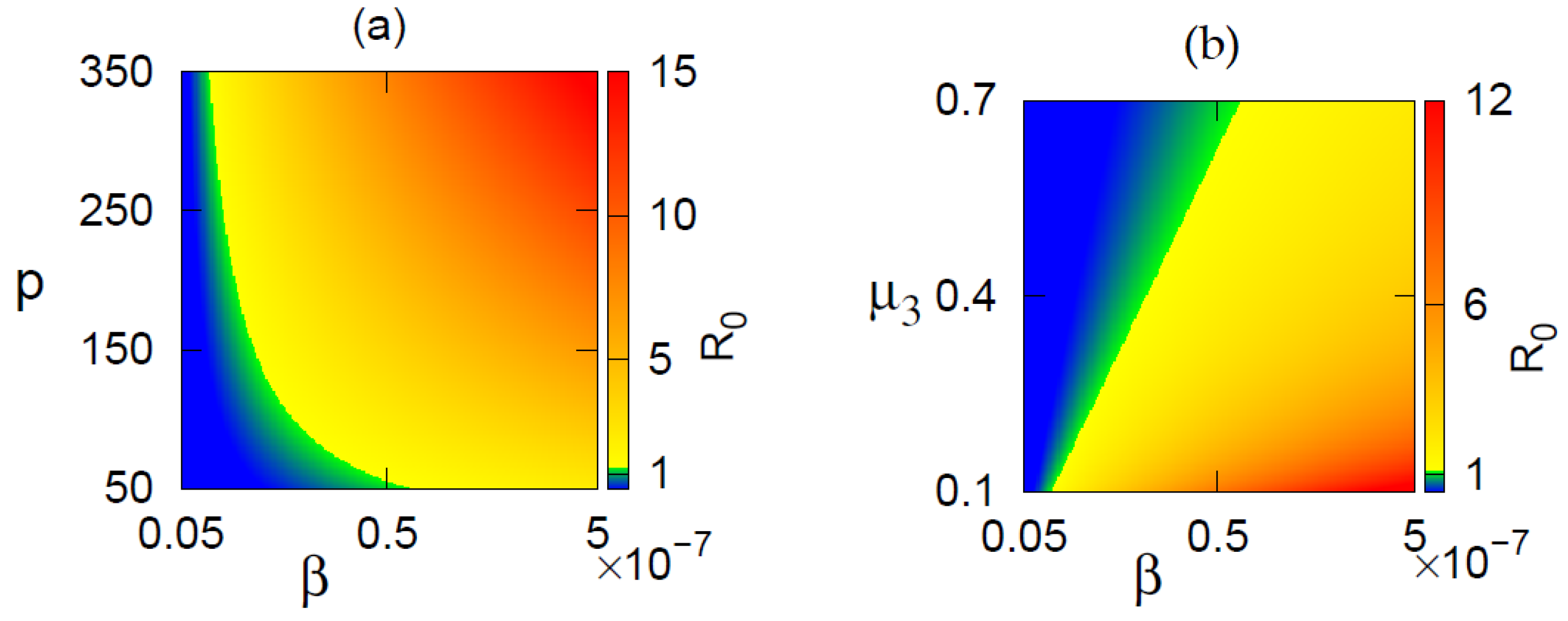
3.2. Basic Reproduction Number
3.3. Existence of Equilibrium Points
3.4. Stability of Equilibrium Points
4. Dynamics of the System with Impulsive Drug Dosing
4.1. Dynamics of the Drug
4.1.1. Impact of Imperfect Drug Dosing
4.2. Dynamics of the Impulsive System (4)
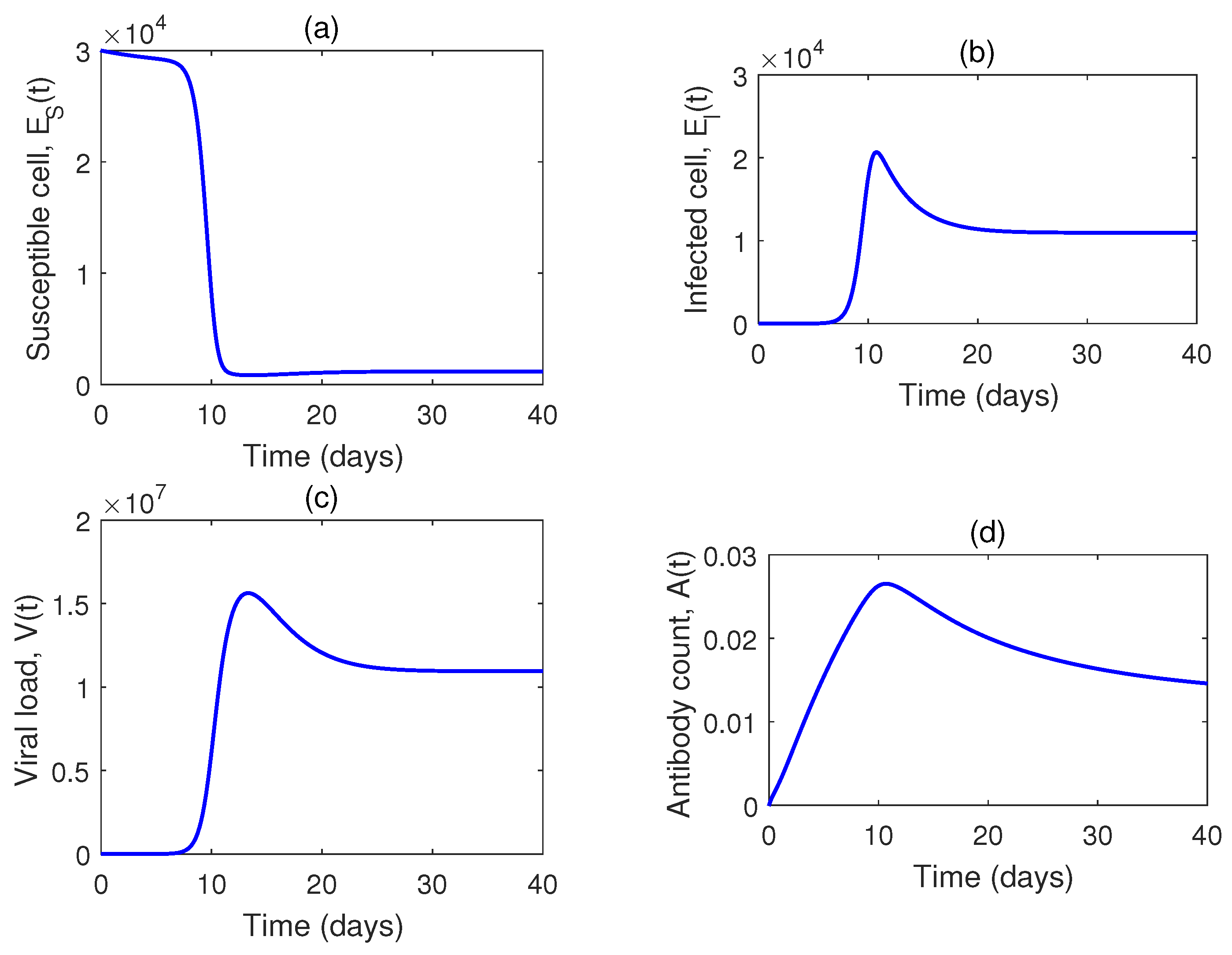
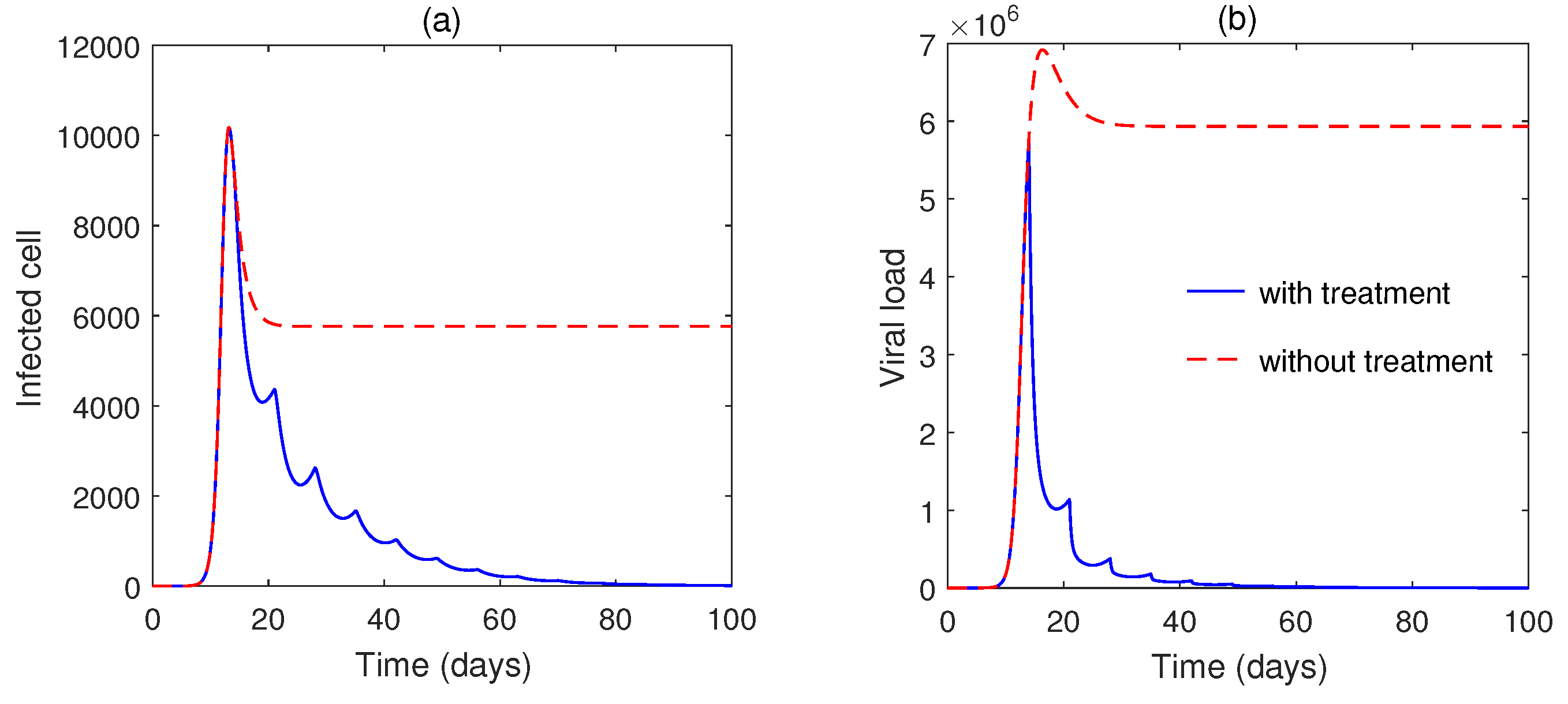
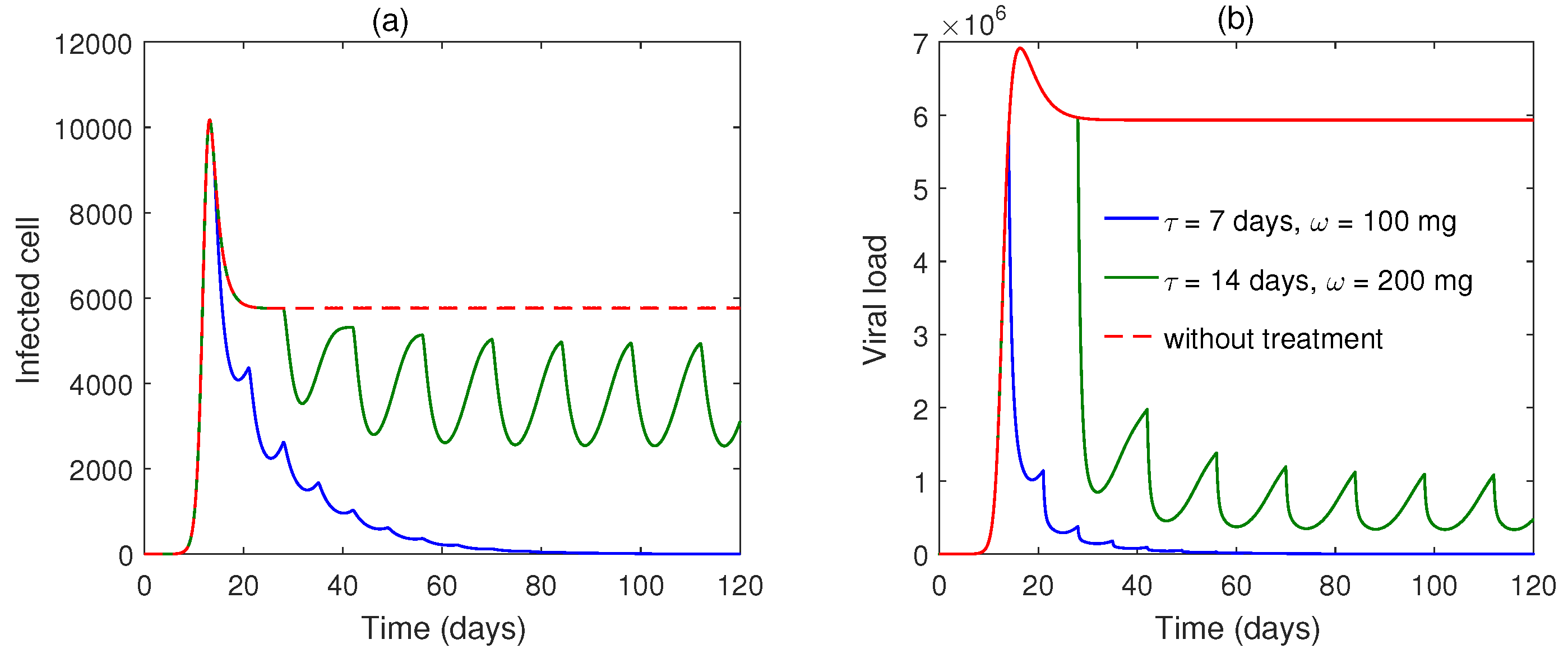
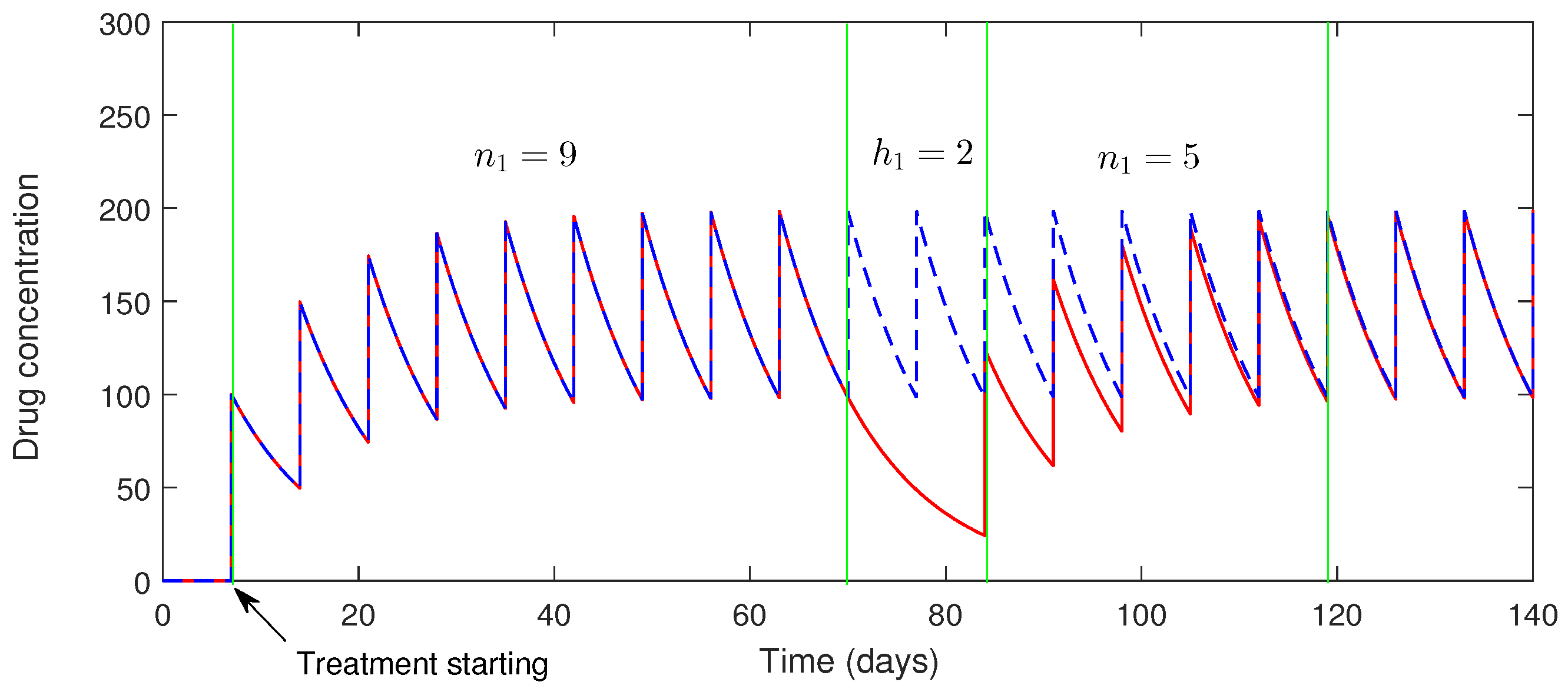
5. Numerical Simulation
6. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef]
- Delikhoon, M.; Guzman, M.I.; Nabizadeh, R.; Norouzian Baghani, A. Modes of transmission of severe acute respiratory syndrome-coronavirus-2 (SARS-CoV-2) and factors influencing on the airborne transmission: A review. Int. J. Environ. Res. Public Health 2021, 18, 395. [Google Scholar] [CrossRef] [PubMed]
- Anand, U.; Cabreros, C.; Mal, J.; Ballesteros, F., Jr.; Sillanpää, M.; Tripathi, V.; Bontempi, E. Novel coronavirus disease 2019 (COVID-19) pandemic: From transmission to control with an interdisciplinary vision. Environ. Res. 2021, 197, 111126. [Google Scholar] [CrossRef] [PubMed]
- Carsetti, R.; Zaffina, S.; Piano Mortari, E.; Terreri, S.; Corrente, F.; Capponi, C.; Palomba, P.; Mirabella, M.; Cascioli, S.; Palange, P.; et al. Different Innate and Adaptive Immune Responses to SARS-CoV-2 Infection of Asymptomatic, Mild, and Severe Cases. Front. Immunol. 2020, 11, 3365. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Xiang, Y.; Du, H.; Wing-Kin Wong, G. SARS-CoV-2 infection in children–Understanding the immune responses and controlling the pandemic. Pediatr. Allergy Immunol. 2020, 31, 449–453. [Google Scholar] [CrossRef]
- Zhou, Z.; Ren, L.; Zhang, L.; Zhong, J.; Xiao, Y.; Jia, Z.; Guo, L.; Yang, J.; Wang, C.; Jiang, S.; et al. Heightened innate immune responses in the respiratory tract of COVID-19 patients. Cell Host Microbe 2020, 27, 883–890. [Google Scholar] [CrossRef]
- Shayakhmetov, D.M. Virus infection recognition and early innate responses to non-enveloped viral vectors. Viruses 2010, 2, 244–261. [Google Scholar] [CrossRef]
- Tosi, M.F. Innate immune responses to infection. J. Allergy Clin. Immunol. 2005, 116, 241–249. [Google Scholar] [CrossRef]
- Azuma, M. Fundamental mechanisms of host immune responses to infection. J. Periodontal Res. 2006, 41, 361–373. [Google Scholar] [CrossRef]
- Spangelo, B.L.; Gorospe, W.C. Role of the cytokines in the neuroendocrine-immune system axis. Front. Neuroendocrinol. 1995, 16, 1–22. [Google Scholar] [CrossRef]
- Chatterjee, A.N.; Al Basir, F.; Almuqrin, M.A.; Mondal, J.; Khan, I. SARS-CoV-2 infection with lytic and non-lytic immune responses: A fractional order optimal control theoretical study. Results Phys. 2021, 26, 104260. [Google Scholar] [CrossRef]
- Okuonghae, D.; Omame, A. Analysis of a mathematical model for COVID-19 population dynamics in Lagos, Nigeria. Chaos Solitons Fractals 2020, 139, 110032. [Google Scholar] [CrossRef]
- Kucharski, A.J.; Russell, T.W.; Diamond, C.; Liu, Y.; Edmunds, J.; Funk, S.; Eggo, R.M.; Sun, F.; Jit, M.; Munday, J.D.; et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 553–558. [Google Scholar] [CrossRef]
- Rahman, B.; Khoshnaw, S.H.; Agaba, G.O.; Al Basir, F. How Containment Can Effectively Suppress the Outbreak of COVID-19: A Mathematical Modeling. Axioms 2021, 10, 204. [Google Scholar] [CrossRef]
- Shahzad, M.; Abdel-Aty, A.H.; Attia, R.A.; Khoshnaw, S.H.; Aldila, D.; Ali, M.; Sultan, F. Dynamics models for identifying the key transmission parameters of the COVID-19 disease. Alex. Eng. J. 2021, 60, 757–765. [Google Scholar] [CrossRef]
- Thomas, D.M.; Sturdivant, R.; Dhurandhar, N.V.; Debroy, S.; Clark, N. A primer on COVID-19 Mathematical Models. Obesity 2020, 28, 1375–1377. [Google Scholar] [CrossRef]
- Soukhovolsky, V.; Kovalev, A.; Pitt, A.; Kessel, B. A new modelling of the COVID 19 pandemic. Chaos Solitons Fractals 2020, 139, 110039. [Google Scholar] [CrossRef]
- Nadim, S.S.; Ghosh, I.; Chattopadhyay, J. Short-term predictions and prevention strategies for COVID-19: A model-based study. Appl. Math. Comput. 2021, 404, 126251. [Google Scholar] [CrossRef]
- Chatterjee, A.N.; Basir, F.A.; Ahmad, B.; Alsaedi, A. A Fractional-Order Compartmental Model of Vaccination for COVID-19 with the Fear Factor. Mathematics 2022, 10, 1451. [Google Scholar] [CrossRef]
- Mondal, J.; Samui, P.; Chatterjee, A.N. Optimal control strategies of non-pharmaceutical and pharmaceutical interventions for COVID-19 control. J. Interdiscip. Math. 2020, 24, 125–153. [Google Scholar] [CrossRef]
- Hattaf, K.; Mohsen, A.A.; Harraq, J.; Achtaich, N. Modeling the dynamics of COVID-19 with carrier effect and environmental contamination. Int. J. Model. Simul. Sci. Comput. 2021, 12, 2150048. [Google Scholar] [CrossRef]
- Maji, C.; Al Basir, F.; Mukherjee, D.; Ravichandran, C.; Nisar, K. COVID-19 propagation and the usefulness of awareness-based control measures: A mathematical model with delay. AIMS Math 2022, 7, 12091–12105. [Google Scholar] [CrossRef]
- Buonomo, B. Effects of information-dependent vaccination behavior on coronavirus outbreak: Insights from a SIRI model. Ric. Di Mat. 2020, 69, 483–499. [Google Scholar] [CrossRef]
- Chatterjee, A.N.; Al Basir, F. A model for SARS-CoV-2 infection with treatment. Comput. Math. Methods Med. 2020, 2020, 1352982. [Google Scholar] [CrossRef]
- Nath, B.J.; Dehingia, K.; Mishra, V.N.; Chu, Y.M.; Sarmah, H.K. Mathematical analysis of a within-host model of SARS-CoV-2. Adv. Differ. Equ. 2021, 2021, 113. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A. Fractional derivatives applied to MSEIR problems: Comparative study with real world data. Eur. Phys. J. Plus 2019, 134, 171. [Google Scholar] [CrossRef]
- Qureshi, S.; Yusuf, A.; Shaikh, A.A.; Inc, M. Transmission dynamics of varicella zoster virus modeled by classical and novel fractional operators using real statistical data. Phys. A Stat. Mech. Its Appl. 2019, 534, 122149. [Google Scholar] [CrossRef]
- Wang, S.; Pan, Y.; Wang, Q.; Miao, H.; Brown, A.N.; Rong, L. Modeling the viral dynamics of SARS-CoV-2 infection. Math. Biosci. 2020, 328, 108438. [Google Scholar] [CrossRef]
- Nath, A.; Ahmad, B. A fractional-order differential equation model of COVID-19 infection of epithelial cells. Chaos Solitons Fractals 2021, 147, 110952. [Google Scholar]
- Tang, S.; Ma, W.; Bai, P. A novel dynamic model describing the spread of the MERS-CoV and the expression of dipeptidyl peptidase 4. Comput. Math. Methods Med. 2017, 2017, 5285810. [Google Scholar] [CrossRef]
- Hernandez-Vargas, E.A.; Velasco-Hernandez, J.X. In-host mathematical modelling of covid-19 in humans. Annu. Rev. Control. 2020, 50, 448–456. [Google Scholar] [CrossRef]
- Wang, B.; Mondal, J.; Samui, P.; Chatterjee, A.N.; Yusuf, A. Effect of an antiviral drug control and its variable order fractional network in host COVID-19 kinetics. Eur. Phys. J. Spec. Top. 2022, 231, 1915–1929. [Google Scholar] [CrossRef]
- Sadria, M.; Layton, A.T. Modeling within-host SARS-CoV-2 infection dynamics and potential treatments. Viruses 2021, 13, 1141. [Google Scholar] [CrossRef]
- Zhou, Y.; Fu, B.; Zheng, X.; Wang, D.; Zhao, C.; Sun, R.; Tian, Z.; Xu, X.; Wei, H. Aberrant pathogenic GM-CSF+ T cells and inflammatory CD14+ CD16+ monocytes in severe pulmonary syndrome patients of a new coronavirus. bioRxiv 2020. [Google Scholar] [CrossRef]
- Encinar, J.A.; Menendez, J.A. Potential drugs targeting early innate immune evasion of SARS-coronavirus 2 via 2′-O-methylation of viral RNA. Viruses 2020, 12, 525. [Google Scholar] [CrossRef]
- Parums, D.V. Post-Exposure Prophylactic Neutralizing Monoclonal Antibodies to SARS-CoV-2 for Individuals at High Risk for COVID-19. Med. Sci. Monit. Int. Med. J. Exp. Clin. Res. 2021, 27, e934393-1–e934393-3. [Google Scholar] [CrossRef]
- Hwang, Y.C.; Lu, R.M.; Su, S.C.; Chiang, P.Y.; Ko, S.H.; Ke, F.Y.; Liang, K.H.; Hsieh, T.Y.; Wu, H.C. Monoclonal antibodies for COVID-19 therapy and SARS-CoV-2 detection. J. Biomed. Sci. 2022, 29, 1–50. [Google Scholar] [CrossRef]
- U.S. Food and Drug Administration. FDA Authorizes REGEN-COV Monoclonal Antibody Therapy for Post-Exposure Prophylaxis (Prevention) for COVID-19. 2021. Available online: https://www.fda.gov/drugs/drug-safety-and-availability/fda-authorizes-regen-cov-monoclonal-antibody-therapy-post-exposure-prophylaxis-prevention-covid-19 (accessed on 1 September 2022).
- Du, S.Q.; Yuan, W. Mathematical modeling of interaction between innate and adaptive immune responses in COVID-19 and implications for viral pathogenesis. J. Med Virol. 2020, 92, 1615–1628. [Google Scholar] [CrossRef]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Lou, J.; Smith, R.J. Modelling the effects of adherence to the HIV fusion inhibitor enfuvirtide. J. Theor. Biol. 2011, 268, 1–13. [Google Scholar] [CrossRef]
- Roy, P.K.; Chatterjee, A.N.; Li, X.Z. The effect of vaccination to dendritic cell and immune cell interaction in HIV disease progression. Int. J. Biomath. 2016, 9, 1650005. [Google Scholar] [CrossRef]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361. [Google Scholar] [CrossRef]
- Yu, H.; Zhong, S.; Agarwal, R.P. Mathematics analysis and chaos in an ecological model with an impulsive control strategy. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 776–786. [Google Scholar] [CrossRef]
- Lakshmikantham, V.; Simeonov, P.S. Theory of Impulsive Differential Equations; World Scientific: Singapore, 1989; Volume 6. [Google Scholar]
- Miron, R.; Smith, R. Modelling imperfect adherence to HIV induction therapy. BMC Infect. Dis. 2010, 10, 6. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N. Dynamics of SARS-CoV-2 infection model with two modes of transmission and immune response. Math. Biosci. Eng 2020, 17, 5326–5340. [Google Scholar] [CrossRef]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Osuna, O.; Villaseñor, G. On the Dulac functions. Qual. Theory Dyn. Syst. 2011, 10, 43–49. [Google Scholar] [CrossRef]




| Parameters | Short Description | Value (Unit) | References |
|---|---|---|---|
| Growth rate of epithelial cells | cells mL day | [48] | |
| Natural death rate of uninfected epithelial cells | day | [11,48] | |
| Blanket death rate of infected epithelial cells | day | [11] | |
| Rate of infection | (5–561) mL (RNA copies) day | [24,31] | |
| p | Growth rate of virus in cells | day | [48] |
| Virus clearance rate | day | [24] | |
| Rate of antibody response from immune cells | day | [48] | |
| r | Viral particles’ rate of neutralization by antibodies | mL (molecules) day | [48] |
| Half-maximal simulation threshold | (RNA copies) mL | [48] | |
| Antibody clearance rate | day | [48] | |
| Antibody production rate by drug | 6 molecules day gm | Assumed | |
| Decay rate of drug | 0.1 mg day | Assumed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chatterjee, A.N.; Basir, F.A.; Biswas, D.; Abraha, T. Global Dynamics of SARS-CoV-2 Infection with Antibody Response and the Impact of Impulsive Drug Therapy. Vaccines 2022, 10, 1846. https://doi.org/10.3390/vaccines10111846
Chatterjee AN, Basir FA, Biswas D, Abraha T. Global Dynamics of SARS-CoV-2 Infection with Antibody Response and the Impact of Impulsive Drug Therapy. Vaccines. 2022; 10(11):1846. https://doi.org/10.3390/vaccines10111846
Chicago/Turabian StyleChatterjee, Amar Nath, Fahad Al Basir, Dibyendu Biswas, and Teklebirhan Abraha. 2022. "Global Dynamics of SARS-CoV-2 Infection with Antibody Response and the Impact of Impulsive Drug Therapy" Vaccines 10, no. 11: 1846. https://doi.org/10.3390/vaccines10111846
APA StyleChatterjee, A. N., Basir, F. A., Biswas, D., & Abraha, T. (2022). Global Dynamics of SARS-CoV-2 Infection with Antibody Response and the Impact of Impulsive Drug Therapy. Vaccines, 10(11), 1846. https://doi.org/10.3390/vaccines10111846