Multidimensional Representation Dynamics for Abstract Visual Objects in Encoded Tangram Paradigms
Abstract
1. Introduction
2. Materials and Methods
2.1. Cognitive-Associative Encoding
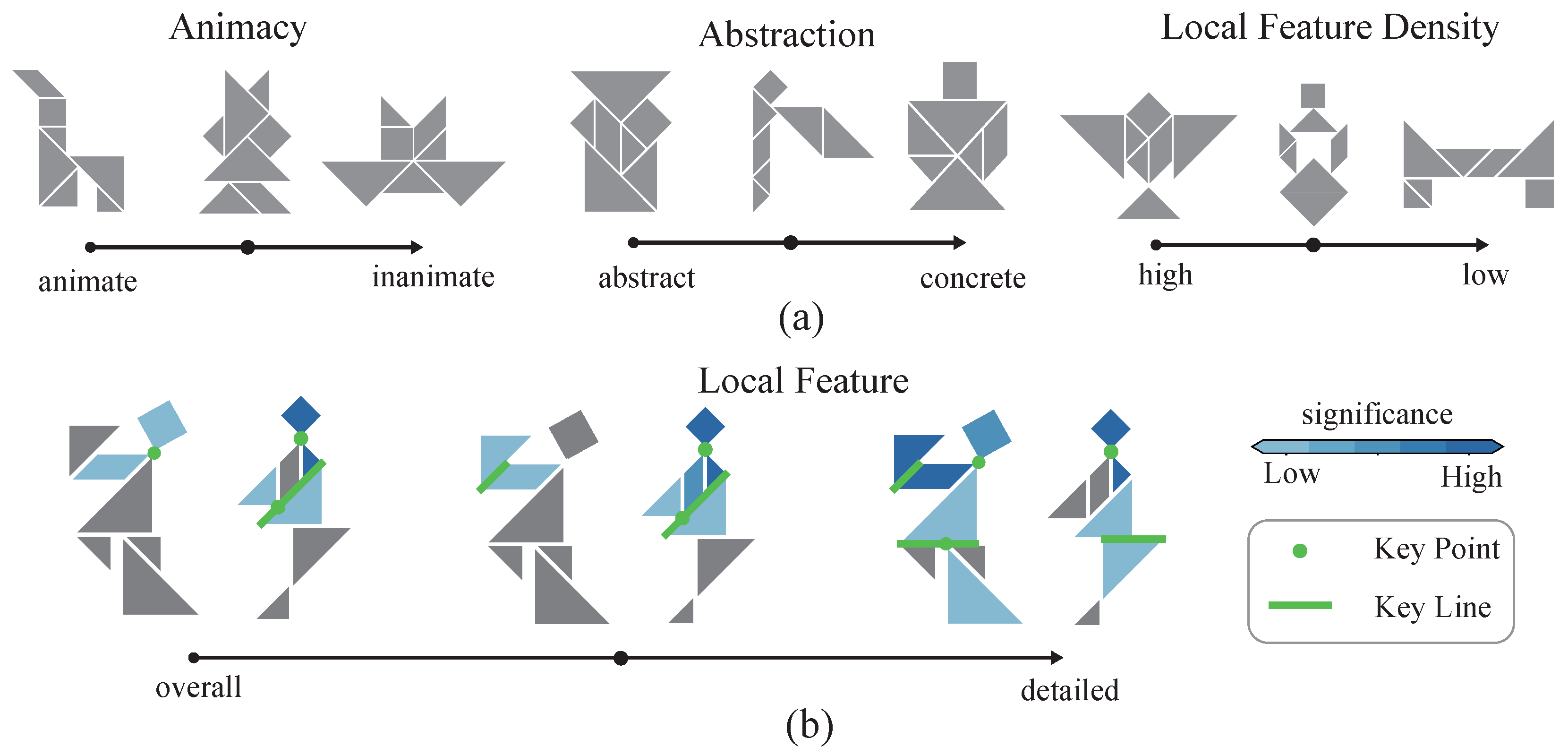
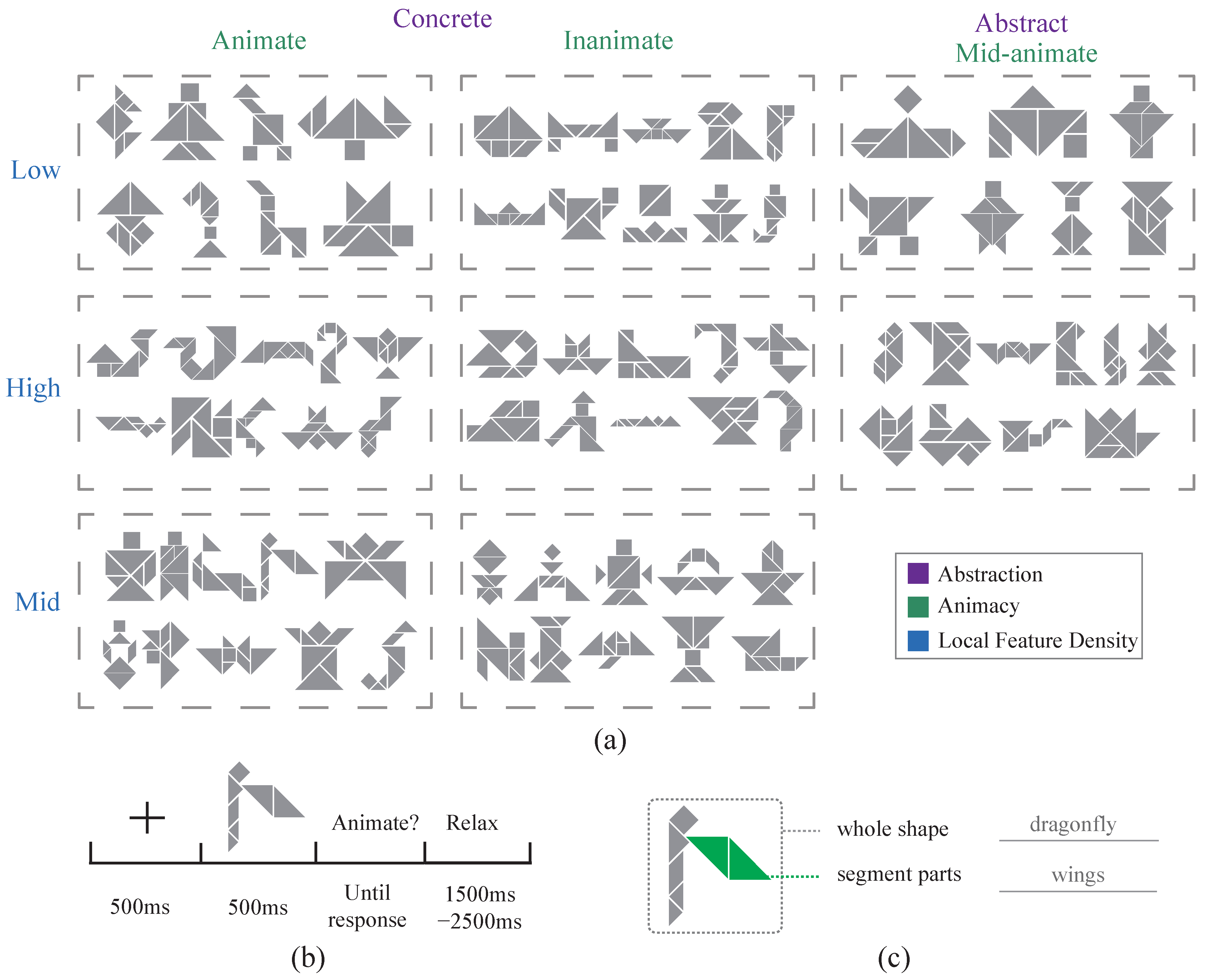
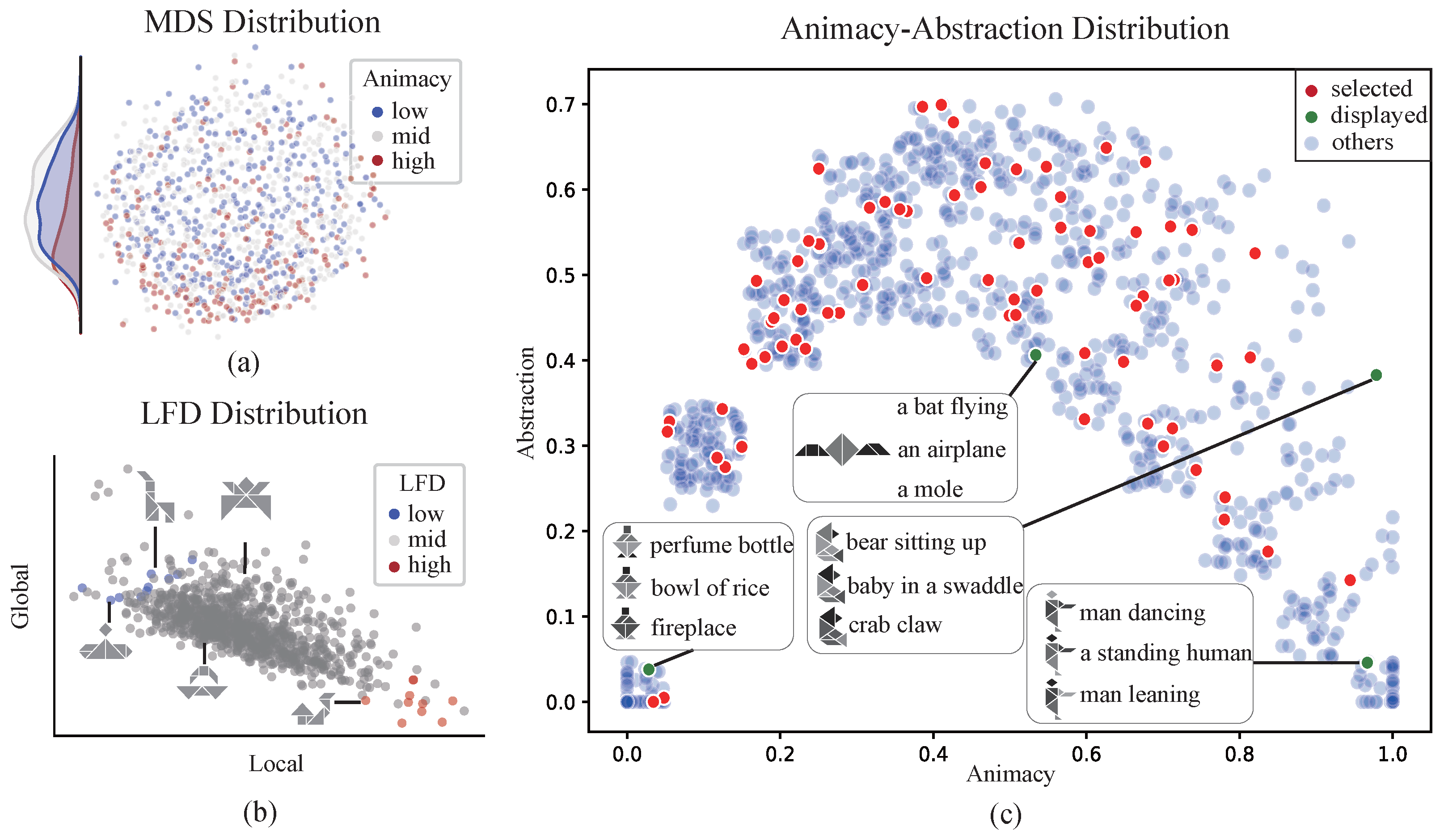
2.2. Visual Stimulus Dataset
2.3. Subjects and Experimental Procedures
2.4. Signal Acquisition and Preprocessing
2.5. Decoding Analysis
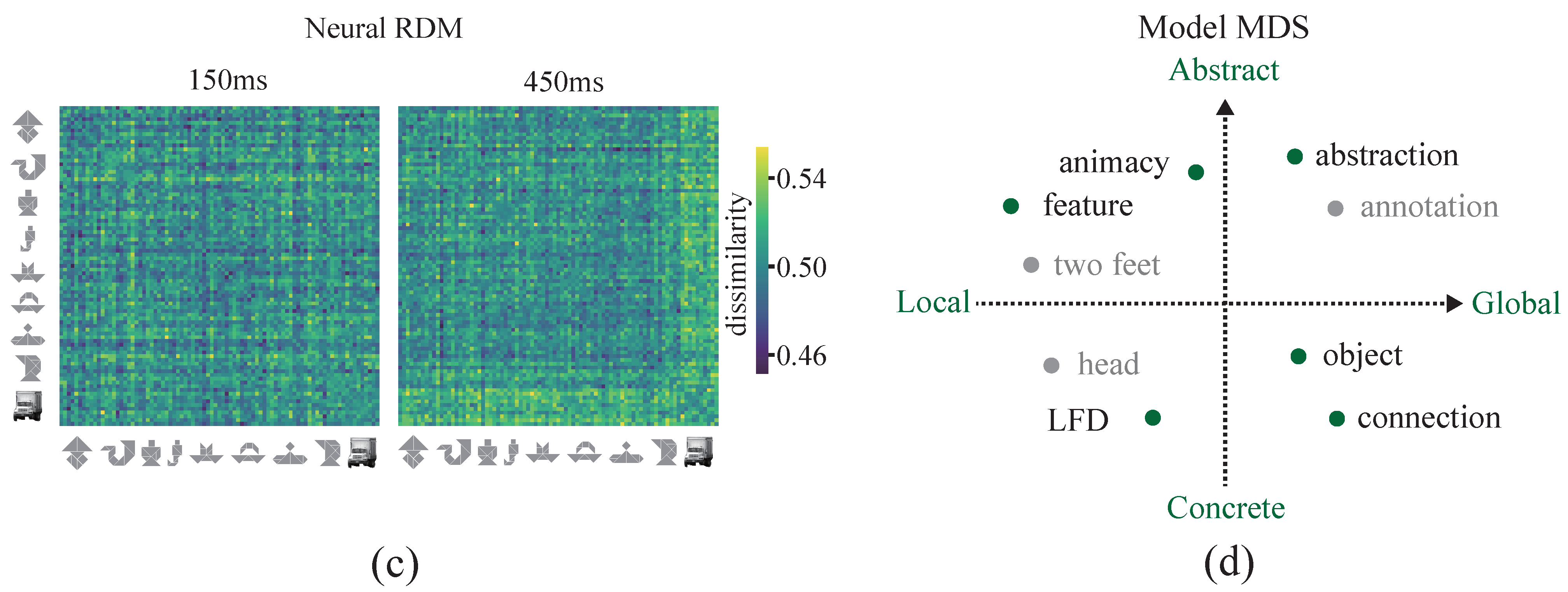
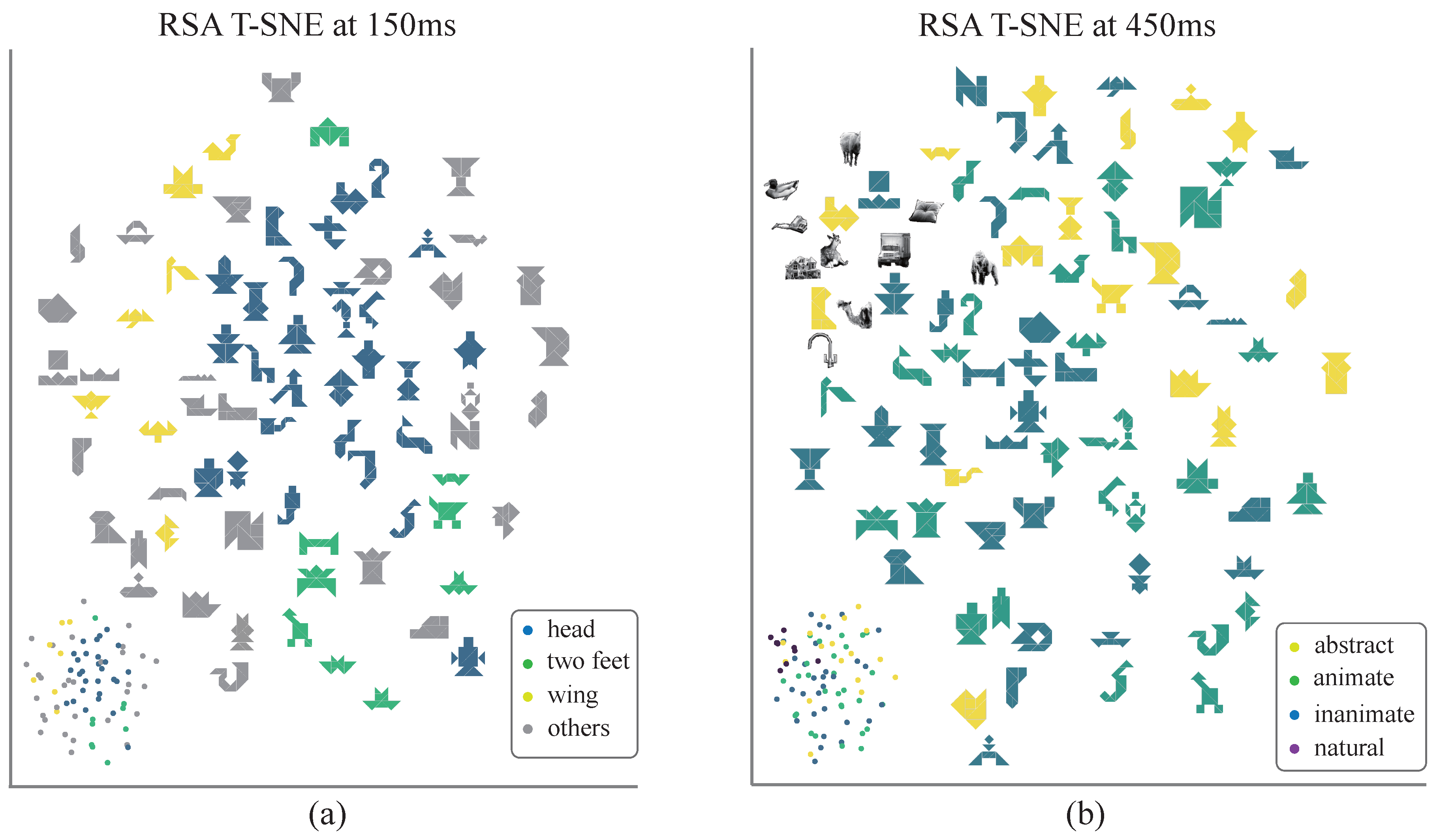
2.6. Representational Similarity Analysis
3. Results
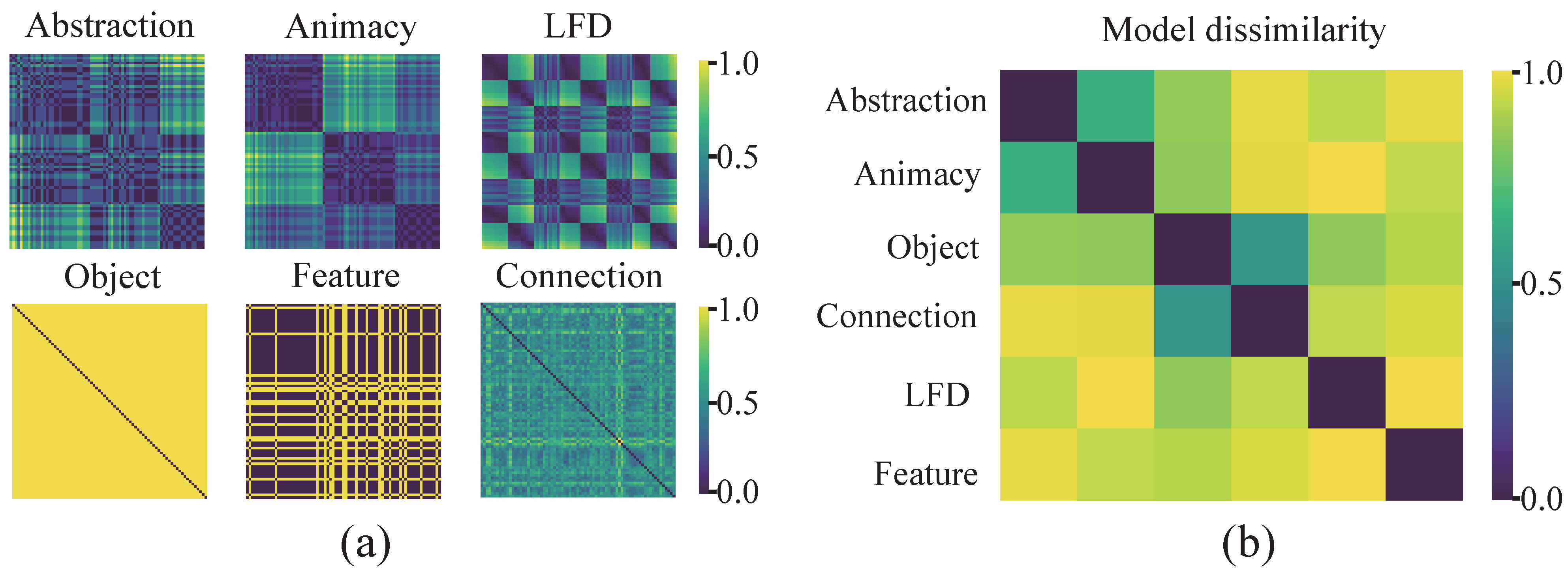
3.1. Cognitive-Associative Encoding Describes the Distributional Structure of Multidimensional Representations
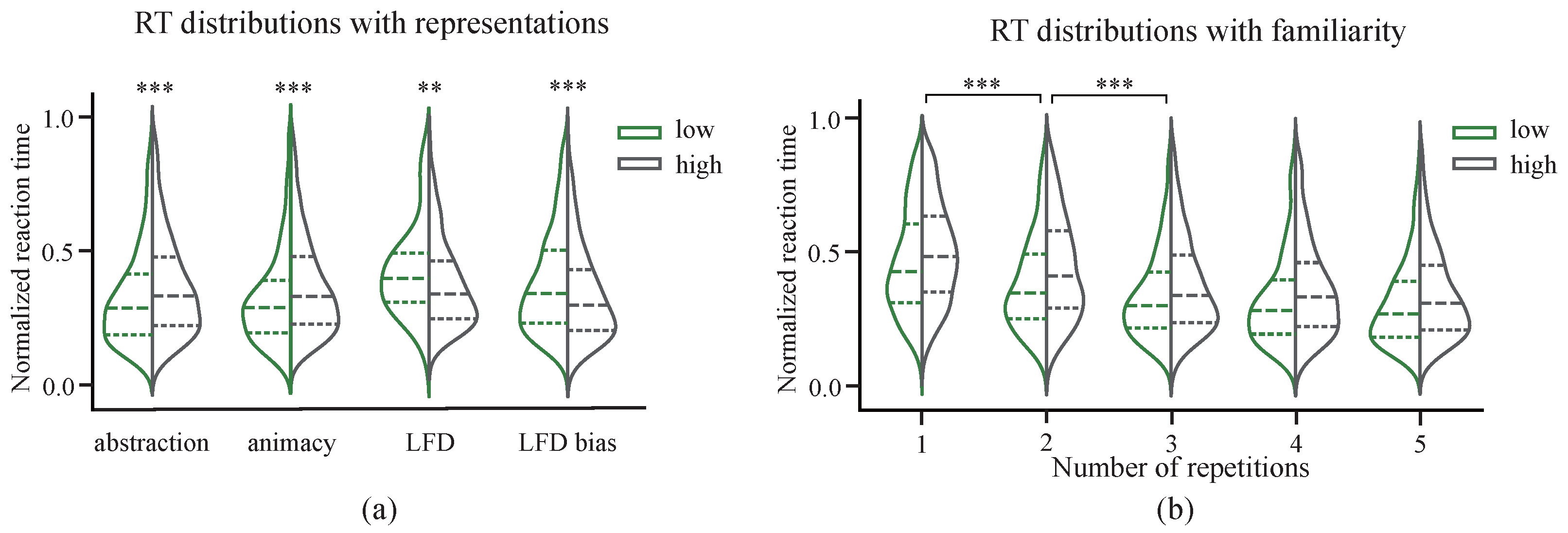
3.2. Behavioral Effects of Representation Dimensions
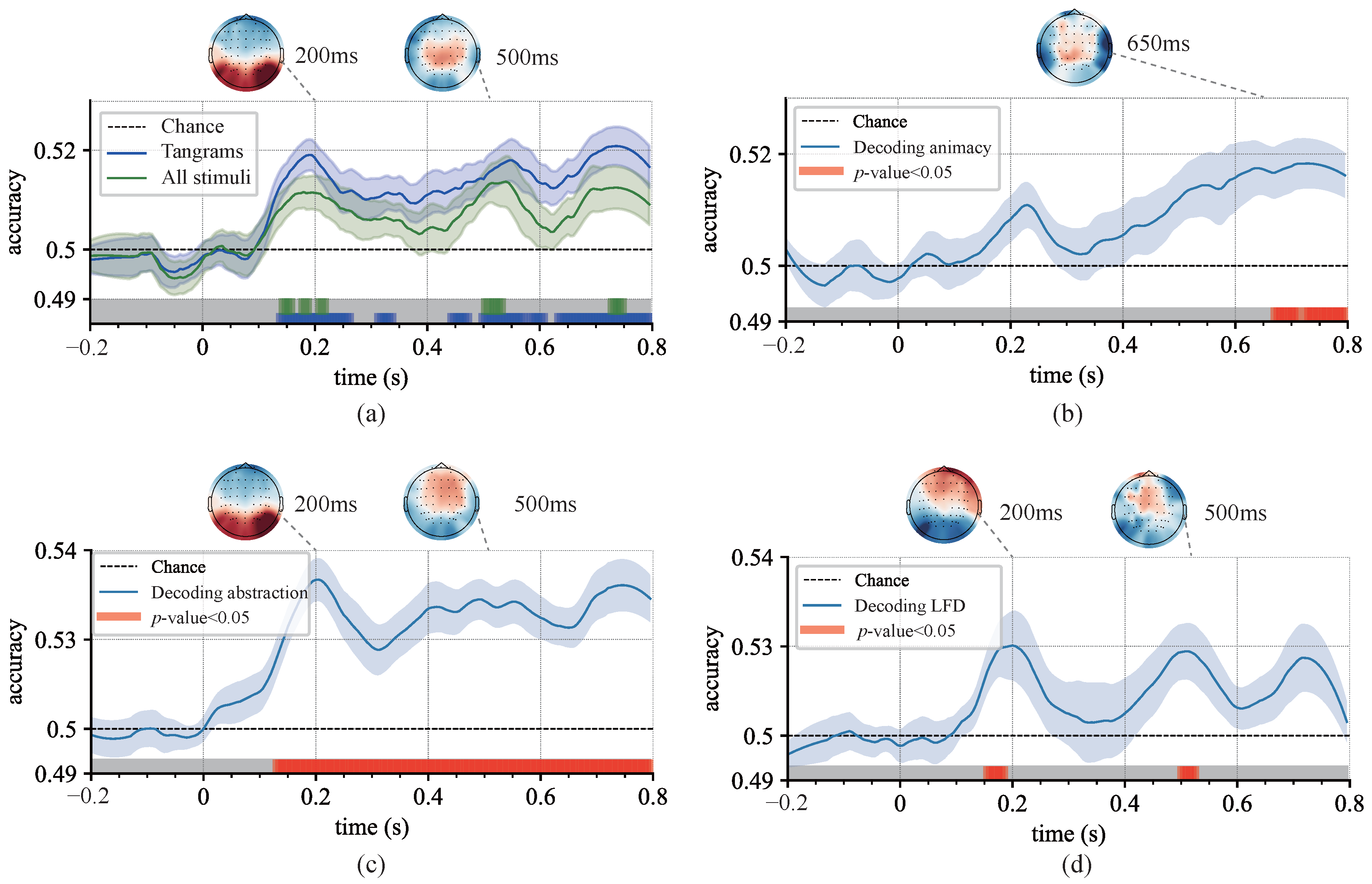
3.3. Decoding the Dynamics of Representation Dimensions
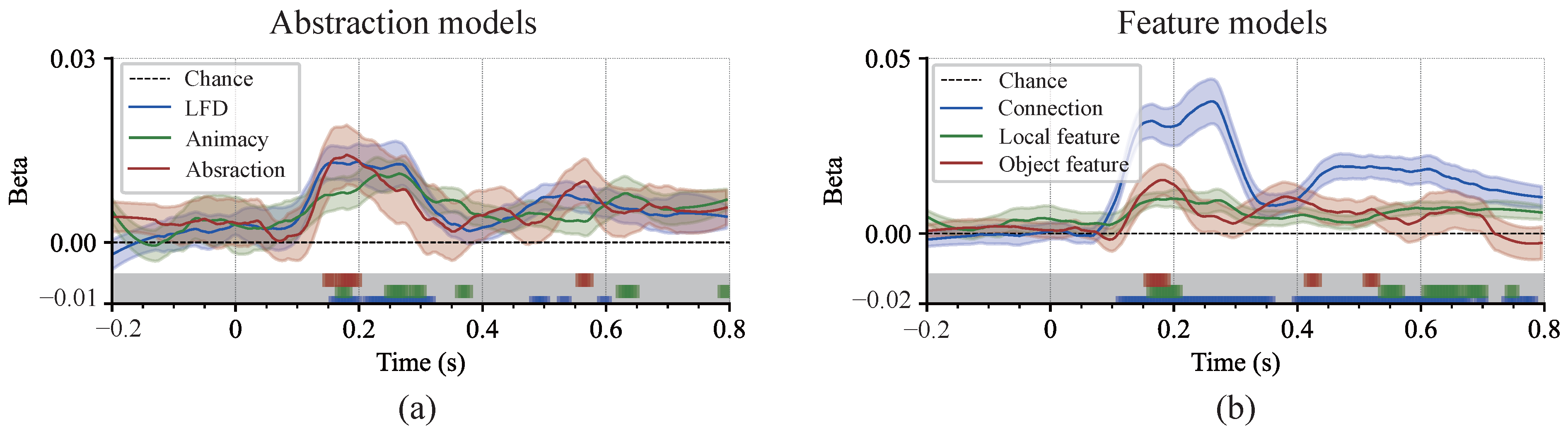
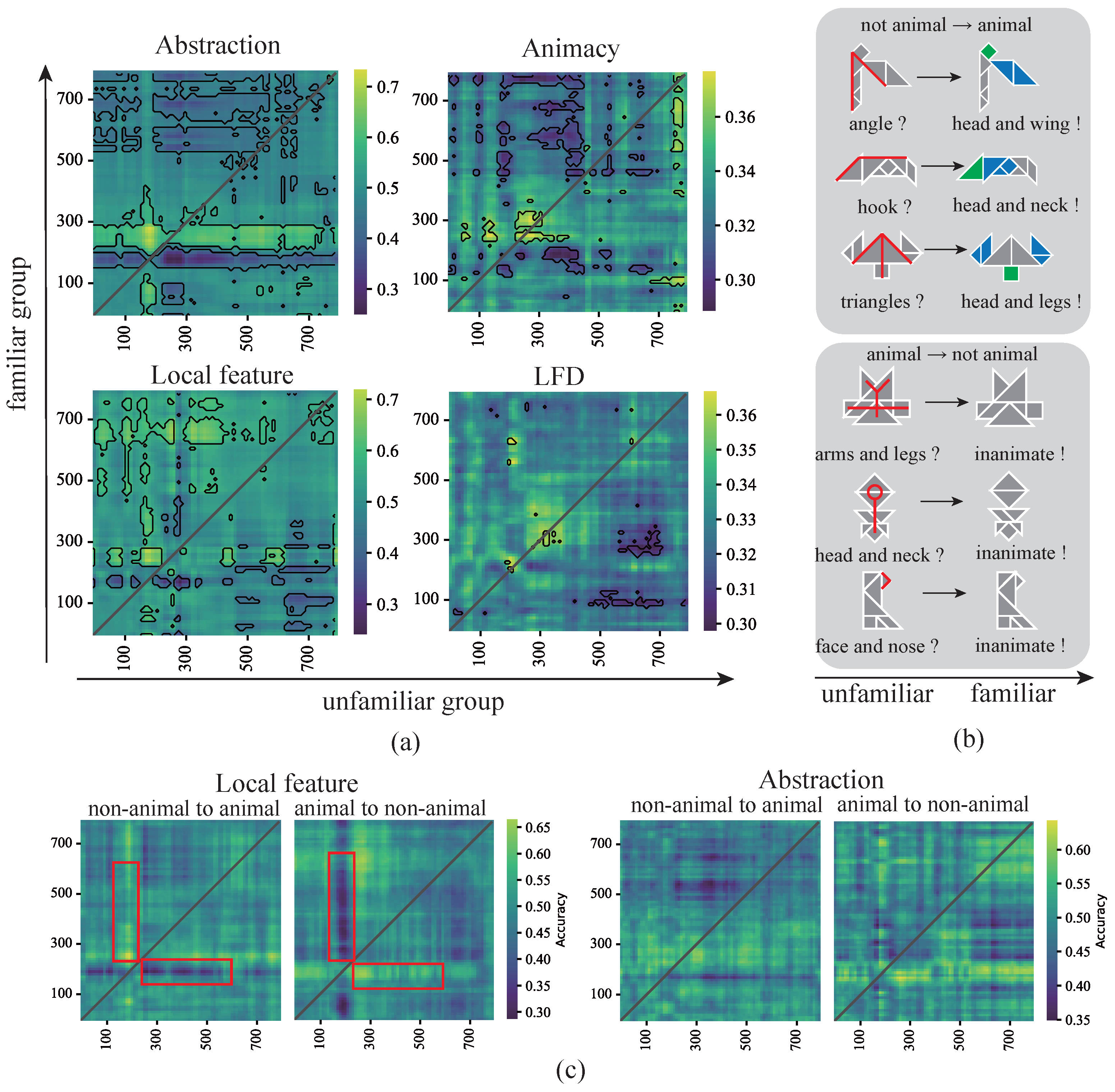
3.4. Cognitive Processes and the Effects of Multidimensional Representation Associations
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| EEG | Electroencephalography |
| fMRI | Functional Magnetic Resonance Imaging |
| MEG | Magnetoencephalography |
| EOG | Electrooculogram |
| RT | Response Time |
| LFD | Local Feature Density |
| MVPA | Multivariate Pattern Analysis |
| LDA | Linear Discriminant Analysis |
| RDM | Representational Dissimilarity Matrices |
| RSA | Representational Similarity Analysis |
Appendix A. Response Time
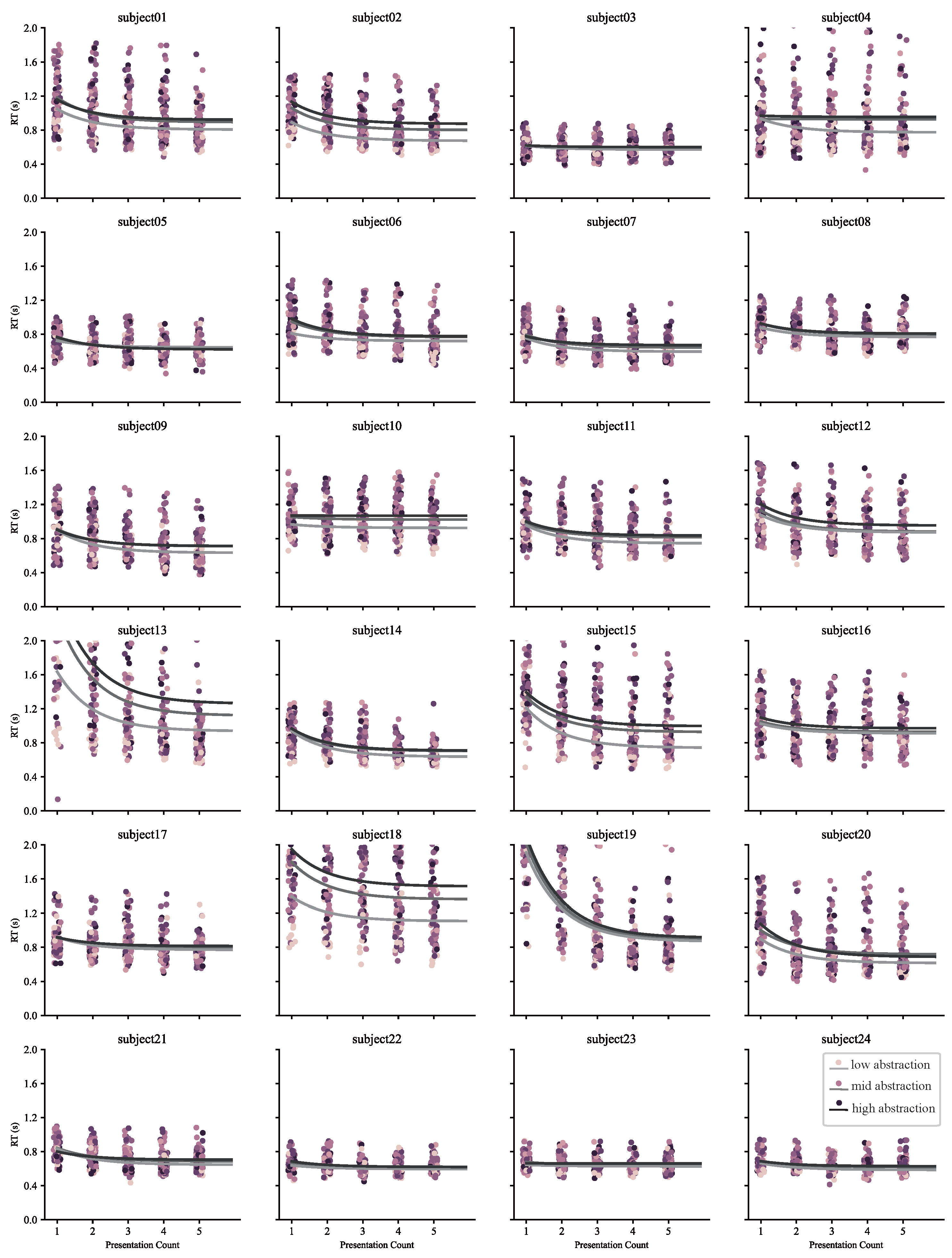
Appendix B. Cognitive-Associative Coding
Appendix B.1. Excellent Characteristics of Coding

Appendix B.2. Validation with MDS
Appendix B.3. Validation with SVM
Appendix B.4. Validation with Decision Tree
Appendix C. Representation Dissimilarity Matrices
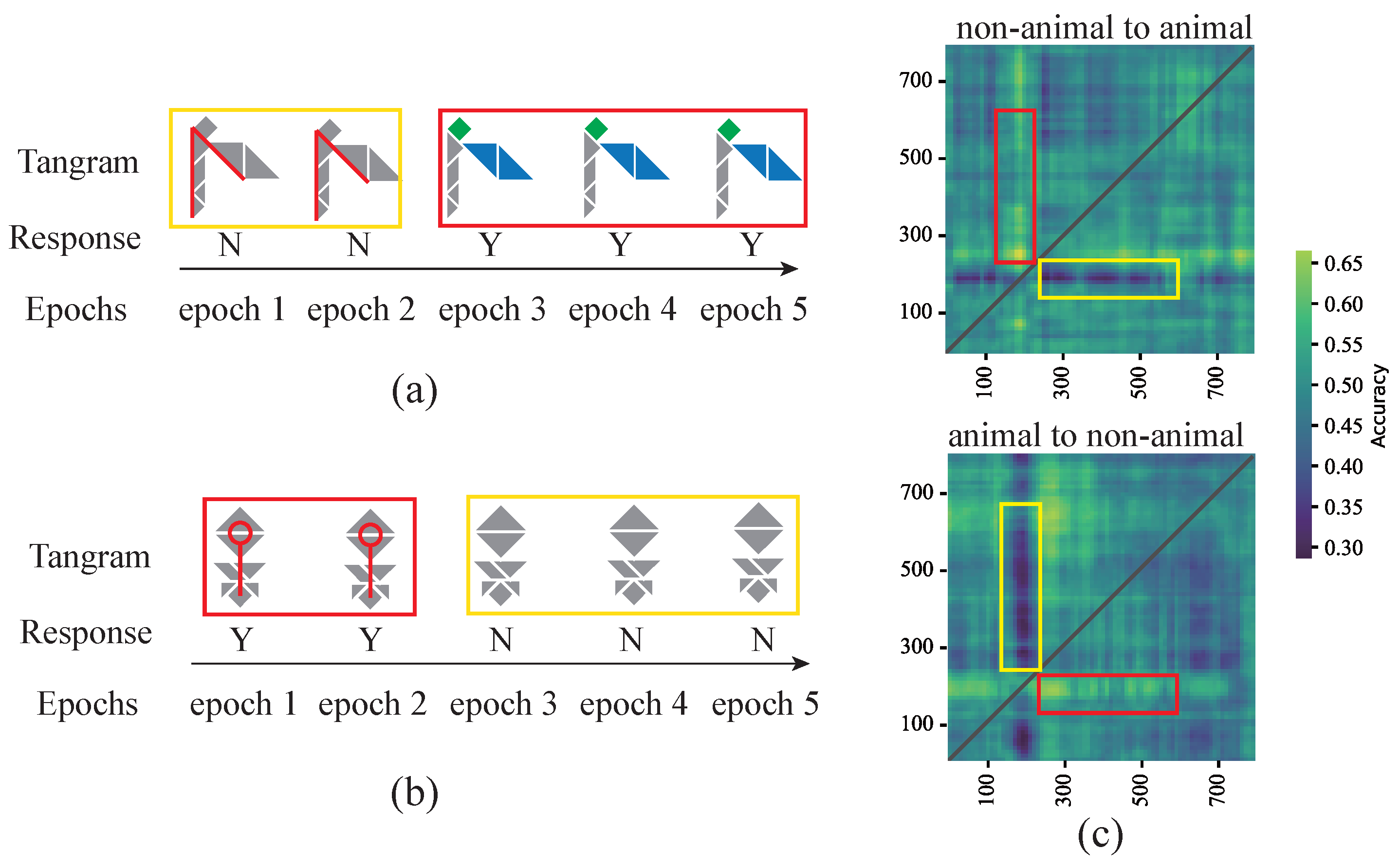
Appendix D. Change-of-Mind Analysis
Appendix D.1. Trials Screening
Appendix D.2. Examples of Change-of-Mind
References
- Contini, E.W.; Wardle, S.G.; Carlson, T.A. Decoding the time-course of object recognition in the human brain: From visual features to categorical decisions. Neuropsychologia 2017, 105, 165–176. [Google Scholar] [CrossRef]
- Carlson, T.A.; Ritchie, J.B.; Kriegeskorte, N.; Durvasula, S.; Ma, J. Reaction time for object categorization is predicted by representational distance. J. Cogn. Neurosci. 2014, 26, 132–142. [Google Scholar] [CrossRef]
- Keysers, C.; Xiao, D.K.; Földiák, P.; Perrett, D.I. The speed of sight. J. Cogn. Neurosci. 2001, 13, 90–101. [Google Scholar] [CrossRef] [PubMed]
- Mack, M.L.; Gauthier, I.; Sadr, J.; Palmeri, T.J. Object detection and basic-level categorization: Sometimes you know it is there before you know what it is. Psychon. Bull. Rev. 2008, 15, 28–35. [Google Scholar] [CrossRef]
- Potter, M.C.; Wyble, B.; Hagmann, C.E.; McCourt, E.S. Detecting meaning in RSVP at 13 ms per picture. Atten. Percept. Psychophys. 2014, 76, 270–279. [Google Scholar] [CrossRef] [PubMed]
- Grootswagers, T.; Robinson, A.K.; Carlson, T.A. The representational dynamics of visual objects in rapid serial visual processing streams. NeuroImage 2019, 188, 668–679. [Google Scholar] [CrossRef]
- Maule, J.; Skelton, A.E.; Franklin, A. The development of color perception and cognition. Annu. Rev. Psychol. 2023, 74, 87–111. [Google Scholar] [CrossRef]
- Konkle, T.; Oliva, A. A real-world size organization of object responses in occipitotemporal cortex. Neuron 2012, 74, 1114–1124. [Google Scholar] [CrossRef] [PubMed]
- Okazawa, G.; Hatch, C.E.; Mancoo, A.; Machens, C.K.; Kiani, R. Representational geometry of perceptual decisions in the monkey parietal cortex. Cell 2021, 184, 3748–3761.e18. [Google Scholar] [CrossRef]
- Grootswagers, T.; McKay, H.; Varlet, M. Unique contributions of perceptual and conceptual humanness to object representations in the human brain. NeuroImage 2022, 257, 119350. [Google Scholar] [CrossRef]
- Fasquel, A.; Brunellière, A.; Knutsen, D. A modified procedure for naming 332 pictures and collecting norms: Using tangram pictures in psycholinguistic studies. Behav. Res. Methods 2023, 55, 2297–2319. [Google Scholar] [CrossRef]
- Ji, A.; Kojima, N.; Rush, N.; Suhr, A.; Vong, W.K.; Hawkins, R.D.; Artzi, Y. Abstract visual reasoning with tangram shapes. arXiv 2022, arXiv:2211.16492. [Google Scholar] [CrossRef]
- Shore, T.; Androulakaki, T.; Skantze, G. KTH tangrams: A dataset for research on alignment and conceptual pacts in task-oriented dialogue. In Proceedings of the 11th International Conference on Language Resources and Evaluation, LREC 2018, Phoenix Seagaia Conference Center, Miyazaki, Japan, 7–12 May 2018; pp. 768–775. [Google Scholar]
- Grootswagers, T.; Robinson, A.K.; Shatek, S.M.; Carlson, T.A. Mapping the dynamics of visual feature coding: Insights into perception and integration. PLoS Comput. Biol. 2024, 20, e1011760. [Google Scholar] [CrossRef]
- Bao, P.; She, L.; McGill, M.; Tsao, D.Y. A map of object space in primate inferotemporal cortex. Nature 2020, 583, 103–108. [Google Scholar] [CrossRef]
- Clarke, A. Dynamic information processing states revealed through neurocognitive models of object semantics. Lang. Cogn. Neurosci. 2015, 30, 409–419. [Google Scholar] [CrossRef] [PubMed]
- Hebart, M.N.; Zheng, C.Y.; Pereira, F.; Baker, C.I. Revealing the multidimensional mental representations of natural objects underlying human similarity judgements. Nat. Hum. Behav. 2020, 4, 1173–1185. [Google Scholar] [CrossRef] [PubMed]
- Huth, A.G.; Nishimoto, S.; Vu, A.T.; Gallant, J.L. A continuous semantic space describes the representation of thousands of object and action categories across the human brain. Neuron 2012, 76, 1210–1224. [Google Scholar] [CrossRef]
- Mitchell, T.M.; Shinkareva, S.V.; Carlson, A.; Chang, K.M.; Malave, V.L.; Mason, R.A.; Just, M.A. Predicting human brain activity associated with the meanings of nouns. Science 2008, 320, 1191–1195. [Google Scholar] [CrossRef]
- Kmetová, M.; Nagyová Lehocká, Z. Using tangram as a manipulative tool for transition between 2D and 3D perception in geometry. Mathematics 2021, 9, 2185. [Google Scholar] [CrossRef]
- Kodak, T.; Bergmann, S.; LeBlanc, B.; Harman, M.J.; Ayazi, M. Examination of the effects of auditory and textual stimuli on response accuracy and latency during a math task and tangram puzzle. Anal. Verbal Behav. 2018, 34, 24–43. [Google Scholar] [CrossRef] [PubMed]
- Barnett, B.; Andersen, L.M.; Fleming, S.M.; Dijkstra, N. Identifying content-invariant neural signatures of perceptual vividness. PNAS Nexus 2024, 3, pgae061. [Google Scholar] [CrossRef]
- Field, D.J.; Hayes, A.; Hess, R.F. Contour integration by the human visual system: Evidence for a local “association field”. Vis. Res. 1993, 33, 173–193. [Google Scholar] [CrossRef] [PubMed]
- Malcolm, G.L.; Groen, I.I.; Baker, C.I. Making sense of real-world scenes. Trends Cogn. Sci. 2016, 20, 843–856. [Google Scholar] [CrossRef]
- Long, B.; Yu, C.P.; Konkle, T. Mid-level visual features underlie the high-level categorical organization of the ventral stream. Proc. Natl. Acad. Sci. USA 2018, 115, E9015–E9024. [Google Scholar] [CrossRef]
- Kravitz, D.J.; Saleem, K.S.; Baker, C.I.; Ungerleider, L.G.; Mishkin, M. The ventral visual pathway: An expanded neural framework for the processing of object quality. Trends Cogn. Sci. 2013, 17, 26–49. [Google Scholar] [CrossRef]
- Marr, D. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Radford, A.; Kim, J.W.; Hallacy, C.; Ramesh, A.; Goh, G.; Agarwal, S.; Sastry, G.; Askell, A.; Mishkin, P.; Clark, J. Learning transferable visual models from natural language supervision. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual, 18–24 July 2021; pp. 8748–8763. [Google Scholar]
- Kim, W.; Son, B.; Kim, I. Vilt: Vision-and-language transformer without convolution or region supervision. In Proceedings of the International Conference on Machine Learning. PMLR, Virtual, 18–24 July 2021; pp. 5583–5594. [Google Scholar]
- Nauta, M.; Van Bree, R.; Seifert, C. Neural prototype trees for interpretable fine-grained image recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Virtual, 19–25 June 2021; pp. 14933–14943. [Google Scholar]
- Peirce, J.W. Generating stimuli for neuroscience using PsychoPy. Front. Neuroinform. 2009, 2, 343. [Google Scholar] [CrossRef]
- Gramfort, A.; Luessi, M.; Larson, E.; Engemann, D.A.; Strohmeier, D.; Brodbeck, C.; Goj, R.; Jas, M.; Brooks, T.; Parkkonen, L. MEG and EEG data analysis with MNE-Python. Front. Neuroinform. 2013, 7, 267. [Google Scholar] [CrossRef]
- Lo, S.; Andrews, S. To transform or not to transform: Using generalized linear mixed models to analyse reaction time data. Front. Psychol. 2015, 6, 1171. [Google Scholar] [CrossRef]
- Grootswagers, T.; Wardle, S.G.; Carlson, T.A. Decoding dynamic brain patterns from evoked responses: A tutorial on multivariate pattern analysis applied to time series neuroimaging data. J. Cogn. Neurosci. 2017, 29, 677–697. [Google Scholar] [CrossRef] [PubMed]
- Oosterhof, N.N.; Connolly, A.C.; Haxby, J.V. CoSMoMVPA: Multi-modal multivariate pattern analysis of neuroimaging data in Matlab/GNU Octave. Front. Neuroinform. 2016, 10, 27. [Google Scholar] [CrossRef] [PubMed]
- Carlson, T.A.; Hogendoorn, H.; Kanai, R.; Mesik, J.; Turret, J. High temporal resolution decoding of object position and category. J. Vis. 2011, 11, 9. [Google Scholar] [CrossRef] [PubMed]
- King, J.R.; Dehaene, S. Characterizing the dynamics of mental representations: The temporal generalization method. Trends Cogn. Sci. 2014, 18, 203–210. [Google Scholar] [CrossRef]
- Meyers, E.M.; Freedman, D.J.; Kreiman, G.; Miller, E.K.; Poggio, T. Dynamic population coding of category information in inferior temporal and prefrontal cortex. J. Neurophysiol. 2008, 100, 1407–1419. [Google Scholar] [CrossRef]
- Kaiser, D.; Azzalini, D.C.; Peelen, M.V. Shape-independent object category responses revealed by MEG and fMRI decoding. J. Neurophysiol. 2016, 115, 2246–2250. [Google Scholar] [CrossRef]
- Kriegeskorte, N.; Mur, M.; Ruff, D.A.; Kiani, R.; Bodurka, J.; Esteky, H.; Tanaka, K.; Bandettini, P.A. Matching categorical object representations in inferior temporal cortex of man and monkey. Neuron 2008, 60, 1126–1141. [Google Scholar] [CrossRef]
- Kriegeskorte, N.; Kievit, R.A. Representational geometry: Integrating cognition, computation, and the brain. Trends Cogn. Sci. 2013, 17, 401–412. [Google Scholar] [CrossRef]
- Proklova, D.; Kaiser, D.; Peelen, M.V. MEG sensor patterns reflect perceptual but not categorical similarity of animate and inanimate objects. NeuroImage 2019, 193, 167–177. [Google Scholar] [CrossRef]
- Foster, J.J.; Sutterer, D.W.; Serences, J.T.; Vogel, E.K.; Awh, E. Alpha-band oscillations enable spatially and temporally resolved tracking of covert spatial attention. Psychol. Sci. 2017, 28, 929–941. [Google Scholar] [CrossRef]
- Meeter, M.; Olivers, C.N. Intertrial priming stemming from ambiguity: A new account of priming in visual search. Vis. Cogn. 2006, 13, 202–222. [Google Scholar] [CrossRef]
- Kaneshiro, B.; Perreau Guimaraes, M.; Kim, H.S.; Norcia, A.M.; Suppes, P. A representational similarity analysis of the dynamics of object processing using single-trial EEG classification. PLoS ONE 2015, 10, e0135697. [Google Scholar] [CrossRef]
- Baldauf, D.; Desimone, R. Neural mechanisms of object-based attention. Science 2014, 344, 424–427. [Google Scholar] [CrossRef]
- Walther, D.B.; Farzanfar, D.; Han, S.; Rezanejad, M. The mid-level vision toolbox for computing structural properties of real-world images. Front. Comput. Sci. 2023, 5, 1140723. [Google Scholar] [CrossRef]
- Shibata, K.; Sagi, D.; Watanabe, T. Two-stage model in perceptual learning: Toward a unified theory. Ann. N. Y. Acad. Sci. 2014, 1316, 18–28. [Google Scholar] [CrossRef] [PubMed]
- Kriegeskorte, N.; Mur, M.; Bandettini, P.A. Representational similarity analysis-connecting the branches of systems neuroscience. Front. Syst. Neurosci. 2008, 2, 249. [Google Scholar] [CrossRef] [PubMed]
- Bracci, S.; de Beeck, H.O. Dissociations and associations between shape and category representations in the two visual pathways. J. Neurosci. 2016, 36, 432–444. [Google Scholar] [CrossRef]
- Ritchie, J.B.; Tovar, D.A.; Carlson, T.A. Emerging object representations in the visual system predict reaction times for categorization. PLoS Comput. Biol. 2015, 11, e1004316. [Google Scholar] [CrossRef] [PubMed]
- Sha, L.; Haxby, J.V.; Abdi, H.; Guntupalli, J.S.; Oosterhof, N.N.; Halchenko, Y.O.; Connolly, A.C. The animacy continuum in the human ventral vision pathway. J. Cogn. Neurosci. 2015, 27, 665–678. [Google Scholar] [CrossRef]
- Schwartenbeck, P.; Baram, A.; Liu, Y.; Mark, S.; Muller, T.; Dolan, R.; Botvinick, M.; Kurth-Nelson, Z.; Behrens, T. Generative replay underlies compositional inference in the hippocampal-prefrontal circuit. Cell 2023, 186, 4885–4897.e14. [Google Scholar] [CrossRef]
- Eom, T.-H. Electroencephalography source localization. Clin. Exp. Pediatr. 2023, 66, 201–209. [Google Scholar] [CrossRef]

| Condition | Cognitive-Associative Code | Pixel Code | Human | |||
|---|---|---|---|---|---|---|
| SVM_line | SVM_poly | SVM_gauss | clip_pt | clip_ft | ||
| Whole + Black | 11.8 | 39.6 | 49.0 | 16.1 | 43.3 | 47.7 |
| Parts + Black | 12.4 | 41.3 | 50.3 | 16.4 | 45.3 | 49.1 |
| Whole + Color | 12.6 | 37.8 | 41.8 | 15.9 | 40.8 | 49.5 |
| Parts + Color | 12.3 | 40.3 | 43.6 | 15.0 | 45.4 | 63.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lian, Y.; Pan, S.; Shi, L. Multidimensional Representation Dynamics for Abstract Visual Objects in Encoded Tangram Paradigms. Brain Sci. 2025, 15, 941. https://doi.org/10.3390/brainsci15090941
Lian Y, Pan S, Shi L. Multidimensional Representation Dynamics for Abstract Visual Objects in Encoded Tangram Paradigms. Brain Sciences. 2025; 15(9):941. https://doi.org/10.3390/brainsci15090941
Chicago/Turabian StyleLian, Yongxiang, Shihao Pan, and Li Shi. 2025. "Multidimensional Representation Dynamics for Abstract Visual Objects in Encoded Tangram Paradigms" Brain Sciences 15, no. 9: 941. https://doi.org/10.3390/brainsci15090941
APA StyleLian, Y., Pan, S., & Shi, L. (2025). Multidimensional Representation Dynamics for Abstract Visual Objects in Encoded Tangram Paradigms. Brain Sciences, 15(9), 941. https://doi.org/10.3390/brainsci15090941






