Functional Importance Backbones of the Brain at Rest, Wakefulness, and Sleep
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
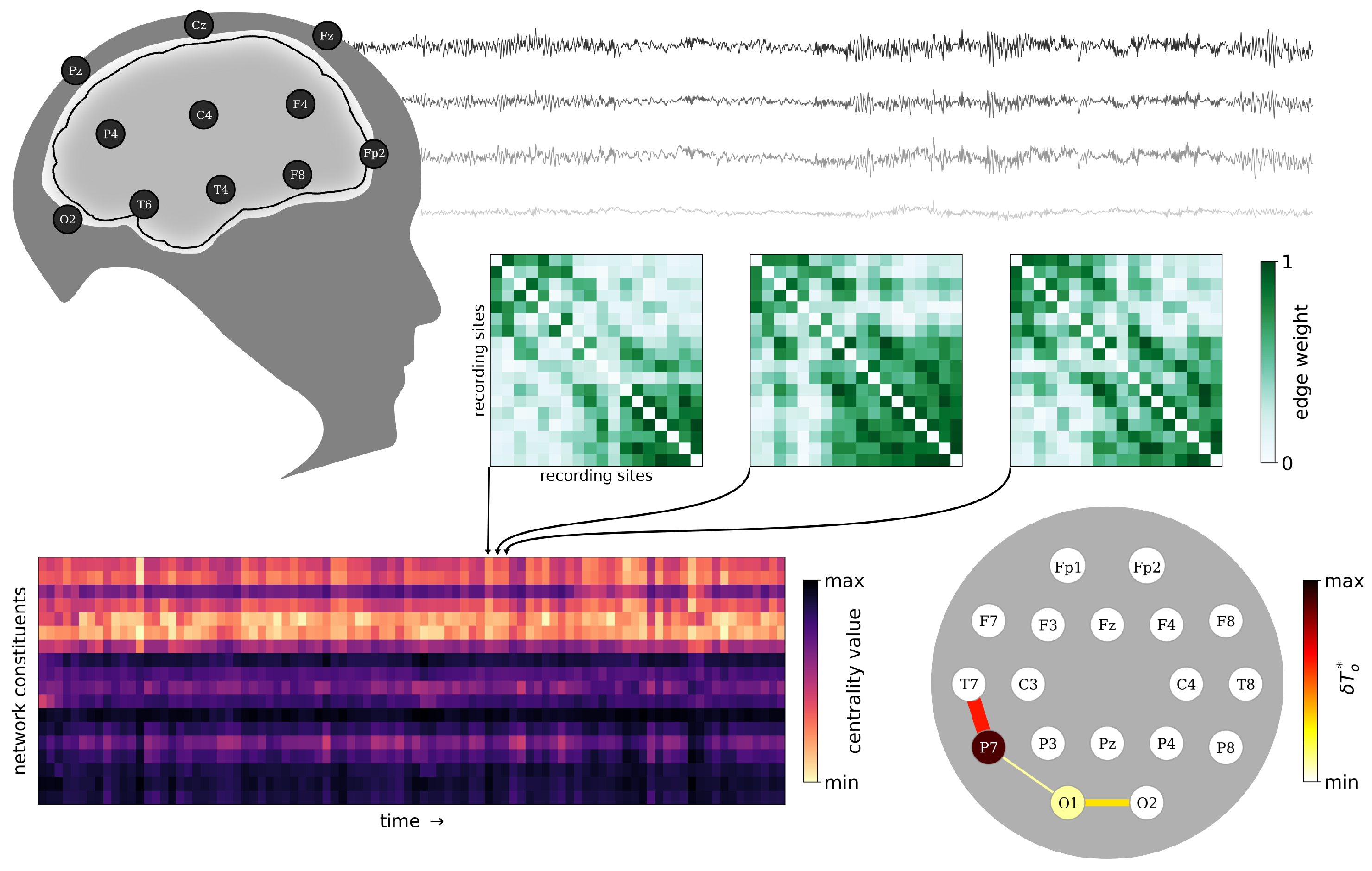
2.2. From EEG Data to Time-Evolving Functional Brain Networks
2.3. Estimating Vertex and Edge Centralities
2.4. Statistical Analyses
3. Results
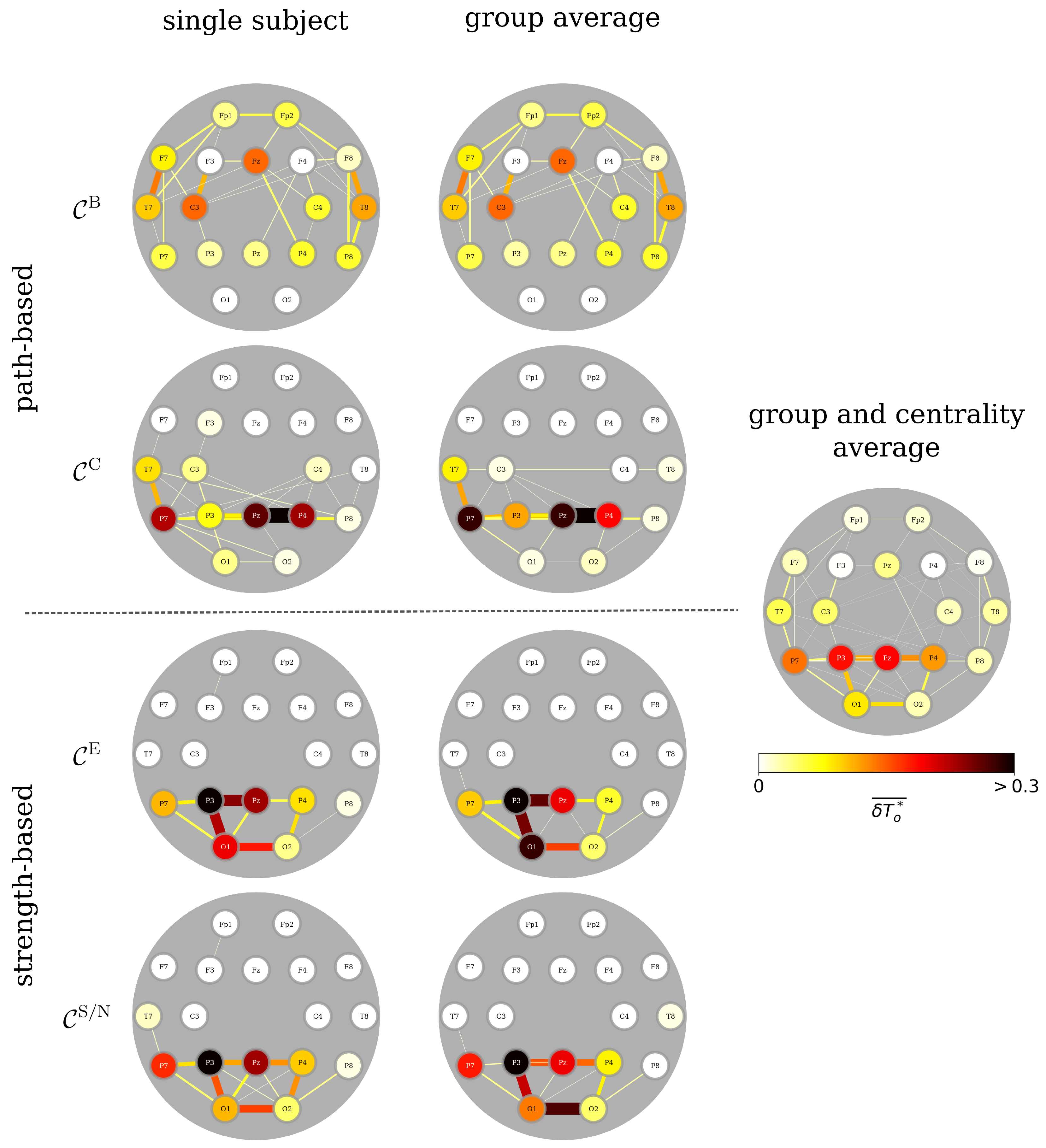
3.1. Identifying Functional Importance Backbones (FIBs) of the Brain
3.2. FIBs Are Insensitive to Epilepsy Types and Handedness
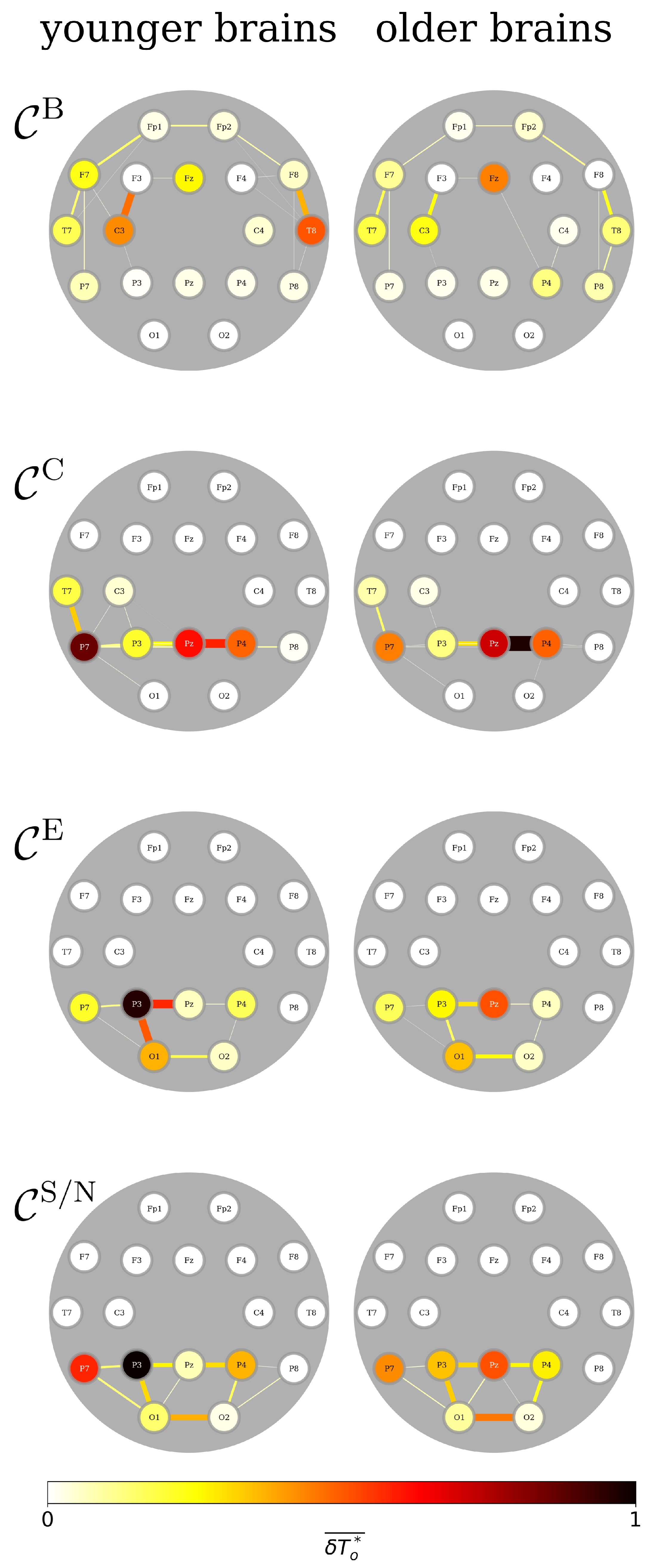
3.3. FIBs Are Sensitive to Sex, Age, and Continuous Attention
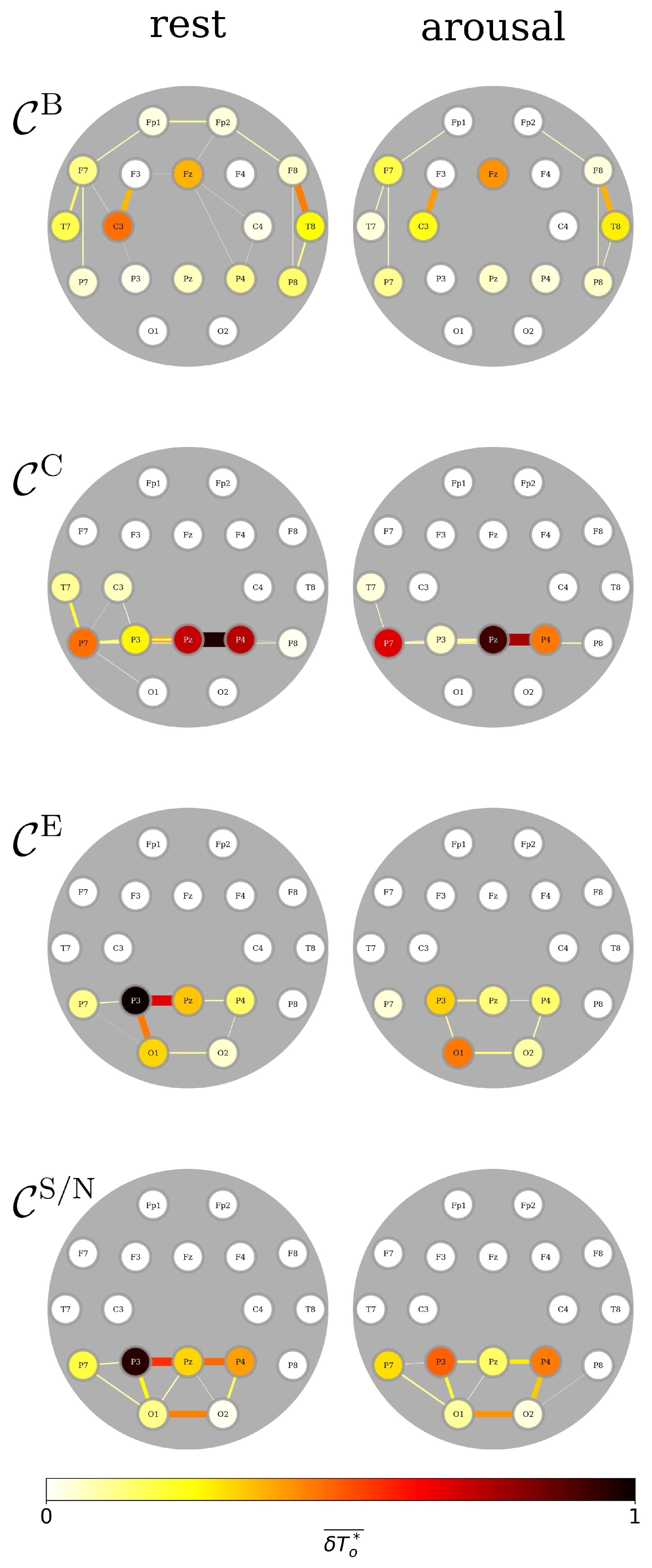
3.4. A Day in the Life of the Brain’s FIBs: Diurnal Variations
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A




References
- James, W.; Burkhardt, F.; Bowers, F.; Skrupskelis, I.K. The Principles of Psychology; Macmillan London: London, UK, 1890; Volume 1. [Google Scholar]
- Berger, H. Über das Elektroenkephalogramm des Menschen. Arch. Psychiat. Nervenkrankh. 1929, 87, 527–570. [Google Scholar] [CrossRef]
- Buckner, R.L.; Andrews-Hanna, J.R.; Schacter, D.L. The brain’s default network: Anatomy, function, and relevance to disease. Ann. N. Y. Acad. Sci. 2008, 1124, 1–38. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Jirsa, V.K.; McIntosh, A.R. Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat. Rev. Neurosci. 2011, 12, 43–56. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Corbetta, M. The dynamical balance of the brain at rest. Neuroscience 2011, 17, 107–123. [Google Scholar] [CrossRef] [PubMed]
- Doucet, G.; Naveau, M.; Petit, L.; Delcroix, N.; Zago, L.; Crivello, F.; Jobard, G.; Tzourio-Mazoyer, N.; Mazoyer, B.; Mellet, E.; et al. Brain activity at rest: A multiscale hierarchical functional organization. J. Neurophysiol. 2011, 105, 2753–2763. [Google Scholar] [CrossRef] [PubMed]
- Cabral, J.; Kringelbach, M.L.; Deco, G. Exploring the network dynamics underlying brain activity during rest. Prog. Neurobiol. 2014, 114, 102–131. [Google Scholar] [CrossRef] [PubMed]
- Callard, F.; Margulies, D.S. What we talk about when we talk about the default mode network. Front. Hum. Neurosci. 2014, 8, 619. [Google Scholar] [CrossRef] [PubMed]
- Raichle, M.E. The brain’s default mode network. Annu. Rev. Neurosci 2015, 38, 433–447. [Google Scholar] [CrossRef] [PubMed]
- Greicius, M.D.; Krasnow, B.; Reiss, A.L.; Menon, V. Functional connectivity in the resting brain: A network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. USA 2003, 100, 253–258. [Google Scholar] [CrossRef] [PubMed]
- Uddin, L.Q.; Clare Kelly, A.; Biswal, B.B.; Xavier Castellanos, F.; Milham, M.P. Functional connectivity of default mode network components: Correlation, anticorrelation, and causality. Hum. Brain Mapp. 2009, 30, 625–637. [Google Scholar] [CrossRef] [PubMed]
- Menon, V. 20 years of the default mode network: A review and synthesis. Neuron 2023, 111, 2469–2487. [Google Scholar] [CrossRef] [PubMed]
- Laufs, H.; Krakow, K.; Sterzer, P.; Eger, E.; Beyerle, A.; Salek-Haddadi, A.; Kleinschmidt, A. Electroencephalographic signatures of attentional and cognitive default modes in spontaneous brain activity fluctuations at rest. Proc. Natl. Acad. Sci. USA 2003, 100, 11053–11058. [Google Scholar] [CrossRef] [PubMed]
- Mantini, D.; Perrucci, M.G.; Del Gratta, C.; Romani, G.L.; Corbetta, M. Electrophysiological signatures of resting state networks in the human brain. Proc. Natl. Acad. Sci. USA 2007, 104, 13170–13175. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, E.; Von Wegner, F.; Morzelewski, A.; Brodbeck, V.; Laufs, H. Dynamic BOLD functional connectivity in humans and its electrophysiological correlates. Front. Hum. Neurosci. 2012, 6, 339. [Google Scholar] [CrossRef] [PubMed]
- Schölvinck, M.L.; Leopold, D.A.; Brookes, M.J.; Khader, P.H. The contribution of electrophysiology to functional connectivity mapping. Neuroimage 2013, 80, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Custo, A.; Van De Ville, D.; Wells, W.M.; Tomescu, M.I.; Brunet, D.; Michel, C.M. Electroencephalographic resting-state networks: Source localization of microstates. Brain Connect. 2017, 7, 671–682. [Google Scholar] [CrossRef] [PubMed]
- Kabbara, A.; El Falou, W.; Khalil, M.; Wendling, F.; Hassan, M. The dynamic functional core network of the human brain at rest. Sci. Rep. 2017, 7, 2936. [Google Scholar] [CrossRef] [PubMed]
- Marino, M.; Liu, Q.; Samogin, J.; Tecchio, F.; Cottone, C.; Mantini, D.; Porcaro, C. Neuronal dynamics enable the functional differentiation of resting state networks in the human brain. Hum. Brain Mapp. 2019, 40, 1445–1457. [Google Scholar] [CrossRef] [PubMed]
- Marino, M.; Arcara, G.; Porcaro, C.; Mantini, D. Hemodynamic correlates of electrophysiological activity in the default mode network. Front. Neurosci. 2019, 13, 1060. [Google Scholar] [CrossRef] [PubMed]
- De Pasquale, F.; Della Penna, S.; Snyder, A.Z.; Lewis, C.; Mantini, D.; Marzetti, L.; Belardinelli, P.; Ciancetta, L.; Pizzella, V.; Romani, G.L.; et al. Temporal dynamics of spontaneous MEG activity in brain networks. Proc. Natl. Acad. Sci. USA 2010, 107, 6040–6045. [Google Scholar] [CrossRef] [PubMed]
- Brookes, M.J.; Woolrich, M.; Luckhoo, H.; Price, D.; Hale, J.R.; Stephenson, M.C.; Barnes, G.R.; Smith, S.M.; Morris, P.G. Investigating the electrophysiological basis of resting state networks using magnetoencephalography. Proc. Natl. Acad. Sci. USA 2011, 108, 16783–16788. [Google Scholar] [CrossRef] [PubMed]
- Jin, S.H.; Jeong, W.; Lee, D.S.; Jeon, B.S.; Chung, C.K. Preserved high-centrality hubs but efficient network reorganization during eyes-open state compared with eyes-closed resting state: An MEG study. J. Neurophysiol. 2014, 111, 1455–1465. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Colclough, G.L.; Woolrich, M.W.; Tewarie, P.K.; Brookes, M.J.; Quinn, A.J.; Smith, S.M. How reliable are MEG resting-state connectivity metrics? NeuroImage 2016, 138, 284–293. [Google Scholar] [CrossRef] [PubMed]
- Duncan, D.; Duckrow, R.B.; Pincus, S.M.; Goncharova, I.; Hirsch, L.J.; Spencer, D.D.; Coifman, R.R.; Zaveri, H.P. Intracranial EEG evaluation of relationship within a resting state network. Clin. Neurophysiol. 2013, 124, 1943–1951. [Google Scholar] [CrossRef] [PubMed]
- Das, A.; de Los Angeles, C.; Menon, V. Electrophysiological foundations of the human default-mode network revealed by intracranial-EEG recordings during resting-state and cognition. NeuroImage 2022, 250, 118927. [Google Scholar] [CrossRef] [PubMed]
- Hutchison, R.M.; Womelsdorf, T.; Allen, E.A.; Bandettini, P.A.; Calhoun, V.D.; Corbetta, M.; Della Penna, S.; Duyn, J.H.; Glover, G.H.; Gonzalez-Castillo, J.; et al. Dynamic functional connectivity: Promise, issues, and interpretations. NeuroImage 2013, 80, 360–378. [Google Scholar] [CrossRef] [PubMed]
- Baker, A.P.; Brookes, M.J.; Rezek, I.A.; Smith, S.M.; Behrens, T.; Smith, P.J.P.; Woolrich, M. Fast transient networks in spontaneous human brain activity. ELIFE 2014, 3, e01867. [Google Scholar] [CrossRef] [PubMed]
- Zalesky, A.; Fornito, A.; Cocchi, L.; Gollo, L.L.; Breakspear, M. Time-resolved resting-state brain networks. Proc. Natl. Acad. Sci. USA 2014, 111, 10341–10346. [Google Scholar] [CrossRef] [PubMed]
- Lehnertz, K.; Geier, C.; Rings, T.; Stahn, K. Capturing time-varying brain dynamics. EPJ Nonlin. Biomed. Phys. 2017, 5, 2. [Google Scholar] [CrossRef]
- Lai, M.; Demuru, M.; Hillebrand, A.; Fraschini, M. A comparison between scalp-and source-reconstructed EEG networks. Sci. Rep. 2018, 8, 12269. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-González, V.; Gómez, C.; Shigihara, Y.; Hoshi, H.; Revilla-Vallejo, M.; Hornero, R.; Poza, J. Consistency of local activation parameters at sensor- and source-level in neural signals. J. Neural Eng. 2020, 17, 056020. [Google Scholar] [CrossRef] [PubMed]
- Lurie, D.J.; Kessler, D.; Bassett, D.S.; Betzel, R.F.; Breakspear, M.; Kheilholz, S.; Kucyi, A.; Liégeois, R.; Lindquist, M.A.; McIntosh, A.R.; et al. Questions and controversies in the study of time-varying functional connectivity in resting fMRI. Netw. Neurosci. 2020, 4, 30–69. [Google Scholar] [CrossRef] [PubMed]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Zuo, X.N.; Ehmke, R.; Mennes, M.; Imperati, D.; Castellanos, F.X.; Sporns, O.; Milham, M.P. Network centrality in the human functional connectome. Cereb. Cortex 2012, 22, 1862–1875. [Google Scholar] [CrossRef] [PubMed]
- van den Heuvel, M.P.; Sporns, O. Network hubs in the human brain. Trends Cogn. Sci. 2013, 17, 683–696. [Google Scholar] [CrossRef] [PubMed]
- Power, J.D.; Schlaggar, B.L.; Lessov-Schlaggar, C.N.; Petersen, S.E. Evidence for hubs in human functional brain networks. Neuron 2013, 79, 798–813. [Google Scholar] [CrossRef] [PubMed]
- De Pasquale, F.; Della Penna, S.; Sporns, O.; Romani, G.L.; Corbetta, M. A dynamic core network and global efficiency in the resting human brain. Cereb. Cortex 2016, 26, 4015–4033. [Google Scholar] [CrossRef] [PubMed]
- Hadriche, A.; Jmail, N.; Blanc, J.L.; Pezard, L. Using centrality measures to extract core pattern of brain dynamics during the resting state. Comput. Methods Programs Biomed. 2019, 179, 104985. [Google Scholar] [CrossRef] [PubMed]
- Lehnertz, K.; Ansmann, G.; Bialonski, S.; Dickten, H.; Geier, C.; Porz, S. Evolving networks in the human epileptic brain. Phys. D 2014, 267, 7–15. [Google Scholar] [CrossRef]
- Bröhl, T.; Rings, T.; Pukropski, J.; von Wrede, R.; Lehnertz, K. The time-evolving epileptic brain network: Concepts, definitions, accomplishments, perspectives. Front. Netw. Physiol. 2024, 3, 1338864. [Google Scholar] [CrossRef] [PubMed]
- Bröhl, T.; Lehnertz, K. Centrality-based identification of important edges in complex networks. Chaos 2019, 29, 033115. [Google Scholar] [CrossRef] [PubMed]
- Bröhl, T.; Lehnertz, K. A straightforward edge centrality concept derived from generalizing degree and strength. Sci. Rep. 2022, 12, 4407. [Google Scholar] [CrossRef] [PubMed]
- Schach, S.; Rings, T.; Bregulla, M.; Witt, J.A.; Bröhl, T.; Surges, R.; von Wrede, R.; Lehnertz, K.; Helmstaedter, C. Electrodermal Activity Biofeedback Alters Evolving Functional Brain Networks in People With Epilepsy, but in a Non-specific Manner. Front. Neurosci. 2022, 16, 828283. [Google Scholar] [CrossRef] [PubMed]
- von Wrede, R.; Bröhl, T.; Rings, T.; Pukropski, J.; Helmstaedter, C.; Lehnertz, K. Modifications of Functional Human Brain Networks by Transcutaneous Auricular Vagus Nerve Stimulation: Impact of Time of Day. Brain Sci. 2022, 12, 546. [Google Scholar] [CrossRef] [PubMed]
- von Wrede, R.; Rings, T.; Bröhl, T.; Pukropski, J.; Schach, S.; Helmstaedter, C.; Lehnertz, K. Transcutaneous Auricular Vagus Nerve Stimulation Differently Modifies Functional Brain Networks of Subjects With Different Epilepsy Types. Front. Hum. Neurosci. 2022, 16, 867563. [Google Scholar] [CrossRef] [PubMed]
- Bröhl, T.; Von Wrede, R.; Lehnertz, K. Impact of biological rhythms on the importance hierarchy of constituents in time-dependent functional brain networks. Front. Netw. Physiol. 2023, 3, 1237004. [Google Scholar] [CrossRef] [PubMed]
- Lehnertz, H.; Broehl, T.; Rings, T.; Von Wrede, R.; Lehnertz, K. Modifying functional brain networks in focal epilepsy by manual visceral-osteopathic stimulation of the vagus nerve at the abdomen. Front. Netw. Physiol. 2023, 3, 1205476. [Google Scholar] [CrossRef] [PubMed]
- Lehnertz, K.; Rings, T.; Bröhl, T. Time in Brain: How Biological Rhythms Impact on EEG Signals and on EEG-Derived Brain Networks. Front. Netw. Physiol. 2021, 1, 755016. [Google Scholar] [CrossRef] [PubMed]
- Seeck, M.; Koessler, L.; Bast, T.; Leijten, F.; Michel, C.; Baumgartner, C.; He, B.; Beniczky, S. The standardized EEG electrode array of the IFCN. Clin. Neurophysiol. 2017, 128, 2070–2077. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, M.; Dan, H.; Sakamoto, K.; Takeo, K.; Shimizu, K.; Kohno, S.; Oda, I.; Isobe, S.; Suzuki, T.; Kohyama, K.; et al. Three-dimensional probabilistic anatomical cranio-cerebral correlation via the international 10–20 system oriented for transcranial functional brain mapping. Neuroimage 2004, 21, 99–111. [Google Scholar] [CrossRef] [PubMed]
- Koessler, L.; Maillard, L.; Benhadid, A.; Vignal, J.P.; Felblinger, J.; Vespignani, H.; Braun, M. Automated cortical projection of EEG sensors: Anatomical correlation via the international 10–10 system. Neuroimage 2009, 46, 64–72. [Google Scholar] [CrossRef] [PubMed]
- Adamovich, T.; Zakharov, I.; Tabueva, A.; Malykh, S. The thresholding problem and variability in the EEG graph network parameters. Sci. Rep. 2022, 12, 18659. [Google Scholar] [CrossRef] [PubMed]
- Varela, F.J.; Lachaux, J.P.; Rodriguez, E.; Martinerie, J. The brain web: Phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2001, 2, 229–239. [Google Scholar] [CrossRef] [PubMed]
- Glass, L. Synchronization and rhythmic processes in physiology. Nature 2001, 410, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Uhlhaas, P.J.; Singer, W. Neural synchrony in brain disorders: Relevance for cognitive dysfunctions and pathophysiology. Neuron 2006, 52, 155–168. [Google Scholar] [CrossRef] [PubMed]
- Fell, J.; Axmacher, N. The role of phase synchronization in memory processes. Nat. Rev. Neurosci. 2011, 12, 105–118. [Google Scholar] [CrossRef] [PubMed]
- Siegel, M.; Donner, T.H.; Engel, A.K. Spectral fingerprints of large-scale neuronal interactions. Nat. Rev. Neurosci. 2012, 13, 121–134. [Google Scholar] [CrossRef] [PubMed]
- Mormann, F.; Lehnertz, K.; David, P.; Elger, C.E. Mean phase coherence as a measure for phase synchronization and its application to the EEG of epilepsy patients. Phys. D 2000, 144, 358–369. [Google Scholar] [CrossRef]
- O’Neill, G.C.; Tewarie, P.; Vidaurre, D.; Liuzzi, L.; Woolrich, M.W.; Brookes, M.J. Dynamics of large-scale electrophysiological networks: A technical review. Neuroimage 2018, 180, 559–576. [Google Scholar] [CrossRef] [PubMed]
- Boashash, B. Time Frequency Signal Analysis: Methods and Applications; Longman Cheshire: Melbourne, Australia, 1992. [Google Scholar]
- Osterhage, H.; Mormann, F.; Staniek, M.; Lehnertz, K. Measuring synchronization in the epileptic brain: A comparison of different approaches. Int. J. Bifurc. Chaos Appl. Sci. Eng. 2007, 17, 3539–3544. [Google Scholar] [CrossRef]
- Bavelas, A. Communication patterns in task-oriented groups. J. Acoust. Soc. Am. 1950, 22, 725–730. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef] [PubMed]
- Freeman, L.C. Centrality in social networks: Conceptual clarification. Soc. Netw. 1979, 1, 215–239. [Google Scholar] [CrossRef]
- Bonacich, P. Power and centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Everett, M.G. A Graph-theoretic perspective on centrality. Soc. Netw. 2006, 28, 466–484. [Google Scholar] [CrossRef]
- Freeman, L.C. A Set of Measures of Centrality Based on Betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
- Bonacich, P. Factoring and weighting approaches to status scores and clique identification. J. Math. Sociol. 1972, 2, 113–120. [Google Scholar] [CrossRef]
- Gonen, O.M.; Kwan, P.; O’Brien, T.J.; Lui, E.; Desmond, P.M. Resting-state functional MRI of the default mode network in epilepsy. Epilepsy Behav. 2020, 111, 107308. [Google Scholar] [CrossRef] [PubMed]
- Esteves, M.; Lopes, S.S.; Almeida, A.; Sousa, N.; Leite-Almeida, H. Unmasking the relevance of hemispheric asymmetries—Break on through (to the other side). Prog Neurobiol. 2020, 192, 101823. [Google Scholar] [CrossRef] [PubMed]
- Oldfield, R.C. The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia 1971, 9, 97–113. [Google Scholar] [CrossRef] [PubMed]
- Papadatou-Pastou, M.; Ntolka, E.; Schmitz, J.; Martin, M.; Munafò, M.R.; Ocklenburg, S.; Paracchini, S. Human handedness: A meta-analysis. Psychol. Bull 2020, 146, 481. [Google Scholar] [CrossRef] [PubMed]
- Raemaekers, M.; Schellekens, W.; Petridou, N.; Ramsey, N.F. Knowing left from right: Asymmetric functional connectivity during resting state. Brain Struct. Func. 2018, 223, 1909–1922. [Google Scholar] [CrossRef] [PubMed]
- Eliot, L.; Ahmed, A.; Khan, H.; Patel, J. Dump the “dimorphism”: Comprehensive synthesis of human brain studies reveals few male-female differences beyond size. Neurosci. Biobehav. Rev. 2021, 125, 667–697. [Google Scholar] [CrossRef] [PubMed]
- Bluhm, R.L.; Osuch, E.A.; Lanius, R.A.; Boksman, K.; Neufeld, R.W.; Théberge, J.; Williamson, P. Default mode network connectivity: Effects of age, sex, and analytic approach. Neuroreport 2008, 19, 887–891. [Google Scholar] [CrossRef] [PubMed]
- Sjøgård, M.; De Tiège, X.; Mary, A.; Peigneux, P.; Goldman, S.; Nagels, G.; Van Schependom, J.; Quinn, A.J.; Woolrich, M.W.; Wens, V. Do the posterior midline cortices belong to the electrophysiological default-mode network? Neuroimage 2019, 200, 221–230. [Google Scholar] [CrossRef] [PubMed]
- Vecchio, F.; Miraglia, F.; Bramanti, P.; Rossini, P.M. Human brain networks in physiological aging: A graph theoretical analysis of cortical connectivity from EEG data. J. Alzheimer’s Dis. 2014, 41, 1239–1249. [Google Scholar] [CrossRef] [PubMed]
- Petti, M.; Toppi, J.; Babiloni, F.; Cincotti, F.; Mattia, D.; Astolfi, L. EEG resting-state brain topological reorganization as a function of age. Comput. Intell. Neurosci. 2016, 2016, 6243694. [Google Scholar] [CrossRef] [PubMed]
- Grayson, D.S.; Fair, D.A. Development of large-scale functional networks from birth to adulthood: A guide to the neuroimaging literature. Neuroimage 2017, 160, 15–31. [Google Scholar] [CrossRef] [PubMed]
- Malagurski, B.; Liem, F.; Oschwald, J.; Mérillat, S.; Jäncke, L. Longitudinal functional brain network reconfiguration in healthy aging. Hum. Brain Mapp. 2020, 41, 4829–4845. [Google Scholar] [CrossRef] [PubMed]
- Sambataro, F.; Murty, V.P.; Callicott, J.H.; Tan, H.Y.; Das, S.; Weinberger, D.R.; Mattay, V.S. Age-related alterations in default mode network: Impact on working memory performance. Neurobiol. Aging 2010, 31, 839–852. [Google Scholar] [CrossRef] [PubMed]
- Tian, Y.; Chen, X.; Xu, D.; Yu, J.; Lei, X. Connectivity within the default mode network mediates the association between chronotype and sleep quality. J. Sleep Res. 2020, 29, e12948. [Google Scholar] [CrossRef] [PubMed]
- Sämann, P.G.; Wehrle, R.; Hoehn, D.; Spoormaker, V.I.; Peters, H.; Tully, C.; Holsboer, F.; Czisch, M. Development of the brain’s default mode network from wakefulness to slow wave sleep. Cereb. Cort. 2011, 21, 2082–2093. [Google Scholar] [CrossRef] [PubMed]
- Rasch, B.; Born, J. About sleep’s role in memory. Physiol. Rev. 2013, 93, 681–766. [Google Scholar] [CrossRef] [PubMed]
- Kaefer, K.; Stella, F.; McNaughton, B.L.; Battaglia, F.P. Replay, the default mode network and the cascaded memory systems model. Nat. Rev. Neurosci. 2022, 23, 628–640. [Google Scholar] [CrossRef] [PubMed]
- Culham, J.C.; Kanwisher, N.G. Neuroimaging of cognitive functions in human parietal cortex. Curr. Opin. Neurobiol. 2001, 11, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Gottlieb, J. From thought to action: The parietal cortex as a bridge between perception, action, and cognition. Neuron 2007, 53, 9–16. [Google Scholar] [CrossRef] [PubMed]
- De Benedictis, A.; Duffau, H.; Paradiso, B.; Grandi, E.; Balbi, S.; Granieri, E.; Colarusso, E.; Chioffi, F.; Marras, C.E.; Sarubbo, S. Anatomo-functional study of the temporo-parieto-occipital region: Dissection, tractographic and brain mapping evidence from a neurosurgical perspective. J. Anat. 2014, 225, 132–151. [Google Scholar] [CrossRef] [PubMed]
- Blank, S.C.; Scott, S.K.; Murphy, K.; Warburton, E.; Wise, R.J. Speech production: Wernicke, Broca and beyond. Brain 2002, 125, 1829–1838. [Google Scholar] [CrossRef] [PubMed]
- Brodt, S.; Inostroza, M.; Niethard, N.; Born, J. Sleep—A brain-state serving systems memory consolidation. Neuron 2023, 111, 1050–1075. [Google Scholar] [CrossRef] [PubMed]
- Giraud, A.L.; Poeppel, D. Cortical oscillations and speech processing: Emerging computational principles and operations. Nat. Neurosci. 2012, 15, 511–517. [Google Scholar] [CrossRef] [PubMed]
- Mudrik, L.; Deouell, L.Y. Neuroscientific evidence for processing without awareness. Annu. Rev. Neurosci. 2022, 45, 403–423. [Google Scholar] [CrossRef] [PubMed]
- Solms, M. Dreaming and REM sleep are controlled by different brain mechanisms. Behav. Brain Sci. 2000, 23, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Nir, Y.; Tononi, G. Dreaming and the brain: From phenomenology to neurophysiology. Trends Cogn. Sci. 2010, 14, 88–100. [Google Scholar] [CrossRef] [PubMed]
- Domhoff, G.W.; Fox, K.C. Dreaming and the default network: A review, synthesis, and counterintuitive research proposal. Conscious. Cogn. 2015, 33, 342–353. [Google Scholar] [CrossRef] [PubMed]
- Hong, C.C.H.; Jin, Y.; Potkin, S.G.; Buchsbaum, M.S.; Wu, J.; Callaghan, G.M.; Nudleman, K.L.; Gillin, J.C. Language in dreaming and regional EEG alpha power. Sleep 1996, 19, 232–235. [Google Scholar] [CrossRef] [PubMed]
- Arnulf, I.; Uguccioni, G.; Gay, F.; Baldayrou, E.; Golmard, J.L.; Gayraud, F.; Devevey, A. What does the sleeping brain say? Syntax and semantics of sleep talking in healthy subjects and in parasomnia patients. Sleep 2017, 40, zsx159. [Google Scholar] [CrossRef] [PubMed]
- Alfonsi, V.; D’Atri, A.; Scarpelli, S.; Mangiaruga, A.; De Gennaro, L. Sleep talking: A viable access to mental processes during sleep. Sleep Med. Rev. 2019, 44, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Fotiadis, P.; Parkes, L.; Davis, K.A.; Satterthwaite, T.D.; Shinohara, R.T.; Bassett, D.S. Structure–function coupling in macroscale human brain networks. Nat. Rev. Neurosci. 2024, 25, 688–704. [Google Scholar] [CrossRef] [PubMed]
- Betzel, R.F.; Faskowitz, J.; Sporns, O. Living on the edge: Network neuroscience beyond nodes. Trends Cogn. Sci. 2023, 27, 1068–1084. [Google Scholar] [CrossRef] [PubMed]
- Raichle, M.E. The restless brain: How intrinsic activity organizes brain function. Philos. Trans. R. Soc. B Biol. Sci. 2015, 370, 20140172. [Google Scholar] [CrossRef] [PubMed]
- Huk, A.; Bonnen, K.; He, B.J. Beyond trial-based paradigms: Continuous behavior, ongoing neural activity, and natural stimuli. J. Neurosci. 2018, 38, 7551–7558. [Google Scholar] [CrossRef] [PubMed]
- He, B.J. Scale-free brain activity: Past, present, and future. Trends Cogn. Sci. 2014, 18, 480–487. [Google Scholar] [CrossRef] [PubMed]
- Dosenbach, N.U.; Raichle, M.E.; Gordon, E.M. The brain’s action-mode network. Nat. Rev. Neurosci. 2025, 26, 158–168. [Google Scholar] [CrossRef] [PubMed]
- Stangl, M.; Maoz, S.L.; Suthana, N. Mobile cognition: Imaging the human brain in the ‘real world’. Nat. Rev. Neurosci. 2023, 24, 347–362. [Google Scholar] [CrossRef] [PubMed]
- Tudisco, F.; Higham, D.J. Node and edge nonlinear eigenvector centrality for hypergraphs. Commun. Phys. 2021, 4, 201. [Google Scholar] [CrossRef]
- Boccaletti, S.; De Lellis, P.; del Genio, C.; Alfaro-Bittner, K.; Criado, R.; Jalan, S.; Romance, M. The structure and dynamics of networks with higher order interactions. Phys. Rep. 2023, 1018, 1–64. [Google Scholar] [CrossRef]
- Tabar, M.R.R.; Nikakhtar, F.; Parkavousi, L.; Akhshi, A.; Feudel, U.; Lehnertz, K. Revealing Higher-Order Interactions in High-Dimensional Complex Systems: A Data-Driven Approach. Phys. Rev. X 2024, 14, 011050. [Google Scholar] [CrossRef]
- Kringelbach, M.L.; Deco, G. Brain states and transitions: Insights from computational neuroscience. Cell Rep. 2020, 32. [Google Scholar] [CrossRef] [PubMed]
- Badr, M.; Bröhl, T.; Dissouky, N.; Helmstaedter, C.; Lehnertz, K. Stable Yet Destabilised: Towards Understanding Brain Network Dynamics in Psychogenic Disorders. J. Clin. Med. 2025, 14, 666. [Google Scholar] [CrossRef] [PubMed]
- Klem, G.; Lüders, H.; Jasper, H.; Elger, C. The international federation of clinical neurophysiology. the ten-twenty electrode system of the international federation. Electroencephalogr. Clin. Neurophysiol. Suppl. 1999, 52, 3–6. [Google Scholar] [PubMed]
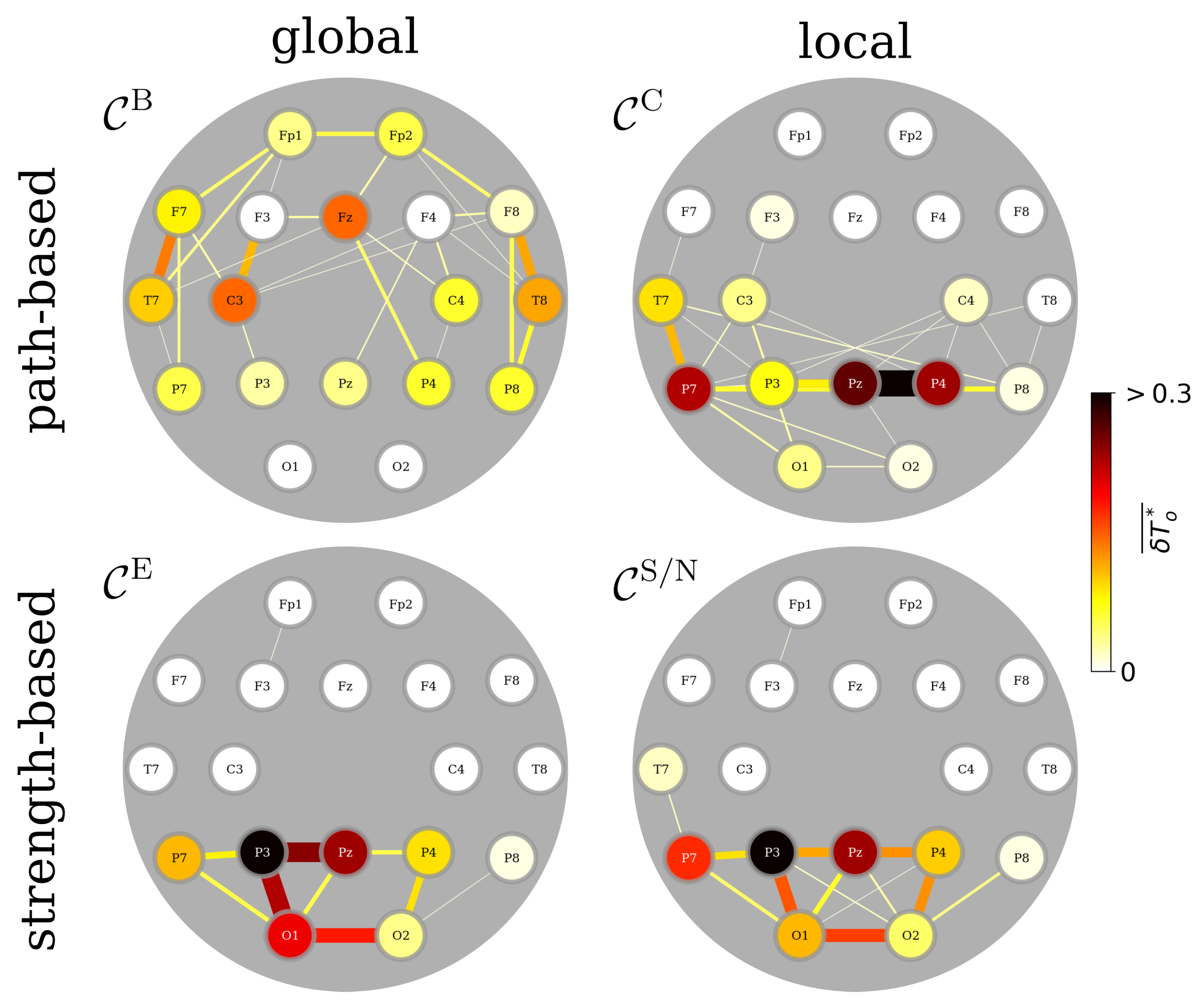
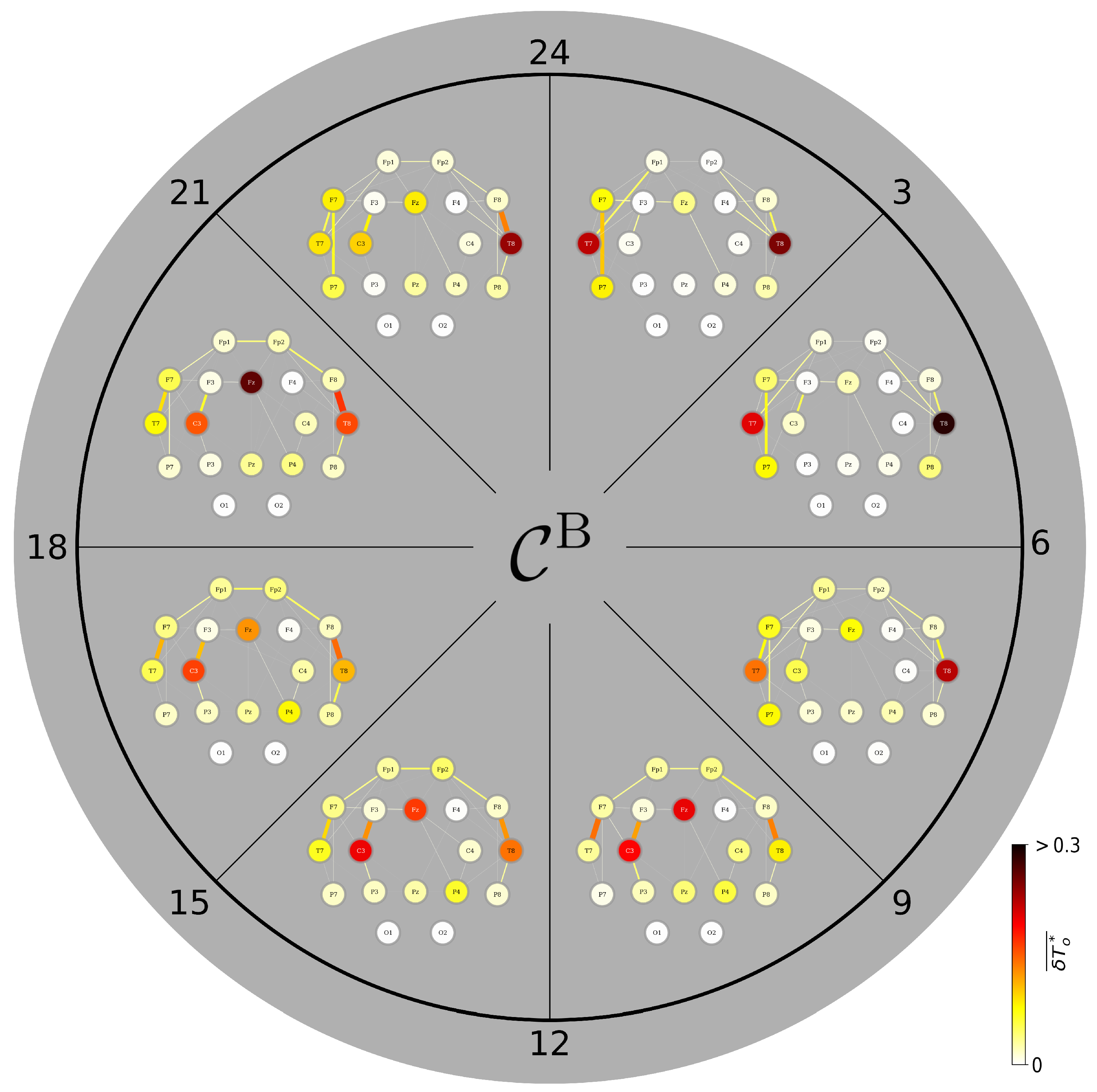
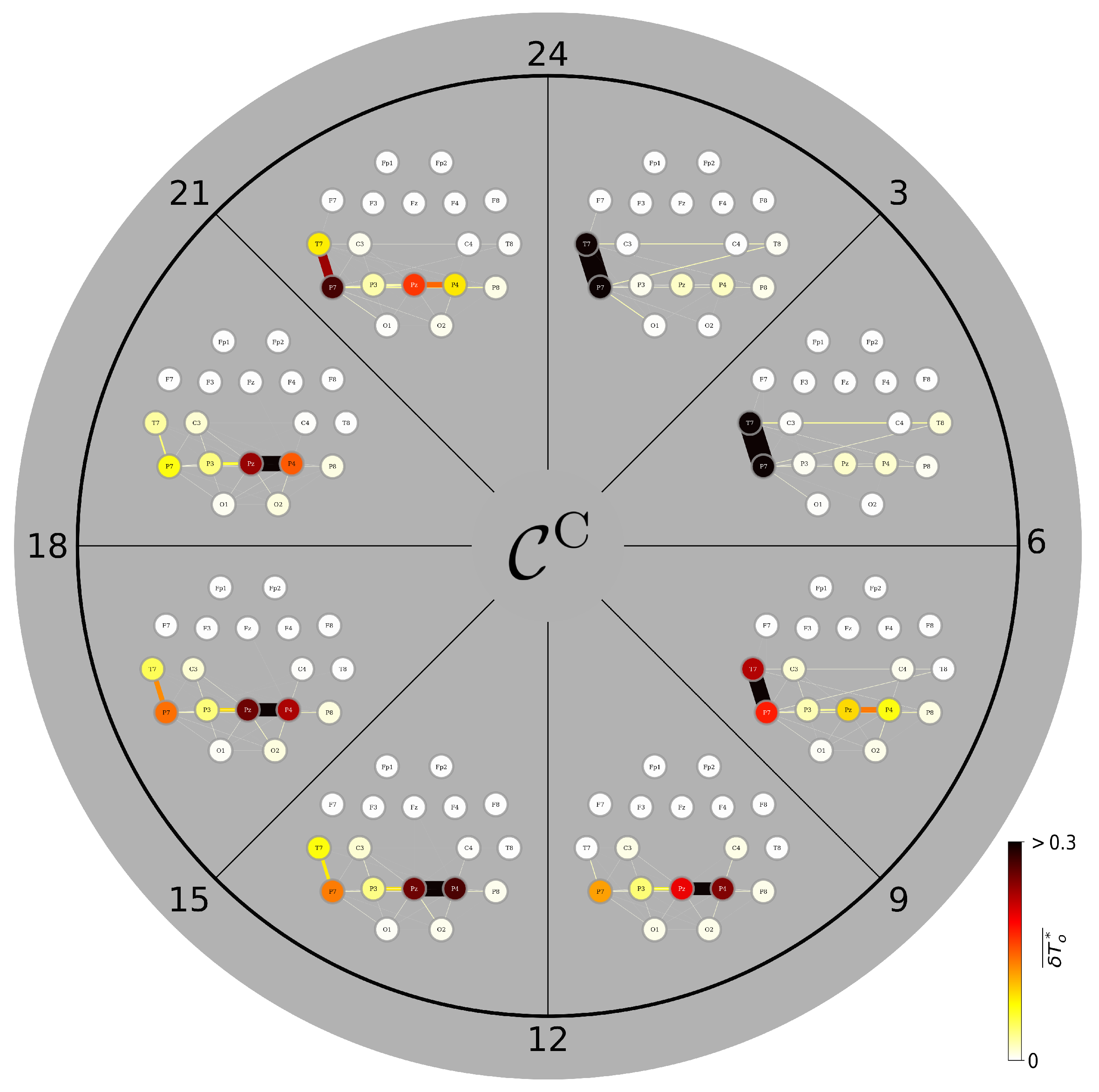
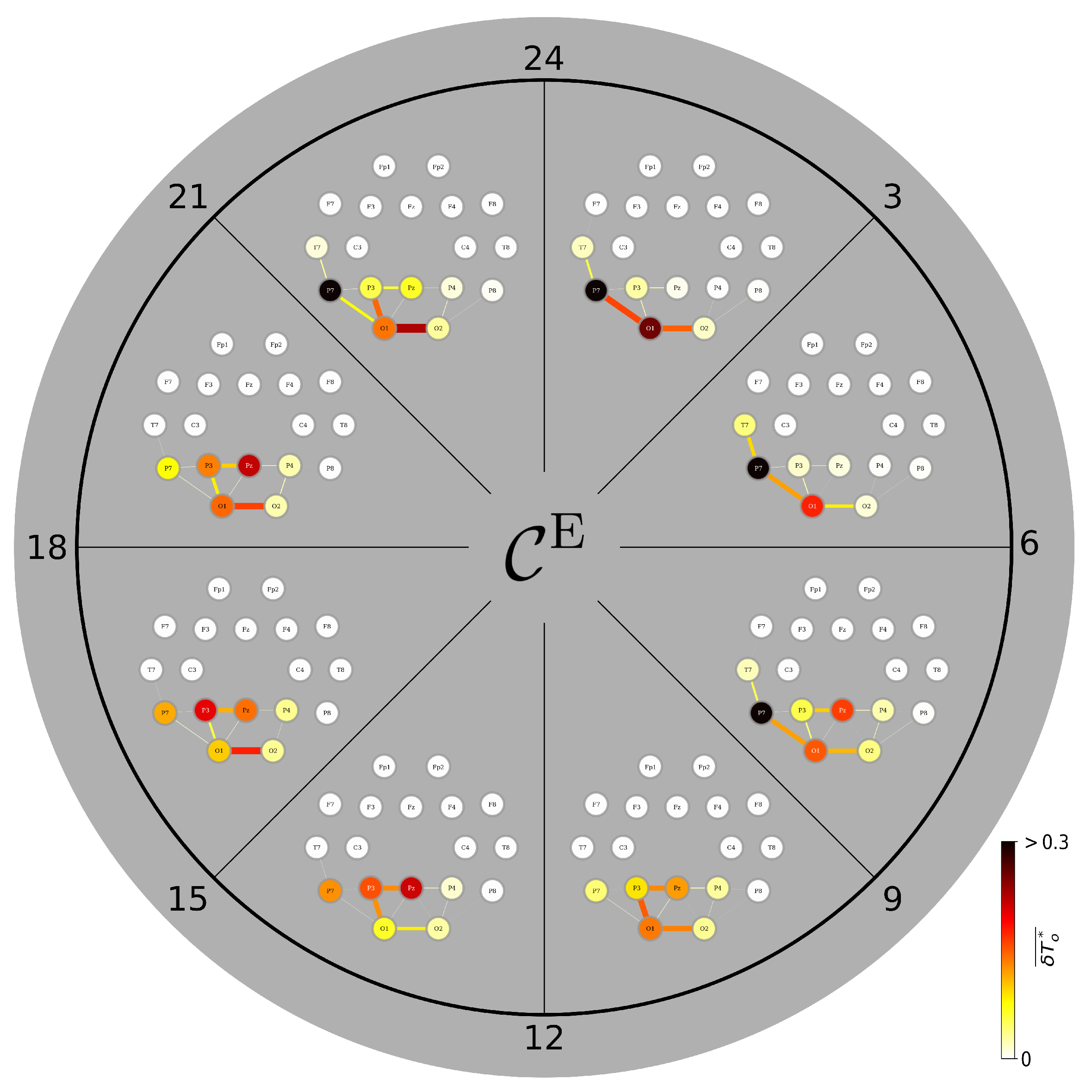
| Electrode | Hemisphere | Lobe | Anatomy | BA |
|---|---|---|---|---|
| Fp1 | L | FL | superior frontal G | 10 |
| Fp2 | R | FL | superior frontal G | 10 |
| Fz | FL | on or near interhemispheral fissure | ||
| F3 | L | FL | middle frontal G | 8 |
| F4 | R | FL | middle frontal G | 8 |
| F7 | L | FL | inferior frontal G | 45 |
| F8 | R | FL | inferior frontal G | 45 |
| C3 | L | PL | postcentral G | 1,2,3 |
| C4 | R | PL | postcentral G | 1,2,3 |
| T7 | L | TL | middle temporal G | 21 |
| T8 | R | TL | middle temporal G | 21 |
| P3 | L | PL | precuneus | 19 |
| P4 | R | PL | precuneus | 19 |
| Pz | PL | on or near interhemispheral fissure | ||
| P7 | L | TL | inferior temporal G | 37 |
| P8 | R | TL | inferior temporal G | 37 |
| O1 | L | OL | middle occipital G | 18 |
| O2 | R | OL | middle occipital G | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehnertz, K.; Bröhl, T. Functional Importance Backbones of the Brain at Rest, Wakefulness, and Sleep. Brain Sci. 2025, 15, 772. https://doi.org/10.3390/brainsci15070772
Lehnertz K, Bröhl T. Functional Importance Backbones of the Brain at Rest, Wakefulness, and Sleep. Brain Sciences. 2025; 15(7):772. https://doi.org/10.3390/brainsci15070772
Chicago/Turabian StyleLehnertz, Klaus, and Timo Bröhl. 2025. "Functional Importance Backbones of the Brain at Rest, Wakefulness, and Sleep" Brain Sciences 15, no. 7: 772. https://doi.org/10.3390/brainsci15070772
APA StyleLehnertz, K., & Bröhl, T. (2025). Functional Importance Backbones of the Brain at Rest, Wakefulness, and Sleep. Brain Sciences, 15(7), 772. https://doi.org/10.3390/brainsci15070772






