Dynamic Synergy Network Analysis Reveals Stage-Specific Regional Dysfunction in Alzheimer’s Disease
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Data Acquisition
2.3. Preprocessing
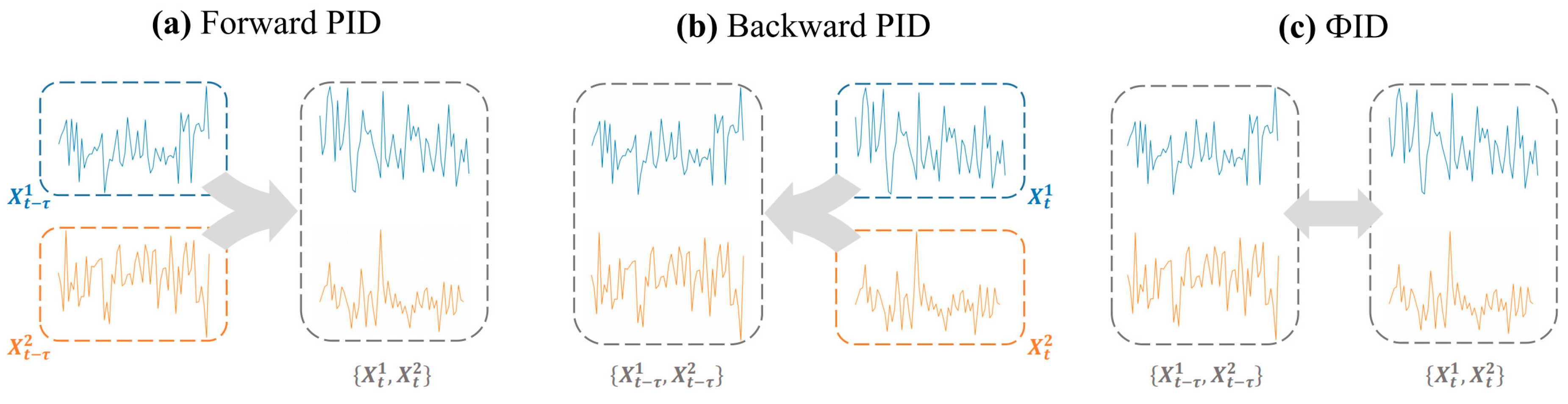
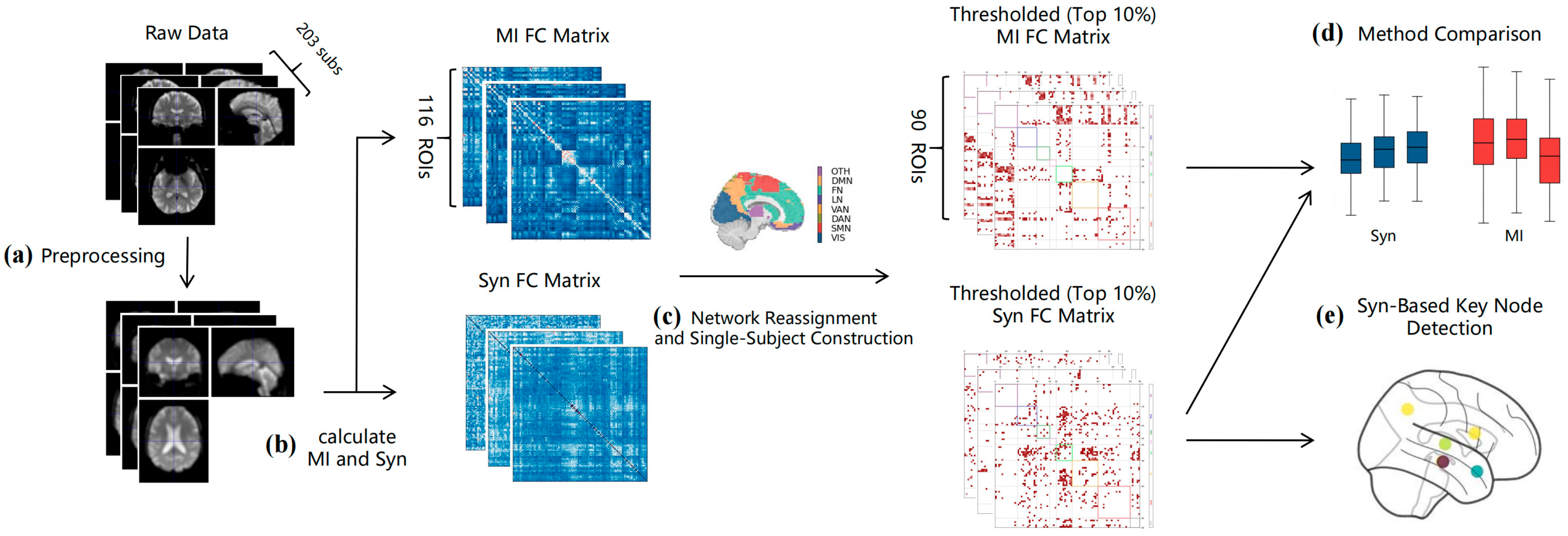
2.4. Mutual Information and Synergy Computation
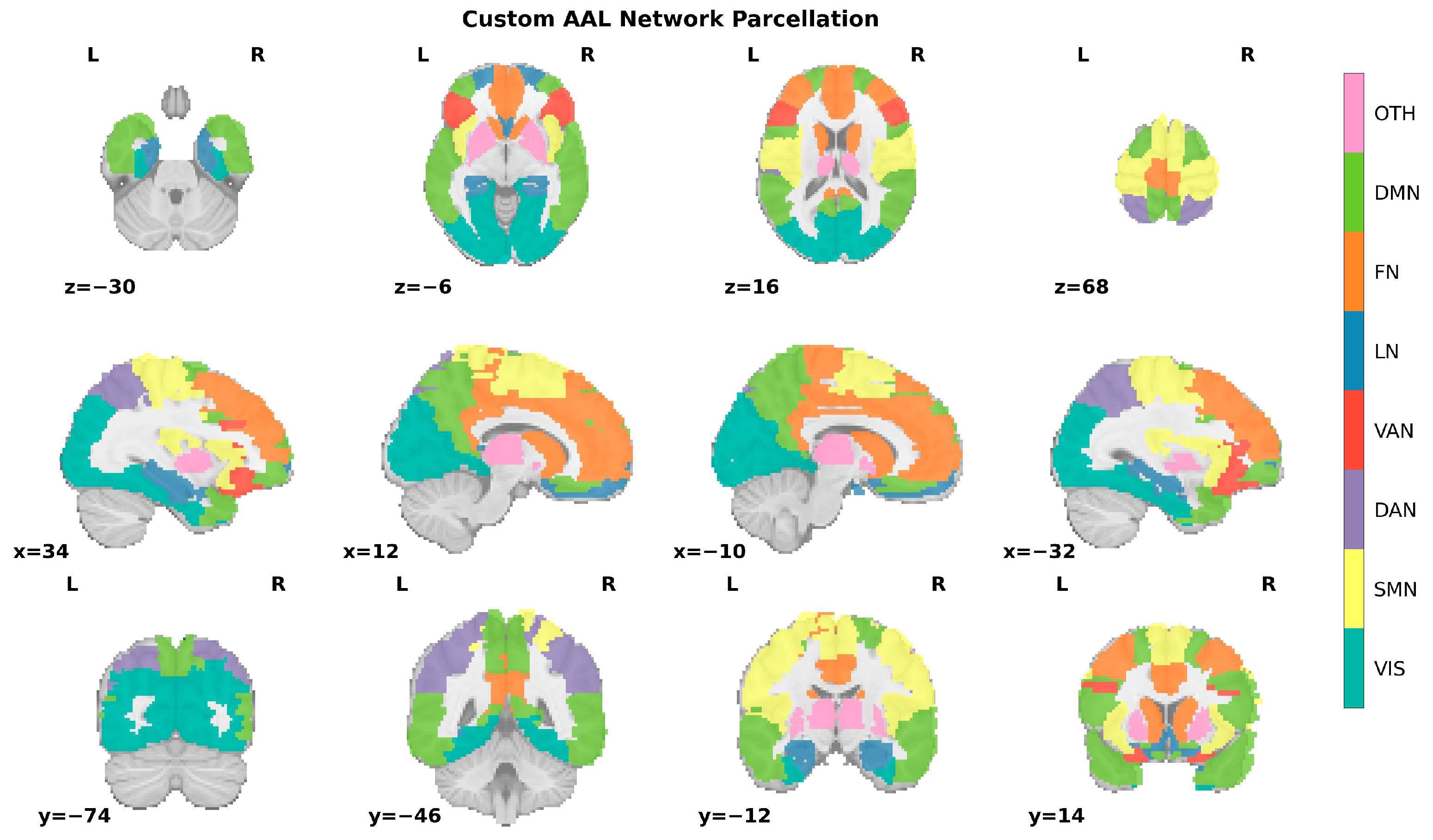
2.5. Computing Functional Connectivity Matrix
2.6. Single-Subject Network Reconstruction
2.7. Graph Theory Metrics and Statistical Analysis
3. Results
3.1. Single-Sample Reconstruction Result Verification
3.2. Inter-Method CV Stability Analysis
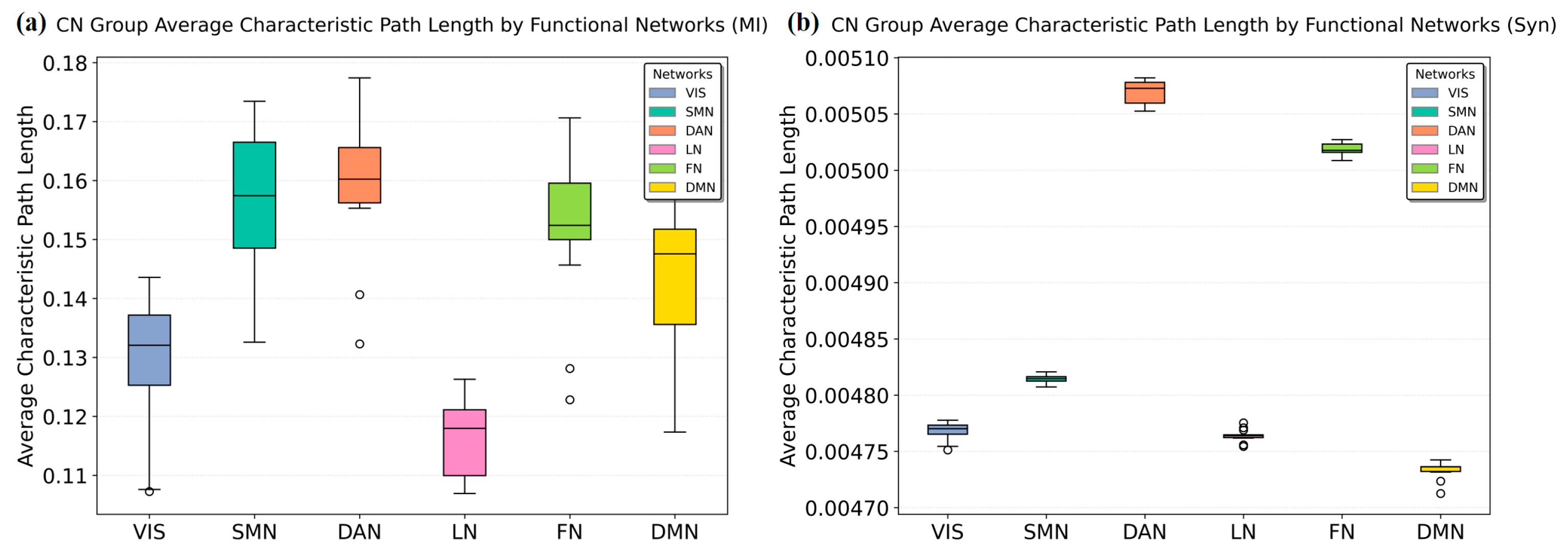
3.3. Resting-State Network Metric Comparison
3.4. Identifying Key Nodes in Alzheimer’s Disease Progression Using Synergy Detection
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tzioras, M.; McGeachan, R.I.; Durrant, C.S.; Spires-Jones, T.L. Synaptic degeneration in Alzheimer disease. Nat. Rev. Neurol. 2023, 19, 19–38. [Google Scholar] [CrossRef] [PubMed]
- Dubois, B.; Villain, N.; Frisoni, G.B.; Rabinovici, G.D.; Sabbagh, M.; Cappa, S.; Bejanin, A.; Bombois, S.; Epelbaum, S.; Teichmann, M.; et al. Clinical diagnosis of Alzheimer’s disease: Recommendations of the International Working Group. Lancet Neurol. 2021, 20, 484–496. [Google Scholar] [CrossRef] [PubMed]
- Roemer-Cassiano, S.N.; Wagner, F.; Evangelista, L.; Rauchmann, B.S.; Dehsarvi, A.; Steward, A.; Dewenter, A.; Biel, D.; Zhu, Z.; Pescoller, J.; et al. Amyloid-associated hyperconnectivity drives tau spread across connected brain regions in Alzheimer’s disease. Sci. Transl. Med. 2025, 17, eadp2564. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, S.; Lee, T.M.; Nayak, A.S.; Glynn, P. Oxygenation-sensitive contrast in magnetic resonance image of rodent brain at high magnetic fields. Magn. Reson. Med. 1990, 14, 68–78. [Google Scholar] [CrossRef]
- Kwong, K.K.; Belliveau, J.W.; Chesler, D.A.; Goldberg, I.E.; Weisskoff, R.M.; Poncelet, B.P.; Kennedy, D.N.; Hoppel, B.E.; Cohen, M.S.; Turner, R. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc. Natl. Acad. Sci. USA 1992, 89, 5675–5679. [Google Scholar] [CrossRef]
- Buckner, R.L.; Krienen, F.M.; Yeo, B.T.T. Opportunities and limitations of intrinsic functional connectivity MRI. Nat. Neurosci. 2013, 16, 832–837. [Google Scholar] [CrossRef]
- Biswal, B.; Yetkin, F.Z.; Haughton, V.M.; Hyde, J.S. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 1995, 34, 537–541. [Google Scholar] [CrossRef]
- Liang, X.; Zou, Q.; He, Y.; Yang, Y. Coupling of functional connectivity and regional cerebral blood flow reveals a physiological basis for network hubs of the human brain. Proc. Natl. Acad. Sci. USA 2013, 110, 1929–1934. [Google Scholar] [CrossRef]
- David, M. Vision: A Computational Investigation into the Human Representation and Processing of Visual Information; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar] [CrossRef]
- Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef]
- Luppi, A.I.; Craig, M.M.; Pappas, I.; Finoia, P.; Williams, G.B.; Allanson, J.; Pickard, J.D.; Owen, A.M.; Naci, L.; Menon, D.K.; et al. Consciousness-specific dynamic interactions of brain integration and functional diversity. Nat. Commun. 2019, 10, 4616. [Google Scholar] [CrossRef]
- Mediano, P.A.M.; Rosas, F.E.; Luppi, A.I.; Carhart-Harris, R.L.; Bor, D.; Seth, A.K.; Barrett, A.B. Towards an Extended Taxonomy of Information Dynamics via Integrated Information Decomposition. arXiv 2021, arXiv:2109.13186. [Google Scholar] [CrossRef]
- Jack, C.R., Jr.; Bernstein, M.A.; Fox, N.C.; Thompson, P.; Alexander, G.; Harvey, D.; Borowski, B.; Britson, P.J.; L Whitwell, J.; Ward, C.; et al. The Alzheimer’s Disease Neuroimaging Initiative (ADNI): MRI Methods. J. Magn. Reson. Imaging 2008, 27, 685–691. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.G.; Zang, Y.F. DPARSF: A MATLAB Toolbox for “Pipeline” Data Analysis of Resting-State fMRI. Front. Syst. Neurosci. 2010, 4, 13. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Tsinghua University Press: Beijing, China, 2006. [Google Scholar]
- Williams, P.L.; Beer, R.D. Nonnegative Decomposition of Multivariate Information. arXiv 2010, arXiv:1004.2515. [Google Scholar] [CrossRef]
- Bim, J.; Feo, V.D.; Chicharro, D.; Hanganu-Opatz, I.L.; Panzeri, S. A non-negative measure of feature-specific information transfer between neural signals. bioRxiv 2019. [Google Scholar] [CrossRef]
- Barrett, A.B. Exploration of synergistic and redundant information sharing in static and dynamical Gaussian systems. Phys. Rev. E 2014, 91, 052802. [Google Scholar] [CrossRef]
- Luppi, A.I.; Mediano, P.A.M.; Rosas, F.E.; Holland, N.; Fryer, T.D.; O’Brien, J.T.; Rowe, J.B.; Menon, D.K.; Bor, D.; Stamatakis , E.A. A synergistic core for human brain evolution and cognition. Nat. Neurosci. 2022, 25, 771–782. [Google Scholar] [CrossRef]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazoyer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage 2002, 15, 273–289. [Google Scholar] [CrossRef]
- Uddin, L.Q.; Betzel, R.F.; Cohen, J.R.; Damoiseaux, J.S.; De Brigard, F.; Eickhoff, S.B.; Fornito, A.; Gratton, C.; Gordon, E.M.; Laird, A.R.; et al. Controversies and progress on standardization of large-scale brain network nomenclature. Netw. Neurosci. 2023, 7, 864–905. [Google Scholar] [CrossRef]
- Yeo, B.T.; Krienen, F.M.; Sepulcre, J.; Sabuncu, M.R.; Lashkari, D.; Hollinshead, M.; Roffman, J.L.; Smoller, J.W.; Zöllei, L.; Polimeni, J.R.; et al. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 2011, 106, 1125–1165. [Google Scholar] [CrossRef]
- Huang, S.Y.; Hsu, J.L.; Lin, K.J.; Hsiao, I.T. A novel individual metabolic brain network for 18F-FDG PET imaging. Front. Neurosci. 2020, 14, 344. [Google Scholar] [CrossRef] [PubMed]
- Rivest, R.L.; Leiserson, C.E.; Cormen, T.H. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barrat, A.; Barthélemy, M.; Pastor-Satorras, R.; Vespignani, A. The architecture of complex weighted networks. Proc. Natl. Acad. Sci. USA 2004, 101, 3747–3752. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function Using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy 2008), Pasadena, CA, USA, 28 June 2008. [Google Scholar] [CrossRef]
- Goodale, M.A.; Milner, A.D. Separate visual pathways for perception and action. Trends Neurosci. 1992, 15, 20–25. [Google Scholar] [CrossRef]
- Wandell, B.A.; Winawer, J. Computational neuroimaging and population receptive fields. Trends Cogn. Sci. 2015, 19, 349–357. [Google Scholar] [CrossRef]
- Bullmore, E.T.; Sporns, O. Complex brain networks: Graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Mega, M.S.; Cummings, J.L.; Salloway, S.; Malloy, P. The limbic system: An anatomic, phylogenetic, and clinical perspective. J. Neuropsychiatry Clin. Neurosci. 1997, 9, 315–330. [Google Scholar] [CrossRef]
- de Araujo, I.E.; Simon, S.A. The gustatory cortex and multisensory integration. Int. J. Obes. 2009, 33 (Suppl. S2), S34–S43. [Google Scholar] [CrossRef]
- Alves, P.N.; Foulon, C.; Karolis, V.; Bzdok, D.; Margulies, D.S.; Volle, E.; de Schotten, M.T. An improved neuroanatomical model of the default-mode network reconciles previous neuroimaging and neuropathological findings. Commun. Biol. 2019, 2, 370. [Google Scholar] [CrossRef]
- Hopper, M.W.; Vogel, F.S. The limbic system in Alzheimer’s disease. A neuropathologic investigation. Am. J. Pathol. 1976, 85, 1–20. Available online: https://pubmed.ncbi.nlm.nih.gov/135514/ (accessed on 6 December 2024). [PubMed]
- Raichle, M.E.; Snyder, A.Z. A default mode of brain function: A brief history of an evolving idea. Neuroimage 2007, 37, 1083–1090. [Google Scholar] [CrossRef]
- Buckner, R.L.; Andrews-Hanna, J.R.; Schacter, D.L. The brain’s default network: Anatomy, function and relevance to disease. Ann. N. Y. Acad. Sci. 2008, 1124, 1–38. [Google Scholar] [CrossRef] [PubMed]
- Smallwood, J.; Bernhardt, B.C.; Leech, R.; Bzdok, D.; Jefferies, E.; Margulies, D.S. The default mode network in cognition: A topographical perspective. Nat. Rev. Neurosci. 2021, 22, 503–513. [Google Scholar] [CrossRef]
- Buckner, R.L.; DiNicola, L.M. The brain’s default network: Updated anatomy, physiology and evolving insights. Nat. Rev. Neurosci. 2019, 20, 593–608. [Google Scholar] [CrossRef]
- Uddin, L.Q.; Yeo, B.T.T.; Spreng, R.N. Towards a Universal Taxonomy of Macro-scale Functional Human Brain Networks. Brain Topogr. 2019, 32, 926–942. [Google Scholar] [CrossRef]
- González-Rueda, A.; Jensen, K.; Noormandipour, M.; de Malmazet, D.; Wilson, J.; Ciabatti, E.; Kim, J.; Williams, E.; Poort, J.; Hennequin, G.; et al. Kinetic features dictate sensorimotor alignment in the superior colliculus. Nature 2024, 631, 378–385. [Google Scholar] [CrossRef]
- Rajmohan, V.; Mohandas, E. The limbic system. Indian J. Psychiatry 2007, 49, 132–139. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, L.; Jiang, Y. Visual mental imagery of nonpredictive central social cues triggers automatic attentional orienting. Cognition 2025, 254, 105968. [Google Scholar] [CrossRef]
- Nee, D.E. Integrative frontal-parietal dynamics supporting cognitive control. eLife 2021, 10, e57244. [Google Scholar] [CrossRef]
- Power, J.D.; Schlaggar, B.L.; Lessov-Schlaggar, C.N.; Petersen, S.E. Evidence for hubs in human functional brain networks. Neuron 2013, 79, 798–813. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, W.; Wang, L.; Liu, D.; Xie, T.; Le, Z.; Li, X.; Gong, H.; Xu, X.H.; Xu, M.; et al. Whole-brain mapping of inputs and outputs of specific orbitofrontal cortical neurons in mice. Neurosci. Bull. 2024, 40, 1681–1698. [Google Scholar] [CrossRef] [PubMed]
- Rolls, E.T. The functions of the orbitofrontal cortex. Brain Cogn. 2004, 55, 11–29. [Google Scholar] [CrossRef] [PubMed]
- Mathys, H.; Boix, C.A.; Akay, L.A.; Xia, Z.; Davila-Velderrain, J.; Ng, A.P.; Jiang, X.; Abdelhady, G.; Galani, K.; Mantero, J.; et al. Single-cell multiregion dissection of Alzheimer’s disease. Nature 2024, 632, 858–868. [Google Scholar] [CrossRef] [PubMed]
- Gnanateja, G.N.; Rupp, K.; Llanos, F.; Hect, J.; German, J.S.; Teichert, T.; Abel, T.J.; Chandrasekaran, B. Cortical processing of discrete prosodic patterns in continuous speech. Nat. Commun. 2025, 16, 1947. [Google Scholar] [CrossRef]
- Tzourio-Mazoyer, N. Intra- and Inter-Hemispheric Connectivity Supporting Hemispheric Specialization. In Micro-, Meso- and Macro-Connectomics of the Brain; Kennedy, H., Van Essen, D., Christen, Y., Eds.; Springer: Cham, Switzerland, 2016; pp. 129–146. [Google Scholar] [CrossRef]
- Xiu, N.; Li, W.; Liu, L.; Liu, Z.; Cai, Z.; Li, L.; Vaxelaire, B.; Sock, R.; Ling, Z.; Chen, J.; et al. A study on voice measures in patients with Alzheimer’s disease. J. Voice 2025, 39, 286.e13–286.e24. [Google Scholar] [CrossRef]
- Yager, L.M.; Garcia, A.F.; Wunsch, A.M.; Ferguson, S.M. The ins and outs of the striatum: Role in drug addiction. Neuroscience 2015, 301, 529–541. [Google Scholar] [CrossRef]
- Li, Y.; Li, W.X.; Xie, D.J.; Wang, Y.; Cheung, E.F.C.; Chan, R.C.K. Grey matter reduction in the caudate nucleus in patients with persistent negative symptoms: An ALE meta-analysis. Schizophr. Res. 2018, 192, 9–15. [Google Scholar] [CrossRef]
- Venkataraman, A.V.; Mansur, A.; Rizzo, G.; Bishop, C.; Lewis, Y.; Kocagoncu, E.; Lingford-Hughes, A.; Huiban, M.; Passchier, J.; Rowe, J.B.; et al. Widespread cell stress and mitochondrial dysfunction occur in patients with early Alzheimer’s disease. Sci. Transl. Med. 2022, 14, eabk1051. [Google Scholar] [CrossRef]
- Guan, X.; Guo, T.; Zhou, C.; Wu, J.; Zeng, Q.; Li, K.; Luo, X.; Bai, X.; Wu, H.; Gao, T.; et al. Altered brain iron depositions from aging to Parkinson’s disease and Alzheimer’s disease: A quantitative susceptibility mapping study. Neuroimage 2022, 264, 119683. [Google Scholar] [CrossRef]
- Klein, M.O.; Battagello, D.S.; Cardoso, A.R.; Hauser, D.N.; Bittencourt, J.C.; Correa, R.G. Dopamine: Functions, signaling, and association with neurological diseases. Cell. Mol. Neurobiol. 2019, 39, 31–59. [Google Scholar] [CrossRef] [PubMed]
- Rockhill, A.P.; Tan, H.; Lopez Ramos, C.G.; Nerison, C.; Shafie, B.; Shahin, M.N.; Fecker, A.; Ismail, M.; Cleary, D.R.; Collins, K.L.; et al. Investigating the Triple Code Model in numerical cognition using stereotactic electroencephalography. PLoS ONE 2024, 19, e0313155. [Google Scholar] [CrossRef] [PubMed]
- Hubel, D.H.; Wiesel, T.N. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol. 1962, 160, 106–154. [Google Scholar] [CrossRef]
- Martin, A.; Wiggs, C.L.; Ungerleider, L.G.; Haxby, J.V. Neural correlates of category-specific knowledge. Nature 1996, 379, 649–652. [Google Scholar] [CrossRef]
- Hodges, J.R.; Patterson, K. Semantic dementia: A unique clinicopathological syndrome. Lancet Neurol. 2007, 6, 1004–1014. [Google Scholar] [CrossRef]
- Yue, J.; Han, S.W.; Liu, X.; Wang, S.; Zhao, W.W.; Cai, L.N.; Cao, D.N.; Mah, J.Z.; Hou, Y.; Cui, X.; et al. Functional brain activity in patients with amnestic mild cognitive impairment: An rs-fMRI study. Front. Neurol. 2023, 14, 1244696. [Google Scholar] [CrossRef]
- Ou, Y.H.; Wu, H.; Lei, Z.; Shi, X.; Xu, Q.; Shi, K.Q.; Liu, X.Y.; Fang, M.; Wang, X.Z.; Cai, X.L.; et al. Diagnosis of mild cognitive impairment using 99mTc-ECD SPECT brain imaging with NeuroGamTM technology. FUDAN Univ. J. Med. Sci. 2022, 49, 753–758. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, L.; Wang, J.; Ding, Y.; Men, W.; Tan, S.; Gao, J.H.; Qin, S.; He, Y.; Dong, Q.; et al. Connections between the middle frontal gyrus and the dorsoventral attention network are associated with the development of attentional symptoms. Biol. Psychiatry 2025, 97, 531–539. [Google Scholar] [CrossRef]
- Caminiti, R.; Chafee, M.V.; Battaglia-Mayer, A.; Averbeck, B.B.; Crowe, D.A.; Georgopoulos, A.P. Understanding the parietal lobe syndrome from a neurophysiological and evolutionary perspective. Eur. J. Neurosci. 2010, 31, 2320–2340. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, J.; Xu, X.; You, Z.; Huang, Q.; Huang, Y.; Guo, Q.; Guan, Y.; Zhao, J.; Liu, J.; et al. In vivo synaptic density loss correlates with impaired functional and related structural connectivity in Alzheimer’s disease. J. Cereb. Blood Flow Metab. 2023, 43, 977–988. [Google Scholar] [CrossRef]
- Zeng, Q.; Luo, X.; Li, K.; Wang, S.; Zhang, R.; Hong, H.; Huang, P.; Jiaerken, Y.; Xu, X.; Xu, J.; et al. Distinct spontaneous brain activity patterns in different biologically-defined Alzheimer’s disease cognitive stage: A preliminary study. Front. Aging Neurosci. 2019, 11, 350. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Zhu, X.; Wu, X.; Gong, Y.; Jones, J.A.; Liu, P.; Chang, Y.; Yan, N.; Chen, X.; Liu, H. Continuous theta burst stimulation over left and right supramarginal gyri demonstrates their involvement in auditory feedback control of vocal production. Cereb. Cortex 2022, 33, 11–22. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, L.; Ding, H.Y.; Zhu, Y.; Wang, T.; Gao, Y.X.; Qi, M. Aberrant spontaneous brain activity of patients in preclinical stages of Alzheimer’s disease based on pre-habilitation: A resting-state fMRI study. Chin. J. Rehabil. Med. 2022, 37, 458–464. [Google Scholar] [CrossRef]
- Gerstmann, J. Some notes on the Gerstmann syndrome. Neurology 1957, 7, 866–869. [Google Scholar] [CrossRef]
- Cabeza, R.; Nyberg, L. Imaging cognition II: An empirical review of 275 PET and fMRI studies. J. Cogn. Neurosci. 2000, 12, 1–47. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Ma, Q.; Shi, C.; Yue, W. Changes in the parietal lobe subregion volume at various stages of Alzheimer’s disease and the role in cognitively normal and mild cognitive impairment conversion. J. Integr. Neurosci. 2025, 24, 25991. [Google Scholar] [CrossRef]





| CN–EMCI | EMCI–LMCI | LMCI–AD | ||
|---|---|---|---|---|
| Before Construction | |t| | 1.4382 | 0.2934 | 0.5274 |
| p | 0.1739 | 0.7701 | 0.5998 | |
| Cohen’s d | 0.31 | 0.05 | 0.10 | |
| After Construction | |t| | 1.4234 | 1.6098 | 1.1095 |
| p | 0.1590 | 0.1119 | 0.2716 | |
| Cohen’s d | 0.30 | 0.30 | 0.21 |
| CN–EMCI | EMCI–LMCI | LMCI–AD | ||
|---|---|---|---|---|
| Before Construction | |t| | 1.2427 | 1.8291 | 1.8453 |
| p | 0.2181 | 0.0716 | 0.0699 | |
| Cohen’s d | 0.27 | 0.34 | 0.35 | |
| After Construction | |t| | 2.2802 | 2.2554 | 2.7684 |
| p | 0.0256 | 0.0272 | 0.0089 | |
| Cohen’s d | 0.49 | 0.41 | 0.53 |
| Method | CN | EMCI | LMCI | AD | |
|---|---|---|---|---|---|
| CV | Syn | 0.0005 | 0.0020 | 0.0032 | 0.0028 |
| MI | 0.0707 | 0.0835 | 0.1583 | 0.1712 |
| Method | CN | EMCI | LMCI | AD | |
|---|---|---|---|---|---|
| CV | Syn | 0.0157 | 0.0182 | 0.0242 | 0.0268 |
| MI | 0.4233 | 0.3223 | 0.3434 | 0.4162 |
| CN–EMCI | EMCI–LMCI | LMCI–AD | |
|---|---|---|---|
| Regions and CS value | Frontal_Inf_Orb_R: 10.02 Heschl_L: 9.56 Frontal_Inf_Orb_L: 9.47 Rectus_L: 6.96 Caudate_R: 6.76 Putamen_L: 6.75 Temporal_Inf_L: 6.57 | Frontal_Mid_R: 12.47 Postcentral_R: 7.64 | SupraMarginal_R: 49.37 |
| CN–EMCI | EMCI–LMCI | LMCI–AD | |
|---|---|---|---|
| Regions and CS value | Frontal_Inf_Orb_R: 11.6 Temporal_Inf_L: 8.9 Temporal_Pole_Sup_L: 6.86 Frontal_Inf_Orb_L: 6.57 Occipital_Inf_L: 6.32 Frontal_Mid_Orb_R: 6.29 | Frontal_Mid_R: 23.21 Postcentral_R: 12.2 | Parietal_Inf_L: 21.26 SupraMarginal_R: 8.47 |
| Key Findings | |
|---|---|
| Syn vs. MI Distribution | Syn-based analysis revealed more pronounced inter-network differences in resting-state connectivity patterns. |
| Characteristic Path Length | Syn methodology revealed stronger connectivity between DMN/SMN and other brain regions. |
| Synergistic Clustering | VIS, FN, and DMN exhibited significantly higher synergistic clustering coefficients than other networks (detectable only via the Syn method). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Han, C.; Xia, J.; Deng, L.; Dong, J. Dynamic Synergy Network Analysis Reveals Stage-Specific Regional Dysfunction in Alzheimer’s Disease. Brain Sci. 2025, 15, 636. https://doi.org/10.3390/brainsci15060636
Zhang X, Han C, Xia J, Deng L, Dong J. Dynamic Synergy Network Analysis Reveals Stage-Specific Regional Dysfunction in Alzheimer’s Disease. Brain Sciences. 2025; 15(6):636. https://doi.org/10.3390/brainsci15060636
Chicago/Turabian StyleZhang, Xiaoyan, Chao Han, Jingbo Xia, Lingli Deng, and Jiyang Dong. 2025. "Dynamic Synergy Network Analysis Reveals Stage-Specific Regional Dysfunction in Alzheimer’s Disease" Brain Sciences 15, no. 6: 636. https://doi.org/10.3390/brainsci15060636
APA StyleZhang, X., Han, C., Xia, J., Deng, L., & Dong, J. (2025). Dynamic Synergy Network Analysis Reveals Stage-Specific Regional Dysfunction in Alzheimer’s Disease. Brain Sciences, 15(6), 636. https://doi.org/10.3390/brainsci15060636







