Dimensionality Reduction Hybrid U-Net for Brain Extraction in Magnetic Resonance Imaging
Abstract
:1. Introduction
2. Materials and Methods
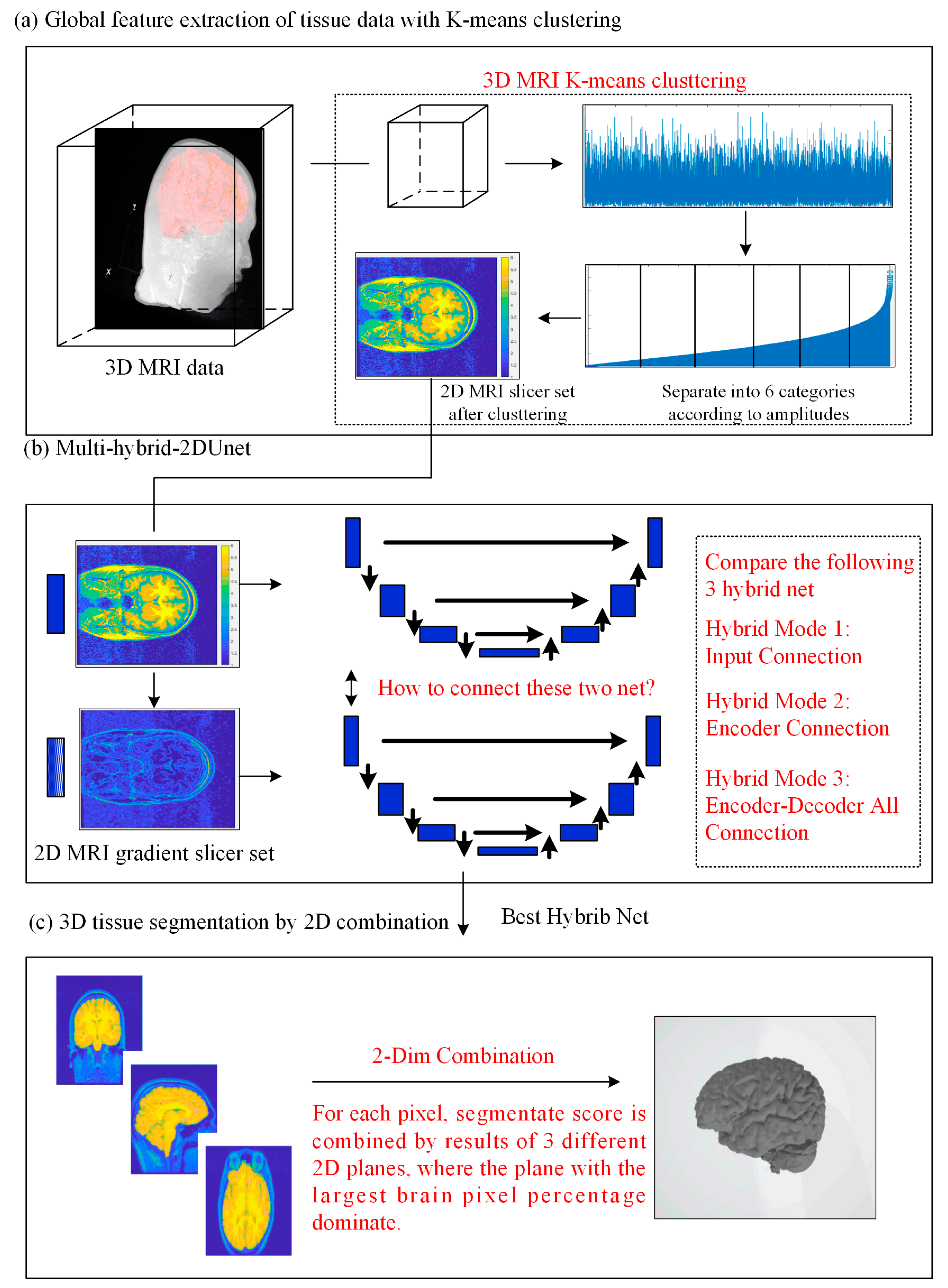
2.1. Network Architecture
2.2. Full Image Information Mining with a K-Means Cluster Preprocessing
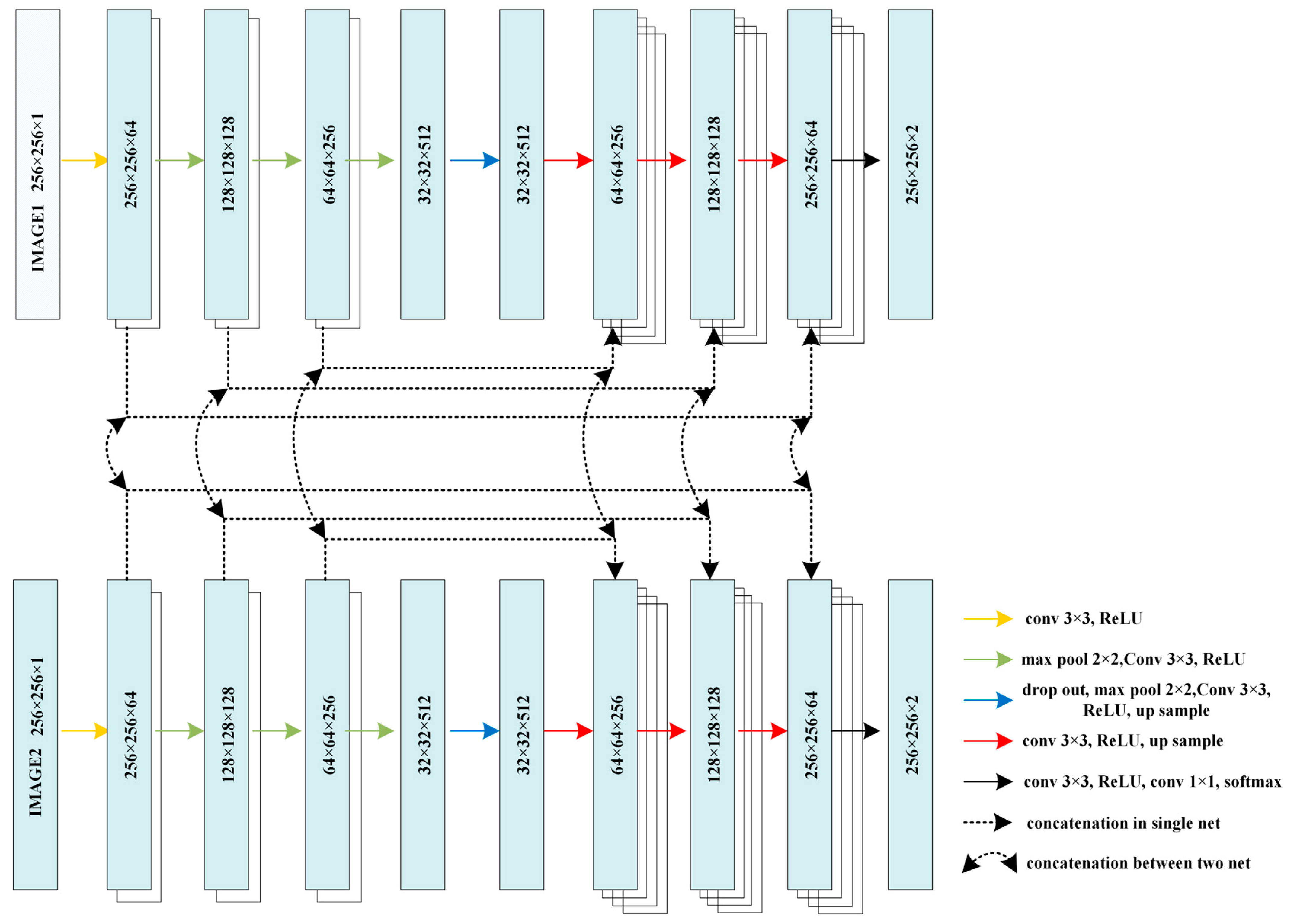
2.3. Hybrid-U-Net Framework
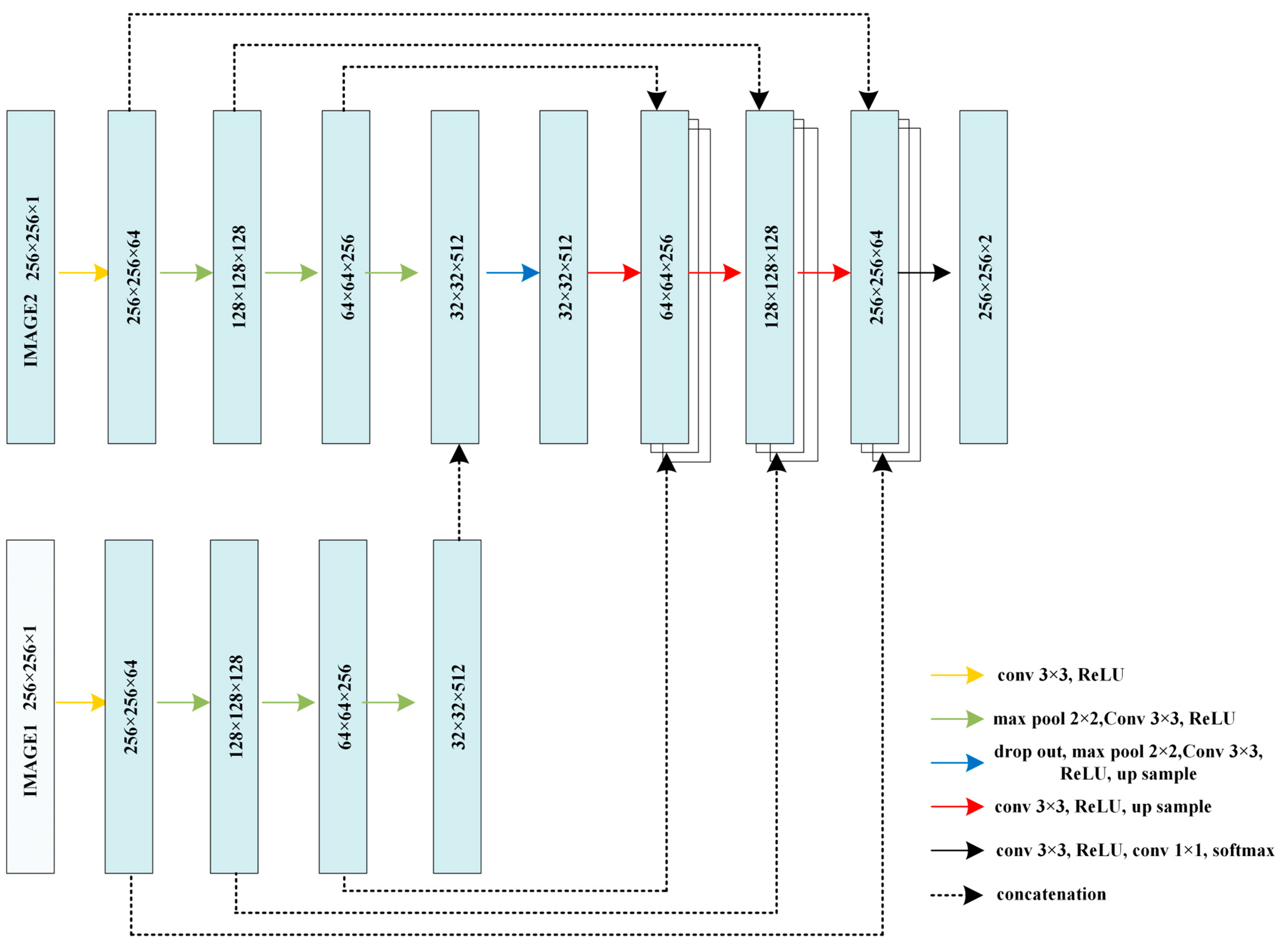
2.4. Dimensionality Reduction U-Net for 3D MRI Data
3. Results
3.1. Datasets
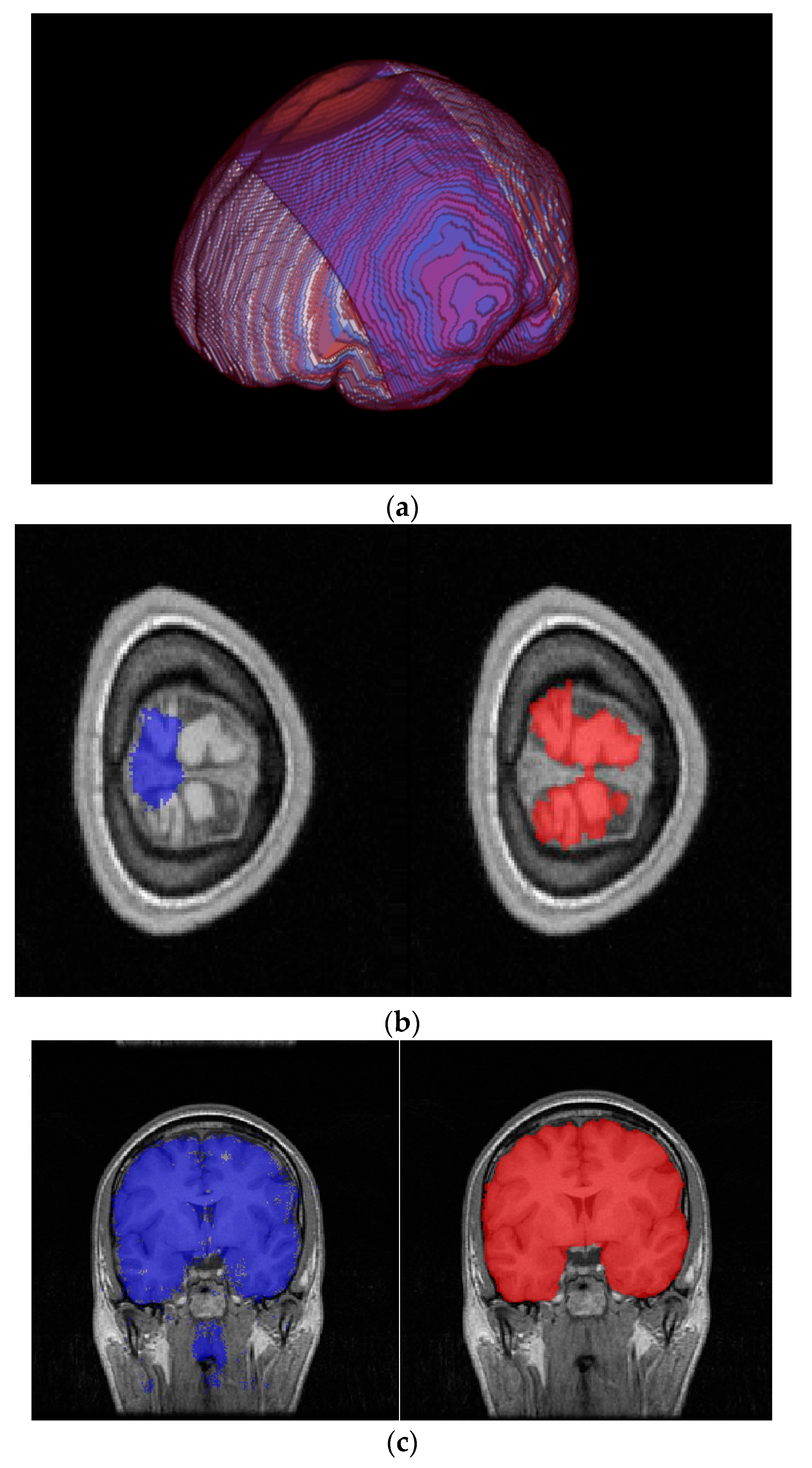
3.2. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Smith, S.M. Fast robust automated brain extraction. Hum. Brain Mapp. 2002, 17, 143–155. [Google Scholar] [CrossRef] [PubMed]
- Jenkinson, M.; Pechaud, M.; Smith, S. BET2: MR-based estimation of brain, skull and scalp surfaces. In Proceedings of the 11th Annual Meeting of the Organization for Human Brain Mapping, Toronto, ON, USA, 12–16 June 2005; Volume 17, p. 167. [Google Scholar]
- Qiu, J.; Cheng, W. Brain tissues extraction based on improved brain extraction tool algorithm. In Proceedings of the 2016 2nd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 14–17 October 2016; pp. 553–556. [Google Scholar]
- Luo, Y.; Gao, B.; Deng, Y.; Zhu, X.; Jiang, T.; Zhao, X.; Yang, Z. Automated brain extraction and immersive exploration of its layers in virtual reality for the rhesus macaque MRI data sets. Comput. Animat. Virtual Worlds 2019, 30, e1841. [Google Scholar] [CrossRef]
- 3dSkullStrip, a Part of the AFNI (Analysis of Functional Neuro Images) Package. Available online: http://afni.nimh.nih.gov (accessed on 1 December 2021).
- Segonne, F.; Dale, A.M.; Busa, E.; Glessner, M.; Salat, D.; Hahn, H.K.; Fischl, B. A hybrid approach to the skull stripping problem in MRI. NeuroImage 2004, 22, 1060–1075. [Google Scholar] [CrossRef] [PubMed]
- Iglesias, J.E.; Liu, C.Y.; Thompson, P.M.; Tu, Z. Robust brain extraction across datasets and comparison with publicly available methods. IEEE Trans. Med. Imaging 2011, 30, 1617–1634. [Google Scholar] [CrossRef] [PubMed]
- Kleesiek, J.; Urban, G.; Hubert, A.; Schwarz, D.; Maier-Hein, K.; Bendszus, M.; Biller, A. Deep MRI brain extraction: A 3D convolutional neural network for skull stripping. NeuroImage 2016, 129, 460–469. [Google Scholar] [CrossRef] [PubMed]
- Brebisson, A.D.; Montana, G. Deep neural networks for anatomeical brain segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Boston, MA, USA, 7–12 June 2015; pp. 20–28. [Google Scholar]
- Glassner, A.S. Deep Learning: From Basics to Practice; The Imaginary Institute: Seattle, WA, USA, 2018; Volume 1. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar]
- Tong, Q.; Ning, M.; Si, W.; Liao, X.; Qin, J. 3D deeply-supervised U-Net based whole heart segmentation. In Proceedings of the International Workshop on Statistical Atlases and Computational Models of the Heart, Quebec City, QC, Canada, 10–14 September 2017; pp. 224–232. [Google Scholar]
- Zeng, G.; Yang, X.; Li, J.; Yu, L.; Heng, P.A.; Zheng, G. 3D U-Net with multi-level deep supervision: Fully automatic segmentation of proximal femur in 3D MR images. In Proceedings of the International Workshop on Machine Learning in Medical Imaging, Quebec City, QC, Canada, 10 September 2017; pp. 274–282. [Google Scholar]
- Bae, H.J.; Hyun, H.; Byeon, Y.; Shin, K.; Cho, Y.; Song, Y.J.; Yi, S.; Kuh, S.U.; Yeom, J.S.; Kim, N. Fully automated 3D segmentation and separation of multiple cervical vertebrae in CT images using a 2D convolutional neural network. Comput. Methods Programs Biomed. 2020, 184, 105119. [Google Scholar] [CrossRef] [PubMed]
- Mehta, R.; Arbel, T. 3D U-Net for brain tumour segmentation. In Proceedings of the International MICCAI Brainlesion Workshop, Granada, Spain, 16 September 2018; pp. 254–266. [Google Scholar]
- Chen, W.; Liu, B.; Peng, S.; Sun, J.; Qiao, X. S3D-UNet: Separable 3D U-Net for brain tumor segmentation. In Proceedings of the International MICCAI Brainlesion Workshop, Granada, Spain, 16 September 2018; pp. 358–368. [Google Scholar]
- Owler, J.; Irving, B.; Ridgeway, G.; Wojciechowska, M.; McGonigle, J.; Brady, M. Comparison of multi-atlas segmentation and U-Net approaches for automated 3D liver delineation in MRI. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Liverpool, UK, 24–26 July 2019; pp. 478–488. [Google Scholar]
- Zhao, C.; Han, J.; Jia, Y.; Gou, F. Lung nodule detection via 3D U-Net and contextual convolutional neural network. In Proceedings of the International Conference on Networking and Network Applications (NaNA), Xi’an, China, 12–15 October 2018; pp. 356–361. [Google Scholar]
- He, Y.; Yu, X.; Liu, C.; Zhang, J.; Hu, K.; Zhu, H.C. A 3D dual path U-Net of cancer segmentation based on MRI. In Proceedings of the IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, 27–29 June 2018; pp. 268–272. [Google Scholar]
- Heinrich, M.P.; Oktay, O.; Bouteldja, N. OBELISK-Net: Fewer layers to solve 3D multi-organ segmentation with sparse deformable convolutions. Med. Image Anal. 2019, 54, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhao, L.; Wang, M.; Song, Z. Organ at risk segmentation in head and neck CT images using a two-stage segmentation framework based on 3D U-Net. IEEE Access 2019, 7, 144591–144602. [Google Scholar] [CrossRef]
- Li, B.; Groot, M.D.; Vernooij, M.W.; Ikram, M.A.; Niessen, W.J.; Bron, E.E. Reproducible white matter tract segmentation using 3D U-Net on a large-scale DTI dataset. In Proceedings of the International Workshop on Machine Learning in Medical Imaging, Granada, Spain, 16 September 2018; pp. 205–213. [Google Scholar]
- Mohseni Salehi, S.S.; Erdogmus, D.; Gholipour, A. Auto-Context Convolutional Neural Network (Auto-Net) for Brain Extraction in Magnetic Resonance Imaging. IEEE Trans. Med. Imaging 2017, 36, 2319–2330. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Lian, S.; Luo, Z.; Li, S. Weighted Res-UNet for High-Quality Retina Vessel Segmentation. In Proceedings of the 2018 9th International Conference on Information Technology in Medicine and Education (ITME), Hangzhou, China, 19–21 October 2018; pp. 327–331. [Google Scholar]
- Lian, S.; Li, L.; Lian, G.; Xiao, X.; Luo, Z.; Li, S. A Global and Local Enhanced Residual U-Net for Accurate Retinal Vessel Segmentation. IEEE/ACM Trans. Comput. Biol. Bioinform. 2021, 18, 852–862. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Guo, L.; Cheng, G.; Chen, X.; Zhang, C.; Chen, Z. Brain Extraction From Brain MRI Images Based on Wasserstein GAN and O-Net. IEEE Access 2021, 9, 136762–136774. [Google Scholar] [CrossRef]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.-W.; Wu, J. UNet 3+: A Full-Scale Connected UNet for Medical Image Segmentation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1055–1059. [Google Scholar]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef] [PubMed]
- Fatima, A.; Madni, T.M.; Anwar, F.; Janjua, U.I.; Sultana, N. Automated 2D slice-based skull stripping multi-view ensemble model on NFBS and IBSR datasets. J. Digit. Imaging 2022, 35, 374–384. [Google Scholar] [CrossRef] [PubMed]
- Pei, L.; Ak, M.; Tahon, N.H.M.; Zenkin, S.; Alkarawi, S.; Kamal, A.; Yilmaz, M.; Chen, L.; Er, M.; Ak, N.; et al. A general skull stripping of multiparametric brain MRIs using 3D convolutional neural network. Sci. Rep. 2022, 12, 10826. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wu, Z.; Chen, L.; Sun, Y.; Lin, W.; Li, G. IBEAT V2.0: A multisite-applicable, deep learning-based pipeline for infant cerebral cortical surface reconstruction. Nat. Protoc. 2023, 18, 1488–1509. [Google Scholar] [CrossRef] [PubMed]
- Ashburner, J.; Friston, K.J. Unified segmentation. NeuroImage 2005, 26, 839–851. [Google Scholar] [CrossRef] [PubMed]
- Shattuck, D.W.; Prasad, G.; Mirza, M.; Narr, K.L.; Toga, A.W. Online resource for validation of brain segmentation methods. NeuroImage 2009, 45, 431–439. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Shao, W.; Zhang, D.; Liu, M. Anatomical Attention Guided Deep Networks for ROI Segmentation of Brain MR Images. IEEE Trans. Med. Imaging 2020, 39, 2000–2012. [Google Scholar] [CrossRef] [PubMed]
- Bhattarai, B.; Subedi, R.; Gaire, R.R.; Vazquez, E.; Stoyanov, D. Histogram of oriented gradients meet deep learning: A novel multi-task deep network for 2D surgical image semantic segmentation. Med. Image Anal. 2023, 85, 102747. [Google Scholar] [CrossRef] [PubMed]

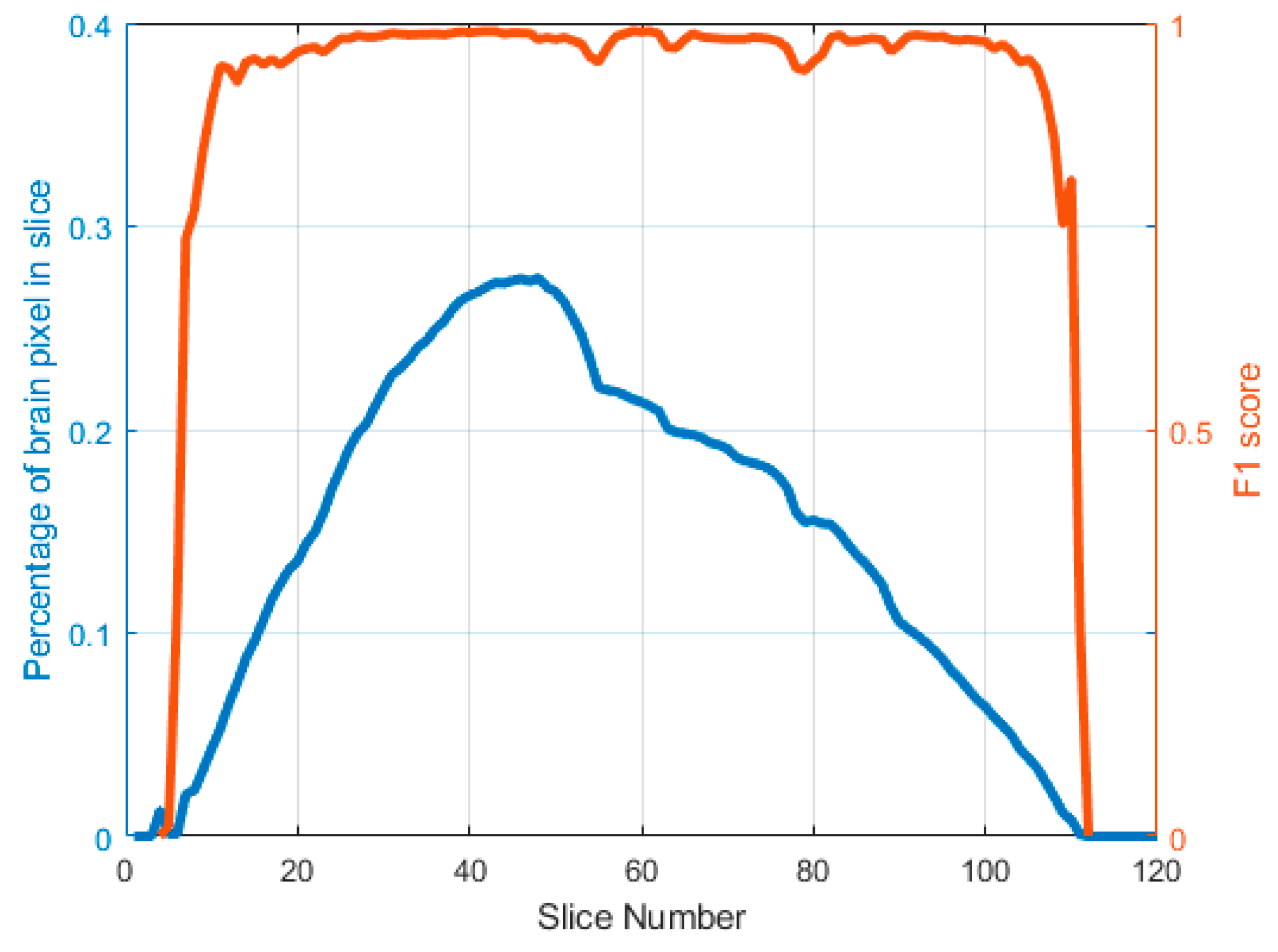
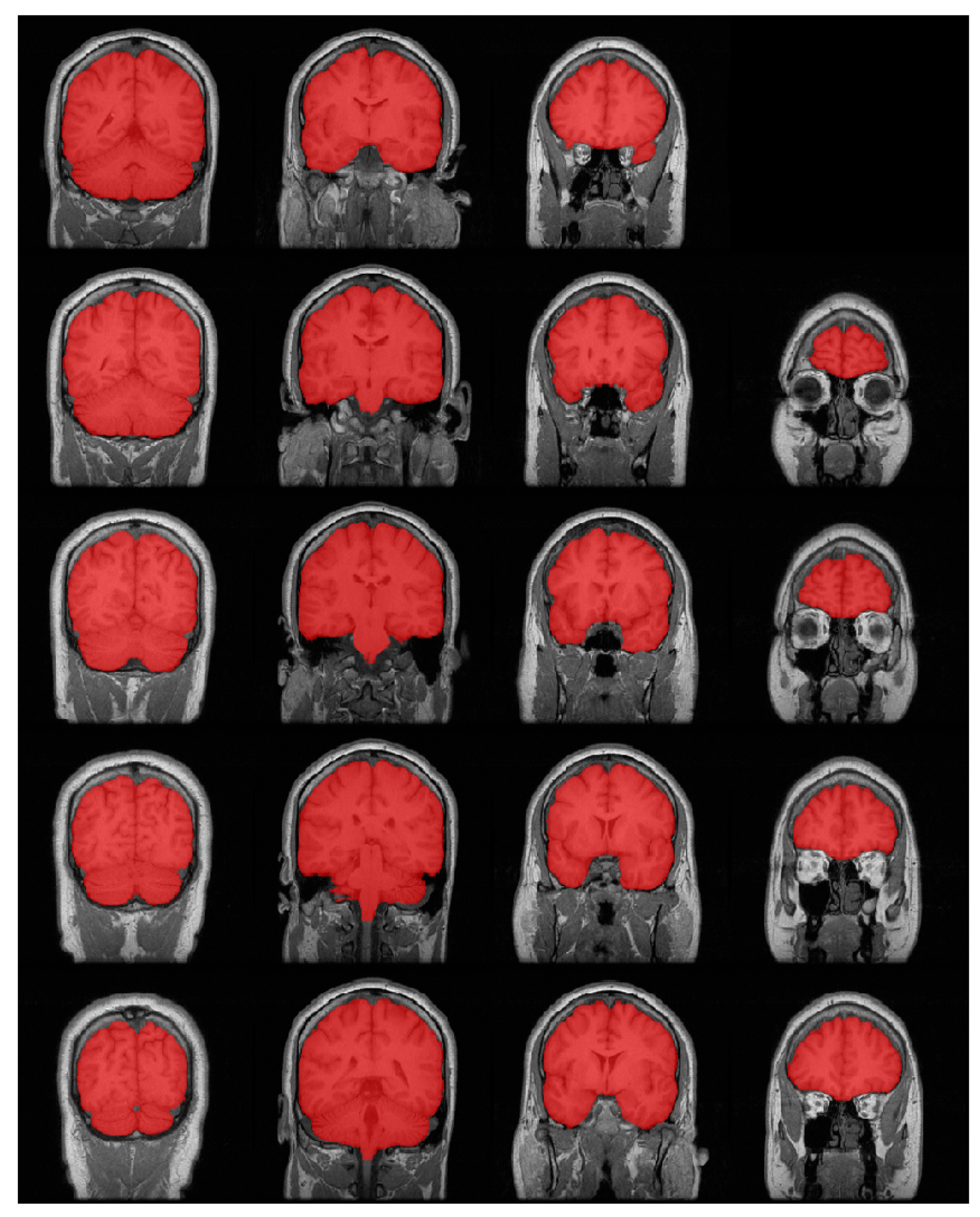

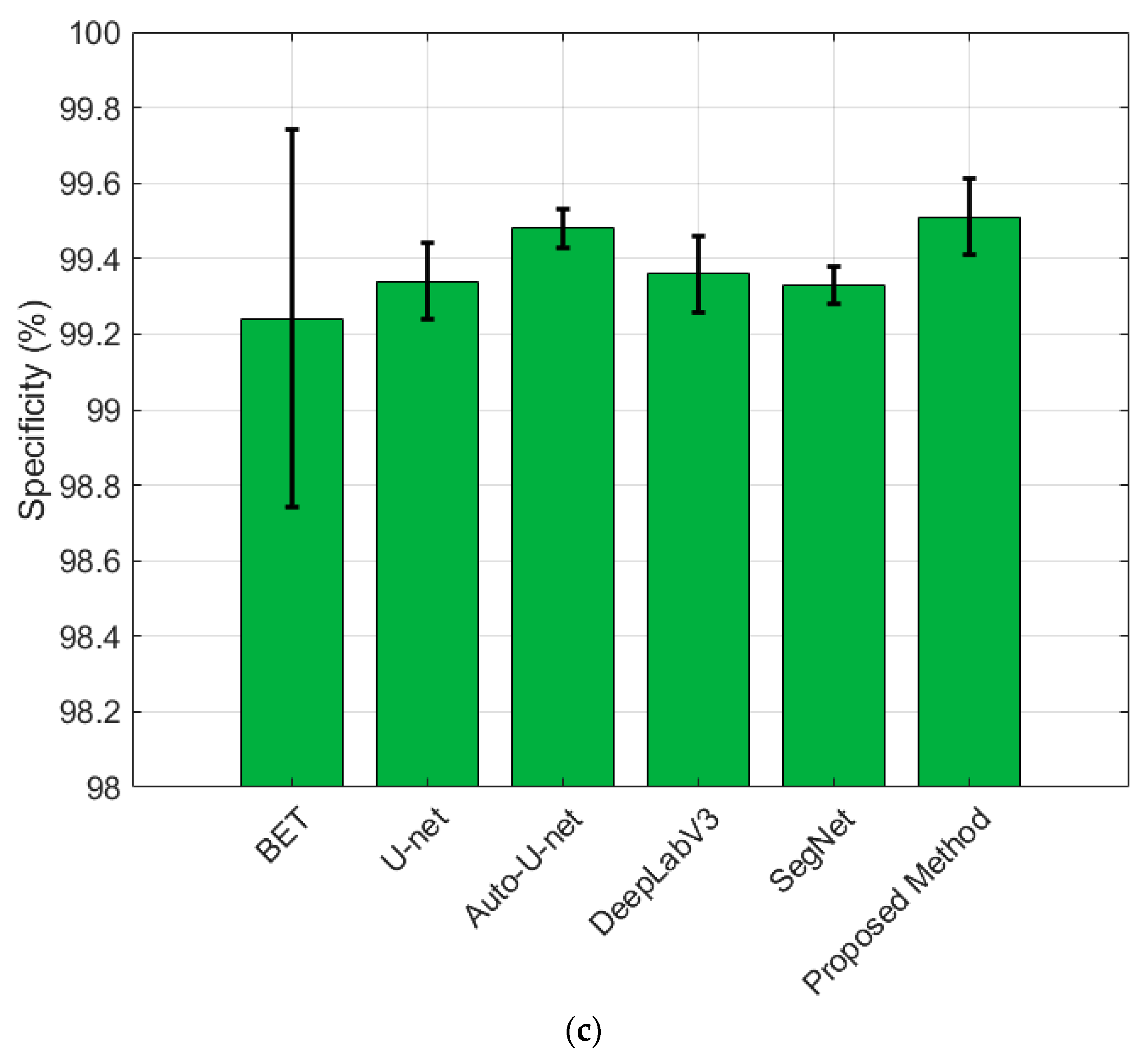

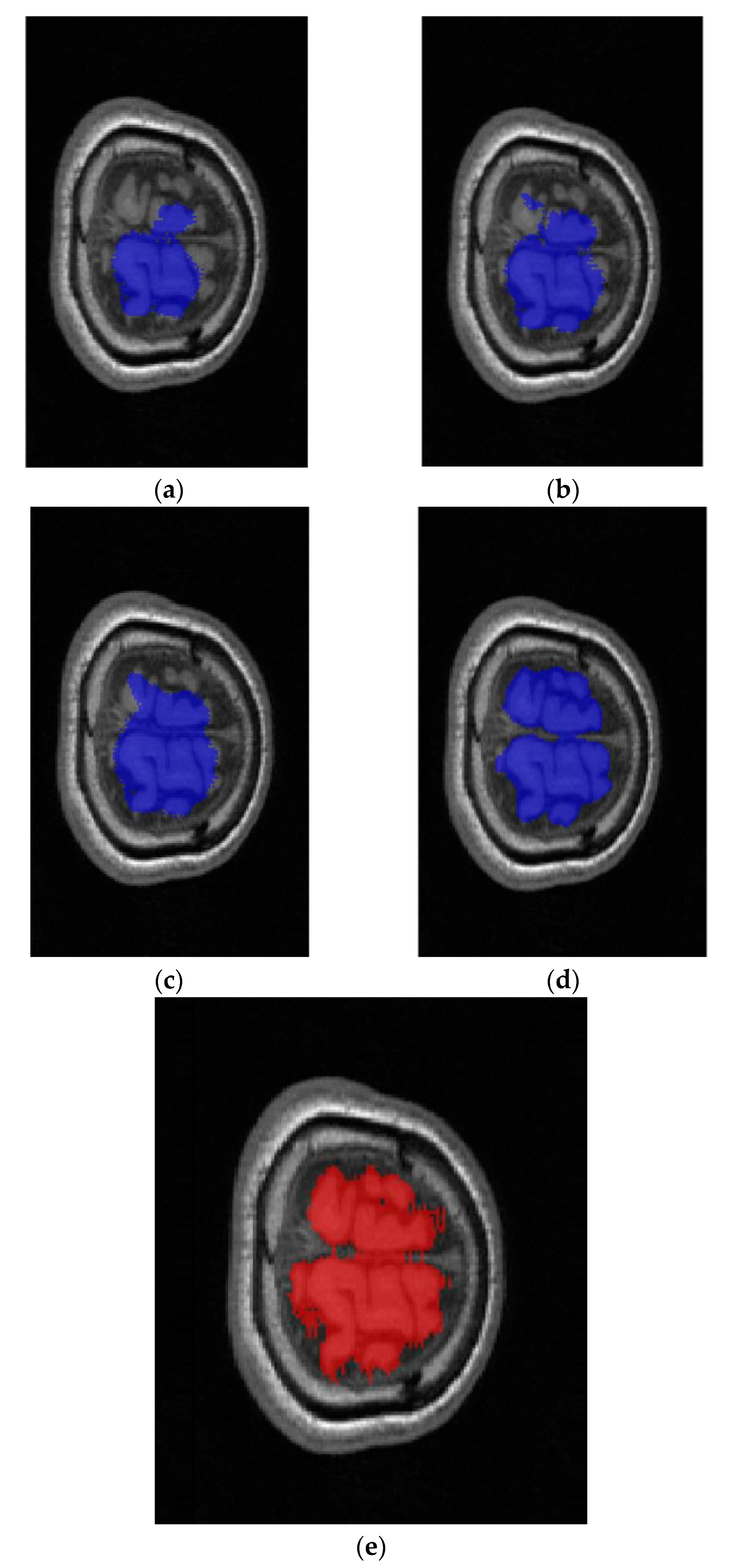
| Method | Dice | Sensitivity | Specificity |
|---|---|---|---|
| BET | 94.57 (±0.02) | 98.52 (±0.005) | 99.24 (±0.01) |
| U-Net | 96.79 (±0.004) | 97.22 (±0.01) | 99.34 (±0.002) |
| Auto-U-Net | 97.73 (±0.003) | 98.31 (±0.006) | 99.48 (±0.001) |
| DeepLabV3+ | 97.72 (±0.005) | 98.23 (±0.004) | 99.36 (±0.002) |
| SegNet | 96.92 (±0.003) | 97.98 (±0.003) | 99.33 (±0.001) |
| Preprocessing-U-Net | 97.69 (±0.005) | 98.27 (±0.007) | 99.39 (±0.002) |
| Prepro-Hybrid1-U-Net | 97.68 (±0.004) | 98.28 (±0.003) | 99.38 (±0.003) |
| Prepro-Hybrid2-U-Net | 97.76 (±0.003) | 98.33 (±0.004) | 99.49 (±0.005) |
| Prepro-Hybrid3-U-Net | 97.72 (±0.002) | 98.29 (±0.003) | 99.41 (±0.004) |
| Prepro-Hybrid2-U-Net with 2D combination (PHC-U-Net) | 98.05 (±0.005) | 98.52 (±0.004) | 99.51 (±0.002) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, W.; Yin, K.; Shi, J. Dimensionality Reduction Hybrid U-Net for Brain Extraction in Magnetic Resonance Imaging. Brain Sci. 2023, 13, 1549. https://doi.org/10.3390/brainsci13111549
Du W, Yin K, Shi J. Dimensionality Reduction Hybrid U-Net for Brain Extraction in Magnetic Resonance Imaging. Brain Sciences. 2023; 13(11):1549. https://doi.org/10.3390/brainsci13111549
Chicago/Turabian StyleDu, Wentao, Kuiying Yin, and Jingping Shi. 2023. "Dimensionality Reduction Hybrid U-Net for Brain Extraction in Magnetic Resonance Imaging" Brain Sciences 13, no. 11: 1549. https://doi.org/10.3390/brainsci13111549
APA StyleDu, W., Yin, K., & Shi, J. (2023). Dimensionality Reduction Hybrid U-Net for Brain Extraction in Magnetic Resonance Imaging. Brain Sciences, 13(11), 1549. https://doi.org/10.3390/brainsci13111549





