Precise Spiking Motifs in Neurobiological and Neuromorphic Data
Abstract
1. Introduction: Importance of Precise Spike Timings in the Brain
1.1. Is There a Neural Code?
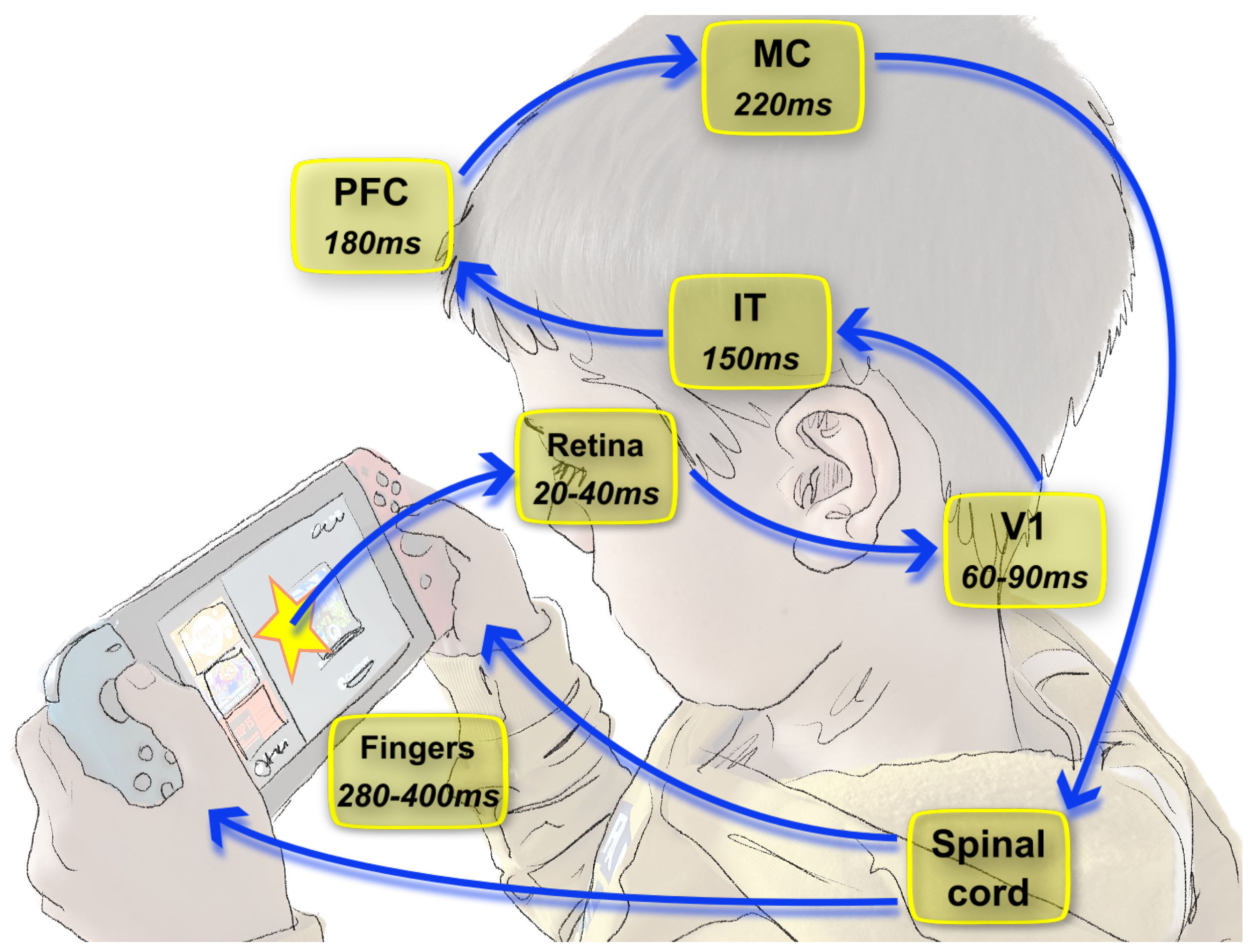
1.2. Dynamics of Vision and Consequences on the Neural Code
1.3. How Precise Spike Timing May Encode Vectors of Real Values
2. Role of Precise Spike Timing in Neural Assemblies
2.1. One First Hypothesis: Synchronous Firing in Cell Assemblies
2.2. A Further Hypothesis: Travelling Waves
2.3. A Rediscovered Hypothesis: Precise Spiking Motifs in Cell Assemblies
3. Understanding Precise Spiking Motifs in Neurobiology
3.1. Decoding Neural Activity from Firing Rates
3.2. Decoding Neural Activity Using Spike Distances
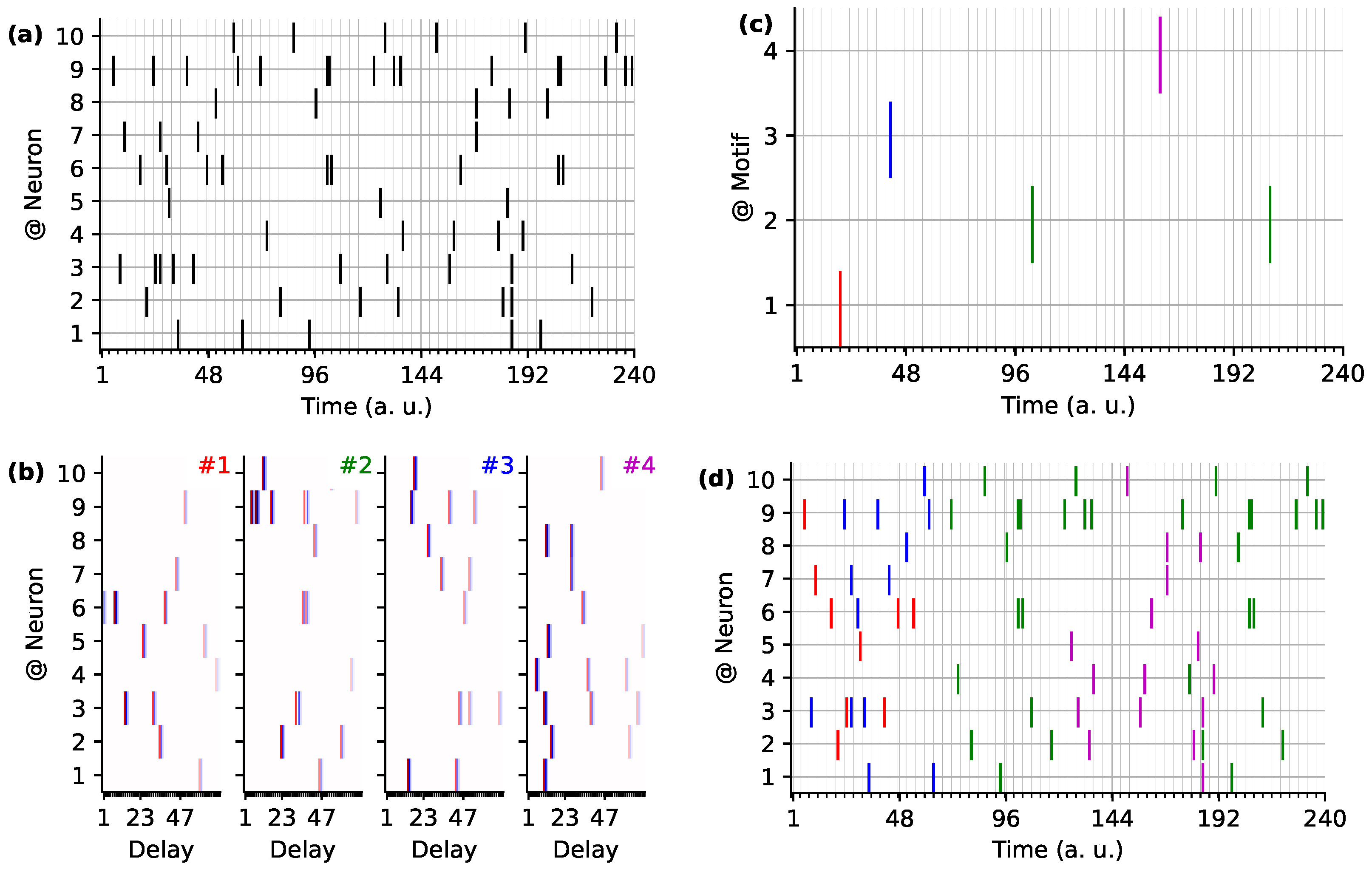
3.3. Scaling up to Very Large Scale Data
4. What Biological Mechanism Could Allow Learning Spiking Motifs?
4.1. Biological Observations of Delay Adaptation
4.2. The Importance of Myelination
4.3. Interplay of Delay Adaptation and Neural Activity
5. Modeling Precise Spiking Motifs in Theoretical and Computational Neuroscience
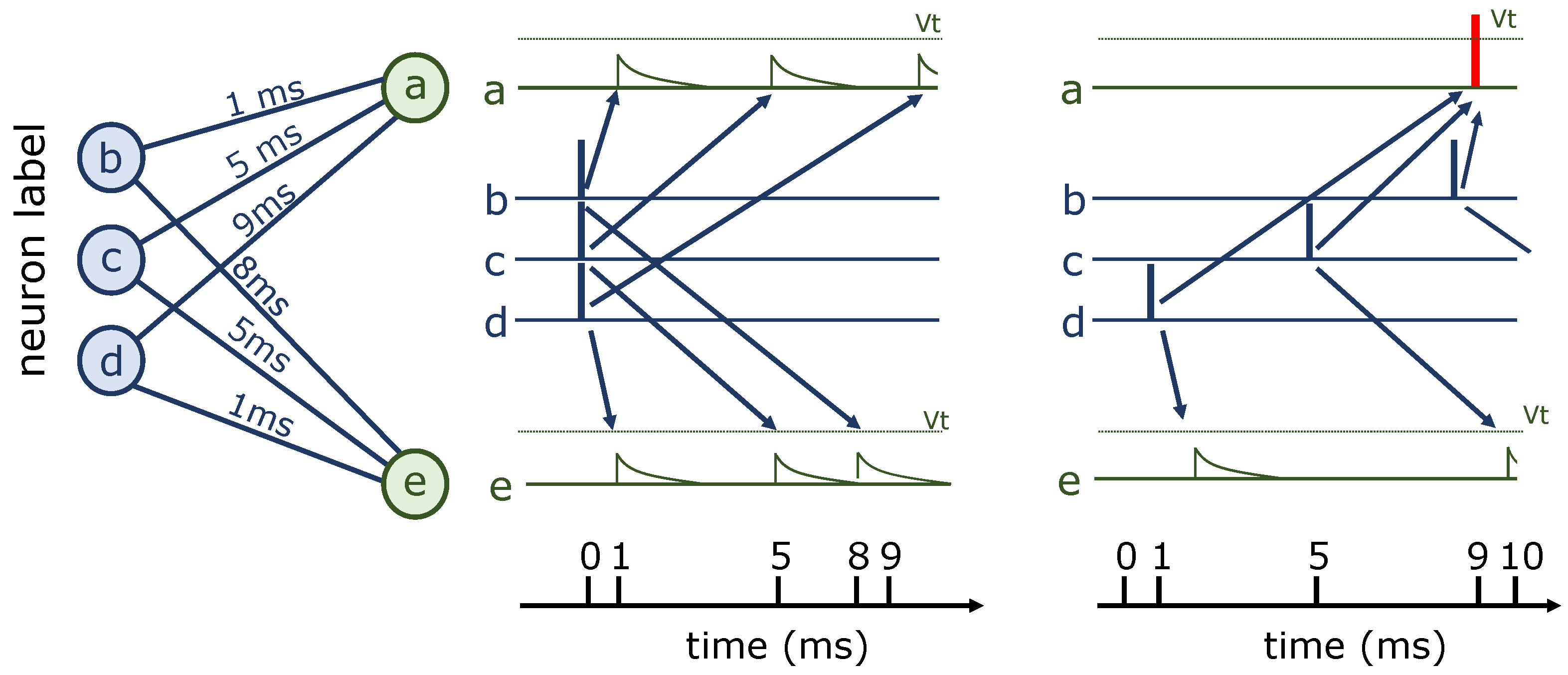
5.1. Izhikevich’s Polychronization Model
5.2. Learning Synaptic Delays
5.3. Real-World Applications
6. Applications of Precise Spiking Motifs in Neuromorphic Engineering
6.1. The Emergence of Novel Computational Architectures
6.2. On the Importance of Spatio-Temporal Information in Silicon Retinas
6.3. Computations with Delays in Neuromorphic Hardware
7. Discussion
7.1. Summary
- The efficiency of neural systems, and in particular the visual system, imposes strong constraints on the structure of neural activity which highlights the importance of precise spike times;
- Growing evidence from neurobiology proves that neural systems are more than integrators and may use synchrony detection in different forms: synfire chains, travelling waves on arbitrary spiking motifs, and notably that an encoding based on precise spiking motifs may provide huge computational benefits;
- Many theoretical models already exist, taking into account the specificity of spiking motifs, notably by using heterogeneous delays;
- Using precise spiking motifs could ultimately be a key ingredient in neuromorphic systems to reach similar efficiencies as biological neural systems.
7.2. Limits
7.3. Perspectives
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Piccolino, M. Luigi Galvani and animal electricity: Two centuries after the foundation of electrophysiology. Trends Neurosci. 1997, 20, 443–448. [Google Scholar] [CrossRef] [PubMed]
- Adrian, E.D.; Zotterman, Y. The impulses produced by sensory nerve endings. J. Physiol. 1926, 61, 465–483. [Google Scholar] [CrossRef] [PubMed]
- Gouras, P. Graded potentials of bream retina. J. Physiol. 1960, 152, 487–505. [Google Scholar] [CrossRef] [PubMed]
- Perkel, D.H.; Gerstein, G.L.; Moore, G.P. Neuronal Spike Trains and Stochastic Point Processes: I. The Single Spike Train. Biophys. J. 1967, 7, 391–418. [Google Scholar] [CrossRef] [PubMed]
- Perkel, D.H.; Gerstein, G.L.; Moore, G.P. Neuronal Spike Trains and Stochastic Point Processes: II. Simultaneous Spike Trains. Biophys. J. 1967, 7, 419–440. [Google Scholar] [CrossRef]
- Abeles, M. Role of the cortical neuron: Integrator or coincidence detector? Isr. J. Med. Sci. 1982, 18, 83–92. [Google Scholar]
- Carr, C.E. Processing of Temporal Information in the Brain. Annu. Rev. Neurosci. 1993, 16, 223–243. [Google Scholar] [CrossRef]
- Davis, Z.W.; Benigno, G.B.; Fletterman, C.; Desbordes, T.; Steward, C.; Sejnowski, T.J.; Reynolds, J.H.; Muller, L. Spontaneous traveling waves naturally emerge from horizontal fiber time delays and travel through locally asynchronous-irregular states. Nat. Commun. 2021, 12, 6057. [Google Scholar] [CrossRef]
- Perrinet, L.; Samuelides, M.; Thorpe, S. Coding static natural images using spiking event times: Do neurons cooperate? IEEE Trans. Neural Netw. 2004, 15, 1164–1175. [Google Scholar] [CrossRef]
- Gollisch, T.; Meister, M. Rapid Neural Coding in the Retina with Relative Spike Latencies. Science 2008, 319, 1108–1111. [Google Scholar] [CrossRef]
- DeWeese, M.R.; Zador, A.M. Binary Coding in Auditory Cortex; Neural Information Processing Systems Foundation: Cambridge, MA, USA; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Carr, C.E.; Konishi, M. A circuit for detection of interaural time differences in the brain stem of the barn owl. J. Neurosci. 1990, 10, 3227–3246. [Google Scholar] [CrossRef] [PubMed]
- Bohte, S.M. The evidence for neural information processing with precise spike-times: A survey. Nat. Comput. 2004, 3, 195–206. [Google Scholar] [CrossRef]
- DiLorenzo, P.M.; Victor, J.D. Spike Timing: Mechanisms and Function; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Roy, K.; Jaiswal, A.; Panda, P. Towards spike-based machine intelligence with neuromorphic computing. Nature 2019, 575, 607–617. [Google Scholar] [CrossRef] [PubMed]
- Flourens, M.J.P. Recherches Expérimentales sur les Propriétés et les Fonctions du Système Nerveux, Dans les Animaux Vertébrés; Hachette BNF: Paris, France, 1842. [Google Scholar]
- Pearce, J. Marie-Jean-Pierre Flourens (1794–1867) and Cortical Localization. Eur. Neurol. 2009, 61, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Hubel, D.H.; Wiesel, T.N. Receptive fields and functional architecture of monkey striate cortex. J. Physiol. 1968, 195, 215–243. [Google Scholar] [CrossRef]
- Carandini, M.; Heeger, D.J. Normalization as a canonical neural computation. Nat. Rev. Neurosci. 2012, 13, 51–62. [Google Scholar] [CrossRef]
- Thorpe, S.; Fize, D.; Marlot, C. Speed of processing in the human visual system. Nature 1996, 381, 520–522. [Google Scholar] [CrossRef]
- Kirchner, H.; Thorpe, S. Ultra-rapid object detection with saccadic eye movements: Visual processing speed revisited. Vis. Res. 2006, 46, 1762–1776. [Google Scholar] [CrossRef]
- Keysers, C.; Xiao, D.K.; Földiák, P.; Perrett, D.I. The Speed of Sight. J. Cogn. Neurosci. 2001, 13, 90–101. [Google Scholar] [CrossRef]
- Schmolesky, M.T.; Wang, Y.; Hanes, D.P.; Thompson, K.G.; Leutgeb, S.; Schall, J.D.; Leventhal, A.G. Signal timing across the macaque visual system. J. Neurophysiol. 1998, 79, 3272–3278. [Google Scholar] [CrossRef]
- Vanni, S.; Tanskanen, T.; Seppä, M.; Uutela, K.; Hari, R. Coinciding early activation of the human primary visual cortex and anteromedial cuneus. Proc. Natl. Acad. Sci. USA 2001, 98, 2776–2780. [Google Scholar] [CrossRef] [PubMed]
- Lamme, V.A.; Roelfsema, P.R. The distinct modes of vision offered by feedforward and recurrent processing. Trends Neurosci. 2000, 23, 571–579. [Google Scholar] [CrossRef] [PubMed]
- Serre, T.; Oliva, A.; Poggio, T. A feedforward architecture accounts for rapid categorization. Proc. Natl. Acad. Sci. USA 2007, 104, 6424–6429. [Google Scholar] [CrossRef] [PubMed]
- Jérémie, J.N.; Perrinet, L.U. Ultrafast image categorization in vivo and in silico. arXiv 2022, arXiv:2205.03635. [Google Scholar]
- Nowak, L.G.; Bullier, J. The Timing of Information Transfer in the Visual System. In Extrastriate Cortex in Primates; Springer: Boston, MA, USA, 1997; pp. 205–241. [Google Scholar]
- Thorpe, S.J.; Fabre-Thorpe, M. Seeking Categories in the Brain. Science 2001, 291, 260–263. [Google Scholar] [CrossRef]
- Rucci, M.; Ahissar, E.; Burr, D. Temporal Coding of Visual Space. Trends Cogn. Sci. 2018, 22, 883–895. [Google Scholar] [CrossRef]
- Softky, W.; Koch, C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 1993, 13, 334–350. [Google Scholar] [CrossRef]
- Bryant, H.L.; Segundo, J.P. Spike initiation by transmembrane current: A white-noise analysis. J. Physiol. 1976, 260, 279–314. [Google Scholar] [CrossRef]
- Mainen, Z.F.; Sejnowski, T.J. Reliability of Spike Timing in Neocortical Neurons. Science 1995, 268, 1503–1506. [Google Scholar] [CrossRef]
- Ermentrout, G.B.; Galán, R.F.; Urban, N.N. Reliability, synchrony and noise. Trends Neurosci. 2008, 31, 428–434. [Google Scholar] [CrossRef]
- Nowak, L. Influence of low and high frequency inputs on spike timing in visual cortical neurons. Cereb. Cortex 1997, 7, 487–501. [Google Scholar] [CrossRef] [PubMed]
- Kenyon, G.T.; Hill, D.; Theiler, J.; George, J.S.; Marshak, D.W. A theory of the Benham Top based on center–surround interactions in the parvocellular pathway. Neural Netw. 2004, 17, 773–786. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Celebrini, S.; Thorpe, S.; Trotter, Y.; Imbert, M. Dynamics of orientation coding in area V1 of the awake primate. Vis. Neurosci. 1993, 10, 811–825. [Google Scholar] [CrossRef] [PubMed]
- Chase, S.M.; Young, E.D. First-spike latency information in single neurons increases when referenced to population onset. Proc. Natl. Acad. Sci. USA 2007, 104, 5175–5180. [Google Scholar] [CrossRef] [PubMed]
- Safaie, M.; Jurado-Parras, M.T.; Sarno, S.; Louis, J.; Karoutchi, C.; Petit, L.F.; Pasquet, M.O.; Eloy, C.; Robbe, D. Turning the body into a clock: Accurate timing is facilitated by simple stereotyped interactions with the environment. Proc. Natl. Acad. Sci. USA 2020, 117, 13084–13093. [Google Scholar] [CrossRef] [PubMed]
- Gautrais, J.; Thorpe, S. Rate coding versus temporal order coding: A theoretical approach. Biosystems 1998, 48, 57–65. [Google Scholar] [CrossRef]
- Delorme, A.; Gautrais, J.; Van Rullen, R.; Thorpe, S. SpikeNET: A simulator for modeling large networks of integrate and fire neurons. Neurocomputing 1999, 26, 989–996. [Google Scholar] [CrossRef]
- Delorme, A.; Richard, G.; Fabre-Thorpe, M. Ultra-rapid categorisation of natural scenes does not rely on colour cues: A study in monkeys and humans. Vis. Res. 2000, 40, 2187–2200. [Google Scholar] [CrossRef]
- Bonilla, L.; Gautrais, J.; Thorpe, S.; Masquelier, T. Analyzing time-to-first-spike coding schemes. Front. Neurosci. 2022, 16, 971937. [Google Scholar] [CrossRef]
- Bohte, S.M.; Kok, J.N.; La Poutré, H. Error-backpropagation in temporally encoded networks of spiking neurons. Neurocomputing 2002, 48, 17–37. [Google Scholar] [CrossRef]
- Zenke, F.; Vogels, T.P. The Remarkable Robustness of Surrogate Gradient Learning for Instilling Complex Function in Spiking Neural Networks. Neural Comput. 2021, 33, 899–925. [Google Scholar] [CrossRef]
- Göltz, J.; Kriener, L.; Baumbach, A.; Billaudelle, S.; Breitwieser, O.; Cramer, B.; Dold, D.; Kungl, A.F.; Senn, W.; Schemmel, J.; et al. Fast and energy-efficient neuromorphic deep learning with first-spike times. arXiv 2021, arXiv:1912.11443. [Google Scholar] [CrossRef]
- Kheradpisheh, S.R.; Ganjtabesh, M.; Thorpe, S.J.; Masquelier, T. STDP-based spiking deep convolutional neural networks for object recognition. Neural Netw. 2018, 99, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Tavanaei, A.; Masquelier, T.; Maida, A. Representation learning using event-based STDP. Neural Netw. 2018, 105, 294–303. [Google Scholar] [CrossRef] [PubMed]
- Gallego, G.; Delbruck, T.; Orchard, G.; Bartolozzi, C.; Taba, B.; Censi, A.; Leutenegger, S.; Davison, A.J.; Conradt, J.; Daniilidis, K.; et al. Event-Based Vision: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 154–180. [Google Scholar] [CrossRef]
- Maunsell, J.H.; Van Essen, D.C. Functional properties of neurons in middle temporal visual area of the macaque monkey. I. Selectivity for stimulus direction, speed, and orientation. J. Neurophysiol. 1983, 49, 1127–1147. [Google Scholar] [CrossRef] [PubMed]
- Montemurro, M.A.; Rasch, M.J.; Murayama, Y.; Logothetis, N.K.; Panzeri, S. Phase-of-Firing Coding of Natural Visual Stimuli in Primary Visual Cortex. Curr. Biol. 2008, 18, 375–380. [Google Scholar] [CrossRef] [PubMed]
- deCharms, R.C.; Merzenich, M.M. Primary cortical representation of sounds by the coordination of action-potential timing. Nature 1996, 381, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Vinje, W.E.; Gallant, J.L. Sparse Coding and Decorrelation in Primary Visual Cortex During Natural Vision. Science 2000, 287, 1273–1276. [Google Scholar] [CrossRef] [PubMed]
- Abeles, M. Corticonics: Neural Circuits of the Cerebral Cortex; Cambridge University Press: Cambridge, MA, USA; New York, NY, USA, 1991. [Google Scholar]
- Paugam-Moisy, H.; Bohte, S.M. Computing with spiking neuron networks. In Handbook of Natural Computing; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hebb, D.O. The Organization of Behavior: A Neuropsychological Theory; Wiley: New York, NY, USA, 1949. [Google Scholar]
- Harris, K.D.; Csicsvari, J.; Hirase, H.; Dragoi, G.; Buzsáki, G. Organization of cell assemblies in the hippocampus. Nature 2003, 424, 552–556. [Google Scholar] [CrossRef]
- Singer, W.; Gray, C.M. Visual Feature Integration and the Temporal Correlation Hypothesis. Annu. Rev. Neurosci. 1995, 18, 555–586. [Google Scholar] [CrossRef] [PubMed]
- Roelfsema, P.R.; Engel, A.K.; König, P.; Singer, W. Visuomotor integration is associated with zero time-lag synchronization among cortical areas. Nature 1997, 385, 157–161. [Google Scholar] [CrossRef] [PubMed]
- Riehle, A.; Grun, S.; Diesmann, M.; Aertsen, A. Spike synchronization and rate modulation differentially involved in motor cortical function. Science 1997, 278, 1950–1953. [Google Scholar] [CrossRef] [PubMed]
- Kilavik, B.E.; Roux, S.; Ponce-Alvarez, A.; Confais, J.; Grun, S.; Riehle, A. Long-Term Modifications in Motor Cortical Dynamics Induced by Intensive Practice. J. Neurosci. 2009, 29, 12653–12663. [Google Scholar] [CrossRef] [PubMed]
- Grammont, F.; Riehle, A. Spike synchronization and firing rate in a population of motor cortical neurons in relation to movement direction and reaction time. Biol. Cybern. 2003, 88, 360–373. [Google Scholar] [CrossRef]
- Denker, M.; Zehl, L.; Kilavik, B.E.; Diesmann, M.; Brochier, T.; Riehle, A.; Grün, S. LFP beta amplitude is linked to mesoscopic spatio-temporal phase patterns. Sci. Rep. 2018, 8, 5200. [Google Scholar] [CrossRef]
- Torre, E.; Canova, C.; Denker, M.; Gerstein, G.; Helias, M.; Grün, S. ASSET: Analysis of Sequences of Synchronous Events in Massively Parallel Spike Trains. PLoS Comput. Biol. 2016, 12, e1004939. [Google Scholar] [CrossRef]
- Ben-yishai, R.; Hansel, D. Traveling Waves and the Processing of Weakly Tuned Inputs in a Cortical Network Module. J. Comput. Neurosci. 1997, 77, 57–77. [Google Scholar] [CrossRef]
- Bruno, R.M.; Sakmann, B. Cortex Is Driven by Weak but Synchronously Active Thalamocortical Synapses. Science 2006, 312, 1622–1627. [Google Scholar] [CrossRef]
- Deneve, S. Bayesian inference in spiking neurons. In Proceedings of the Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2004; Volume 17. [Google Scholar]
- Ballard, D.; Jehee, J. Dual Roles for Spike Signaling in Cortical Neural Populations. Front. Comput. Neurosci. 2011, 5, 22. [Google Scholar] [CrossRef]
- Gewaltig, M.O.; Diesmann, M.; Aertsen, A. Propagation of cortical synfire activity: Survival probability in single trials and stability in the mean. Neural Netw. 2001, 14, 657–673. [Google Scholar] [CrossRef] [PubMed]
- Gerstner, W. Time structure of the activity in neural network models. Phys. Rev. E 1995, 51, 738–758. [Google Scholar] [CrossRef] [PubMed]
- Azouz, R.; Gray, C.M. Stimulus-selective spiking is driven by the relative timing of synchronous excitation and disinhibition in cat striate neurons in vivo. Eur. J. Neurosci. 2008, 28, 1286–1300. [Google Scholar] [CrossRef] [PubMed]
- Kremkow, J.; Perrinet, L.U.; Monier, C.; Alonso, J.M.; Aertsen, A.; Frégnac, Y.; Masson, G.S. Push-Pull Receptive Field Organization and Synaptic Depression: Mechanisms for Reliably Encoding Naturalistic Stimuli in V1. Front. Neural Circuits 2016, 10, 37. [Google Scholar] [CrossRef] [PubMed]
- Aviel, Y.; Mehring, C.; Abeles, M.; Horn, D. On Embedding Synfire Chains in a Balanced Network. Neural Comput. 2003, 15, 1321–1340. [Google Scholar] [CrossRef][Green Version]
- Kremkow, J.; Perrinet, L.U.; Masson, G.S.; Aertsen, A. Functional consequences of correlated excitatory and inhibitory conductances in cortical networks. J. Comput. Neurosci. 2010, 28, 579–594. [Google Scholar] [CrossRef]
- Davison, A.P. PyNN: A common interface for neuronal network simulators. Front. Neuroinform. 2008, 2, 11. [Google Scholar] [CrossRef]
- Pfeil, T.; Grübl, A.; Jeltsch, S.; Müller, E.; Müller, P.; Petrovici, M.A.; Schmuker, M.; Brüderle, D.; Schemmel, J.; Meier, K. Six Networks on a Universal Neuromorphic Computing Substrate. Front. Neurosci. 2013, 7, 11. [Google Scholar] [CrossRef]
- Schrader, S.; Grün, S.; Diesmann, M.; Gerstein, G.L. Detecting Synfire Chain Activity Using Massively Parallel Spike Train Recording. J. Neurophysiol. 2008, 100, 2165–2176. [Google Scholar] [CrossRef]
- Grammont, F.; Riehle, A. Precise spike synchronization in monkey motor cortex involved in preparation for movement. Exp. Brain Res. 1999, 128, 118–122. [Google Scholar] [CrossRef]
- Brette, R. Computing with Neural Synchrony. PLoS Comput. Biol. 2012, 8, e1002561. [Google Scholar] [CrossRef] [PubMed]
- Fries, P. A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. Trends Cogn. Sci. 2005, 9, 474–480. [Google Scholar] [CrossRef] [PubMed]
- VanRullen, R.; Reddy, L.; Koch, C. The Continuous Wagon Wheel Illusion Is Associated with Changes in Electroencephalogram Power at 13 Hz. J. Neurosci. 2006, 26, 502–507. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Dugue, L.; Marque, P.; VanRullen, R. The Phase of Ongoing Oscillations Mediates the Causal Relation between Brain Excitation and Visual Perception. J. Neurosci. 2011, 31, 11889–11893. [Google Scholar] [CrossRef]
- Bringuier, V.; Chavane, F.; Glaeser, L.; Frégnac, Y. Horizontal Propagation of Visual Activity in the Synaptic Integration Field of Area 17 Neurons. Science 1999, 283, 695–699. [Google Scholar] [CrossRef]
- Benvenuti, G.; Chemla, S.; Boonman, A.; Perrinet, L.U.; Masson, G.S.; Chavane, F. Anticipatory responses along motion trajectories in awake monkey area V1. bioRxiv Prepr. Serv. Biol. 2020. [Google Scholar] [CrossRef]
- Le Bec, B.; Troncoso, X.G.; Desbois, C.; Passarelli, Y.; Baudot, P.; Monier, C.; Pananceau, M.; Frégnac, Y. Horizontal connectivity in V1: Prediction of coherence in contour and motion integration. PLoS ONE 2022, 17, e0268351. [Google Scholar] [CrossRef]
- Feller, M.B.; Butts, D.A.; Aaron, H.L.; Rokhsar, D.S.; Shatz, C.J. Dynamic Processes Shape Spatiotemporal Properties of Retinal Waves. Neuron 1997, 19, 293–306. [Google Scholar] [CrossRef]
- Bienenstock, E. A model of neocortex. Netw. Comput. Neural Syst. 1995, 6, 179–224. [Google Scholar] [CrossRef]
- Muller, L.; Reynaud, A.; Chavane, F.; Destexhe, A. The stimulus-evoked population response in visual cortex of awake monkey is a propagating wave. Nat. Commun. 2014, 5, 3675. [Google Scholar] [CrossRef]
- Muller, L.; Chavane, F.; Reynolds, J.; Sejnowski, T.J. Cortical travelling waves: Mechanisms and computational principles. Nat. Rev. Neurosci. 2018, 19, 255–268. [Google Scholar] [CrossRef] [PubMed]
- Lindén, H.; Petersen, P.C.; Vestergaard, M.; Berg, R.W. Movement is governed by rotational neural dynamics in spinal motor networks. Nature 2022, 610, 526–531. [Google Scholar] [CrossRef] [PubMed]
- Chemla, S.; Reynaud, A.; diVolo, M.; Zerlaut, Y.; Perrinet, L.U.; Destexhe, A.; Chavane, F.Y. Suppressive waves disambiguate the representation of long-range apparent motion in awake monkey V1. J. Neurosci. 2019, 2792, 18. [Google Scholar] [CrossRef]
- Pillow, J.W.; Shlens, J.; Paninski, L.; Sher, A.; Litke, A.M.; Chichilnisky, E.J.; Simoncelli, E.P. Spatio-temporal correlations and visual signalling in a complete neuronal population. Nature 2008, 454, 995–999. [Google Scholar] [CrossRef]
- Schneidman, E.; Berry, M.J.; Segev, R.; Bialek, W. Weak pairwise correlations imply strongly correlated network states in a neural population. Nature 2006, 440, 1007–1012. [Google Scholar] [CrossRef]
- Puchalla, J.; Berry, M.J. Spike Trains of Retinal Ganglion Cells Viewing a Repeated Natural Movie; Princeton University: Princeton, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Miller, J.e.K.; Ayzenshtat, I.; Carrillo-Reid, L.; Yuste, R. Visual stimuli recruit intrinsically generated cortical ensembles. Proc. Natl. Acad. Sci. USA 2014, 111, E4053–E4061. [Google Scholar] [CrossRef]
- Ikegaya, Y.; Aaron, G.; Cossart, R.; Aronov, D.; Lampl, I.; Ferster, D.; Yuste, R. Synfire Chains and Cortical Songs: Temporal Modules of Cortical Activity. Science 2004, 304, 559–564. [Google Scholar] [CrossRef]
- Luczak, A.; Barthó, P.; Marguet, S.L.; Buzsáki, G.; Harris, K.D. Sequential structure of neocortical spontaneous activity in vivo. Proc. Natl. Acad. Sci. USA 2007, 104, 347–352. [Google Scholar] [CrossRef]
- Pastalkova, E.; Itskov, V.; Amarasingham, A.; Buzsáki, G. Internally Generated Cell Assembly Sequences in the Rat Hippocampus. Science 2008, 321, 1322–1327. [Google Scholar] [CrossRef]
- Villette, V.; Malvache, A.; Tressard, T.; Dupuy, N.; Cossart, R. Internally Recurring Hippocampal Sequences as a Population Template of Spatiotemporal Information. Neuron 2015, 88, 357–366. [Google Scholar] [CrossRef]
- Branco, T.; Clark, B.A.; Häusser, M. Dendritic Discrimination of Temporal Input Sequences in Cortical Neurons. Science 2010, 329, 1671–1675. [Google Scholar] [CrossRef] [PubMed]
- Luczak, A.; McNaughton, B.L.; Harris, K.D. Packet-based communication in the cortex. Nat. Rev. Neurosci. 2015, 16, 745–755. [Google Scholar] [CrossRef] [PubMed]
- Meister, M.; Lagnado, L.; Baylor, D.A. Concerted Signaling by Retinal Ganglion Cells. Science 1995, 270, 1207–1210. [Google Scholar] [CrossRef] [PubMed]
- Cleland, T.A. Construction of Odor Representations by Olfactory Bulb Microcircuits. In Progress in Brain Research; Elsevier: Amsterdam, The Netherlands, 2014; Volume 208, pp. 177–203. [Google Scholar] [CrossRef]
- Kashiwadani, H.; Sasaki, Y.F.; Uchida, N.; Mori, K. Synchronized Oscillatory Discharges of Mitral/Tufted Cells With Different Molecular Receptive Ranges in the Rabbit Olfactory Bulb. J. Neurophysiol. 1999, 82, 1786–1792. [Google Scholar] [CrossRef] [PubMed]
- Rinberg, D.; Koulakov, A.; Gelperin, A. Speed-Accuracy Tradeoff in Olfaction. Neuron 2006, 51, 351–358. [Google Scholar] [CrossRef]
- Johansson, R.S.; Birznieks, I. First spikes in ensembles of human tactile afferents code complex spatial fingertip events. Nat. Neurosci. 2004, 7, 170–177. [Google Scholar] [CrossRef]
- Buzsáki, G.; Tingley, D. Space and Time: The Hippocampus as a Sequence Generator. Trends Cogn. Sci. 2018, 22, 853–869. [Google Scholar] [CrossRef]
- Malvache, A.; Reichinnek, S.; Villette, V.; Haimerl, C.; Cossart, R. Awake hippocampal reactivations project onto orthogonal neuronal assemblies. Science 2016, 353, 1280–1283. [Google Scholar] [CrossRef]
- Haimerl, C.; Angulo-Garcia, D.; Villette, V.; Reichinnek, S.; Torcini, A.; Cossart, R.; Malvache, A. Internal representation of hippocampal neuronal population spans a time-distance continuum. Proc. Natl. Acad. Sci. USA 2019, 116, 7477–7482. [Google Scholar] [CrossRef]
- Agus, T.R.; Thorpe, S.J.; Pressnitzer, D. Rapid Formation of Robust Auditory Memories: Insights from Noise. Neuron 2010, 66, 610–618. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Polychronization: Computation with Spikes. Neural Comput. 2006, 18, 245–282. [Google Scholar] [CrossRef] [PubMed]
- Simoncelli, E.P.; Paninski, L.; Pillow, J.; Schwartz, O. Characterization of Neural Responses with Stochastic Stimuli. In The New Cognitive Neurosciences, 3rd ed.; Gazzaniga, M., Ed.; MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Jazayeri, M.; Movshon, J.A. Optimal representation of sensory information by neural populations. Nat. Neurosci. 2006, 9, 690–696. [Google Scholar] [CrossRef] [PubMed]
- Berens, P.; Ecker, A.S.; Cotton, R.J.; Ma, W.J.; Bethge, M.; Tolias, A.S. A Fast and Simple Population Code for Orientation in Primate V1. J. Neurosci. 2012, 32, 10618–10626. [Google Scholar] [CrossRef] [PubMed]
- Bellec, G.; Wang, S.; Modirshanechi, A.; Brea, J.; Gerstner, W. Fitting summary statistics of neural data with a differentiable spiking network simulator. arXiv 2021, arXiv:2106.10064. [Google Scholar]
- Kohn, A.; Smith, M. Utah Array Extracellular Recordings of Spontaneous and Visually Evoked Activity from Anesthetized Macaque Primary Visual Cortex (V1). 2016. Available online: https://doi.org/10.6080/K0NC5Z4X (accessed on 25 December 2022).
- Warner, C.; Ruda, K.; Sommer, F.T. A probabilistic latent variable model for detecting structure in binary data. arXiv 2022, arXiv:2201.11108. [Google Scholar]
- Victor, J.D.; Purpura, K.P. Nature and precision of temporal coding in visual cortex: A metric-space analysis. J. Neurophysiol. 1996, 76, 1310–1326. [Google Scholar] [CrossRef]
- van Rossum, M.C. A novel spike distance. Neural Comput. 2001, 13, 751–763. [Google Scholar] [CrossRef]
- Kreuz, T.; Haas, J.S.; Morelli, A.; Abarbanel, H.D.I.; Politi, A. Measuring spike train synchrony. J. Neurosci. Methods 2007, 165, 151–161. [Google Scholar] [CrossRef]
- Moser, B.A.; Natschlager, T. On Stability of Distance Measures for Event Sequences Induced by Level-Crossing Sampling. IEEE Trans. Signal Process. 2014, 62, 1987–1999. [Google Scholar] [CrossRef]
- Weyl, H. Ueber die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 1916, 77, 313–352. [Google Scholar] [CrossRef]
- Aronov, D.; Victor, J.D. Non-Euclidean properties of spike train metric spaces. Phys. Rev. E 2004, 69, 061905. [Google Scholar] [CrossRef] [PubMed]
- Levakova, M.; Tamborrino, M.; Ditlevsen, S.; Lansky, P. A review of the methods for neuronal response latency estimation. Biosystems 2015, 136, 23–34. [Google Scholar] [CrossRef] [PubMed]
- Grün, S.; Diesmann, M.; Aertsen, A. Unitary Events in Multiple Single-Neuron Spiking Activity: II. Nonstationary Data. Neural Comput. 2002, 14, 81–119. [Google Scholar] [CrossRef] [PubMed]
- Grün, S.; Diesmann, M.; Aertsen, A. Unitary Event Analysis. In Analysis of Parallel Spike Trains; Springer: Boston, MA, USA, 2010; pp. 191–220. [Google Scholar]
- Grün, S.; Diesmann, M.; Aertsen, A. Unitary Events in Multiple Single-Neuron Spiking Activity: I. Detection and Significance. Neural Comput. 2002, 14, 43–80. [Google Scholar] [CrossRef]
- Torre, E.; Picado-Muiño, D.; Denker, M.; Borgelt, C.; Grün, S. Statistical evaluation of synchronous spike patterns extracted by frequent item set mining. Front. Comput. Neurosci. 2013, 7, 132. [Google Scholar] [CrossRef]
- Quaglio, P.; Rostami, V.; Torre, E.; Grün, S. Methods for identification of spike patterns in massively parallel spike trains. Biol. Cybern. 2018, 112, 57–80. [Google Scholar] [CrossRef]
- Stella, A.; Quaglio, P.; Torre, E.; Grün, S. 3d-SPADE: Significance evaluation of spatio-temporal patterns of various temporal extents. Biosystems 2019, 185, 104022. [Google Scholar] [CrossRef]
- Stella, A.; Bouss, P.; Palm, G.; Grün, S. Comparing Surrogates to Evaluate Precisely Timed Higher-Order Spike Correlations. eNeuro 2022, 9, ENEURO.0505–21.2022. [Google Scholar] [CrossRef]
- Grossberger, L.; Battaglia, F.P.; Vinck, M. Unsupervised clustering of temporal patterns in high-dimensional neuronal ensembles using a novel dissimilarity measure. PLoS Comput. Biol. 2018, 14, e1006283. [Google Scholar] [CrossRef]
- Nádasdy, Z.; Hirase, H.; Czurkó, A.; Csicsvari, J.; Buzsáki, G. Replay and Time Compression of Recurring Spike Sequences in the Hippocampus. J. Neurosci. 1999, 19, 9497–9507. [Google Scholar] [CrossRef]
- Lee, A.K.; Wilson, M.A. A Combinatorial Method for Analyzing Sequential Firing Patterns Involving an Arbitrary Number of Neurons Based on Relative Time Order. J. Neurophysiol. 2004, 92, 2555–2573. [Google Scholar] [CrossRef] [PubMed]
- Sotomayor-Gómez, B.; Battaglia, F.P.; Vinck, M. SpikeShip: A method for fast, unsupervised discovery of high-dimensional neural spiking patterns. bioRxiv Prepr. Serv. Biol. 2021. [Google Scholar] [CrossRef]
- Pachitariu, M.; Stringer, C.; Harris, K.D. Robustness of Spike Deconvolution for Neuronal Calcium Imaging. J. Neurosci. 2018, 38, 7976–7985. [Google Scholar] [CrossRef]
- Stringer, C. MouseLand/Rastermap: A Multi-Dimensional Embedding Algorithm. 2020. Available online: https://github.com/MouseLand/rastermap (accessed on 25 December 2022).
- Stringer, C.; Pachitariu, M.; Steinmetz, N.; Reddy, C.B.; Carandini, M.; Harris, K.D. Spontaneous behaviors drive multidimensional, brainwide activity. Science 2019, 364, 255. [Google Scholar] [CrossRef] [PubMed]
- Stringer, C.; Michaelos, M.; Tsyboulski, D.; Lindo, S.E.; Pachitariu, M. High-precision coding in visual cortex. Cell 2021, 184, 2767–2778.e15. [Google Scholar] [CrossRef] [PubMed]
- Russo, E.; Durstewitz, D. Cell assemblies at multiple time scales with arbitrary lag constellations. eLife 2017, 6, e19428. [Google Scholar] [CrossRef]
- Pipa, G.; Wheeler, D.W.; Singer, W.; Nikolić, D. NeuroXidence: Reliable and efficient analysis of an excess or deficiency of joint-spike events. J. Comput. Neurosci. 2008, 25, 64–88. [Google Scholar] [CrossRef]
- Torre, E.; Quaglio, P.; Denker, M.; Brochier, T.; Riehle, A.; Grun, S. Synchronous Spike Patterns in Macaque Motor Cortex during an Instructed-Delay Reach-to-Grasp Task. J. Neurosci. 2016, 36, 8329–8340. [Google Scholar] [CrossRef]
- Williams, A.H.; Degleris, A.; Wang, Y.; Linderman, S.W. Point process models for sequence detection in high-dimensional neural spike trains. arXiv 2020, arXiv:2010.04875. [Google Scholar]
- Kass, R.E.; Ventura, V.; Brown, E.N. Statistical issues in the analysis of neuronal data. J. Neurophysiol. 2005, 94, 8–25. [Google Scholar] [CrossRef]
- van Kempen, J.; Gieselmann, M.A.; Boyd, M.; Steinmetz, N.A.; Moore, T.; Engel, T.A.; Thiele, A. Top-down coordination of local cortical state during selective attention. Neuron 2021, 109, 894–904.e8. [Google Scholar] [CrossRef] [PubMed]
- Pasturel, C.; Montagnini, A.; Perrinet, L.U. Humans adapt their anticipatory eye movements to the volatility of visual motion properties. PLoS Comput. Biol. 2020, 16, e1007438. [Google Scholar] [CrossRef] [PubMed]
- Von Helmholz, H. Messungen über den zeitlichen Verlauf der Zuckung animalischer Muskeln und die Fortpflanzungsgeschwindigkeit der Reizung in den Nerven. Arch. Anat. Physiol. Wiss. Med. 1850, 17, 176–364. [Google Scholar]
- Peyrard, M. How is information transmitted in a nerve? J. Biol. Phys. 2020, 46, 327–341. [Google Scholar] [CrossRef] [PubMed]
- Young, J.Z. The Functioning of the Giant Nerve Fibres of the Squid. J. Exp. Biol. 1938, 15, 170–185. [Google Scholar] [CrossRef]
- Madadi Asl, M.; Valizadeh, A.; Tass, P.A. Dendritic and Axonal Propagation Delays May Shape Neuronal Networks With Plastic Synapses. Front. Physiol. 2018, 9, 1849. [Google Scholar] [CrossRef]
- Stetson, D.S.; Albers, J.W.; Silverstein, B.A.; Wolfe, R.A. Effects of age, sex, and anthropometric factors on nerve conduction measures. Muscle Nerve 1992, 15, 1095–1104. [Google Scholar] [CrossRef]
- Jeffress, L.A. A place theory of sound localization. J. Comp. Physiol. Psychol. 1948, 41, 35–39. [Google Scholar] [CrossRef]
- Konishi, M. Coding of auditory space. Annu. Rev. Neurosci. 2003, 26, 31–55. [Google Scholar] [CrossRef]
- Gerstner, W.; Kempter, R.; van Hemmen, J.L.; Wagner, H. A neuronal learning rule for sub-millisecond temporal coding. Nature 1996, 383, 76–78. [Google Scholar] [CrossRef]
- Seidl, A.H.; Rubel, E.W.; Harris, D.M. Mechanisms for adjusting interaural time differences to achieve binaural coincidence detection. J. Neurosci. Off. J. Soc. Neurosci. 2010, 30, 70–80. [Google Scholar] [CrossRef] [PubMed]
- Camon, J.; Hugues, S.; Erlandson, M.A.; Robbe, D.; Lagoun, S.; Marouane, E.; Bureau, I. The Timing of Sensory-Guided Behavioral Response is Represented in the Mouse Primary Somatosensory Cortex. Cereb. Cortex 2019, 29, 3034–3047. [Google Scholar] [CrossRef]
- Gasser, H.S.; Grundfest, H. Axon Diameters in Relation to the Spike Dimensions and the Conduction Velocity in Mammalian A Fibers. Am. J.-Physiol.-Leg. Content 1939. [Google Scholar] [CrossRef]
- Brill, M.H.; Waxman, S.G.; Moore, J.W.; Joyner, R.W. Conduction velocity and spike configuration in myelinated fibres: Computed dependence on internode distance. J. Neurol. Neurosurg. Psychiatry 1977, 40, 769–774. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Cerdá, F.; Sánchez-Gómez, M.V.; Matute, C. Pío del Río Hortega and the discovery of the oligodendrocytes. Front. Neuroanat. 2015, 9, 92. [Google Scholar] [CrossRef] [PubMed]
- Schmitt, F.O.; Bear, R.S. The Ultrastructure of the Nerve Axon Sheath. Biol. Rev. 1939, 14, 27–50. [Google Scholar] [CrossRef]
- Simons, M.; Nave, K.A. Oligodendrocytes: Myelination and Axonal Support. Cold Spring Harb. Perspect. Biol. 2016, 8, a020479. [Google Scholar] [CrossRef] [PubMed]
- Duncan, G.J.; Simkins, T.J.; Emery, B. Neuron-Oligodendrocyte Interactions in the Structure and Integrity of Axons. Front. Cell Dev. Biol. 2021, 9, 653101. [Google Scholar] [CrossRef]
- Fields, R.D. A new mechanism of nervous system plasticity: Activity-dependent myelination. Nat. Rev. Neurosci. 2015, 16, 756–767. [Google Scholar] [CrossRef]
- Fields, R.D.; Bukalo, O. Myelin makes memories. Nat. Neurosci. 2020, 23, 469–470. [Google Scholar] [CrossRef]
- Reynolds, F.E.; Slater, J.K. A Study of the Structure and Function of the Interstitial Tissue of the Central Nervous System. Edinb. Med. J. 1928, 35, 49–57. [Google Scholar]
- Steadman, P.E.; Xia, F.; Ahmed, M.; Mocle, A.J.; Penning, A.R.; Geraghty, A.C.; Steenland, H.W.; Monje, M.; Josselyn, S.A.; Frankland, P.W. Disruption of Oligodendrogenesis Impairs Memory Consolidation in Adult Mice. Neuron 2020, 105, 150–164.e6. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Mayoral, S.R.; Choi, H.S.; Chan, J.R.; Kheirbek, M.A. Preservation of a remote fear memory requires new myelin formation. Nat. Neurosci. 2020, 23, 487–499. [Google Scholar] [CrossRef] [PubMed]
- Wan, R.; Cheli, V.T.; Santiago-González, D.A.; Rosenblum, S.L.; Wan, Q.; Paez, P.M. Impaired Postnatal Myelination in a Conditional Knockout Mouse for the Ferritin Heavy Chain in Oligodendroglial Cells. J. Neurosci. 2020, 40, 7609–7624. [Google Scholar] [CrossRef] [PubMed]
- Xue, J.; Zhu, Y.; Liu, Z.; Lin, J.; Li, Y.; Li, Y.; Zhuo, Y. Demyelination of the Optic Nerve: An Underlying Factor in Glaucoma? Front. Aging Neurosci. 2021, 13, 701322. [Google Scholar] [CrossRef]
- Kuhn, S.; Gritti, L.; Crooks, D.; Dombrowski, Y. Oligodendrocytes in Development, Myelin Generation and Beyond. Cells 2019, 8, 1424. [Google Scholar] [CrossRef]
- Baraban, M.; Koudelka, S.; Lyons, D.A. Ca2+ activity signatures of myelin sheath formation and growth in vivo. Nat. Neurosci. 2018, 21, 19–23. [Google Scholar] [CrossRef]
- Nave, K.A.; Salzer, J.L. Axonal regulation of myelination by neuregulin 1. Curr. Opin. Neurobiol. 2006, 16, 492–500. [Google Scholar] [CrossRef] [PubMed]
- Cullen, C.L.; Pepper, R.E.; Clutterbuck, M.T.; Pitman, K.A.; Oorschot, V.; Auderset, L.; Tang, A.D.; Ramm, G.; Emery, B.; Rodger, J.; et al. Periaxonal and nodal plasticities modulate action potential conduction in the adult mouse brain. Cell Rep. 2021, 34, 108641. [Google Scholar] [CrossRef]
- Gibson, E.M.; Purger, D.; Mount, C.W.; Goldstein, A.K.; Lin, G.L.; Wood, L.S.; Inema, I.; Miller, S.E.; Bieri, G.; Zuchero, J.B.; et al. Neuronal Activity Promotes Oligodendrogenesis and Adaptive Myelination in the Mammalian Brain. Science 2014, 344, 1252304. [Google Scholar] [CrossRef]
- Spencer, M.J.; Meffin, H.; Burkitt, A.N.; Grayden, D.B. Compensation for Traveling Wave Delay Through Selection of Dendritic Delays Using Spike-Timing-Dependent Plasticity in a Model of the Auditory Brainstem. Front. Comput. Neurosci. 2018, 12, 36. [Google Scholar] [CrossRef]
- Mel, B.W.; Schiller, J.; Poirazi, P. Synaptic plasticity in dendrites: Complications and coping strategies. Curr. Opin. Neurobiol. 2017, 43, 177–186. [Google Scholar] [CrossRef] [PubMed]
- Golding, N.L.; Staff, N.P.; Spruston, N. Dendritic spikes as a mechanism for cooperative long-term potentiation. Nature 2002, 418, 326–331. [Google Scholar] [CrossRef] [PubMed]
- Maass, W. Networks of spiking neurons: The third generation of neural network models. Neural Netw. 1997, 10, 1659–1671. [Google Scholar] [CrossRef]
- Neftci, E.O.; Mostafa, H.; Zenke, F. Surrogate Gradient Learning in Spiking Neural Networks: Bringing the Power of Gradient-Based Optimization to Spiking Neural Networks. IEEE Signal Process. Mag. 2019, 36, 51–63. [Google Scholar] [CrossRef]
- Rueckauer, B.; Lungu, I.A.; Hu, Y.; Pfeiffer, M.; Liu, S.C. Conversion of Continuous-Valued Deep Networks to Efficient Event-Driven Networks for Image Classification. Front. Neurosci. 2017, 11, 682. [Google Scholar] [CrossRef]
- Susi, G.; Antón-Toro, L.F.; Maestú, F.; Pereda, E.; Mirasso, C. nMNSD-A Spiking Neuron-Based Classifier That Combines Weight-Adjustment and Delay-Shift. Front. Neurosci. 2021, 15, 582608. [Google Scholar] [CrossRef]
- Davies, M.; Srinivasa, N.; Lin, T.H.; Chinya, G.; Cao, Y.; Choday, S.H.; Dimou, G.; Joshi, P.; Imam, N.; Jain, S.; et al. Loihi: A Neuromorphic Manycore Processor with On-Chip Learning. IEEE Micro 2018, 38, 82–99. [Google Scholar] [CrossRef]
- Lazar, A.A. Time encoding with an integrate-and-fire neuron with a refractory period. Neurocomputing 2004, 58–60, 53–58. [Google Scholar] [CrossRef]
- Markram, H.; Lübke, J.; Frotscher, M.; Sakmann, B. Regulation of Synaptic Efficacy by Coincidence of Postsynaptic APs and EPSPs. Science 1997, 275, 213–215. [Google Scholar] [CrossRef]
- Caporale, N.; Dan, Y. Spike Timing–Dependent Plasticity: A Hebbian Learning Rule. Annu. Rev. Neurosci. 2008, 31, 25–46. [Google Scholar] [CrossRef] [PubMed]
- Hüning, H.; Glünder, H.; Palm, G. Synaptic Delay Learning in Pulse-Coupled Neurons. Neural Comput. 1998, 10, 555–565. [Google Scholar] [CrossRef] [PubMed]
- Eurich, C.W.; Pawelzik, K.; Ernst, U.; Cowan, J.D.; Milton, J.G. Dynamics of Self-Organized Delay Adaptation. Phys. Rev. Lett. 1999, 82, 1594–1597. [Google Scholar] [CrossRef]
- Gütig, R.; Sompolinsky, H. The tempotron: A neuron that learns spike timing–based decisions. Nat. Neurosci. 2006, 9, 420–428. [Google Scholar] [CrossRef] [PubMed]
- Gütig, R. To spike, or when to spike? Curr. Opin. Neurobiol. 2014, 25, 134–139. [Google Scholar] [CrossRef]
- Pauli, R.; Weidel, P.; Kunkel, S.; Morrison, A. Reproducing Polychronization: A Guide to Maximizing the Reproducibility of Spiking Network Models. Front. Neuroinformatics 2018, 12, 46. [Google Scholar] [CrossRef]
- Guise, M.; Knott, A.; Benuskova, L. A Bayesian Model of Polychronicity. Neural Comput. 2014, 26, 2052–2073. [Google Scholar] [CrossRef]
- Zhang, M.; Wu, J.; Belatreche, A.; Pan, Z.; Xie, X.; Chua, Y.; Li, G.; Qu, H.; Li, H. Supervised learning in spiking neural networks with synaptic delay-weight plasticity. Neurocomputing 2020, 409, 103–118. [Google Scholar] [CrossRef]
- Ghosh, D.; Frasca, M.; Rizzo, A.; Majhi, S.; Rakshit, S.; Alfaro-Bittner, K.; Boccaletti, S. Synchronization in time-varying networks. arXiv 2021, arXiv:2109.07618. [Google Scholar]
- Ghosh, D.; Frasca, M.; Rizzo, A.; Majhi, S.; Rakshit, S.; Alfaro-Bittner, K.; Boccaletti, S. The synchronized dynamics of time-varying networks. Phys. Rep. 2022, 949, 1–63. [Google Scholar] [CrossRef]
- Izhikevich, E.M.; Hoppensteadt, F.C. Polychronous Wavefront Computations. Int. J. Bifurc. Chaos 2009, 19, 1733–1739. [Google Scholar] [CrossRef]
- Grimaldi, A.; Perrinet, L.U. Learning hetero-synaptic delays for motion detection in a single layer of spiking neurons. In Proceedings of the 2022 IEEE International Conference on Image Processing (ICIP), Bordeaux, France, 16–19 October 2022; pp. 3591–3595. [Google Scholar] [CrossRef]
- Madadi Asl, M.; Ramezani Akbarabadi, S. Delay-dependent transitions of phase synchronization and coupling symmetry between neurons shaped by spike-timing-dependent plasticity. Cogn. Neurodyn. 2022, 1–14. [Google Scholar] [CrossRef]
- Perrinet, L.; Samuelides, M. Coherence detection in a spiking neuron via Hebbian learning. Neurocomputing 2002, 44-46, 133–139. [Google Scholar] [CrossRef]
- Perrinet, L.; Delorme, A.; Samuelides, M.; Thorpe, S. Networks of integrate-and-fire neuron using rank order coding A: How to implement spike time dependent Hebbian plasticity. Neurocomputing 2001, 38–40, 817–822. [Google Scholar] [CrossRef]
- Gilson, M. STDP in recurrent neuronal networks. Front. Comput. Neurosci. 2010, 4, 23. [Google Scholar] [CrossRef]
- Datadien, A.; Haselager, P.; Sprinkhuizen-Kuyper, I. The Right Delay—Detecting Specific Spike Patterns with STDP and Axonal Conduction Delays; Springer: Berlin/Heidelberg, Germany, 2011; pp. 90–99. [Google Scholar]
- Kerr, R.R.; Burkitt, A.N.; Thomas, D.A.; Gilson, M.; Grayden, D.B. Delay Selection by Spike-Timing-Dependent Plasticity in Recurrent Networks of Spiking Neurons Receiving Oscillatory Inputs. PLoS Comput. Biol. 2013, 9, e1002897. [Google Scholar] [CrossRef]
- Burkitt, A.N.; Hogendoorn, H. Predictive Visual Motion Extrapolation Emerges Spontaneously and without Supervision at Each Layer of a Hierarchical Neural Network with Spike-Timing-Dependent Plasticity. J. Neurosci. 2021, 41, 4428–4438. [Google Scholar] [CrossRef]
- Nadafian, A.; Ganjtabesh, M. Bio-plausible Unsupervised Delay Learning for Extracting Temporal Features in Spiking Neural Networks. arXiv 2020, arXiv:2011.09380. [Google Scholar]
- Wang, X.; Lin, X.; Dang, X. A Delay Learning Algorithm Based on Spike Train Kernels for Spiking Neurons. Front. Neurosci. 2019, 13, 252. [Google Scholar] [CrossRef]
- Hazan, H.; Caby, S.; Earl, C.; Siegelmann, H.; Levin, M. Memory via Temporal Delays in weightless Spiking Neural Network. arXiv 2022, arXiv:2202.07132. [Google Scholar]
- Luo, X.; Qu, H.; Wang, Y.; Yi, Z.; Zhang, J.; Zhang, M. Supervised Learning in Multilayer Spiking Neural Networks With Spike Temporal Error Backpropagation. IEEE Trans. Neural Netw. Learn. Syst. 2022, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Sourina, O.; Huang, G.B. Learning polychronous neuronal groups using joint weight-delay spike-timing-dependent plasticity. Neural Comput. 2016, 28, 2181–2212. [Google Scholar] [CrossRef] [PubMed]
- Ghosh, R.; Gupta, A.; Silva, A.N.; Soares, A.; Thakor, N.V. Spatiotemporal filtering for event-based action recognition. arXiv 2019, arXiv:1903.07067. [Google Scholar]
- Perrinet, L.U.; Adams, R.A.; Friston, K.J. Active inference, eye movements and oculomotor delays. Biol. Cybern. 2014, 108, 777–801. [Google Scholar] [CrossRef]
- Hogendoorn, H.; Burkitt, A.N. Predictive Coding with Neural Transmission Delays: A Real-Time Temporal Alignment Hypothesis. eNeuro 2019, 6, ENEURO.0412-18.2019. [Google Scholar] [CrossRef]
- Khoei, M.A.; Masson, G.S.; Perrinet, L.U. Motion-based prediction explains the role of tracking in motion extrapolation. J. Physiol.-Paris 2013, 107, 409–420. [Google Scholar] [CrossRef]
- Kaplan, B.A.; Lansner, A.; Masson, G.S.; Perrinet, L.U. Anisotropic connectivity implements motion-based prediction in a spiking neural network. Front. Comput. Neurosci. 2013, 7, 112. [Google Scholar] [CrossRef]
- Khoei, M.A.; Masson, G.S.; Perrinet, L.U. The Flash-Lag Effect as a Motion-Based Predictive Shift. PLoS Comput. Biol. 2017, 13, e1005068. [Google Scholar] [CrossRef]
- Javanshir, A.; Nguyen, T.T.; Mahmud, M.A.P.; Kouzani, A.Z. Advancements in Algorithms and Neuromorphic Hardware for Spiking Neural Networks. Neural Comput. 2022, 34, 1289–1328. [Google Scholar] [CrossRef]
- Marković, D.; Mizrahi, A.; Querlioz, D.; Grollier, J. Physics for neuromorphic computing. Nat. Rev. Phys. 2020, 2, 499–510. [Google Scholar] [CrossRef]
- Rasetto, M.; Wan, Q.; Akolkar, H.; Shi, B.; Xiong, F.; Benosman, R. The Challenges Ahead for Bio-inspired Neuromorphic Event Processors: How Memristors Dynamic Properties Could Revolutionize Machine Learning. arXiv 2022, arXiv:2201.12673. [Google Scholar]
- Diesmann, M.; Gewaltig, M.O. NEST: An Environment for Neural Systems Simulations. GWDG-Bericht Nr. 58 Theo Plesser, Volker Macho (Hrsg.). 2003, p. 29. Available online: https://paper.idea.edu.cn/paper/85561255 (accessed on 25 December 2022).
- Hazan, H.; Saunders, D.J.; Khan, H.; Patel, D.; Sanghavi, D.T.; Siegelmann, H.T.; Kozma, R. BindsNET: A Machine Learning-Oriented Spiking Neural Networks Library in Python. Front. Neuroinform. 2018, 12, 89. [Google Scholar] [CrossRef] [PubMed]
- Stimberg, M.; Brette, R.; Goodman, D.F. Brian 2, an intuitive and efficient neural simulator. eLife 2019, 8, e47314. [Google Scholar] [CrossRef]
- Zenke, F.; Bohté, S.M.; Clopath, C.; Comşa, I.M.; Göltz, J.; Maass, W.; Masquelier, T.; Naud, R.; Neftci, E.O.; Petrovici, M.A.; et al. Visualizing a joint future of neuroscience and neuromorphic engineering. Neuron 2021, 109, 571–575. [Google Scholar] [CrossRef]
- Mead, C.; Ismail, M. Analog VLSI Implementation of Neural Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Bartolozzi, C.; Indiveri, G. Synaptic Dynamics in Analog VLSI. Neural Comput. 2007, 19, 2581–2603. [Google Scholar] [CrossRef]
- Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A Survey of Neuromorphic Computing and Neural Networks in Hardware. arXiv 2017, arXiv:1705.06963. [Google Scholar]
- Furber, S.B.; Lester, D.R.; Plana, L.A.; Garside, J.D.; Painkras, E.; Temple, S.; Brown, A.D. Overview of the SpiNNaker System Architecture. IEEE Trans. Comput. 2013, 62, 2454–2467. [Google Scholar] [CrossRef]
- Furber, S.; Bogdan, P. (Eds.) SpiNNaker: A Spiking Neural Network Architecture; Now Publishers: Norwell, MA, USA, 2020. [Google Scholar] [CrossRef]
- Merolla, P.A.; Arthur, J.V.; Alvarez-Icaza, R.; Cassidy, A.S.; Sawada, J.; Akopyan, F.; Jackson, B.L.; Imam, N.; Guo, C.; Nakamura, Y.; et al. A million spiking-neuron integrated circuit with a scalable communication network and interface. Science 2014, 345, 668–673. [Google Scholar] [CrossRef]
- Benjamin, B.V.; Gao, P.; McQuinn, E.; Choudhary, S.; Chandrasekaran, A.R.; Bussat, J.M.; Alvarez-Icaza, R.; Arthur, J.V.; Merolla, P.A.; Boahen, K. Neurogrid: A Mixed-Analog-Digital Multichip System for Large-Scale Neural Simulations. Proc. IEEE 2014, 102, 699–716. [Google Scholar] [CrossRef]
- Neckar, A.; Fok, S.; Benjamin, B.V.; Stewart, T.C.; Oza, N.N.; Voelker, A.R.; Eliasmith, C.; Manohar, R.; Boahen, K. Braindrop: A mixed-signal neuromorphic architecture with a dynamical systems-based programming model. Proc. IEEE 2019, 107, 144–164. [Google Scholar] [CrossRef]
- Schemmel, J.; Brüderle, D.; Grübl, A.; Hock, M.; Meier, K.; Millner, S. A wafer-scale neuromorphic hardware system for large-scale neural modeling. In Proceedings of the 2010 IEEE International Symposium on Circuits and Systems (ISCAS), Paris, France, 30 May–2 June 2010; pp. 1947–1950. [Google Scholar] [CrossRef]
- Markram, H.; Meier, K.; Lippert, T.; Grillner, S.; Frackowiak, R.; Dehaene, S.; Knoll, A.; Sompolinsky, H.; Verstreken, K.; DeFelipe, J.; et al. Introducing the Human Brain Project. Procedia Comput. Sci. 2011, 7, 39–42. [Google Scholar] [CrossRef][Green Version]
- Farquhar, E.; Gordon, C.; Hasler, P. A Field Programmable Neural Array. In Proceedings of the 2006 IEEE International Symposium on Circuits and Systems, Kos, Greece, 21–24 May 2006; pp. 4114–4117. [Google Scholar] [CrossRef]
- Liu, M.; Yu, H.; Wang, W. FPAA Based on Integration of CMOS and Nanojunction Devices for Neuromorphic Applications. In Nano-Net; Cheng, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 3, pp. 44–48. [Google Scholar]
- Chan, V.; Liu, S.C.; van Schaik, A. AER EAR: A Matched Silicon Cochlea Pair With Address Event Representation Interface. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 48–59. [Google Scholar] [CrossRef]
- Haessig, G.; Milde, M.B.; Aceituno, P.V.; Oubari, O.; Knight, J.C.; van Schaik, A.; Benosman, R.B.; Indiveri, G. Event-Based Computation for Touch Localization Based on Precise Spike Timing. Front. Neurosci. 2020, 14, 420. [Google Scholar] [CrossRef] [PubMed]
- Lagorce, X.; Orchard, G.; Galluppi, F.; Shi, B.E.; Benosman, R.B. HOTS: A Hierarchy of Event-Based Time-Surfaces for Pattern Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1346–1359. [Google Scholar] [CrossRef]
- Sironi, A.; Brambilla, M.; Bourdis, N.; Lagorce, X.; Benosman, R. HATS: Histograms of Averaged Time Surfaces for Robust Event-Based Object Classification. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 1731–1740. [Google Scholar] [CrossRef]
- Maro, J.M.; Ieng, S.H.; Benosman, R. Event-Based Gesture Recognition With Dynamic Background Suppression Using Smartphone Computational Capabilities. Front. Neurosci. 2020, 14, 275. [Google Scholar] [CrossRef]
- Grimaldi, A.; Boutin, V.; Perrinet, L.; Ieng, S.H.; Benosman, R. A homeostatic gain control mechanism to improve event-driven object recognition. In Proceedings of the 2021 International Conference on Content-Based Multimedia Indexing (CBMI), Lille, France, 28–30 June 2021. [Google Scholar] [CrossRef]
- Grimaldi, A.; Boutin, V.; Ieng, S.H.; Benosman, R.; Perrinet, L.U. A robust event-driven approach to always-on object recognition. TechRxiv 2022. [Google Scholar] [CrossRef]
- Yu, C.; Gu, Z.; Li, D.; Wang, G.; Wang, A.; Li, E. STSC-SNN: Spatio-Temporal Synaptic Connection with Temporal Convolution and Attention for Spiking Neural Networks. arXiv 2022, arXiv:2210.05241. [Google Scholar] [CrossRef]
- Benosman, R.; Clercq, C.; Lagorce, X.; Ieng, S.-H.; Bartolozzi, C. Event-Based Visual Flow. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 407–417. [Google Scholar] [CrossRef]
- Clady, X.; Clercq, C.; Ieng, S.H.; Houseini, F.; Randazzo, M.; Natale, L.; Bartolozzi, C.; Benosman, R.B. Asynchronous visual event-based time-to-contact. Front. Neurosci. 2014, 8, 9. [Google Scholar] [CrossRef]
- Tschechne, S.; Sailer, R.; Neumann, H. Bio-Inspired Optic Flow from Event-Based Neuromorphic Sensor Input. In Proceedings of the Artificial Neural Networks in Pattern Recognition; El Gayar, N., Schwenker, F., Suen, C., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 171–182. [Google Scholar] [CrossRef]
- Hidalgo-Carrió, J.; Gehrig, D.; Scaramuzza, D. Learning Monocular Dense Depth from Events. arXiv 2020, arXiv:2010.08350. [Google Scholar]
- Dardelet, L.; Benosman, R.; Ieng, S.H. An Event-by-Event Feature Detection and Tracking Invariant to Motion Direction and Velocity. TechRxiv 2021. [Google Scholar] [CrossRef]
- Stoffregen, T.; Gallego, G.; Drummond, T.; Kleeman, L.; Scaramuzza, D. Event-Based Motion Segmentation by Motion Compensation. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 February 2019; pp. 7243–7252. [Google Scholar] [CrossRef]
- Kim, H.; Leutenegger, S.; Davison, A.J. Real-Time 3D Reconstruction and 6-DoF Tracking with an Event Camera. In Proceedings of the Computer Vision—ECCV 2016; Leibe, B., Matas, J., Sebe, N., Welling, M., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 349–364. [Google Scholar] [CrossRef]
- Hussain, S.; Basu, A.; Wang, M.; Hamilton, T.J. DELTRON: Neuromorphic architectures for delay based learning. In Proceedings of the 2012 IEEE Asia Pacific Conference on Circuits and Systems, Kaohsiung, Taiwan, 2–5 December 2012; pp. 304–307. [Google Scholar] [CrossRef]
- Wang, R.M.; Hamilton, T.J.; Tapson, J.C.; van Schaik, A. A neuromorphic implementation of multiple spike-timing synaptic plasticity rules for large-scale neural networks. Front. Neurosci. 2015, 9, 180. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Hamilton, T.J.; Tapson, J.; van Schaik, A. An FPGA design framework for large-scale spiking neural networks. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014; pp. 457–460. [Google Scholar] [CrossRef]
- Pfeil, T.; Scherzer, A.C.; Schemmel, J.; Meier, K. Neuromorphic learning towards nano second precision. In Proceedings of the The 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Boerlin, M.; Denève, S. Spike-Based Population Coding and Working Memory. PLoS Comput. Biol. 2011, 7, e1001080. [Google Scholar] [CrossRef] [PubMed]
- Renner, A.; Sandamirskaya, Y.; Sommer, F.T.; Frady, E.P. Sparse Vector Binding on Spiking Neuromorphic Hardware Using Synaptic Delays. In Proceedings of the International Conference on Neuromorphic Systems; ACM Digital Library: Knoxville, TN, USA, 2022. [Google Scholar] [CrossRef]
- Dard, R.F.; Leprince, E.; Denis, J.; Rao Balappa, S.; Suchkov, D.; Boyce, R.; Lopez, C.; Giorgi-Kurz, M.; Szwagier, T.; Dumont, T.; et al. The rapid developmental rise of somatic inhibition disengages hippocampal dynamics from self-motion. eLife 2022, 11, e78116. [Google Scholar] [CrossRef]
- Coull, J.T.; Giersch, A. The distinction between temporal order and duration processing, and implications for schizophrenia. Nat. Rev. Psychol. 2022, 1, 257–271. [Google Scholar] [CrossRef]
- Panahi, M.R.; Abrevaya, G.; Gagnon-Audet, J.C.; Voleti, V.; Rish, I.; Dumas, G. Generative Models of Brain Dynamics—A review. arXiv 2021, arXiv:2112.12147. [Google Scholar]
- Tolle, K.M.; Tansley, D.S.W.; Hey, A.J.G. The Fourth Paradigm: Data-Intensive Scientific Discovery [Point of View]. Proc. IEEE 2011, 99, 1334–1337. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grimaldi, A.; Gruel, A.; Besnainou, C.; Jérémie, J.-N.; Martinet, J.; Perrinet, L.U. Precise Spiking Motifs in Neurobiological and Neuromorphic Data. Brain Sci. 2023, 13, 68. https://doi.org/10.3390/brainsci13010068
Grimaldi A, Gruel A, Besnainou C, Jérémie J-N, Martinet J, Perrinet LU. Precise Spiking Motifs in Neurobiological and Neuromorphic Data. Brain Sciences. 2023; 13(1):68. https://doi.org/10.3390/brainsci13010068
Chicago/Turabian StyleGrimaldi, Antoine, Amélie Gruel, Camille Besnainou, Jean-Nicolas Jérémie, Jean Martinet, and Laurent U. Perrinet. 2023. "Precise Spiking Motifs in Neurobiological and Neuromorphic Data" Brain Sciences 13, no. 1: 68. https://doi.org/10.3390/brainsci13010068
APA StyleGrimaldi, A., Gruel, A., Besnainou, C., Jérémie, J.-N., Martinet, J., & Perrinet, L. U. (2023). Precise Spiking Motifs in Neurobiological and Neuromorphic Data. Brain Sciences, 13(1), 68. https://doi.org/10.3390/brainsci13010068





