Reevaluating the Language of Learning Advantage in Bilingual Arithmetic: An ERP Study on Spoken Multiplication Verification
Abstract
1. Introduction
The Current Study
2. Materials and Methods
2.1. Experiment 1: Multiplication Verification Task
2.1.1. Participants
2.1.2. Offline Behavioral Assessments
2.1.3. Stimuli
2.1.4. Experiment 1A Procedure
2.1.5. Experiment 1B Procedure
2.2. Experiment 2: Word–Picture Verification (WPV) Task
2.2.1. Participants
2.2.2. Stimuli and Procedure
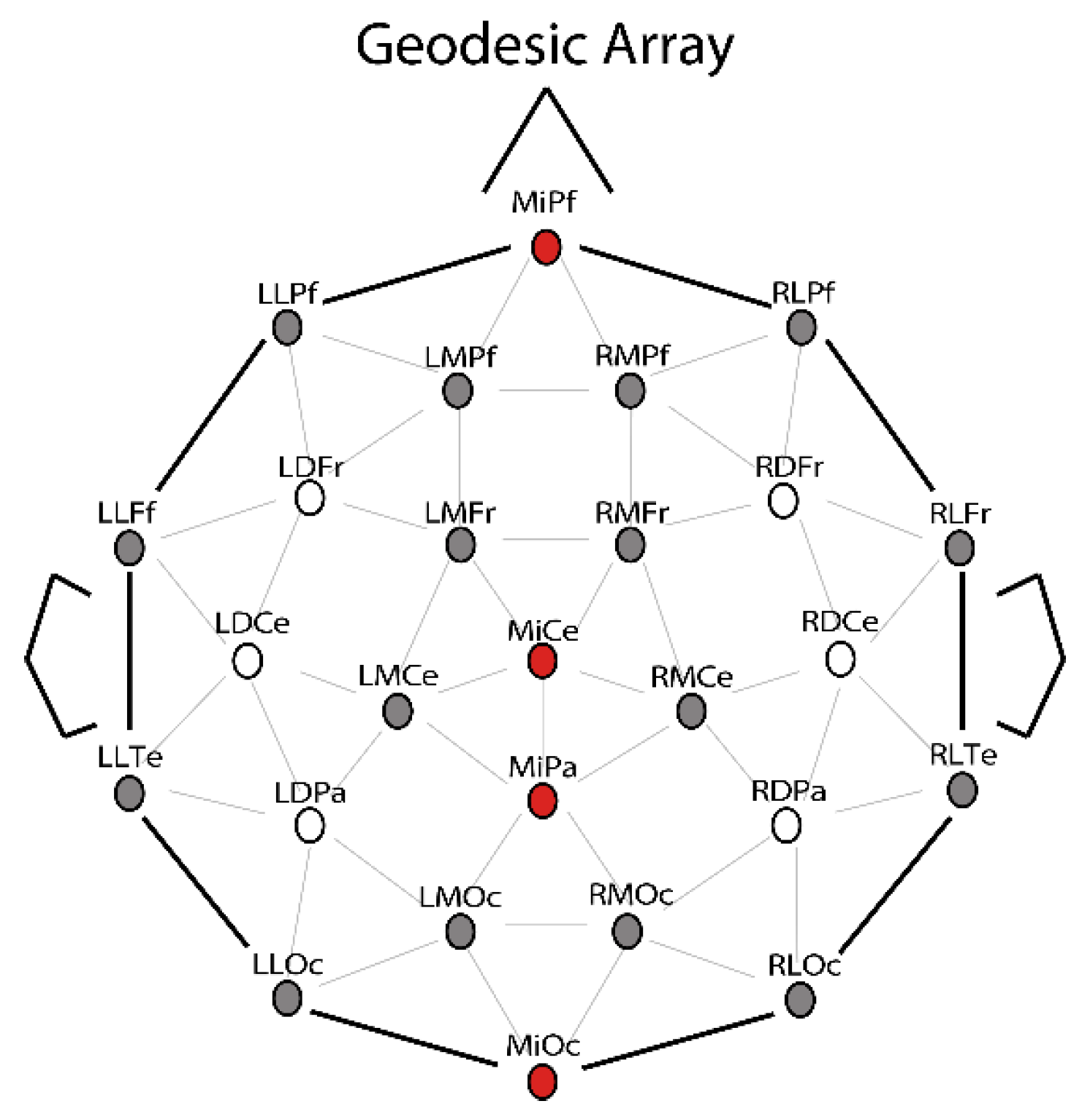
2.3. EEG Recording
3. Results
3.1. ISI Multiplication Task—Experiment 1A
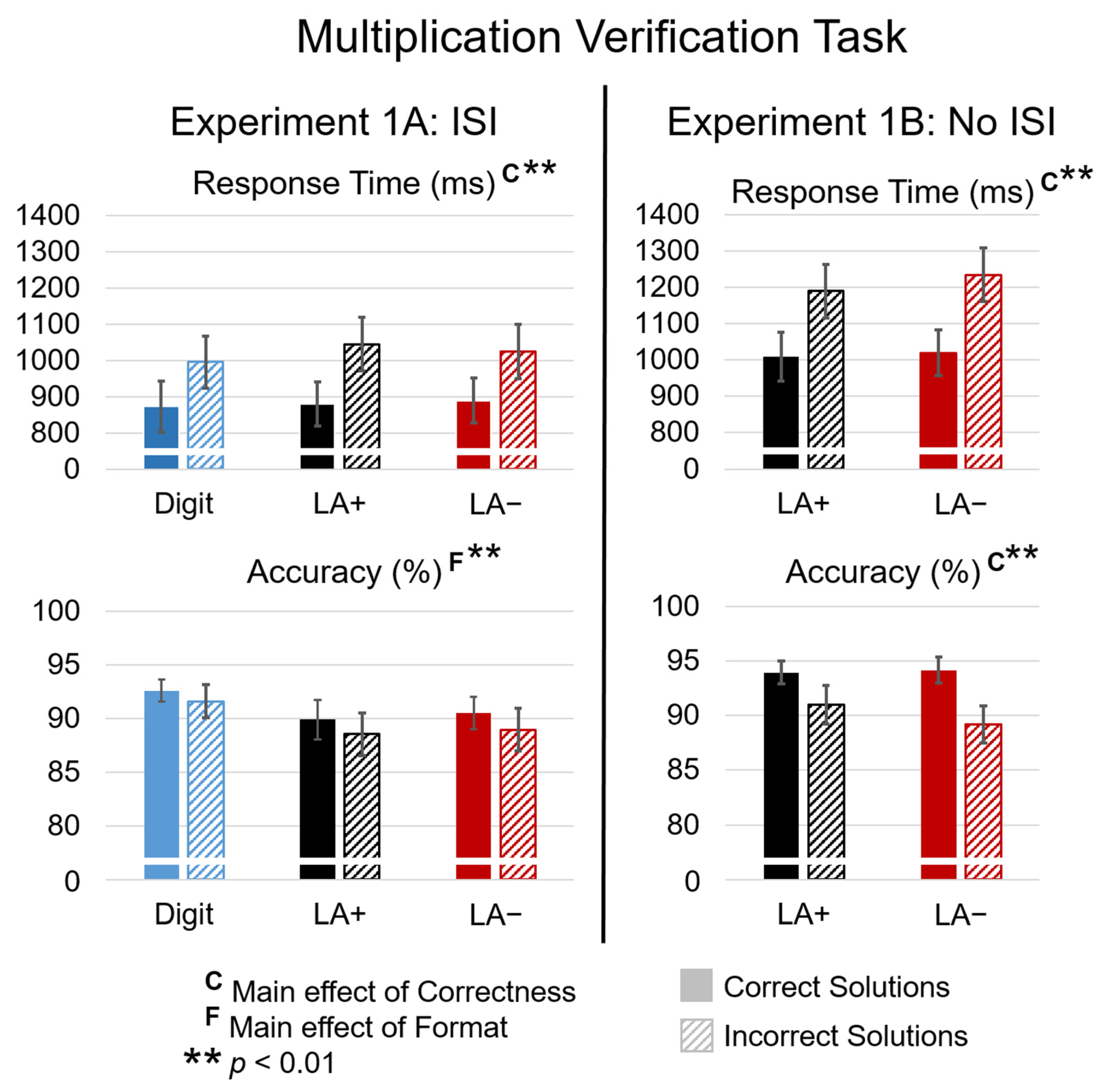
3.1.1. Behavior
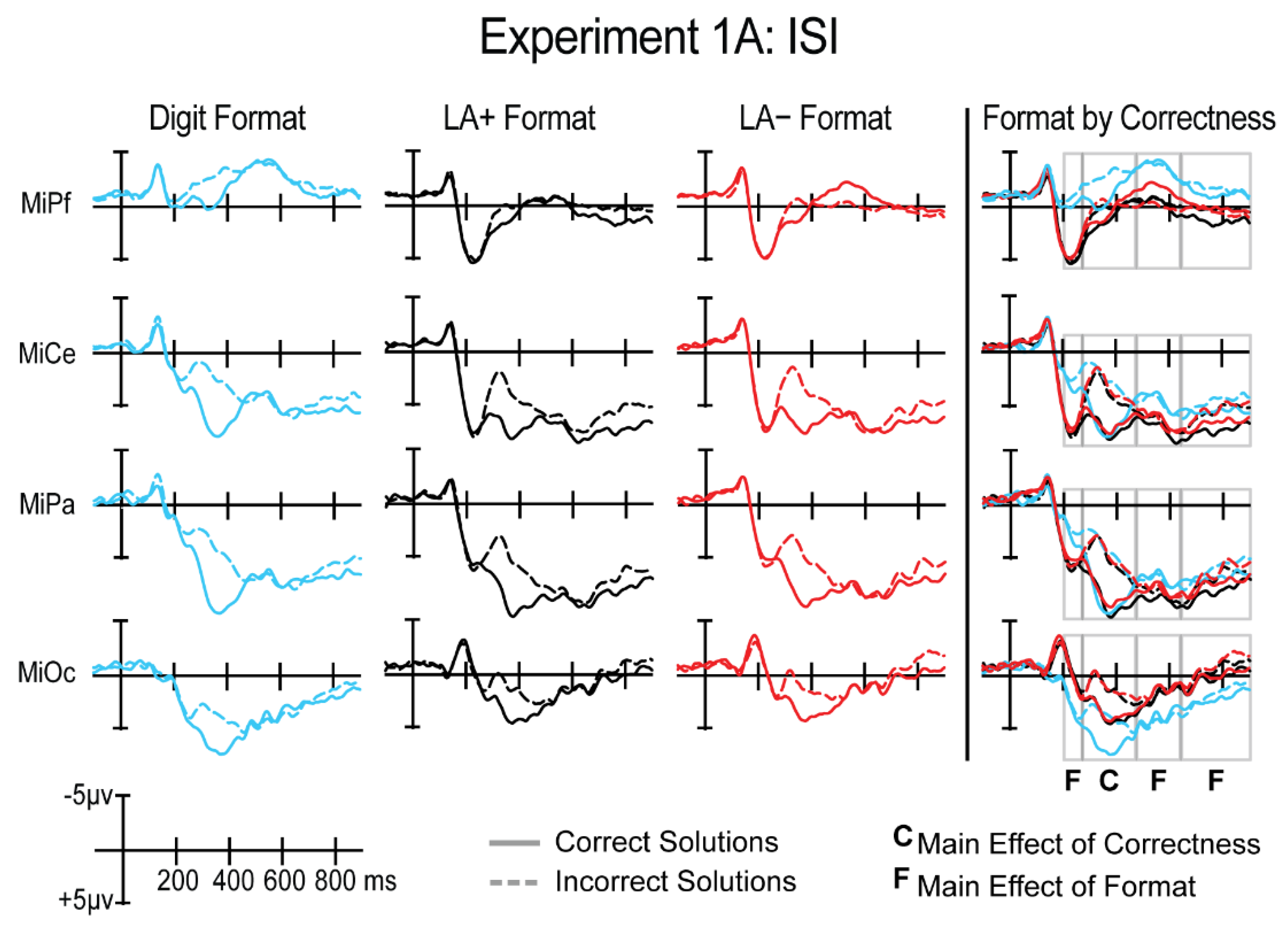
3.1.2. ERPs
3.1.3. P200 Time Window (200–270 ms)
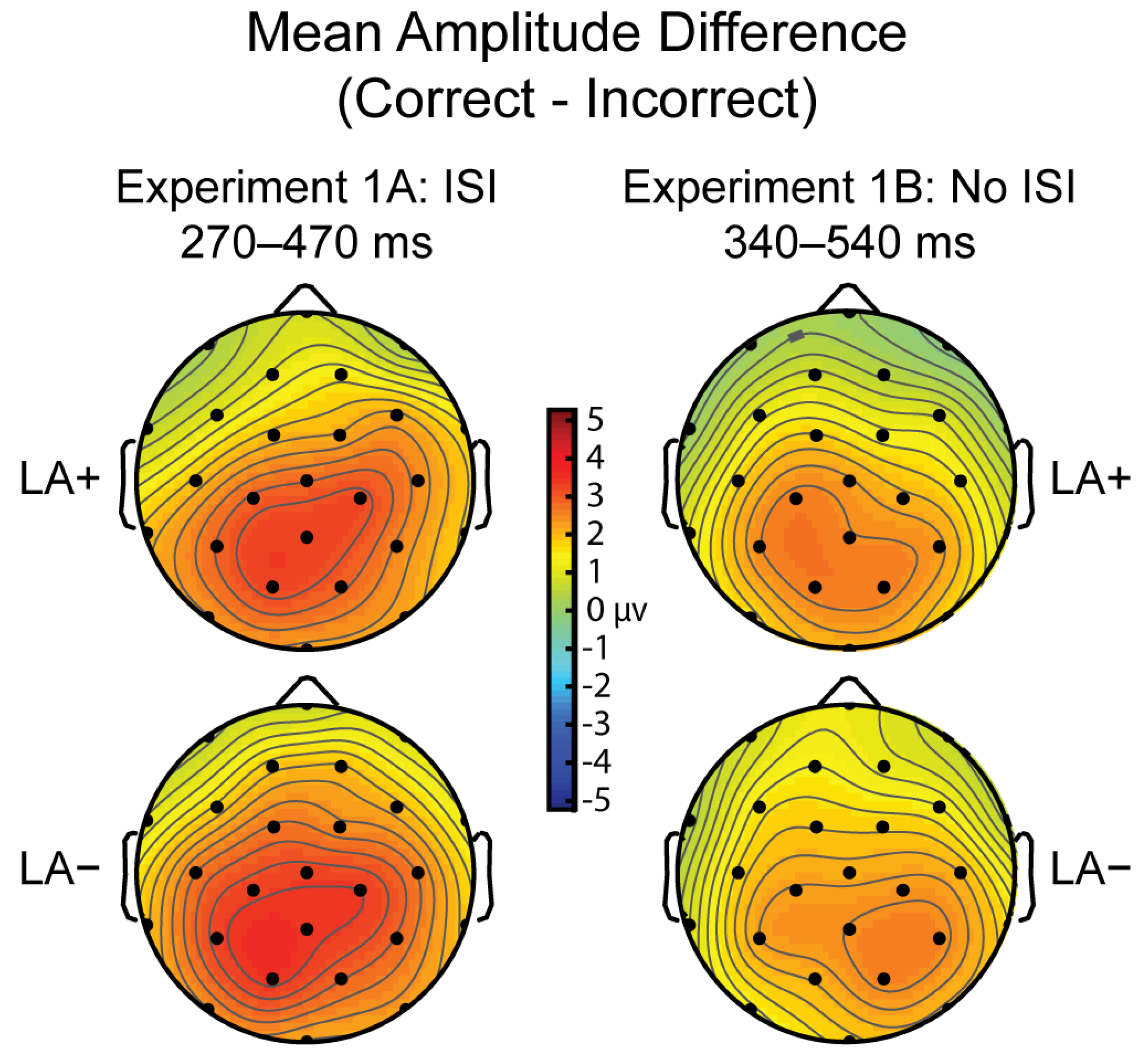
3.1.4. P300 Time Window (270–470 ms)
3.1.5. Post-P300—Early (475–640 ms)
3.1.6. Post-P300—Late (640–900 ms)
3.1.7. Experiment 1A Summary of Results
3.2. Speeded Multiplication Task—Experiment 1B
3.2.1. Behavior
3.2.2. ERPs
3.2.3. P200 (200–270 ms)
3.2.4. P300 (340–540 ms)
3.2.5. Post-P300 (640–900 ms)
3.2.6. Experiment 1B Summary of Results
3.3. Baysian Analyses
3.4. Comparison of Experiment 1A and B
3.4.1. Behavior
3.4.2. P200 (200–270 ms)
3.4.3. P300 (Variable Time Window)
3.4.4. Post-P300 (640–900 ms)
3.4.5. Comparison of 1A and 1B Summary of Results
3.5. Word–Picture Verification (WPV)
3.5.1. Behavior
3.5.2. N400 (280 ms–480 ms)
3.5.3. Post-N400 (500–900 ms)
3.5.4. WPV Task Summary of Results
4. Discussion
4.1. N400 versus P300 Interpretation of the Correctness Effect
4.2. Language of Learning Effects
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dehaene, S.; Spelke, E.; Dehaene, S.; Spelke, E.; Pinel, P.; Stanescu, R.; Tsivkin, S. Sources of Mathematical Thinking: Behavioral and Brain-Imaging Evidence. Science 1999, 284, 970–974. [Google Scholar] [CrossRef] [PubMed]
- Spelke, E.S.; Tsivkin, S. Language and number: A bilingual training study. Cognition 2001, 78, 45–88. [Google Scholar] [CrossRef]
- Dewaele, J.M. Multilinguals’ language choice for mental calculation. Intercult. Pragmat. 2007, 4, 343–376. [Google Scholar] [CrossRef]
- Salillas, E.; Wicha, N.Y.Y. Early Learning Shapes the Memory Networks for Arithmetic: Evidence from Brain Potentials in Bilinguals. Psychol. Sci. 2012, 23, 745–755. [Google Scholar] [CrossRef]
- Vaid, J.; Menon, R. Correlates of bilinguals’ preferred language for mental computations. Span. Appl. Linguist. 2000, 4, 325–342. [Google Scholar]
- Cerda, V.R.; Grenier, A.E.; Wicha, N.Y.Y. Bilingual children access multiplication facts from semantic memory equivalently across languages: Evidence from the N400. Brain Lang. 2019, 198, 104679. [Google Scholar] [CrossRef] [PubMed]
- Frenck-Mestre, C.; Vaid, J. Activation of number facts in bilinguals. Mem. Cognit. 1993, 21, 809–818. [Google Scholar] [CrossRef]
- Lotus Lin, J.-F.; Imada, T.; Kuhl, P.K. Neuroplasticity, bilingualism, and mental mathematics: A behavior-MEG study. Brain Cogn. 2019, 134, 122–134. [Google Scholar]
- Marsh, L.G.; Maki, R.H. Efficiency of arithmetic operations in bilinguals as a function of language. Mem. Cognit. 1976, 4, 459–464. [Google Scholar] [CrossRef]
- Tamamaki, K. Language Dominance in Bilinguals’ Arithmetic Operations According to Their Language Use. Lang. Learn. 1993, 43, 239–261. [Google Scholar] [CrossRef]
- Van Rinsveld, A.; Dricot, L.; Guillaume, M.; Rossion, B.; Schiltz, C. Mental arithmetic in the bilingual brain: Language matters. Neuropsychologia 2017, 101, 17–29. [Google Scholar] [CrossRef] [PubMed]
- Van Rinsveld, A.; Schiltz, C.; Brunner, M.; Landerl, K.; Ugen, S. Solving arithmetic problems in first and second language: Does the language context matter? Learn. Instr. 2016, 42, 72–82. [Google Scholar] [CrossRef]
- Garcia, O.; Faghihi, N.; Raola, A.R.; Vaid, J. Factors influencing bilinguals’ speed and accuracy of number judgments across languages: A meta-analytic review. J. Mem. Lang. 2021, 118, 104211. [Google Scholar] [CrossRef]
- Martinez-Lincoln, A.; Cortinas, C.; Wicha, N.Y.Y. Arithmetic memory networks established in childhood are changed by experience in adulthood. Neurosci. Lett. 2015, 584, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Dickson, D.S.; Cerda, V.R.; Beavers, R.N.; Ruiz, A.; Castaneda, R.; Wicha, N.Y.Y. When 2 × 4 is meaningful: The N400 and P300 reveal operand format effects in multiplication verification. Psychophysiology 2018, 55, e13212. [Google Scholar] [CrossRef] [PubMed]
- Campbell, J.I.D.; Epp, L.J. An Encoding-Complex Approach to Numerical Cognition in Chinese-English Bilinguals. Can. J. Exp. Psychol. Can. Psychol. Exp. 2004, 58, 229–244. [Google Scholar] [CrossRef] [PubMed]
- Dehaene, S. Varieties of numerical abilities. Cognition 1992, 44, 1–42. [Google Scholar] [CrossRef]
- Dehaene, S.; Cohen, L. Towards an Anatomical and Functional Model of Number Processing. Math. Cogn. 1995, 1, 83–120. [Google Scholar]
- Venkatraman, V.; Siong, S.C.; Chee, M.W.L.; Ansari, D. Effect of Language Switching on Arithmetic: A Bilingual fMRI Study. J. Cogn. Neurosci. 2006, 81, 64–74. [Google Scholar] [CrossRef]
- Dickson, D.S.; Federmeier, K.D. The language of arithmetic across the hemispheres: An event-related potential investigation. Brain Res. 2017, 1662, 46–56. [Google Scholar] [CrossRef]
- Dickson, D.S.; Wicha, N.Y.Y. P300 amplitude and latency reflect arithmetic skill: An ERP study of the problem size effect. Biol. Psychol. 2019, 148, 107745. [Google Scholar] [CrossRef] [PubMed]
- Jasinski, E.C.; Coch, D. ERPs across arithmetic operations in a delayed answer verification task. Psychophysiology 2012, 49, 943–958. [Google Scholar] [CrossRef] [PubMed]
- Niedeggen, M.; Rösler, F. N400 effects reflect activation spread during retrieval of arithmetic facts. Psychol. Sci. 1999. [Google Scholar] [CrossRef]
- Niedeggen, M.; Rösler, F.; Jost, K. Processing of incongruous mental calculation problems: Evidence for an arithmetic N400 effect. Psychophysiology 1999, 36, 307–324. [Google Scholar] [CrossRef]
- Jost, K.; Hennighausen, E.; Rösler, F. Comparing arithmetic and semantic fact retrieval: Effects of problem size and sentence constraint on event-related brain potentials. Psychophysiology 2004, 41, 46–59. [Google Scholar] [CrossRef]
- Coch, D.; Holcomb, P.J. The N400 in beginning readers. Dev. Psychobiol. 2003, 43, 146–166. [Google Scholar] [CrossRef]
- Hasko, S.; Groth, K.; Bruder, J.; Bartling, J.; Schulte-Körne, G. The time course of reading processes in children with and without dyslexia: An ERP study. Front. Hum. Neurosci. 2013, 7, 570. [Google Scholar] [CrossRef]
- Campbell, J.I.D. Architectures for numerical cognition. Cognition 1994, 53, 1–44. [Google Scholar] [CrossRef]
- Grosjean, F. Transfer and language mode. Biling. Lang. Cogn. 1998, 1, 175–176. [Google Scholar] [CrossRef]
- Grosjean, F. Studying bilinguals: Methodological and conceptual issues. Biling. Lang. Cogn. 1998, 1, 131–149. [Google Scholar] [CrossRef]
- Hernandez, A.E.; Martinez, A.; Kohnert, K. In Search of the Language Switch: An fMRI Study of Picture Naming in Spanish–English Bilinguals. Brain Lang. 2000, 73, 421–431. [Google Scholar] [CrossRef] [PubMed]
- Misra, M.; Guo, T.; Bobb, S.; Kroll, J. When bilinguals choose a single word to speak: Electrophysiological evidence for inhibition of the native language. J. Mem. Lang. 2012, 67, 224–237. [Google Scholar] [CrossRef] [PubMed]
- McClain, L.; Huang, J.Y. Speed of simple arithmetic in bilinguals. Mem. Cognit. 1982, 10, 591–596. [Google Scholar] [CrossRef]
- Martinez, A. Language and Math: What if we have two separate naming systems? Languages 2019, 4, 68. [Google Scholar] [CrossRef]
- Kutas, M.; Federmeier, K.D. Thirty Years and Counting: Finding Meaning in the N400 Component of the Event-Related Brain Potential (ERP). Annu. Rev. Psychol. 2011, 62, 621–647. [Google Scholar] [CrossRef] [PubMed]
- Kutas, M.; Hillyard, S.A. Reading senseless sentences: Brain potentials reflect semantic incongruity. Science 1980, 207, 203–205. [Google Scholar] [CrossRef]
- Wicha, N.Y.Y.; Moreno, E.M.; Kutas, M. Anticipating words and their gender: An event-related brain potential study of semantic integration, gender expectancy, and gender agreement in Spanish sentence reading. J. Cogn. Neurosci. 2004, 16, 1272–1288. [Google Scholar] [CrossRef]
- DeLong, K.; Urbach, T.; Kutas, M. Probabilistic word pre-activation during language comprehension inferred from electrical brain activity. Nat. Neurosci. 2005, 8, 1117–1121. [Google Scholar] [CrossRef]
- Sutton, S.; Ruchkin, D.S.; Munson, R.; Kietzman, M.L.; Hammer, M. Event-related potentials in a two-interval forced-choice detection task. Percept. Psychophys. 1982, 32, 360–374. [Google Scholar] [CrossRef]
- Polich, J. Task difficulty, probability, and inter-stimulus interval as determinants of P300 from auditory stimuli. Electroencephalogr. Clin. Neurophysiol. Potentials Sect. 1987, 68, 311–320. [Google Scholar] [CrossRef]
- Polich, J. Updating P300: An integrative theory of P3a and P3b. Clin. Neurophysol. 2007, 118, 2128–2148. [Google Scholar] [CrossRef] [PubMed]
- Polich, J. Neuropsychology of P300. In The Oxford Handbook of Event-Related Potential Components; Luck, S.J., Kappenman, E.S., Eds.; Oxford University Press: Oxford, UK, 2012; pp. 159–188. [Google Scholar]
- Johnson, R.; Donchin, E. P300 and Stimulus Categorization: Two Plus One is not so Different from One Plus One. Psychophysiology 1980, 17, 167–178. [Google Scholar] [CrossRef] [PubMed]
- Grenier, A.E.; Dickson, D.S.; Sparks, C.S.; Wicha, N.Y.Y. Meaning to multiply: Electrophysiological evidence that children and adults treat multiplication facts differently. Dev. Cogn. Neurosci. 2020, 46, 100873. [Google Scholar] [CrossRef] [PubMed]
- Prieto-Corona, B.; Rodríguez-Camacho, M.; Silva-Pereyra, J.; Marosi, E.; Fernández, T.; Guerrero, V. Event-related potentials findings differ between children and adults during arithmetic-fact retrieval. Neurosci. Lett. 2010, 468, 220–224. [Google Scholar] [CrossRef]
- Liu, H.; Cao, F. L1 and L2 processing in the bilingual brain: A meta-analysis of neuroimaging studies. Brain Lang. 2016, 159, 60–73. [Google Scholar] [CrossRef]
- Marian, V.; Shildkrot, Y.; Blumenfeld, H.; Kaushanskaya, M.; Faroqi-Shah, Y.; Hirsch, J. Cortical activation during word processing in late bilinguals: Similarities and differences as revealed by functional magnetic resonance imaging. J. Clin. Exp. Neuropsychol. 2007, 29, 247–265. [Google Scholar] [CrossRef]
- Wei, M.; Joshi, A.; Zhang, M.; Mei, L.; Manis, F.; He, Q.; Beattie, R.; Xue, G.; Shattuck, D.; Leahy, R.; et al. How age of acquisition influences brain architecture in bilinguals. J. Neurolinguist. 2015, 36, 35–55. [Google Scholar] [CrossRef]
- Kim, K.H.S.; Relkin, N.R.; Lee, K.-M.; Hirsch, J. Distinct cortical areas associated with native and second languages. Nature 1997, 388, 171–174. [Google Scholar] [CrossRef]
- Moreno, E.M.; Kutas, M. Processing semantic anomalies in two languages: An electrophysiological exploration in both languages of Spanish–English bilinguals. Cogn. Brain Res. 2005, 22, 205–220. [Google Scholar] [CrossRef]
- Saalbach, H.; Eckstein, D.; Andri, N.; Hobi, R.; Grabner, R.H. When language of instruction and language of application differ: Cognitive costs of bilingual mathematics learning. Learn. Instr. 2013, 26, 36–44. [Google Scholar] [CrossRef]
- Bernardo, A.B.I. Asymmetric activation of number codes in bilinguals: Further evience for the encoding complex model of number processing. Mem. Cognit. 2001, 29, 968–976. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bernardo, A.B.I.; Calleja, M.O. The Effects of Stating Problems in Bilingual Students’ First and Second Languages on Solving Mathematical Word Problems. J. Genet. Psychol. 2005, 166, 117–129. [Google Scholar] [CrossRef] [PubMed]
- Oldfield, R.C. The assessment and analysis of handedness: The Edinburgh inventory. Neuropsychologia 1971, 9, 97–113. [Google Scholar] [CrossRef]
- Woodcock, R.; McGrew, K.; Mather, N. Woodcock-Johnson III Tests of Achievement; Riverside Publishing: Itasca, IL, USA, 2001. [Google Scholar]
- Woodcock, R.W.; McGrew, K.S.; Mather, N. Woodcock-Johnson III Tests of Cognitive Abilities; Riverside Publishing: Itasca, IL, USA, 2001. [Google Scholar]
- Muñoz-Sandoval, A.F.; Woodcock, R.W.; McGrew, K.S.; Mather, N. Batería III Woodcock-Muñoz: Pruebas de Aprovechamiento; Riverside Publishing: Itasca, IL, USA, 2005. [Google Scholar]
- Marian, V.; Blumenfeld, H.K.; Kaushanskaya, M. The Language Experience and Proficiency Questionnaire (LEAP-Q): Assessing language profiles in bilinguals and multilinguals. J. Speech Lang. Hear. Res. 2007, 50, 940–967. [Google Scholar] [CrossRef]
- Wechsler, D. Wechsler Individual Achievement Test; Pearson: London, UK, 1992. [Google Scholar]
- Campbell, J.I.D.; Graham, D.J. Mental multiplication skill: Structure, process, and acquisition. Can. J. Psychol. Can. Psychol. 1985, 39, 338–366. [Google Scholar] [CrossRef]
- Stazyk, E.H.; Ashcraft, M.H.; Hamann, M.S. A network approach to mental multiplication. J. Exp. Psychol. Learn. Mem. Cogn. 1982, 8, 320–335. [Google Scholar] [CrossRef]
- Snodgrass, J.G.; Vanderwart, M. A standardized set of 260 pictures: Norms for name agreement, image agreement, familiarity, and visual complexity. J. Exp. Psychol. Hum. Learn. Mem. 1980, 6, 174–215. [Google Scholar] [CrossRef]
- Davis, C.J. N-Watch: A program for deriving neighborhood size and other psycholinguistic statistics. Behav. Res. Methods 2005, 37, 65–70. [Google Scholar] [CrossRef]
- Davis, C.J.; Perea, M. BuscaPalabras: A program for deriving orthographic and phonological neighborhood statistics and other psycholinguistic indices in Spanish. Behav. Res. Methods 2005, 37, 665–671. [Google Scholar] [CrossRef]
- Lopez-Calderon, J.; Luck, S.J. ERPLAB: An open-source toolbox for the analysis of event-related potentials. Front. Hum. Neurosci. 2014, 8, 1–14. [Google Scholar] [CrossRef]
- Watanabe, S. A Widely Applicable Bayesian Information Criterion. J. Mach. Learn. Res. 2013, 14, 867–897. [Google Scholar]
- Campbell, J.I.D.; Clark, J.M. Cognitive number processing: An encoding-complex perspective. Adv. Psychol. 1992, 91, 457–491. [Google Scholar] [CrossRef]
- Federmeier, K.D. Connecting and considering: Electrophysiology provides insights into comprehension. Psychophysiology 2022, 59, e13940. [Google Scholar] [CrossRef] [PubMed]
- Näätänen, R. The role of attention in auditory information processing as revealed by event-related potentials and other brain measures of cognitive function. Behav. Brain Sci. 1990, 13, 201–233. [Google Scholar] [CrossRef]
- Fruhstorfer, H.; Soveri, P.; Jarvilehto, T. Short-term habituation of the auditory evoked response in man. Electroencephalogr. Clin. Neurophysiol. 1970, 28, 153–161. [Google Scholar] [CrossRef]
- Ashcraft, M.H.; Fierman, B.A.; Bartolotta, R. The production and verification tasks in mental addition: An empirical comparison. Dev. Rev. 1984, 4, 157–170. [Google Scholar] [CrossRef]
- Dagenbach, D.; McCloskey, M. The organization of arithmetic facts in memory: Evidence from a brain-damaged patient. Brain Cogn. 1992, 20, 345–366. [Google Scholar] [CrossRef]
- Zbrodoff, N.J.; Logan, G.D. When it hurts to be misled: A Stroop-like effect in a simple addition production task. Mem. Cognit. 2000, 28, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Dewi, J.D.; Bagnoud, J.; Thevenot, C. Do production and verification tasks in arithmetic rely on the same cognitive mechanisms? A test using alphabet arithmetic. Q. J. Exp. Psychol. 2021, 74, 2182–2192. [Google Scholar] [CrossRef]
- Moschkovich, J. A Situated and Sociocultural Perspective on Bilingual Mathematics Learners. Math. Think. Learn. 2002, 4, 189–212. [Google Scholar] [CrossRef]
- Bermejo, V.; Ester, P.; Morales, I. How the Language of Instruction Influences Mathematical Thinking Development in the First Years of Bilingual Schoolers. Front. Psychol. 2021, 12, 1194. [Google Scholar] [CrossRef] [PubMed]
- Moschkovich, J. Using Two Languages When Learning Mathematics. Educ. Stud. Math. 2007, 64, 121–144. [Google Scholar] [CrossRef]




| Test | English Standard Score | Spanish Standard Score |
|---|---|---|
| Experiment 1A (n = 29) | ||
| Picture Vocabulary | 87.69 (SD = 10.86) | 87.31 (SD = 10.12) |
| Oral Comprehension | 97.69 (SD = 6.05) | 97.37 (SD = 9.21) |
| Incomplete Words | 93.10 (SD = 15.48) | 88.89 (SD = 8.05) |
| Experiment 1B (n = 28) | ||
| Picture Vocabulary | 84.89 (SD = 11.12) | 89.85 (SD = 11.25) |
| Oral Comprehension | 95.07 (SD = 7.82) | 97.68 (SD = 10.28) |
| Incomplete Words | 87.68 (SD = 18.80) | 91.75 (SD = 8.95) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerda, V.R.; Montufar Soria, P.; Wicha, N.Y. Reevaluating the Language of Learning Advantage in Bilingual Arithmetic: An ERP Study on Spoken Multiplication Verification. Brain Sci. 2022, 12, 532. https://doi.org/10.3390/brainsci12050532
Cerda VR, Montufar Soria P, Wicha NY. Reevaluating the Language of Learning Advantage in Bilingual Arithmetic: An ERP Study on Spoken Multiplication Verification. Brain Sciences. 2022; 12(5):532. https://doi.org/10.3390/brainsci12050532
Chicago/Turabian StyleCerda, Vanessa R., Paola Montufar Soria, and Nicole Y. Wicha. 2022. "Reevaluating the Language of Learning Advantage in Bilingual Arithmetic: An ERP Study on Spoken Multiplication Verification" Brain Sciences 12, no. 5: 532. https://doi.org/10.3390/brainsci12050532
APA StyleCerda, V. R., Montufar Soria, P., & Wicha, N. Y. (2022). Reevaluating the Language of Learning Advantage in Bilingual Arithmetic: An ERP Study on Spoken Multiplication Verification. Brain Sciences, 12(5), 532. https://doi.org/10.3390/brainsci12050532






