Differentiating High-Grade Gliomas from Brain Metastases at Magnetic Resonance: The Role of Texture Analysis of the Peritumoral Zone
Abstract
1. Introduction
2. Materials and Methods
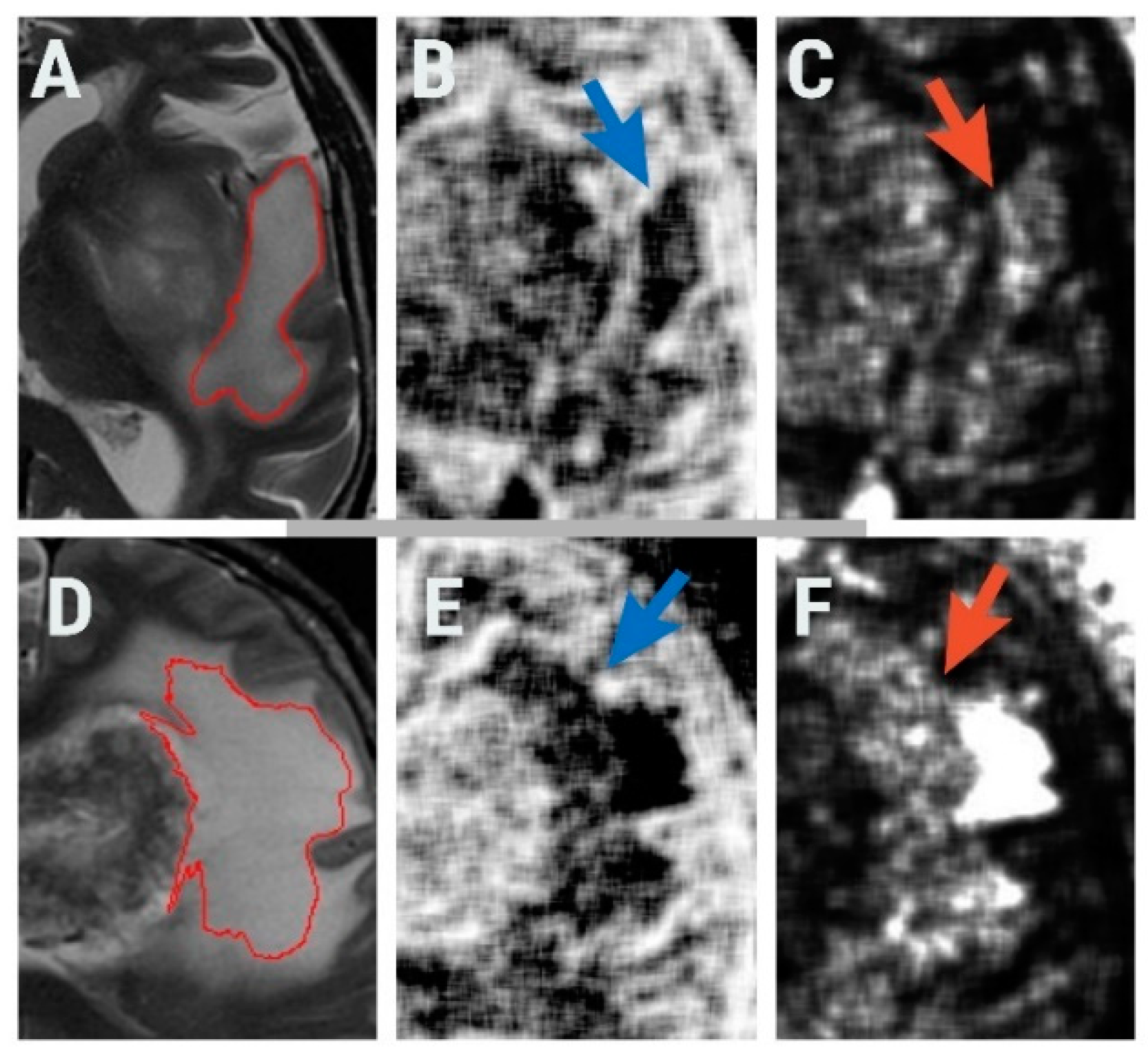
2.1. Patients
2.2. MRI Protocol
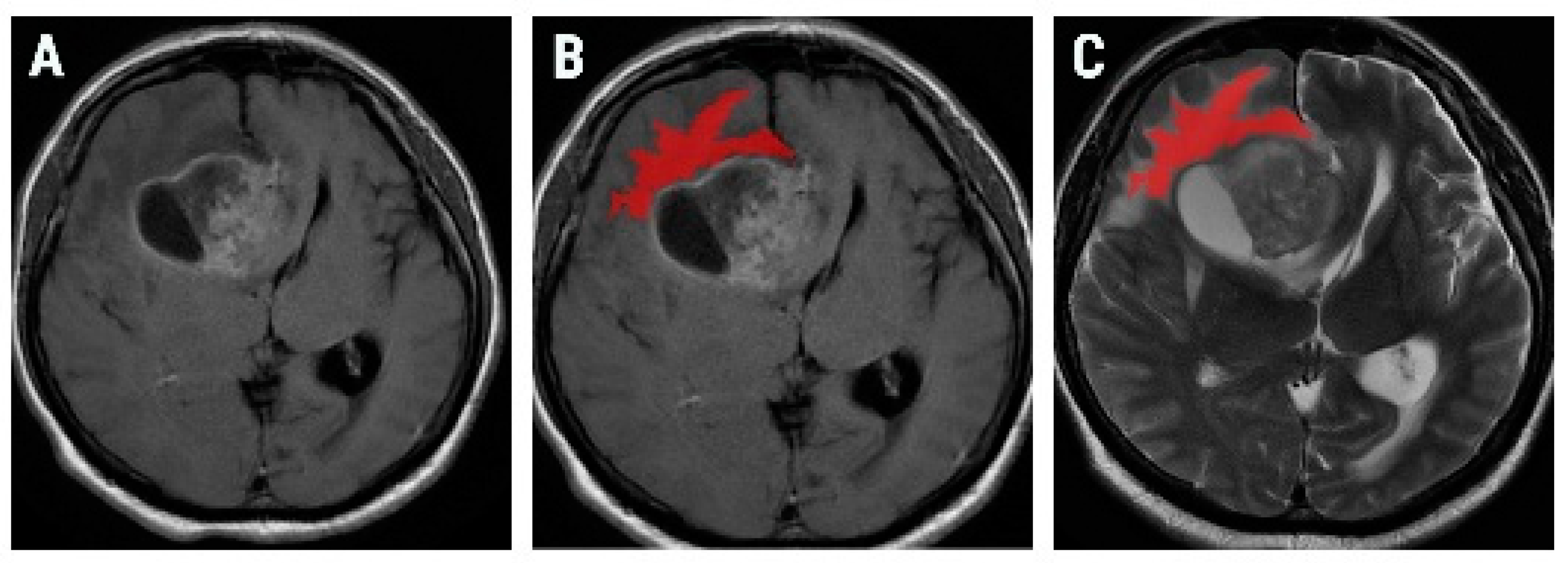
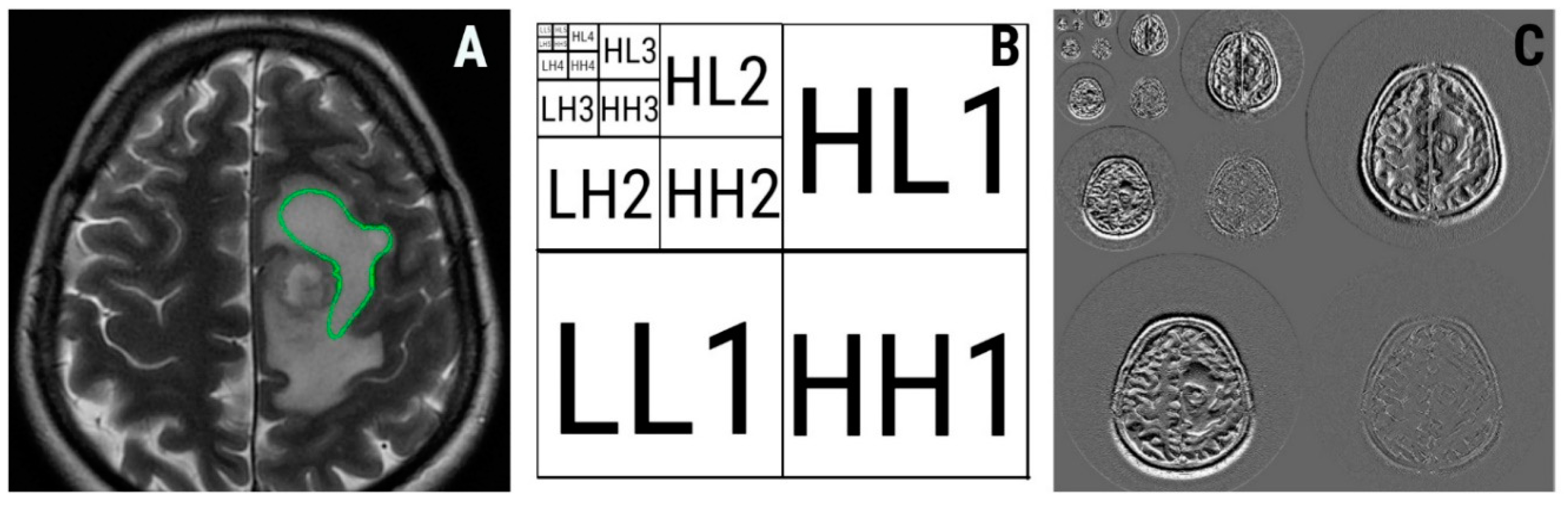
2.3. Texture Analysis Protocol
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Caravan, I.; Ciortea, C.A.; Contis, A.; Lebovici, A. Diagnostic value of apparent diffusion coefficient in differentiating between high-grade gliomas and brain metastases. Acta Radiol. 2017. [Google Scholar] [CrossRef] [PubMed]
- Giese, A.; Westphal, M. Treatment of malignant glioma: A problem beyond the margins of resection. J. Cancer Res. Clin. Oncol. 2001, 127, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Ho, M.-L.; Rojas, R.; Eisenberg, R.L. Cerebral edema. Am. J. Roentgenol. 2012. [Google Scholar] [CrossRef]
- Lu, S.; Ahn, D.; Johnson, G.; Cha, S. Peritumoral diffusion tensor imaging of high-grade gliomas and metastatic brain tumors. Am. J. Neuroradiol. 2003, 24, 937–941. [Google Scholar] [PubMed]
- Oh, J.; Cha, S.; Aiken, A.H.; Han, E.T.; Crane, J.C.; Stainsby, J.A.; Wright, G.A.; Dillon, P.D.; Nelson, S.J. Quantitative apparent diffusion coefficients and T2 relaxation times in characterizing contrast enhancing brain tumors and regions of peritumoral edema. J. Magn. Reason. Imaging 2005, 21, 701–708. [Google Scholar] [CrossRef]
- Byrnes, T.J.D.; Barrick, T.R.; Bell, B.A.; Clark, C.A. Diffusion tensor imaging discriminates between glioblastoma and cerebral metastases in vivo. NMR Biomed. 2011, 24, 54–60. [Google Scholar] [CrossRef]
- Blanchet, L.; Krooshof, P.W.T.; Postma, G.J.; Idema, A.J.; Goraj, B.; Heerschap, A.; Buydens, L.M.C. Discrimination between metastasis and glioblastoma multiforme based on morphometric analysis of MR images. AJNR Am. J. Neuroradiol. 2011, 32, 67–73. [Google Scholar] [CrossRef]
- Wang, W.; Steward, C.E.; Desmond, P.M. Diffusion tensor imaging in glioblastoma multiforme and brain metastases: The role of p, q, L, and fractional anisotropy. AJNR Am. J. Neuroradiol. 2009, 30, 203–208. [Google Scholar] [CrossRef]
- Neves, S.; Mazal, P.R.; Wanschitz, J.; Rudnay, A.C.; Drlicek, M.; Czech, T.; Wüstinger, C.; Budka, H. Pseudogliomatous growth pattern of anaplastic small cell carcinomas metastatic to the brain. Clin. Neuropathol. 2001, 20, 38–42. [Google Scholar]
- Lee, E.J.; terBrugge, K.; Mikulis, D.; Choi, D.S.; Bae, J.M.; Lee, S.K.; Moon, S.Y. Diagnostic value of peritumoral minimum apparent diffusion coefficient for differentiation of glioblastoma multiforme from solitary metastatic lesions. AJR Am. J. Roentgenol. 2011, 196, 71–76. [Google Scholar] [CrossRef]
- Upadhyay, N.; Waldman, A.D. Conventional MRI evaluation of gliomas. Br. J. Radiol. 2011, 84, 107–111. [Google Scholar] [CrossRef] [PubMed]
- Price, S.J.; Young, A.M.H.; Scotton, W.J.; Ching, J.; Mohsen, L.A.; Boonzaier, N.R.; Lupsor, V.C.; Griffiths, J.R.; McLean, M.A.; Larkin, T.J. Multimodal MRI can identify perfusion and metabolic changes in the invasive margin of glioblastomas. J. Magn. Reason. Imaging 2016, 43, 487–494. [Google Scholar] [CrossRef]
- Price, S.J.; Green, H.a.L.; Dean, A.F.; Joseph, J.; Hutchinson, P.J.; Gillard, J.H. Correlation of MR relative cerebral blood volume measurements with cellular density and proliferation in high-grade gliomas: An image-guided biopsy study. AJNR Am. J. Neuroradiol. 2011, 32, 501–506. [Google Scholar] [CrossRef] [PubMed]
- Doi, K. Computer-Aided Diagnosis in Medical Imaging: Historical Review, Current Status and Future Potential. Comput. Med. Imaging Graph. 2007, 31, 198–211. [Google Scholar] [CrossRef]
- Tourassi, G.D. Journey toward computer-aided diagnosis: Role of image texture analysis. Radiology 1999, 213, 317–320. [Google Scholar] [CrossRef] [PubMed]
- Livens, S.; Scheunders, P.; Wouwer, G.; Dyck, D. Wavelets for texture analysis, an overview. In Proceedings of the 6th International Conference on Image Processing and its Applications, Dublin, Ireland, 14–17 July 1997; pp. 581–585. [Google Scholar] [CrossRef]
- Raveane, W.; Arrieta, M.A.G. Texture Classification with Neural Networks. In Distributed Computing and Artificial Intelligence; Omatu, S., Neves, J., Rodriguez, J.M.C., Paz Santana, J.F., Gonzalez, S.R., Eds.; Springer International Publishing: Cham, Switzerland, 2013; pp. 325–332. [Google Scholar] [CrossRef]
- Soni, N.; Priya, S.; Bathla, G. Texture Analysis in Cerebral Gliomas: A Review of the Literature. AJNR Am. J. Neuroradiol. 2019, 40, 928–934. [Google Scholar] [CrossRef]
- Varghese, B.A.; Cen, S.Y.; Hwang, D.H.; Duddalwar, V.A. Texture Analysis of Imaging: What Radiologists Need to Know. AJR Am. J. Roentgenol. 2019, 212, 520–528. [Google Scholar] [CrossRef]
- Kang, Y.; Choi, S.H.; Kim, Y.-J.; Kim, K.G.; Sohn, C.-H.; Kim, J.-H.; Yun, T.J.; Chang, K.-H. Gliomas: Histogram analysis of apparent diffusion coefficient maps with standard- or high-b-value diffusion-weighted MR imaging—Correlation with tumor grade. Radiology 2011, 261, 882–890. [Google Scholar] [CrossRef]
- Raja, R.; Sinha, N.; Saini, J.; Mahadevan, A.; Rao, K.N.; Swaminathan, A. Assessment of tissue heterogeneity using diffusion tensor and diffusion kurtosis imaging for grading gliomas. Neuroradiology 2016, 58, 1217–1231. [Google Scholar] [CrossRef]
- Strzelecki, M.; Szczypinski, P.; Materka, A.; Klepaczko, A. A software tool for automatic classification and segmentation of 2D/3D medical images. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2013, 702, 137–140. [Google Scholar] [CrossRef]
- Collewet, G.; Strzelecki, M.; Mariette, F. Influence of MRI acquisition protocols and image intensity normalization methods on texture classification. Magn. Reason. Imaging 2004, 22, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Materka, A. Texture analysis methodologies for magnetic resonance imaging. Dialogues Clin. Neurosci. 2004, 6, 243–250. [Google Scholar] [PubMed]
- Herlidou-Même, S.; Constans, J.M.; Carsin, B.; Olivie, D.; Eliat, P.A.; Nadal-Desbarats, L.; Gondry, C.; Rumeur, E.; Idy-Perreti, I.; de Certaines, J.D. MRI texture analysis on texture test objects, normal brain and intracranial tumors. Magn. Reason. Imaging 2003, 21, 989–993. [Google Scholar] [CrossRef]
- DeLong, E.R.; DeLong, D.M.; Clarke-Pearson, D.L. Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach. Biometrics 1988, 44, 837–845. [Google Scholar] [CrossRef]
- Larroza, A.; Bodí, V.; Moratal, D. Texture Analysis in Magnetic Resonance Imaging: Review and Considerations for Future Applications. In Assessment of Cellular and Organ Function and Dysfunction Using Direct and Derived MRI Methodologies; Constantinides, C., Ed.; IntechOpen: London, UK, 2016. [Google Scholar] [CrossRef]
- Muccio, C.F.; Tedeschi, E.; Ugga, L.; Cuocolo, R.; Esposito, G.; Caranci, F. Solitary Cerebral Metastases vs. High-grade Gliomas: Usefulness of Two MRI Signs in the Differential Diagnosis. Anticancer Res. 2019, 39, 4905–4909. [Google Scholar] [CrossRef]
- Han, C.; Huang, S.; Guo, J.; Zhuang, X.; Han, H. Use of a high b-value for diffusion weighted imaging of peritumoral regions to differentiate high-grade gliomas and solitary metastases. J. Magn. Reason. Imaging 2015, 42, 80–86. [Google Scholar] [CrossRef]
- Pavlisa, G.; Rados, M.; Pavic, L.; Potocki, K.; Mayer, D. The differences of water diffusion between brain tissue infiltrated by tumor and peritumoral vasogenic edema. Clin. Imaging 2009, 33, 96–101. [Google Scholar] [CrossRef]
- Server, A.; Kulle, B.; Maehlen, J.; Josefsen, R.; Schellhorn, T.; Kumar, T.; Langberg, P.H.; Nakstad, P.H. Quantitative apparent diffusion coefficients in the characterization of brain tumors and associated peritumoral edema. Acta Radiol. 2009, 50, 682–689. [Google Scholar] [CrossRef]
- Bertossi, M.; Virgintino, D.; Maiorano, E.; Occhiogrosso, M.; Roncali, L. Ultrastructural and morphometric investigation of human brain capillaries in normal and peritumoral tissues. Ultrastruct. Pathol. 1997, 21, 41–49. [Google Scholar] [CrossRef]
- Tsougos, I.; Svolos, P.; Kousi, E.; Fountas, K.; Theodorou, K.; Fezoulidis, I.; Theodorou, K.; Frezoulidis, I.; Kapsalaki, E. Differentiation of glioblastoma multiforme from metastatic brain tumor using proton magnetic resonance spectroscopy, diffusion and perfusion metrics at 3 T. Cancer Imaging 2012, 12, 423–436. [Google Scholar] [CrossRef]
- Yan, J.-L.; Li, C.; Boonzaier, N.R.; Fountain, D.M.; Larkin, T.J.; Matys, T.; van der Hoorn, A.; Price, S.J. Multimodal MRI characteristics of the glioblastoma infiltration beyond contrast enhancement. Ther. Adv. Neurol. Disord. 2019, 12, 1756286419844664. [Google Scholar] [CrossRef] [PubMed]
- Wijnen, J.P.; Idema, A.J.S.; Stawicki, M.; Lagemaat, M.W.; Wesseling, P.; Wright, A.J.; Scheenen, T.W.J.; Heerschap, A. Quantitative short echo time 1H MRSI of the peripheral edematous region of human brain tumors in the differentiation between glioblastoma, metastasis, and meningioma. J. Magn. Reason. Imaging 2012, 36, 1072–1082. [Google Scholar] [CrossRef]
- Jain, R.; Poisson, L.M.; Gutman, D.; Scarpace, L.; Hwang, S.N.; Holder, C.A.; Wintermark, M.; Rao, A.; Colen, R.R.; Kirby, J.; et al. Outcome prediction in patients with glioblastoma by using imaging, clinical, and genomic biomarkers: Focus on the nonenhancing component of the tumor. Radiology 2014, 272, 484–493. [Google Scholar] [CrossRef] [PubMed]
- Bette, S.; Huber, T.; Wiestler, B.; Boeckh-Behrens, T.; Gempt, J.; Ringel, F.; Meyer, B.; Zimmer, C.; Kirsche, J.S. Analysis of fractional anisotropy facilitates differentiation of glioblastoma and brain metastases in a clinical setting. Eur. J. Radiol. 2016, 85, 2182–2187. [Google Scholar] [CrossRef]
- Ryu, Y.J.; Choi, S.H.; Park, S.J.; Yun, T.J.; Kim, J.-H.; Sohn, C.-H. Glioma: Application of whole-tumor texture analysis of diffusion-weighted imaging for the evaluation of tumor heterogeneity. PLoS ONE 2014, 9, e108335. [Google Scholar] [CrossRef]
- Kinoshita, M.; Sakai, M.; Arita, H.; Shofuda, T.; Chiba, Y.; Kagawa, N.; Watanabe, Y.; Hashimoto, N.; Fujimoto, Y.; Yoshimine, T.; et al. Introduction of High Throughput Magnetic Resonance T2-Weighted Image Texture Analysis for WHO Grade 2 and 3 Gliomas. PLoS ONE 2016, 11, e0164268. [Google Scholar] [CrossRef]
- Skogen, K.; Schulz, A.; Dormagen, J.B.; Ganeshan, B.; Helseth, E.; Server, A. Diagnostic performance of texture analysis on MRI in grading cerebral gliomas. Eur. J. Radiol. 2016, 85, 824–829. [Google Scholar] [CrossRef]
- Skogen, K.; Schulz, A.; Helseth, E.; Ganeshan, B.; Dormagen, J.B.; Server, A. Texture analysis on diffusion tensor imaging: Discriminating glioblastoma from single brain metastasis. Acta Radiol. 2019, 60, 356–366. [Google Scholar] [CrossRef]
- Mouthuy, N.; Cosnard, G.; Abarca-Quinones, J.; Michoux, N. Multiparametric magnetic resonance imaging to differentiate high-grade gliomas and brain metastases. J. Neuroradiol. 2012, 39, 301–307. [Google Scholar] [CrossRef]
- Artzi, M.; Liberman, G.; Blumenthal, D.T.; Aizenstein, O.; Bokstein, F.; Ben Bashat, D. Differentiation between vasogenic edema and infiltrative tumor in patients with high-grade gliomas using texture patch-based analysis. J. Magn. Reason. Imaging 2018. [Google Scholar] [CrossRef] [PubMed]
- Szczypinski, P.M.; Klepaczko, A. MaZda—A Framework for Biomedical Image Texture Analysis and Data Exploration In Biomedical Texture Analysis: Fundamentals, Tools and Challenges; Szczypinski, P.M., Klepaczko, A., Depeursinge, A., Al-Kadi, O.S., Mitchell, J.R., Eds.; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Miles, K.A.; Ganeshan, B.; Hayball, M.P. CT texture analysis using the filtration-histogram method: What do the measurements mean? Cancer Imaging 2013, 13, 400–406. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.-Q.; Liang, H.-Y.; Yang, Z.-X.; Ding, Y.; Zeng, M.-S.; Rao, S.-X. Value of MR histogram analyses for prediction of microvascular invasion of hepatocellular carcinoma. Medicine 2016, 95, e4034. [Google Scholar] [CrossRef] [PubMed]
- Castellano, G.; Bonilha, L.; Li, L.M.; Cendes, F. Texture analysis of medical images. Clin. Radiol. 2004, 59, 1061–1069. [Google Scholar] [CrossRef] [PubMed]
- Mayerhoefer, M.E.; Breitenseher, M.J.; Kramer, J.; Aigner, N.; Hofmann, S.; Materka, A. Texture analysis for tissue discrimination on T1-weighted MR images of the knee joint in a multicenter study: Transferability of texture features and comparison of feature selection methods and classifiers. J. Magn. Reason. Imaging 2005, 22, 674–680. [Google Scholar] [CrossRef]
- Kairuddin, W.N.H.W.; Mahmud, W.M.H.W. Texture Feature Analysis for Different Resolution Level of Kidney Ultrasound Images. IOP Conf. Ser. Mater. Sci. Eng. 2017, 226, 12136. [Google Scholar] [CrossRef]
- Grey-Level Run Length Matrix (GLRLM) n.d. Available online: https://www.lifexsoft.org/index.php/resources/19-texture/radiomic-features/68-grey-level-run-length-matrix-glrlm (accessed on 21 May 2020).
- cerr/CERR. GitHub n.d. Available online: https://github.com/cerr/CERR (accessed on 21 May 2020).
- Yadav, A.K.; Roy, R.; Ch, S.; Kumar, E.; Praveen, A. Vaishali, Wavelet Based Texture Analysis for MedicalImages. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2015. [Google Scholar] [CrossRef]
- Classifying Image data n.d. Available online: https://www.debugmode.com/imagecmp/classify.htm (accessed on 21 May 2020).
- Dutra da Silva, R.; Minneto, R.; Schwartz, W.; Pedrini, H. Satellite Image Segmentation Using Wavelet Transform Based on Color and Texture Features. In Advances in Visual Computing: 4th International Symposium, ISVC 2008, Las Vegas, NV, USA, 1–3 December 2008; Boyle, R., Parvin, B., Koracin, D., Porikli, F., Peters, J., Klosowski, J., Eds.; Part, II. Springer: Berlin, Germany, 2008; pp. 114–132. [Google Scholar]
- Mori, S.; Zhang, J. Principles of Diffusion Tensor Imaging and Its Applications to Basic Neuroscience Research. Neuron 2006, 51, 527–539. [Google Scholar] [CrossRef]
- Buch, K.; Kuno, H.; Qureshi, M.M.; Li, B.; Sakai, O. Quantitative variations in texture analysis features dependent on MRI scanning parameters: A phantom model. J. Appl. Clin. Med. Phys. 2018, 19, 253–264. [Google Scholar] [CrossRef]
- Duffau, H. Long-term outcomes after supratotal resection of diffuse low-grade gliomas: A consecutive series with 11-year follow-up. Acta Neurochir. 2016, 158, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Nabors, L.B.; Portnow, J.; Ammirati, M.; Baehring, J.; Brem, H.; Butowski, N.; Fenstermaker, R.A.; Forsyth, P.; Hattangadi-Gluth, J.; Holdoff, M.; et al. NCCN Guidelines Insights: Central Nervous System Cancers, Version 1.2017. J. Natl. Compr. Cancer Netw. 2017, 15, 1331–1345. [Google Scholar] [CrossRef]
- Blystad, I.; Warntjes, J.B.M.; Smedby, Ö.; Lundberg, P.; Larsson, E.-M.; Tisell, A. Quantitative MRI for analysis of peritumoral edema in malignant gliomas. PLoS ONE 2017, 12, e0177135. [Google Scholar] [CrossRef] [PubMed]
- Kousi, E.; Tsougos, I.; Tsolaki, E.; Fountas, K.N.; Theodorou, K.; Fezoulidis, I.; Kapsalaki, E.; Kappas, C. Spectroscopic Evaluation of Glioma Grading at 3T: The Combined Role of Short and Long TE. Sci. World J. 2012, 2012, 546171. [Google Scholar] [CrossRef]
- Lee, K.H. Computers in Nuclear Medicine: A Practical Approach; SNMMI: Reston, VA, USA, 2005; pp. 106–112. [Google Scholar]
- Pirzkall, A.; McKnight, T.R.; Graves, E.E.; Carol, M.P.; Sneed, P.K.; Wara, W.W.; Nelson, S.J.; Verhey, L.J.; Larson, D.A. MR-spectroscopy guided target delineation for high-grade gliomas. Int. J. Radiat. Oncol. Biol. Phys. 2001, 50, 915–928. [Google Scholar] [CrossRef]
- Price, S.J.; Gillard, J.H. Imaging biomarkers of brain tumour margin and tumour invasion. Br. J. Radiol. 2011, 84, 159–167. [Google Scholar] [CrossRef]
- Herr, K.; Muglia, V.F.; Koff, W.J.; Westphalen, A.C. Imaging of the adrenal gland lesions. Radiol. Bras. 2014, 47, 228–239. [Google Scholar] [CrossRef]
- Yagi, T.; Yamazaki, M.; Ohashi, R.; Ogawa, R.; Ishikawa, H.; Yoshimura, N.; Tsuchida, M.; Ajioka, Y.; Aoyama, H. HRCT texture analysis for pure or part-solid ground-glass nodules: Distinguishability of adenocarcinoma in situ or minimally invasive adenocarcinoma from invasive adenocarcinoma. Jpn. J. Radiol. 2018, 36, 113–121. [Google Scholar] [CrossRef]
- Hassan, I.; Kotrotsou, A.; Bakhtiari, A.S.; Thomas, G.A.; Weinberg, J.S.; Kumar, A.J.; Sawaya, R.; Luedi, M.K.; Zinn, P.O.; Colen, R.R. Radiomic Texture Analysis Mapping Predicts Areas of True Functional MRI Activity. Sci. Rep. 2016, 6, 25295. [Google Scholar] [CrossRef]
- Mayerhoefer, M.E.; Breitenseher, M.; Amann, G.; Dominkus, M. Are signal intensity and homogeneity useful parameters for distinguishing between benign and malignant soft tissue masses on MR images? Objective evaluation by means of texture analysis. Magn. Reason. Imaging 2008, 26, 1316–1322. [Google Scholar] [CrossRef]
- Ng, F.; Kozarski, R.; Ganeshan, B.; Goh, V. Assessment of tumor heterogeneity by CT texture analysis: Can the largest cross-sectional area be used as an alternative to whole tumor analysis? Eur. J. Radiol. 2013, 82, 342–348. [Google Scholar] [CrossRef] [PubMed]
- Lewis, M.A.; Ganeshan, B.; Barnes, A.; Bisdas, S.; Jaunmuktane, Z.; Brandner, S.; Endozo, R.; Groves, A.; Thust, S.C. Filtration-histogram based magnetic resonance texture analysis (MRTA) for glioma IDH and 1p19q genotyping. Eur. J. Radiol. 2019, 113, 116–123. [Google Scholar] [CrossRef] [PubMed]
- Win, T.; Miles, K.A.; Janes, S.M.; Ganeshan, B.; Shastry, M.; Endozo, R.; Meagher, M.; Shortman, R.I.; Wan, S.; Kayani, I.; et al. Tumor heterogeneity and permeability as measured on the CT component of PET/CT predict survival in patients with non-small cell lung cancer. Clin. Cancer Res. 2013, 19, 3591–3599. [Google Scholar] [CrossRef]
- Dohan, A.; Gallix, B.; Guiu, B.; Le Malicot, K.; Reinhold, C.; Soyer, P.; Bennouna, J.; Ghiringhelli, F.; Barbier, E.; Boige, V. Early evaluation using a radiomic signature of unresectable hepatic metastases to predict outcome in patients with colorectal cancer treated with FOLFIRI and bevacizumab. Gut 2020, 69, 531–539. [Google Scholar] [CrossRef]
- Miles, K.A.; Ganeshan, B.; Griffiths, M.R.; Young, R.C.D.; Chatwin, C.R. Colorectal cancer: Texture analysis of portal phase hepatic CT images as a potential marker of survival. Radiology 2009, 250, 444–452. [Google Scholar] [CrossRef]
- Yasaka, K.; Akai, H.; Mackin, D.; Court, L.; Moros, E.; Ohtomo, K.; Kiryu, S. Precision of quantitative computed tomography texture analysis using image filtering: A phantom study for scanner variability. Medicine 2017, 96, e6993. [Google Scholar] [CrossRef] [PubMed]
- Gourtsoyianni, S.; Doumou, G.; Prezzi, D.; Taylor, B.; Stirling, J.J.; Taylor, N.J.; Siddique, M.; Cook, C.J.R.; Glyme-Jones, R.; Goh, V. Primary Rectal Cancer: Repeatability of Global and Local-Regional MR Imaging Texture Features. Radiology 2017, 284, 552–561. [Google Scholar] [CrossRef]
- Cui, H.W.; Devlies, W.; Ravenscroft, S.; Heers, H.; Freidin, A.J.; Cleveland, R.O.; Ganeshan, B.; Turney, B.W. CT Texture Analysis of Ex Vivo Renal Stones Predicts Ease of Fragmentation with Shockwave Lithotripsy. J. Endourol. 2017, 31, 694–700. [Google Scholar] [CrossRef]
- Mayerhoefer, M.E.; Schima, W.; Trattnig, S.; Pinker, K.; Berger-Kulemann, V.; Ba-Ssalamah, A. Texture-based classification of focal liver lesions on MRI at 3.0 Tesla: A feasibility study in cysts and hemangiomas. J. Magn. Reason. Imaging 2010, 32, 352–359. [Google Scholar] [CrossRef]
| Fisher | F | p-Value | POE + ACC | PP | p-Value |
|---|---|---|---|---|---|
| Perc01 * | 2.31 | <0.0001 | CV5S6SumOfSqs | 0.39 | 0.0883 |
| Perc10 * | 1.73 | 0.0002 | CV4S6InvDfMom | 0.41 | 0.0997 |
| Mean | 1.27 | 0.0013 | WavEnHH_s-1 | 0.46 | 0.0067 |
| Perc50 | 1.22 | 0.0015 | WavEnHL_s-4 | 0.47 | 0.3853 |
| WavEnLL_s-4 * | 1.2 | 0.0062 | Perc10 * | 0.47 | 0.0002 |
| RNS6ShrtREmp | 0.96 | 0.0045 | RNS6Fraction * | 0.49 | 0.0057 |
| Perc90 | 0.92 | 0.0053 | WavEnLL_s-4 * | 0.49 | 0.0062 |
| RNS6Fraction * | 0.9 | 0.0057 | CZ5S6SumAverg | 0.49 | 0.5007 |
| RNS6LngREmph | 0.81 | 0.0083 | WavEnLH_s-4 | 0.49 | 0.7559 |
| Perc99 | 0.78 | 0.0096 | Perc01 * | 0.64 | <0.0001 |
| Parameter | HGGs | BMs |
|---|---|---|
| Perc01 | 33,848.43 ±328.15 | 34,308.65 ± 298.8 |
| Perc10 | 33,994.5 ± 363.17 | 34,437 ± 322.34 |
| Perc50 | 34,182.12 ± 433.34 | 34,581.69 ± 325.32 |
| Perc90 | 34,331.18 ± 466.79 | 34,699.46 ± 341.39 |
| Perc99 | 34,411.31 ± 489.28 | 34,765.03 ± 352.9 |
| Mean | 34,171.97 ± 420.92 | 34,573.13 ± 325.66 |
| WavEnLL_s-4 | 10,272.3 ± 4385.84 | 6579.94 ± 2732.81 |
| WavEnHH_s-1 | 6.25 ± 3.47 | 10.96 ± 7.11 |
| RNS6Fraction | 0.9 ± 0.02 | 0.93 ± 0.02 |
| RNS6ShrtREmp | 0.93 ± 0.01 | 0.94 ± 0.01 |
| RNS6LngREmph | 1.32 ± 0.11 | 1.23 ± 0.08 |
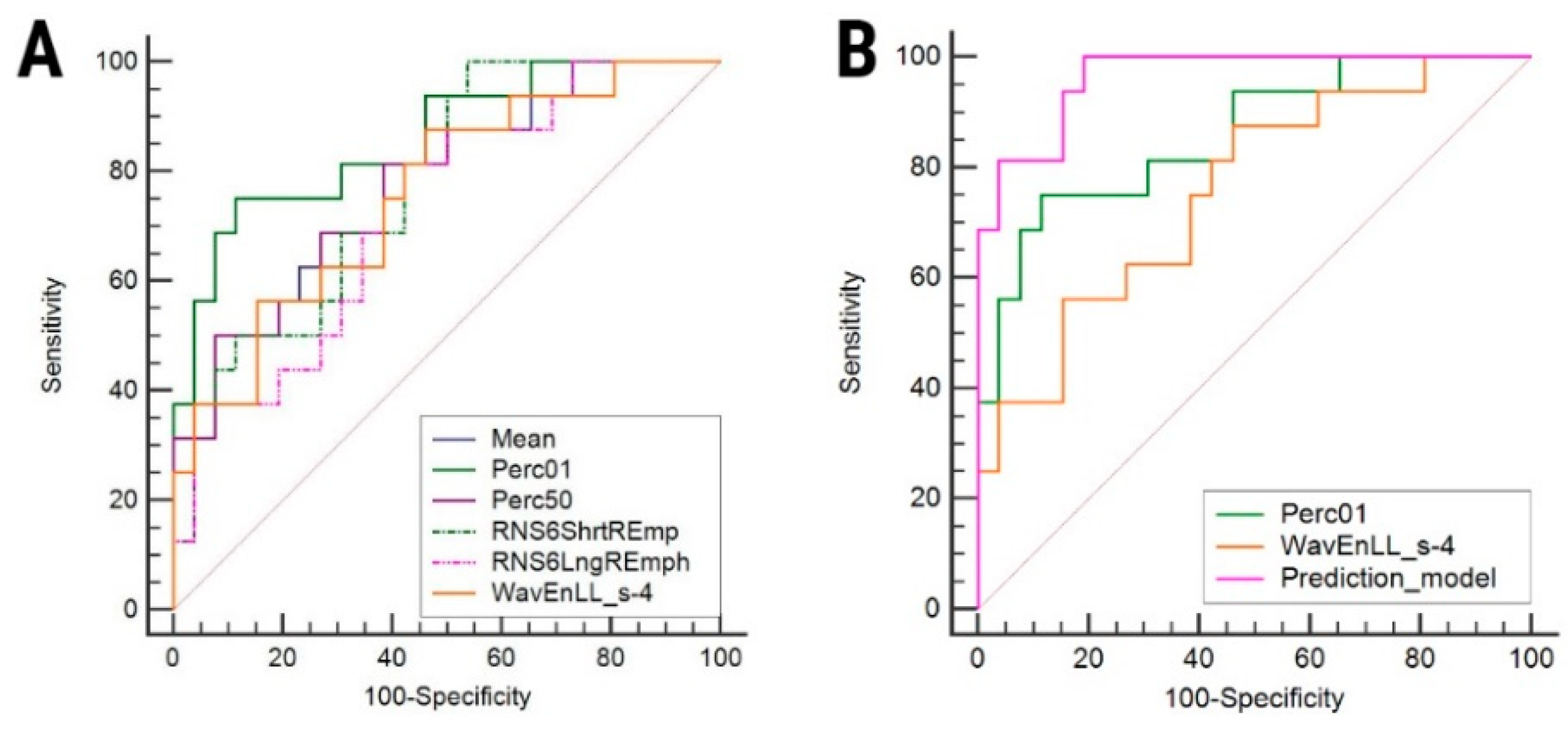
| Parameter | Sign. Lvl. | AUC | J | Cut-Off | Sensitivity (%) | Specificity (%) |
|---|---|---|---|---|---|---|
| Perc01 | <0.0001 | 0.858 (0.716–0.946) | 0.63 | ≤34,039 | 75 (47.6–92.7) | 88.46 (69.8–97.6) |
| Perc10 | 0.0031 | 0.748 (0.59–0.869) | 0.53 | ≤34,081 | 68.75 (41.3–89) | 84.62 (65.1–95.6) |
| Perc50 | 0.0003 | 0.772 (0.616–0.887) | 0.42 | ≤34,466 | 81.25 (54.4–96) | 61.54 (40.6–79.8) |
| Perc90 | 0.006 | 0.726 (0.567–0.852) | 0.37 | ≤34,728 | 87.5 (61.7–98.4) | 87.5 (61.7–98.4) |
| Perc99 | 0.0084 | 0.719 (0.559–0.846) | 0.37 | ≤34,831 | 87.5 (61.7–98.4) | 87.5 (61.7–98.4) |
| Mean | 0.0002 | 0.774 (0.619–0.889) | 0.42 | ≤34,154.86 | 50 (24.7–75.3) | 92.31 (74.9–99.1) |
| WavEnLL_s-4 | 0.0009 | 0.757 (0.6–0.876) | 0.41 | >6458.11 | 87.5 (61.7–98.4) | 53.85 (33.4–73.4) |
| WavEnHH_s-1 | 0.0294 | 0.68 (0.519–0.816) | 0.38 | ≤14.8 | 100 (79.4–100) | 38.46 (20.2–59.4) |
| RNS6Fraction | 0.0004 | 0.748 (0.606–0.88) | 0.46 | ≤0.94 | 100 (79.4–100) | 46.15 (22.6–66.6) |
| RNS6ShrtREmp | 0.0001 | 0.776 (0.622–0.89) | 0.46 | ≤0.95 | 100 (79.4–100) | 46.15 (22.6–66.6) |
| RNS6LngREmph | 0.0041 | 0.728 (0.596–0.854) | 0.38 | >1.23 | 81.25 (54.4–96) | 57.69 (36.9–76.6) |
| Perc01 | REF | 0.0021 | 0.0362 | 0.0109 | 0.0095 | 0.0231 | 0.2766 | 0.0572 | 0.2933 | 0.3627 | 0.17 |
| Perc10 | 0.0021 | REF | 0.5385 | 0.6518 | 0.5633 | 0.4581 | 0.9311 | 0.552 | 0.9007 | 0.7992 | 0.872 |
| Perc50 | 0.0362 | 0.5385 | REF | 0.0203 | 0.0264 | 0.7778 | 0.8862 | 0.3996 | 0.7568 | 0.964 | 0.7041 |
| Perc90 | 0.0109 | 0.6518 | 0.0203 | REF | 0.3795 | 0.0233 | 0.7691 | 0.6882 | 0.7568 | 0.6589 | 0.9843 |
| Perc99 | 0.0095 | 0.5633 | 0.0264 | 0.3795 | REF | 0.0256 | 0.7191 | 0.7373 | 0.7122 | 0.6169 | 0.9377 |
| Mean | 0.0231 | 0.4581 | 0.7778 | 0.0233 | 0.0256 | REF | 0.8668 | 0.1105 | 0.9103 | 0.9817 | 0.6822 |
| WavEnLL_s-4 | 0.2766 | 0.9311 | 0.8862 | 0.7691 | 0.7191 | 0.8668 | REF | 0.4324 | 0.9553 | 0.8246 | 0.7434 |
| WavEnHH_s-1 | 0.0572 | 0.552 | 0.3996 | 0.6882 | 0.7373 | 0.1105 | 0.4324 | REF | 0.1105 | 0.0655 | 0.3928 |
| RNS6Fraction | 0.2933 | 0.9007 | 0.7568 | 0.7568 | 0.7122 | 0.9103 | 0.9553 | 0.1105 | REF | 0.358 | 0.0693 |
| RNS6ShrtREmp | 0.3627 | 0.7992 | 0.964 | 0.6589 | 0.6169 | 0.9817 | 0.8246 | 0.0655 | 0.358 | REF | 0.0705 |
| RNS6LngREmph | 0.17 | 0.872 | 0.7041 | 0.9843 | 0.9377 | 0.6822 | 0.7434 | 0.3928 | 0.0693 | 0.0705 | REF |
| Independent Variable | Coefficient | Standard Error | p-Value | VIF |
|---|---|---|---|---|
| Perc01 | −0.002 | 0.001 | 0.0370 | 67.869 |
| Perc10 | 0.001 | 0.002 | 0.4061 | 247.596 |
| Perc50 | 0.0008 | 0.003 | 0.7806 | 555.997 |
| Perc90 | −0.006 | 0.006 | 0.3198 | 2433.857 |
| Perc99 | 0.005 | 0.004 | 0.2162 | 1245.022 |
| RNS6Fraction | 0.91 | 77.72 | 0.9906 | 1224.984 |
| RNS6LngREmph | 3.08 | 10.38 | 0.7682 | 405.915 |
| RNS6ShrtREmp | −19.75 | 49.49 | 0.6925 | 270.604 |
| WavEnHH_s-1 | −0.004157 | 0.01405 | 0.7692 | 2.693 |
| WavEnLL_s-4 | 0.0000413 | 0.0000182 | 0.0311 | 1.672 |
| Sign. level. | 0.0002 | |||
| R2 | 0.6180 | |||
| R2 adjusted | 0.4948 | |||
| M.R. Coef. | 0.7861 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Csutak, C.; Ștefan, P.-A.; Lenghel, L.M.; Moroșanu, C.O.; Lupean, R.-A.; Șimonca, L.; Mihu, C.M.; Lebovici, A. Differentiating High-Grade Gliomas from Brain Metastases at Magnetic Resonance: The Role of Texture Analysis of the Peritumoral Zone. Brain Sci. 2020, 10, 638. https://doi.org/10.3390/brainsci10090638
Csutak C, Ștefan P-A, Lenghel LM, Moroșanu CO, Lupean R-A, Șimonca L, Mihu CM, Lebovici A. Differentiating High-Grade Gliomas from Brain Metastases at Magnetic Resonance: The Role of Texture Analysis of the Peritumoral Zone. Brain Sciences. 2020; 10(9):638. https://doi.org/10.3390/brainsci10090638
Chicago/Turabian StyleCsutak, Csaba, Paul-Andrei Ștefan, Lavinia Manuela Lenghel, Cezar Octavian Moroșanu, Roxana-Adelina Lupean, Larisa Șimonca, Carmen Mihaela Mihu, and Andrei Lebovici. 2020. "Differentiating High-Grade Gliomas from Brain Metastases at Magnetic Resonance: The Role of Texture Analysis of the Peritumoral Zone" Brain Sciences 10, no. 9: 638. https://doi.org/10.3390/brainsci10090638
APA StyleCsutak, C., Ștefan, P.-A., Lenghel, L. M., Moroșanu, C. O., Lupean, R.-A., Șimonca, L., Mihu, C. M., & Lebovici, A. (2020). Differentiating High-Grade Gliomas from Brain Metastases at Magnetic Resonance: The Role of Texture Analysis of the Peritumoral Zone. Brain Sciences, 10(9), 638. https://doi.org/10.3390/brainsci10090638