Whole-Brain Models to Explore Altered States of Consciousness from the Bottom Up
Abstract
1. Introduction
2. What Is an Altered State of Consciousness? Examples and Defining Features
3. Top-Down Signatures of Consciousness from Brain Signals
3.1. Functionalist and Non-Functionalist Positions on the Mind-Brain Problem
3.2. Examples of Signatures of Consciousness
3.2.1. The Entropic Brain Hypothesis
3.2.2. Integrated Information Theory
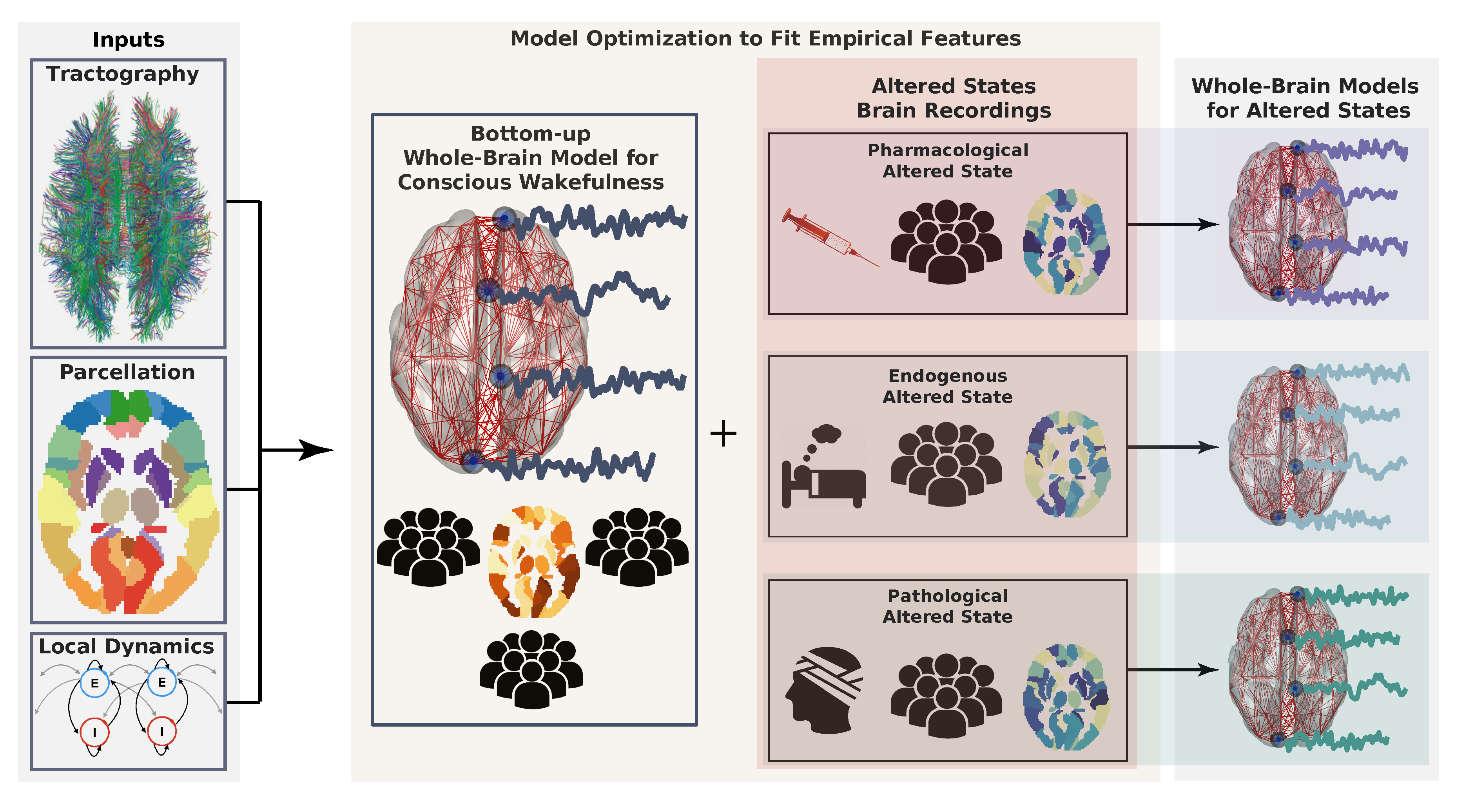
4. Bottom-Up Whole-Brain Models
4.1. What Are Whole-Brain Models?
- Brain parcellation: A brain parcellation determines the number of regions and the spatial resolution at which the brain dynamics take place. The parcellation may include cortical, sub-cortical, and cerebellar regions. Examples of well-known parcellations are the Hagmann parcellation [105], and the automated anatomical labeling (AAL) atlas [106].
- Anatomical connectivity matrix: This matrix defines the network of connections between brain regions. Most studies are based on the human connectome, obtained by estimating the number of white-matter fibers connecting brain areas from DTI data combined with probabilistic tractography [28]. For control purposes, randomized versions of the connectome (null hypothesis networks) may also be employed.
- Local dynamics: The activity of each brain region is typically determined by the chosen local dynamics plus interaction terms with other regions. A variety of approaches have been proposed to model whole-brain dynamics, including cellular automata [107,108], the Ising spin model [109,110,111], autoregressive models [112], stochastic linear models [113], non-linear oscillators [114,115], neural field theory [116,117], neural mass models [118,119], and dynamic mean-field models [120,121,122]. A detailed review of the different models that can be explored within this context can be found in Reference [15,29].
4.2. Examples
4.2.1. Dynamic Mean-Field (DMF) Model
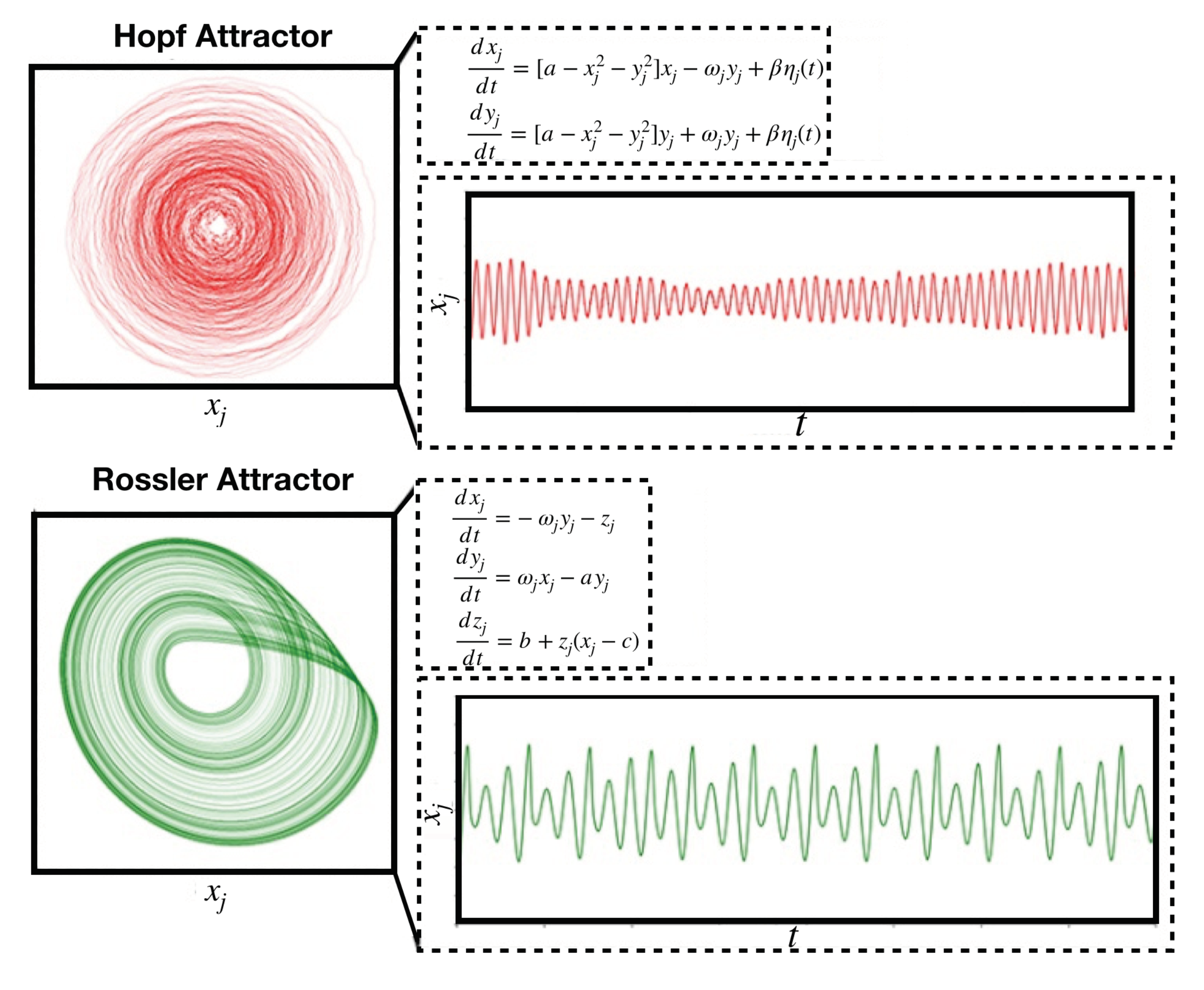
4.2.2. Stuart-Landau Non-Linear Oscillator Model
4.3. How to Fit Whole-Brain Models to Neuroimaging Data?
4.4. Whole-Brain Models Applied to the Study of Consciousness
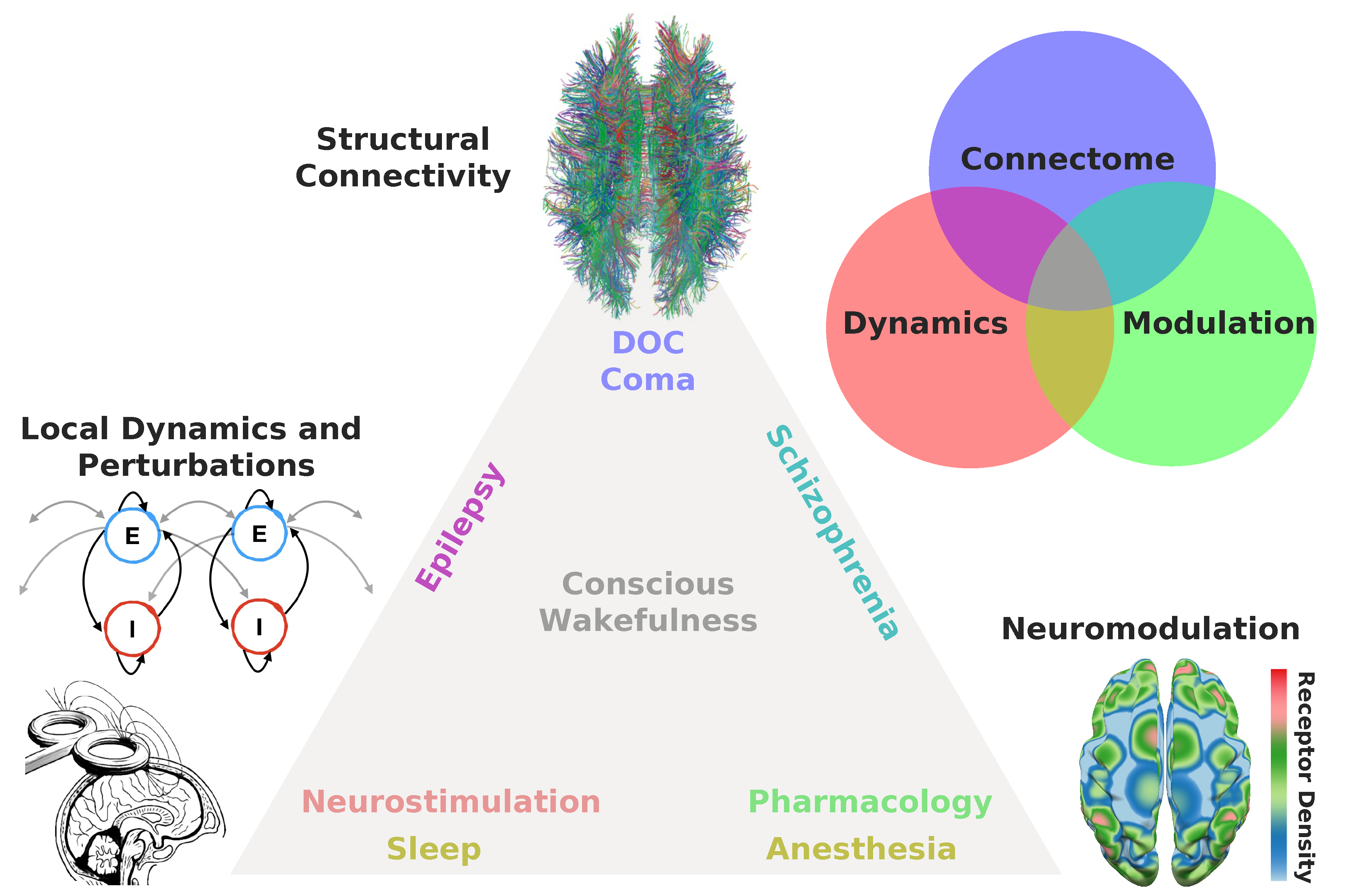
5. Proposed Research Agenda
5.1. Motivation
5.2. Proposal
- Connectome: Is the state of consciousness implicated with local or diffuse structural abnormalities? This is frequently the case for neurological conditions, such as coma and post-comatose disorders of consciousness (e.g., unresponsive wakefulness syndrome, minimally conscious state) [145]. In addition, subtler structural modifications can be implicated in certain psychiatric conditions presenting episodes of altered consciousness, such as different forms of schizophrenia [146]. While several papers have investigated localized (e.g., stroke, tumors, focal epilepsy) structural damage from this perspective [147,148,149,150,151,152,153,154], the literature on whole-brain models applied to patients suffering from neurological impairments and from disorders of consciousness is very limited. The project of modeling pathological brain states perforce necessitates to incorporate individualized structural connectomes and lesion maps, thus moving towards simulation at the single patient level [155,156].
- Modulation: Is the state of consciousness a consequence of neuromodulatory changes, either endogenous or induced externally by means of pharmacological manipulation? Two typical examples are the altered states of consciousness induced by psychedelics/dissociatives, which are linked to agonism/antagonism at serotonin/glutamate receptors [157]. Certain psychiatric conditions are believed to arise as a consequence of neuromodulatory imbalances, e.g., dopaminergic imbalances are believed to play an important role in the pathophysiology of schizophrenia [158]. Most anaesthetic drugs reduce the complexity of the brain activity by targeting specific neuromodulatory sites, such as those activated by gamma-aminobutyric acid (GABA) [159]. Finally, sleep is a state of reduced consciousness triggered by activity in monoaminergic neurons with diffuse projections throughout the brain [160].
- Dynamics: Is the altered state of consciousness captured by well-understood dynamical mechanisms? Does the model include parametrically controlled external perturbations? While changes in the local excitation/inhibition balance are ultimately caused by neurochemical processes, they are best understood in terms of their dynamical consequences. States such as epilepsy, deep sleep and general anaesthesia are believed to involve unbalanced excitation/inhibition [161]. In some cases, dynamics may be sufficiently idiosyncratic to be captured by low dimensional phenomenological models, as in the case of certain forms of epileptic activity [162]. Finally, local dynamics could be modified to simulate the effects of external neurostimulation [123,139].
5.3. What Can We Learn?
5.4. Case Study: Modeling Neural Entropy Increases Induced by Psychedelics
6. Future Directions
6.1. What Should Be the “Bottom” of Bottom-Up Models?
6.2. Transitions between Canonical Dynamics as Primitives to Construct Whole-Brain Models
7. Final Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| NCC | Neural correlates of consciousness |
| DMF | Dynamic mean-field |
| fMRI | Functional magnetic resonance imaging |
| BOLD | Blood oxygen level–dependent |
| PET | Positron emission tomography |
| DTI | Diffusion tensor imaging |
| EEG | Electroencephalography |
| MEG | Magnetoencephalography |
| IIT | Integrated Information Theory |
| GNW | Global neuronal workspace |
| EBH | Entropic brain hypothesis |
| LZc | Lempel-Ziv complexity |
| FCD | Functional connectivity dynamics |
| PCI | Perturbational complexity index |
| PILI | Perturbative Integration Latency Index |
| LSD | Lysergic acid diethylamide |
| AAL | Automated anatomical labeling |
| DOC | Disorder of consciousness |
| GABA | Gamma-aminobutyric acid |
| RSN | Resting-state networks |
| Glossary of Technical Terms | |
| 5- receptor | Serotonin receptor in which acute activation by serotonergic psychedelics produces a transient altered state of consciousness. |
| Attractor | Set of points in the phase space of a dynamical system towards which the system approaches during its temporal evolution. |
| Bifurcation | Phenomena in the field of dynamical systems that occurs when a small change in the parameter values causes a sharp qualitative change in the behavior of the system. |
| Bottom-up approach | Defines the local dynamics of interacting units (such as neurons or groups of neurons) in order to generate features as similar as possible to the ones observed in the brain during different experimental conditions. |
| Entropic brain hypothesis | An example of top-down approach. Postulates that the richness of conscious experience depends on the complexity of the underlying population-level neuronal activity, which determines the repertoire of states available for the brain to explore. |
| Functional connectivity (FC) and Functional Connectivity Dynamics (FCD) | Second order statistics summarizing the pair-wise dependence between the activity of brain regions. The FCD is obtained from computing the similarity between the FCs associated with different time windows. |
| Integrated information theory (IIT) | An example of top-down approach. Based on certain first-person qualities of subjective experience, which are accessed by introspection and can be taken as “postulates” or “axioms” for the theory. This theory strives to provide a quantitative characterization of consciousness analyzing the causal relationships of brain activity using multivariate information theory. |
| Hopf bifurcation | Example of a bifurcation of a nonlinear dynamical system where steady dynamics change their stability and a limit cycle emerges, giving rise to periodical solutions. |
| Lempel-Ziv complexity | Lossless compression algorithm that provides an effective tool to estimate the entropy rate of a signal. |
| Lyapunov exponent | An exponent that indicates how two trajectories with similar initial conditions diverge in their temporal evolution along each dimension. A positive value for the Lyapunov exponent is indicative of deterministic chaos. |
| Mind-brain problem | Dualistic perspective addressing the relationship between the mental and the embodied brain processes. |
| Neural correlates of consciousness (NCC) | Minimal set of neural events associated with a certain subjective experience. |
| Perturbational complexity index | Measure of the complexity of the cortical activity evoked by transcranial magnetic stimulation. |
| Phenomenal and access consciousness | The first represents the subjective experience of sensory perception, emotion, thoughts, etc. The second represents the global availability of conscious content for cognitive functions, such as speech, reasoning, and decision-making, enabling the capacity to issue first-person reports. |
| Psychedelic drugs | Psychoactive drugs in which the primary effect is to produce profound changes in perception, mood, and cognitive processes, triggering non-ordinary states of consciousness. There are two major types: serotonergic (e.g., LSD, DMT), which activate the serotonin 2A receptor (5- ), and glutamatergic dissociatives (e.g., ketamine, PCP), in which action blocks the PCP site of NMDA glutamate receptors. |
| Resting state networks | Represent specific patterns of synchronous activity between brain regions in whole-brain recordings. They are consistently found in healthy subjects in fMRI data when no explicit task is being performed. |
| Stuart-Landau oscillators | Non-linear oscillating system near a Hopf bifurcation. |
| Top-down approach | Focuses on the use of subjective signatures of consciousness as guiding principles to analyze brain signals in order to narrow down the possible biophysical mechanisms compatible with those signatures. |
| Whole-brain computational models | An implementation of bottom-up approach. Defines a set of differential equations ruling the dynamics and interactions between simulated brain regions in order to reproduce observables from neuroimaging data. |
References
- LeDoux, J.E.; Michel, M.; Lau, H. A little history goes a long way toward understanding why we study consciousness the way we do today. Proc. Natl. Acad. Sci. USA 2020, 117, 6976–6984. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K. Consciousness: The last 50 years (and the next). Brain Neurosci. Adv. 2018, 2, 2398212818816019. [Google Scholar] [CrossRef] [PubMed]
- Overgaard, M. The status and future of consciousness research. Front. Psychol. 2017. [Google Scholar] [CrossRef] [PubMed]
- Crick, F.; Koch, C. Towards a neurobiological theory of consciousness. In Seminars in the Neurosciences; Salk Institute: La Jolla, California, USA, 1990. [Google Scholar]
- Crick, F.; Koch, C. A framework for consciousness. Nat. Neurosci. 2003. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, N.; Wilke, M.; Frässle, S.; Lamme, V.A. No-report paradigms: Extracting the true neural correlates of consciousness. Trends Cogn. Sci. 2015, 19, 757–770. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.A.; Dennett, D.C. Consciousness cannot be separated from function. Trends Cogn. Sci. 2011, 15, 358–364. [Google Scholar] [CrossRef]
- Koch, C.; Massimini, M.; Boly, M.; Tononi, G. Neural correlates of consciousness: Progress and problems. Nat. Rev. Neurosci. 2016. [Google Scholar] [CrossRef]
- Chalmers, D.J. What is a neural correlate of consciousness? In Neural Correlates of Consciousness: Empirical and Conceptual Questions; Metzinger, T., Ed.; MIT Press: Cambridge, MA, USA, 2000; pp. 17–39. [Google Scholar]
- Noë, A.; Thompson, E. Are there neural correlates of consciousness? J. Conscious. Stud. 2004, 11, 3–28. [Google Scholar]
- De Graaf, T.A.; Hsieh, P.J.; Sack, A.T. The ‘correlates’ in neural correlates of consciousness. Neurosci. Biobehav. Rev. 2012, 36, 191–197. [Google Scholar] [CrossRef]
- Seth, A. Models of consciousness. Scholarpedia 2007, 2, 1328. [Google Scholar] [CrossRef]
- Sergent, C.; Naccache, L. Imaging neural signatures of consciousness:‘What’,‘When’,‘Where’and ‘How’does it work? Arch. Ital. Biol. 2012, 150, 91–106. [Google Scholar] [PubMed]
- Stinson, C.; Sullivan, J. Mechanistic explanation in neuroscience. In The Routledge Handbook of Mechanisms and Mechanical Philosophy; Routledge Books, Taylor and Francis Group: Oxfordshire, UK, 2018; pp. 375–387. [Google Scholar]
- Deco, G.; Jirsa, V.K.; Robinson, P.A.; Breakspear, M.; Friston, K. The dynamic brain: From spiking neurons to neural masses and cortical fields. PLoS Comput. Biol. 2008, 4, e1000092. [Google Scholar] [CrossRef] [PubMed]
- Vaitl, D.; Birbaumer, N.; Gruzelier, J.; Jamieson, G.A.; Kotchoubey, B.; Kübler, A.; Lehmann, D.; Miltner, W.H.; Ott, U.; Pütz, P.; et al. Psychobiology of altered states of consciousness. Psychol. Bull. 2005, 131, 98. [Google Scholar] [CrossRef] [PubMed]
- Revonsuo, A.; Kallio, S.; Sikka, P. What is an altered state of consciousness? Philos. Psychol. 2009, 22, 187–204. [Google Scholar] [CrossRef]
- Overgaard, M.; Overgaard, R. Neural correlates of contents and levels of consciousness. Front. Psychol. 2010, 1, 164. [Google Scholar] [CrossRef] [PubMed]
- Tassi, P.; Muzet, A. Defining the states of consciousness. Neurosci. Biobehav. Rev. 2001, 25, 175–191. [Google Scholar] [CrossRef]
- Ludwig, A.M. Altered states of consciousness. Arch. Gen. Psychiatry 1966, 15, 225–234. [Google Scholar] [CrossRef]
- Tart, C. The basic nature of altered states of consciousness, a system approach. J. Transpers. Psychol. 1976, 8, 45–64. [Google Scholar]
- Bayne, T. Conscious states and conscious creatures: Explanation in the scientific study of consciousness. Philos. Perspect. 2007, 21, 1–22. [Google Scholar] [CrossRef]
- Michel, M. Consciousness science underdetermined: A short history of endless debates. Ergo Open Access J. Philos. 2019, 6, 2019–2020. [Google Scholar] [CrossRef]
- Reardon, S. Rival Theories Face off over Brain’s Source of Consciousness. Science 2019, 366, 293. [Google Scholar] [CrossRef]
- Freeman, W.J. Indirect biological measures of consciousness from field studies of brains as dynamical systems. Neural Netw. 2007, 20, 1021–1031. [Google Scholar] [CrossRef] [PubMed]
- Thompson, E.; Varela, F.J. Radical embodiment: Neural dynamics and consciousness. Trends Cogn. Sci. 2001, 5, 418–425. [Google Scholar] [CrossRef]
- Edelman, G.M.; Tononi, G. Reentry and the dynamic core: Neural correlates of conscious experience. In Neural Correlates of Consciousness: Empirical and Conceptual Questions; Metzinger, T., Ed.; MIT Press: Cambridge, MA, USA, 2000; pp. 139–151. [Google Scholar]
- Sporns, O.; Tononi, G.; Kötter, R. The human connectome: A structural description of the human brain. PLoS Comput. Biol. 2005, 1, e42. [Google Scholar] [CrossRef] [PubMed]
- Breakspear, M. Dynamic models of large-scale brain activity. Nat. Neurosci. 2017, 20, 340–352. [Google Scholar] [CrossRef] [PubMed]
- Ritter, P.; Schirner, M.; McIntosh, A.R.; Jirsa, V.K. The virtual brain integrates computational modeling and multimodal neuroimaging. Brain Connect. 2013, 3, 121–145. [Google Scholar] [CrossRef] [PubMed]
- Block, N. On a confusion about a function of consciousness. Behav. Brain Sci. 1995, 18, 227–247. [Google Scholar] [CrossRef]
- Tart, C.T. Altered States of Consciousness; Doubleday: New York, NY, USA, 1972. [Google Scholar]
- Natsoulas, T. Basic problems of consciousness. J. Personal. Soc. Psychol. 1981. [Google Scholar] [CrossRef]
- Deutsch, D. A Musical Paradox. Music. Percept. 1986. [Google Scholar] [CrossRef]
- Kunzendorf, R.G.; Wallace, B.E. Individual Differences in Conscious Experience; John Benjamins: Amsterdam, The Netherelands; Philadelphia, PA, USA, 2000. [Google Scholar]
- Pasricha, S.; Stevenson, I. Near-death experiences in india: A preliminary report. J. Nerv. Ment. Dis. 1986. [Google Scholar] [CrossRef]
- Cardeña, E.; Winkelman, M.J.E. Altering Consciousness: Multidisciplinary Perspectives; Praeger: Santa Barbara, CA, USA, 2011. [Google Scholar]
- Carhart-Harris, R.L.; Leech, R.; Hellyer, P.J.; Shanahan, M.; Feilding, A.; Tagliazucchi, E.; Chialvo, D.R.; Nutt, D. The entropic brain: A theory of conscious states informed by neuroimaging research with psychedelic drugs. Front. Hum. Neurosci. 2014, 8, 20. [Google Scholar] [CrossRef] [PubMed]
- Bayne, T.; Hohwy, J.; Owen, A.M. Are there levels of consciousness? Trends Cogn. Sci. 2016, 20, 405–413. [Google Scholar] [CrossRef] [PubMed]
- Bayne, T.; Carter, O. Dimensions of consciousness and the psychedelic state. Neurosci. Conscious. 2018, 2018, niy008. [Google Scholar] [CrossRef] [PubMed]
- Sitt, J.D.; King, J.R.; El Karoui, I.; Rohaut, B.; Faugeras, F.; Gramfort, A.; Cohen, L.; Sigman, M.; Dehaene, S.; Naccache, L. Large scale screening of neural signatures of consciousness in patients in a vegetative or minimally conscious state. Brain 2014, 137, 2258–2270. [Google Scholar] [CrossRef] [PubMed]
- Watt, D.F.; Pincus, D.I. Neural substrates of consciousness: Implications for clinical psychiatry. In Textbook of Biological Psychiatry; Panksepp, J., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2004; p. 75. [Google Scholar]
- Dennet, D. Consciousness Explained; Penguin Science, Theory & Psychology: London, UK, 1997. [Google Scholar]
- Dennett, D. Who’s on first? Heterophenomenology explained. J. Conscious. Stud. 2003, 10, 19–30. [Google Scholar]
- Block, N. Troubles with Functionalism; University of Minnesota Press: Minneapolis, MN, USA, 1978. [Google Scholar]
- Lutz, A.; Lachaux, J.P.; Martinerie, J.; Varela, F.J. Guiding the study of brain dynamics by using first-person data: Synchrony patterns correlate with ongoing conscious states during a simple visual task. Proc. Natl. Acad. Sci. USA 2002, 99, 1586–1591. [Google Scholar] [CrossRef]
- Shear, J.; Varela, F.J. The View from within: First-Person Approaches to the Study of Consciousness; Imprint Academic: Thorverton, UK, 1999. [Google Scholar]
- Chalmers, D.J. First-person methods in the science of consciousness. Conscious. Bull. 1999. Available online: http://consc.net/papers/firstperson.html (accessed on 1 September 2020).
- Frankish, K. Illusionism as a theory of consciousness. J. Conscious. Stud. 2016, 23, 11–39. [Google Scholar]
- Nida-Rümelin, M. The illusion of illusionism. J. Conscious. Stud. 2016, 23, 160–171. [Google Scholar]
- Seager, W. Could consciousness be an illusion? Mind Matter 2017, 15, 7–28. [Google Scholar]
- Baars, B.J. Global workspace theory of consciousness: Toward a cognitive neuroscience of human experience. Prog. Brain Res. 2005. [Google Scholar] [CrossRef]
- Dehaene, S.; Naccache, L. Towards a cognitive neuroscience of consciousness: Basic evidence and a workspace framework. Cognition 2001. [Google Scholar] [CrossRef]
- Mashour, G.A.; Roelfsema, P.; Changeux, J.P.; Dehaene, S. Conscious processing and the global neuronal workspace hypothesis. Neuron 2020, 105, 776–798. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G. An information integration theory of consciousness. BMC Neurosci. 2004. [Google Scholar] [CrossRef]
- Balduzzi, D.; Tononi, G. Integrated information in discrete dynamical systems: Motivation and theoretical framework. PLoS Comput. Biol. 2008. [Google Scholar] [CrossRef]
- Oizumi, M.; Albantakis, L.; Tononi, G. From the phenomenology to the mechanisms of consciousness: Integrated information theory 3.0. PLoS Comput. Biol. 2014, 10, e1003588. [Google Scholar] [CrossRef] [PubMed]
- Barrett, A.B.; Mediano, P.A. The Phi measure of integrated information is not well-defined for general physical systems. J. Conscious. Stud. 2019, 26, 11–20. [Google Scholar]
- Block, N. Perceptual consciousness overflows cognitive access. Trends Cogn. Sci. 2011, 15, 567–575. [Google Scholar] [CrossRef]
- Aru, J.; Bachmann, T.; Singer, W.; Melloni, L. Distilling the neural correlates of consciousness. Neurosci. Biobehav. Rev. 2012, 36, 737–746. [Google Scholar] [CrossRef]
- Lamme, V.A. Towards a true neural stance on consciousness. Trends Cogn. Sci. 2006, 10, 494–501. [Google Scholar] [CrossRef]
- Doerig, A.; Schurger, A.; Hess, K.; Herzog, M.H. The unfolding argument: Why IIT and other causal structure theories cannot explain consciousness. Conscious. Cogn. 2019, 72, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Tsuchiya, N.; Andrillon, T.; Haun, A. A reply to “the unfolding argument”: Beyond functionalism/behaviorism and towards a truer science of causal structural theories of consciousness. Conscious. Cogn. 2020, 79, 102877. [Google Scholar] [CrossRef] [PubMed]
- Seth, A.K.; Izhikevich, E.; Reeke, G.N.; Edelman, G.M. Theories and measures of consciousness: An extended framework. Proc. Natl. Acad. Sci. USA 2006, 103, 10799–10804. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, E. The signatures of conscious access and its phenomenology are consistent with large-scale brain communication at criticality. Conscious. Cogn. 2017, 55, 136–147. [Google Scholar] [CrossRef] [PubMed]
- Laureys, S.; Owen, A.M.; Schiff, N.D. Brain function in coma, vegetative state, and related disorders. Lancet Neurol. 2004. [Google Scholar] [CrossRef]
- Laureys, S.; Goldman, S.; Phillips, C.; Van Bogaert, P.; Aerts, J.; Luxen, A.; Franck, G.; Maquet, P. Impaired effective cortical connectivity in vegetative state: Preliminary investigation using PET. NeuroImage 1999. [Google Scholar] [CrossRef] [PubMed]
- Carhart-Harris, R.L. The entropic brain-revisited. Neuropharmacology 2018, 142, 167–178. [Google Scholar] [CrossRef]
- Lempel, A.; Ziv, J. On the complexity of finite sequences. IEEE Trans. Inf. Theory 1976. [Google Scholar] [CrossRef]
- Ziv, J. Coding theorems for individual sequences. IEEE Trans. Inf. Theory 1978. [Google Scholar] [CrossRef]
- Zhang, X.S.; Roy, R.J.; Jensen, E.W. EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans. Biomed. Eng. 2001, 48, 1424–1433. [Google Scholar] [CrossRef]
- Nenadovic, V.; Perez Velazquez, J.L.; Hutchison, J.S. Phase synchronization in electroencephalographic recordings prognosticates outcome in paediatric coma. PLoS ONE 2014. [Google Scholar] [CrossRef] [PubMed]
- Schartner, M.M.; Pigorini, A.; Gibbs, S.A.; Arnulfo, G.; Sarasso, S.; Barnett, L.; Nobili, L.; Massimini, M.; Seth, A.K.; Barrett, A.B. Global and local complexity of intracranial EEG decreases during NREM sleep. Neurosci. Conscious. 2017, 2017, niw022. [Google Scholar] [CrossRef] [PubMed]
- Dominguez, L.G.; Wennberg, R.A.; Gaetz, W.; Cheyne, D.; Snead, O.C.; Perez Velazquez, J.L. Enhanced synchrony in epileptiform activity? Local versus distant phase synchronization in generalized seizures. J. Neurosci. 2005. [Google Scholar] [CrossRef] [PubMed]
- Vivot, R.M.; Pallavicini, C.; Zamberlan, F.; Vigo, D.; Tagliazucchi, E. Meditation increases the entropy of brain oscillatory activity. Neuroscience 2020. [Google Scholar] [CrossRef]
- Schartner, M.M.; Carhart-Harris, R.L.; Barrett, A.B.; Seth, A.K.; Muthukumaraswamy, S.D. Increased spontaneous MEG signal diversity for psychoactive doses of ketamine, LSD and psilocybin. Sci. Rep. 2017, 7, 46421. [Google Scholar] [CrossRef] [PubMed]
- Timmermann, C.; Roseman, L.; Schartner, M.; Milliere, R.; Williams, L.T.; Erritzoe, D.; Muthukumaraswamy, S.; Ashton, M.; Bendrioua, A.; Kaur, O.; et al. Neural correlates of the DMT experience assessed with multivariate EEG. Sci. Rep. 2019, 9, 1–13. [Google Scholar] [CrossRef]
- Stam, C.J. Nonlinear dynamical analysis of EEG and MEG: Review of an emerging field. Clin. Neurophysiol. 2005, 116, 2266–2301. [Google Scholar] [CrossRef]
- Peng, H.; Hu, B.; Zheng, F.; Fan, D.; Zhao, W.; Chen, X.; Yang, Y.; Cai, Q. A method of identifying chronic stress by EEG. Pers. Ubiquitous Comput. 2013, 17, 1341–1347. [Google Scholar] [CrossRef]
- Xu, R.; Zhang, C.; He, F.; Zhao, X.; Qi, H.; Zhou, P.; Zhang, L.; Ming, D. How physical activities affect mental fatigue based on EEG energy, connectivity, and complexity. Front. Neurol. 2018, 9, 915. [Google Scholar] [CrossRef]
- Dolan, D.; Jensen, H.J.; Mediano, P.; Molina-Solana, M.; Rajpal, H.; Rosas, F.; Sloboda, J.A. The improvisational state of mind: A multidisciplinary study of an improvisatory approach to classical music repertoire performance. Front. Psychol. 2018, 9, 1341. [Google Scholar] [CrossRef]
- Casali, A.G.; Gosseries, O.; Rosanova, M.; Boly, M.; Sarasso, S.; Casali, K.R.; Casarotto, S.; Bruno, M.A.; Laureys, S.; Tononi, G.; et al. A theoretically based index of consciousness independent of sensory processing and behavior. Sci. Transl. Med. 2013. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G. Consciousness as integrated information: A provisional manifesto. Biol. Bull. 2008. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994. [Google Scholar] [CrossRef] [PubMed]
- Mediano, P.A.; Rosas, F.; Carhart-Harris, R.L.; Seth, A.K.; Barrett, A.B. Beyond integrated information: A taxonomy of information dynamics phenomena. arXiv 2019, arXiv:1909.02297. [Google Scholar]
- Mediano, P.A.; Seth, A.K.; Barrett, A.B. Measuring integrated information: Comparison of candidate measures in theory and simulation. Entropy 2019. [Google Scholar] [CrossRef]
- Mindt, G. The problem with the ’information’ in integrated information theory. J. Conscious. Stud. 2017, 24, 130–154. [Google Scholar]
- Morch, H.H. Is consciousness intrinsic?: A problem for the integrated information theory. J. Conscious. Stud. 2019, 26, 133–162. [Google Scholar]
- Bayne, T. On the axiomatic foundations of the integrated information theory of consciousness. Neurosci. Conscious. 2018, 2018, niy007. [Google Scholar] [CrossRef]
- Krohn, S.; Ostwald, D. Computing integrated information. Neurosci. Conscious. 2017. [Google Scholar] [CrossRef]
- Kitazono, J.; Kanai, R.; Oizumi, M. Efficient algorithms for searching the minimum information partition in integrated information theory. Entropy 2018, 20, 173. [Google Scholar] [CrossRef]
- Toker, D.; Sommer, F.T. Information integration in large brain networks. PLoS Comput. Biol. 2019, 15, e1006807. [Google Scholar] [CrossRef] [PubMed]
- Mediano, P. Integrated Information in Complex Neural Systems. PhD Thesis, Imperial College London, London, UK, 2020. [Google Scholar]
- Chang, J.Y.; Pigorini, A.; Massimini, M.; Tononi, G.; Nobili, L.; Van Veen, B.D. Multivariate autoregressive models with exogenous inputs for intracerebral responses to direct electrical stimulation of the human brain. Front. Hum. Neurosci. 2012. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Hudetz, A.G.; Lee, J.; Mashour, G.A.; Lee, U.C.; Avidan, M.S.; Bel-Bahar, T.; Blain-Moraes, S.; Golmirzaie, G.; Janke, E.; et al. Estimating the integrated information measure Phi from high-density electroencephalography during states of consciousness in humans. Front. Hum. Neurosci. 2018. [Google Scholar] [CrossRef] [PubMed]
- Mediano, P.A.; Farah, J.C.; Shanahan, M. Integrated information and metastability in systems of coupled oscillators. arXiv 2016, arXiv:1606.08313. [Google Scholar]
- Gerstner, W.; Sprekeler, H.; Deco, G. Theory and simulation in neuroscience. Science 2012, 338, 60–65. [Google Scholar] [CrossRef]
- Ramsey, J.D.; Hanson, S.J.; Hanson, C.; Halchenko, Y.O.; Poldrack, R.A.; Glymour, C. Six problems for causal inference from fMRI. NeuroImage 2010, 49, 1545–1558. [Google Scholar] [CrossRef] [PubMed]
- Kriegeskorte, N.; Douglas, P.K. Cognitive computational neuroscience. Nat. Neurosci. 2018, 21, 1148–1160. [Google Scholar] [CrossRef] [PubMed]
- Kriegeskorte, N.; Mur, M.; Bandettini, P.A. Representational similarity analysis-connecting the branches of systems neuroscience. Front. Syst. Neurosci. 2008, 2, 4. [Google Scholar] [CrossRef]
- Kriegeskorte, N.; Kievit, R.A. Representational geometry: Integrating cognition, computation, and the brain. Trends Cogn. Sci. 2013, 17, 401–412. [Google Scholar] [CrossRef] [PubMed]
- Friston, K.J.; Harrison, L.; Penny, W. Dynamic causal modelling. Neuroimage 2003, 19, 1273–1302. [Google Scholar] [CrossRef]
- Schirner, M.; McIntosh, A.R.; Jirsa, V.; Deco, G.; Ritter, P. Inferring multi-scale neural mechanisms with brain network modelling. Elife 2018, 7, e28927. [Google Scholar] [CrossRef] [PubMed]
- Markram, H. The blue brain project. Nat. Rev. Neurosci. 2006, 7, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Hagmann, P.; Cammoun, L.; Gigandet, X.; Meuli, R.; Honey, C.J.; Van Wedeen, J.; Sporns, O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008. [Google Scholar] [CrossRef] [PubMed]
- Tzourio-Mazoyer, N.; Landeau, B.; Papathanassiou, D.; Crivello, F.; Etard, O.; Delcroix, N.; Mazoyer, B.; Joliot, M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. NeuroImage 2002. [Google Scholar] [CrossRef] [PubMed]
- Tagliazucchi, E.; Chialvo, D.R.; Siniatchkin, M.; Amico, E.; Brichant, J.F.; Bonhomme, V.; Noirhomme, Q.; Laufs, H.; Laureys, S. Large-scale signatures of unconsciousness are consistent with a departure from critical dynamics. J. R. Soc. Interface 2016. [Google Scholar] [CrossRef] [PubMed]
- Haimovici, A.; Tagliazucchi, E.; Balenzuela, P.; Chialvo, D.R. Brain organization into resting state networks emerges at criticality on a model of the human connectome. Phys. Rev. Lett. 2013. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Jirsa, V.K. Ongoing cortical activity at rest: Criticality, multistability, and ghost attractors. J. Neurosci. 2012. [Google Scholar] [CrossRef] [PubMed]
- Marinazzo, D.; Pellicoro, M.; Wu, G.; Angelini, L.; Cortés, J.M.; Stramaglia, S. Information transfer and criticality in the Ising model on the human connectome. PLoS ONE 2014, 9, e93616. [Google Scholar] [CrossRef]
- Abeyasinghe, P.M.; Aiello, M.; Nichols, E.S.; Cavaliere, C.; Fiorenza, S.; Masotta, O.; Borrelli, P.; Owen, A.M.; Estraneo, A.; Soddu, A. Consciousness and the Dimensionality of DOC Patients via the Generalized Ising Model. J. Clin. Med. 2020, 9, 1342. [Google Scholar] [CrossRef]
- Messé, A.; Rudrauf, D.; Benali, H.; Marrelec, G. Relating structure and function in the human brain: Relative contributions of anatomy, stationary dynamics, and non-stationarities. PLoS Comput. Biol. 2014. [Google Scholar] [CrossRef]
- Saggio, M.L.; Ritter, P.; Jirsa, V.K. Analytical operations relate structural and functional connectivity in the brain. PLoS ONE 2016. [Google Scholar] [CrossRef] [PubMed]
- Cabral, J.; Kringelbach, M.L.; Deco, G. Exploring the network dynamics underlying brain activity during rest. Prog. Neurobiol. 2014. [Google Scholar] [CrossRef] [PubMed]
- Jobst, B.M.; Hindriks, R.; Laufs, H.; Tagliazucchi, E.; Hahn, G.; Ponce-Alvarez, A.; Stevner, A.B.; Kringelbach, M.L.; Deco, G. Increased stability and breakdown of brain effective connectivity during slow-wave sleep: Mechanistic insights from whole-brain computational modelling. Sci. Rep. 2017. [Google Scholar] [CrossRef] [PubMed]
- Robinson, P.A.; Roy, N. Neural field theory of nonlinear wave-wave and wave-neuron processes. Phys. Rev. E 2015. [Google Scholar] [CrossRef] [PubMed]
- Babaie Janvier, T.; Robinson, P.A. Neural field theory of corticothalamic prediction with control systems analysis. Front. Hum. Neurosci. 2018. [Google Scholar] [CrossRef] [PubMed]
- Breakspear, M.; Terry, J.R.; Friston, K.J. Modulation of excitatory synaptic coupling facilitates synchronization and complex dynamics in a biophysical model of neuronal dynamics. Netw. Comput. Neural Syst. 2003. [Google Scholar] [CrossRef]
- Honey, C.J.; Sporns, O.; Cammoun, L.; Gigandet, X.; Thiran, J.P.; Meuli, R.; Hagmann, P. Predicting human resting-state functional connectivity from structural connectivity. Proc. Natl. Acad. Sci. USA 2009. [Google Scholar] [CrossRef]
- Deco, G.; Ponce-Alvarez, A.; Hagmann, P.; Romani, G.L.; Mantini, D.; Corbetta, M. How local excitation-inhibition ratio impacts the whole brain dynamics. J. Neurosci. 2014. [Google Scholar] [CrossRef]
- Deco, G.; Cruzat, J.; Cabral, J.; Knudsen, G.M.; Carhart-Harris, R.L.; Whybrow, P.C.; Logothetis, N.K.; Kringelbach, M.L. Whole-brain multimodal neuroimaging model using serotonin receptor maps explains non-linear functional effects of LSD. Curr. Biol. 2018. [Google Scholar] [CrossRef]
- Kringelbach, M.L.; Cruzat, J.; Cabral, J.; Knudsen, G.M.; Carhart-Harris, R.; Whybrow, P.C.; Logothetis, N.K.; Deco, G. Dynamic coupling of whole-brain neuronal and neurotransmitter systems. Proc. Natl. Acad. Sci. USA 2020. [Google Scholar] [CrossRef]
- Deco, G.; Cruzat, J.; Cabral, J.; Tagliazucchi, E.; Laufs, H.; Logothetis, N.K.; Kringelbach, M.L. Awakening: Predicting external stimulation to force transitions between different brain states. Proc. Natl. Acad. Sci. USA 2019. [Google Scholar] [CrossRef] [PubMed]
- Ipiña, I.P.; Kehoe, P.D.; Kringelbach, M.; Laufs, H.; Ibañez, A.; Deco, G.; Perl, Y.S.; Tagliazucchi, E. Modeling regional changes in dynamic stability during sleep and wakefulness. NeuroImage 2020. [Google Scholar] [CrossRef] [PubMed]
- Renart, A.; Brunel, N.; Wang, X.J. Mean-field theory of irregularly spiking neuronal populations and working memory in recurrent cortical networks. In Computational Neuroscience: A Comprehensive Approach; Feng, J., Ed.; CRC: Boca Raton, FL, USA, 2004; pp. 431–490. [Google Scholar]
- Friston, K.J.; Mechelli, A.; Turner, R.; Price, C.J. Nonlinear responses in fMRI: The Balloon model, Volterra kernels, and other hemodynamics. NeuroImage 2000, 12, 466–477. [Google Scholar] [CrossRef] [PubMed]
- Deco, G.; Cabral, J.; Saenger, V.M.; Boly, M.; Tagliazucchi, E.; Laufs, H.; Van Someren, E.; Jobst, B.; Stevner, A.; Kringelbach, M.L. Perturbation of whole-brain dynamics in silico reveals mechanistic differences between brain states. NeuroImage 2018. [Google Scholar] [CrossRef] [PubMed]
- Marsden, J.E.; McCracken, M. The Hopf Bifurcation and Its Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 19. [Google Scholar]
- Deco, G.; Kringelbach, M.L.; Jirsa, V.K.; Ritter, P. The dynamics of resting fluctuations in the brain: Metastability and its dynamical cortical core. Sci. Rep. 2017. [Google Scholar] [CrossRef] [PubMed]
- Shanahan, M. Metastable chimera states in community-structured oscillator networks. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 013108. [Google Scholar] [CrossRef]
- Dehaene, S.; Changeux, J.P. Experimental and theoretical approaches to conscious processing. Neuron 2011. [Google Scholar] [CrossRef]
- Tononi, G.; Edelman, G.M. Consciousness and complexity. Science 1998, 282, 1846–1851. [Google Scholar] [CrossRef]
- Bocaccio, H.; Pallavicini, C.; Castro, M.N.; Sánchez, S.M.; De Pino, G.; Laufs, H.; Villarreal, M.F.; Tagliazucchi, E. The avalanche-like behaviour of large-scale haemodynamic activity from wakefulness to deep sleep. J. R. Soc. Interface 2019. [Google Scholar] [CrossRef]
- Solovey, G.; Alonso, L.M.; Yanagawa, T.; Fujii, N.; Magnasco, M.O.; Cecchi, G.A.; Proekt, A. Loss of consciousness is associated with stabilization of cortical activity. J. Neurosci. 2015, 35, 10866–10877. [Google Scholar] [CrossRef]
- Alonso, L.M.; Proekt, A.; Schwartz, T.H.; Pryor, K.O.; Cecchi, G.A.; Magnasco, M.O. Dynamical criticality during induction of anesthesia in human ECoG recordings. Front. Neural Circuits 2014, 8, 20. [Google Scholar] [CrossRef] [PubMed]
- Cavanna, F.; Vilas, M.G.; Palmucci, M.; Tagliazucchi, E. Dynamic functional connectivity and brain metastability during altered states of consciousness. Neuroimage 2018, 180, 383–395. [Google Scholar] [CrossRef]
- Chialvo, D.R. Emergent complex neural dynamics: The brain at the edge. Nat. Phys. 2010, 6, 744–750. [Google Scholar] [CrossRef]
- Damoiseaux, J.S.; Rombouts, S.; Barkhof, F.; Scheltens, P.; Stam, C.J.; Smith, S.M.; Beckmann, C.F. Consistent resting-state networks across healthy subjects. Proc. Natl. Acad. Sci. USA 2006, 103, 13848–13853. [Google Scholar] [CrossRef] [PubMed]
- Perl, Y.S.; Pallavicini, C.; Ipina, I.P.; Demertzi, A.; Bonhomme, V.; Martial, C.; Panda, R.; Annen, J.; Ibanez, A.; Kringelbach, M.; et al. Perturbations in dynamical models of whole-brain activity dissociate between the level and stability of consciousness. bioRxiv 2020. [Google Scholar] [CrossRef]
- Smith, S.M.; Vidaurre, D.; Beckmann, C.F.; Glasser, M.F.; Jenkinson, M.; Miller, K.L.; Nichols, T.E.; Robinson, E.C.; Salimi-Khorshidi, G.; Woolrich, M.W.; et al. Functional connectomics from resting-state fMRI. Trends Cogn. Sci. 2013, 17, 666–682. [Google Scholar] [CrossRef]
- Cavanna, A.E.; Trimble, M.R. The precuneus: A review of its functional anatomy and behavioural correlates. Brain 2006, 129, 564–583. [Google Scholar] [CrossRef]
- Andersen, L.M.; Pedersen, M.N.; Sandberg, K.; Overgaard, M. Occipital MEG activity in the early time range (<300 ms) predicts graded changes in perceptual consciousness. Cereb. Cortex 2016. [Google Scholar] [CrossRef]
- Utevsky, A.V.; Smith, D.V.; Huettel, S.A. Precuneus is a functional core of the default-mode network. J. Neurosci. 2014. [Google Scholar] [CrossRef]
- Thom, R. Prédire n’est pas Expliquer; Eshel: Paris, France, 1997. [Google Scholar]
- Fernández-Espejo, D.; Bekinschtein, T.; Monti, M.M.; Pickard, J.D.; Junque, C.; Coleman, M.R.; Owen, A.M. Diffusion weighted imaging distinguishes the vegetative state from the minimally conscious state. Neuroimage 2011, 54, 103–112. [Google Scholar] [CrossRef]
- Kubicki, M.; Park, H.; Westin, C.F.; Nestor, P.G.; Mulkern, R.V.; Maier, S.E.; Niznikiewicz, M.; Connor, E.E.; Levitt, J.J.; Frumin, M.; et al. DTI and MTR abnormalities in schizophrenia: Analysis of white matter integrity. Neuroimage 2005, 26, 1109–1118. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, M.H.; Hacker, C.D.; Siegel, J.S.; Griffa, A.; Hagmann, P.; Deco, G.; Corbetta, M. Decreased integration and information capacity in stroke measured by whole brain models of resting state activity. Brain 2017, 140, 1068–1085. [Google Scholar] [CrossRef] [PubMed]
- Haimovici, A.; Balenzuela, P.; Tagliazucchi, E. Dynamical signatures of structural connectivity damage to a model of the brain posed at criticality. Brain Connect. 2016, 6, 759–771. [Google Scholar] [CrossRef] [PubMed]
- Beuter, A.; Balossier, A.; Vassal, F.; Hemm, S.; Volpert, V. Cortical stimulation in aphasia following ischemic stroke: Toward model-guided electrical neuromodulation. Biol. Cybern. 2020, 114, 5–21. [Google Scholar] [CrossRef] [PubMed]
- Váša, F.; Shanahan, M.; Hellyer, P.J.; Scott, G.; Cabral, J.; Leech, R. Effects of lesions on synchrony and metastability in cortical networks. Neuroimage 2015, 118, 456–467. [Google Scholar] [CrossRef] [PubMed]
- Hellyer, P.J.; Scott, G.; Shanahan, M.; Sharp, D.J.; Leech, R. Cognitive flexibility through metastable neural dynamics is disrupted by damage to the structural connectome. J. Neurosci. 2015, 35, 9050–9063. [Google Scholar] [CrossRef]
- Sinha, N.; Dauwels, J.; Kaiser, M.; Cash, S.S.; Brandon Westover, M.; Wang, Y.; Taylor, P.N. Predicting neurosurgical outcomes in focal epilepsy patients using computational modelling. Brain 2017, 140, 319–332. [Google Scholar] [CrossRef]
- Richardson, M.P. Large scale brain models of epilepsy: Dynamics meets connectomics. J. Neurol. Neurosurg. Psychiatry 2012, 83, 1238–1248. [Google Scholar] [CrossRef]
- Aerts, H.; Schirner, M.; Dhollander, T.; Jeurissen, B.; Achten, E.; Van Roost, D.; Ritter, P.; Marinazzo, D. Modeling brain dynamics after tumor resection using The Virtual Brain. NeuroImage 2020, 213, 116738. [Google Scholar] [CrossRef]
- Bansal, K.; Nakuci, J.; Muldoon, S.F. Personalized brain network models for assessing structure–function relationships. Curr. Opin. Neurobiol. 2018, 52, 42–47. [Google Scholar] [CrossRef]
- Jirsa, V.K.; Proix, T.; Perdikis, D.; Woodman, M.M.; Wang, H.; Gonzalez-Martinez, J.; Bernard, C.; Bénar, C.; Guye, M.; Chauvel, P.; et al. The virtual epileptic patient: Individualized whole-brain models of epilepsy spread. Neuroimage 2017, 145, 377–388. [Google Scholar] [CrossRef] [PubMed]
- Nichols, D.E. Psychedelics. Pharmacol. Rev. 2016, 68, 264–355. [Google Scholar] [CrossRef] [PubMed]
- Howes, O.D.; Kapur, S. The dopamine hypothesis of schizophrenia: Version III—The final common pathway. Schizophr. Bull. 2009, 35, 549–562. [Google Scholar] [CrossRef] [PubMed]
- Peduto, V.; Concas, A.; Santoro, G.; Biggio, G.; Gessa, G. Biochemical and electrophysiologic evidence that propofol enhances GABAergic transmission in the rat brain. Anesthesiol. J. Am. Soc. Anesthesiol. 1991, 75, 1000–1009. [Google Scholar] [CrossRef]
- Jouvet, M. The role of monoamines and acetylcholine-containing neurons in the regulation of the sleep-waking cycle. In Neurophysiology and Neurochemistry of Sleep and Wakefulness; Springer: Berlin/Heidelberg, Germany, 1972; pp. 166–307. [Google Scholar]
- Gao, R.; Peterson, E.J.; Voytek, B. Inferring synaptic excitation/inhibition balance from field potentials. Neuroimage 2017, 158, 70–78. [Google Scholar] [CrossRef]
- El Houssaini, K.; Bernard, C.; Jirsa, V.K. The Epileptor model: A systematic mathematical analysis linked to the dynamics of seizures, refractory status epilepticus and depolarization block. Eneuro 2020, 7. [Google Scholar] [CrossRef]
- Hermann, B.; Raimondo, F.; Hirsch, L.; Huang, Y.; Denis-Valente, M.; Pérez, P.; Engemann, D.; Faugeras, F.; Weiss, N.; Demeret, S.; et al. Combined behavioral and electrophysiological evidence for a direct cortical effect of prefrontal tDCS on disorders of consciousness. Sci. Rep. 2020, 10, 1–16. [Google Scholar] [CrossRef]
- An, S.; Bartolomei, F.; Guye, M.; Jirsa, V. Optimization of surgical intervention outside the epileptogenic zone in the Virtual Epileptic Patient (VEP). PLoS Comput. Biol. 2019, 15, e1007051. [Google Scholar] [CrossRef] [PubMed]
- Perl, Y.S.; Pallacivini, C.; Ipina, I.P.; Kringelbach, M.L.; Deco, G.; Laufs, H.; Tagliazucchi, E. Data augmentation based on dynamical systems for the classification of brain states. bioRxiv 2020. [Google Scholar] [CrossRef]
- Perl, Y.S.; Boccacio, H.; Pérez-Ipiña, I.; Zamberlán, F.; Laufs, H.; Kringelbach, M.; Deco, G.; Tagliazucchi, E. Generative embeddings of brain collective dynamics using variational autoencoders. arXiv 2020, arXiv:2007.01378. [Google Scholar]
- Herzog, R.; Mediano, P.A.; Rosas, F.E.; Carhart-Harris, R.; Sanz, Y.; Tagliazucchi, E.; Cofré, R. A mechanistic model of the neural entropy increase elicited by psychedelic drugs. bioRxiv 2020. [Google Scholar] [CrossRef]
- Kraehenmann, R.; Pokorny, D.; Vollenweider, L.; Preller, K.; Pokorny, T.; Seifritz, E.; Vollenweider, F. Dreamlike effects of LSD on waking imagery in humans depend on serotonin 2A receptor activation. Psychopharmacology 2017, 234, 2031–2046. [Google Scholar] [CrossRef] [PubMed]
- Preller, K.H.; Burt, J.B.; Ji, J.L.; Schleifer, C.H.; Adkinson, B.D.; Stämpfli, P.; Seifritz, E.; Repovs, G.; Krystal, J.H.; Murray, J.D.; et al. Changes in global and thalamic brain connectivity in LSD-induced altered states of consciousness are attributable to the 5-HT2A receptor. eLife 2018, 7, e35082. [Google Scholar] [CrossRef] [PubMed]
- Searle, J.R. Biological naturalism. In Blackwell Companion Conscious; Wiley: Hoboken, NJ, USA, 2007; Chapter 23; pp. 325–334. [Google Scholar]
- Stuart, H. Quantum computation in brain microtubules? The Penrose–Hameroff ‘Orch OR ‘model of consciousness. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 356, 1869–1896. [Google Scholar] [CrossRef]
- Murdock, J. Normal forms. Scholarpedia 2006, 1, 1902. [Google Scholar] [CrossRef]
- Berry, R.B.; Budhiraja, R.; Gottlieb, D.J.; Gozal, D.; Iber, C.; Kapur, V.K.; Marcus, C.L.; Mehra, R.; Parthasarathy, S.; Quan, S.F.; et al. Rules for scoring respiratory events in sleep: Update of the 2007 AASM manual for the scoring of sleep and associated events: Deliberations of the sleep apnea definitions task force of the American Academy of Sleep Medicine. J. Clin. Sleep Med. 2012, 8, 597–619. [Google Scholar] [CrossRef]
- Rosow, C.; Manberg, P.J. Bispectral index monitoring. Anesthesiol. Clin. N. Am. 2001, 19, 947–966. [Google Scholar] [CrossRef]
- Schiff, N.D.; Nauvel, T.; Victor, J.D. Large-scale brain dynamics in disorders of consciousness. Curr. Opin. Neurobiol. 2014, 25, 7–14. [Google Scholar] [CrossRef]
- Schartner, M.; Seth, A.; Noirhomme, Q.; Boly, M.; Bruno, M.A.; Laureys, S.; Barrett, A. Complexity of multi-dimensional spontaneous EEG decreases during propofol induced general anaesthesia. PLoS ONE 2015. [Google Scholar] [CrossRef]
- Batterman, R.W. Multiple realizability and universality. Br. J. Philos. Sci. 2000, 51, 115–145. [Google Scholar] [CrossRef]
- Northoff, G.; Wainio-Theberge, S.; Evers, K. Is temporo-spatial dynamics the “common currency” of brain and mind? In Quest of “Spatiotemporal Neuroscience”. Phys. Life Rev. 2019, 33, 34–54. [Google Scholar] [CrossRef] [PubMed]
- Guckenheimer, J.; Kuznetsov, Y.A. Bogdanov-Takens bifurcation. Scholarpedia 2007, 2, 1854. [Google Scholar] [CrossRef]
- Mindlin, G. Dinámica no Lineal; Universidad Nacional de Quilmes: Bernal, Argentina, 2017. [Google Scholar]
- Rolls, E.T.; Deco, G. The Noisy Brain: Stochastic Dynamics as a Principle of Brain Function; Oxford University Press: Oxford, UK, 2010; Volume 34. [Google Scholar]
- Chizhov, A.V.; Zefirov, A.V.; Amakhin, D.V.; Smirnova, E.Y.; Zaitsev, A.V. Minimal model of interictal and ictal discharges “Epileptor-2”. PLoS Comput. Biol. 2018, 14, e1006186. [Google Scholar] [CrossRef] [PubMed]
- Letellier, C.; Rossler, O.E. Rossler attractor. Scholarpedia 2006, 1, 1721. [Google Scholar] [CrossRef]
- Shulgin, A.; Shulgin, A. PiHKAL. In A Chemical Love Story; Transform Press: Berkeley, CA, USA, 1992. [Google Scholar]
- Shulgin, A.; Shulgin, A. TIHKAL the Continuation; Transform Press: Berkeley, CA, USA, 1997. [Google Scholar]
- Velmans, M. Towards a Deeper Understanding of Consciousness. Selected Works of Max Velmans; Routledge: Abingdon, UK, 2016. [Google Scholar]
- Kelly, E.F.; Kelly, E.W.; Crabtree, A.; Gauld, A.; Grosso, M. Irreducible Mind: Toward a Psychology for the 21st Century; Rowman and Littlefield: Lanham, MD, USA, 2007. [Google Scholar]
- Miller, G. Beyond DSM: Seeking a brain-based classification of mental illness. Science 2010, 327, 1437. [Google Scholar] [CrossRef]
- Deco, G.; Kringelbach, M.L. Great expectations: Using whole-brain computational connectomics for understanding neuropsychiatric disorders. Neuron 2014, 84, 892–905. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D.; Demirtaş, M.; Anticevic, A. Biophysical modeling of large-scale brain dynamics and applications for computational psychiatry. Biol. Psychiatry Cogn. Neurosci. Neuroimaging 2018, 3, 777–787. [Google Scholar] [CrossRef] [PubMed]

| Category | Examples | Reversibility |
|---|---|---|
| Natural or endogenous | deep sleep dreaming | transitory transitory |
| Pharmacological | general anaesthesia psychedelic state | transitory transitory |
| Induced by other means | meditation hypnosis | transitory transitory |
| Pathological | epilepsy psychotic episodes disorders of consciousness brain death | transitory transitory transitory or permanent permanent |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cofré, R.; Herzog, R.; Mediano, P.A.M.; Piccinini, J.; Rosas, F.E.; Sanz Perl, Y.; Tagliazucchi, E. Whole-Brain Models to Explore Altered States of Consciousness from the Bottom Up. Brain Sci. 2020, 10, 626. https://doi.org/10.3390/brainsci10090626
Cofré R, Herzog R, Mediano PAM, Piccinini J, Rosas FE, Sanz Perl Y, Tagliazucchi E. Whole-Brain Models to Explore Altered States of Consciousness from the Bottom Up. Brain Sciences. 2020; 10(9):626. https://doi.org/10.3390/brainsci10090626
Chicago/Turabian StyleCofré, Rodrigo, Rubén Herzog, Pedro A.M. Mediano, Juan Piccinini, Fernando E. Rosas, Yonatan Sanz Perl, and Enzo Tagliazucchi. 2020. "Whole-Brain Models to Explore Altered States of Consciousness from the Bottom Up" Brain Sciences 10, no. 9: 626. https://doi.org/10.3390/brainsci10090626
APA StyleCofré, R., Herzog, R., Mediano, P. A. M., Piccinini, J., Rosas, F. E., Sanz Perl, Y., & Tagliazucchi, E. (2020). Whole-Brain Models to Explore Altered States of Consciousness from the Bottom Up. Brain Sciences, 10(9), 626. https://doi.org/10.3390/brainsci10090626






