Theoretical Framework for Characterizing Strain-Dependent Dynamic Soil Properties

Abstract

This paper proposes a theoretical framework for the characterization of the strain-dependent dynamic properties of soils. The analysis begins with an analytical constitutive model for soils under steady-state cyclic loading. The model describes the dominant soil characteristics, i.e., the hysteresis and nonlinearity with an intrinsic material property α, which physically represents the degree of the hysteresis nonlinearity in a medium. Explicit formulas for the backbone curve, tangent shear modulus, secant shear modulus, and damping ratio as a function of shear strain are derived directly from the constitutive model. A procedure is then developed to determine the parameter α in which the derived damping ratio equation is fitted to damping ratio data measured from the resonant column test (RCT). Clay and sand under three different levels of confinement stress are considered in the numerical evaluation. The capability of the proposed theoretical framework in predicting strain-dependent soil properties and responses is demonstrated.

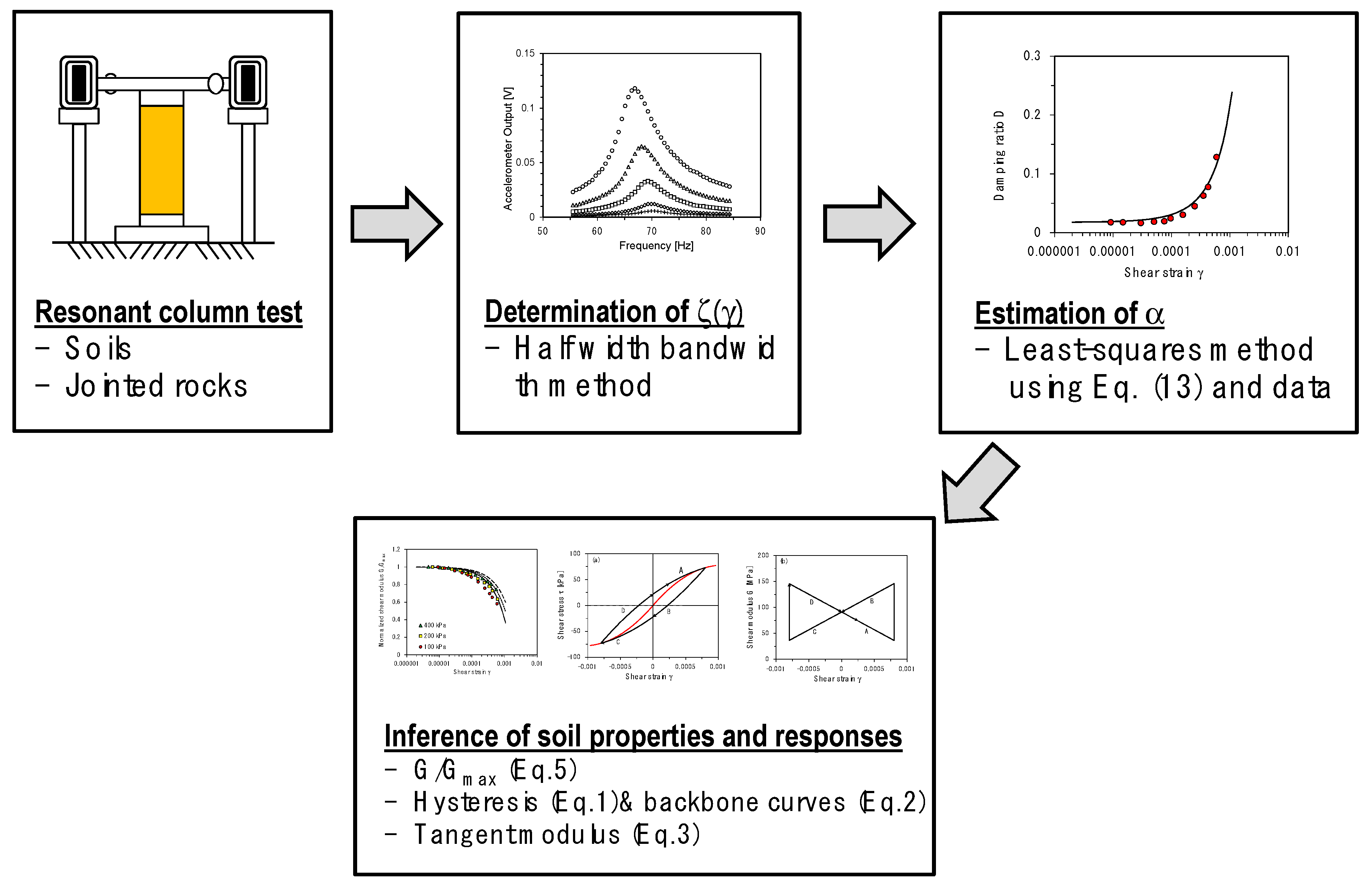
1. Introduction

When the ground motion is severely affected by shear waves propagating vertically from the underlying rock, the soil deposits may undergo cyclic shear deformations. The dynamic properties of soils, including the strain-dependent shear modulus and damping ratio, are the basic input parameters in the analysis of the seismic ground response and site amplification [1]. The soil properties exhibit strong nonlinear responses; the shear modulus decreases, and the damping capacity increases with the amplitude of shear strain. The increasing damping capacity is directly associated with the hysteresis. These macroscopic, hysteretic, nonlinear behaviors of soils are the consequences of complex physics at microscales including inter-grain contact, friction and adhesion, and rearrangement of grain structures under loading–unloading.

Numerous stress-strain models have been proposed for the analysis of dynamic soil responses [2,3]. Classical models in terms of empirical fitting parameters are often used for their simplicity [4,5,6,7,8]. More sophisticated models for cyclic loading require more fitting parameters to better describe the soil hysteresis loops. The hysteresis models have been proposed to capture a closed hysteresis loop characterized by imposed shear strain amplitude, and state of stress [9,10,11,12,13,14,15,16,17]. While these models have been successful in expressing the complex strain-dependency for certain soil types under the steady-state cyclic loading, they still have lack of robustness and universality due to physical uncertainty of the input parameters and their uses are quite limited to other soils. Therefore, a simple but robust model is needed to describe inherently hysteretic nonlinear nature of soils.

The present study is to develop a new theoretical framework for the purpose of characterizing the strain-dependent dynamic shear modulus and damping ratio of soils. This paper extends the previous study by the author of [18] to (1) derive the explicit formula with the second model order; (2) to test damping ratio data obtained from resonant column test (RCT); and (3) to explore the effect of confinement stress on the hysteretic parameters. In particular, the modified procedure of conventional data interpretation is proposed to accurately characterize the hysteretic soil properties and responses from resonant column.

2. Explicit Formulas to Describe Nonlinear-Hysteretic Response

2.1. Constitutive Model: Stress-Strain Relation

Considerable progress in modeling such hysteretic nonlinear behaviors of granular materials has been made in the geophysics community. The constitutive models are derived within the mathematical framework of the Preisach-Mayergoyz space representation from a unit physical mechanism [19,20,21,22]. This study uses the relevant stress-strain relationship of soils for one-dimensional cyclic shear motion [23,24,25,26]. In particular, the classical nonlinearity terms (higher order power series in strain) are neglected

$${\tau }_H=G_{\max }\left\{\gamma -\frac{\alpha }{2}\left[2\Delta \gamma \cdot \gamma -\mathrm{sgn}\left(\dot{\gamma }\right)\left({\left(\Delta \gamma \right)}^2-{\gamma }^2\right)\right]\right\}$$

(1)

where Gmax is the shear modulus in the limit of infinitesimal strain, γ is the shear strain, α is a non-dimensional parameter that measures the degree of hysteretic nonlinearity, $\dot{\gamma }\left(=\partial \gamma /\partial t\right)$ is strain rate, Δγ is shear strain amplitude, and sgn(x) is signum function.

2.2. Backbone Curve

The nonlinear-hysteretic soil models follow the basic and extended Masing’s rules, which are adopted in conjunction with the backbone curve to express unloading, reloading, and cyclic degradation behavior. It represents trajectory of the extrema of the hysteresis curves. By replacing the strain amplitude (Δγ) with the shear strain γ in Equation (1), the backbone curve can be readily obtained for the entire strain range:

$${\tau }_b=G_{\max }\gamma \left[1-\mathrm{sgn}(\dot{\gamma })\alpha \gamma \right]$$

(2)

The backbone curves are superimposed on the stress-strain curves for three different strain amplitudes (Figure 1). The results show increasing hysteresis (nonlinear damping) and decreasing slope (the strain-softening effect) with increasing strain amplitude. In addition, the backbone curve is constructed by two quadratic functions joined at the coordinate origin. In fact, similar hysteresis loops are observed in many soils and other granular materials. While the stress–strain model in Equation (1) may not describe all of complex constitutive behaviors of granular materials, it has been shown to capture some essential features in the stress–strain relationship under steady-state cyclic loading.

2.3. Modulus Degradation

The instantaneous shear modulus (Gtan = dτ_H/dγ), defined as the slope on the stress-strain hysteresis loop along the loading path, can be obtained by taking the derivative with respect to shear strain in Equation (1):

$$G_{\tan }^H=\mathrm{d}{\tau }_H/\mathrm{d}\gamma =G_{\max }\left[1-\alpha \left(\mathrm{sgn}(\dot{\gamma })\cdot \gamma +\Delta \gamma \right)\right]$$

(3)

Given the $\dot{\gamma }>0$ and Δγ = γ, the tangent shear modulus can be expressed:

$$\frac{G_{\tan }}{G_{\max }}=1-2\alpha \gamma$$

(4)

This explicit form of the tangent modulus can be useful in the numerical simulations to reflect strain-softening response of granular materials under cyclic loading. The tangent stiffness G_tan instantaneously captures the soil fabric change during a large strain test. It is not related with small strain stiffness G_max measured under constant fabric [27,28].

The secant shear modulus (G_sec = τ_b/γ), where the secant slope drawn from the origin to any specified point on the stress-strain curve can be derived using Equation (2):

$$\frac{G_{\sec }}{G_{\max }}=1-\alpha \gamma$$

(5)

The ratio between the secant and backbone tangent moduli is given:

$$\frac{G_{\tan }^{}}{G_{\sec }}=\frac{1-2\alpha \gamma }{1-\alpha \gamma }<1$$

(6)

The small positive quantity in αγ indicates that the secant modulus is always larger than the backbone tangential modulus.

2.4. Damping Ratio

The damping ratio of a granular material is the summation of the linear damping ratio in the limit of small strain (ζ^L) that represents the inherent viscoelastic absorption and a nonlinear damping ratio due to the hysteresis that increases with the strain (ζ^NL(γ)), i.e.,

$$\zeta \left(\gamma \right)={\zeta }^L+{\zeta }^{NL}\left(\gamma \right)$$

(7)

The nonlinear damping ratio is defined [1,26]:

$${\zeta }^{NL}(\gamma )=\frac{W_D}{4\pi W_S}$$

(8)

where W_S is the maximum strain energy stored during the cycle (= G_sec·Δγ²/2), and W_D is the area closed by the hysteresis loop in the stress-strain curve, which represents the dissipated energy per cycle. The energy dissipation per cycle can be obtained by integrating Equation (1):

$$\begin{array}{ll}W=& {\displaystyle \tau d\gamma }={\displaystyle G\left\{\gamma -\frac{\alpha }{2}\left[2\Delta \gamma \cdot \gamma -\left((\Delta \gamma \right)-\gamma )\right]\right\}d\gamma }\\ & +{\displaystyle G\left\{\gamma -\frac{\alpha }{2}\left[2\Delta \gamma \cdot \gamma +\left((\Delta \gamma \right)-\gamma )\right]\right\}d\gamma }=\frac{4}{3}G\alpha (\Delta \gamma )\end{array}$$

(9)

The dissipated energy depends on the strain amplitude, hysteretic nonlinearity parameter, and shear modulus in the limit of infinitesimal strain. Thus, the nonlinear damping ratio can be obtained from Equation (8):

$${\zeta }^{NL}(\gamma )=\frac{2}{3\pi }\frac{G_{\max }}{G_{\sec }}\alpha \gamma =\frac{2}{3\pi }\frac{\alpha \gamma }{1-\alpha \gamma }\stackrel{\alpha \gamma \ll 1}{\cong }\frac{2}{3\pi }\alpha \gamma$$

(10)

The strain-dependent damping ratio response cannot be described with the Kelvin-Voigt model that consists of a linear spring element and a linear dashpot element in parallel system:

$$\tau =G\gamma +\eta \dot{\gamma }=G\gamma \pm \eta \omega \sqrt{{\left(\Delta \gamma \right)}^2-{\gamma }^2}$$

(11)

where η is the viscosity and γ is the harmonically varying strain as Δγsin(ωt). The damping ratio can be expressed:

$${\zeta }_{KV}^L=\frac{\eta \omega }{2G}$$

(12)

There is no strain-dependence in the shear modulus and the damping ratio. These correspond to the constant damping ratio and resonant frequency monitored at low shear strains.

3. Results and Analysis

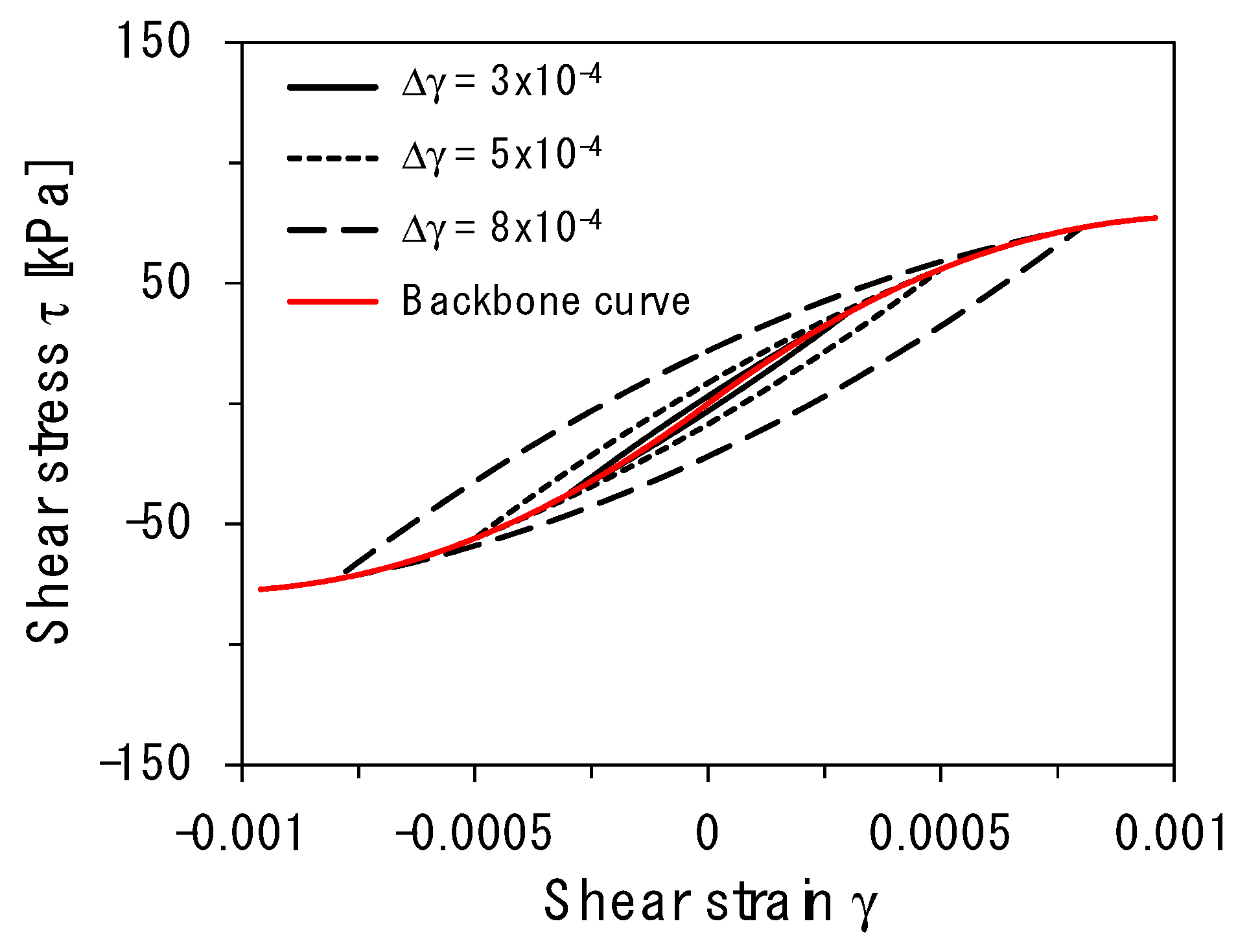
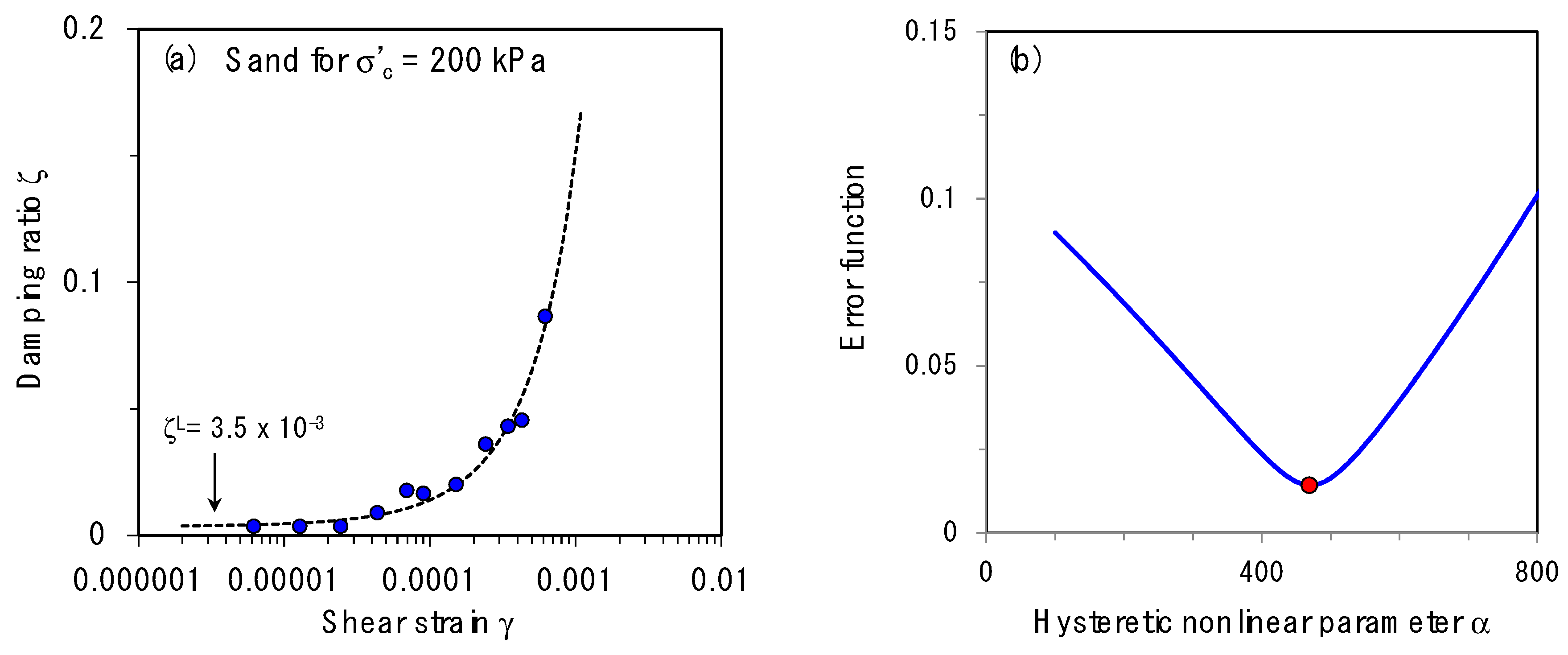
3.1. Examples

Resonant column test (RCT) characterizes the resonance frequency and damping ratio as a function of shear strain. The shear modulus is obtained from the resonance frequency using the characteristic equation derived from the linear vibration of the column-mass system. In fact, the hysteretic nonlinear nature of the vibration problem is ignored on the calculation of the shear modulus. Thus, this study uses damping ratio data to avoid data interpretation errors. The linear damping ratio ζ^L is experimentally constrained below elastic threshold regime. Meanwhile, the nonlinear damping ratio is defined by using the least-squares method:

$$E(\alpha )=\min {\displaystyle \sum _i{[{\zeta }_i^{Exp}-{\zeta }_i^{Model}(\alpha )]}^2}$$

(13)

Figure 2 presents fitted damping ratio and slices of the error surface presenting the inevitability of the hysteretic nonlinear parameter.

Figure 3 shows the data points and fitted models for damping ratios and the estimated values are tabulated in

Table 1. Hysteretic nonlinearity parameter determined with the damping ratio data, measured from the resonant column test for sand and clay under the three different confinement stress levels.

Sand				Clay
#	σ’c [kPa]	α [ ]	References	#	σ’c [kPa]	α [ ]	References
1	42	613	[9]	1	100	276	[29]
2	83	565		2	200	246
3	214	469		3	400	192
4	300	371		4	124	238
5	84	594		5	140	263
6	84	640		6	131	277
7	331	370		7	70	282	[9]
8	359	296		8	276	206
9	214	529		9	250	210
10	470	342		10	100	260
11	275	462		11	100	259
12	250	417		12	100	270
13	320	419		13	200	230
14	480	223		14	400	200
15	550	209
16	100	590	[29]
17	200	469
18	400	370
19	70	610
20	138	518
21	207	390
22	83	437
23	83	500
24	100	482

. Since, the α values are on the order of 10² and the maximum shear strain is less than 10⁻³, αγ is at most 10⁻¹, which proves the inequality in Equation (6). Higher confinement stress extends the elastic threshold region with lower values. In addition, clay is expected to be lower nonlinear than sand. These results show trend of the α values, implying that the α parameter involves physical information about the soil fabric changes. With the fitted parameters, the secant shear modulus data was compared with the proposed model (Figure 4). As the shear strain levels are increased beyond the elastic threshold strain, the conventional method predicted larger reductions in the shear modulus. These deviations show that the use of the linear characteristic equation produces data interpretation errors on the shear modulus. However, larger reductions in the shear modulus would be more conservative data for design purpose. Figure 5 shows the hysteresis curves, corresponding backbone curves, and the instantaneous tangent shear moduli for sand under confinement stresses, 100 and 400 kPa. The instantaneous tangent shear moduli have a bow-tie shape with end-point discontinuities, thereby, showing that the shear modulus is dependent on the loading path and exhibits a significant drop with the strain amplitude again due to the strain softening effect. The secant modulus at the maximum strains is superimposed at its tangent counterpart. Note that the tangent modulus at γ = 0 is equal to the average of two secant modulus at each shear strain amplitude.

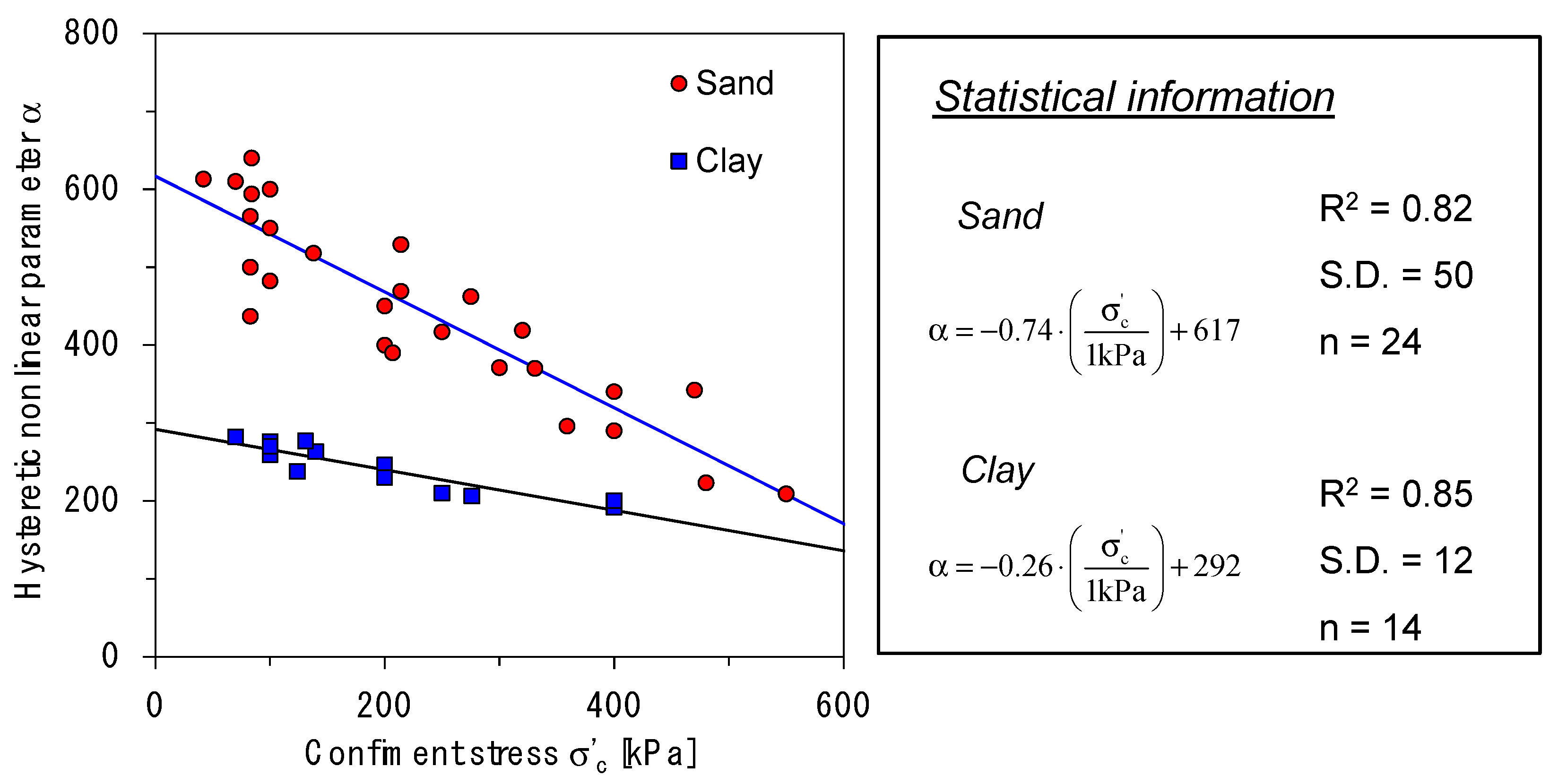
3.2. Correlation: Hysteretic Parameter and Confinement Stress

The 38 data sets of resonant column test (RCT) compiled from the literature are compared with the proposed model for different confinement stress levels and soils. Figure 6 presents that (1) there is an inverse relation between hysteretic nonlinear parameter α and confinement stress σ’_c; (2) sand leads to higher α value than clay at the same confinement stress.

3.3. Comments: Shear Strain Range

The constitutive model in Equation (1) has been validated for many different granular material systems [25,30,31], while this research for the first time applies the constitutive model to characterize the soil properties of geotechnical interest. The functional form determines the shape of hysteresis, while the hysteretic nonlinearity parameter α quantifies the amount of the macroscopic hysteretic nonlinear effect caused by microscopic sources of nonlinearity. In addition, this parameter is not a meaningless fitting parameter but it has its own full physical meaning related to the sources of nonlinearity [24,32]. Thus, the ad-hoc fitting procedure is not required to characterize strain-dependent soil properties. It was revealed that the constitutive model in Equation (1) is valid in the strain range up to 10⁻² [25]. For example, the α parameters for the sand and clay considered in this research are on the order of 10². This means αγ < 1 for γ < 10⁻², and thus Gsec > 0 and Gtan > 0 in this model. The upper validity limit shear strain of 10⁻² is high enough in most of geotechnical applications. Figure 7 summarizes the entire procedure based on the RCT data. While the data from RCT are used as an example in this research, data from the torsional shear test can additionally be used in a similar procedure.

4. Conclusions

This paper addresses a theoretical framework for characterizing the dynamic behavior of soils. In particular, the simple but robust constitutive model involved with a single physical parameter α was used to capture the strain-dependent response of granular materials under steady-state cyclic loading condition. The main conclusions can be drawn as follows:

• The constitutive model derives explicit formulas to describe the hysteretic nonlinear response. Note that all other models derived from this study model depend on the hysteretic nonlinear parameter α.
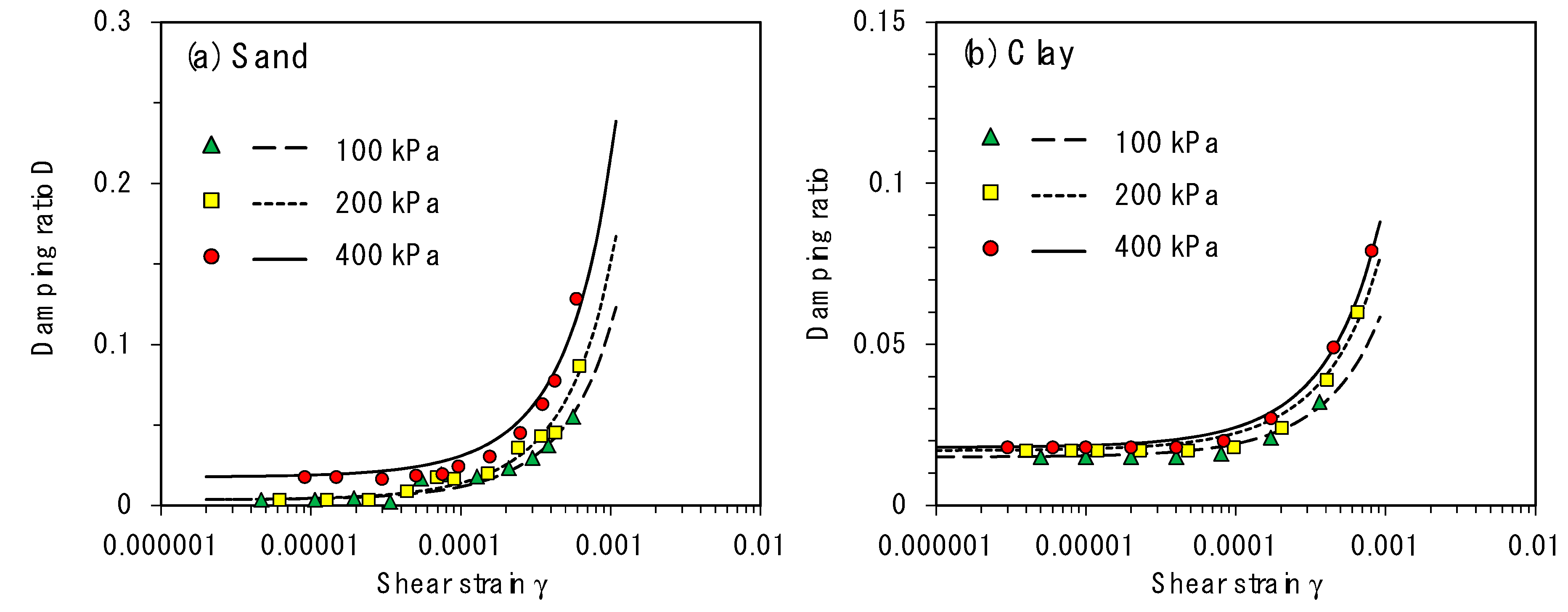
• The 36 damping ratio data sets measured from resonant column test were compared with the proposed model for different confinement stress levels and soils. It shows the inverse relation between the α parameter and confinement stress and higher α values for sand.
• The data analysis reveals that the model is valid for αγ < 1, and thus the explicit formula can be used to simulate the ground motion within intermediate strain range.