Flexibility Based Day-Ahead Generation–Reserve Bilevel Decision Model

Abstract

With the increasing penetration rate of renewable energy like fluctuating wind and solar energy, the power system has to equip itself with a more reasonable reserve capacity. Therefore, how to quantify the reserve capacity needed for dealing with the uncertainty and fluctuation has turned out to be a new problem faced by the power system integrated with large-scale renewable energy. This paper proposes a flexibility based day-ahead generation–reserve bilevel decision model. In the upper level, the day-ahead unit commitment model is constrained by flexibility reserve, which is calculated in the lower level. In the lower level, taking into account various factors of uncertainty and fluctuation, e.g., wind power ramping, load ramping and random failure of conventional units, the ramping probability distribution of an equivalent system is obtained by the universal generating function method, then the quantified relationship between operating reserve and flexibility is established ultimately. If the unit commitment scheme gained from the upper level could not provide sufficient reserve, a feedback for the correction of the upper level is needed. The rationality and validity of the proposed model are verified through the simulation of a modified IEEE-118 bus system.

1. Introduction

Renewable energy (RE) represented by wind power and solar power has become the main player of the energy industry revolution in China. Due to the uncertainty and fluctuation nature of RE, the integration of large-scale RE has brought about great risks to the safe and reliable operation of the power system, leading to the curtailment of RE [1], which therefore requires the power system to equip itself with a more reasonable reserve capacity [2,3,4]. Therefore, it remains an important issue how to reasonably quantify the reserve capacity needed under the background of integrating large-scale renewable energy into the power system [5].

The reserve capacity of the power system mainly comes from the generation side. Seen from the system level, the reserve capacity at the generation side in dispatch issues refers to the generator operating reserve dealing with net load uncertainty and fluctuation. With the reform of the power industry in China, reserve service will become a major product [6,7]. It can be seen that reasonable decision of system operating reserve capacity has become the key to both the economy and security of the power system. Hence, it is essential to reasonably evaluate the system operation state, develop operating reserve decision method that considers both security and efficiency and research on the generation–reserve optimization method for power system integrated with large-scale RE.

Traditionally, the operating reserve in the power system is served by conventional units, and the formulation of operating reserve is closely related to the operation scheme of conventional units, so the operating reserve is usually coordinative optimized with the generation dispatch [8,9,10,11]. Reference [12] proposed an energy and reserve bilevel co-optimization model based on the two compensation mechanisms of loss probability and uplift payment under deregulated market environment, realizing the maximization of market efficiency. Paterakis et al. [13] presented a multi-objective energy and reserve joint optimization model with the objective of minimum total expected cost and conditional risk value, and meanwhile proposed an improved variant of the epsilon-constraint algorithm. These methods add economic factors like expected outage cost in the objective function, thereby realizing the coordinated optimization of generation and reserve. However, they fail to establish the quantitative relationship between the reserve and system operating state.

Flexibility of the power system is defined as the ability to meet power fluctuations by system resources [14,15,16], and it has become one of the most important performance indices of the power system in addition to security, reliability and economy [17]. There is already some research on quantitative evaluation of flexibility. The flexibility envelope method was developed to describe the flexibility potential dynamics of a power system and its individual resources in the operational planning time-frame [18]. The International Energy Agency proposed a flexibility evaluation method with an expert scoring system that has comprehensively considered power grid strength, power balance scale, schedulable flexible resource ratio and so on [19]. Lu et al. [17] presented a flexibility evaluation method for power system planning issue that has comprehensively considered system resources regulation features and renewable energy sources fluctuation based on a conditional probability convolution algorithm. Based on a Monte Carlo simulation, Li et al. [20] proposes a power system flexibility assessment system considering wind power correlation. A novel flexibility index (FLEXIN) is proposed by Mazidi et al. [21]. The FLEXIN takes generation reserve, transmission reserve, renewables, storage, demand and market into consideration, provides several opportunities for analysis and improving the operation. However, flexibility assessments in these studies are based on the given system operating reserve, and there are few researches about reserve decision based on flexibility requirements.

This paper proposes a day-ahead generation–reserve bilevel decision model. Based on historical data and forecast information, the proposed model establishes the quantitative relationship between reserve and flexibility, and ensures system flexibility to meet the requirements while realizing conventional unit output scheduling. In the upper level, the unit commitment (UC) model is solved on the basis of predicted load and wind power output, and what is different is the relationship between reserve and flexibility established by the lower level is taken as a constraint. In the lower level, the ramping state of load and wind power is formulated based on historical data and forecast information. As well as, the conventional unit is modeled by forced outage rate and planned output. Then, the ramping probability distribution of the equivalent system is obtained by universal generating function algorithm. In this way, the relationship between reserve and flexibility is established. Then, the UC scheme is verified by the flexibility requirement, and if it could not that provide enough reserve capacity, the UC model of upper level is corrected and re-solved.

The remainder of the paper is arranged as follows. Day-ahead unit commitment model considering flexibility constraint of the upper level is introduced in Section 2. The flexibility based reserve decision method of lower level is developed in Section 3. Section 4 presents case studies, followed by the conclusion in Section 5.

2. Day-Ahead Unit Commitment Model Considering Flexibility Constraint

Given that operating reserve and conventional unit output state are closely related, it is essential for a day-ahead unit commitment model to provide necessary boundary conditions if the system flexibility is to be rational measured to assess the reserve capacity required. In the upper level, the day-ahead unit commitment model schedules the conventional unit start-up and output plan of 96 time periods based on the short-term forecast of wind power and load. Meanwhile, the constraints of the UC model also include the flexibility-based reserve obtained by the lower level. The specific model is as follows:

2.1. Objective Function

The objective function of day-ahead UC features system operation cost minimization, and the operation cost includes generation cost and unit start-up cost, expressed as:

$$\min {\displaystyle \sum _t^T\left(C_1+C_2\right)}$$

(1)

(1) Generation cost C₁

The generation cost of conventional unit is normally expressed as quadratic function, namely:

$$C_1={\displaystyle \sum _{i\in \mathsf{\Omega }}{u}_{i,t}f(P_{i,t}^{\mathrm{G}})}={\displaystyle \sum _{i\in \mathsf{\Omega }}{u}_{i,t}\cdot }{a}_i+b_i{P}_{i,t}^{\mathrm{G}}+c_i(P_{i,t}^{\mathrm{G}}{)}^2$$

(2)

where T is the total number of time period, Ω is the conventional unit set; u_i,t is the state of unit i at the time t, 1 for operation and 0 for outage, $P_{i,t}^{\mathrm{G}}$ is the planned output of unit i at the time t and a_i, b_i, c_i is the generation cost coefficient of unit i.

(2) Start-up cost C₂

$$C_2={\displaystyle \sum _{t\in T}{\displaystyle \sum _{i\in \mathsf{\Omega }}{u}_{i,t}^{}(1-u_{i,t-1}^{})C_{i,t}^{st}}}$$

(3)

where the unit start cost $C_{i,t}^{st}$ can be expressed as:

$$C_{i,t}^{st}=\{\begin{array}{l}{C}_i^{hot},T_i^{off}\le t_{i,t}^{off}\le T_i^{off}+T_i^{col\mathrm{d}}\\ C_i^{col\mathrm{d}},t_{i,t}^{off}\ge T_i^{off}+T_i^{col\mathrm{d}}\end{array}$$

(4)

where $C_i^{hot}$ and $C_i^{col\mathrm{d}}$ represent hot start-up cost and cold start-up cost of unit i, respectively, $T_i^{off}$ and $T_i^{col\mathrm{d}}$ respectively represent minimum off time and cold start time, $t_{i,t}^{off}$ is the actual continuous off time. As the stop cost is small, it is normally expressed as constant, which is not considered here.

2.2. Constraints

(1) Power balance

$${\displaystyle \sum _{i\in \mathsf{\Omega }}{P}_{i,t}^{\mathrm{G}}}+{\displaystyle \sum _{j\in \mathrm{W}}{P}_{j,t}^{\mathrm{W}}}-{\displaystyle \sum _{k\in \mathrm{D}}{P}_{k,t}^{\mathrm{D}}}=0$$

(5)

where W and D respectively represent wind farm set and load set, $P_{j,t}^{\mathrm{W}}$ is the predicted output of wind farm j at time t and $P_{k,t}^{\mathrm{D}}$ is the predicted load k at time t.

(2) The generation constraints for the power unit are:

$$u_{i,t}{P}_{i,\min }^{\mathrm{G}}\le P_{i,t}^{\mathrm{G}}\le u_{i,t}{P}_{i,\max }^{\mathrm{G}}$$

(6)

where $P_{i,\max }^{\mathrm{G}}$ and $P_{i,\min }^{\mathrm{G}}$ refer respectively to the upper and lower limits of unit i.

(3) The ramping constraints of the power unit are:

$$-\Delta T{r}_i^{\mathrm{d}}\le P_{i,t}^{\mathrm{G}}-P_{i,t-1}^{\mathrm{G}}\le \Delta T{r}_i^{\mathrm{u}}$$

(7)

$$R_{i,t}^{\mathrm{U}}\le \Delta T_{\mathrm{R}}{r}_i^{\mathrm{u}}$$

(8)

$$R_{i,t}^{\mathrm{D}}\le \Delta T_{\mathrm{R}}{r}_i^{\mathrm{d}}$$

(9)

where △T is the length of time interval, △T_R is the spinning reserve response time, $R_{i,t}^{\mathrm{U}}$ and $R_{i,t}^{\mathrm{D}}$ refer to the up and down reserve of unit i at time t, $r_i^u$ and $r_i^{\mathrm{d}}$ refer to the up and down ramping rate of unit i.

(4) Minimum up and down time

$$t_{i,on}^{\min }\ge T_{i,on}^{\min }$$

(10)

$$t_{i,off}^{\min }\ge T_{i,off}^{\min }$$

(11)

where $t_{i,on}^{\min }$ and $T_{i,off}^{\min }$ refer to the minimum up and down duration of unit i, $T_{i,on}^{\min }$ and $T_{i,off}^{\min }$ are the allowable minimum up and down time of unit i.

(5) Flexibility constraint

The UC model must keep enough flexibility resources to maintain the safe and reliable operation of the power system. Loss of flexibility probability (LOFP) is a flexibility index [17]. The UC model needs to keep the LOFP lower than the requirement set by operator to ensure the flexibility of system. Since the calculation of the LOFP is complicated, it is difficult to consider the LOFP in the optimization process. The quantitative relationship between the LOFP and reserve capacity is established by the reserve decision model in the lower level. In this way, the flexibility constraint is converted into the reserve constraint. In other words, in order to ensure that the flexibility of system meets the given requirement, the total up and down reserve capacity $R_t^{\mathrm{U}}$ and $R_t^{\mathrm{D}}$ provided by conventional unit must meet the reserve requirements calculated by the reserve decision model in the lower level.

$$\left(R_t^{\mathrm{U}},R_t^{\mathrm{D}}\right)=f_{\mathrm{R}}(\alpha ,t)$$

(12)

$${\displaystyle \sum _{i\in \mathsf{\Omega }}{R}_{i,t}^{\mathrm{U}}}=R_t^{\mathrm{U}}$$

(13)

$${\displaystyle \sum _{i\in \mathsf{\Omega }}{R}_{i,t}^{\mathrm{D}}}=R_t^{\mathrm{D}}$$

(14)

$$R_{i,t}^{\mathrm{U}}\le u_{i,t}\left(P_{i,\max }^{\mathrm{G}}-P_{i,t}^{\mathrm{G}}\right)$$

(15)

$$R_{i,t}^{\mathrm{D}}\le u_{i,t}\left(P_{i,t}^{\mathrm{G}}-P_{i,\min }^{\mathrm{G}}\right)$$

(16)

where f_R(α, t) is the function of reserve established by the reserve decision model in the lower level at time t, and it will be detailed in Section 3, α refers to the given tolerance of the LOFP. The initial values of $R_t^{\mathrm{U}}$ and $R_t^{\mathrm{D}}$ are set as a certain proportion of the total load.

The solution of the UC model in the upper level, including the start-up plan and output scheme of conventional unit, provides boundary conditions for the reserve decision model in the lower level.

3. Flexibility Based Reserve Decision Method

The universal generating function is an effective discrete random variable expression and calculation tool proposed by Professor Ushakov in the 1980s [22]. It has been widely used in the reliability analysis of multi-state systems [23,24,25,26]. The UGF theory establishes a one-to-one correspondence between the discrete probability distribution and u-function. Then, the discrete probability distribution of random variable function can be calculated by the corresponding UGF operator in a recursive way. Other stochastic approaches in optimization, e.g., interval optimization, only considers limited scenarios and probability information is lost. The adoption of the UGF theory makes it possible to evaluate the flexibility of the power system at every time period effectively. Thus, the UGF based flexibility assessment method in this section provides the basis for the flexibility-based UC. In the lower level, the proposed reserve decision model considers various factors of uncertainty and fluctuation like the wind power output feature and conventional unit forced outage comprehensively, establishes the quantitative relationship between operating reserve and flexibility index.

Flexibility refers to the ability of the system to cope with power fluctuations. For the issue of day-ahead scheduling, the system responds to the deviation of the dispatch scheme by the operating reserve. Therefore, the operating reserve can be quantified based on the flexibility assessment. The system ramping is defined as the power change between adjacent time intervals. The key of the reserve decision based on the flexibility is how to evaluate the system ramping reasonably. The power system is considered as a multi-state model, and the UGF models of ramping state for each component are built; then UGF combination operators are used to obtain the ramping state distribution of the equivalent system. The relationship between the flexibility index LOFP and reserve capacity is established by the ramping state probability distribution of the equivalent system, thereby the reserve capacity is calculated by the given LOFP.

3.1. Universal Generating Function Model for Load

The load forecasting error of the power system obeys a normal distribution [27] so the actual load at time t P^D(t) conforms to normal distribution N($\overline{P}$_d(t), σ_d(t)), where $\overline{P}$_d(t) is the predicted load value at time t and σ_d(t) is the load forecasting standard deviation. σ_d(t) can be obtained through statistics of historical data, or comes from empirical value.

Step P_intv is set for discretization of probability load model. According to probability theory, the study is limited in the range of [$\overline{P}$_d(t)−3σ_d(t), $\overline{P}$_d(t)+3σ_d(t)] for efficiency. The load is divided into N_d states. In a certain load state k, the load value is $P_k^{\mathrm{d}}$(t) and the error is Δ$P_k^{\mathrm{d}}$(t), then the corresponding probability $p_k^{\mathrm{d}}$(t) is:

$$\begin{array}{ll}{p}_k^{\mathrm{d}}\left(t\right)& =\mathrm{Pr}\left\{P_k^{\mathrm{d}}\left(t\right)-\frac{P_{\mathrm{intv}}}{2}<P^{\mathrm{D}}\left(t\right)<P_k^{\mathrm{d}}\left(t\right)+\frac{P_{\mathrm{intv}}}{2}\right\}\\ & =\Phi \left(\frac{2\Delta P_k^{\mathrm{d}}\left(t\right)+P_{\mathrm{intv}}}{2{\sigma }_{\mathrm{d}}\left(t\right)}\right)-\Phi \left(\frac{2\Delta P_k^{\mathrm{d}}\left(t\right)-P_{\mathrm{intv}}}{2{\sigma }_{\mathrm{d}}\left(t\right)}\right)\end{array}$$

(17)

where Pr{·} is the probability of event {·}, Δ$P_k^{\mathrm{d}}$ is the error of load state k and Φ(·) is the standard normal distribution function. Then the UGF model of load can be obtained:

$$u_{\mathrm{d}}(z,t)={\displaystyle \sum _{k=1}^{N_{\mathrm{d}}}{p}_k^{\mathrm{d}}(t)\cdot z^{P_k^{\mathrm{d}}(t)}}$$

(18)

Similar to the ramping of generator, the load change at time t is R^d(t) = P^D(t + 1) − P^D(t), the prediction errors of load at adjacent time are independent so the UGF model of load change is:

$$u_{\mathrm{D}}(z,t)=u_d(z,t+1){\otimes }_{-}{u}_d(z,t)={\displaystyle \sum _{k=1}^{S_{\mathrm{D}}}{p}_k^{\mathrm{d}}(t)\cdot z^{R_k^{\mathrm{d}}(t)}}$$

(19)

where ${\otimes }_{-}$ is the difference operator of UGF method, S_D is the total number of load change states, $R_k^{\mathrm{d}}$(t) refers to the load change value of state k and $p_k^{\mathrm{D}}$(t) is the corresponding probability.

3.2. Universal Generating Function Model for Wind Power

The wind power prediction error is formulated as a normal distribution model [28], and the modeling method is also applicable to other distribution forms. The output of wind farm P^w(t) at the time t obeys normal distribution N($\overline{P}$_w(t), σ_w(t)), where $\overline{P}$_w(t) is the wind farm output predictive value at time t, σ_w(t) is the standard deviation. Same as load, the study was limited in the range of [$\overline{P}$_w(t) − 3σ_w(t), $\overline{P}$_w(t) + 3σ_w(t)] for efficiency. The output of wind farm is divided into N_w states, the power value of state i is $P_i^{\mathrm{w}}$(t), the prediction error is Δ$P_i^{\mathrm{w}}$(t), then the corresponding probability $p_i^{\mathrm{w}}$(t):

$$\begin{array}{ll}{p}_i^{\mathrm{w}}\left(t\right)& =\mathrm{P}\mathrm{r}\left\{P_i^{\mathrm{w}}\left(t\right)-\frac{P_{\mathrm{intv}}}{2}<P_{\mathrm{w}}^{}\left(t\right)<P_i^{\mathrm{w}}\left(t\right)+\frac{P_{\mathrm{intv}}}{2}\right\}\\ & =\Phi \left(\frac{2\Delta P_i^{\mathrm{w}}\left(t\right)+P_{\mathrm{intv}}}{2{\sigma }_{\mathrm{w}}\left(t\right)}\right)-\Phi \left(\frac{2\Delta P_i^{\mathrm{w}}\left(t\right)-P_{\mathrm{intv}}}{2{\sigma }_{\mathrm{w}}\left(t\right)}\right)\end{array}$$

(20)

The transition probability $p_{ij}^{\mathrm{w}1}$(t) from the output state i at time t to the output state j at time t + 1 is obtained through the historical data statistics of wind farm W1. The difference in output from the next moment to the current moment is the wind power ramping state of current moments. From this, the conditional probability of wind power ramping on output is obtained. While the output of W1 is in state i, the conditional probability of the ramping state k can be described as $p_{k|i}^{\mathrm{w}1}$(t):

$$\begin{array}{ll}{p}_{k|i}^{\mathrm{w}1}\left(t\right)& =\mathrm{Pr}\left\{R_k^{\mathrm{w}1}\left(t\right)|P_i^{\mathrm{w}1}\left(t\right)\right\}\\ & =p_{ij}^{\mathrm{w}1}\left(t\right)|R_k^{\mathrm{w}1}\left(t\right)=P_j^{\mathrm{w}1}\left(t+1\right)-P_i^{\mathrm{w}1}\left(t\right)\end{array}$$

(21)

According to conditional probability formula, the probability $p_k^{\mathrm{w}1}$(t) of ramping state k is:

$$p_k^{\mathrm{w}1}\left(t\right)={\displaystyle \sum _{i=1}^{N_{\mathrm{w}1}}\left(p_{k|i}^{\mathrm{w}1}\left(t\right)·p_{i,t}^{\mathrm{w}1}\left(t\right)\right)}={\displaystyle \sum _{i,j\in {\mathsf{\Pi }}_k}\left(p_{ij}^{\mathrm{w}1}\left(t\right)·p_{i,t}^{\mathrm{w}1}\left(t\right)\right)}$$

(22)

where N_w1 is the total number of output states of wind farm W1; Π_k is the state set that satisfy $R_k^{\mathrm{w}1}$(t) = $P_j^{\mathrm{W}1}$(t + 1) − $P_i^{\mathrm{W}1}$(t). In formula (22), the ramping probability distribution of wind farm W1 is established on the basis of predicted output and ramping state transition distribution, then the ramping UGF model for wind farm W1 at time t is as follows:

$$u_{\mathrm{w}1}\left(z,t\right)={\displaystyle \sum _{k=1}^{S_{\mathrm{w}1}}{p}_k^{\mathrm{w}1}\left(t\right)}{z}^{R_k^{\mathrm{w}1}\left(t\right)}$$

(23)

where S_w1 is the total number of ramping states. Repeat the process listed above until the ramping probability distribution of all wind farms is obtained.

If wind farms are independent, then the total ramping probability distribution of wind farms is:

$$u_{\mathrm{W}}\left(z,t\right)=u_{\mathrm{w}1}\left(z,t\right){\otimes }_{+}{u}_{\mathrm{w}2}\left(z,t\right){\otimes }_{+}\dots u_{{\mathrm{wN}}^{\mathrm{w}}}\left(z,t\right)={\displaystyle \sum _{j=1}^{S_{\mathrm{W}}}{p}_j^{\mathrm{W}}\cdot z^{R_j^{\mathrm{W}}\left(t\right)}}$$

(24)

where ${\otimes }_{+}$ is the summation operator of the UGF method, N^w refers to the total number of wind farms, S_w is the total number of wind farm total ramping states, $R_j^{\mathrm{W}}$(t) and $p_j^{\mathrm{W}}$(t) are the ramping value and probability of the j^th ramping state of total wind farms at time t.

3.3. Universal Generating Function Model for Conventional Unit

In the flexibility analysis, it is necessary to consider the forced outage of the conventional unit for the accuracy. On the basis of the operating scheme obtained in the upper level and forced outage rate, the conventional units are modeled as follows.

There are only two states for the ramping of conventional unit caused by forced by outage in flexibility analysis: (1) If conventional generation unit fault at the time t + 1 and causes outage of the unit, then the ramping of conventional unit at time t is the negative value of the planned output at time t + 1, and the corresponding probability is the forced outage rate. (2) If the conventional unit operates normally, then there is no ramping. Therefore, the UGF model of conventional unit g at time t is:

$$u_g(z,t)=\left(1-p_g\right)z^0+p_g{z}^{-P_{g,t+1}^{\mathrm{G}}}$$

(25)

where p_g is the forced outage rate of unit g, $P_{g,t+1}^{\mathrm{G}}$ is the planned output of unit g at time t + 1.

The forced outage events of conventional units are independent so the equivalent multi-state UGF model for conventional units is:

$$\begin{array}{ll}{u}_{\mathrm{G}}(z,t)& ={\otimes }_{+}(u_1(z,t),u_2(z,t),\cdots ,u_N(z,t))\\ & ={\displaystyle \sum _{i=1}^{S_{\mathrm{G}}}{p}_i^{\mathrm{G}}(t)\cdot z^{R_i^{\mathrm{G}}(t)}}\end{array}$$

(26)

where S_G is the total number of ramping states of equivalent conventional units, N refers to the total number of conventional units, $R_i^{\mathrm{G}}$(t) and $p_i^{\mathrm{G}}$(t) are the ramping value and probability of the i^th ramping state of equivalent conventional units at time t.

3.4. Flexibility Based Reserve Capacity Calculation

The system ramping, which refers to the power fluctuation between adjacent time, is the algebraic sum of load change, conventional unit ramping caused by forced outage and wind power ramping so the UGF model for system ramping is:

$$\begin{array}{ll}{u}_{\mathrm{R}}(z,t)& =u_{\mathrm{D}}(z,t){\otimes }_{-}{u}_{\mathrm{G}}(z,t){\otimes }_{-}{u}_{\mathrm{W}}(z,t)\\ & ={\displaystyle \sum _{k=1}^{S_{\mathrm{D}}}{p}_k^{\mathrm{dr}}\cdot z^{R_k^{\mathrm{d}}}}{\otimes }_{-}{\displaystyle \sum _{j=1}^{S_{\mathrm{W}}}{p}_j^{\mathrm{W}}\cdot z^{R_j^{\mathrm{W}}}}{\otimes }_{-}{\displaystyle \sum _{i=1}^{S_{\mathrm{G}}}{p}_i^{\mathrm{G}}\cdot z^{R_i^{\mathrm{G}}}}\\ & ={\displaystyle \sum _{k=1}^{S_{\mathrm{eq}}}{p}_k^{\mathrm{eq}}(t)\cdot z^{R_k^{\mathrm{eq}}(t)}}\end{array}$$

(27)

where S_eq is the total number of ramping states of the equivalent system, $R_k^{\mathrm{eq}}$(t) is the system ramping power at state k, and $p_k^{\mathrm{eq}}$(t) is the corresponding probability. In this way, the probability distribution function $F_t^{\mathrm{eq}}$(·) of the system ramping at time t is obtained.

Loss of flexibility probability means the probability that the system ramp more than the operating reserve. It is an intuitive index of system flexibility. The up and down operating reserves are R^U(t) and R^D(t), respectively. For ramping state k, if $R_k^{\mathrm{eq}}$(t) > R^U(t), the system cannot provide sufficient generation power in transition from time t to t + 1, causing loss of load; if $R_k^{\mathrm{eq}}$(t) < −R^D(t), it cannot lower output in transition from time t to t+1, resulting in wind power curtailment. Therefore, the system LOFP can be defined as:

$$LOFP\left(t\right)={\displaystyle \sum _{R_i^{\mathrm{eq}}\left(t\right)>R^{\mathrm{U}}\left(t\right)}{p}_i^{\mathrm{eq}}\left(t\right)}+{\displaystyle \sum _{R_j^{\mathrm{eq}}\left(t\right)<-R^{\mathrm{D}}\left(t\right)}{p}_j^{\mathrm{eq}}\left(t\right)}$$

(28)

The relationship between LOFP and operating reserve is shown in Figure 1.

The quantified relationship between the system operating reserve and LOFP is established in definition (28) but this definition cannot be calculated directly. The explicit form of f_R(α, t) still needs further derivation. As the probability distribution function $F_t^{\mathrm{eq}}$(·) of the system ramping at time t obtained in u-function (27), R^U(t) and R^D(t) can be calculated by the inverse function of $F_t^{\mathrm{eq}}$(·). When the LOFP is set as α, the f_R(α, t) can be expressed as:

$$R^{\mathrm{U}}\left(t\right)={\mathrm{G}}_t^{\mathrm{eq}}\left(1-\alpha /2\right)$$

(29a)

$$R^{\mathrm{D}}\left(t\right)={\mathrm{G}}_t^{\mathrm{eq}}\left(\alpha /2\right)$$

(29b)

where ${\mathrm{G}}_t^{\mathrm{eq}}$(·) refers to the inverse function of $F_t^{\mathrm{eq}}$(·).

Just like reliability, the power system needs to keep the LOFP lower than a certain value. According to this flexibility requirement, the total system operating reserve can be calculated through the formula (29). If the reserve obtained in the lower level is greater than the maximal reserve capacity that can be provided by the UC scheme, then the solution of the upper level is not feasible. Therefore, the feedback mechanism between the upper and lower levels is necessary. If the obtained reserve is greater than the reserve capacity that can be provided by the UC scheme, then the flexibility constraint (12) in the UC model of upper level is to be modified, then re-solve the whole model; or otherwise, output the results.

Meanwhile, it has to be noted that there is no coupling relationship among the time period in the reserve decision models so this model can conduct parallel calculation over a different time period. Moreover, the calculation of the universal generating function features recursiveness, so it significantly improves the efficiency and is extremely applicable to large-scale computer analysis.

The flowchart of proposed model is as shown in Figure 2.

4. Case Studies

4.1. Test System

The proposed unit commitment model in the upper level is converted into a mixed integer linear planning problem, and it was solved by the CPLEX solver on Matlab using the Yalmip toolbox [29,30]. The parallel computing programming of the reserve decision in the lower level was conducted in the Matlab. The test was carried out on the computer with CPU i7 3.5GHz and 16G RAM.

A modified IEEE-118 bus test system was used in case studies, which contained 54 conventional units, and the 24h load curve is as shown in Figure 3 [31]. In addition, two wind farms were added to the IEEE-118 system with the capacities of 200 MW and 150 MW. The wind farms were modeled by the historical data of two wind farms in northwest China, and the historical wind output data of 24 h as showed in Figure 4 was used as the predicted value.

4.2. Flexibility Based Reserve Decision Method

Traditional reserve decision model only considers uncertainty in the system, but the flexibility based reserve model proposed in this paper has comprehensively considered the uncertainty and fluctuation of net load as well as the forced outage of conventional unit. Under the joint influence of uncertainty and fluctuation, the system needs reserve in both up and down directions. In order to demonstrate the effectiveness of the proposed method in a more intuitive way, the flexibility based reserve only considered the uncertainty and fluctuation of load in this case. The LOFP is set as 5%, and the load prediction errors SD is 3% of forecasted load. 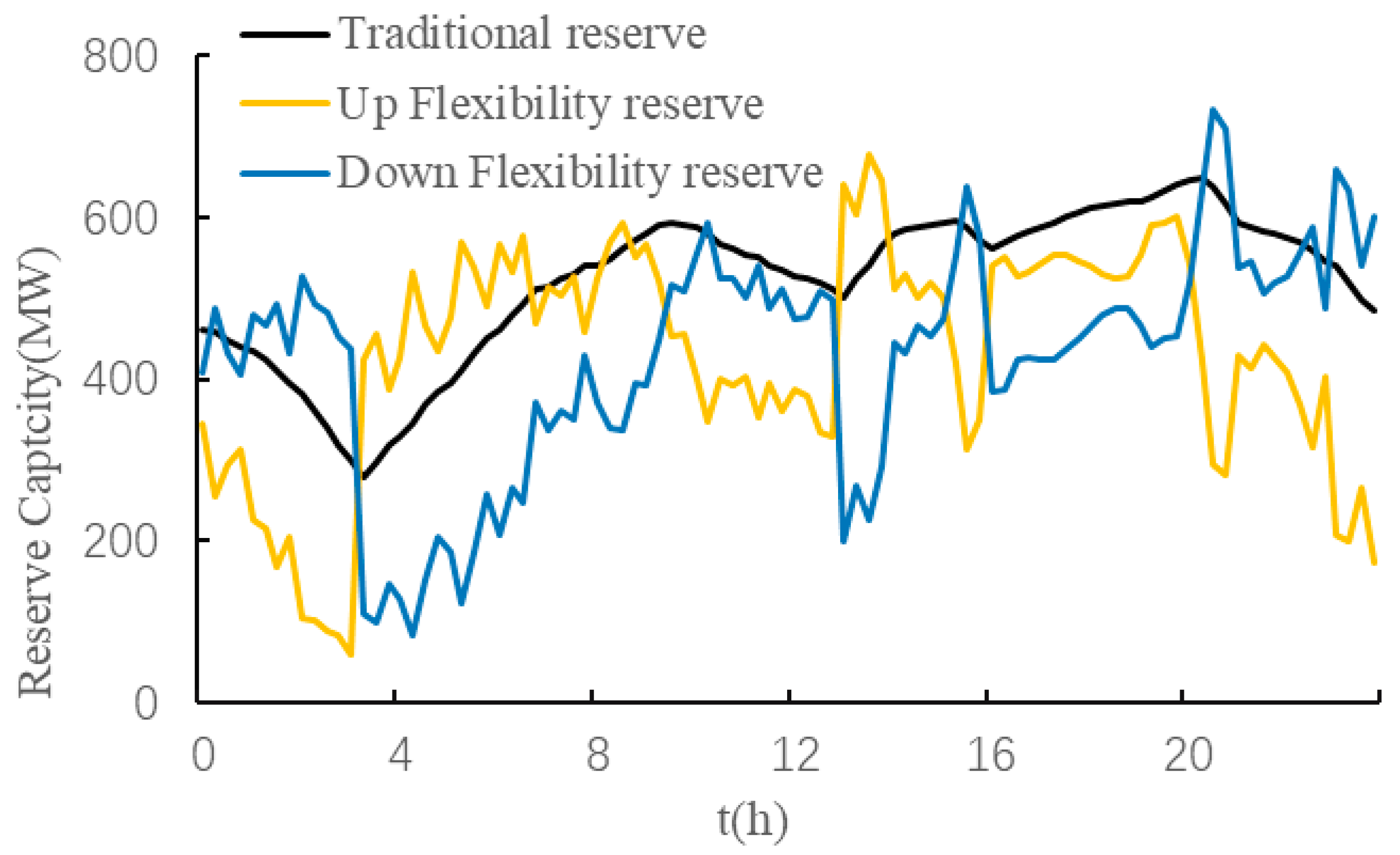Figure 5 shows the comparison of reserve between the proposed method and the traditional method, which values the reserve as 10% of forecasted load.

As showed in Figure 5, the reserve obtained by the proposed method is less than the traditional method most of the time. However, when the load sees a rapid rising, such as around six o’clock, the up flexibility reserve is greater than the traditional one; and when the load sees a rapid dropping such as around 22 o’clock, the down flexibility reserve is greater than the traditional one. This indicates that the traditional reserve model may not be able to satisfy the ramping requirement of the system when load changes rapidly. For traditional reserve model, the operator will increase the reserve ratio if the reserve fails frequently but the insufficient of reserve may have caused losses already before the operator takes action. The risk of loss flexibility is uncontrollable. What is more, increasing the reserve ratio for all time interval will lead to a waste of system resources, which is uneconomical.

Meanwhile, at the load rising stage, e.g., 5–10 a.m., the up flexibility reserve is greater than the down flexibility reserve; at the load dropping stage, e.g., 0–3 a.m., the up flexibility reserve is smaller than the down flexibility reserve. The flexibility based reserve is a measure of system ramping. It captures the characteristics of system power changes between adjacent time. It shows a better performance of indicating the potential changes of the system power, which the traditional one fails to measure. This shows that the proposed method can more accurately describe the net load characteristics. It can be seen that the proposed flexibility based reserve decision method is more applicable to the reliable operation of the power system containing fluctuating RE.

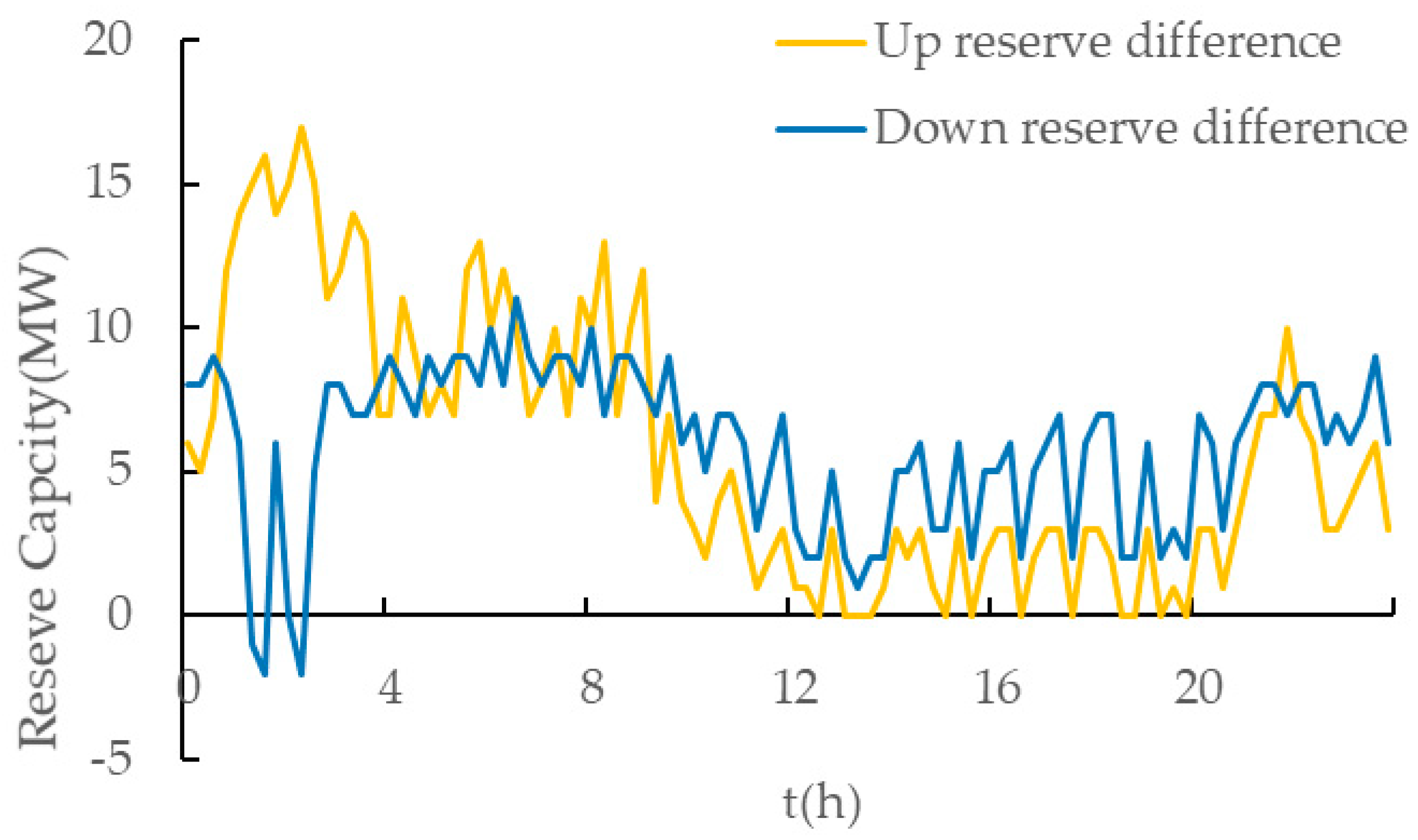
In order to analyze the influence of RE upon the flexibility based reserve, flexibility based reserve (R_DW) comprehensively considering load and wind farm A and flexibility based reserve (R_D) only considering the load fluctuation were compared, and the difference between R_DW–R_D could directly reflect the influence of wind farm fluctuation upon flexibility reserve. The curve is as shown in Figure 6.

Due to the intensive uncertainty and fluctuation of the wind farm, the introduction of the wind farm increases the up and down flexibility based reserves of the system in general. According to the statistical results of historical data, when the wind farm output is high, the downward ramping probability is larger than upward ramping; when the wind power output is low, it is the opposite. With wind farm A taken into consideration, when the wind farm output is high, for example at 3 a.m., the downward ramping probability of the wind power is greater, so the increment of the up reserve is larger than that of the down reserve. Particularly, when the wind farm output approximates to the rated value, its downward fluctuation probability is far larger than the upward fluctuation. At this moment, the up reserve significantly increases while the down reserve may drop. When the wind farm output is low, for example 8 p.m., the upward ramping probability is larger than the downward ramping, so the increment of down flexibility is larger than that of the up flexibility.

Meanwhile, to verify the effect of parallel computing, serial computing, 2 threads parallelism, 4 threads parallelism, 6 threads parallelism and 8 threads parallelism were adopted. The computing time for different computing means is as shown in

Table 1. Computing time of different computing means.

Computing Means	Serial Computing	2 Threads Parallelism	4 Threads Parallelism	6 Threads Parallelism	8 Threads Parallelism
Calculation Time	1207 s	924 s	642 s	563 s	526 s

. The comparison of different computing means indicates that parallel computing could reduce the solution time effectively.

Based on the above analyses, the proposed flexibility based reserve decision model can accurately reflect the uncertainty and fluctuation of load and RE. When compared with the traditional reserve decision method, the proposed flexibility based reserve can make the dispatch scheme stronger and safer.

4.3. Flexibility Based Generation-Reserve Bilevel Decision Model

In order to verify the accuracy of the proposed model, four scenarios were studied in the first case of Section 4.3. The parameters of each scenario are listed in

Table 2. Parameters of each scenario.

Scenarios	LOFP	Load Prediction Errors SD in Percentage of Forecasted Load	Wind Power Prediction Errors SD in Percentage of Forecasted Wind Power
Scenario 1	5%	3%	5%
Scenario 2	2%	3%	5%
Scenario 3	5%	5%	5%
Scenario 4	5%	3%	3%

.

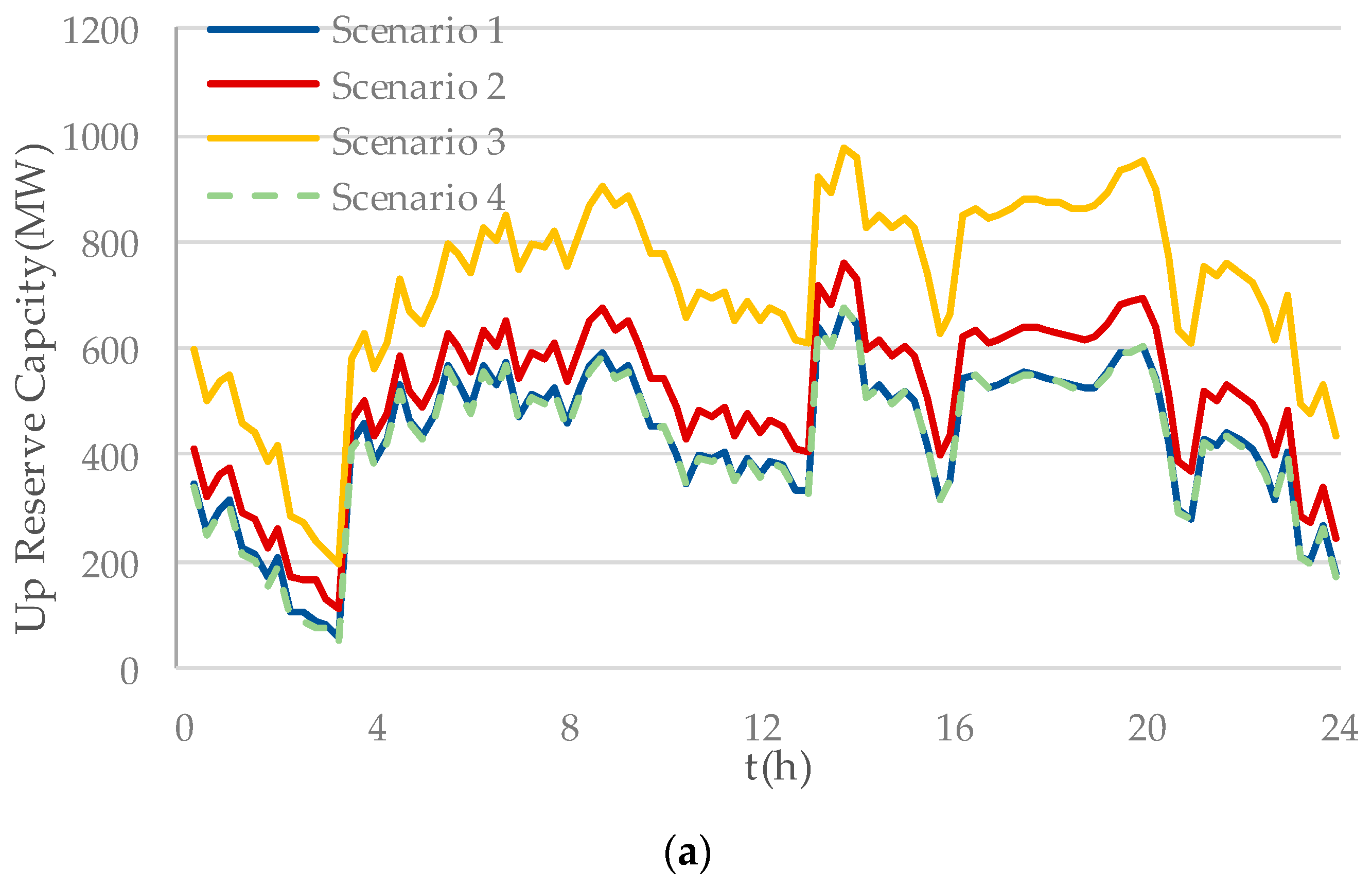
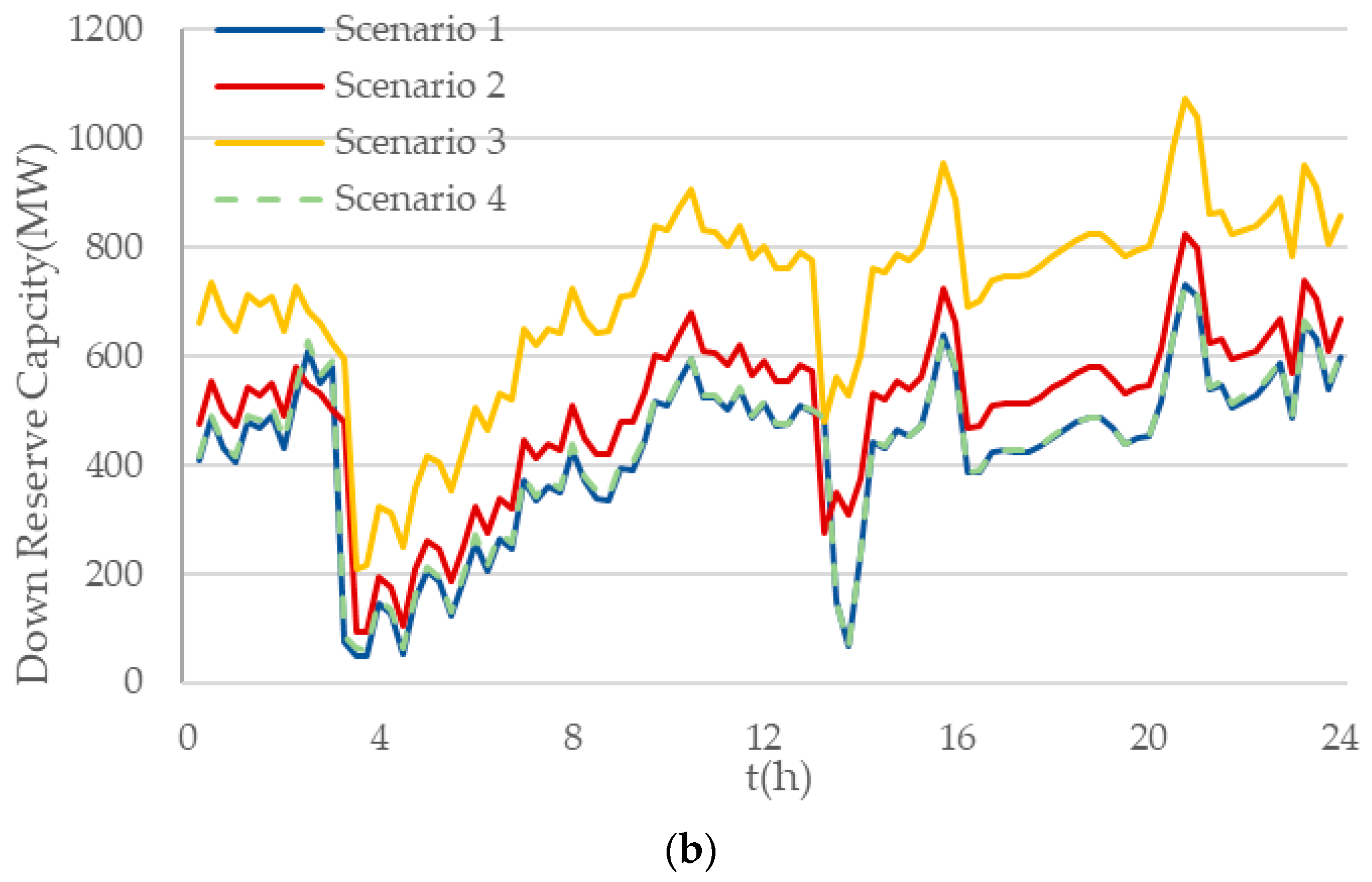
The obtained unit commitment schemes of the four scenarios were the same. As the predicted value of the load and wind power remained consistent, the objective function value of the four scenarios were the same, which was $1.96 × 10⁶. As all solution are obtained through one iteration, the solution time is about 52 min. Figure 7 shows the UC scheme of partial conventional units. In Figure 7, the gray represents unit on operation while the white represents unit shutdown. The comparison of reserve in different scenarios is shown in Figure 8.

The comparison of scenario 1 and 2 shows the influence of different flexibility requirements upon reserve. When the flexibility requirement rises, the system reserve significantly increases. The comparison of scenario 1 and 3 displays the impact of load prediction error upon reserve. Compared to scenario 1, the load prediction error in scenario 3 is larger, and the reserve significantly increases. The reserve of scenario 4 is almost the same with scenario 1. This is because the total capacity of wind power is relatively small, so the increase in wind power output fluctuation caused by the increase in wind power prediction error has less impact on system flexibility.

The above simulation results showed that the reserve increased as flexibility requirement rose. When the uncertainty of the system diminishes, such as the lowered load prediction SD and wind speed prediction SD, the operating reserve will decrease. Those cases listed above demonstrate that the reserve capacity obtained by the proposed model could accurately reflect the system uncertainty and flexibility, hence verifying the validity of the proposed model and algorithm.

In order to further analyze the influence of wind power upon the operating reserve, the system reserve was calculated under different wind power penetration rates. In scenario 1, the total wind power capacity was 350 MW, with a penetration rate of 5%. The scenarios of no wind power and integrated wind power capacity of 800 MW, 1250 MW and 1800 MW were calculated separately, corresponding to wind power penetration rates of 0%, 10%, 15% and 20%, respectively. The solution information is listed in

Table 3. Solution information under different wind power penetration rates.

Wind Power Penetration Rates	Solution Time	Number of Iterations	Objective Function Value
0%	51′31″	1	$2.00 × 106
5%	52′08″	1	$1.96 × 106
10%	93′32″	2	$1.92 × 106
15%	91′17″	2	$1.92 × 106
20%	94′43″	2	$1.95 × 106

.

When the wind power penetration rate was relatively low, the UC scheme of initial solution by the upper level model could provide sufficient reserve capacity. However, the uncertainty in the system increased with the rising of the wind power penetration rate. Although wind power generation cost was neglected, the unit generation cost increased as wind power penetration increased. When the penetration rate reached 10% or more, the UC scheme of first iteration failed to meet the reserve requirement, and the reserve model in the lower level corrected the flexibility constraint and then re-solved the entire model. To facilitate analysis, Figure 9 only displays the reserve at 2 a.m. under different wind power penetration rates.

Figure 9 shows that wind power had a significant influence on system flexibility. The flexibility based reserve was positively correlated with the wind power penetration rate. The growth rate of the flexibility based reserve also shows a positively correlation with the wind power penetration rate.

5. Conclusions

For the issue of the reserve decision and coordinated optimization of generation and reserve of power system integrated with large-scale renewable energy, this paper proposed a day-ahead generation–reserve bilevel decision model. The flexibility models of the load and wind power are built on the basis of historical data and forecast information, while the conventional unit are modeled by the output plan and forced outage rate. Then the quantitative relationship between flexibility and operating reserve is established by the universal generating function theory. Taking it as a constraint, the day-ahead power generation-reserve bilevel decision model is formulated.

The generation-reserve joint dispatching scheme obtained from the proposed model cannot only meet the load, but also ensure the flexibility to meet given requirements. In this way, the dispatching scheme ensures that there is sufficient reserve capability to cope with uncertainties and fluctuation within the system. Other players, e.g., demand response, storage and electric vehicle, will also provide reserve services. The quantitative relationship between the flexibility and operating reserve established in this paper can provide reference for the auxiliary service market.