Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations
Abstract
1. Introduction
2. Related Work
3. Navigation Process
4. Victim Detection
4.1. Formation Control
4.2. Distributed Estimation Consensus
5. Simulation Results
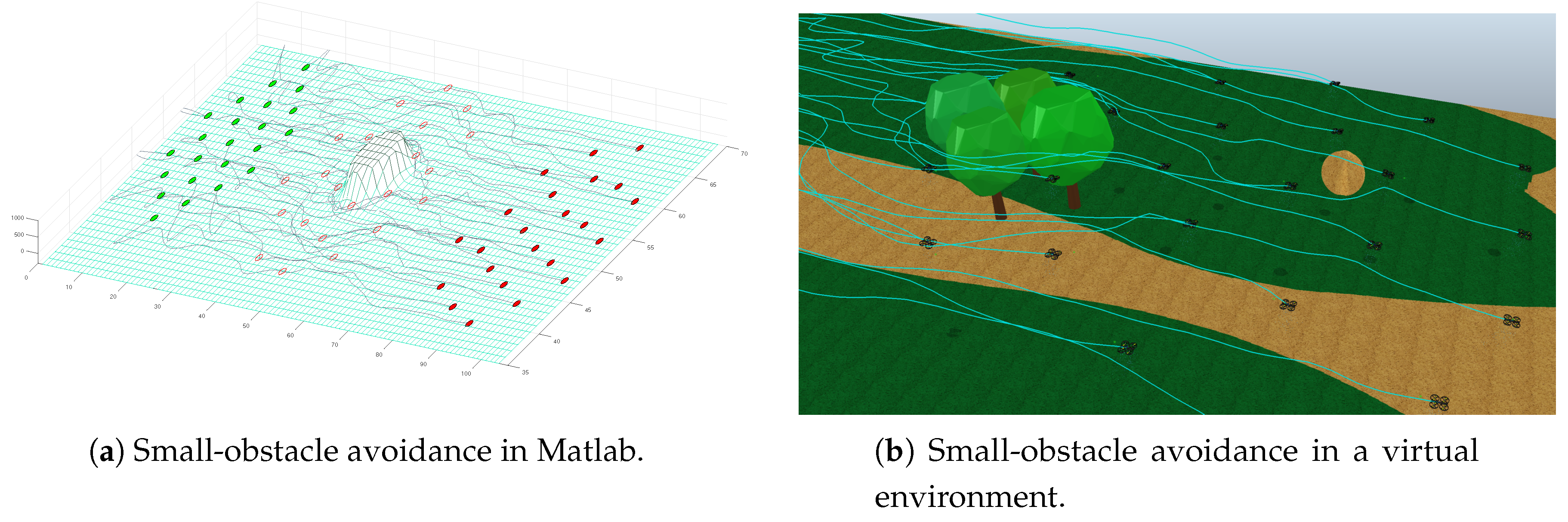
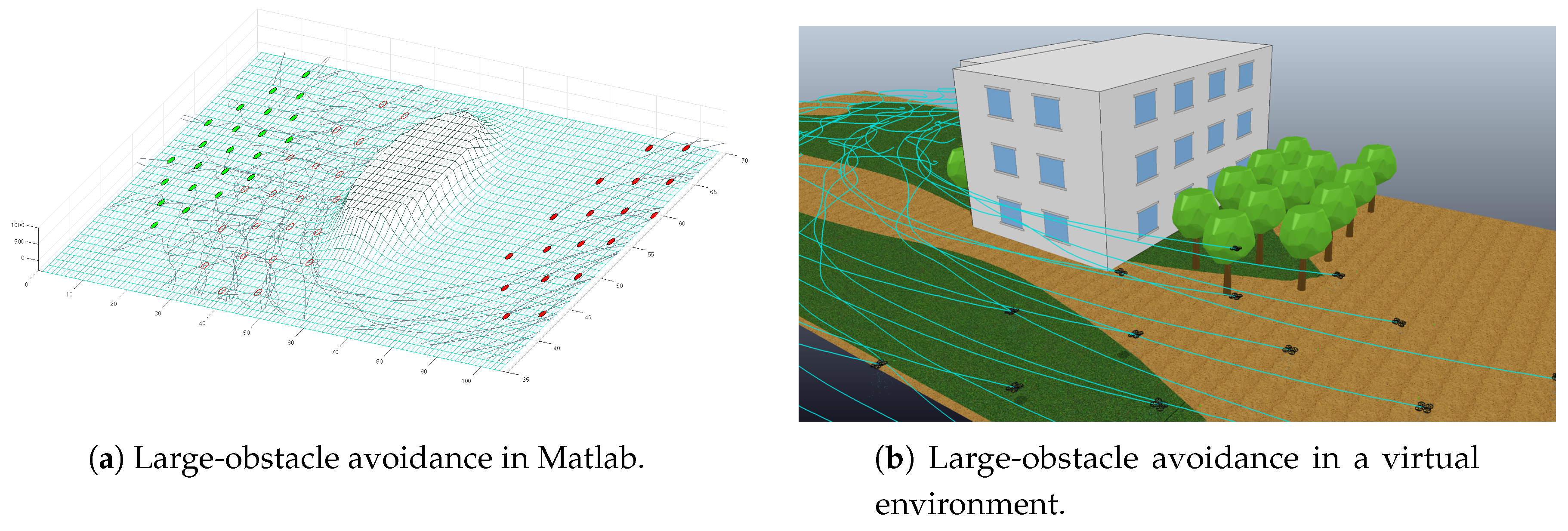
5.1. Obstacle Avoidance
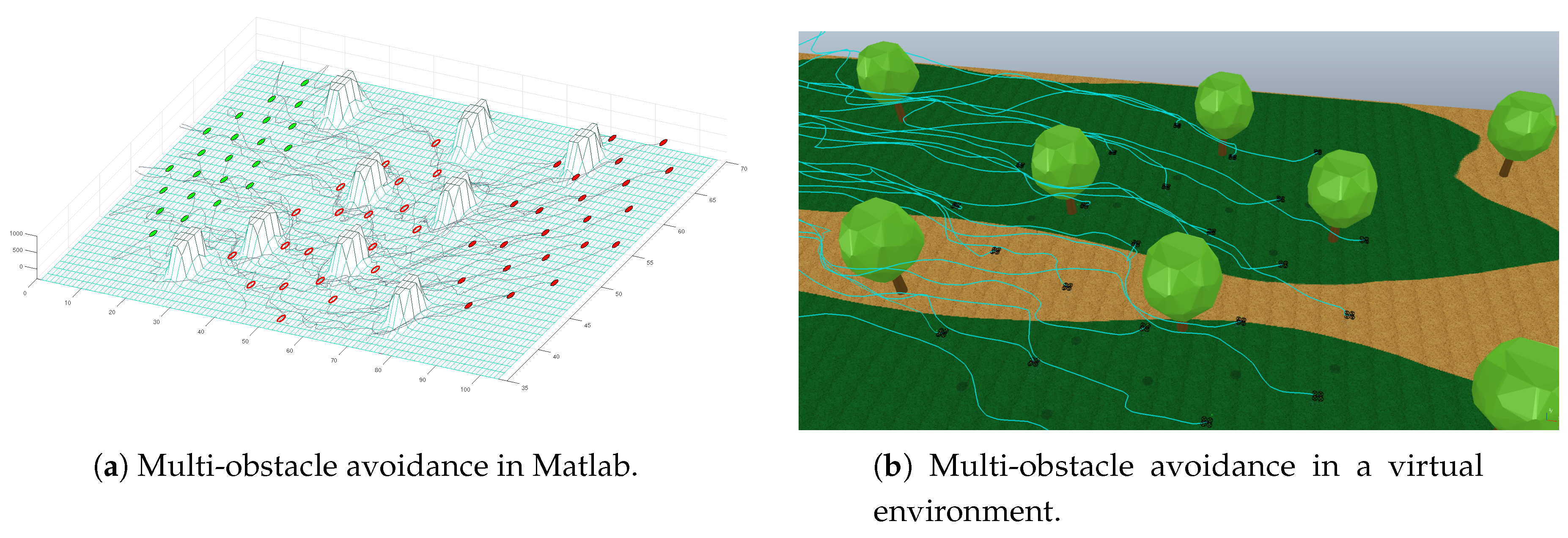
5.2. Multiple Obstacles
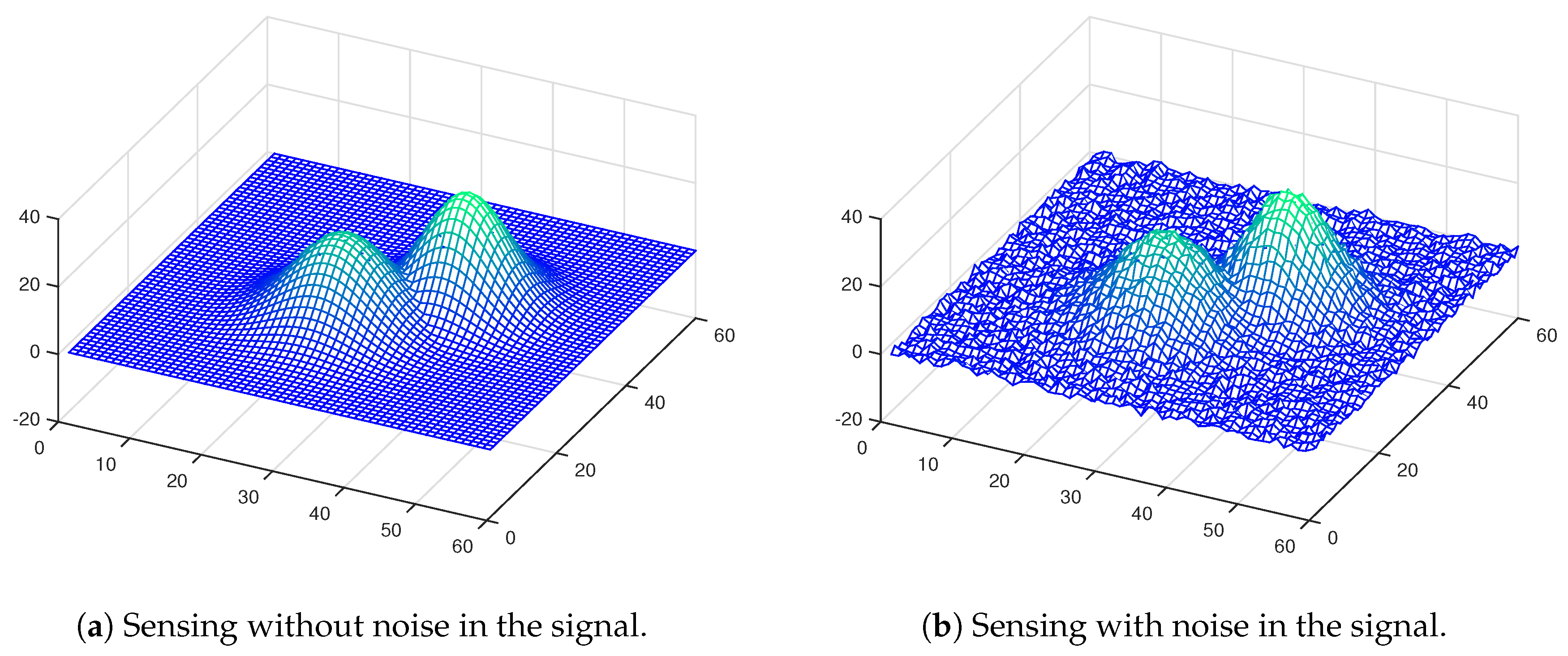
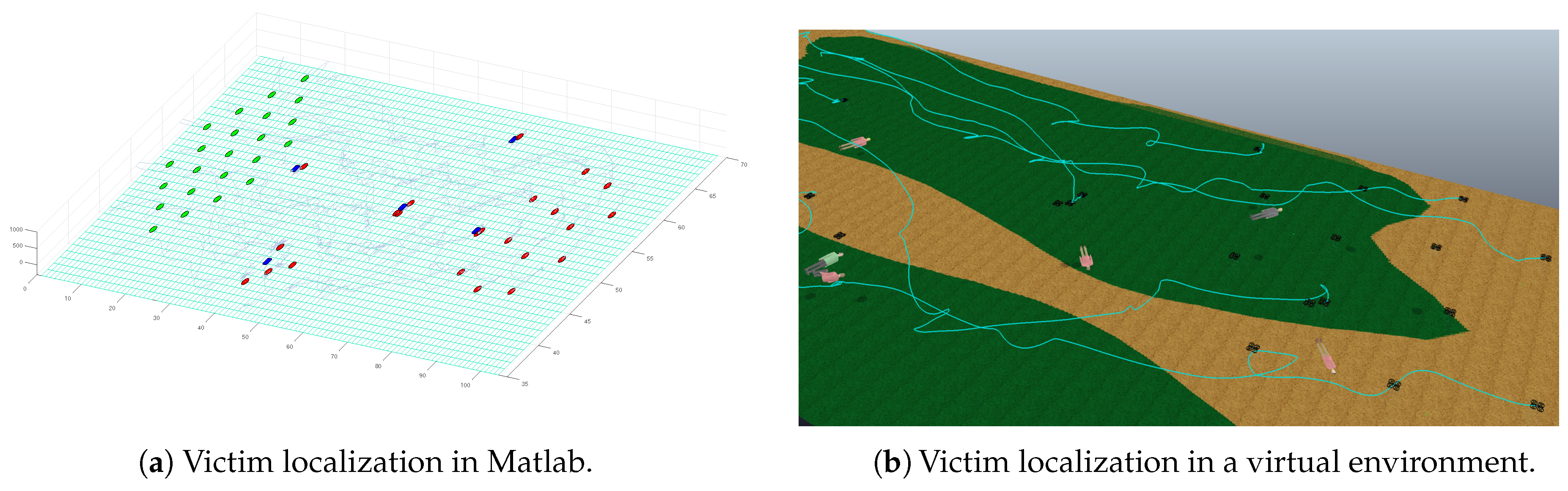
5.3. Victim Localization
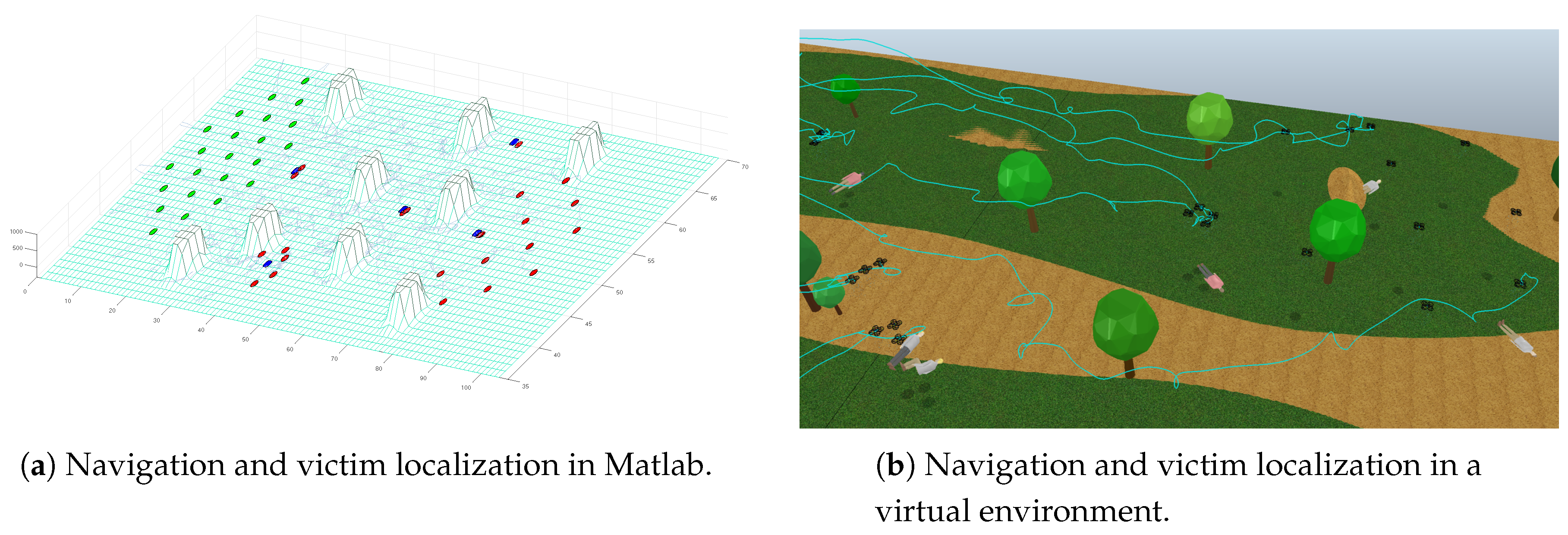
5.4. Navigation and Victim Localization
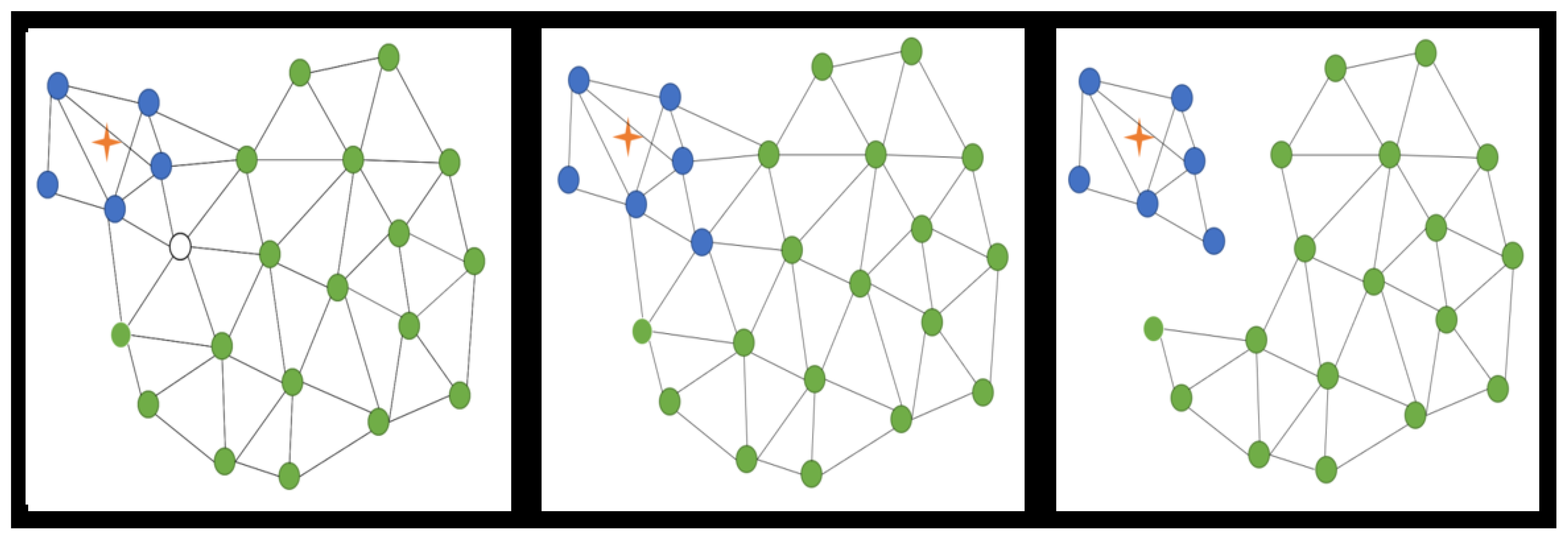
5.5. Sub-Swarm Formation for Distributed Estimation Consensus
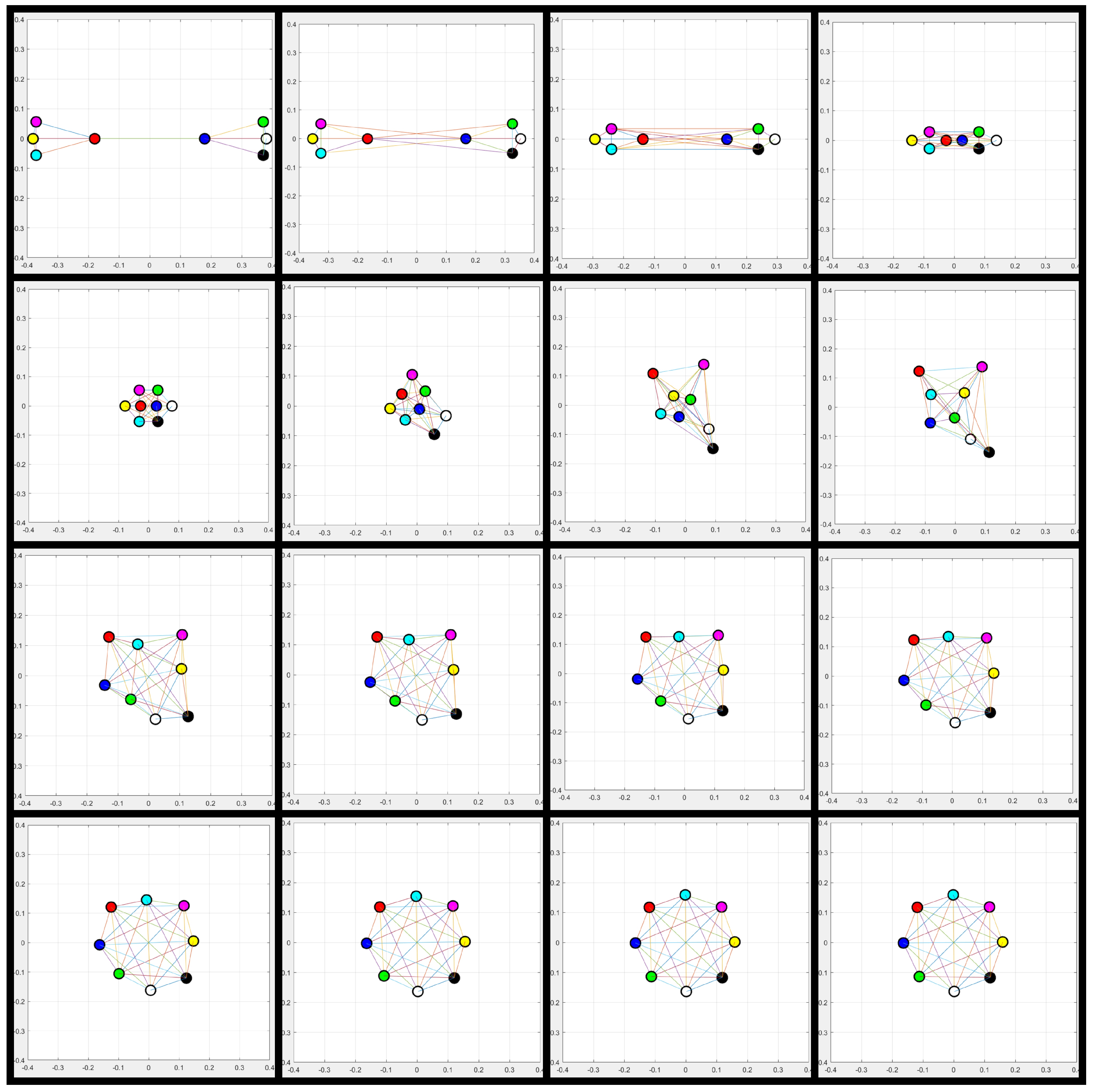
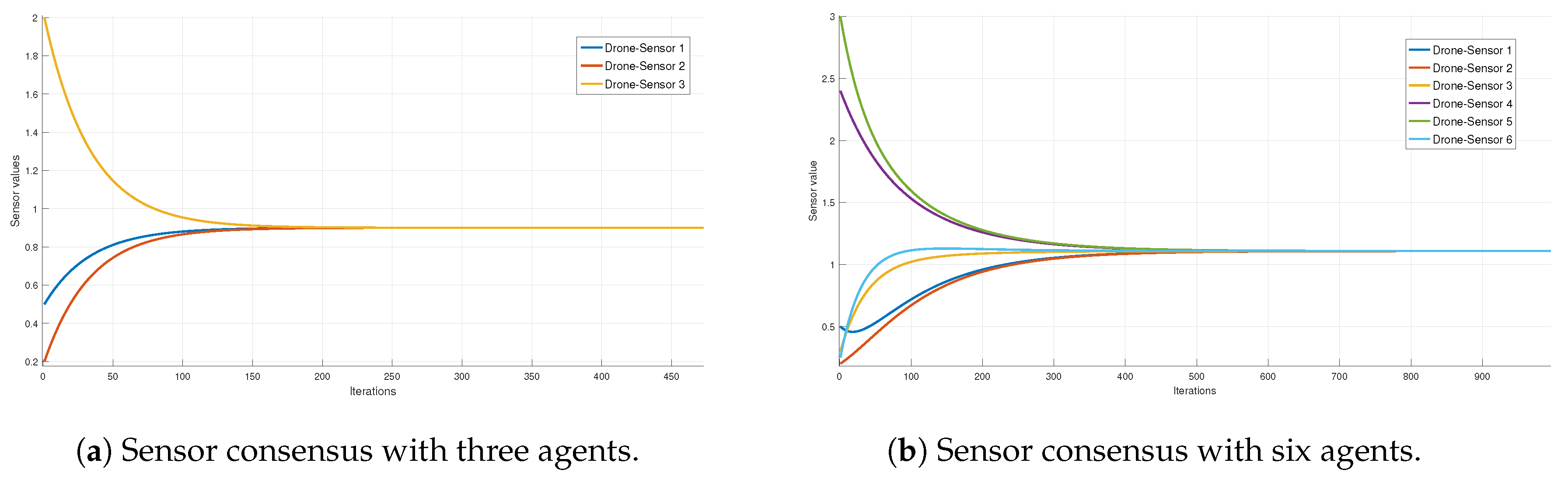
5.6. Convergence Analysis of the Distributed Estimation Consensus
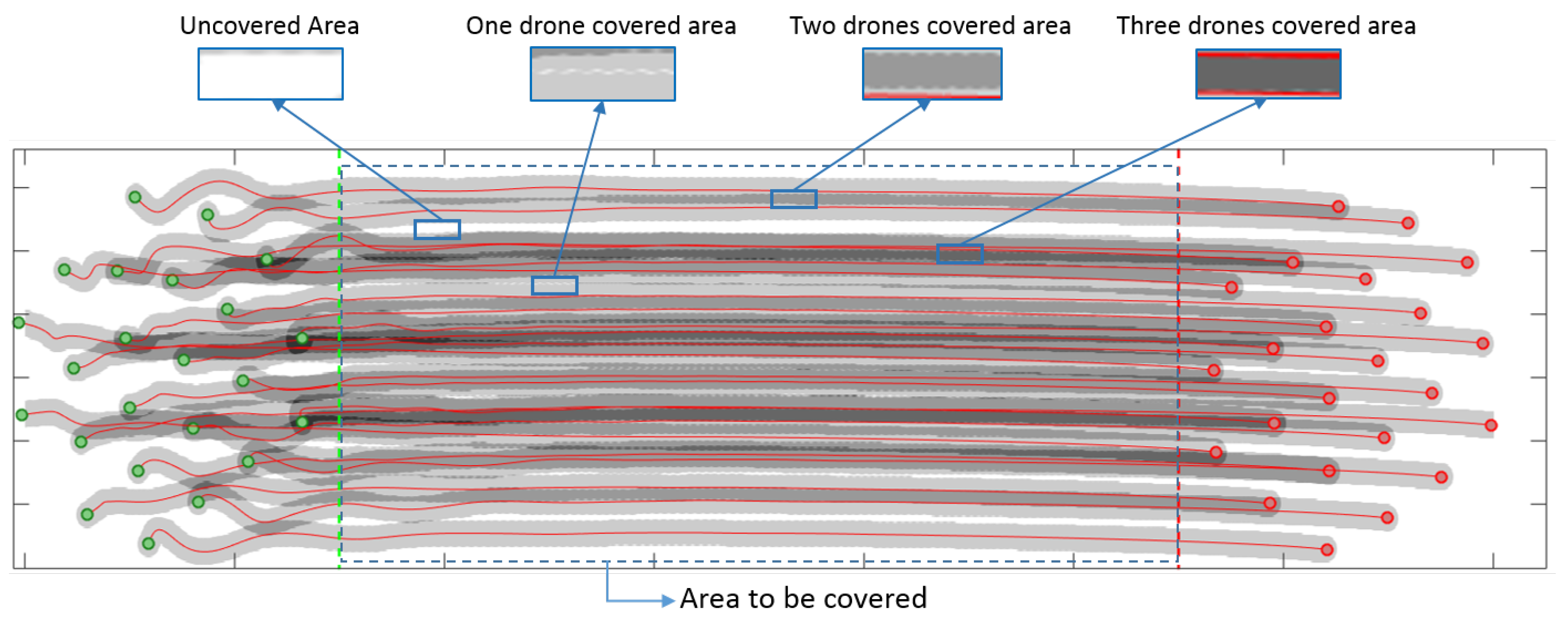
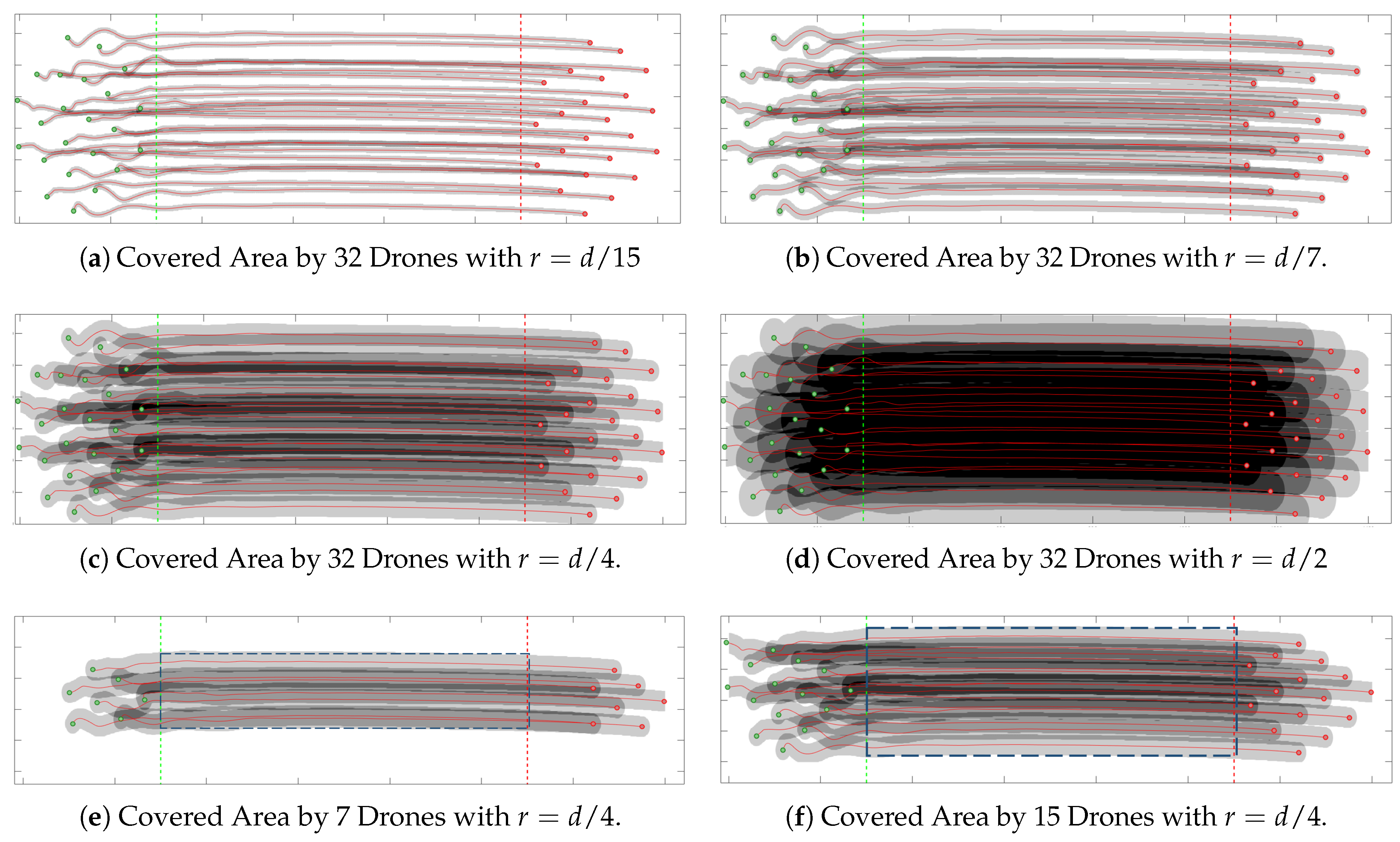
5.7. Effective Coverage Area
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Basic Concepts of Graph Theory
References
- Casper, J.; Murphy, R.R. Human-robot interactions during the robot-assisted urban search and rescue response at the world trade center. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2003, 33, 367–385. [Google Scholar] [CrossRef] [PubMed]
- Ventura, R.; Lima, P.U. Search and rescue robots: The civil protection teams of the future. In Proceedings of the 2012 Third International Conference on Emerging Security Technologies, Lisbon, Portugal, 5–7 September 2012; pp. 12–19. [Google Scholar]
- Latscha, S.; Kofron, M.; Stroffolino, A.; Davis, L.; Merritt, G.; Piccoli, M.; Yim, M. Design of a Hybrid Exploration Robot for Air and Land Deployment (HERALD) for urban search and rescue applications. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 1868–1873. [Google Scholar]
- Seljanko, F. Low-cost electronic equipment architecture proposal for urban search and rescue robot. In Proceedings of the 2013 IEEE International Conference on Mechatronics and Automation (ICMA), Takamatsu, Japan, 4–7 August 2013; pp. 1245–1250. [Google Scholar]
- Doroodgar, B.; Ficocelli, M.; Mobedi, B.; Nejat, G. The search for survivors: Cooperative human-robot interaction in search and rescue environments using semi-autonomous robots. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–8 May 2010; pp. 2858–2863. [Google Scholar]
- Pfotzer, L.; Ruehl, S.; Heppner, G.; Rönnau, A.; Dillmann, R. KAIRO 3: A modular reconfigurable robot for search and rescue field missions. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics (ROBIO), Bali, Indonesia, 5–10 December 2014; pp. 205–210. [Google Scholar]
- Tan, Y.; Zheng, Z.Y. Research advance in swarm robotics. Def. Technol. 2013, 9, 18–39. [Google Scholar] [CrossRef]
- Husni, N.L.; Handayani, A.S.; Nurmaini, S.; Yani, I. Cooperative searching strategy for swarm robot. In Proceedings of the 2017 International Conference on Electrical Engineering and Computer Science (ICECOS), Palembang, Indonesia, 22–23 August 2017; pp. 92–97. [Google Scholar]
- Yanguas-Rojas, D.; Cardona, G.A.; Ramirez-Rugeles, J.; Mojica-Nava, E. Victims search, identification, and evacuation with heterogeneous robot networks for search and rescue. In Proceedings of the 2017 IEEE 3rd Colombian Conference on Automatic Control (CCAC), Cartagena, Colombia, 18–20 October 2017; pp. 1–6. [Google Scholar]
- Cardona, G.A.; Yanguas-Rojas, D.; Arevalo-Castiblanco, M.F.; Mojica-Nava, E. Ant-Based Multi-Robot Exploration in Non-Convex Space without Global-Connectivity Constraints. In Proceedings of the 2019 European Control Conference (ECC), Naples, Italy, 25–28 June 2019. [Google Scholar]
- Zavlanos, M.M.; Egerstedt, M.B.; Pappas, G.J. Graph-theoretic connectivity control of mobile robot networks. Proc. IEEE 2011, 99, 1525–1540. [Google Scholar] [CrossRef]
- Torres-Torriti, M.; Arredondo, T.; Castillo-Pizarro, P. Survey and comparative study of free simulation software for mobile robots. Robotica 2016, 34, 791–822. [Google Scholar] [CrossRef]
- Zhang, F.; Leitner, J.; Milford, M.; Corke, P. Sim-to-real transfer of visuo-motor policies for reaching in clutter: Domain randomization and adaptation with modular networks. World 2017, 7, 8. [Google Scholar]
- León, J.; Cardona, G.A.; Botello, A.; Calderon, J.M. Robot swarms theory applicable to seek and rescue operation. In Proceedings of the International Conference on Intelligent Systems Design and Applications, Porto, Portugal, 16–18 December 2016; Springer: Cham, Switzerland, 2016; pp. 1061–1070. [Google Scholar]
- León, J.; Cardona, G.A.; Jaimes, L.G.; Calderon, J.M.; Rodriguez, P.O. Rendezvous Consensus Algorithm Applied to the Location of Possible Victims in Disaster Zones. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 3–7 June 2018; Springer: Cham, Switzerland, 2018; pp. 700–710. [Google Scholar]
- Quesada, W.O.; Rodriguez, J.I.; Murillo, J.C.; Cardona, G.A.; Yanguas-Rojas, D.; Jaimes, L.G.; Calderon, J.M. Leader-Follower Formation for UAV Robot Swarm Based on Fuzzy Logic Theory. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 3–7 June 2018; Springer: Cham, Switzerland, 2018; pp. 740–751. [Google Scholar]
- de Sousa Paula, P.; de Castro, M.F.; Paillard GA, L.; Sarmento, W.W. A swarm solution for a cooperative and self-organized team of UAVs to search targets. In Proceedings of the 2016 8th Euro American Conference on Telematics and Information Systems (EATIS), Cartagena, Colombia, 28–29 April 2016; pp. 1–8. [Google Scholar]
- Couceiro, M.S.; Rocha, R.P.; Ferreira, N.M. A novel multi-robot exploration approach based on particle swarm optimization algorithms. In Proceedings of the 2011 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Kyoto, Japan, 1–5 November 2011; pp. 327–332. [Google Scholar]
- Edlinger, R.; Zauner, M.; Rokitansky, W. RRTLAN-A real-time robot communication protocol stack with multi threading option. In Proceedings of the 2013 IEEE International Symposium on Safety, Security, and Rescue Robotics (SSRR), Linkpoping, Sweden, 21–26 October 2013; pp. 1–5. [Google Scholar]
- Wiltsche, C.; Lygeros, J.; Ramponi, F.A. Synthesis of an asynchronous communication protocol for search and rescue robots. In Proceedings of the 2013 European Control Conference (ECC), Zurich, Switzerland, 17–19 July 2013; pp. 1256–1261. [Google Scholar]
- Pan, Q.W.; Lowe, D. Search and rescue robot team RF communication via power cable transmission line—A proposal. In Proceedings of the International Symposium on Signals, Systems and Electronics, ISSSE’07, Montreal, QC, Canada, 30 July–2 August 2007; pp. 287–290. [Google Scholar]
- Araujo, F.; Santos, J.; Rocha, R.P. Implementation of a routing protocol for Ad Hoc networks in search and rescue robotics. In Proceedings of the 2014 IFIP Wireless Days (WD), Rio de Janeiro, Brazil, 12–14 November 2014; pp. 1–7. [Google Scholar]
- Nurellari, E.; McLernon, D.C.; Ghogho, M. Distributed two-step quantized fusion rules via consensus algorithm for distributed detection in wireless sensor networks. IEEE Trans. Signal Inf. Process. Netw. 2016, 2. [Google Scholar] [CrossRef]
- Ghassemian, H. A review of remote sensing image fusion methods. Inf. Fusion 2016, 32, 75–89. [Google Scholar] [CrossRef]
- Misra, S.; Vasilakos, A.V.; Obaidat, M.S.; Krishna, P.V.; Agarwal, H.; Saritha, V. A fault-tolerant routing protocol for dynamic autonomous unmanned vehicular networks. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 3525–3529. [Google Scholar]
- Chelbi, S.; Duvallet, C.; Abdouli, M.; Bouaziz, R. Event-driven wireless sensor networks based on consensus. In Proceedings of the 2016 IEEE/ACS 13th International Conference of Computer Systems and Applications (AICCSA), Agadir, Morocco, 29 November–2 December 2016; pp. 1–6. [Google Scholar]
- Li, X.; Qiao, D.; Li, Y.; Dai, H. A novel through-wall respiration detection algorithm using uwb radar. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 1013–1016. [Google Scholar]
- Li, J.; Liu, L.; Zeng, Z.; Liu, F. Advanced signal processing for vital sign extraction with applications in UWB radar detection of trapped victims in complex environments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 783–791. [Google Scholar]
- Friedman, M.; Haddad, Y.; Blekhman, A. ACOUFIND: Acoustic ad-hoc network system for trapped person detection. In Proceedings of the 2015 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems (COMCAS), Tel-Aviv, Israel, 2–4 November 2015; pp. 1–4. [Google Scholar]
- Couceiro, M.S.; Portugal, D.; Rocha, R.P. A collective robotic architecture in search and rescue scenarios. In Proceedings of the 28th Annual ACM Symposium on Applied Computing, Coimbra, Portugal, 18–22 March 2013; pp. 64–69. [Google Scholar]
- Alvissalim, M.S.; Zaman, B.; Hafizh, Z.A.; Ma’sum, M.A.; Jati, G.; Jatmiko, W.; Mursanto, P. Swarm quadrotor robots for telecommunication network coverage area expansion in disaster area. In Proceedings of the 2012 SICE Annual Conference (SICE), Akita, Japan, 20–23 August 2012; pp. 2256–2261. [Google Scholar]
- Rocha, R.; Dias, J.; Carvalho, A. Cooperative multi-robot systems: A study of vision-based 3-d mapping using information theory. Robot. Auton. Syst. 2005, 53, 282–311. [Google Scholar] [CrossRef]
- Rohmer, E.; Singh, S.P.; Freese, M. V-REP: A versatile and scalable robot simulation framework. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Tokyo, Japan, 3–8 November 2013; pp. 1321–1326. [Google Scholar]
- Messina, E.R.; Jacoff, A.S. Measuring the performance of urban search and rescue robots. In Proceedings of the 2007 IEEE Conference on Technologies for Homeland Security, Woburn, MA, USA, 16–17 May 2007; pp. 28–33. [Google Scholar]
- Chiou, A.; Wynn, C. Urban search and rescue robots in test arenas: Scaled modeling of disasters to test intelligent robot prototyping. In Proceedings of the UIC-ATC’09—Symposia and Workshops on Ubiquitous, Autonomic and Trusted Computing, Brisbane, Australia, 7–9 July 2009; pp. 200–205. [Google Scholar]
- Saeedi, P.; Sorensen, S.A.; Hailes, S. Performance-aware exploration algorithm for search and rescue robots. In Proceedings of the 2009 IEEE International Workshop on Safety, Security & Rescue Robotics (SSRR), Denver, CO, USA, 3–6 November 2009; pp. 1–6. [Google Scholar]
- Seeley, T.D.; Buhrman, S.C. Group decision making in swarms of honey bees. Behav. Ecol. Sociobiol. 1999, 45, 19–31. [Google Scholar] [CrossRef]
- Mesbahi, M.; Egerstedt, M. Graph Theoretic Methods in Multiagent Networks; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Reynolds, C.W. Flocks, herds and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Gr. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Bullo, F.; Cortes, J.; Martinez, S. Distributed Control of Robotic Networks: A Mathematical Approach to Motion Coordination Algorithms; Princeton University Press: Princeton, NJ, USA, 2009; Volume 27. [Google Scholar]
- Calderon, J. Mobile Robotics & Intelligent Systems. Robot Swarm Navigation-Obstacles. 2018. Available online: https://youtu.be/6B5TVmT8knI (accessed on 21 March 2019).
- Calderon, J. Mobile Robotics & Intelligent Systems. Robot Swarm Navigation. 2018. Available online: https://youtu.be/F2tsg9jzIoY (accessed on 21 March 2019).




| Agents Number | Average Convergence Iteration | Standard Deviation | Average Convergence Time |
|---|---|---|---|
| 3 | 176.6 | 8.3 | 90.6 (mS) |
| 5 | 404.9 | 22.4 | 103.9 (mS) |
| 7 | 602.6 | 39.4 | 144.5 (mS) |
| 10 | 1162.4 | 102.3 | 226.6 (mS) |
| r | Uncovered | Covered | +2 Drones | +3 Drones | +4 Drones | +5 Drones |
|---|---|---|---|---|---|---|
| d/15 | 43.10% | 56.89% | 9.55% | 0.0014% | 0.0% | 0.0% |
| d/8 | 13.51% | 86.48% | 42.01% | 4.35% | 0.0069% | 0.0% |
| d/5 | 1.73% | 98.26% | 73.28% | 24.57% | 3.06% | 0.0% |
| d/4 | 0.0% | 100% | 87.77% | 54.55% | 20.53% | 0.20% |
| d/3 | 0.0% | 100% | 94.34% | 80.14% | 52.72% | 14.56% |
| d/2 | 0.0% | 100% | 98.17% | 94.04% | 85.42% | 71.26% |
| d | 0.0% | 100% | 100% | 100% | 97.57% | 96.11% |
| Drone Number | Uncovered | Covered | +2 Drones | +3 Drones | +4 Drones | +5 Drones |
|---|---|---|---|---|---|---|
| 7 | 0.0% | 100% | 93.14% | 16.63% | 0.01% | 0.0% |
| 12 | 1.02% | 98.87% | 83.88% | 29.8% | 5.03% | 0.0% |
| 17 | 0.0% | 100% | 89.10% | 48.48% | 11.87% | 0.0% |
| 23 | 0.0% | 100% | 87.77% | 54.55% | 20.53% | 0.20% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardona, G.A.; Calderon, J.M. Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations. Appl. Sci. 2019, 9, 1702. https://doi.org/10.3390/app9081702
Cardona GA, Calderon JM. Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations. Applied Sciences. 2019; 9(8):1702. https://doi.org/10.3390/app9081702
Chicago/Turabian StyleCardona, Gustavo A., and Juan M. Calderon. 2019. "Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations" Applied Sciences 9, no. 8: 1702. https://doi.org/10.3390/app9081702
APA StyleCardona, G. A., & Calderon, J. M. (2019). Robot Swarm Navigation and Victim Detection Using Rendezvous Consensus in Search and Rescue Operations. Applied Sciences, 9(8), 1702. https://doi.org/10.3390/app9081702




