Abstract
Novel methods of coherent short-wavelength sources generation require thorough analysis for their further amendments and practical implementations. In this work, we report on the quasi-phase matching (QPM) of high-order harmonics generation during the propagation of single- and two-color femtosecond pulses through multi-jet plasmas, which allows the enhancement of groups of harmonics in different ranges of extreme ultraviolet. The role of the number of coherent zones; sizes of plasma jets and the distance between them; plasma formation conditions, and the characteristics of the fundamental radiation on the harmonic efficiency at quasi-phase matching (QPM) conditions are analyzed. We demonstrate the ~40× enhancement factor of the maximally-enhanced harmonic with respect to the one generated at ordinary conditions in the imperforated plasma.
1. Introduction
The interaction of ultrashort laser pulses with gases, plasmas, surfaces, and solids allows the conversion of longer-wavelength laser sources towards the extreme ultraviolet (XUV) region. This approach took special attention due to relative easiness in generating coherent short-wavelength radiation. Increasing the length of laser-matter interaction to attain stronger nonlinear optical response from extended media is one of the methods that has been applied to enhance the coherent XUV yield during high-order harmonic generation (HHG). This method, though attractive in the case of ablation of extended targets, has a significant drawback related to the phase mismatch between the interacting waves of the driving pulse and the generated harmonic when the length of medium exceeds the coherence length of the generated harmonic order.
To diminish the effect of phase mismatch in laser-produced plasmas (LPP) on the HHG efficiency, the concept of quasi-phase matching (QPM) using the modulated shape of the LPP, was employed to minimize the difference between the phases of two waves. This modulation is based on the division of extended plasma into a set of equidistantly-separated plasma jets either by inserting multi-slit mask (MSM) in front of ablating surface [1], or by using perforated targets [2].
Initially, QPM concept for HHG was introduced in the gaseous media and was studied both theoretically and experimentally using different methods of gaseous medium modulation [3,4,5,6,7,8,9,10,11,12,13,14]. Previously, phase mismatch compensation was obtained by using counter-propagating driving beams, off-axis phase matching, phase-matching in low-frequency fields, control of the pressure in modulated waveguides, the addition of a buffer gas with anomalous dispersion, self-focusing by the Kerr nonlinearity, and the application of gaseous multi-jet structures.
The conditions of QPM in multi-jet plasmas are similar to those reported in the case of gaseous multi-jet structures [6,9,10]. The principles of QPM developed in those studies, as well as the theoretical approaches proposed in the case of QPM in plasmas [15,16,17], allow describing the main peculiarities of this approach and comparing the theoretical predictions and experimental observations of QPM. In the study of QPM conditions, it is usually assumed that the target is in some fixed state with some given degree and level of ionization. The model that is used in the numerical calculations takes into account the amplitudes and phases of the harmonics generated by single atoms placed in any point of the medium. The values of the amplitudes and phases are calculated by solving the quantum-mechanical problem of a single atom interacting with laser field. However, while using the single atom response under different laser parameters, it is also important to take into account the change in the profile of the driving pulse while propagating in the medium [18].
Currently, the use of two-color pumps (TCP) in gases and plasmas is a reliable approach to enhance the HHG conversion efficiency. Strong harmonic generation in the case of TCP is possible due to the formation of a quasi-linear field, and a selection of a short quantum path component, which has a denser electron wave packet and higher ionization rate compared to the single-color pump (SCP) [19]. The orthogonally-polarized second field also participates in the modification of the trajectory of accelerated electrons from being two-dimensional to three-dimensional, which may lead to the removal of the medium symmetry. With suitable control of the relative phase between the fundamental and the second harmonic radiation, the latter field enhances the short path contribution resulting in a clean spectrum of harmonics.
This TCP-induced enhancement of harmonics has been earlier realized through the generation of 400-nm radiation in a separate channel with further mixing with 800-nm radiation in gases, as well as through direct generation of second harmonic in thin barium borate (BBO) crystals followed by focusing two co-propagating beams in gases [20,21]. The following studies of TCP in LPPs [22,23] have also shown the advantages of the TCP in LPP, in comparison with the SCP, using both 800 nm and 1300 nm fundamental sources and their second harmonic.
The installation of the nonlinear crystal inside the vacuum chamber on the path of focused radiation allows excluding the spatial walk-off effect and the influence of the dispersion of window and focusing lens [24]. The temporal and spatial overlaps between the two beams become sufficient for the interaction of two waves in the extended plasma plume, provided that the thickness of BBO crystal is chosen properly and optimized from various points of view.
In this paper, we analyze different schemes, allowing the modifications of harmonic spectra at the conditions of QPM in silver, indium, and gold multi-jet plasmas using single- and two-color femtosecond pumps at the peak intensities of 5 × 1014 and 1.4 × 1014 W cm−2, for 800 and 1320 nm pumps, respectively. We report the role of the number of coherent zones, sizes of plasma jets, plasma formation conditions, and the characteristics of fundamental radiation on the HHG efficiency at QPM conditions in different ranges of XUV. We demonstrate the TCP-induced QPM at different regimes of laser-plasma interaction. We also present the theoretical approach describing the observed peculiarities of HHG spectra modulation based on the model described in Ref. [18], and compare our calculations with the experimental data.
2. Experiment
2.1. Scheme for the Formation of QPM Conditions in Plasma
The experimental setup consists of Ti:Sapphire laser, traveling-wave optical parametric amplifier (OPA) of white-light continuum, and HHG scheme using the propagation of two pulses (the amplified signal radiation from OPA and 800 nm radiation, as well as their second harmonics) through the extended LPP. We used the mode-locked Ti:Sapphire laser (TSUNAMI, Spectra−Physics Lasers) pumped by diode-pumped, cw laser (MILLENIA Vs, Spectra−Physics Lasers) as the source of 803 nm, 55 fs, 82 MHz, 450 mW pulses for injection in the pulsed Ti:sapphire regenerative amplifier with pulse stretcher and additional double-pass linear amplifier (TSA−10, Spectra−Physics Lasers). The output characteristics of uncompressed radiation from this laser were as follows: central wavelength 800 nm, pulse duration 370 ps, pulse energy 4 mJ, 10 Hz pulse repetition rate. This radiation was further amplified up to 22 mJ in the home-made three-pass Ti:Sapphire linear amplifier. Part of the amplified radiation with pulse energy of 5 mJ was separated from the whole beam and used as a heating pulse for homogeneous extended plasma formation using cylindrical lens of 200 mm focal length installed in front of the 5-mm long target placed in the vacuum chamber (Figure 1). The intensity and fluence of the heating pulse on the target surface were varied up to 4 × 109 W cm−2 and 1.4 J cm−2, respectively. We used 5-mm-long targets for ablation and formation of extended homogeneous and structured plasmas. The ablation area was 5 × 0.08 mm2.
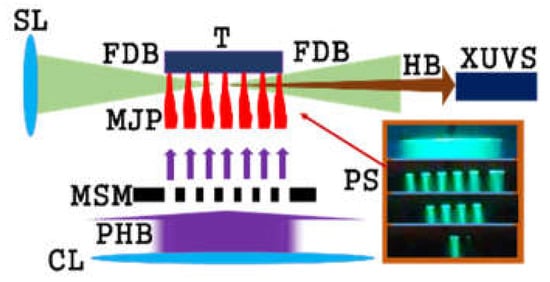
Figure 1.
Experimental setup for high-order harmonic generation (HHG) in MJP. CL, cylindrical lens; PHB, picosecond heating beam; MSM, multi-slit mask; MJP, multi-jet plasma; T, target; SL, spherical lens; FDB, femtosecond driving beam; HB, harmonic beam; XUVS, extreme ultraviolet spectrometer. Inset: The extended, six-, four-, and single-jet plasma images are shown from the top to bottom. PS, plasma shapes.
The remaining part of the amplified radiation was delayed with respect to the heating pulse in such a way that, after compression and pump of OPA, the signal pulse from parametric amplifier propagated through the plasma plume 40 ns after the beginning of target irradiation by heating pulses, which is assumed to be optimal for ablation of used samples and harmonic generation. After propagation through the compressor stage, laser pulses of 810 nm central wavelength, 8 mJ energy, 50 fs duration, 10 Hz repetition rate, and pulse bandwidth of 17 nm were produced. This radiation pumped the OPA (HE-TOPAS Prime, Light Conversion). The signal and idler pulses from the OPA allowed tuning in the 1200–1600 nm, and 1600–2600 nm ranges, respectively.
In our HHG experiments we mostly used the signal pulses, which were ~1.5 times stronger than the idler pulses. Most of the experiments were carried out using the 1 mJ, 70 fs signal pulses tunable in the range of 1200–1600 nm; and 3 mJ, 50 fs, 810 nm pulses. The spectral bandwidth of the tunable near infrared (NIR) pulses was 40 nm. The intensity of the 1310 nm pulses, showing the highest yield from OPA, was 2 × 1014 W cm−2. The driving pulses were focused onto the extended plasma at a distance of ~100–150 µm above the target surface. The harmonic yield was maximized by adjusting the position of target with regard to the optical axis of propagation of two driving pulses and by varying their focusing positions relative to the extended plasma. The harmonic emission was analyzed using an XUV spectrometer containing a cylindrical mirror and a 1200 grooves/mm flat field grating with variable line spacing. The spectrum was recorded on a micro-channel plate detector backed by phosphor screen, which was imaged onto a CCD camera.
The multi-slit mask (MSM) was installed between the cylindrical lens and the target to produce multi-jet plasma (MJP, Figure 1). The width of each slit was varied between 0.3 and 0.8 mm with similar distance between slits.
The electron density of plasma (7 × 1016 cm−3) was estimated using the hydrodynamic code HYADES [25]. Similar estimates were reported in [26]. We also estimated the electron density using the relation for QPM (Ne ≈ 1 × 1018/Lcoh × Hqpm), where (Hqpm) is the maximally enhanced harmonic of the NIR radiation, and Lcoh is the coherence length, which is actually the length of single plasma jet [27]. This approach of determining the electron density provided almost similar value (~1 × 1017 cm−3), considering the uncertainties of some parameters.
The plasma plume had a cone shape with angle of divergence of 200. The delay between driving and heating pulses was chosen from the point of view of maximal harmonic yield, which means that the driving femtosecond pulse propagated through the most “optimal” part of the plasma plume. The meaning of “optimal plasma” refers to the complex conditions when different impeding processes play a minimal role in the formation of the maximally favorable conditions for HHG.
The fundamental radiation (810 nm or tunable NIR radiation) and its second harmonic, which was produced by propagating the fundamental beam through 0.3-mm thick (BBO) crystal installed inside the vacuum chamber, were focused onto the MJP. The same BBO was used to double both 810 nm and 1320 nm radiation at appropriate phase matching angle (290 and 210, respectively). The duration of the driving pulses was sufficiently long to provide the phase matching bandwidth in this crystal for both wavelengths. The position of the focused femtosecond beam was approximately 0.15 mm away from the targets surface. The Rayleigh range of femtosecond beam was 4 mm, i.e., close to the whole length of plasma, thus assuming that the driving beam propagated through the 5 mm long plasma at the condition of almost plane wave-plasma interaction, which was exactly simulated during this study. Thus, the role of Gouy phase was neglected in this study. The peak intensities of 810 nm and 1320 nm pumps in the plasma area were 5 × 1014 and 1.4 × 1014 W cm−2, respectively.
In the case of the TCP comprising of 1320 and 660 nm waves, due to the group velocity dispersion in type-I BBO crystal, the 1320-nm pulse was delayed by 26 fs with respect to the second harmonic pulse when using 0.3-mm-long BBO crystal. This delay is obtained from (Δcryst = d[(noω)group/c − (ne2ω)group/c], where d is the crystal length, c/(noω)group and c/(ne2ω)group are the group velocities of the ω and 2ω waves in the BBO crystal, c is the light velocity, and noω and ne2ω are the refractive indices of the ω (1320 nm) and 2ω (660 nm) waves. The duration of second harmonic pulse at the output of the 0.3-mm-long BBO crystal has a value of ~ 90 fs assuming the application of 1320 nm, 70-fs driving pulses. This value was estimated using t2ω ≈ [(Δcryst)2 + 0.5(tω)2]1/2 [28]. Hence, the 660 nm beam has longer pulse duration, corresponding to the induced delay and a certain percentage (~50%) of the fundamental pulse duration. The latter results from the fact that the energy of the fundamental radiation is in general not high enough in the pulse wings to effectively generate the second-order harmonic. In the case of 810 nm driving pulses, the influence of group velocity dispersion is larger on the temporal overlap of this radiation and its second harmonic in the plasma area.
As it is mentioned above, the group velocity dispersion in the BBO crystal leads to some temporal separation of two pulses. However, this temporal mismatch in the area of laser plasma did not prevent converting them to the odd and even harmonics, especially in the case of NIR driving pulses. The appearance of all even harmonics revealed sufficient overlapping of the 1320 nm and 660 nm pulses in the plasma area. In the case of TCP using second harmonic generation, the ratio of the pulse energies of second harmonic and fundamental waves of Ti:sapphire laser was in the range between 0.05 and 0.2 for 800 nm and 1320 nm fundamental waves. TCP of plasmas using conventional scheme (810 nm + 405 nm) has been analyzed for the first time in [29,30,31], where notable enhancement of harmonic yield compared with SCP was achieved. With suitable control of the relative phase between the fundamental and the second harmonic radiation, the latter field enhances the short path contribution, resulting in a clean spectrum of harmonics [19].
The 26-fs delay between 1320 nm and 660 nm waves that occurred during the propagation through the 0.3-mm thick type-I BBO crystal would decrease the ratio between the overlapped second harmonic and driving radiation in plasma and would reduce the influence of the second field on the output spectrum of generated harmonics. Nevertheless, as will be shown below, even at these unfavorable conditions the efficiencies of even and odd harmonics were comparable. It is worth mentioning that when longer crystals (type-I BBO, d = 0.7 mm and beyond) are used, considerable change in the role of the second-harmonic wave will be produced. While the conversion efficiency toward the second-harmonic wave in the case of longer crystals (11% for 0.7-mm long BBO) is higher than in the case of shorter (0.3-mm long) BBO crystal, the much faster growing delay of the pump pulses allowed only insignificant partial overlap in the plasma (0.01 in the case of 0.7-mm long crystal and 1320 nm and 660 nm driving waves). The calculations showed that, for 0.3 mm long BBO crystal at 5% conversion efficiency and 90 fs duration of broadened second harmonic pulse and delay of 26 fs between the maximums of two pulses, the ratio between overlapping 2ω and ω waves becomes equal to 0.03 [32]. As already mentioned, in the case of 810 nm and 405 nm pulses, due to the larger group velocity dispersion in BBO, worse features will be observed when longer crystals are used.
2.2. QPM in LPPs
Figure 2 shows the raw images of the harmonic spectra from different LPPs. The saturated images of harmonics are intentionally chosen to present the spectra for better viewing. Note that for the line-outs of the HHG spectra, unsaturated images are used. The difference between the so-called plateulike harmonics and the group of enhanced harmonics in the plateau range is clearly displayed.

Figure 2.
Raw images of harmonic spectra from (a) extended homogeneous (top to bottom) indium, silver and gold laser-produced plasmas (LPPs) pumped by 810 nm, 50 fs pulses and (b) multi-jet indium LPP produced using tilted MSM with the single plasma jet sizes of (top to bottom) 0.23, 0.28, and 0.31 mm pumped by two-color NIR + visible (1320 nm + 660 nm), 70 fs pulses. The peak intensities of 800 and 1320 nm pumps in the plasma area were 5 × 1014 and 1.4 × 1014 W cm−2, respectively, while the intensity of the second harmonic of 1320 nm pump was ~1 × 1013 W cm−2. Maximally enhanced harmonics (H34, H31, and H28) are clearly distinguished for each of these plasma configurations. Bottom spectrum corresponds to the HHG from the homogeneous extended indium plasma produced at similar conditions.
Figure 2a shows the plateaulike shapes of the odd harmonics generated in indium, silver and gold plasmas in the case of 810 nm, 50 fs driving pulses. The harmonics between the 17th (H17) and 33rd (H33) orders are shown. Nearly similar distributions, with almost equal intensities of these harmonics, are observed.
The plateaulike shape of harmonic spectra drastically changed once the MSM was inserted in the path of the heating picosecond radiation. The examples of three strongly modulated and enhanced spectra of the groups of odd and even harmonics of two-color NIR pump (1320 nm + 660 nm, 70 fs pulses) compared to the case of extended homogeneous indium plasma are shown in Figure 2b. The three upper spectra containing significantly enhanced groups of harmonics centered at H34, H31, and H28 were observed when tilting the MSM at angles of 350, 200 and 00 and creating the 11-, 9-, and 8-jet indium plasmas, with the sizes of single jet of 0.23, 0.28, and 0.31 mm, respectively. Meanwhile, the bottom spectrum shows the HHG from the homogeneous extended indium plasma produced at similar conditions. The collection times of these four spectra and the energy fluencies of target ablation were similar to each other. When the MSM was used, the whole energy of heating pulses interacting with target was two times smaller when compared with the case of extended homogeneous plasma, while the energy fluencies of heating radiation on the target surface were equal to each other. The enhancement factors of these harmonics (three upper spectra) with respect to those generated in the case of imperforated plasma (bottom spectrum) were measured to be 38×, 36×, and 27× respectively. A two-fold decrease of the whole length of multi-jet plasma compared with extended imperforated plasma (2.5 and 5 mm respectively) did not play an important role in the harmonic yield, which underlines the importance of the collective processes over single-atom ones.
The bottom spectrum of Figure 2b, as well as the three upper spectra, shows the strong resonance-induced enhancement of H21. On the other hand, the formation of QPM conditions (three upper spectra) demonstrates the significant enhancement of the groups of harmonics surrounded the one (Hqpm) for which conditions of QPM became most favorable.
Similar pattern, though without resonance-induced enhancement of harmonics, was observed in the case of the silver plasma pumped by 1310 nm + 655 nm radiation (Figure 3). Again, in the case of imperforated 5-mm-long Ag plasma, plateaulike harmonics were barely seen (bottom image). The groups of strong harmonics appeared once the MSM was inserted between the target and heating pulse. They were centered at H43, H36, and H31 (see Figure 3 from top to bottom) and corresponded to the MJP structures with the sizes of single jet of 0.25, 0.31, and 0.35 mm.

Figure 3.
Raw images of harmonic spectra from the multi-jet silver LPP produced using tilted MSM with single plasma jet sizes of (top to bottom) 0.25, 0.31, and 0.35 mm pumped by two-color (1310 nm + 655 nm), 70 fs pulses. The intensities of 1310 nm and 655 nm pumps in plasma area were 1.3 × 1014 and 1 × 1013 W cm−2, respectively. Maximally enhanced harmonics (H43, H36, and H31) are determined for each of these plasma configurations. Bottom spectrum corresponds to homogeneous extended silver plasma. Similar conditions of plasma ablation using the same energy fluence of heating pulses and data collection times are applied for these four cases.
The analysis of the harmonics intensity as a function of the number of plasma jets (n) can provide a proof of the decisive role of the QPM in the variations of harmonic spectrum. The coherent accumulation of harmonic yield along the whole length of divided nonlinear optical medium is demonstrated in the present studies. We used the indium target for ablation and the two-color pump (1300 nm + 650 nm) for HHG in indium plasma. The heating areas on the target (shown in the inset in Figure 1) were shielded one by one to allow the generation of harmonics in different numbers of plasma jets. The number of jets was increased one by one from single jet to 8 jets. The width of each jet was 0.3 mm and the empty area on the target surface between jets was also equal to 0.3 mm. The whole length of the 8-jet structure was ~5 mm.
The harmonic spectrum in the case of single jet showed a plateau-like shape of weak harmonics. Each addition of the next jet caused growth of the group of harmonics centered at around H34. This harmonic had the coherent length of ~0.3 mm at the used fluence of heating pulses on the surface of In target (1.2 J cm−2) and the intensity of driving NIR pulses (1.4 × 1014 W cm−2).
The coherence length (in mm) of some harmonics at the conditions of using the 1300-nm driving laser could be presented as Lcoh ≈ 1 × 1018/(Ne × Hqpm) [1,16]. Here Hqpm is the maximally-enhanced harmonic at QPM conditions and Ne is the electron density in cm−3. H34 has coherence length of ~0.3 mm at the used fluence (1.2 J cm−2) of the heating pulses on the surface of In target, and 1.4 × 1014 W cm−2 intensity of the driving NIR pulses. We used the MSM containing slits with the sizes of 0.3 mm and excited the target in such a manner that electron density satisfied the above relation for the H34 at the length of single jet of 0.3 mm. Correspondingly, at another excitation of target the electron concentration of plasma may satisfy to another harmonic order at the fixed sizes of single jet in the MJP.
The yield of H34 increased as IH34~n2 up to n = 4. Further addition of jets led to deviation from quadratic dependence [Figure 4a] due to some inequality of plasma jets, which led to violation of the optimal phase relations between driving and H34 waves. At these conditions of the imperfect coherent accumulation of nonlinear optical response we were able to observe the 40-fold growth of H34 in the case of 8-jet plasma compared with the single-jet one.
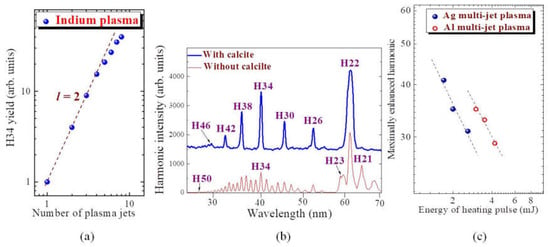
Figure 4.
(a) Dependence of H34 intensity on the number (n) of jets of the indium MJP. The multi-jet indium LPP was produced using the tilted MSM with the single plasma jet sizes of 0.23 mm and pumped by two-color near infrared (NIR) + visible (1320 nm + 660 nm), 70 fs pulses. The peak intensity of 1320 nm pump was 1.4 × 1014 W cm−2. The dashed line shows the slope l = 2 of the experimental dependence up to n = 4. (b) Harmonic distribution obtained from indium MJP in the case of propagation of driving pulses (1360 nm + 680 nm) through the plasma [bottom spectrum, similarly to the case shown in the upper panel of Figure 2b] and calcium quarter-wavelength plate and plasma (upper panel, see text). (c) Influence of heating pulse energy on the maximally enhanced harmonic in the case of silver (filled spheres) and aluminum (empty circles) MJPs.
H34 was perfectly suited for comparative analysis of the role of number of separated jets on the variation of the intensity of generated harmonic. The coherence length in these experiments has a direct relation with the coherent addition of harmonic emission after propagation of H34 through each next jet. As it was shown, even at these favorable conditions for coherent summing of harmonic waves in each next jet, the additional impeding processes did not allow following the theoretically predicted quadratic rule once the number of jets exceeded four coherence zones. As for non-phase matched harmonics, for example H18 of 1320 nm + 660 nm pump, this consideration (i.e., quadratic growth of harmonic efficiency with the growth of the number of jets) is not applicable, since phase mismatch between harmonic and fundamental waves does not allow the growth of harmonic yield.
We also analyzed the QPM-enhanced spectrum from indium MJP using 1360 nm + 680 nm two-color pump at the conditions when the calcite quarter-wave plate was inserted before the BBO crystal. In that case the polarization of the driving 1360 nm pulses was changed from linear to circular. The pump radiation after propagating in the BBO crystal consisted of a circularly polarized 1360 nm pump and a linearly polarized 680 nm pump. The variation of polarization conditions caused the generation of high-order harmonics only from the 680 nm pump. The generated spectrum of harmonics is seen in the upper panel of Figure 4b showing the strong odd harmonics of 680 nm radiation. In the case of absence of calcite, the spectral pattern (bottom graph) contained a whole set of two groups of enhanced harmonics, as has already been shown in the above-described results [Figure 2b].
The aim of this study is to show the QPM at different combinations of the driving fields. The results presented in Fig. 4b are related to QPM studies at variable polarization conditions of the driving waves, when the linearly polarized second harmonic field (680 nm) and two linearly polarized fields (1360 nm and 680 nm) were applied for HHG. The harmonics occur at the conditions of the interaction of linearly polarized radiation and plasma. Circularly-polarized 1360 nm radiation splits into two orthogonally polarized waves during the propagation through BBO. One of these waves partially converts to the second harmonic. After propagation through the BBO crystal, these two orthogonally-polarized 1360 nm waves combine to create the circularly polarized 1360 nm radiation, which does not participate in HHG. Then only the second harmonic radiation serves as the driving field for HHG at the conditions of QPM.
The optimization of QPM for shorter wavelengths at lesser excitation of the target during formation of multi-jet plasmas can be observed in different materials. We analyzed the dependence of the highest enhanced harmonic order on the energy of the heating pulse producing MJPs on the surfaces of silver and aluminum [Figure 4c]. This dependence underlines the influence of over-dense plasmas and electrons on the formation of QPM conditions in different plasmas. We observed the tuning of the maximum of spectral envelope towards the higher-order harmonics at smaller fluence of heating radiation. A decrease of electron concentration at weaker excitation of the target led to optimization of the QPM for higher orders of harmonics to keep the product Hqpm × Ne unchanged at the fixed spatial characteristics of the plasma jets. Figure 4c, showing the log-log dependence of Hqpm on the energy of heating pulses for two different targets (Ag and Al), confirms the relation Hqpm × Ne ~ constant.
There are four factors that contribute to the phase mismatch: atomic dispersion, Gouy phase shift, intensity-dependent dynamical phase shift in nonlinear dipole moments, and plasma dispersion. The first one refers to the variation in the refractive index of the neutral components of plasma, which shows considerably less influence than the dispersion induced by the presence of free electrons (fourth factor) in the plasma in the spectral ranges far from the resonance transitions, especially in the case of low-density plasma medium, thus allowing us to exclude the influence of atomic dispersion on the phase mismatch. Gouy phase shift could be also dismissed when the confocal parameter of the focused radiation exceeds the sizes of plasma, which was the case of our experiments (correspondingly 8 and 5 mm). The Gouy phase mismatch [33] at our conditions was 0.6 cm−1. The intensity of NIR femtosecond radiation used in the plasma area did not exceed 3 × 1014 W cm−2. At these conditions the phase mismatch between the harmonics emitted at different ends of the 5-mm-long plasma medium can be estimated as 8 cm−1 [34]. Finally, the phase mismatch due to plasma electrons [35] was considerably higher (~50 cm−1 for the 34th harmonic) compared to other components. Thus, at our conditions, the only component influencing the phase mismatch is related to the presence of electrons in the laser-produced plasma. Our studies confirmed that the above-mentioned formula (Lcoh ≈ 1 × 1018/Hqpm×Ne) for the coherence length can be used at the conditions of low-density plasma (≤1018 cm−3), relatively long confocal parameters (b > lplasma), and relatively low intensities of the driving pulse (<5 × 1014 W cm−2).
3. Theory
To support our experimental investigations, we used the 1D model described in Ref. [18]. Within this model, the nonlinear medium is simulated by 1D chain of atoms oriented along the propagation direction of laser pulses. The response of each atom in the chain is calculated using the non-perturbative theory [36,37]. The two-color laser field parameters that were chosen for the single-atom response calculations on one hand coincide with the ones used in the experiments, and on the other hand depend on the position of the atoms in the chain. The generated harmonic radiation from each atom is calculated in the far-field zone by a numerical summation over a chain of atoms [18,38,39]. As a result, the spatial distribution of generated radiation is calculated, which is integrated for analysis of the overall intensity of the harmonic radiation.
In the numerical calculation we deal with silver plasma having the following parameters related to the above described experimental conditions: density of plasma is equal to ~2 × 1017 cm−3, and the density of free electron is equal to ~2 × 1016 cm−3. Other parameters, such as the intensities of two-color pulses, their durations, and the length of nonlinear medium were chosen to be the same as in experiment.
We studied the dependence of harmonic spectra on the size of the individual jet under conditions of the constant length (~5 mm) of nonlinear medium. The number of jets changed with variation of their length. The harmonic spectra are presented in Figure 5a. It is seen that decreasing of d leads to the shift of Hqpm towards the shorter wavelength region. The position of Hqpm as a function of d is shown in Figure 5b. The results of numerical calculations are shown by open circles. It can be seen that the positions of the center of the enhanced groups of harmonics are inversely proportional to d. Empty and filled squares correspond to experimental data for indium [Figure 2b] and silver (Figure 3) plasmas, respectively. Here we also show some other reported data in the case of silver plasma [40,41,42]. The slopes of the dotted lines (l = −1) correspond to the Hqpm(Ag) ∞ 1/d dependence. The data in the case of indium plasma shows similar tendency [(Hqpm(In) ∞ 1/d], while the graph is slightly shifted with respect to the data and that is due to the different role of two groups of free electrons in phase mismatch at specific ablation conditions for these two metals. A similar shift has been earlier observed in the case of silver plasma ablated at higher energies of heating pulses (see pentagons in Figure 5b; where the data shown was taken from Ref. [40]).
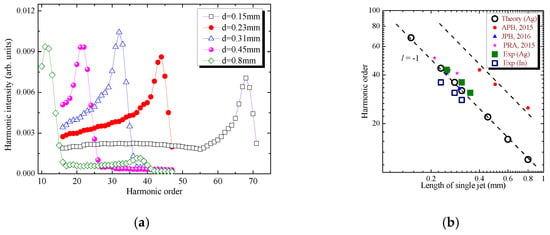
Figure 5.
(a) Harmonic distribution from silver MJP in the case of propagation of two-color driving pulses (1310 nm + 655 nm) through the plasma of ~5 mm length containing the jets with the sizes (d) equal to 0.15 mm (black empty squares), 0.23 mm (red filled circles), 0.31 mm (blue empty triangles), 0.45 mm (pink filled spheres), and 0.8 mm (green empty rhombs). (b) Influence of the jet sizes on the order of maximally enhanced harmonic Hqpm in the case of silver MJP. Black empty circles correspond to theoretical calculations and green filled squares correspond to experiment with Ag plasma. Triangles, stars and pentagons correspond to earlier reported data for silver plasma [40,41,42]. Here we also show the experimental data for indium plasma (blue empty squares). The slopes of all dependences correspond to l = −1.
We also investigated the influence of the number of jets on the characteristics of generated radiation. In the numerical investigations we used d = 0.23 mm. The calculated spectra are presented in Figure 6a. It can be seen that the harmonic’s yield increases with the increase of n. At the same time the maximally enhanced harmonic depended on n. To show it more precisely we analyzed the position of Hqpm and its intensity as a function of n (see blue filled circles and red empty squares in Figure 6b). It is seen that the position of Hqpm shifts towards the higher order harmonic region, and the value of the harmonic intensity quadratically grows with the increase of the number of jets. It is worth mentioning that in experiment we also observed the shift of Hqpm with the increase of n, though this shift was less pronounced in comparison with the calculations.
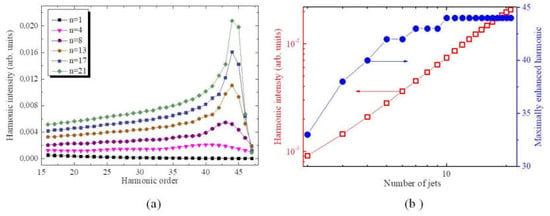
Figure 6.
(a) Harmonic distribution in the case of silver MJP during propagation of two-color pulses (1310 nm + 655 nm) through the plasmas consisting of different number of jets. Single jet sizes were 0.23 mm. (b) Hqpm and its intensity as the functions of n (blue filled circles and black empty squares).
Finally, we simulated new possibilities for the control of Hqpm and peak intensity in the case of the two-color pump of MJP. It assumes application of the jets of two different lengths (d1 and d2). In all calculations the whole length of nonlinear medium was kept the same (5 mm). We took d1 = 0.15 mm and d2 = 0.31 mm and simulated the HHG in the nonlinear medium consisting of 8 jets of d1 and four jets of d2.
The resulting spectrum is shown in Figure 7 as blue filled squares. The HHG spectrum has two maxima (green dotted lines) at the same place as for similar jets (H32 and H67 as compared with Figure 5a). The decrease in the amplitude of the peaks in comparison with the cases shown in Figure 5a is explained by the fact that in the former case the number of jets of different ds is two times smaller. We also constructed the blocks of two groups of jets separated by the free space of the same sizes using d1 and d2 jets (i.e., d1 jet −d1 free space −d2 jet −d2 free space −d1 jet −d1 free space…). This group of jets forms the nonlinear medium with the same length as in the previous case (i.e., eight jets of d1 and four jets of d2).
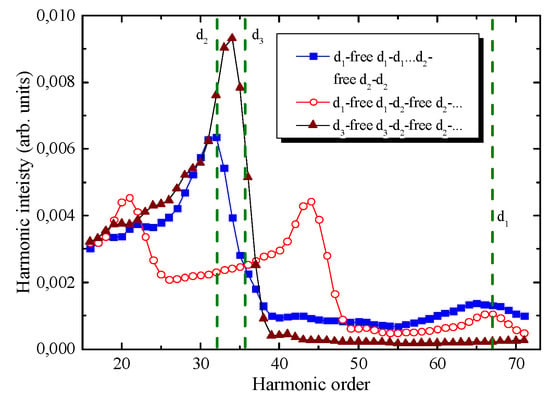
Figure 7.
Harmonic distribution in the case of propagation of two-color pulses (1310 nm + 655 nm) through silver MJP of 5 mm length consisting of different combinations of two groups of jets (see text).
The HHG spectrum in this case is presented in Figure 7 by red empty circles. It can be seen that this HHG spectrum has three peaks. The peak corresponded to the d2 becoming divided into two peaks, at H21 and H44, and the third peak remained at the same place corresponding to d1 (H67). To investigate the observed changes of the spectrum more precisely we changed the value of one sort of jets from d1 to d3 = 0.28 mm and formed the nonlinear medium in the same way as in the previous case. The resulting harmonic spectrum is presented by the brown filled triangles in Figure 7. It is seen that the main peak of the spectrum became centered at H34 and the harmonic intensity increased by a factor of 2 in comparison with previous cases.
4. Discussion
The practical aspects of our presented approach require answers to a few questions in order to provide a reliable pattern of the QPM in plasmas.
(1) For practical purposes, one would like to know: what is the most optimal number of jets for a given harmonic? The meaning of most optimal number of jets cannot be clarified without understanding the impeding processes, which stop the quadratic growth of harmonic yield with the increase of number of jets. Our studies revealed that this deviation from the anticipated quadratic dependence occurs at n > 5. This quadratic rule is fulfilled only for the maximally quasi-phase matched harmonic (i.e., the one which has highest enhancement). For non-phase matched harmonic, the enhancement is not realized at all.
(2) Another question is: what would be the corresponding jet characteristics in the case of “optimal” (i.e., most effective) QPM? The characterization of jets requires the knowledge of the ions/neutrals and free electron densities. The latter parameter defines the maximally-enhanced harmonic at a given jet length. For a given size of individual plasma jet, the QPM for maximally enhanced harmonic could be maintained at a fixed product Hqpm × Ne (since Lcoh ≈ 1 × 1018(Hqpm × Ne)−1 [5,6]). The electron density depends on the ablation conditions and the ionization of the target species by the heating pulse in addition to the tunneling ionization by femtosecond driving pulse. The conditions of ablation are easily adjustable and can be used for variation of Ne and the corresponding Hqpm.
(3) What would be the most optimal material for this purpose? Currently, the most optimal material is silver. The reasons for that include the extended plateau-like shape of harmonic distribution in the non-QPM regime, the relatively high conversion efficiency, and the easiness in stable Ag plasma formation, etc. Other materials, which also allow observation of this effect, are indium, manganese, gold and arsenic plasmas.
(4) How much is the most attainable gain? Until now, the 20× to 40× enhancement factors for QPM harmonics were reported. This is the ratio of the intensities of QPM-enhanced harmonic propagated through eight to 11 plasma jets and of the same harmonic propagated through the extended imperforated (i.e., homogeneous) plasma, which has a length that is equivalent to length of all jets.
(5) Can we use the QPM measurements to determine the electron density? Previously reported studies have shown this opportunity [40]. The developed plasma QPM technique allows achieving some groups of notably enhanced harmonics at fixed Ne such that one can assume this technique could be a method to determine the value of electron density of the plasma. Determining the value of electron density of the plasma is a well-recognized problem in plasma physics especially with the case of dynamically changed Ne. Numerous techniques and theories were proposed and realized to resolve this issue. Particularly, in the case of laser-produced plasmas, the code HYADES was used to estimate the electron density of plasma at different regimes of plasma formation. The plasma QPM method allows determining the electron density from direct measurements of two other parameters from the aforementioned relation, and those parameters are the coherence length and the maximally-enhanced harmonic order.
(6) What is the ultimate limit from the point of view of tuning the maximally enhanced harmonic towards the shorter wavelengths? Our aim is to demonstrate the effect of different experimental parameters on the modulation of homogeneous harmonic distribution. We did not aim to determine the limits of Hqpm variations since this task has already been analyzed in previous studies [1,16,42]. Particularly, H43 of 800 nm pump was the maximally-enhanced harmonic in the case of 11-jet silver plasma structure. Similar pattern is also seen in Figure 3 (upper panel) in the case of indium plasma pumped by 1310 nm + 655 nm pulses. However, the enhancement in that case was lesser compared with longer wavelength XUV region. As shown in the upper panel of Figure 3, the maximally available cutoff for harmonics extended towards shorter wavelength region once optimal conditions for QPM were realized. This spectrum does not show the cutoff but rather demonstrates the attractiveness of the method when almost invisible harmonics (see bottom panel) appear next to the enhanced ones.
5. Conclusions
TCP allows stronger yield of odd harmonics and appearance of almost similar intensities of odd and even harmonics in the case of TCP. Meanwhile, QPM allows tuning a group of enhanced harmonics in the XUV range. The practical issue here is the search for optimal experimental conditions for each particular case of laser-plasma interaction using different concepts of harmonic enhancement. TCP and QPM notably enhance the potential of laser-ablation-induced HHG spectroscopy of any solid material.
We have demonstrated some peculiarities of quasi-phase matching in laser produced plasma, which allows us to analyze the advantages and disadvantages, as well as further amend the developed technique. Since first demonstration of this effect in plasma [1], new opportunities and schemes were developed and analyzed. Inevitably, they overlap, to some extent, with each other to explain, in some cases from the very basic rules, the advantages (and in some case disadvantages) of the QPM in plasmas. This overlap may cause some confusion; however, it would be difficult to clarify some new findings without the description of the basics and practical issues of this method.
Apart from the novelty of the approach employed in the present work (comparison of single and two color pumps of QPM plasmas, role of number of coherent zones, competitiveness of macro-processes (QPM) and micro-processes (resonance enhancement of single harmonic), analysis of dimensional parameters of plasma jets, etc.), we have developed a new approach in the theoretical description of the process, which shows peculiarities that are not mentioned in earlier theoretical studies of QPM in plasmas.
We have analyzed different patterns of experimentally-observed modifications of harmonic spectra at the conditions of QPM in silver, indium, and aluminum multi-jet plasmas. In particular, we have studied the role of the number of coherent zones, sizes of plasma jets and distance between them, plasma formation conditions and the characteristics of fundamental and heating radiation on the HHG efficiency at QPM conditions. We have demonstrated TCP-induced QPM at different regimes of laser-plasma interaction.
The results of the theoretical simulations have shown good agreement with the experimental findings. The calculated spectra qualitatively coincide with the measured ones. The deeper insight into the mechanisms of the investigated phenomena can be obtained from the analysis of relationships between the characteristics of the processes like those shown in Figure 4. Figure 4a shows that the yield of H34 increases as IH34~n2 up to number of jets (n) equal to 4. The quadratic dependence is correct in a wide range of harmonic spectra. However, further deviation of IH34(n) dependence from the quadratic one can be explained by the violation of equality of the conditions for each next added jet (i.e., non-ideal conditions of propagation through jets, and/or low-order nonlinear optical properties of plasma, etc.). New possibilities for controlling QPM conditions using combined multi-jet plasmas are readily proposed. The results of our experimental and theoretical studies of the QPM conditions provide reliable interpretation of this phenomenon.
Author Contributions
Conceptualization, R.A.G. and A.S.A.; Software, S.Y.S.; Formal Analysis, S.Y.S. and A.V.A; Investigation, R.A.G.; Writing—Original Draft Preparation, R.A.G. and S.Y.S.; Writing—Review & Editing, A.S.A.; Supervision, A.S.A.
Funding
This research was funded by the Russian Foundation for Basic Research, grant number 18-02-40014. The APC was funded by Materials Science and Engineering Research Institute, UAE.
Acknowledgments
R.A.G. acknowledges the support from H. Kuroda.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ganeev, R.A.; Suzuki, M.; Kuroda, H. Quasi-phase-matching of high-order harmonics in multiple plasma jets. Phys. Rev. A 2014, 89, 033821. [Google Scholar] [CrossRef]
- Wöstmann, M.; Splitthoff, L.; Zacharias, H. Control of quasi-phase-matching of high-harmonics in a spatially structured plasma. Opt. Express 2018, 26, 14524–14532. [Google Scholar] [CrossRef]
- Paul, A.; Bartels, R.A.; Tobey, R.; Green, H.; Weiman, S.; Christov, I.P.; Murnane, M.M.; Kapteyn, H.C.; Backus, S. Quasi-phase-matched generation of coherent extreme-ultraviolet light. Nature 2013, 421, 51–54. [Google Scholar] [CrossRef]
- Zhang, X.; Lytle, A.L.; Popmintchev, T.; Zhou, X.; Kaptayn, H.C.; Murnane, M.M.; Cohen, O. Quasi-phase-matching and quantum-path control of high-harmonic generation using counterpropagating light. Nat. Phys. 2007, 3, 270–275. [Google Scholar] [CrossRef]
- Auguste, T.; Carre, B.; Salieres, P. Quasi-phase-matching of high-order harmonics using a modulated atomic density. Phys. Rev. A 2007, 76, 011802. [Google Scholar] [CrossRef]
- Seres, J.; Yakovlev, V.S.; Seres, E.; Streli, C.H.; Wobrauschek, P.; Spielmann, C.H.; Krausz, F. Coherent superposition of laser-driven soft-X-ray harmonics from successive sources. Nat. Phys. 2007, 3, 878–883. [Google Scholar] [CrossRef]
- Zepf, M.; Dromey, B.; Landreman, M.; Foster, P.; Hooker, S.M. Bright quasi-phase-matched soft-X-ray harmonic radiation from argon ions. Phys. Rev. Lett. 2007, 99, 143901. [Google Scholar] [CrossRef] [PubMed]
- Lytle, A.L.; Zhang, X.; Sandberg, R.L.; Cohen, O.; Kapteyn, H.C.; Murnane, M.M. Quasi-phase matching and characterization of high-order harmonic generation in hollow waveguides using counterpropagating light. Opt. Express 2008, 16, 6544–6566. [Google Scholar] [CrossRef]
- Pirri, A.; Corsi, C.; Bellini, M. Enhancing the yield of high-order harmonics with an array of gas jets. Phys. Rev. A 2008, 78, 011801. [Google Scholar] [CrossRef]
- Tosa, V.; Yakovlev, V.S.; Krausz, F. Generation of tunable isolated attosecond pulses in multi-jet systems. New J. Phys. 2008, 10, 025016. [Google Scholar] [CrossRef]
- Bahabad, A.; Murnane, M.M.; Kapteyn, H.C. Quasi-phase-matching of momentum and energy in nonlinear optical processes. Nature Phot. 2010, 4, 570. [Google Scholar] [CrossRef]
- Willner, A.; Tavella, F.; Yeung, M.; Dzelzainis, T.; Kamperidis, C.; Bakarezos, M.; Adams, D.; Schulz, M.; Riedel, R.; Hoffmann, M.C.; et al. Coherent control of high harmonic generation via dual-gas multijet arrays. Phys. Rev. Lett. 2011, 107, 175002. [Google Scholar] [CrossRef]
- O’Keeffe, K.; Robinson, T.; Hooker, S.M. Quasi-phase-matching high harmonic generation using trains of pulses produced using an array of birefringent plates. Opt. Express 2012, 20, 6236–6247. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Chini, M.; Zhang, Q.; Zhao, K.; Wu, Y.; Telnov, D.A.; Chu, S.-I.; Chang, Z. Mechanism of quasi-phase-matching in a dual-gas multijet array. Phys. Rev. A 2012, 86, 021802. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Redkin, P.V.; Kuroda, H. Quasi-phase-matching of laser harmonics using variable multi-jet plasmas. J. Nonlin. Opt. Phys. Mater. 2014, 23, 1450013. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Husakou, A.; Suzuki, M.; Kuroda, H. Application of mid-infrared pulses for quasi-phase-matching of high-order harmonics in silver plasma. Opt. Express 2016, 24, 3414. [Google Scholar] [CrossRef] [PubMed]
- Strelkov, V.V.; Ganeev, R.A. Quasi-phase-matching of high-order harmonics in plasma plumes: Theory and experiment. Opt. Express 2017, 25, 21068–21083. [Google Scholar] [CrossRef]
- Stremoukhov, S.Y.; Andreev, A.V. Quantum-mechanical elaboration for the description of low- and high-order harmonics generated by extended gas media: Prospects to the efficiency enhancement in spatially modulated media. Laser Phys. 2018, 28, 035403. [Google Scholar] [CrossRef]
- Kim, I.J.; Lee, G.H.; Park, S.B.; Lee, Y.S.; Kim, T.K.; Nam, C.H.; Mocek, T.; Jakubczak, K. Generation of submicrojoule high harmonics using a long gas jet in a two-color laser field. Appl. Phys. Lett. 2008, 92, 021125. [Google Scholar] [CrossRef]
- Kim, I.J.; Kim, C.M.; Kim, H.T.; Lee, G.H.; Lee, Y.S.; Park, J.Y.; Cho, D.J.; Nam, C.H. Highly efficient high-harmonic generation in an orthogonally polarized two-color laser field. Phys. Rev. Lett. 2005, 94, 243901. [Google Scholar] [CrossRef]
- Mauritsson, J.; Johnsson, P.; Gustafsson, E.; L’Huillier, A.; Schafer, K.J.; Gaarde, M.B. Attosecond pulse trains generated using two color laser fields. Phys. Rev. Lett. 2006, 97, 013001. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Singhal, H.; Naik, P.A.; Kulagin, I.A.; Redkin, P.V.; Chakera, J.A.; Tayyab, M.; Khan, R.A.; Gupta, P.D. Enhancement of high-order harmonic generation using two-color pump in plasma plumes. Phys. Rev. A 2009, 80, 033845. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Hutchison, C.; Zaïr, A.; Witting, T.; Frank, F.; Okell, W.A.; Tisch, J.W.G.; Marangos, J.P. Enhancement of high harmonics from plasmas using two-color pump and chirp variation of 1 kHz Ti:sapphire laser pulses. Opt. Express 2012, 20, 90–100. [Google Scholar] [CrossRef]
- Wang, H.-C.; Lu, Y.-C.; Chen, C.-Y.; Yang, C.C. Ultrafast pump-probe spectroscopy in the UV-blue range with an extremely broad probe spectrum for the carrier relaxation study in an InGaN thin film with indium-rich nano-clusters. Opt. Express 2007, 15, 3417–3425. [Google Scholar] [CrossRef]
- Rubenchik, A.M.; Feit, M.D.; Perry, M.D.; Larsen, J.T. Numerical simulation of ultra-short laser pulse energy deposition and bulk transport for material processing. Appl. Surf. Sci. 1998, 129, 193–198. [Google Scholar] [CrossRef]
- Bom, L.B.E.; Kieffer, J.-C.; Ganeev, R.A.; Suzuki, M.; Kuroda, H.; Ozaki, T. Influence of the main pulse and prepulse intensity on high-order harmonic generation in silver plasma ablation. Phys. Rev. A 2007, 75, 033804. [Google Scholar]
- Sheinfux, A.H.; Henis, Z.; Levin, M.; Zigler, A. Plasma structures for quasiphase matched high harmonic generation. Appl. Phys. Lett. 2011, 98, 141110. [Google Scholar] [CrossRef]
- Lambert, G.; Gautier, J.; Hauri, C.P.; Zeitoun, P.; Valentin, C.; Marchenko, T.; Tissandier, F.; Goddet, J.P.; Ribiere, M.; Rey, G.; et al. An optimized kHz two-colour high harmonic source for seeding free-electron lasers and plasma-based soft X-ray lasers. New J. Phys. 2009, 11, 083033. [Google Scholar] [CrossRef]
- Wang, H.-C.; Lu, Y.-C.; Chen, C.-Y.; Yang, C.C. Non-degenerate fs pump-probe study on InGaN with multi-wavelength second-harmonic generation. Opt. Express 2005, 13, 5245–5252. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.-C.; Lu, Y.-C.; Chen, C.-Y.; Yang, C.C. Carrier capture times of the localized states in an InGaN thin film with indium-rich nano-cluster structures. Appl. Phys. Lett. 2006, 89, 011906. [Google Scholar] [CrossRef]
- Ganeev, R.A. High-order sum and difference frequency generation using tunable two- and three-color commensurate and incommensurate mid-infrared pumps of graphite plasma. J. Opt. Soc. Am. B 2016, 33, 93–101. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Kuroda, H. Enhanced harmonic generation using different second-harmonic sources for the two-color pump of extended laser-produced plasmas. J. Opt. Soc. Am. B 2014, 31, 911–918. [Google Scholar] [CrossRef]
- Lindner, F.; Paulus, G.G.; Walther, H.; Baltuska, A.; Goulielmakis, E.; Lezius, M.; Krausz, F. Gouy phase shift for few-cycle laser pulses. Phys. Rev. Lett. 2004, 92, 113001. [Google Scholar] [CrossRef]
- Tamaki, Y.; Itatani, J.; Obara, M.; Midorikawa, K. Optimization of conversion efficiency and spatial quality of high-order harmonic generation. Phys. Rev. A 2000, 62, 063802. [Google Scholar] [CrossRef]
- Singhal, H.; Ganeev, R.A.; Naik, P.A.; Arora, V.; Chakravarty, U.; Gupta, P.D. Dependence of high order harmonics intensity on laser focal spot position in pre-formed plasma plumes. J. Appl. Phys. 2008, 103, 013107. [Google Scholar] [CrossRef]
- Andreev, A.V.; Stremoukhov, S.Y.; Shoutova, O.A. Light-induced anisotropy of atomic response: Prospects for emission spectrum control. Eur. Phys. J. D 2012, 66, 16. [Google Scholar] [CrossRef]
- Stremoukhov, S.; Andreev, A.; Vodungbo, B.; Salières, P.; Mahieu, B.; Lambert, G. Origin of ellipticity of high-order harmonics generated by a two-color laser field in the cross-polarized configuration. Phys. Rev. A 2016, 94, 013855. [Google Scholar] [CrossRef]
- Stremoukhov, S.; Andreev, A. Quantum-mechanical fingerprints in generation of elliptical terahertz radiation by extended media interacting with two-color laser field. J. Opt. Soc. Am. B 2017, 34, 232–237. [Google Scholar] [CrossRef]
- Stremoukhov, S.Y.; Andreev, A.V. Spatial variations of the intensity of THz radiation emitted by extended media in two-color laser fields. Laser Phys. Lett. 2015, 12, 015402. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Suzuki, M.; Yoneya, S.; Kuroda, H. Electron density measurements using high-order harmonic generation in laser-produced plasmas. Appl. Phys. B 2015, 121, 307. [Google Scholar] [CrossRef]
- Ganeev, R.A.; Tosa, V.; Kovács, K.; Suzuki, M.; Yoneya, S.; Kuroda, H. Influence of ablated and tunneled electrons on the quasi-phase-matched high-order harmonic generation in laser-produced plasma. Phys. Rev. A 2015, 91, 043823. [Google Scholar] [CrossRef]
- Ganeev, R.A. On- and off-axis studies of the quasi-phase-matching-enhanced harmonics generated in the multi-jet laser-produced plasmas. J. Phys. B 2016, 49, 095402. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).