A Trimmed Clustering-Based l1-Principal Component Analysis Model for Image Classification and Clustering Problems with Outliers
Abstract
:1. Introduction
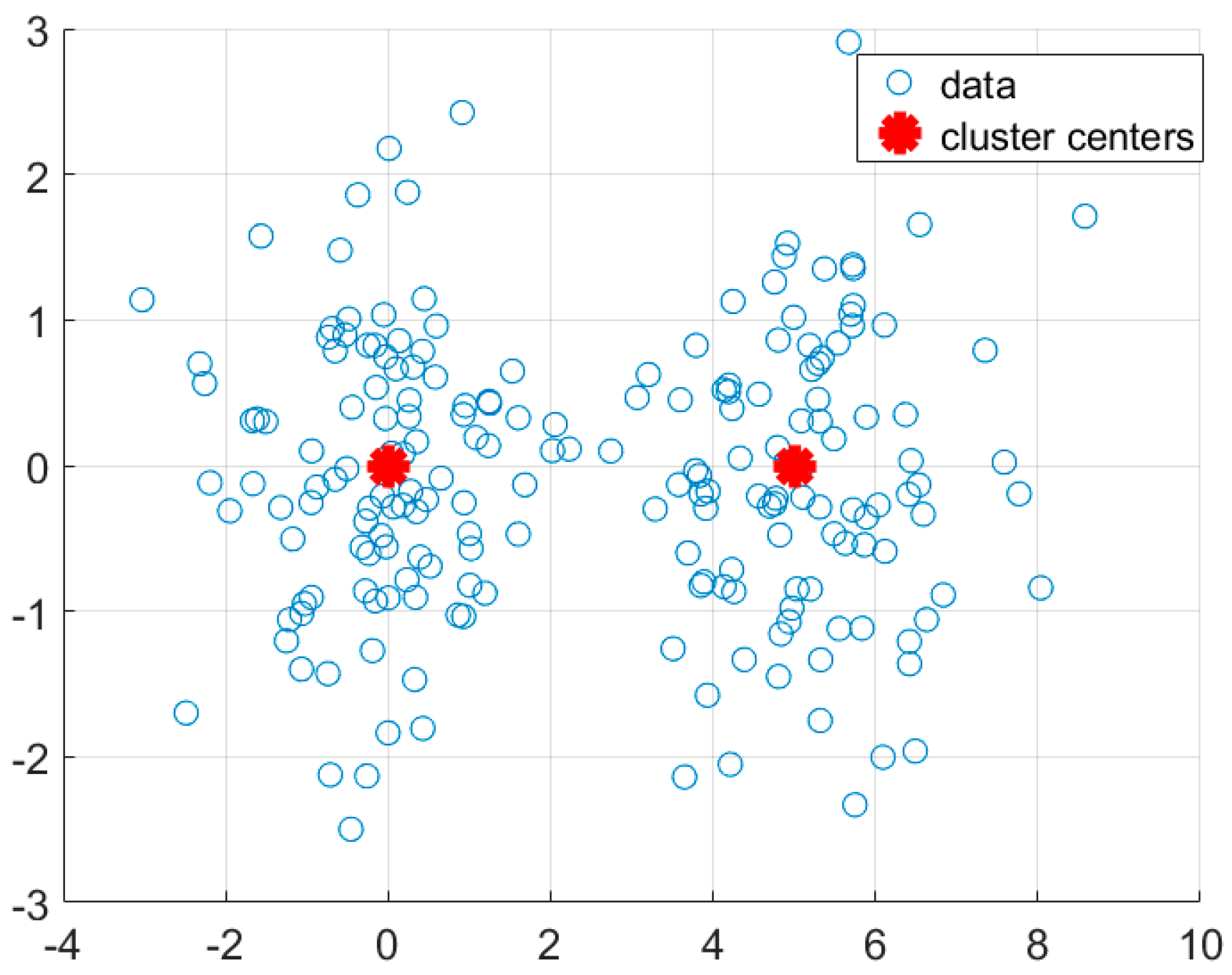
- We prove that the l1-PCA is equivalent to a two-group k-means clustering model. The projection vector estimated by the -PCA is the vector difference between the two cluster centers that are obtained by the -means clustering algorithm. In other words, the projection vector of the -PCA represents the inter-cluster direction, that is beneficial to distinguish data objects from different classes.
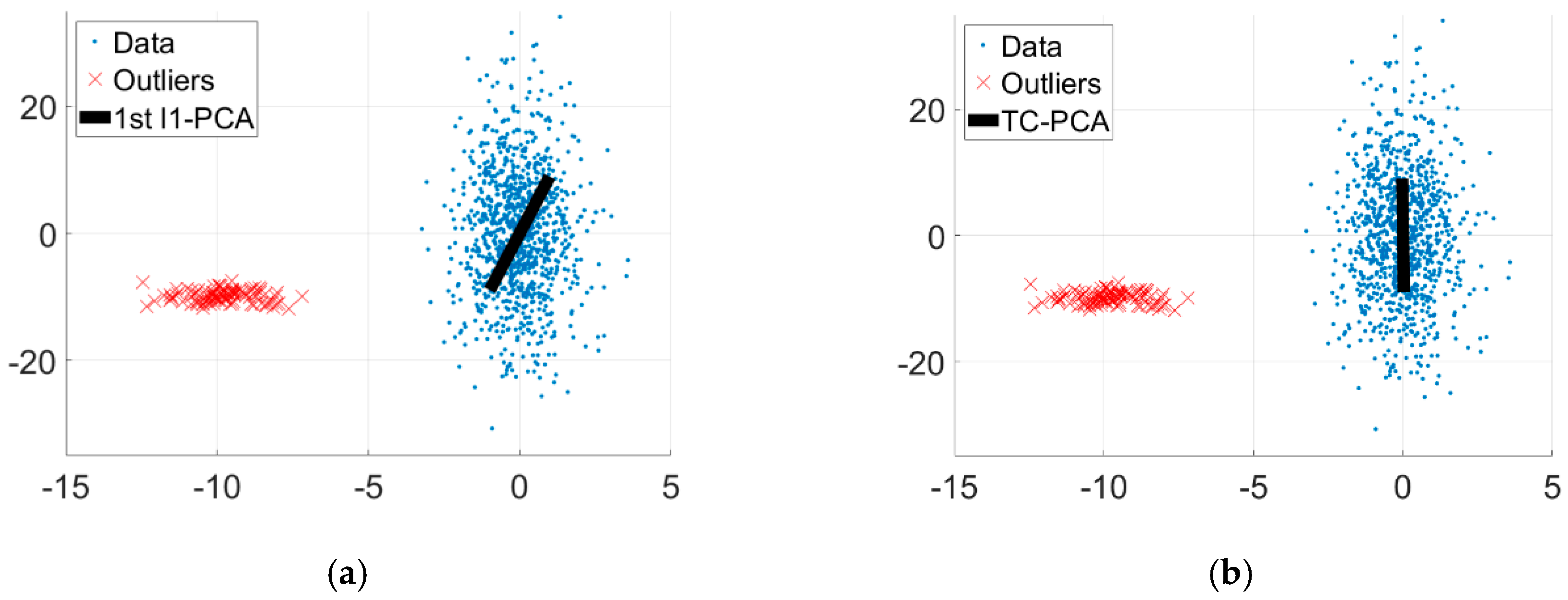
- We propose a novel TC-PCA model by integrating a trimming set into the two-group k-means clustering model, which makes the proposed method not sensitive to outliers.
- We mathematically prove that the estimator of TC-PCA is insensitive to outliers, which shows the robustness of the proposed method. In addition, we mathematically prove the convergence of the proposed algorithm.
2. Related Work
3. A Trimmed-Clustering Based l1-PCA Model
3.1. Relating l1-PCA to Two-Groups K-Means Clustering
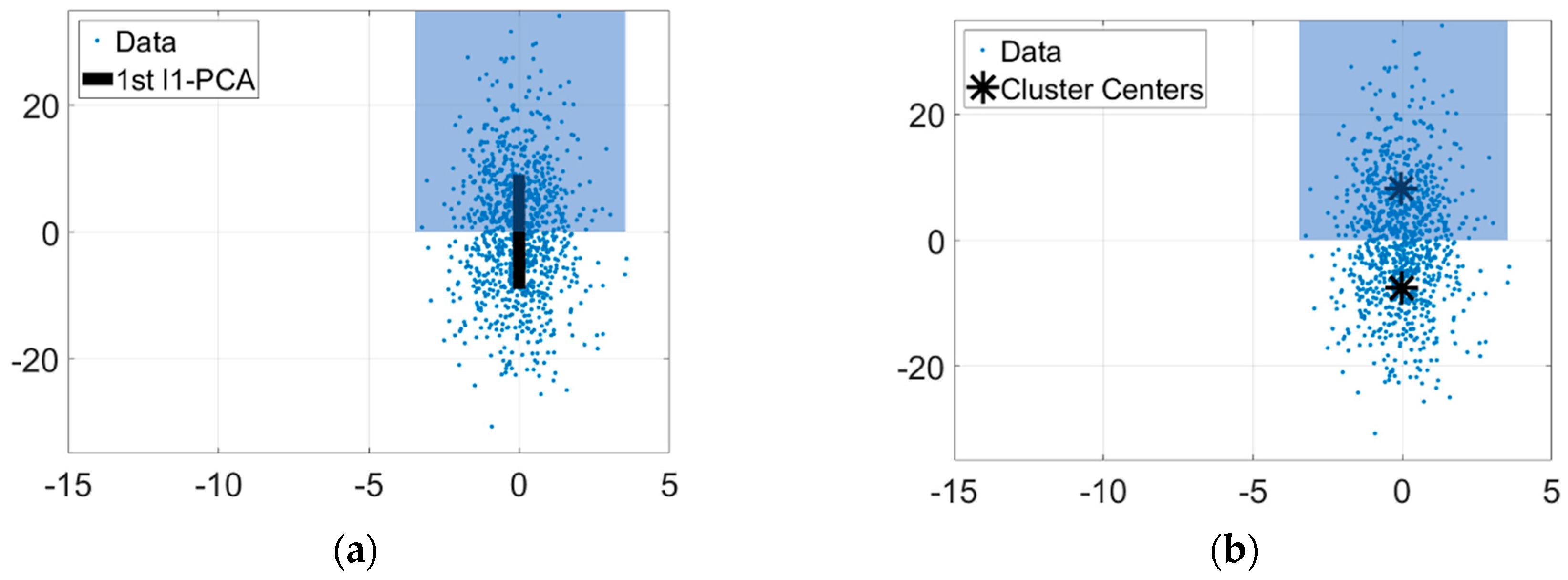
3.2. The Proposed Model
3.3. The Overall Implementation
| Algorithm 1. Single Projection Vector Extraction | |
| Step 1. | Input p and . Set and . |
| Step 2. | Randomly choose two samples from the dataset as initial cluster centers. |
| Step 3. | Update the trimming set via (9). |
| Step 4. | Update the cluster center via (11). |
| Step 5. | Update the indicator function via (12). |
| Step 6. | If there is a change of the indicator functions , go to Step 3. Otherwise, compute via (8). |
| Step 7. | If , compute via (10) and and set . Otherwise, set . |
| Step 8. | If , go to Step 2. Otherwise, Compute and stop. |
| Algorithm 2. Trimmed-Clustering based l1-PCA | |
| Step 1. | Input D and set . Apply the SPVEA (Algorithm 1) to obtain . |
| Step 2. | Obtain the subspace via (13). |
| Step 3. | Use as an input dataset of SPVEA (Algorithm 1) to obtain . Set . |
| Step 4. | If , go to Step 2; otherwise, output and stop. |
3.4. Mathematical Properties
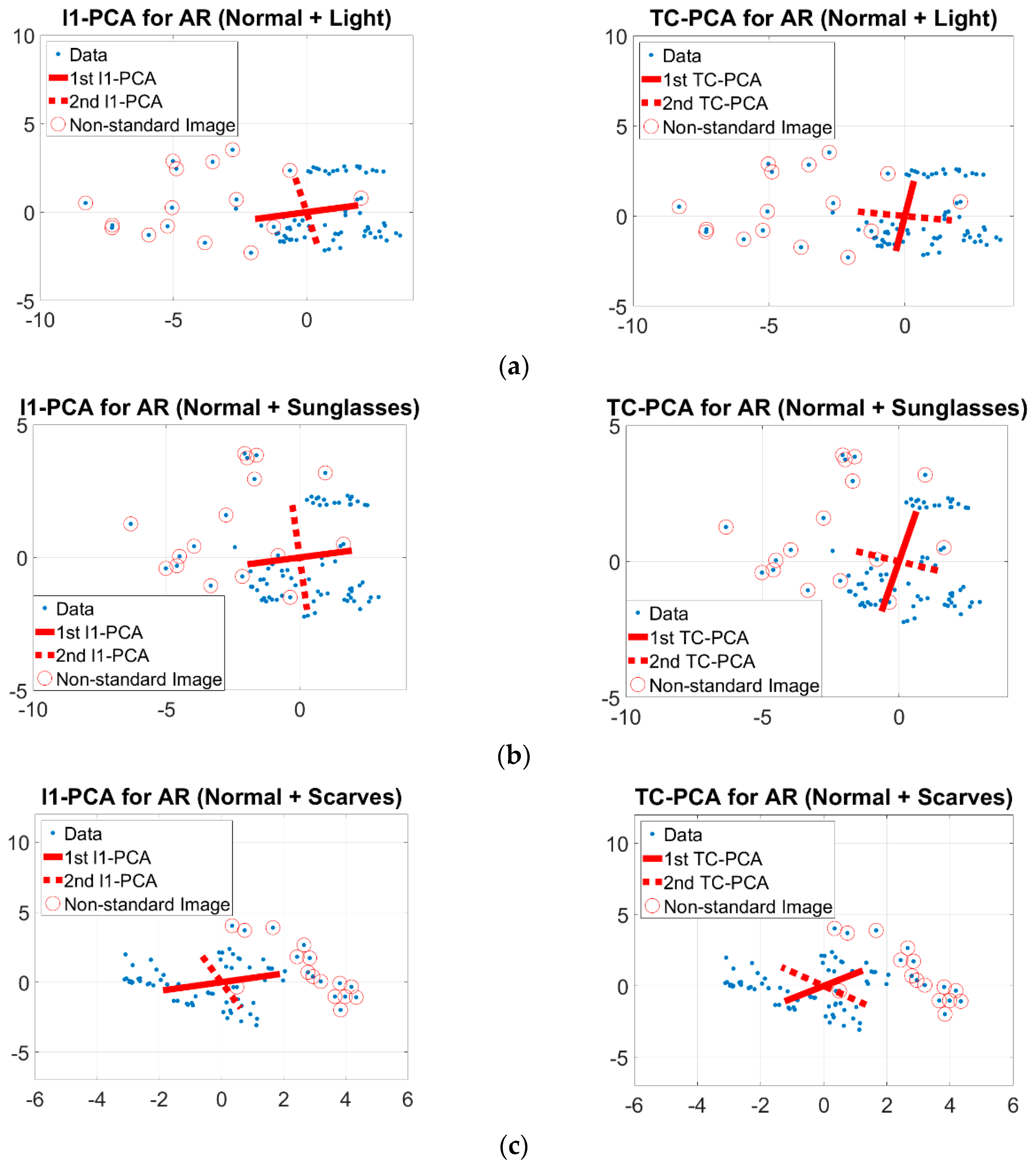
3.5. Synthetic Analysis
4. Experiments
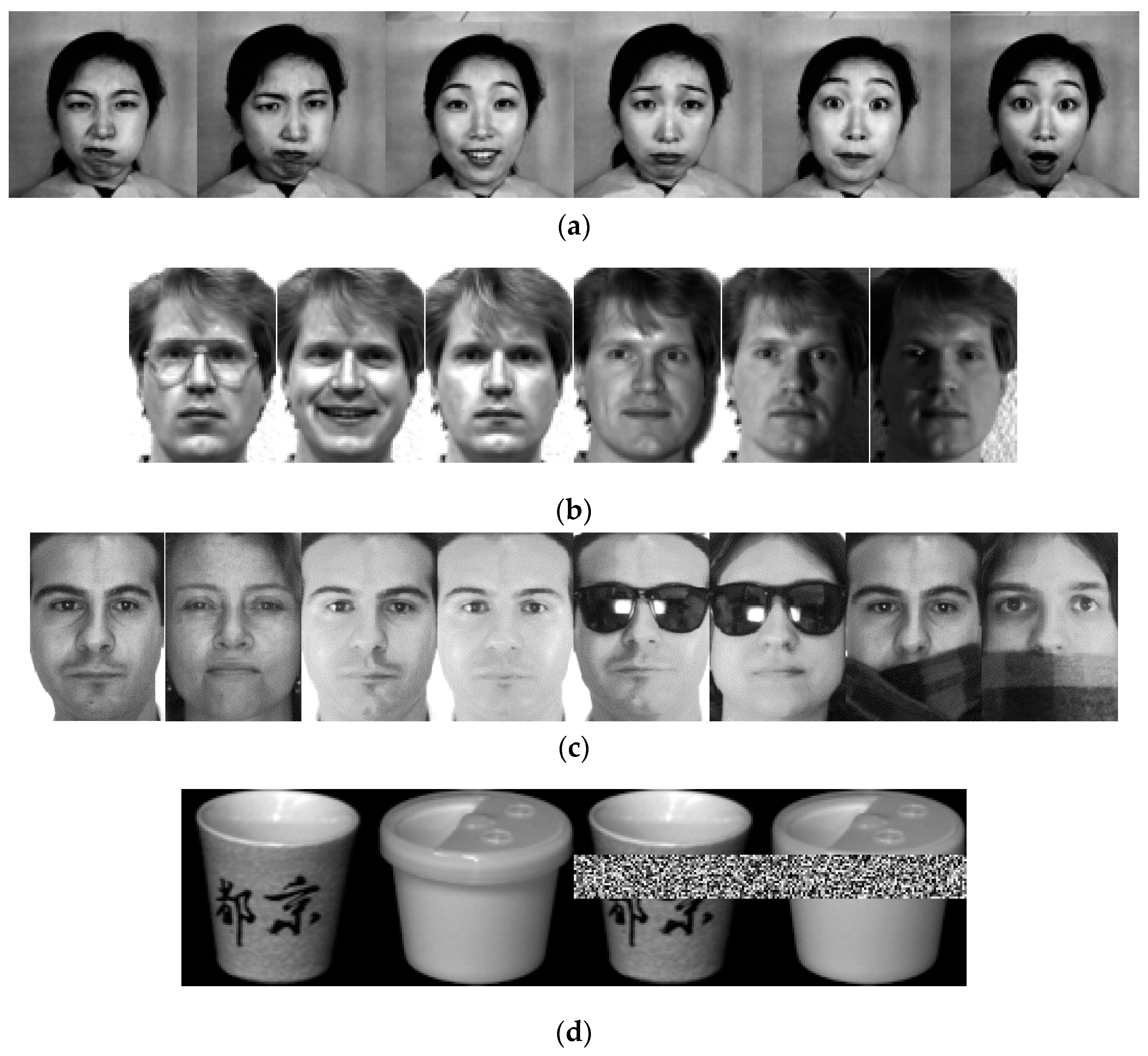
4.1. Image Classification
- The overall AMCR and AMF1-score of TC-PCA is usually the highest among the PCA methods for any number of testing images. It is higher than other PCA methods up to 4.6% for both AMCR and AMF1-score. When the number of testing images is one (i.e., r = 1), the proposed method performs better than the second best, OM-RPCA method by 2.4% for AMCR and 1.4% for AMF1-score. Besides, the overall AMCR and AMF1-score of any PCA method increases with the number of testing images and approximately converges to 81%. As the number of standard images increases (i.e., more testing images), the recognition problems are easier for most methods, which lead to higher overall AMCRs and AMF1-scores. For a smaller number of testing images, the portion of non-standard images are higher in the testing set and the method must learn more precise features to correctly classify the images. This shows that the proposed method learns more effective features than other PCA methods.
- The TC-PCA outperforms other methods in classifying non-standard images up to 8.26% for AMCR and 7.2% for AMF1-score. These results experimentally justify that the proposed method can successfully discard information given by the non-standard images such as face images under various lighting conditions. On the other hand, the performance of all methods in classifying standard images are similar (around 97%–100%), which is consistent with the findings of JAFFE face database shown in Table 1.
- The overall classification accuracy and F1-score vary with the number of testing images for the Yale face database whereas the classification performance is not sensitive to the number of testing images for the JAFFE face database. Such a difference is mainly due to the ability of each methodology in recognizing non-standard images. Our experimental results reveal that the proposed method has a superior classification performance in classifying standard images and moreover, the use of trimming set in the TC-PCA model makes the proposed method not sensitive to outliers, which can improve the non-standard image classification performance. These results indicate that the overall classification performance of all methods is comparable for the face databases with only standard images while the proposed method outperforms all other methods for the face databases consisting of both standard and non-standard images.
- The proposed method needs 9 to 21 fewer number of projection vectors to achieve high classification rates and F1-scores compared with other PCA methods. Experiments also show that the TC-PCA method usually performs better than the classifier with all dimensions (i.e., the size of an image, which is ) and it only needs 18 to 35 dimensions to achieve good results. This may not be the case for other dimensionality reduction techniques. This shows that the TC-PCA method can effectively discard the noisy information caused by the curse of dimensionality and also better represent the key characteristics of the data.
4.2. Image Clustering
4.3. Parameter Study
4.3.1. Effectiveness of the Trimming Parameter
4.3.2. Sensitivity Analysis of Cluster Centers Initialization of the SPVEA
4.4. Discussions for Large Number of Outliers
5. Conclusions
- The proposed TC-PCA model works well in image classification and clustering. More analysis of the proposed method to different applications such as video surveillance and image segmentation should be done.
- We adopt the hold-out method to estimate the optimal number of projection vectors for classification problems. However, this method did not give the best solutions in the experiments. A more robust estimation should be developed.
- Many PCA methods such as the traditional PCA can be extended to the so-called 2D-PCA. Like these methods, a nature extension of the proposed method to 2D-PCA should be investigated.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nam, G.; Heeseung, C.; Junghyun, C.; Kim, I. PSI-CNN: A pyramid-based scale-invariant CNN architecture for face recognition robust to various image resolutions. Appl. Sci. 2018, 8, 1561. [Google Scholar] [CrossRef]
- Basaran, E.; Gökmen, M.; Kamasak, M. An efficient multiscale scheme using local zernike moments for face recognition. Appl. Sci. 2018, 8, 827. [Google Scholar] [CrossRef]
- Shnain, N.; Hussain, Z.; Lu, S. A feature-based structural measure: An image similarity measure for face recognition. Appl. Sci. 2017, 7, 786. [Google Scholar] [CrossRef]
- Liu, Z.; Song, R.; Zeng, D.; Zhang, J. Principal components adjusted variable screening. Comput. Stat. Data Anal. 2017, 110, 134–144. [Google Scholar] [CrossRef]
- Julie, J.; Francois, H. Selecting the number of components in PCA using cross-validation approximations. Comput. Stat. Data Anal. 2012, 56, 1869–1879. [Google Scholar]
- Yang, J.; Zhang, D.; Frangi, A.F.; Yang, J.-Y. Two-dimensional PCA: A New approach to appearance-based face representation and recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Yang, J.; Qian, J.; Xu, Y. Nuclear norm-based 2-DPCA for extracting features from images. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 2247–2260. [Google Scholar] [CrossRef]
- Wang, Q.; Gao, Q. Two-dimensional PCA with F-norm minimization. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 2718–2724. [Google Scholar]
- Gao, Q.; Gao, F.; Zhang, H.; Hao, X.-J.; Wang, X. Two-dimensional maximum local variation based on image euclidean distance for face recognition. IEEE Trans. Image Process. 2013, 22, 3807–3817. [Google Scholar] [PubMed]
- Lai, Z.; Xu, Y.; Yang, J.; Tang, J.; Zhang, D. Sparse tensor discriminant analysis. IEEE Trans. Image Process. 2013, 22, 3904–3915. [Google Scholar] [PubMed]
- Gao, Q.; Wang, Q.; Huang, Y.; Gao, X.; Hong, X.; Zhang, H. Dimensionality reduction by integrating sparse representation and fisher criterion and its applications. IEEE Trans. Image Process. 2015, 24, 5684–5695. [Google Scholar] [CrossRef]
- Navarrete, P.; Ruiz-del-Solar, J. Analysis and comparison of eigenspace-based face recognition approaches. Int. J. Pattern Recognit. Artif. Intell. 2002, 16, 817–830. [Google Scholar] [CrossRef]
- Brooks, J.P.; Dulá, J.H.; Boone, E.L. A Pure L1-norm principal component analysis. Comput. Stat. Data Anal. 2013, 61, 83–98. [Google Scholar] [CrossRef] [PubMed]
- Kwak, N. Principal component analysis based on L1-norm maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1672–1680. [Google Scholar] [CrossRef]
- Candes, E.; Li, X.; Ma, Y.; Wright, J. Robust principal component analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Xu, H.; Caramanis, C.; Sanghavi, S. Robust PCA by outlier pursuit. IEEE Trans. Inf. Theory 2012, 58, 3047–3064. [Google Scholar] [CrossRef]
- Wright, J.; Ganesh, A.; Rao, S.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. Adv. Neural Inf. Process. Syst. 2009, 22, 2080–2088. [Google Scholar]
- McCoy, M.; Tropp, J. Two proposals for robust PCA using semidefinite programming. Electron. J. Stat. 2011, 5, 1123–1160. [Google Scholar] [CrossRef]
- Nie, F.; Huang, H.; Ding, C.; Luo, D.; Wang, H. Robust principal component analysis with non-greedy l1-norm maximization. In Proceedings of the International Joint Conference on Artificial Intelligence, Barcelona, Spain, 16–22 July 2011; pp. 1433–1438. [Google Scholar]
- Zhou, T.; Tao, D. Double shrinking sparse dimension deduction. IEEE Trans. Image Process. 2013, 22, 244–257. [Google Scholar] [CrossRef] [PubMed]
- Markopoulos, P.P.; Karystinos, G.N.; Pados, D.A. Optimal algorithms for L1-subspace signal processing. IEEE Trans. Signal Process. 2014, 62, 5046–5058. [Google Scholar] [CrossRef]
- Markopoulos, P.P.; Kundu, S.; Chamadia, S.; Pados, D.A. Efficient L1-norm principal-component analysis via bit flipping. IEEE Trans. Signal Process. 2017, 65, 4252–4264. [Google Scholar] [CrossRef]
- Kwak, N. Principal component analysis by Lp-norm Maximization. IEEE Trans. Cybern. 2014, 44, 594–609. [Google Scholar] [CrossRef]
- Luo, M.; Nie, F.; Chang, X.; Yang, Y.; Hauptmann, A.; Zheng, Q. Avoiding optimal mean robust PCA/2DPCA with non-greedy l1-norm maximization. In Proceedings of the International Joint Conference on Artificial Intelligence, New York, NY, USA, 9–16 July 2016; pp. 1802–1808. [Google Scholar]
- Luo, M.; Nie, F.; Chang, X.; Yang, Y.; Hauptmann, A.G.; Zheng, Q. Avoiding optimal mean l2,1-norm maximization-based robust PCA for reconstruction. Neural Comput. 2017, 29, 1124–1150. [Google Scholar] [CrossRef]
- Ke, Q.; Kanade, T. Robust L1-norm factorization in the presence of outliers and missing data by alternative convex programming. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (IEEE CVPR), San Diego, CA, USA, 20–25 June 2005; pp. 739–746. [Google Scholar]
- Meng, D. Divide-and-conquer method for l1-norm matrix factorization in the presence of outliers and missing data. arXiv 2012, arXiv:1202.5844. [Google Scholar]
- Nie, F.; Yuan, J.; Huang, H. Optimal mean robust principal component analysis. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1062–1070. [Google Scholar]
- He, R.; Hu, B.G.; Zheng, W.S.; Kong, X.W. Robust principal component analysis based on maximum correntropy criterion. IEEE Trans. Image Process. 2011, 20, 1485–1494. [Google Scholar]
- Wang, Q.; Gao, Q.; Gao, X.; Nie, F. l2,p-norm based PCA for image recognition. IEEE Trans. Image Process. 2018, 27, 1336–1346. [Google Scholar] [CrossRef]
- Li, X.; Pang, Y.; Yuan, Y. L1-norm-based 2DPCA. IEEE Trans. Syst. Man Cybern. Part B 2010, 40, 1170–1175. [Google Scholar]
- Ju, F.; Sun, Y.; Gao, J.; Hu, Y.; Yin, B. Image outlier detection and feature extraction via l1-norm-based 2D probabilistic PCA. IEEE Trans. Image Process. 2015, 24, 4834–4846. [Google Scholar] [CrossRef]
- Zhong, F.; Zhang, J. Linear discriminant analysis based on L1-norm maximization. IEEE Trans. Image Process. 2013, 22, 3018–3027. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Q.; Miao, S.; Gao, X.; Nie, F.; Li, Y. A non-greedy algorithm for l1-norm LDA. IEEE Trans. Image Process. 2017, 26, 684–695. [Google Scholar] [CrossRef]
- Wang, R.; Nie, F.; Yang, X.; Gao, F.; Yao, M. Robust 2DPCA with non-greedy L1-norm maximization for image analysis. IEEE Trans. Cybern. 2015, 45, 1108–1112. [Google Scholar] [CrossRef]
- Ding, X.; He, L.; Carin, L. Bayesian robust principal component analysis. IEEE Trans. Image Process. 2011, 20, 3419–3430. [Google Scholar] [CrossRef]
- Parker, J.T.; Schniter, P.; Cevher, V. Bilinear generalized approximate message passing—Part I: Derivation. IEEE Trans. Signal Process. 2014, 62, 5839–5853. [Google Scholar] [CrossRef]
- Parker, J.T.; Schniter, P.; Cevher, V. Bilinear generalized approximate message passing—Part II: Application. IEEE Trans. Signal Process. 2014, 62, 5854–5867. [Google Scholar] [CrossRef]
- Khan, Z.; Shafait, F.; Mian, A. Joint group sparse PCA for compressed hyperspectral imaging. IEEE Trans. Image Process. 2015, 24, 4934–4942. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, F.; Zhao, M.; Zhang, L.; Yan, S. Joint low-rank and sparse principal feature coding for enhanced robust representation and visual classification. IEEE Trans. Image Process. 2016, 25, 2429–2443. [Google Scholar] [CrossRef]
- Wang, N.; Yao, T.; Wang, J.; Yeung, D. A probabilistic approach to robust matrix factorization. In European Conference on Computer Vision; Springer: Berlin/Heidelberg, Germany, 2012; pp. 126–139. [Google Scholar]
- Wang, N.; Yeung, D. Bayesian robust matrix factorization for image and video processing. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Zhao, Q.; Meng, D.; Xu, Z.; Zuo, W.; Zhang, L. Robust principal component analysis with complex noise. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014. [Google Scholar]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J. Total variation and rank-1 constraint RPCA for background subtraction. IEEE Access 2018, 6, 49955–49966. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Mittal, S.; Anand, S.; Meer, P. Generalized projection-based M-estimator. IEEE Trans. Pattern Anal. Mach. Int. 2012, 34, 2351–2364. [Google Scholar] [CrossRef]
- Mittal, S.; Anand, S.; Meer, P. Generalized projection-based M-estimator: Theory and application. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 2689–2696. [Google Scholar]
- Fauconnier, C.; Haesbroeck, G. Outliers detection with the minimum covariance determinant estimator in practice. Stat. Methodol. 2009, 6, 363–379. [Google Scholar] [CrossRef]
- Rousseeuw, P.J.; Driessen, K.V. A fast algorithm for the minimum covariance determinant estimator. Technometrics 1999, 41, 212–223. [Google Scholar] [CrossRef]
- Zhang, J.; Li, G. Breakdown point properties of location M-estimators. Ann. Stat. 1998, 26, 1170–1189. [Google Scholar]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- The Japanese Female Facial Expression (JAFFE) Database. Available online: http://www.kasrl.org/jaffe.html (accessed on 27 July 2018).
- The Yale Face Database. Available online: http://cvc.cs.yale.edu/cvc/projects/yalefaces/yalefaces.html (accessed on 27 July 2018).
- Martinez, A.M.; Benavente, R. The AR Face Database; CVC Technical Report 24; Computer Vision Centar: Barcelona, Spain, 1998. [Google Scholar]
- Columbia University Image Library. Available online: http://www.cs.columbia.edu/CAVE/software/softlib/coil-20.php (accessed on 27 July 2018).
- Nene, S.A.; Nayar, S.K.; Murase, H. Columbia Object Image Library (COIL-20); Technical Report CUCS-005-96; Department of Computer Science, Columbia University: New York, NY, USA, 1996. [Google Scholar]
- Wang, X.; Tang, X. A unified framework for subspace face recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1222–1228. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Florero-Salinas, W.; Li, D. Simple, fast and accurate hyper-parameter tuning in Gaussian-kernel SVM. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 14–19 July 2017; pp. 348–355. [Google Scholar]
- Ding, C.; Zhou, D.; He, X.; Zha, H. R1-PCA: Rotational Invariant L1-norm principal component analysis for robust subspace factorization. In Proceedings of the International Conference on Machine Learning, Pittsburgh, PA, USA, 25–19 June 2006; pp. 281–288. [Google Scholar]
- Ding, C.; He, X. K-means clustering via principal component analysis. In Proceedings of the International Conference on Machine Learning, Banff, Canada, 4–8 July 2004; pp. 225–232. [Google Scholar]

| r | All Dim. | AMCR (Avg. Dim.) [AMF1-Score] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | |||
| 1 | Overall | 1.000 ( – ) | 1.000 (34.30) | 1.000 (40.40) | 1.000 (29.50) | 1.000 (26.80) | 1.000 (30.50) | 1.000 (31.60) | 1.000 (34.80) |
| [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | ||
| 2 | Overall | 0.975 ( – ) | 0.980 (32.80) | 0.990 (31.40) | 0.980 (27.70) | 0.990 (21.50) | 0.980 (25.30) | 0.980 (30.50) | 0.990 (31.80) |
| [0.973] | [0.979] | [0.989] | [0.979] | [0.989] | [0.979] | [0.979] | [0.989] | ||
| 3 | Overall | 0.983 ( – ) | 0.987 (21.50) | 0.990 (35.80) | 0.987 (28.00) | 0.990 (30.90) | 0.987 (27.90) | 0.983 (22.40) | 0.990 (30.20) |
| [0.983] | [0.986] | [0.99] | [0.986] | [0.99] | [0.986] | [0.983] | [0.99] | ||
| 4 | Overall | 0.995 ( – ) | 0.995 (31.30) | 0.995 (48.00) | 0.995 (28.40) | 0.995 (34.30) | 0.995 (34.30) | 0.995 (30.30) | 0.995 (35.10) |
| [0.995] | [0.995] | [0.995] | [0.995] | [0.995] | [0.995] | [0.995] | [0.995] | ||
| 5 | Overall | 0.994 ( – ) | 0.996 (31.70) | 0.996 (44.00) | 0.996 (32.60) | 0.996 (38.90) | 0.996 (31.30) | 0.996 (32.40) | 0.996 (36.00) |
| [0.994] | [0.994] | [0.994] | [0.994] | [0.996] | [0.994] | [0.996] | [0.998] | ||
| 6 | Overall | 0.983 ( – ) | 0.987 (30.20) | 0.993 (37.00) | 0.988 (30.90) | 0.992 (36.70) | 0.988 (35.20) | 0.987 (27.10) | 0.993 (37.50) |
| [0.983] | [0.987] | [0.992] | [0.987] | [0.992] | [0.988] | [0.987] | [0.993] | ||
| 7 | Overall | 0.981 ( – ) | 0.986 (25.00) | 0.986 (48.10) | 0.983 (34.00) | 0.984 (33.10) | 0.983 (26.90) | 0.984 (30.20) | 0.987 (32.90) |
| [0.981] | [0.981] | [0.985] | [0.981] | [0.985] | [0.984] | [0.981] | [0.988] | ||
| 8 | Overall | 0.984 ( – ) | 0.989 (28.40) | 0.990 (44.20) | 0.988 (35.20) | 0.993 (34.50) | 0.988 (41.80) | 0.986 (26.80) | 0.984 (26.30) |
| [0.984] | [0.987] | [0.991] | [0.99] | [0.989] | [0.987] | [0.986] | [0.985] | ||
| 9 | Overall | 0.990 ( – ) | 0.991 (28.00) | 0.990 (46.50) | 0.991 (35.40) | 0.989 (36.00) | 0.989 (28.70) | 0.989 (29.70) | 0.991 (34.30) |
| [0.99] | [0.992] | [0.988] | [0.988] | [0.99] | [0.991] | [0.988] | [0.991] | ||
| r | All Dim. | AMCR (Avg. Dim.) [AMF1-Score] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | |||
| 1 | Overall | 0.670 ( – ) | 0.654 (43.10) | 0.635 (47.70) | 0.651 (42.70) | 0.641 (39.60) | 0.657 (40.80) | 0.654 (43.10) | 0.681 (32.50) |
| [0.681] | [0.669] | [0.642] | [0.666] | [0.648] | [0.67] | [0.667] | [0.684] | ||
| Non-standard | 0.470 | 0.443 | 0.413 | 0.439 | 0.422 | 0.448 | 0.443 | 0.487 | |
| [0.429] | [0.408] | [0.37] | [0.399] | [0.379] | [0.41] | [0.407] | [0.429] | ||
| Standard | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | ||
| 2 | Overall | 0.750 ( – ) | 0.744 (34.70) | 0.731 (33.40) | 0.742 (38.80) | 0.731 (34.10) | 0.742 (43.60) | 0.746 (38.90) | 0.763 (18.7) |
| [0.761] | [0.756] | [0.739] | [0.753] | [0.74] | [0.753] | [0.756] | [0.77] | ||
| Non-standard | 0.443 | 0.430 | 0.404 | 0.426 | 0.400 | 0.430 | 0.435 | 0.483 | |
| [0.386] | [0.372] | [0.353] | [0.377] | [0.346] | [0.371] | [0.378] | [0.425] | ||
| Standard | 0.993 | 0.993 | 0.990 | 0.993 | 0.993 | 0.990 | 0.993 | 0.986 | |
| [0.993] | [0.993] | [0.989] | [0.993] | [0.993] | [0.989] | [0.993] | [0.986] | ||
| 3 | Overall | 0.809 ( – ) | 0.809 (39.20) | 0.800 (36.20) | 0.801 (44.90) | 0.796 (37.20) | 0.803 (41.70) | 0.809 (44.90) | 0.809 (35.20) |
| [0.821] | [0.821] | [0.81] | [0.813] | [0.805] | [0.815] | [0.82] | [0.814] | ||
| Non-standard | 0.470 | 0.457 | 0.435 | 0.448 | 0.426 | 0.452 | 0.461 | 0.457 | |
| [0.414] | [0.405] | [0.382] | [0.399] | [0.375] | [0.409] | [0.405] | [0.393] | ||
| Standard | 0.986 | 0.993 | 0.991 | 0.986 | 0.989 | 0.986 | 0.991 | 0.993 | |
| [0.986] | [0.993] | [0.99] | [0.985] | [0.988] | [0.986] | [0.99] | [0.985] | ||
| 4 | Overall | 0.816 ( – ) | 0.816 (50.70) | 0.809 (37.60) | 0.813 (51.70) | 0.813 (32.00) | 0.812 (43.40) | 0.813 (48.70) | 0.816 (30.60) |
| [0.826] | [0.825] | [0.817] | [0.823] | [0.823] | [0.82] | [0.822] | [0.826] | ||
| Non-standard | 0.400 | 0.400 | 0.387 | 0.396 | 0.378 | 0.400 | 0.391 | 0.400 | |
| [0.375] | [0.368] | [0.351] | [0.365] | [0.352] | [0.371] | [0.363] | [0.37] | ||
| Standard | 0.978 | 0.978 | 0.973 | 0.976 | 0.983 | 0.973 | 0.978 | 0.978 | |
| [0.978] | [0.978] | [0.972] | [0.976] | [0.983] | [0.973] | [0.978] | [0.978] | ||
| r | All Dim. | AMCR (Avg. Dim.) [AMF1-Score] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | |||
| 1 | Overall | 0.588 ( – ) | 0.556 (32.30) | 0.580 (52.80) | 0.564 (36.10) | 0.552 (32.80) | 0.556 (27.40) | 0.564 (32.50) | 0.680 (20.80) |
| [0.605] | [0.573] | [0.598] | [0.581] | [0.57] | [0.578] | [0.581] | [0.692] | ||
| Non-standard | 0.333 | 0.267 | 0.320 | 0.287 | 0.253 | 0.273 | 0.287 | 0.467 | |
| [0.325] | [0.248] | [0.318] | [0.275] | [0.24] | [0.268] | [0.274] | [0.446] | ||
| Standard | 0.970 | 0.990 | 0.970 | 0.980 | 1.000 | 0.980 | 0.980 | 1.000 | |
| [0.96] | [0.987] | [0.96] | [0.973] | [1.000] | [0.973] | [0.973] | [1.000] | ||
| 2 | Overall | 0.674 ( – ) | 0.666 (31.60) | 0.657 (26.10) | 0.663 (33.90) | 0.669 (31.10) | 0.671 (29.10) | 0.666 (36.70) | 0.726 (27.70) |
| [0.693] | [0.687] | [0.684] | [0.682] | [0.692] | [0.693] | [0.685] | [0.744] | ||
| Non-standard | 0.273 | 0.260 | 0.207 | 0.253 | 0.227 | 0.260 | 0.260 | 0.380 | |
| [0.282] | [0.277] | [0.222] | [0.252] | [0.223] | [0.276] | [0.269] | [0.367] | ||
| Standard | 0.975 | 0.970 | 0.995 | 0.970 | 1.000 | 0.980 | 0.970 | 0.985 | |
| [0.973] | [0.965] | [0.995] | [0.968] | [1.000] | [0.979] | [0.968] | [0.984] | ||
| 3 | Overall | 0.758 ( – ) | 0.742 (33.40) | 0.749 (32.80) | 0.742 (33.10) | 0.751 (39.20) | 0.751 (35.30) | 0.744 (35.40) | 0.773 (20.90) |
| [0.766] | [0.75] | [0.76] | [0.751] | [0.761] | [0.76] | [0.753] | [0.776] | ||
| Non-standard | 0.347 | 0.313 | 0.293 | 0.307 | 0.280 | 0.333 | 0.313 | 0.373 | |
| [0.319] | [0.291] | [0.279] | [0.278] | [0.259] | [0.312] | [0.292] | [0.361] | ||
| Standard | 0.963 | 0.957 | 0.977 | 0.960 | 0.987 | 0.960 | 0.960 | 0.973 | |
| [0.962] | [0.955] | [0.976] | [0.958] | [0.985] | [0.958] | [0.958] | [0.969] | ||
| 4 | Overall | 0.782 ( – ) | 0.775 (26.30) | 0.776 (28.40) | 0.776 (28.50) | 0.793 (23.90) | 0.784 (25.20) | 0.771 (23.00) | 0.784 (23.90) |
| [0.786] | [0.779] | [0.785] | [0.781] | [0.799] | [0.789] | [0.776] | [0.79] | ||
| Non-standard | 0.313 | 0.293 | 0.273 | 0.300 | 0.267 | 0.300 | 0.280 | 0.293 | |
| [0.329] | [0.299] | [0.287] | [0.305] | [0.265] | [0.308] | [0.28] | [0.286] | ||
| Standard | 0.958 | 0.955 | 0.965 | 0.955 | 0.990 | 0.965 | 0.955 | 0.968 | |
| [0.956] | [0.953] | [0.964] | [0.954] | [0.99] | [0.964] | [0.953] | [0.967] | ||
| r | All Dim. | AMCR (Avg. Dim.) [AMF1-Score] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | |||
| 1 | Overall | 0.588 ( – ) | 0.592 (31.70) | 0.576 (40.10) | 0.592 (28.30) | 0.572 (36.30) | 0.592 (24.40) | 0.588 (29.30) | 0.816 (15.10) |
| [0.595] | [0.598] | [0.582] | [0.599] | [0.588] | [0.599] | [0.597] | [0.817] | ||
| Non-standard | 0.333 | 0.333 | 0.313 | 0.333 | 0.300 | 0.333 | 0.333 | 0.693 | |
| [0.312] | [0.309] | [0.28] | [0.312] | [0.284] | [0.31] | [0.316] | [0.665] | ||
| Standard | 0.97 | 0.980 | 0.970 | 0.980 | 0.980 | 0.980 | 0.970 | 1.000 | |
| [0.96] | [0.973] | [0.96] | [0.973] | [0.973] | [0.973] | [0.96] | [1.000] | ||
| 2 | Overall | 0.694 ( – ) | 0.669 (20.90) | 0.691 (31.30) | 0.680 (25.60) | 0.663 (38.50) | 0.680 (24.80) | 0.671 (27.90) | 0.840 (18.10) |
| [0.708] | [0.69] | [0.711] | [0.697] | [0.685] | [0.696] | [0.691] | [0.845] | ||
| Non-standard | 0.32 | 0.253 | 0.287 | 0.280 | 0.220 | 0.287 | 0.260 | 0.647 | |
| [0.329] | [0.266] | [0.308] | [0.277] | [0.235] | [0.292] | [0.271] | [0.597] | ||
| Standard | 0.975 | 0.980 | 0.995 | 0.980 | 0.995 | 0.975 | 0.980 | 0.985 | |
| [0.973] | [0.979] | [0.995] | [0.979] | [0.995] | [0.973] | [0.979] | [0.984] | ||
| 3 | Overall | 0.744 ( – ) | 0.738 (28.60) | 0.742 (45.80) | 0.736 (35.60) | 0.753 (35.80) | 0.744 (37.20) | 0.736 (34.60) | 0.869 (16.10) |
| [0.749] | [0.744] | [0.748] | [0.74] | [0.761] | [0.751] | [0.741] | [0.871] | ||
| Non-standard | 0.307 | 0.287 | 0.293 | 0.273 | 0.273 | 0.300 | 0.300 | 0.660 | |
| [0.286] | [0.267] | [0.284] | [0.248] | [0.274] | [0.278] | [0.285] | [0.614] | ||
| Standard | 0.963 | 0.963 | 0.967 | 0.967 | 0.993 | 0.967 | 0.953 | 0.973 | |
| [0.962] | [0.962] | [0.965] | [0.965] | [0.993] | [0.965] | [0.948] | [0.973] | ||
| 4 | Overall | 0.794 ( – ) | 0.776 (30.60) | 0.780 (29.90) | 0.771 (32.70) | 0.795 (31.80) | 0.789 (26.10) | 0.776 (33.50) | 0.815 (26.70) |
| [0.788] | [0.785] | [0.787] | [0.779] | [0.799] | [0.785] | [0.777] | [0.822] | ||
| Non-standard | 0.32 | 0.280 | 0.300 | 0.280 | 0.273 | 0.307 | 0.287 | 0.38 0 | |
| [0.314] | [0.312] | [0.297] | [0.292] | [0.259] | [0.293] | [0.282] | [0.38] | ||
| Standard | 0.958 | 0.963 | 0.960 | 0.955 | 0.990 | 0.970 | 0.960 | 0.978 | |
| [0.956] | [0.959] | [0.962] | [0.957] | [0.99] | [0.964] | [0.956] | [0.977] | ||
| r | All Dim. | AMCR (Avg. Dim.) [AMF1-Score] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | |||
| 1 | Overall | 0.472 ( – ) | 0.444 (30.90) | 0.444 (37.60) | 0.452 (34.80) | 0.440 (39.30) | 0.448 (30.30) | 0.444 (26.90) | 0.512 (36.30) |
| [0.494] | [0.467] | [0.469] | [0.473] | [0.462] | [0.475] | [0.468] | [0.531] | ||
| Non-standard | 0.14 | 0.093 | 0.093 | 0.107 | 0.087 | 0.100 | 0.093 | 0.200 | |
| [0.136] | [0.086] | [0.077] | [0.099] | [0.077] | [0.09] | [0.087] | [0.191] | ||
| Standard | 0.97 | 0.970 | 0.970 | 0.970 | 0.970 | 0.970 | 0.970 | 0.980 | |
| [0.96] | [0.96] | [0.96] | [0.96] | [0.96] | [0.96] | [0.96] | [0.973] | ||
| 2 | Overall | 0.617 ( – ) | 0.594 (20.90) | 0.609 (30.60) | 0.589 (16.30) | 0.606 (36.50) | 0.594 (14.90) | 0.600 (24.70) | 0.629 (20.70) |
| [0.633] | [0.61] | [0.632] | [0.603] | [0.623] | [0.61] | [0.615] | [0.641] | ||
| Non-standard | 0.14 | 0.080 | 0.100 | 0.073 | 0.087 | 0.073 | 0.100 | 0.153 | |
| [0.107] | [0.054] | [0.086] | [0.052] | [0.068] | [0.046] | [0.07] | [0.124] | ||
| Standard | 0.975 | 0.980 | 0.990 | 0.975 | 0.995 | 0.985 | 0.975 | 0.985 | |
| [0.973] | [0.979] | [0.989] | [0.973] | [0.995] | [0.984] | [0.973] | [0.984] | ||
| 3 | Overall | 0.691 ( – ) | 0.684 (23.10) | 0.691 (30.70) | 0.680 (24.40) | 0.696 (31.80) | 0.689 (23.10) | 0.673 (24.30) | 0.713 (19.40) |
| [0.704] | [0.699] | [0.706] | [0.693] | [0.713] | [0.701] | [0.688] | [0.727] | ||
| Non-standard | 0.147 | 0.120 | 0.127 | 0.120 | 0.113 | 0.127 | 0.093 | 0.180 | |
| [0.158] | [0.12] | [0.137] | [0.119] | [0.122] | [0.126] | [0.098] | [0.165] | ||
| Standard | 0.963 | 0.967 | 0.973 | 0.960 | 0.987 | 0.970 | 0.963 | 0.980 | |
| [0.962] | [0.965] | [0.972] | [0.957] | [0.985] | [0.968] | [0.961] | [0.979] | ||
| 4 | Overall | 0.723 ( – ) | 0.751 (22.60) | 0.756 (32.30) | 0.760 (23.40) | 0.773 (21.40) | 0.758 (22.30) | 0.747 (25.90) | 0.762 (18.70) |
| [0.759] | [0.758] | [0.765] | [0.768] | [0.782] | [0.769] | [0.755] | [0.769] | ||
| Non-standard | 0.207 | 0.200 | 0.193 | 0.200 | 0.187 | 0.200 | 0.187 | 0.200 | |
| [0.191] | [0.187] | [0.181] | [0.2] | [0.178] | [0.194] | [0.177] | [0.199] | ||
| Standard | 0.958 | 0.958 | 0.968 | 0.970 | 0.993 | 0.968 | 0.958 | 0.973 | |
| [0.956] | [0.957] | [0.967] | [0.969] | [0.992] | [0.967] | [0.957] | [0.972] | ||
| r | All Dim. | AMCR (Avg. Dim.) [AMF1-Score] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | |||
| 1 | Overall | 1.000 ( – ) | 0.97 (2.7) | 0.985 (4.1) | 0.995 (5.5) | 0.98 (5.5) | 0.95 (5.6) | 0.995 (4.2) | 1.000 (3.6) |
| [1.000] | [0.973] | [0.985] | [0.995] | [0.984] | [0.956] | [0.996] | [1.000] | ||
| Non-standard | 1.000 | 0.94 | 0.97 | 0.99 | 0.96 | 0.9 | 0.99 | 1.000 | |
| [1.000] | [0.962] | [1.000] | [1.000] | [0.964] | [0.93] | [0.99] | [1.000] | ||
| Standard | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | ||
| 2 | Overall | 1.000 ( – ) | 0.98 (3.8) | 0.983 (2.5) | 0.987 (4.4) | 0.967 (4.5) | 0.99 (3.9) | 0.987 (4.4) | 1.000 (2.9) |
| [1.000] | [0.98] | [0.983] | [0.988] | [0.969] | [0.99] | [0.988] | [1.000] | ||
| Non-standard | 1.000 | 0.94 | 0.95 | 0.96 | 0.9 | 0.97 | 0.96 | 1.000 | |
| [1.000] | [0.951] | [0.942] | [0.963] | [0.891] | [0.971] | [0.959] | [1.000] | ||
| Standard | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | ||
| 3 | Overall | 1.000 ( – ) | 0.993 (7.5) | 0.995 (7.2) | 0.995 (9) | 0.985 (6.5) | 0.995 (8.4) | 0.993 (8.8) | 0.998 (14.7) |
| [1.000] | 0.993 | 0.996 | 0.996 | 0.986 | 0.996 | 0.993 | 0.997 | ||
| Non-standard | 1.000 | 0.97 | 0.98 | 0.98 | 0.94 | 0.98 | 0.97 | 0.99 | |
| [1.000] | 0.972 | 0.983 | 0.981 | 0.943 | 0.981 | 0.973 | 0.99 | ||
| Standard | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 | |
| [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | [1.000] | ||
| All Dim. | NAUC | |||||||
|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | ||
| Synthetic Data 3 | 0.354 | 0.596 | 0.605 | 0.653 | 0.409 | 0.652 | 0.650 | 0.654 |
| JAFFE | 0.676 | 0.673 | 0.686 | 0.680 | 0.684 | 0.677 | 0.674 | 0.691 |
| Yale | 0.545 | 0.519 | 0.538 | 0.521 | 0.525 | 0.528 | 0.520 | 0.547 |
| AR (Normal + Lighting) | 0.476 | 0.491 | 0.495 | 0.490 | 0.498 | 0.487 | 0.489 | 0.509 |
| AR (Normal + Sunglasses) | 0.491 | 0.464 | 0.467 | 0.469 | 0.465 | 0.467 | 0.465 | 0.509 |
| AR (Normal + Scarves) | 0.464 | 0.434 | 0.441 | 0.437 | 0.440 | 0.436 | 0.436 | 0.484 |
| p | Database | r | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 95 | JAFFE | 1.000 | 0.995 | 0.993 | 0.988 |
| Yale | 0.643 | 0.737 | 0.806 | 0.811 | |
| AR (Normal + Lighting) | 0.568 | 0.663 | 0.753 | 0.787 | |
| AR (Normal + Sunglasses) | 0.604 | 0.683 | 0.751 | 0.784 | |
| AR (Normal + Scarves) | 0.448 | 0.600 | 0.693 | 0.742 | |
| 90 | JAFFE | 1.000 | 0.995 | 0.993 | 0.988 |
| Yale | 0.646 | 0.744 | 0.802 | 0.810 | |
| AR (Normal + Lighting) | 0.556 | 0.657 | 0.749 | 0.787 | |
| AR (Normal + Sunglasses) | 0.596 | 0.683 | 0.760 | 0.787 | |
| AR (Normal + Scarves) | 0.472 | 0.600 | 0.702 | 0.742 | |
| 85 | JAFFE | 1.000 | 0.995 | 0.997 | 0.990 |
| Yale | 0.654 | 0.739 | 0.796 | 0.805 | |
| AR (Normal + Lighting) | 0.588 | 0.709 | 0.753 | 0.786 | |
| AR (Normal + Sunglasses) | 0.652 | 0.714 | 0.782 | 0.800 | |
| AR (Normal + Scarves) | 0.476 | 0.603 | 0.722 | 0.744 | |
| 80 | JAFFE | 1.000 | 0.995 | 0.997 | 0.99 |
| Yale | 0.681 | 0.729 | 0.794 | 0.816 | |
| AR (Normal + Lighting) | 0.604 | 0.726 | 0.747 | 0.789 | |
| AR (Normal + Sunglasses) | 0.820 | 0.803 | 0.791 | 0.820 | |
| AR (Normal + Scarves) | 0.504 | 0.620 | 0.716 | 0.747 | |
| 75 | JAFFE | 1.000 | 0.990 | 0.990 | 0.995 |
| Yale | 0.681 | 0.763 | 0.809 | 0.816 | |
| AR (Normal + Lighting) | 0.680 | 0.726 | 0.773 | 0.784 | |
| AR (Normal + Sunglasses) | 0.816 | 0.840 | 0.869 | 0.815 | |
| AR (Normal + Scarves) | 0.512 | 0.629 | 0.713 | 0.762 | |
| Database | r | |||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| JAFFE | 1.000 | 0.975 | 0.987 | 0.995 |
| Yale | 0.659 | 0.744 | 0.809 | 0.812 |
| AR (Normal + Lighting) | 0.632 | 0.683 | 0.773 | 0.795 |
| AR (Normal + Sunglasses) | 0.812 | 0.860 | 0.829 | 0.802 |
| AR (Normal + Scarves) | 0.480 | 0.617 | 0.709 | 0.767 |
| Database | No. of Projection Vectors | ||
|---|---|---|---|
| 1 | 10 | 20 | |
| JAFFE | |||
| Yale | |||
| AR (Normal + Lighting) | |||
| AR (Normal + Sunglasses) | |||
| AR (Normal + Scarves) | |||
| Database | All Dim. | AMCR (Avg. Dim.) [AMF1-Score] | |||||||
|---|---|---|---|---|---|---|---|---|---|
| PCA | HQ-PCA | l1-PCA | RPCA | OM-RPCA | AM-PCA | TC-PCA | |||
| Yale | Overall | 0.804 ( – ) | 0.80 (25) | 0.758 (27.5) | 0.797 (22.70) | 0.821 (26.80) | 0.80 (28.70) | 0.802 (24.30) | 0.806 (31.40) |
| [0.799] | [0.796] | [0.754] | [0.792] | [0.821] | [0.796] | [0.798] | [0.801] | ||
| Non-standard | 0.339 | 0.33 | 0.317 | 0.335 | 0.313 | 0.335 | 0.33 | 0.352 | |
| [0.316] | [0.308] | [0.3] | [0.318] | [0.3] | [0.315] | [0.304] | [0.325] | ||
| Standard | 0.907 | 0.904 | 0.856 | 0.899 | 0.934 | 0.903 | 0.906 | 0.907 | |
| [0.898] | [0.897] | [0.845] | [0.89] | [0.93] | [0.894] | [0.899] | [0.897] | ||
| AR (Normal + Lighting) | Overall | 0.785 ( – ) | 0.702 (13.10) | 0.648 (13.45) | 0.702 (14.50) | 0.742 (14.40) | 0.739 (17.15) | 0.746 (15.10) | 0.71 (12.75) |
| [0.781] | [0.697] | [0.64] | [0.695] | [0.742] | [0.733] | [0.741] | [0.705] | ||
| Non-standard | 0.367 | 0.283 | 0.257 | 0.283 | 0.24 | 0.303 | 0.297 | 0.28 | |
| [0.313] | [0.267] | [0.242] | [0.267] | [0.225] | [0.282] | [0.283] | [0.253] | ||
| Standard | 0.874 | 0.792 | 0.732 | 0.791 | 0.849 | 0.832 | 0.843 | 0.802 | |
| [0.868] | [0.781] | [0.719] | [0.778] | [0.846] | [0.822] | [0.833] | [0.792] | ||
| AR (Normal + Sunglasses) | Overall | 0.793 ( – ) | 0.774 (14.90) | 0.634 (9.80) | 0.731 (13.30) | 0.726 (14.20) | 0.754 (16.20) | 0.712 (14.20) | 0.74 (12.90) |
| [0.79] | [0.771] | [0.622] | [0.723] | [0.723] | [0.752] | [0.708] | [0.737] | ||
| Non-standard | 0.427 | 0.427 | 0.313 | 0.38 | 0.32 | 0.413 | 0.367 | 0.353 | |
| [0.405] | [0.391] | [0.293] | [0.335] | [0.29] | [0.384] | [0.324] | [0.335] | ||
| Standard | 0.871 | 0.849 | 0.703 | 0.806 | 0.813 | 0.827 | 0.786 | 0.823 | |
| [0.865] | [0.844] | [0.687] | [0.795] | [0.804] | [0.822] | [0.779] | [0.814] | ||
| AR (Normal + Scarves) | Overall | 0.767 ( – ) | 0.645 (9.60) | 0.581 (10.10) | 0.582 (7.40) | 0.486 (7.90) | 0.676 (11.20) | 0.655 (10.9) | 0.669 (11.60) |
| [0.767] | [0.643] | [0.578] | [0.578] | [0.48] | [0.674] | [0.656] | [0.667] | ||
| Non-standard | 0.28 | 0.213 | 0.187 | 0.167 | 0.18 | 0.253 | 0.227 | 0.2 | |
| [0.271] | [0.185] | [0.158] | [0.158] | [0.154] | [0.242] | [0.219] | [0.191] | ||
| Standard | 0.871 | 0.737 | 0.666 | 0.671 | 0.551 | 0.767 | 0.747 | 0.77 | |
| [0.865] | [0.735] | [0.662 | [0.662] | [0.543] | [0.76] | [0.742] | [0.764] | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lam, B.S.Y.; Choy, S.K. A Trimmed Clustering-Based l1-Principal Component Analysis Model for Image Classification and Clustering Problems with Outliers. Appl. Sci. 2019, 9, 1562. https://doi.org/10.3390/app9081562
Lam BSY, Choy SK. A Trimmed Clustering-Based l1-Principal Component Analysis Model for Image Classification and Clustering Problems with Outliers. Applied Sciences. 2019; 9(8):1562. https://doi.org/10.3390/app9081562
Chicago/Turabian StyleLam, Benson S. Y., and S. K. Choy. 2019. "A Trimmed Clustering-Based l1-Principal Component Analysis Model for Image Classification and Clustering Problems with Outliers" Applied Sciences 9, no. 8: 1562. https://doi.org/10.3390/app9081562
APA StyleLam, B. S. Y., & Choy, S. K. (2019). A Trimmed Clustering-Based l1-Principal Component Analysis Model for Image Classification and Clustering Problems with Outliers. Applied Sciences, 9(8), 1562. https://doi.org/10.3390/app9081562





