Time-Delayed Feedback Control of Piezoelectric Elastic Beams under Superharmonic and Subharmonic Excitations
Abstract
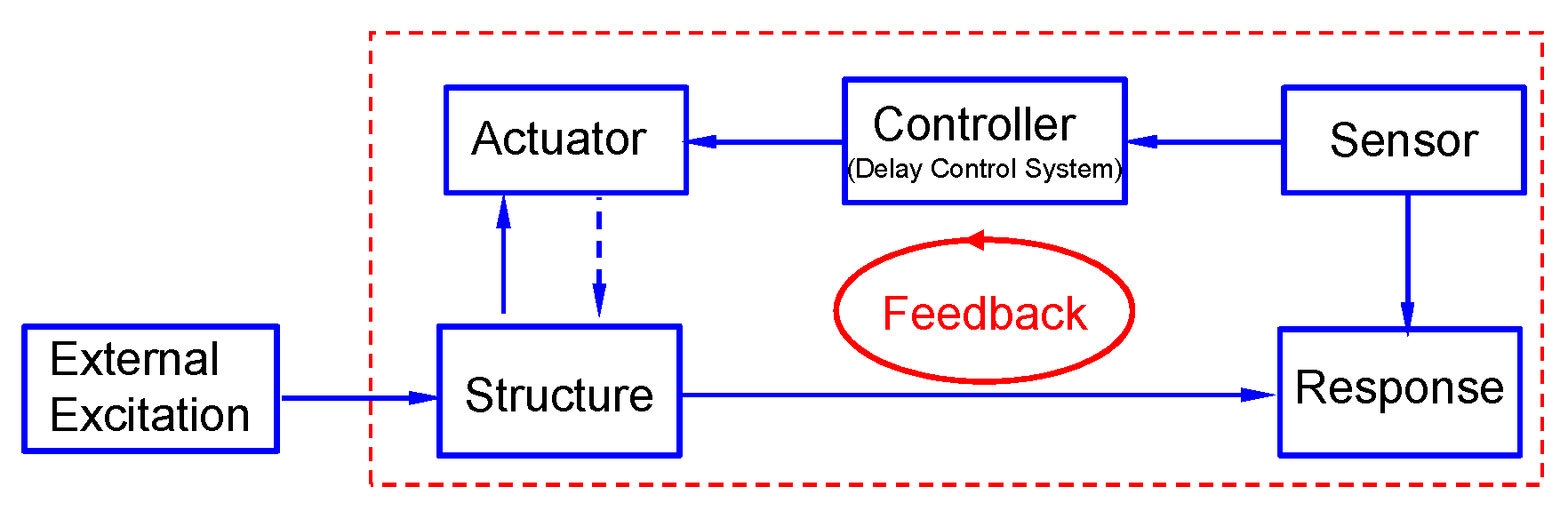
1. Introduction
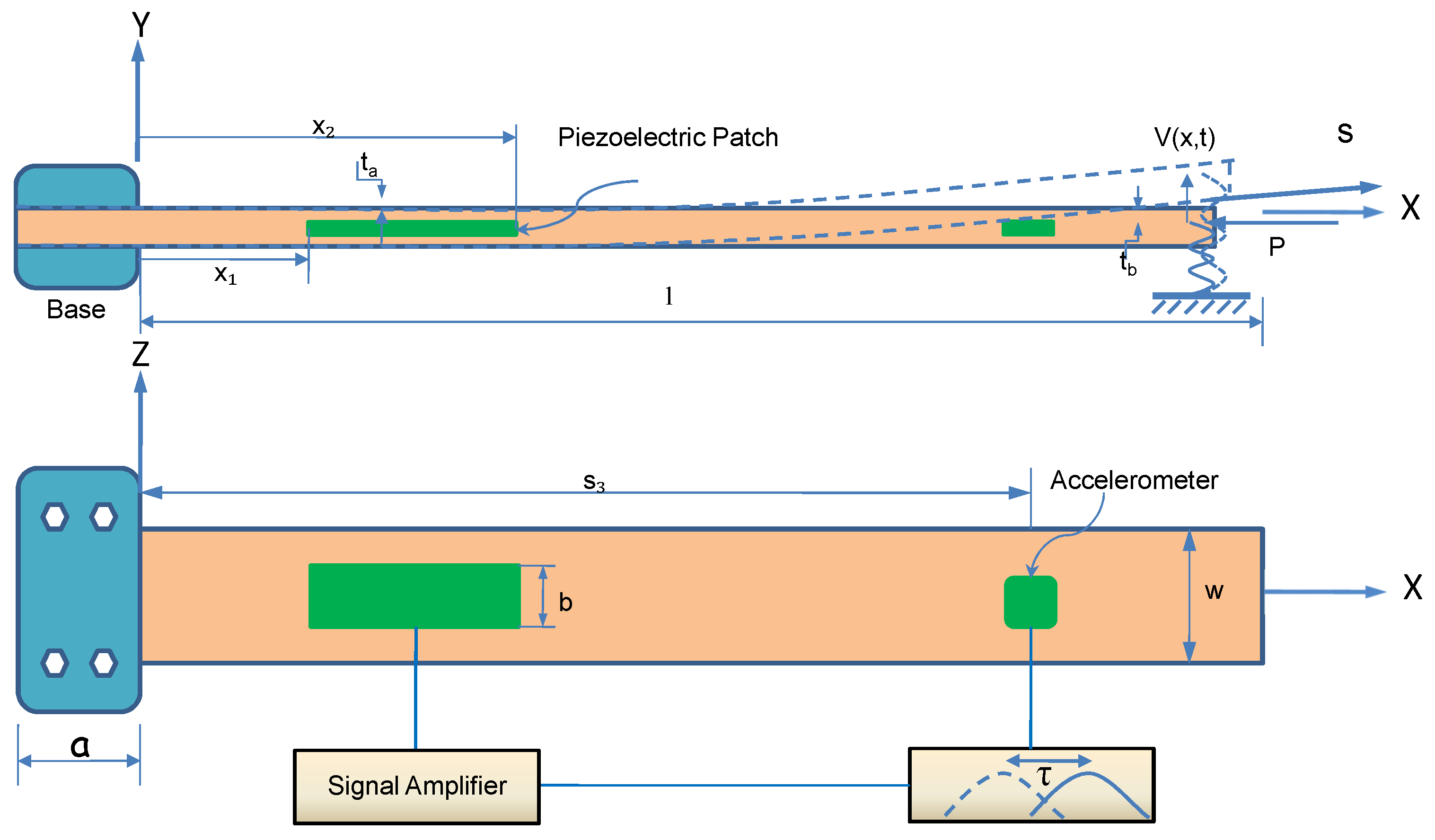
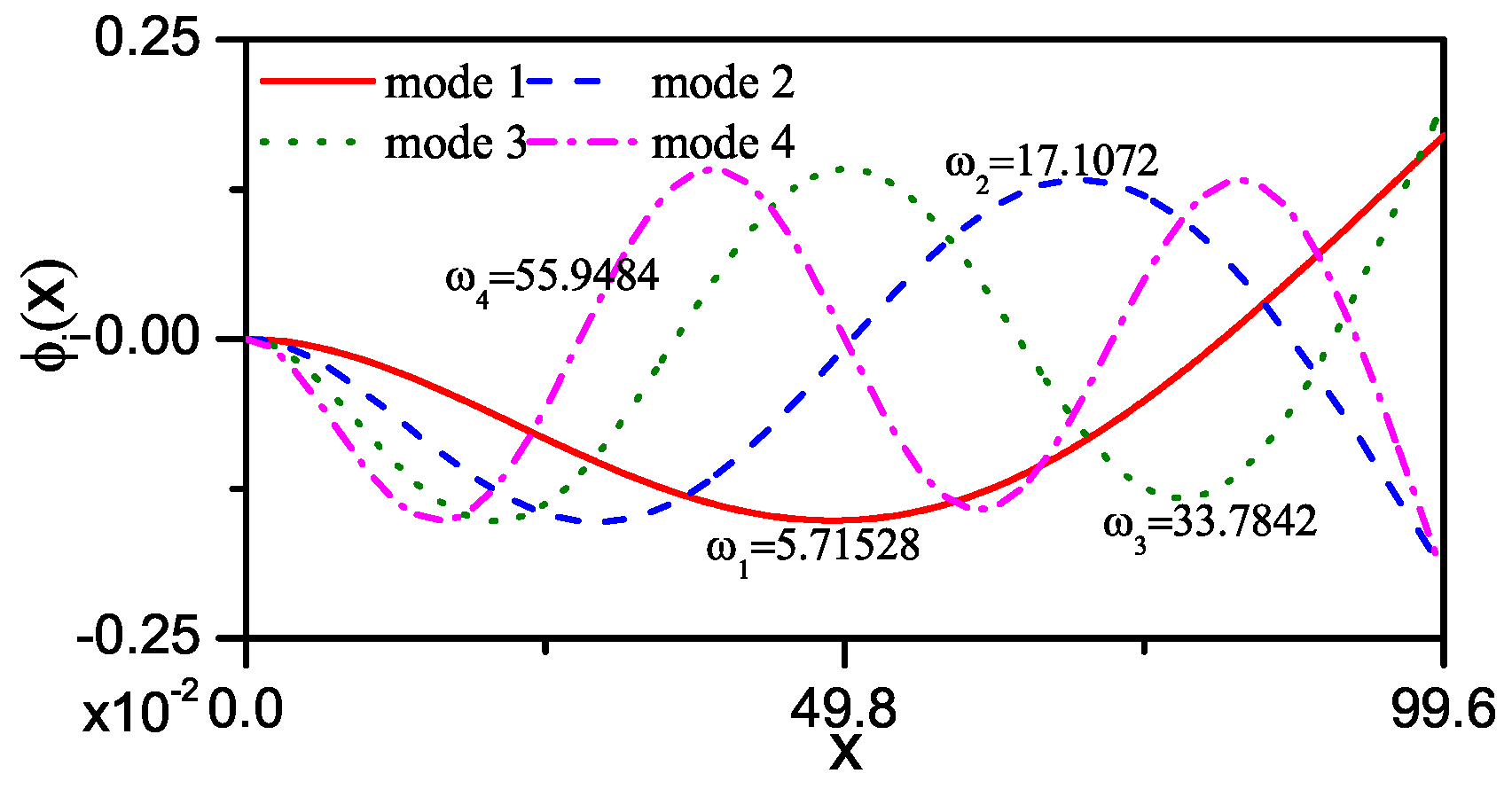
2. Equations of Motion
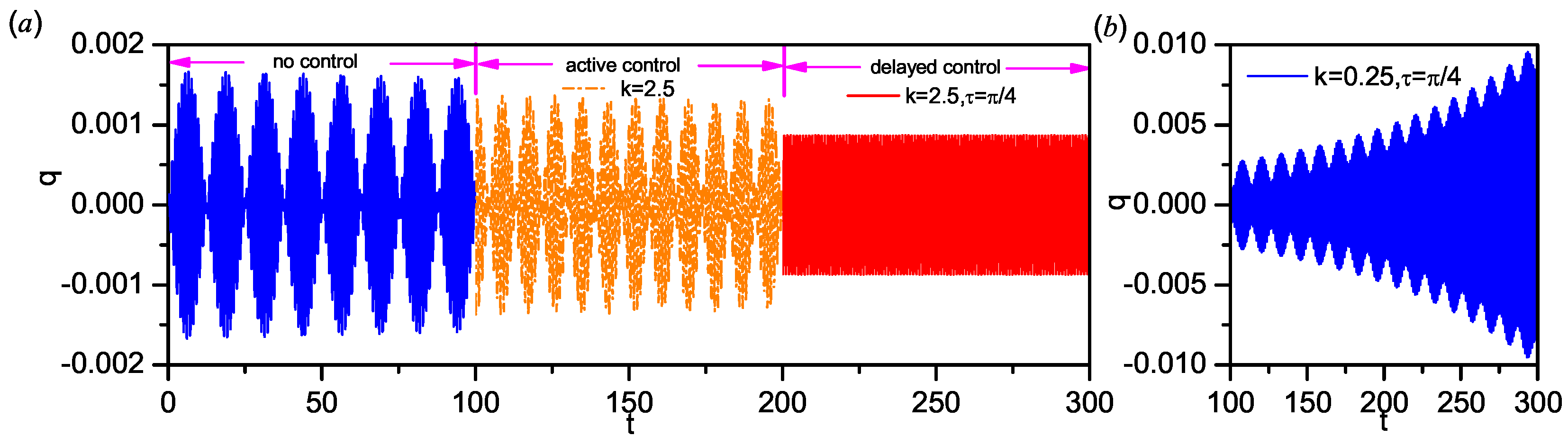
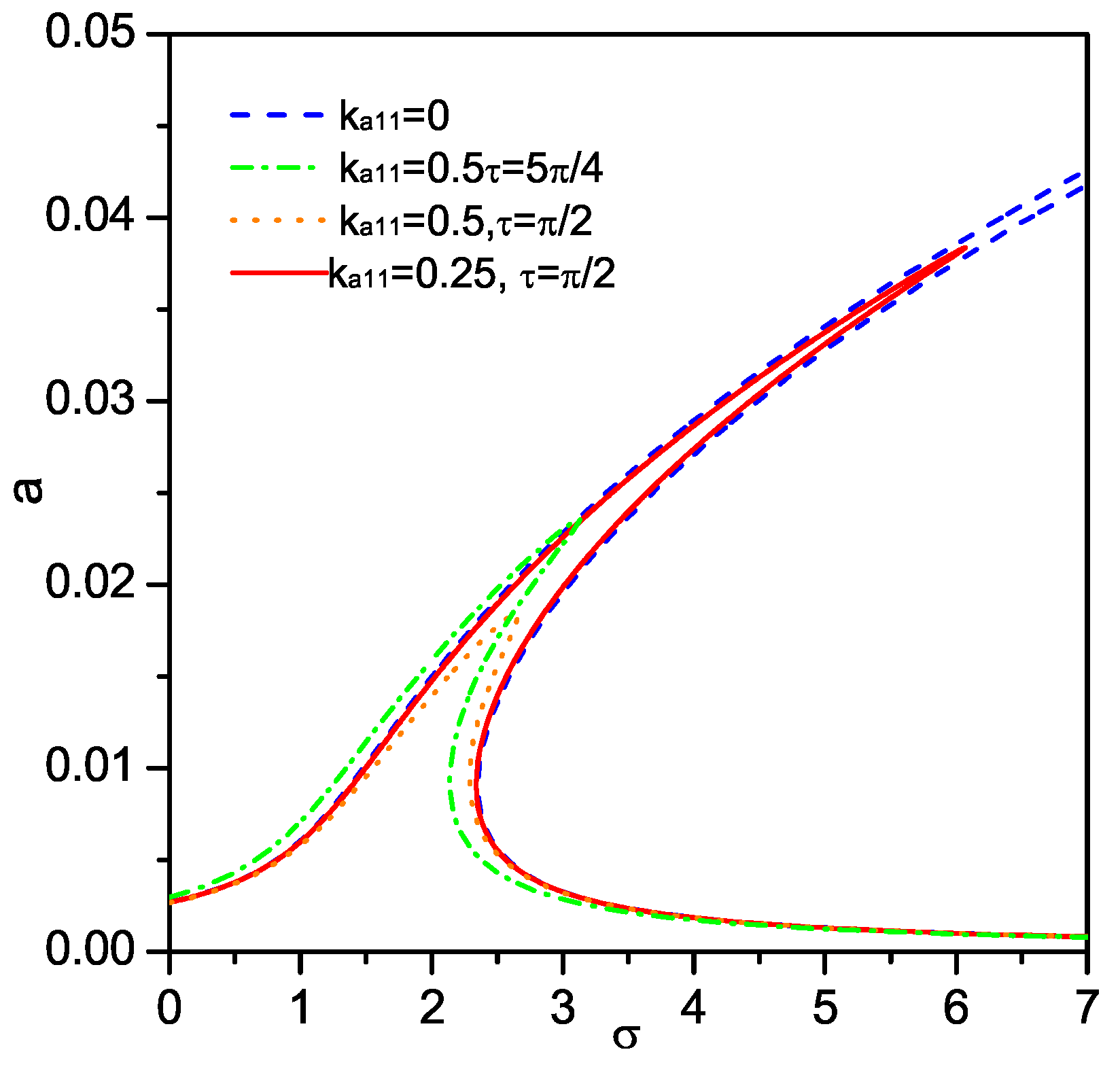
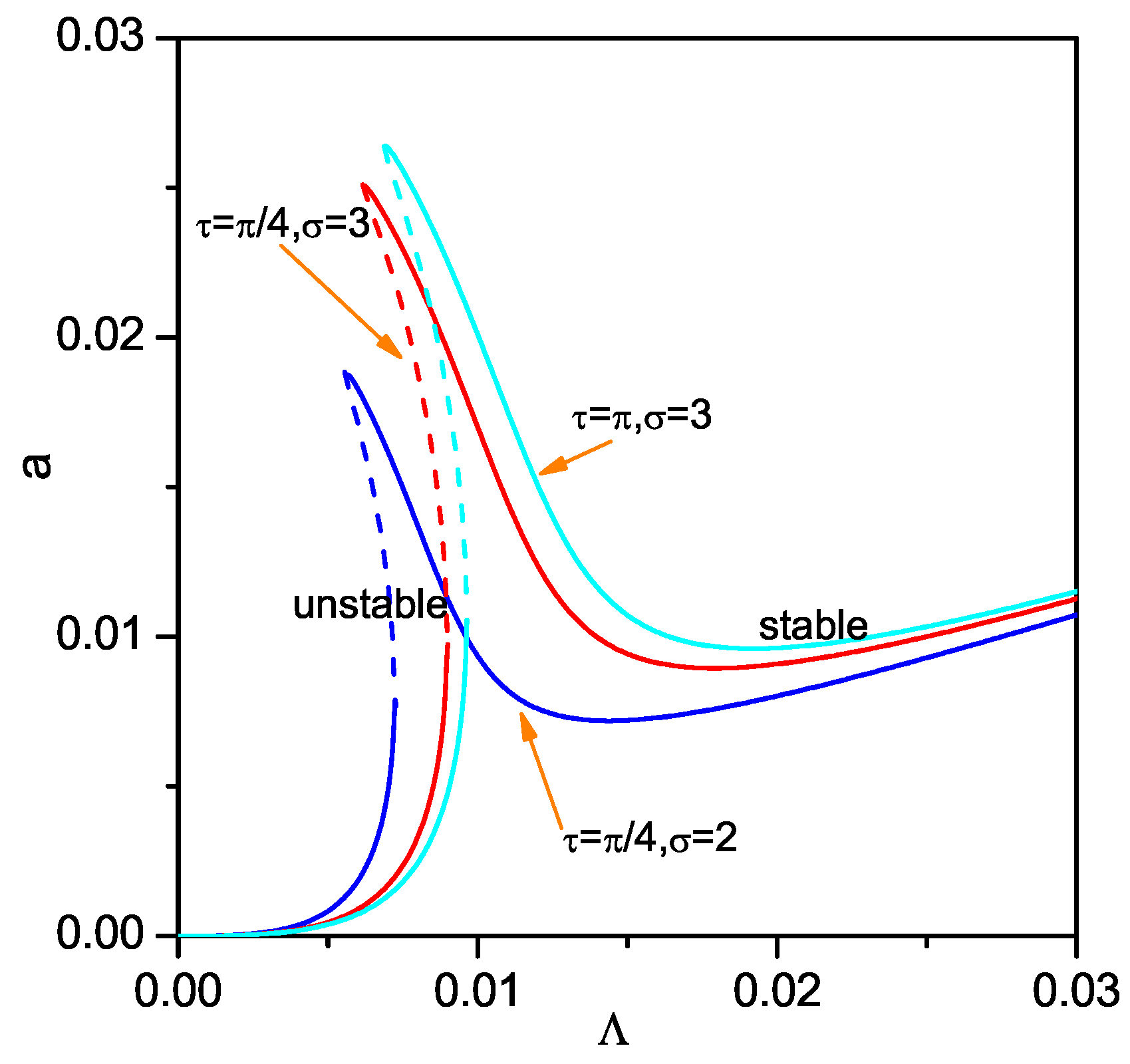
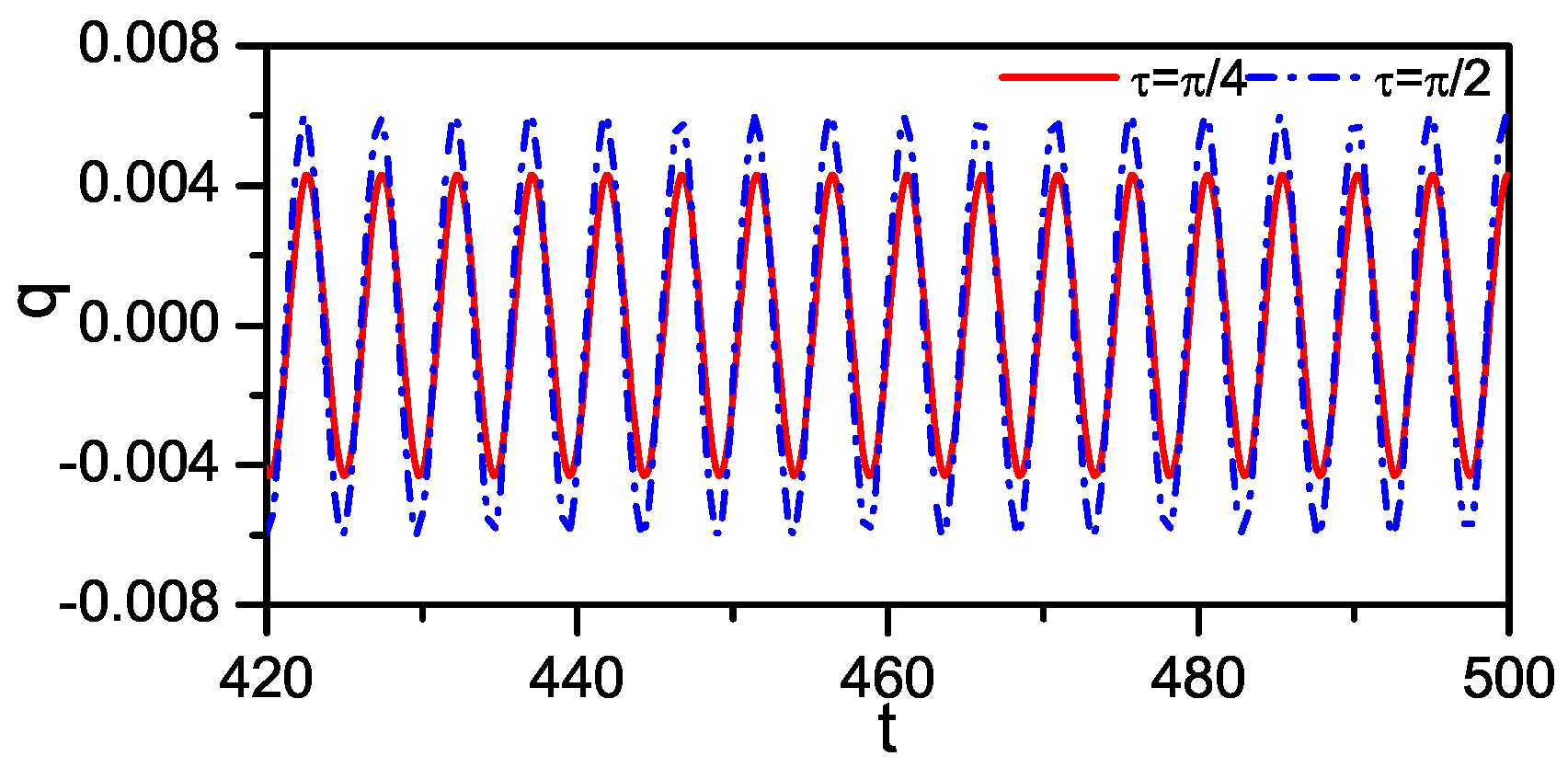
3. Superharmonic Resonance
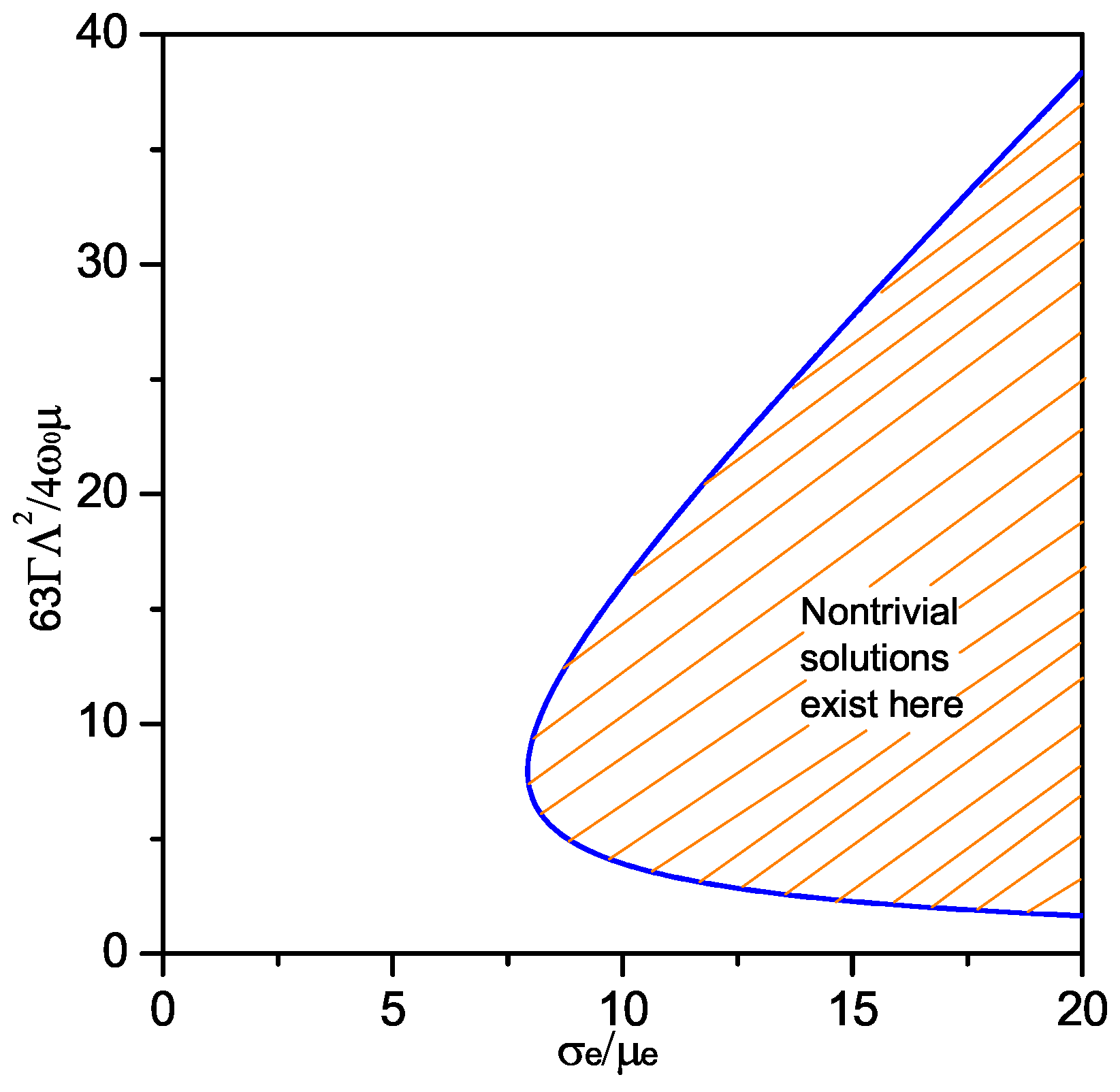
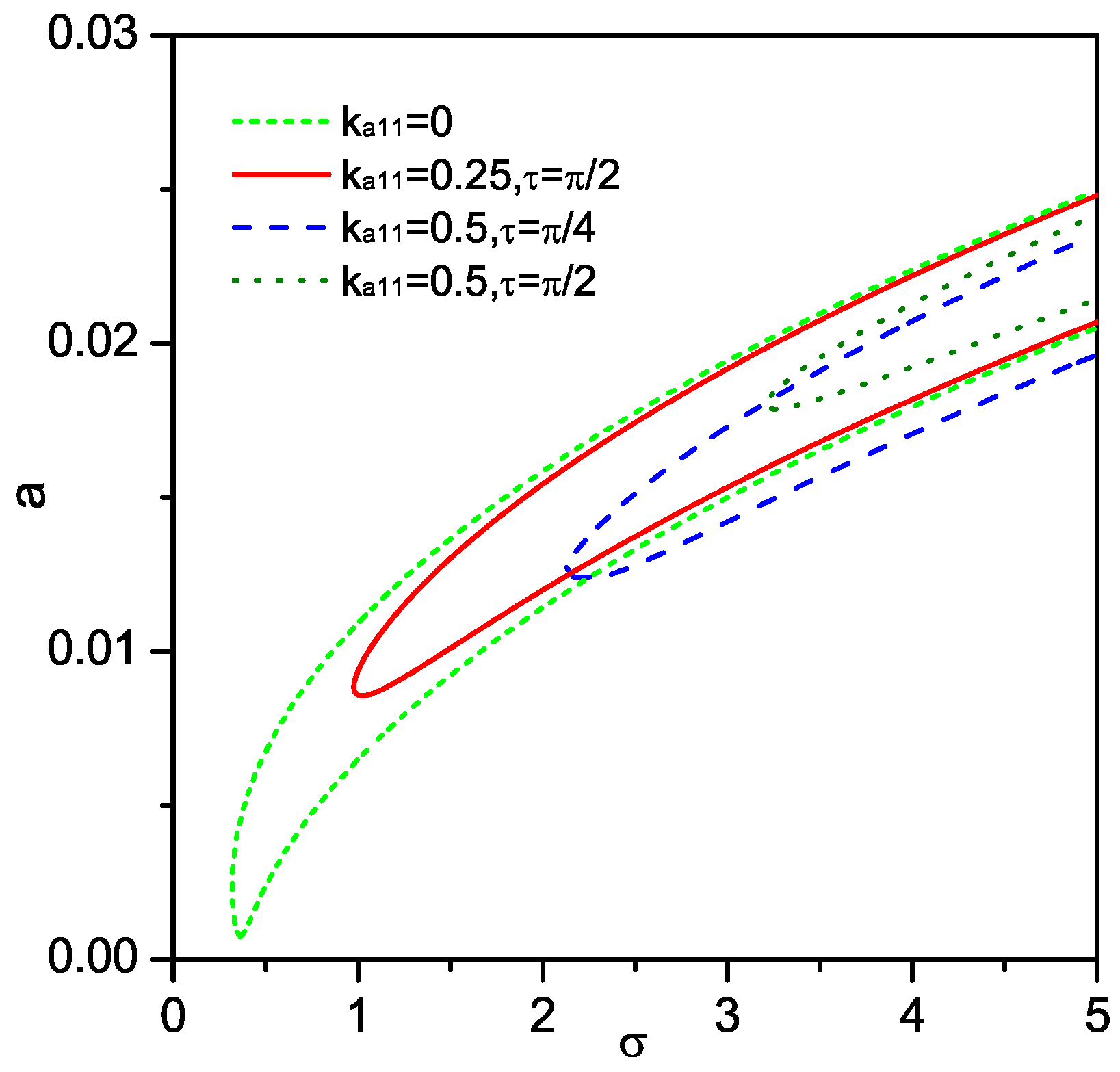
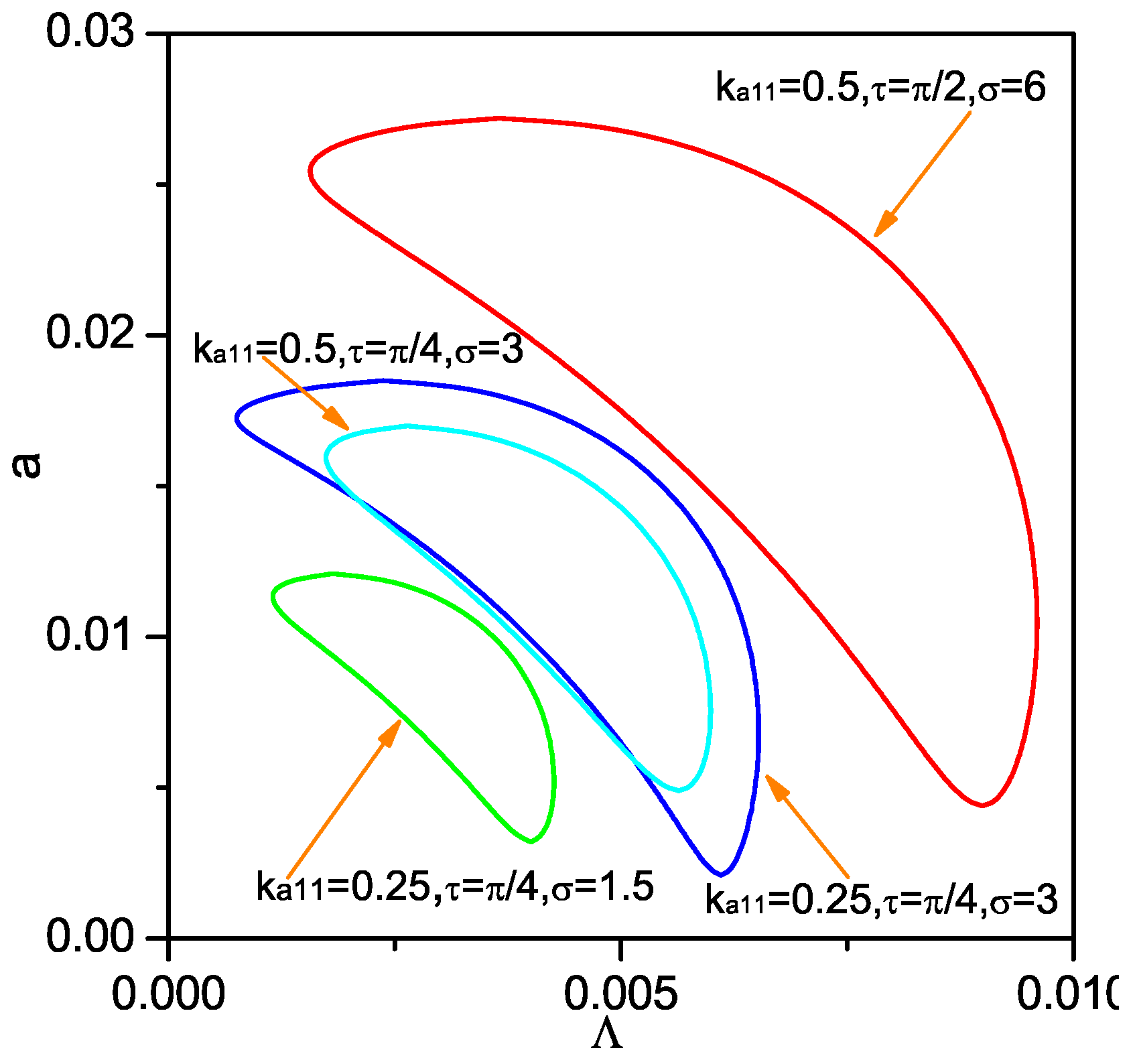
4. 1/3 Subharmonic Resonance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ma, J.J.; Liu, F.J.; Nie, M.Q.; Wang, J.B. Nonlinear free vibration of a beam on Winkler foundation with consideration of soil mass motion of finite depth. Nonlinear Dyn. 2018, 92, 429–441. [Google Scholar] [CrossRef]
- Ma, J.J.; Gao, X.J.; Liu, F.J. Nonlinear lateral vibrations and two-to-one resonant responses of a single pile with soil-structure interaction. Meccanica 2017, 52, 3549–3562. [Google Scholar] [CrossRef]
- Zhong, X.G.; Peng, X.; Yan, S.K.; Shen, M.Y.; Zhai, Y.Y. Assessment of the feasibility of detecting concrete cracks in images acquired by unmanned aerial vehicles. Autom. Constr. 2018, 89, 49–57. [Google Scholar] [CrossRef]
- Wang, W.X.; Wang, X.Y.; Hua, X.G.; Song, G.B.; Chen, Z.Q. Vibration control of vortex-induced vibrations of a bridge deck by a single-side pounding tuned mass damper. Eng. Struct. 2018, 173, 61–75. [Google Scholar] [CrossRef]
- Wang, W.X.; Hua, X.G.; Wang, X.Y.; Chen, Z.Q.; Song, G.B. Optimum design of a novel pounding tuned mass damper under harmonic excitation. Smart Mater. Struct. 2017, 26, 055024. [Google Scholar] [CrossRef]
- Wen, Q.; Hua, X.G.; Lei, X.; Chen, Z.Q.; Niu, H.W. Experimental study of wake-induced instability of coupled parallel hanger ropes for suspension bridges. Eng. Struct. 2018, 167, 175–187. [Google Scholar] [CrossRef]
- Wen, Q.; Hua, X.G.; Chen, Z.Q.; Niu, H.W.; Wang, X.Y. AMD-Based Random Decrement Technique for Modal Identification of Structures with Close Modes. J. Aerosp. Eng. 2018, 5, 04018057. [Google Scholar] [CrossRef]
- Lin, W.; Song, G.B.; Chen, S.H. PTMD control on a benchmark tv tower under earthquake and wind load excitations. Appl. Sci. 2017, 7, 425. [Google Scholar] [CrossRef]
- Sun, H.; Zuo, L.; Wang, X.; Peng, J.; Wang, W. Exact H2 optimal solutions to inerter-based isolation systems for building structures. Struct. Control Health Monit. 2019, e2357. [Google Scholar] [CrossRef]
- Qian, H.; Li, H.N.; Song, G.B. Experimental investigations of building structure with a superelastic shape memory alloy friction damper subject to seismic loads. Smart Mater. Struct. 2016, 25, 125026. [Google Scholar] [CrossRef]
- Lin, W.; Lin, Y.L.; Song, G.B.; Li, J. Multiple Pounding Tuned Mass Damper (MPTMD) control on benchmark tower subjected to earthquake excitations. Earthq. Struct. 2016, 11, 1123–1141. [Google Scholar] [CrossRef]
- Li, H.N.; Zhang, P.; Song, G.B.; Patil, D.; Mo, Y.L. Robustness study of the pounding tuned mass damper for vibration control of subsea jumpers. Smart Mater. Struct. 2015, 24, 095001. [Google Scholar] [CrossRef]
- Wang, W.X.; Hua, X.G.; Wang, X.Y.; Wu, J.L.; Sun, H.X.; Song, G.B. Mechanical behavior of magnetorheological dampers after long-term operation in a cable vibration control system. Struct. Control Health 2019, 26, e2280. [Google Scholar] [CrossRef]
- Yu, Y.; Li, L.Y.; Leng, X.Z.; Song, G.B.; Liu, Z.Q.; Ou, J.P. A wireless decentralized control experimental platform for vibration control of civil structures. Smart. Struct. Syst. 2017, 19, 47–56. [Google Scholar] [CrossRef]
- Wang, H.; Li, L.Y.; Song, G.B.; Dabney, J.B.; Harman, T.L. A new approach to deal with sensor errors in structural controls with MR damper. Smart. Struct. Syst. 2015, 16, 329–345. [Google Scholar] [CrossRef]
- Shivashankar, P.; Kandagal, S.B. Characterization of elastic and electromechanical nonlinearities in piezoceramic plate actuators from vibrations of a piezoelectric-beam. Mech. Syst. Signal Process. 2019, 116, 624–640. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Ni, Y.W.; Zhu, S.B.; Tong, Z.Z.; Sun, J.B.; Xu, X.S. An accurate and straightforward approach to thermo-electro-mechanical vibration of piezoelectric fiber-reinforced composite cylindrical shells. Compos. Struct. 2019, 207, 292–303. [Google Scholar] [CrossRef]
- Bricault, C.; Pezerat, C.; Collet, M.; Pyski, A.; Perrard, P.; Matten, G.; Romero-Garcia, V. Multimodal reduction of acoustic radiation of thin plates by using a single piezoelectric patch with a negative capacitance shunt. Appl. Acoust. 2019, 145, 320–327. [Google Scholar] [CrossRef]
- Feng, Q.; Liang, Y.B.; Song, G.B. Real-time monitoring of early-age concrete strength using piezoceramic-based smart aggregates. J. Aerosp. Eng. 2019, 32, 04018115. [Google Scholar] [CrossRef]
- Lim, Y.Y.; Tang, Z.S.; Smith, S.T. Piezoelectric-based monitoring of the curing of structural adhesives: A novel experimental study. Smart Mater. Struct. 2019, 28, 107532. [Google Scholar] [CrossRef]
- Jiang, T.Y.; Zhang, Y.W.; Wang, L.; Zhang, L.; Song, G.B. Monitoring fatigue damage of modular bridge expansion joints using piezoceramic transducers. Sensors 2018, 18, 3973. [Google Scholar] [CrossRef]
- Chen, M.F.; Chen, H.L.; Ma, X.L.; Jin, G.Y.; Ye, T.G.; Zhang, Y.T.; Liu, Z.G. The isogeometric free vibration and transient response of functionally graded piezoelectric curved beam with elastic restraints. Results Phys. 2018, 11, 71225. [Google Scholar] [CrossRef]
- Przybylski, J.; Gasiorski, G. Nonlinear vibrations of elastic beam with piezoelectric actuators. J. Sound Vib. 2018, 437, 150–165. [Google Scholar] [CrossRef]
- Ling, M.X.; Cao, J.Y.; Li, Q.S.; Zhuang, J. Design, pseudostatic model, and pvdf-based motion sensing of a piezo-actuated XYZ flexure manipulator. IEEE ASME Trans. Mech. 2018, 23, 2837–2848. [Google Scholar] [CrossRef]
- Presas, A.; Luo, Y.; Wang, Z.; Valentin, D.; Egusquiza, M. A Review of PZT Patches Applications in Submerged Systems. Sensors 2018, 18, 2251. [Google Scholar] [CrossRef]
- Wang, T.; Wei, D.L.; Shao, J.H.; Li, Y.R.; Song, G.B. Structural stress monitoring based on piezoelectric impedance frequency shift. J. Aerosp. Eng. 2018, 31, 8. [Google Scholar] [CrossRef]
- Olgac, N.; Holm-Hansen, B.A. Novel Active Vibration Absorption Technique: Delayed Resonator. J. Sound Vib. 1994, 176, 93–104. [Google Scholar] [CrossRef]
- Vyhlal, T.; Olgac, N.; Kucera, V. Delayed resonator with acceleration feedback-Complete stability analysis by spectral methods and vibration absorber. J. Sound Vib. 2014, 333, 6781–6795. [Google Scholar] [CrossRef]
- Kammer, A.S.; Olgac, N. Delayed-feedback vibration absorbers to enhance energy harvesting. J. Sound Vib. 2016, 363, 54–67. [Google Scholar] [CrossRef]
- Ma, J.Z.; Zhang, S.J.; Luan, M.Y.; Wang, J.P. Experimental investigation on delay time phenomenon in rotating detonation engine. Aerosp. Sci. Technol. 2019, 88, 395–404. [Google Scholar] [CrossRef]
- Yan, G.; Fang, M.X.; Xu, J. Analysis and experiment of time-delayed optimal control for vehicle suspension system. J. Sound Vib. 2019, 446, 144–158. [Google Scholar] [CrossRef]
- Zheng, P.X.; Long, X.H. Active control of time-delay in cutting vibration. Theor. Appl. Mech. Lett. 2013, 3, 063003. [Google Scholar] [CrossRef]
- Salehi, H.; Das, S.; Chakrabartty, S.; Biswas, S.; Burgueño, R. An algorithmic framework for reconstruction of time-delayed and incomplete binary signals from an energy-lean structural health monitoring system. Eng. Struct. 2019, 180, 603–620. [Google Scholar] [CrossRef]
- Chen, L.X.; Cai, G.P. Design method of multiple time-delay controller for active structural vibration control. Appl. Math. Mech. Engl. 2009, 30, 1405–1414. [Google Scholar] [CrossRef]
- Hu, H.Y.; Wang, Z.H. Dynamics of Controlled Mechanical Systems with Delayed Feedback; Springer: Berlin/Heidelbeg, Germany, 2002. [Google Scholar]
- Wang, Z.H.; Hu, H.Y. Stabilization of vibration systems via delayed state difference feedback. J. Sound Vib. 2006, 296, 117–129. [Google Scholar] [CrossRef]
- Masoud, Z.; Daqaq, M.F.; Nayfeh, N.H. Pendulation reduction of small telescopic cranes. J. Vib. Control 2004, 10, 1167–1179. [Google Scholar]
- Daqaq, M.F.; Alhazza, K.A.; Arafat, H.N. Non-linear vibrations of cantilever beams with feedback delays. Int. J. Nonlinear Mech. 2008, 43, 962–978. [Google Scholar] [CrossRef]
- Qian, C.Z.; Tang, J.S. A time delay control for a nonlinear dynamic beam under moving load. J. Sound Vib. 2008, 309, 1–8. [Google Scholar] [CrossRef]
- Xu, J.; Yu, P. Delay-induced bifurcations in a nonautonomous system with delayed velocity feedbacks. Int. J. Bifurc. Chaos 2004, 14, 2777–2798. [Google Scholar] [CrossRef]
- Kalmar-Nagy, T.; Stepan, G.; Moon, F.C. Subcritical Hopf bifurcation in the delay equation model for machine tool vibrations. Nonlinear Dyn. 2001, 26, 121–142. [Google Scholar] [CrossRef]
- Peng, J.; Wang, L.H.; Zhao, Y.Y.; Zhao, Y.B. Bifurcation analysis in active control system with time delay feedback. Appl. Math. Comput. 2013, 219, 10073–10081. [Google Scholar] [CrossRef]
- Li, X.Y.; Ji, J.C.; Hansen, C.H.; Tan, C.X. The response of a Duffing-van der Pol oscillator under delayed feedback control. J. Sound Vib. 2006, 291, 644–655. [Google Scholar] [CrossRef]
- Jin, Y.F.; Hu, H.Y. Stabilization of traffic flow in optimal velocity model via delayed-feedback control. Commun. Nonlinear Sci. 2013, 18, 1027–1034. [Google Scholar] [CrossRef]
- Omidi, E.; Mahmoodi, S.N. Sensitivity analysis of the nonlinear integral positive position feedback and integral resonant controllers on vibration suppression of nonlinear oscillatory systems. Commun. Nonlinear Sci. 2015, 22, 149–166. [Google Scholar] [CrossRef]
- Omidi, E.; Mahmoodi, S.N. Nonlinear vibration suppression of flexible structures using nonlinear modified positive position feedback approach. Nonlinear Dyn. 2015, 79, 835–849. [Google Scholar] [CrossRef]
- El-Ganaini, W.A.; Saeed, N.A.; Eissa, M. Positive position feedback (PPF) controller for suppression of nonlinear system vibration. Nonlinear Dyn. 2013, 72, 517–537. [Google Scholar] [CrossRef]
- Warminski, J.; Bochenski, M.; Jarzyna, W.; Filipek, P.; Augustyniak, M. Active suppression of nonlinear composite beam vibrations by selected control algorithms. Commun. Nonlinear Sci. 2011, 16, 2237–2248. [Google Scholar] [CrossRef]
- Belhaq, M.; Ghouli, Z.; Hamdi, M. Energy harvesting in a Mathieu-van der Pol-Duffing MEMS device using time delay. Nonlinear Dyn. 2018, 94, 2537–2546. [Google Scholar] [CrossRef]
- Hamdi, M.; Belhaq, M. Quasi-periodic vibrations in a delayed van der Pol oscillator with time-periodic delay amplitude. J. Vib. Control 2018, 24, 5726–5734. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, J.; Ji, J. Modelling and tuning for a time-delayed vibration absorber with friction. J. Sound Vib. 2018, 424, 137–157. [Google Scholar] [CrossRef]
- Ji, J.C.; Zhou, J. Coexistence of two families of sub-harmonic resonances in a time-delayed nonlinear system at different forcing frequencies. Mech. Syst. Signal Process. 2017, 93, 151–163. [Google Scholar] [CrossRef]
- Ji, J.C.; Brown, T. Periodic and Chaotic Motion of a Time-Delayed Nonlinear System under Two Coexisting Families of Additive Resonances. Int. J. Bifurc. Chaos 2017, 27, 1750066. [Google Scholar] [CrossRef]
- Nayfeh, A.H. Linear and Nonlinear Structure Mechanics; Wiley Interscience: New York, NY, USA, 2004. [Google Scholar]
- Ma, J.J.; Liu, F.J.; Gao, X.J.; Nie, M.Q. Buckling and free vibration of a single pile considering the effect of soil-structure interaction. Int. J. Struct. Stab. Dyn. 2017, 18, 1850061. [Google Scholar] [CrossRef]
- Ma, J.J.; Peng, J.; Gao, X.J.; Xie, L. Effect of soil-structure interaction on the nonlinear response of an inextensional beam on elastic foundation. Arch. Appl. Mech. 2014, 85, 273–285. [Google Scholar] [CrossRef]
- Nayfeh, A.H.; Mook, D.T. Nonlinear Oscillations; Wiley: Hoboken, NJ, USA, 1979. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Xiang, M.; Li, L.; Sun, H.; Wang, X. Time-Delayed Feedback Control of Piezoelectric Elastic Beams under Superharmonic and Subharmonic Excitations. Appl. Sci. 2019, 9, 1557. https://doi.org/10.3390/app9081557
Peng J, Xiang M, Li L, Sun H, Wang X. Time-Delayed Feedback Control of Piezoelectric Elastic Beams under Superharmonic and Subharmonic Excitations. Applied Sciences. 2019; 9(8):1557. https://doi.org/10.3390/app9081557
Chicago/Turabian StylePeng, Jian, Mingjiao Xiang, Luxin Li, Hongxin Sun, and Xiuyong Wang. 2019. "Time-Delayed Feedback Control of Piezoelectric Elastic Beams under Superharmonic and Subharmonic Excitations" Applied Sciences 9, no. 8: 1557. https://doi.org/10.3390/app9081557
APA StylePeng, J., Xiang, M., Li, L., Sun, H., & Wang, X. (2019). Time-Delayed Feedback Control of Piezoelectric Elastic Beams under Superharmonic and Subharmonic Excitations. Applied Sciences, 9(8), 1557. https://doi.org/10.3390/app9081557




