A New Coverage Flight Path Planning Algorithm Based on Footprint Sweep Fitting for Unmanned Aerial Vehicle Navigation in Urban Environments
Abstract
:1. Introduction
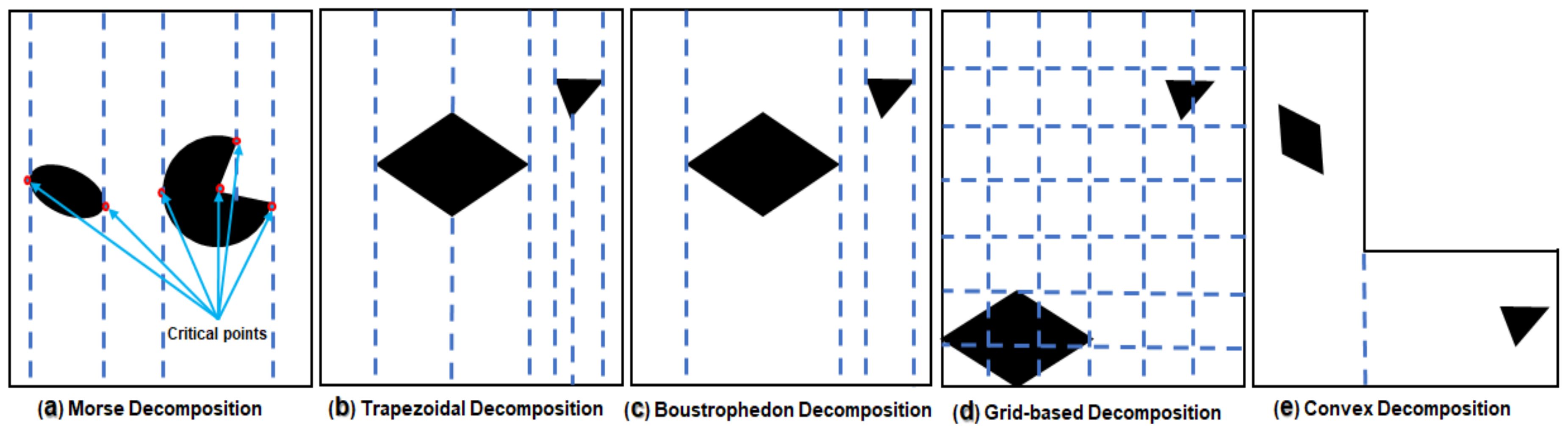
2. Background and Related Work
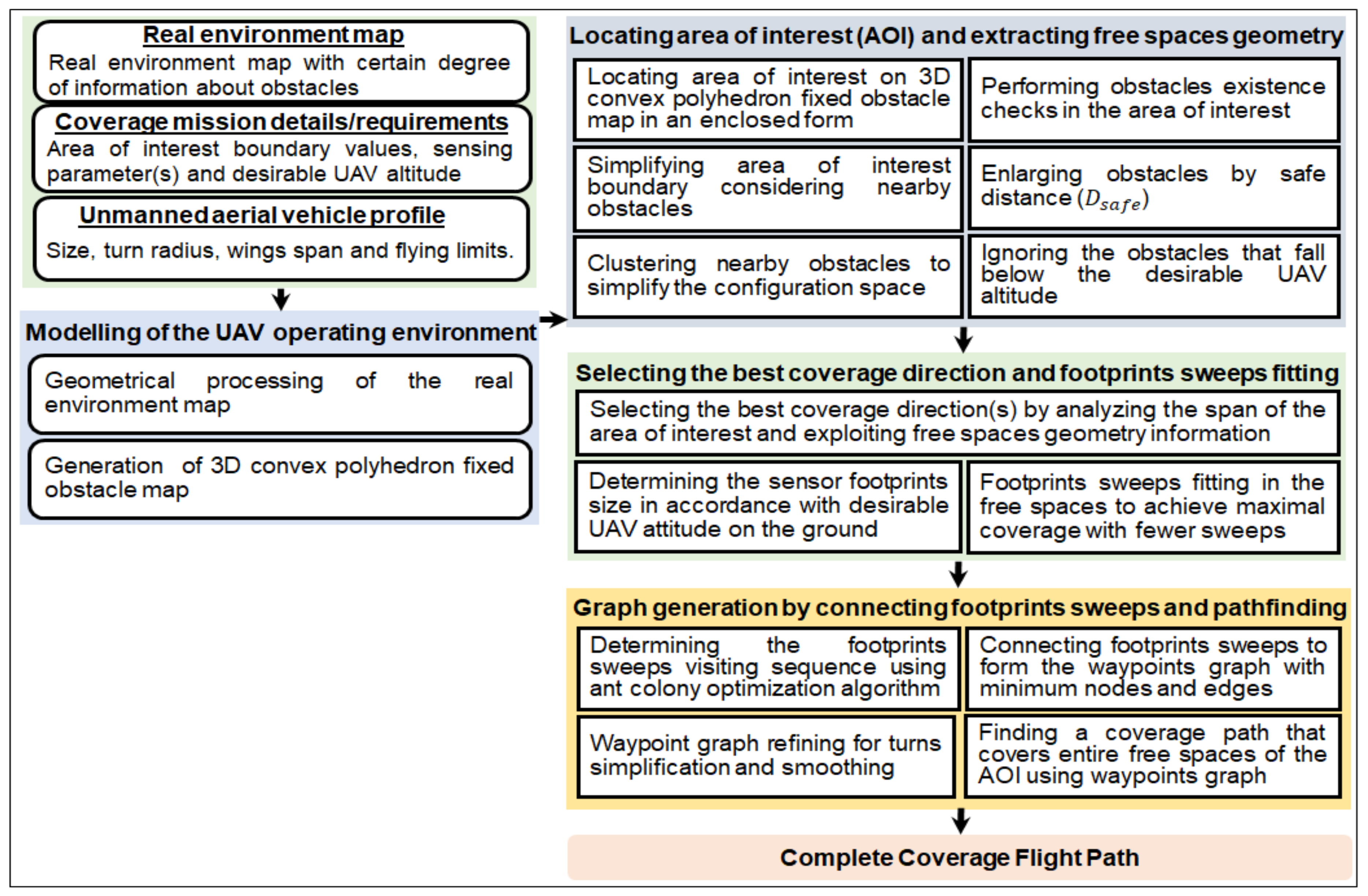
3. The Proposed Coverage Flight Path Planning Algorithm
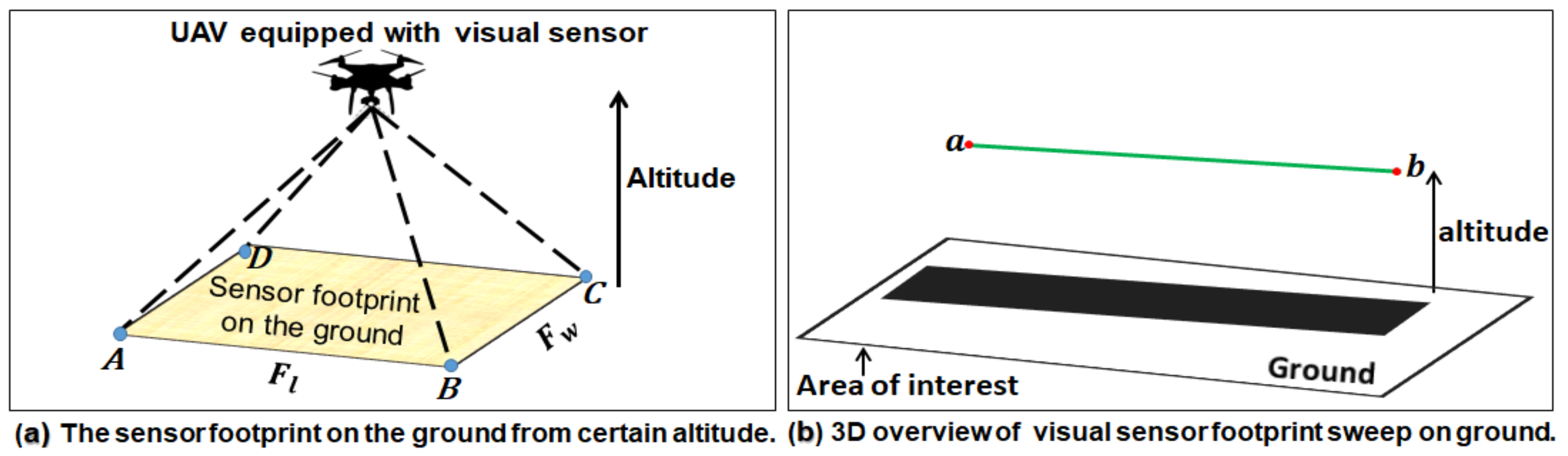
3.1. Modelling of the UAV Operating Environment
3.2. Locating Area of Interest on the Modelled Map and Extracting Free Spaces Geometry
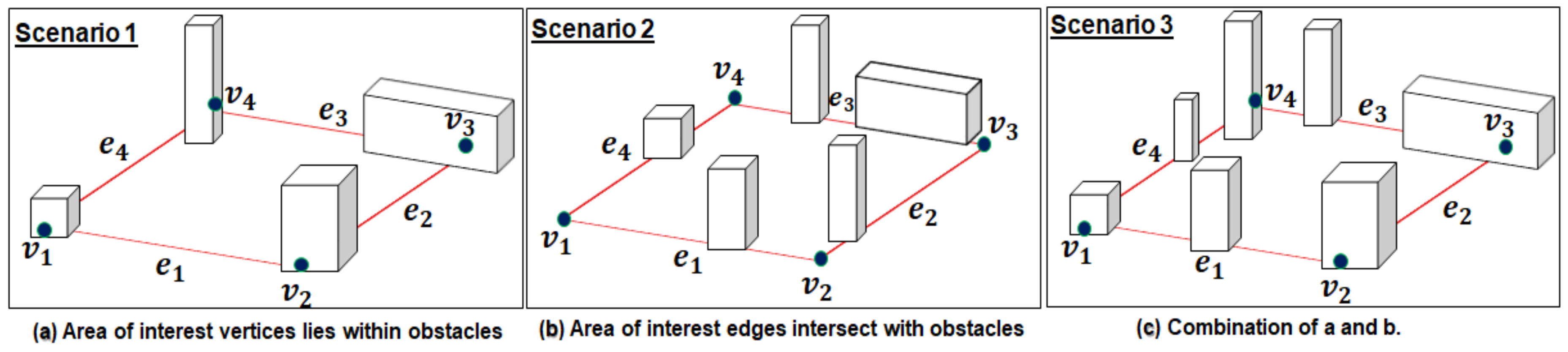
3.2.1. Locating Area of Interest on the 3D Modelled Map
3.2.2. Extracting Free Spaces Geometry
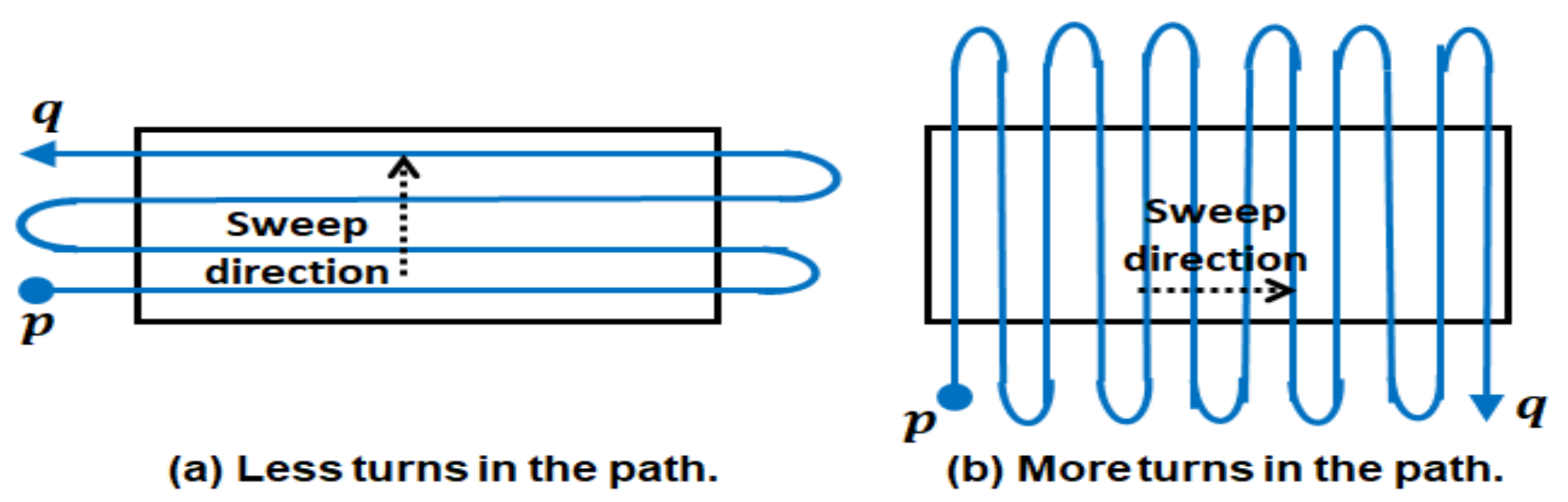
3.3. Selecting the Best Coverage Direction (s) by Analyzing the Span of the Area of Interest and Exploiting Free Spaces Geometry Information
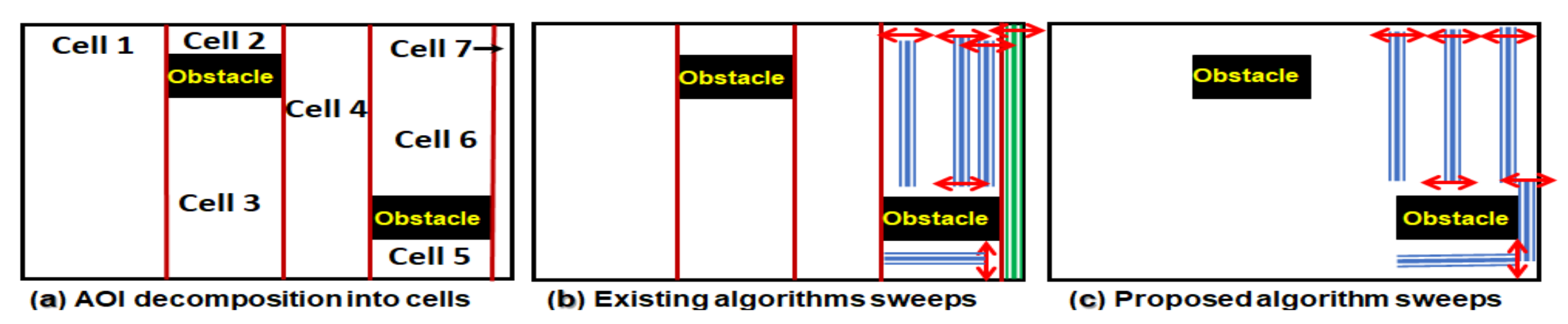
3.4. Sensor Footprints Sweeps Fitting in Free Spaces of the Area of Interest
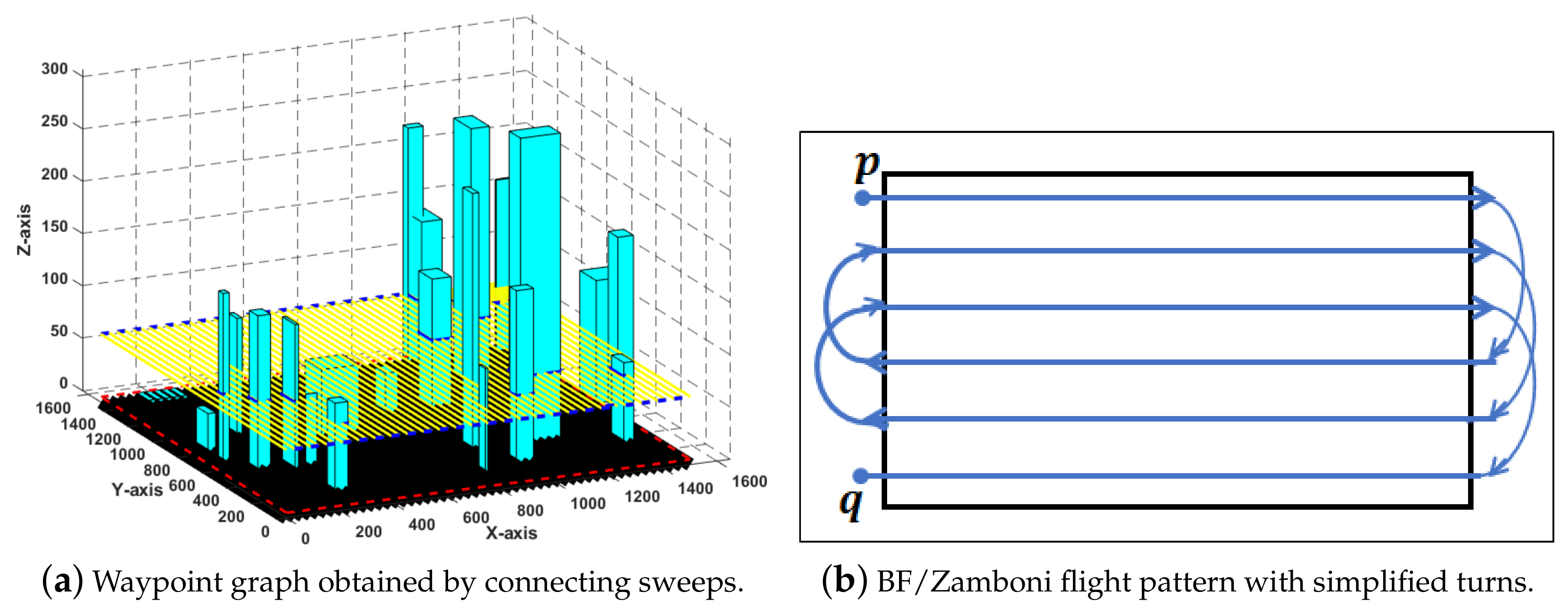
3.5. Determining the Footprints’ Sweeps Visiting Sequence
3.6. Waypoints Graph Generation by Connecting Footprints’ Sweeps
| Algorithm 1: Waypoint graph generation from the AOI located in a 3D map. |
| Input :(1) AOI Q containing N number of obstacles, where . (2) Set R of footprints’ sweeps, where and . (3) Sweeps visitng sequence set S, where (4) Sweeps connection gap (g). Output :Way point graph Procedure: for each footprint sweep , where = to ∈ R do Find next footprint sweep considering the g value and optimized visiting sequence. Identify the relevant endpoint pair using for connection if INTERSECTS(,) then Evaluate and select the appropriate obstacle avoidance option using Equation (7). Connect the footprints’ sweeps and with the relevant endpoints. else Connect the footprints’ sweeps and with the relevant endpoints. End if End for return |
3.7. Path Searching on the Waypoints Graph
4. Simulation Results and Discussion
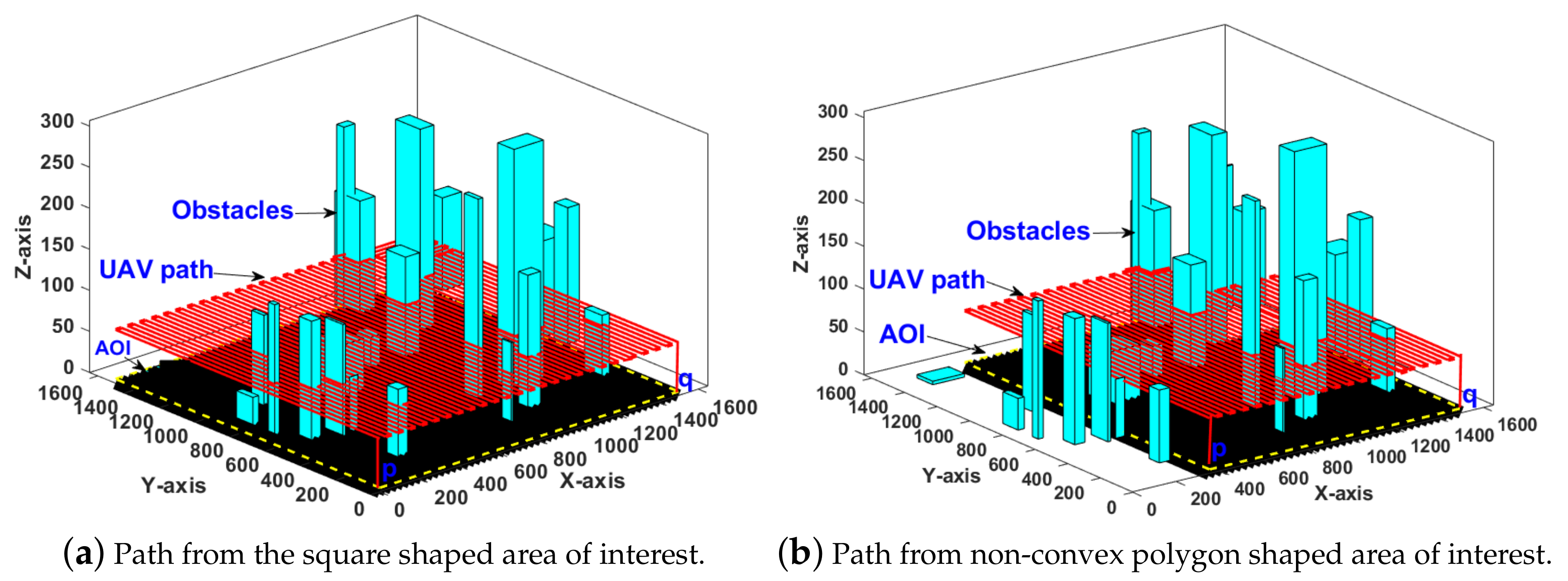
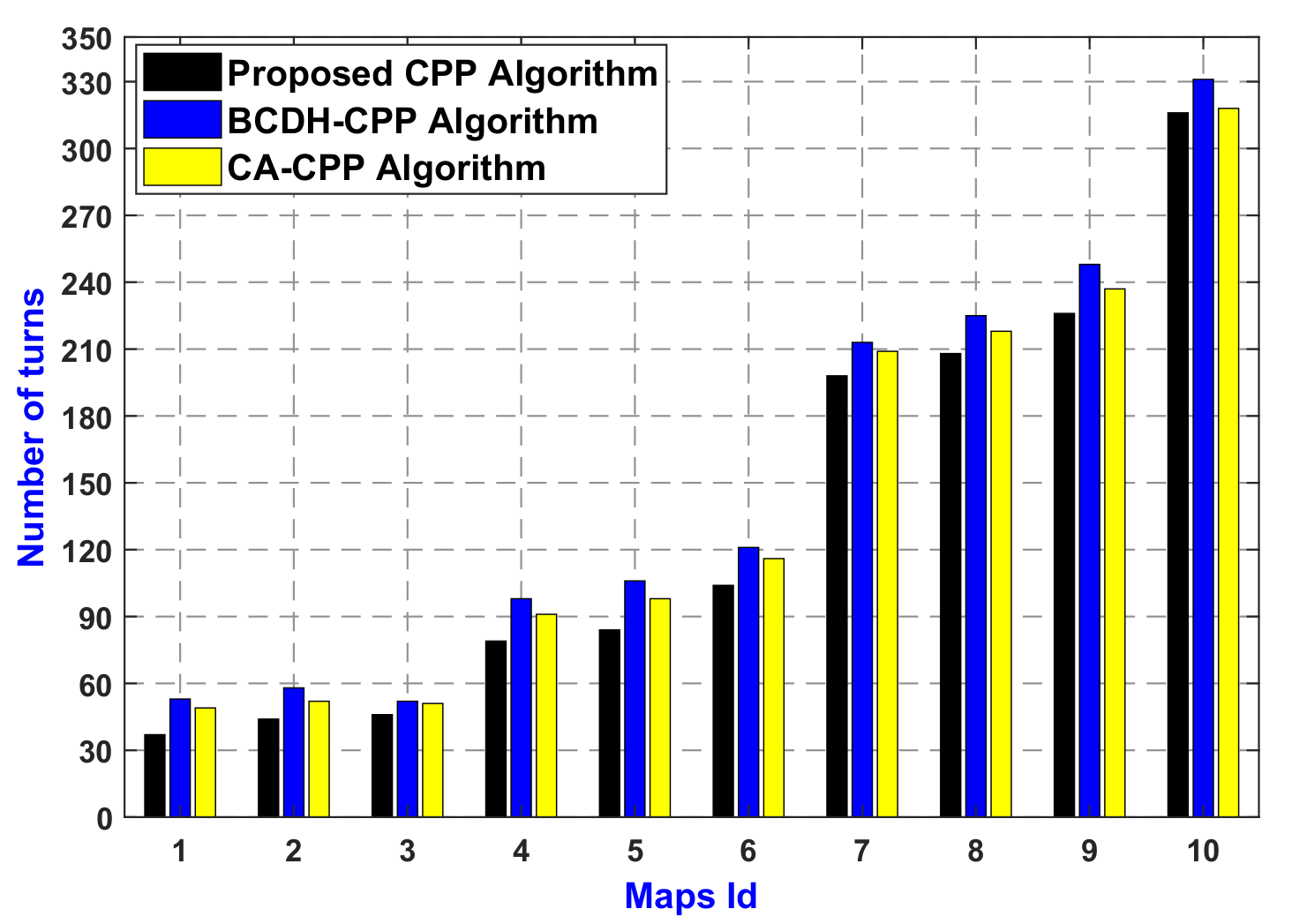
4.1. Comparisons with the Existing Algorithms Based on Obstacles’ Densities
4.2. Comparisons with the Existing Algorithms Based on the Shape of the Area of Interest
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
References
- Kyrkou, C.; Timotheou, S.; Kolios, P.; Theocharides, T.; Panayiotou, C. Drones: Augmenting Our Quality of Life. IEEE Potentials 2019, 38, 30–36. [Google Scholar]
- Wong, C.; Yang, E.; Yan, X.T.; Gu, D. Autonomous robots for harsh environments: A holistic overview of current solutions and ongoing challenges. Syst. Sci. Control Eng. 2018, 6, 213–219. [Google Scholar] [CrossRef]
- Pinto, M.F.; Marcato, A.L.; Melo, A.G.; Honório, L.M.; Urdiales, C. A Framework for Analyzing Fog-Cloud Computing Cooperation Applied to Information Processing of UAVs. Wirel. Commun. Mob. Comput. 2019. [Google Scholar] [CrossRef]
- Karaduman, M.; Çınar, A.; Eren, H. UAV Traffic Patrolling via Road Detection and Tracking in Anonymous Aerial Video Frames. J. Intell. Robot. Syst. 2019, 1–16. [Google Scholar] [CrossRef]
- Wang, Y.C. Mobile Solutions to Air Quality Monitoring. In Mobile Solutions and Their Usefulness in Everyday Life; Springer: Cham, Switzerland, 2019; pp. 225–249. [Google Scholar]
- Luo, C.; Miao, W.; Ullah, H.; McClean, S.; Parr, G.; Min, G. Unmanned Aerial Vehicles for Disaster Management. In Geological Disaster Monitoring Based on Sensor Networks; Springer: Singapore, 2019; pp. 83–107. [Google Scholar]
- Ullah, S.; Kim, K.I.; Kim, K.H.; Imran, M.; Khan, P.; Tovar, E.; Ali, F. UAV-enabled healthcare architecture: Issues and challenges. Future Gener. Comput. Syst. 2019, 97, 425–432. [Google Scholar] [CrossRef]
- Long, D.; Rehm, P.J.; Ferguson, S. Benefits and challenges of using unmanned aerial systems in the monitoring of electrical distribution systems. Electr. J. 2018, 31, 26–32. [Google Scholar] [CrossRef]
- Choset, H. Coverage for robotics—A survey of recent results. Ann. Math. Artif. Intell. 2001, 31, 113–126. [Google Scholar] [CrossRef]
- Dai, R.; Fotedar, S.; Radmanesh, M.; Kumar, M. Quality-aware UAV coverage and path planning in geometrically complex environments. Ad Hoc Netw. 2018, 73, 95–105. [Google Scholar] [CrossRef]
- Yao, P.; Cai, Y.; Zhu, Q. Time-optimal trajectory generation for aerial coverage of urban building. Aerosp. Sci. Technol. 2019, 84, 387–398. [Google Scholar] [CrossRef]
- Kim, D.; Liu, M.; Lee, S.; Kamat, V.R. Remote proximity monitoring between mobile construction resources using camera-mounted UAVs. Autom. Constr. 2019, 99, 168–182. [Google Scholar]
- Oliveira, R.A.; Tommaselli, A.M.; Honkavaara, E. Generating a hyperspectral digital surface model using a hyperspectral 2D frame camera. ISPRS J. Photogramm. Remote Sens. 2019, 147, 345–360. [Google Scholar] [CrossRef]
- Díaz-Delgado, R.; Ónodi, G.; Kröel-Dulay, G.; Kertész, M. Enhancement of Ecological Field Experimental Research by Means of UAV Multispectral Sensing. Drones 2019, 3, 7. [Google Scholar] [CrossRef]
- Lingelbach, F. Path planning using probabilistic cell decomposition. In Proceedings of the 2004 IEEE International Conference on Robotics and Automation, ICRA’04, New Orleans, LA, USA, 26 April–1 May 2004; Volume 1, pp. 467–472. [Google Scholar]
- Acar, E.U.; Choset, H.; Rizzi, A.A.; Atkar, P.N.; Hull, D. Morse decompositions for coverage tasks. Int. J. Robot. Res. 2002, 21, 331–344. [Google Scholar] [CrossRef]
- Wong, S. Qualitative Topological Coverage of Unknown Environments by Mobile Robots. Doctoral Dissertation, The University of Auckland, Auckland, New Zealand, 2006. [Google Scholar]
- Shivashankar, V.; Jain, R.; Kuter, U.; Nau, D.S. Real-Time Planning for Covering an Initially-Unknown Spatial Environment. In Proceedings of the Twenty-Fourth International Florida Artificial Intelligence Research Society Conference, Palm Beach, FL, USA, 18–20 May 2011. [Google Scholar]
- Butler, Z.J.; Rizzi, A.A.; Hollis, R.L. Contact sensor-based coverage of rectilinear environments. In Proceedings of the 1999 IEEE International Symposium on Intelligent Control/Intelligent Systems and Semiotics, Cambridge, MA, USA, 17 September 1999; pp. 266–271. [Google Scholar]
- Xu, L. Graph Planning for Environmental Coverage. Ph.D. Thesis, Robotics Institute, Carnegie Mellon University, Pittsburgh, PA, USA, August 2011. [Google Scholar]
- Li, Y.; Chen, H.; Er, M.J.; Wang, X. Coverage path planning for UAVs based on enhanced exact cellular decomposition method. Mechatronics 2011, 21, 876–885. [Google Scholar] [CrossRef]
- Nasr, S.; Mekki, H.; Bouallegue, K. A multi-scroll chaotic system for a higher coverage path planning of a mobile robot using flatness controller. Chaos Solitons Fractals 2019, 118, 366–375. [Google Scholar] [CrossRef]
- Morgenthal, G.; Hallermann, N.; Kersten, J.; Taraben, J.; Debus, P.; Helmrich, M.; Rodehorst, V. Framework for automated UAS-based structural condition assessment of bridges. Autom. Constr. 2019, 97, 77–95. [Google Scholar] [CrossRef]
- Zhou, K.; Jensen, A.L.; Sørensen, C.G.; Busato, P.; Bothtis, D.D. Agricultural operations planning in fields with multiple obstacle areas. Comput. Electron. Agric. 2014, 109, 12–22. [Google Scholar] [CrossRef]
- Coombes, M.; Fletcher, T.; Chen, W.H.; Liu, C. Optimal polygon decomposition for UAV survey coverage path planning in wind. Sensors 2018, 18, 2132. [Google Scholar] [CrossRef]
- Montanari, A.; Kringberg, F.; Valentini, A.; Mascolo, C.; Prorok, A. Surveying Areas in Developing Regions Through Context Aware Drone Mobility. In Proceedings of the 4th ACM Workshop on Micro Aerial Vehicle Networks, Systems, and Applications, Munich, Germany, 10–15 June 2018; ACM: New York, NY, USA, 2018; pp. 27–32. [Google Scholar]
- Valente, J.; Del Cerro, J.; Barrientos, A.; Sanz, D. Aerial coverage optimization in precision agriculture management: A musical harmony inspired approach. Comput. Electron. Agric. 2013, 99, 153–159. [Google Scholar] [CrossRef]
- Cabreira, T.; Brisolara, L.; Ferreira, P.R. Survey on Coverage Path Planning with Unmanned Aerial Vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Cao, Z.L.; Huang, Y.; Hall, E.L. Region filling operations with random obstacle avoidance for mobile robots. J. Robot. Syst. 1988, 5, 87–102. [Google Scholar] [CrossRef]
- Galceran, E.; Carreras, M. A survey on coverage path planning for robotics. Robot. Auton. Syst. 2013, 61, 1258–1276. [Google Scholar] [CrossRef]
- Lee, T.K.; Baek, S.H.; Choi, Y.H.; Oh, S.Y. Smooth coverage path planning and control of mobile robots based on high-resolution grid map representation. Robot. Auton. Syst. 2011, 59, 801–812. [Google Scholar] [CrossRef]
- Lin, L.; Goodrich, M.A. Hierarchical heuristic search using a Gaussian Mixture Model for UAV coverage planning. IEEE Trans. Cybern. 2014, 44, 2532–2544. [Google Scholar] [CrossRef] [PubMed]
- Choset, H. Coverage of known spaces: The boustrophedon cellular decomposition. Auton. Robots 2000, 9, 247–253. [Google Scholar] [CrossRef]
- Choset, H.M.; Hutchinson, S.; Lynch, K.M.; Kantor, G.; Burgard, W.; Kavraki, L.E.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementation; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Milnor, J.W.; Spivak, M.; Wells, R.; Wells, R. Morse Theory; Princeton University Press: Princeton, NJ, USA, 1963. [Google Scholar]
- Nam, L.H.; Huang, L.; Li, X.J.; Xu, J.F. An approach for coverage path planning for UAVs. In Proceedings of the 2016 IEEE 14th International Workshop on Advanced Motion Control (AMC), Auckland, New Zealand, 22–24 April 2016; pp. 411–416. [Google Scholar]
- Bochkarev, S.; Smith, S.L. On minimizing turns in robot coverage path planning. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 August 2016; pp. 1237–1242. [Google Scholar]
- Andersen, H.L. Path Planning for Search and Rescue Mission Using Multicopters. Master’s Thesis, Institutt for Teknisk Kybernetikk, Trondheim, Norway, 2014. [Google Scholar]
- Jiao, Y.S.; Wang, X.M.; Chen, H.; Li, Y. Research on the coverage path planning of uavs for polygon areas. In Proceedings of the 2010 5th IEEE Conference on Industrial Electronics and Applications (ICIEA), Taichung, Taiwan, 15–17 June 2010; pp. 1467–1472. [Google Scholar]
- Levcopoulos, C.; Krznaric, D. Quasi-Greedy Triangulations Approximating the Minimum Weight Triangulation. In Proceedings of the Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, Atlanta, GA, USA, 28–30 January 1996; pp. 392–401. [Google Scholar]
- Xu, A.; Viriyasuthee, C.; Rekleitis, I. Optimal complete terrain coverage using an unmanned aerial vehicle. In Proceedings of the 2011 IEEE International Conference On Robotics and automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 2513–2519. [Google Scholar]
- Öst, G. Search Path Generation With UAV Applications Using Approximate Convex Decomposition. Master Thesis, Linkoping University, Linkoping, Sweden, 2012. [Google Scholar]
- Sadat, S.A.; Wawerla, J.; Vaughan, R.T. Recursive non-uniform coverage of unknown terrains for uavs. In Proceedings of the 2014 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2014), Chicago, IL, USA, 14–18 September 2014; pp. 1742–1747. [Google Scholar]
- Sadat, S.A.; Wawerla, J.; Vaughan, R. Fractal trajectories for online non-uniform aerial coverage. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 2971–2976. [Google Scholar]
- Barrientos, A.; Colorado, J.; Cerro, J.D.; Martinez, A.; Rossi, C.; Sanz, D.; Valente, J. Aerial remote sensing in agriculture: A practical approach to area coverage and path planning for fleets of mini aerial robots. J. Field Robot. 2011, 28, 667–689. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Dorigo, M.; Maniezzo, V.; Colorni, A. Ant system: Optimization by a colony of cooperating agents. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 1996, 26, 29–41. [Google Scholar] [CrossRef]
- Larranaga, P.; Kuijpers, C.M.H.; Murga, R.H.; Inza, I.; Dizdarevic, S. Genetic algorithms for the travelling salesman problem: A review of representations and operators. Artif. Intell. Rev. 1999, 13, 129–170. [Google Scholar] [CrossRef]
- Zelinsky, A.; Jarvis, R.A.; Byrne, J.C.; Yuta, S. Planning paths of complete coverage of an unstructured environment by a mobile robot. In Proceedings of the International Conference on Advanced Robotics, Tsukuba, Japan, 8–9 November 1993; Volume 13, pp. 533–538. [Google Scholar]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Nash, A.; Daniel, K.; Koenig, S.; Felner, A. Theta*: Any-Angle Path Planning on Grids. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 22–26 July 2007; pp. 1177–1183. [Google Scholar]
- Fu, Y.; Ding, M.; Zhou, C.; Hu, H. Route planning for unmanned aerial vehicle (UAV) on the sea using hybrid differential evolution and quantum-behaved particle swarm optimization. IEEE Trans. Syst. Man Cybern. Syst. 2013, 43, 1451–1465. [Google Scholar] [CrossRef]
- Xu, A.; Viriyasuthee, C.; Rekleitis, I. Efficient complete coverage of a known arbitrary environment with applications to aerial operations. Auton. Robots 2014, 36, 365–381. [Google Scholar] [CrossRef]
- Torres, M.; Pelta, D.A.; Verdegay, J.L.; Torres, J.C. Coverage path planning with unmanned aerial vehicles for 3D terrain reconstruction. Expert Syst. Appl. 2016, 55, 441–451. [Google Scholar] [CrossRef]
- Majeed, A.; Lee, S. A Fast Global Flight Path Planning Algorithm Based on Space Circumscription and Sparse Visibility Graph for Unmanned Aerial Vehicle. Electronics 2018, 7, 375. [Google Scholar] [CrossRef]

| Area of Intrest Size | BCDH-CPP Algorithm | CA-CPP Algorithm | Proposed-CPP Algorithm | |||||
|---|---|---|---|---|---|---|---|---|
| Avg. Time (s) | Avg. Length (m) | Avg. Time (s) | Avg. Length (m) | Avg. Time (s) | Avg. Length (m) | |||
| 500 × 600 × 300 | 13.53 | 8910.34 | 17.94 | 7901.12 | 10.54 | 8201.56 | ||
| 1000 × 1200 × 300 | 18.40 | 35,997.11 | 22.89 | 34,807.45 | 15.64 | 35,417.67 | ||
| 12,000 × 1400 × 300 | 23.19 | 55,920.19 | 28.81 | 55,429.12 | 18.29 | 53,120.09 | ||
| 1500 × 1500 × 400 | 27.13 | 72,995.22 | 33.09 | 72,810.21 | 24.54 | 71,030.42 | ||
| 2000 × 2000 × 400 | 31.21 | 124,991.10 | 39.19 | 123,951.10 | 26.75 | 122,367.15 | ||
| Algorithms | Evaluation Criteria | Maps Id | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| CA-CPP | Avg. path overlapping (m) | 129.59 | 289.37 | 990.45 | 1258.98 | 2039.51 |
| BCDH-CPP | Avg. path overlapping (m) | 209.21 | 330.89 | 1023.07 | 1455.45 | 2237.98 |
| Proposed | Avg. path overlapping (m) | 171.09 | 301.12 | 810.95 | 1125.12 | 1927.45 |
| Algorithms | Evaluation Criteria | Shape of the Area of Interest | ||||
|---|---|---|---|---|---|---|
| Square | Rectangle | Polygon (Convex) | Polygon (Non-Convex) | Irregular | ||
| CA-CPP | Avg. computing time (s) Avg. path length (m) Avg. path overlapping (m) | 31.59 70,810.21 1153.40 | 15.84 8193.11 169.19 | 24.98 51,900.12 671.65 | 36.51 55,723.41 755.35 | 23.88 48,611.16 976.51 |
| BCDH-CPP | Avg. computing time (s) Avg. path length (m) Avg. path overlapping (m) | 25.13 70,998.52 1365.23 | 11.85 8710.24 189.31 | 19.08 52,100.32 698.12 | 27.91 55,925.41 795.35 | 18.53 48,914.09 1001.31 |
| Proposed | Avg. computing time (s) Avg. path length (m) Avg. path overlapping (m) | 19.55 68,730.42 1025.12 | 8.17 8001.96 161.99 | 14.78 50,300.32 621.34 | 18.91 54,605.21 705.15 | 13.43 47,410.89 954.21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majeed, A.; Lee, S. A New Coverage Flight Path Planning Algorithm Based on Footprint Sweep Fitting for Unmanned Aerial Vehicle Navigation in Urban Environments. Appl. Sci. 2019, 9, 1470. https://doi.org/10.3390/app9071470
Majeed A, Lee S. A New Coverage Flight Path Planning Algorithm Based on Footprint Sweep Fitting for Unmanned Aerial Vehicle Navigation in Urban Environments. Applied Sciences. 2019; 9(7):1470. https://doi.org/10.3390/app9071470
Chicago/Turabian StyleMajeed, Abdul, and Sungchang Lee. 2019. "A New Coverage Flight Path Planning Algorithm Based on Footprint Sweep Fitting for Unmanned Aerial Vehicle Navigation in Urban Environments" Applied Sciences 9, no. 7: 1470. https://doi.org/10.3390/app9071470
APA StyleMajeed, A., & Lee, S. (2019). A New Coverage Flight Path Planning Algorithm Based on Footprint Sweep Fitting for Unmanned Aerial Vehicle Navigation in Urban Environments. Applied Sciences, 9(7), 1470. https://doi.org/10.3390/app9071470






