Flocking of Multi-Agent System with Nonlinear Dynamics via Distributed Event-Triggered Control
Abstract
:1. Introduction
2. Preliminaries and Problems Formulation
2.1. Notation
2.2. Preliminaries
- (i)
- The eigenvalues of L satisfy , if is connected, one has
- (ii)
- L is a positive semi-definite matrix that satisfies the following sum-of-squares (SOS) property:
2.3. System Model
2.4. Problem Statement
3. Flocking via Distributed ETC
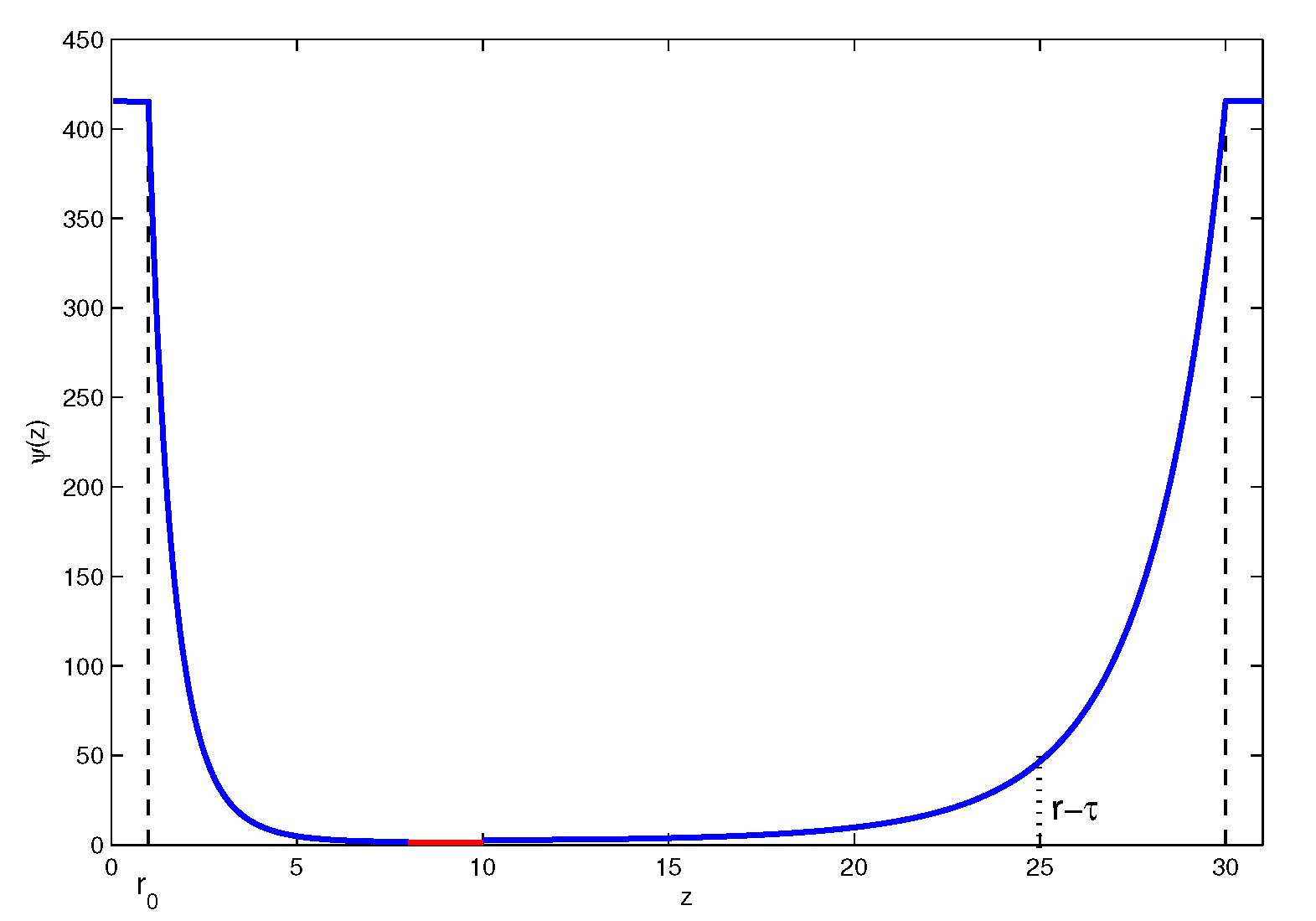
3.1. Design of Action Function
3.2. Controller Design and Stability Analysis
- (i)
- is connected and no collisions occur for ;
- (ii)
- Flocking motion is achieved asymptotically.
- (i)
- is connected and no collisions occur for ;
- (ii)
- Flocking motion is achieved asymptotically.
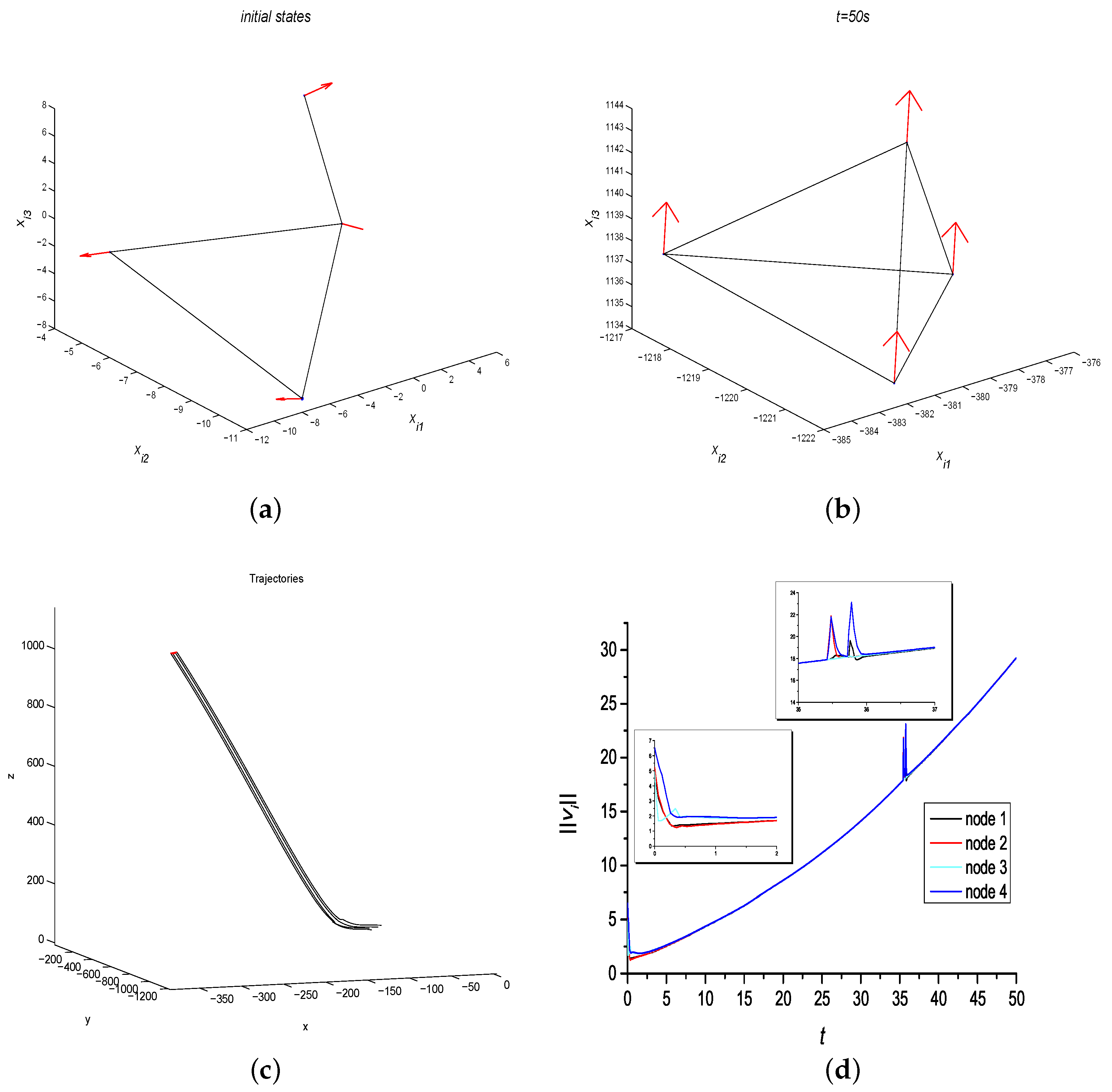
4. Simulations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Åström, K.J.; Bernhardsson, B. Comparison of periodic and event based sampling for first-order stochastic systems. IFAC Proc. Vol. 1999, 32, 5006–5011. [Google Scholar] [CrossRef]
- Miskowicz, M. Send-On-Delta Concept: An Event-Based Data Reporting Strategy. Sensors 2006, 6, 49–63. [Google Scholar] [CrossRef]
- Losada, M.G. Contributions to Networked and Event-Triggered of Linear Systems; Springer: Berlin, Germany, 2016. [Google Scholar]
- Miskowicz, M. Event-Based Control and Signal Processing; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Mazo, M.; Tabuada, P. Decentralized event-triggered control over wireless sensor/actuator networks. IEEE Trans. Autom. Control 2011, 56, 2456–2461. [Google Scholar] [CrossRef]
- Santos, C.; Martínez-Rey, M.; Espinosa, F.; Gardel, A.; Santiso, E. Event-based sensing and control for remote robot guidance: An experimental case. Sensors 2017, 17, 2034. [Google Scholar] [CrossRef] [PubMed]
- Acho, L.; Buenestado, P. A robust asynchronous sampled-data control design for nonlinear systems with actuator failures. Appl. Sci. 2017, 7, 875. [Google Scholar] [CrossRef]
- Barrios-Avilés, J.; Rosado-Muñoz, A.; Medus, L.; Bataller-Mompeán, M.; Guerrero-Martínez, J. Less Data Same Information for Event-Based Sensors: A Bioinspired Filtering and Data Reduction Algorithm. Sensors 2018, 18, 4122. [Google Scholar] [CrossRef] [PubMed]
- Thakur, S.; Abdul, S.; Chiu, H.Y.; Roy, R.B.; Huang, P.-Y.; Malwade, S.; Nursetyo, A.A.; Li, Y.-C. Artificial-intelligence-based prediction of clinical events among hemodialysis patients using non-contact sensor data. Sensors 2018, 18, 2833. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Lu, Q.; Yin, K.; Zhang, B. Signal Source Localization of Multiple Robots Using an Event-Triggered Communication Scheme. Appl. Sci. 2018, 8, 977. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, Q.; Hu, Y. Event-Based Communication and Finite-Time Consensus Control of Mobile Sensor Networks for Environmental Monitoring. Sensors 2018, 88, 2547. [Google Scholar] [CrossRef] [PubMed]
- Socas, R.; Dormido, R.; Dormido, S. New control paradigms for resources saving: An approach for mobile robots navigation. Sensors 2018, 18, 281. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Torres, R.; Torres-Huitzil, C.; Galeana-Zapién, H. A Cognitive-Inspired Event-Based Control for Power-Aware Human Mobility Analysis in IoT Devices. Sensors 2019, 19, 832. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.R.; Wang, Z.D.; Shen, B.; Wei, G.L. Event-triggered consensus control for discrete-time stochastic multi-agent systems: The input-to-state stability in probability. Automatica 2015, 62, 284–291. [Google Scholar] [CrossRef]
- Wang, Z.D.; Ding, D.R.; Dong, H.L.; Shu, H.S. H∞ consensus control for multi-agent systems with missing measurements: The finite-horizon case. Syst. Control Lett. 2013, 62, 827–836. [Google Scholar] [CrossRef]
- Dimarogonas, D.V.; Frazzoli, E.; Johansson, K.H. Distributed event-triggered control for multi-agent systems. IEEE Trans. Autom. Control 2012, 57, 1291–1297. [Google Scholar] [CrossRef]
- Wang, X.F.; Lemmon, M. On event design in event-triggered feedback systems. Automatica 2011, 47, 2319–2322. [Google Scholar] [CrossRef]
- Fan, Y.; Feng, G.; Wang, Y.; Song, C. Distributed event-triggered control of multi-agent systems with combinational measurements. Automatica 2013, 49, 671–675. [Google Scholar] [CrossRef]
- Seyboth, G.S.; Dimarogonas, D.V.; Johansson, K.H. Event-based broadcasting for multi-agent average consensus. Automatica 2013, 49, 245–252. [Google Scholar] [CrossRef]
- Garcia, E.; Cao, Y.; Giua, A.; Casbeer, D. Decentralized event-triggered consensus with general linear dynamics. Automatica 2014, 50, 2633–2640. [Google Scholar] [CrossRef]
- Yang, D.; Ren, W.; Liu, X.; Chen, W. Decentralized event-triggered consensus for linear multi-agent systems under general directed graphs. Automatica 2016, 69, 242–249. [Google Scholar] [CrossRef]
- Chen, Z.; Li, D.; Huang, Y.; Tang, C. Event-triggered communication for time synchronization in WSNs. Neurocomputing 2016, 177, 416–426. [Google Scholar] [CrossRef]
- Zhou, F.; Huang, Z.; Yang, Y.; Wang, J.; Li, L.; Peng, J. Decentralized event-triggered cooperative control for multi-agent systems with uncertain dynamics using local estimators. Neurocomputing 2017, 237, 388–396. [Google Scholar] [CrossRef]
- Reynolds, C.W. Flocks, herds, and schools: A distributed behavioral model. ACM SIGGRAPH Comput. Graph. 1987, 21, 25–34. [Google Scholar] [CrossRef]
- Saber, R.O.; Murray, R.M. Flocking for multi-agent dynamic systems: Algorithms and theory. IEEE Trans. Autom. Control 2006, 51, 401–419. [Google Scholar] [CrossRef]
- Su, H.S.; Zhang, N.; Chen, M.Z.Q.; Wang, H.; Wang, X.F. Adaptive flocking with a virtual leader of multiple agents governed by locally Lipschitz nonlinearity. Nonlinear Anal. Real World Appl. 2013, 14, 798–806. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Su, H.; Chen, G.; Yu, W. A Connectivity-preserving flocking algorithm for multi-agent dynamical systems with bounded potential function. IET Control Theory Appl. 2011, 6, 813–821. [Google Scholar] [CrossRef]
- Yu, W.W.; Chen, G.R.; Cao, M. Distributed leader-follower flocking control for multi-agent dynamical systems with time-varying velocities. Syst. Cont. Lett. 2010, 59, 543–552. [Google Scholar] [CrossRef]
- Mecholsky, N.A.; Edward, O.; Antonsen, T.M. Obstacle and predator avoidance in a model for flocking. Physcia D Nonlinear Phenom. 2010, 239, 988–996. [Google Scholar] [CrossRef]
- Hwang, C.; Talipov, E.; Cha, H. Distributed geographic service discovery for mobile sensor networks. Comput. Net. 2011, 55, 1069–1082. [Google Scholar] [CrossRef]
- Crowther, B. Flocking of autonomous unmanned air vehicles. Aero-Naut. J. 2003, 107, 99–109. [Google Scholar]
- Yu, P.; Ding, L.; Liu, Z.W.; Guan, Z.H.; Hu, M.X. Flocking with a virtual leader based on distributed event-triggered hybrid control. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26–28 July 2013; pp. 6947–6952. [Google Scholar]
- Yu, P.; Ding, L.; Liu, Z.W.; Guan, Z.H. Leader-follower flocking based on distributed event-triggered hybrid control. Int. J. Robust Nonlinear Control 2016, 26, 143–153. [Google Scholar] [CrossRef]
- Fang, C.; Zhang, Y.; Huang, S. Distributed event-triggered flocking control of nonlinear multi-agent systems. In Proceedings of the 2017 Chinese Automation Congress (CAC), Jinan, China, 20–22 October 2017; pp. 2965–2970. [Google Scholar]
- Sun, F.; Wang, R.; Zhu, W.; Li, Y. Flocking in nonlinear multi-agent systems with time-varying delay via event-triggered control. Appl. Math. Comput. 2019, 350, 66–77. [Google Scholar] [CrossRef]
- Merris, R. Laplacian matrices of graph: A survey. Linear Algebr. Appl. 1994, 197, 143–176. [Google Scholar] [CrossRef]
- Ji, M.; Egerstedt, M. Distributed coordination control of multiagent systems while preserving connectedness. IEEE Trans. Robot. 2007, 23, 693–703. [Google Scholar] [CrossRef]
- Balch, T.; Arkin, R.C. Behavior-based formation control for multirobot teams. IEEE Trans. Robot. Autom. 1998, 14, 926–939. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Y.; Kong, Z.; Ding, L. Flocking of Multi-Agent System with Nonlinear Dynamics via Distributed Event-Triggered Control. Appl. Sci. 2019, 9, 1336. https://doi.org/10.3390/app9071336
Shen Y, Kong Z, Ding L. Flocking of Multi-Agent System with Nonlinear Dynamics via Distributed Event-Triggered Control. Applied Sciences. 2019; 9(7):1336. https://doi.org/10.3390/app9071336
Chicago/Turabian StyleShen, Yanhua, Zhengmin Kong, and Li Ding. 2019. "Flocking of Multi-Agent System with Nonlinear Dynamics via Distributed Event-Triggered Control" Applied Sciences 9, no. 7: 1336. https://doi.org/10.3390/app9071336
APA StyleShen, Y., Kong, Z., & Ding, L. (2019). Flocking of Multi-Agent System with Nonlinear Dynamics via Distributed Event-Triggered Control. Applied Sciences, 9(7), 1336. https://doi.org/10.3390/app9071336






