Dynamic Parameter Identification of a Long-Span Arch Bridge Based on GNSS-RTK Combined with CEEMDAN-WP Analysis
Abstract
1. Introduction
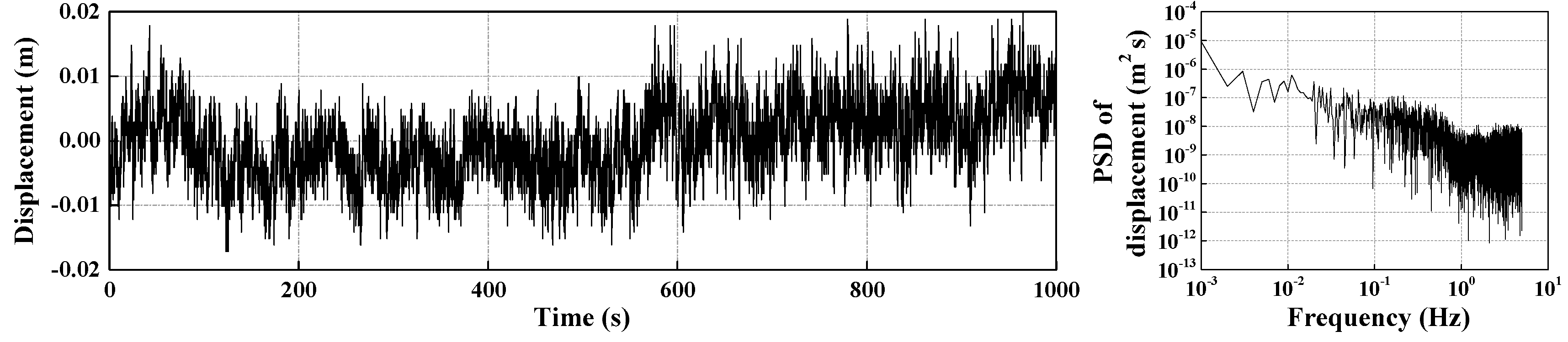
2. Stability Test of GNSS-RTK Receivers
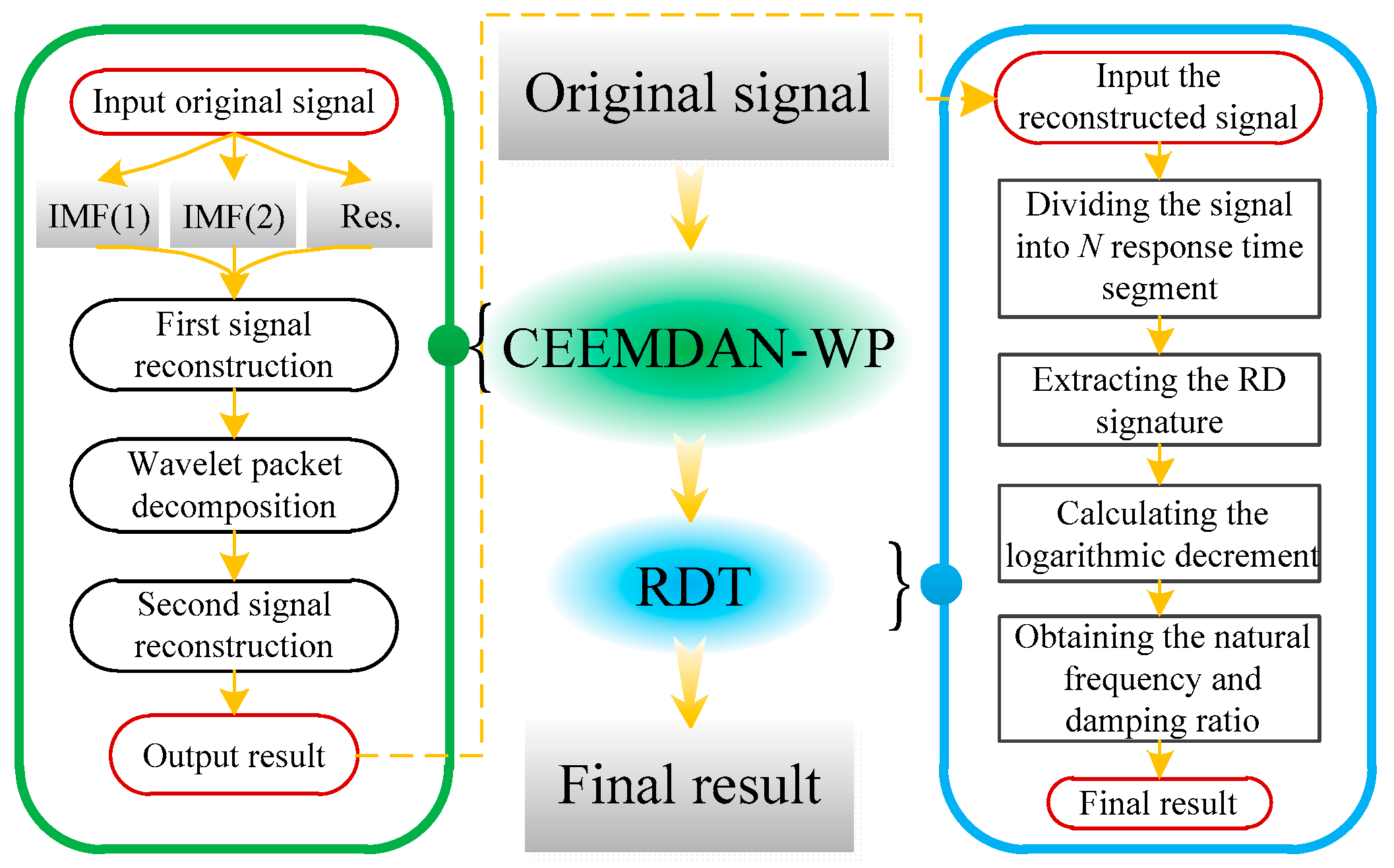
3. The Principle of CEEMDAN-WP and RDT
3.1. EEMD, CEEMD, and CEEMDAN Algorithms
- Add Gauss white noise into the original signal and thus produce a new signal .
- Using the EMD algorithm, is decomposed into a number of IMF components and a residual component .
- By repeating the above two steps, the IMFs are obtained, where is the iteration number and is the mode.
- Compute the average of the IMF components to eliminate the effects of additional white noise.
- Add positive and negative white noise into the original signal , and generate two new signals .
- Repeat the above step, and decompose the new signals using EMD.
- Derive two sets of IMF components for the new signals.
- Calculate decomposition results by averaging multiple components.
- Define as the operator which produces the -th IMF which has been decomposed based on the EMD algorithm. The first mode is derived by EMD from the signal .where is the amplitude of the added white noise and is the white noise with unit variance.
- Calculate the first residual signal.
- Decompose the signal to derive the first mode, after which the second mode is defined.
- For , calculate the -th residual signal.
- For , decompose the signal to derive the first mode, after which the -th mode is defined.
- Turn to step 4 for the next .
3.2. WP Method
3.3. The CEEMDAN-WP Model
- CEEMDAN is employed for decomposition to obtain a series of IMFs.
- Because of the existence of background noise, some IMF components are noise dominated. Reconstruct signals after removing the components which are noise dominated.
- A three-level WP is used to decompose the signal obtained in Step 2.
- Determine the classic wavelet basis.
- Select proper thresholds and quantify the decomposed coefficients.
- Reconstruct the signal and export.
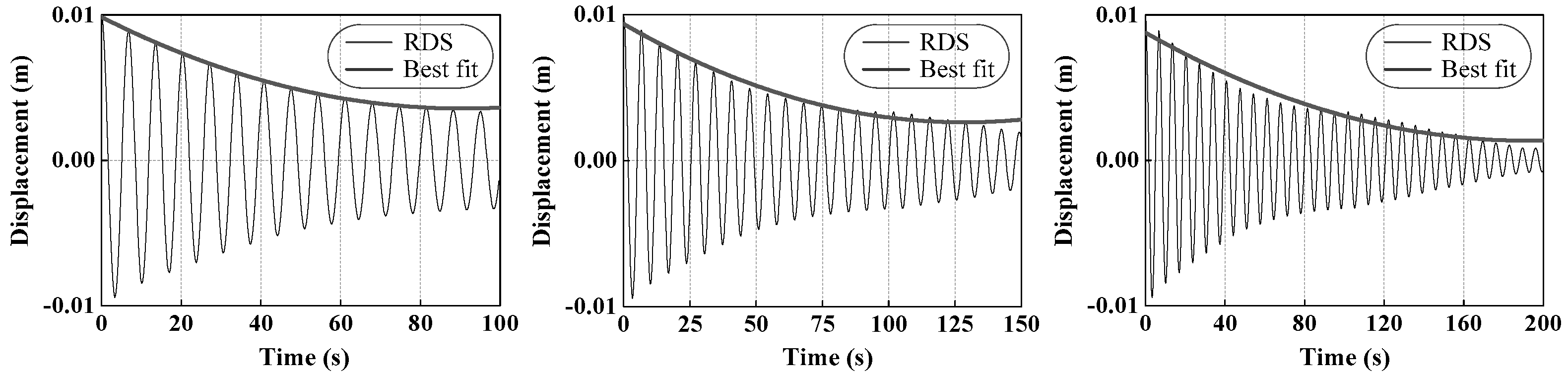
3.4. The RDT Method
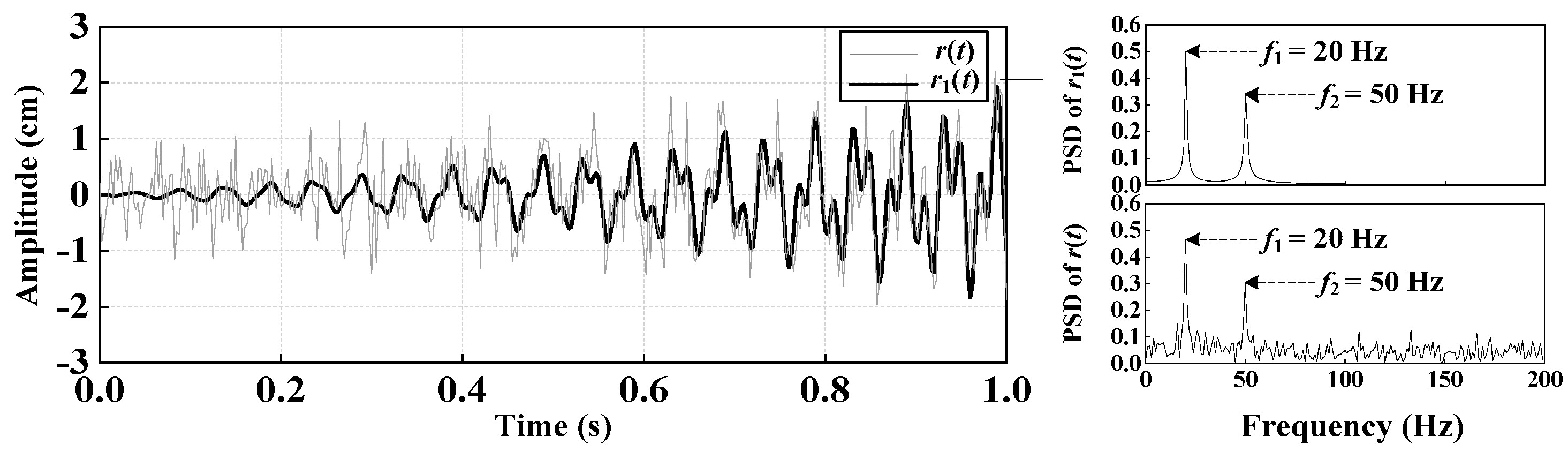
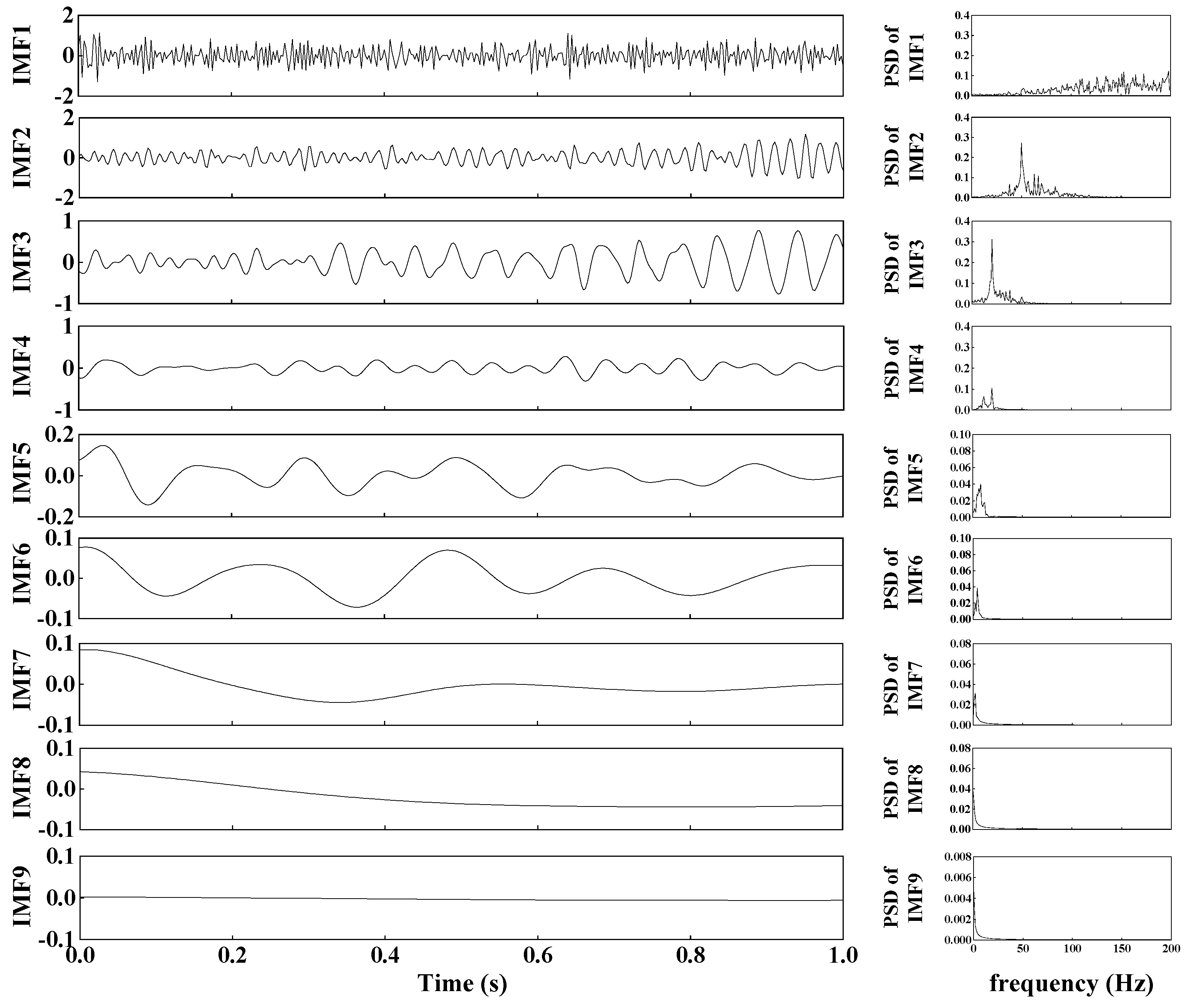
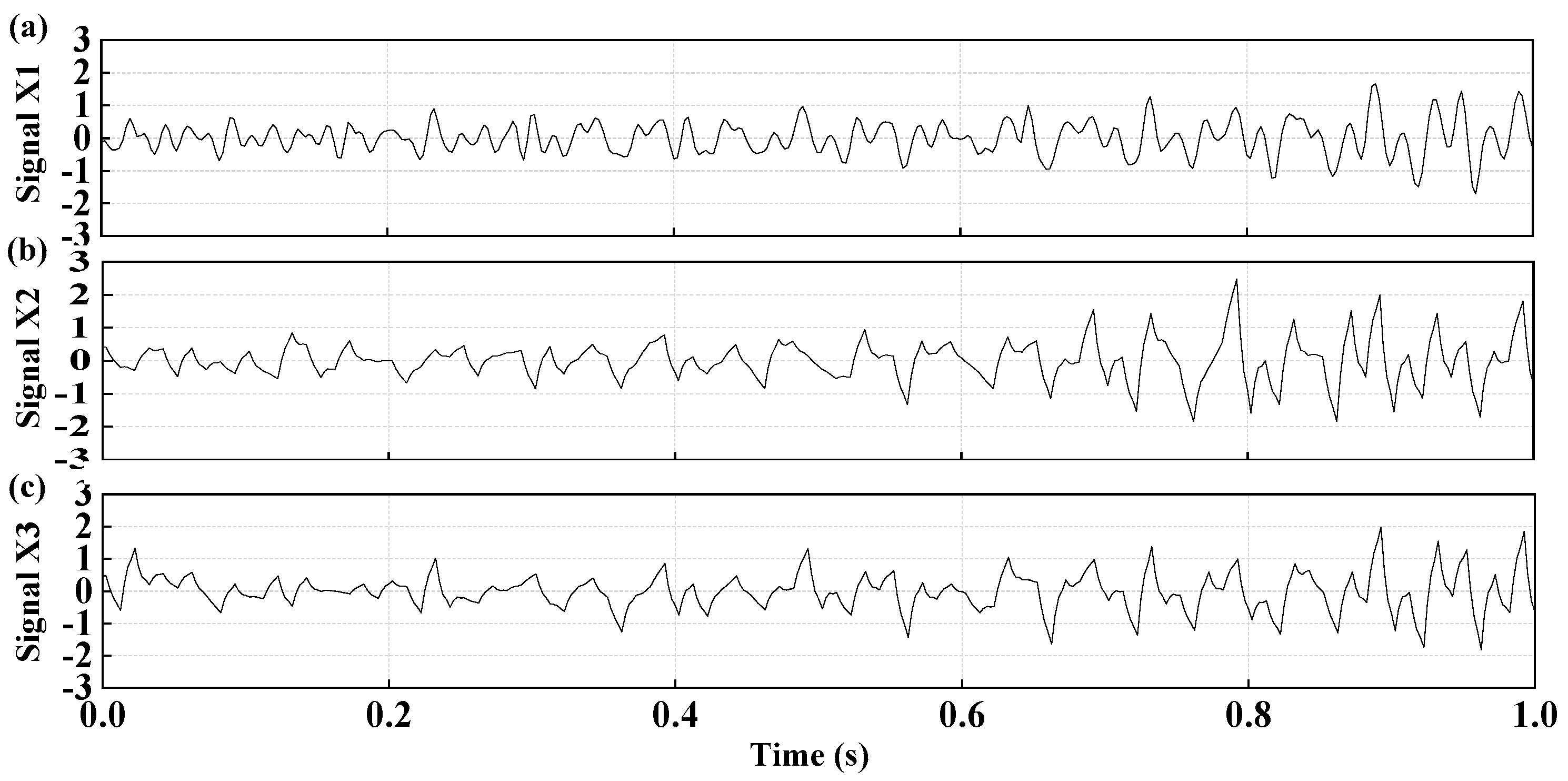
4. Performance Evaluation of the CEEMDAN-WP
5. Structural Dynamic Deformation Monitoring of Rainbow Bridge
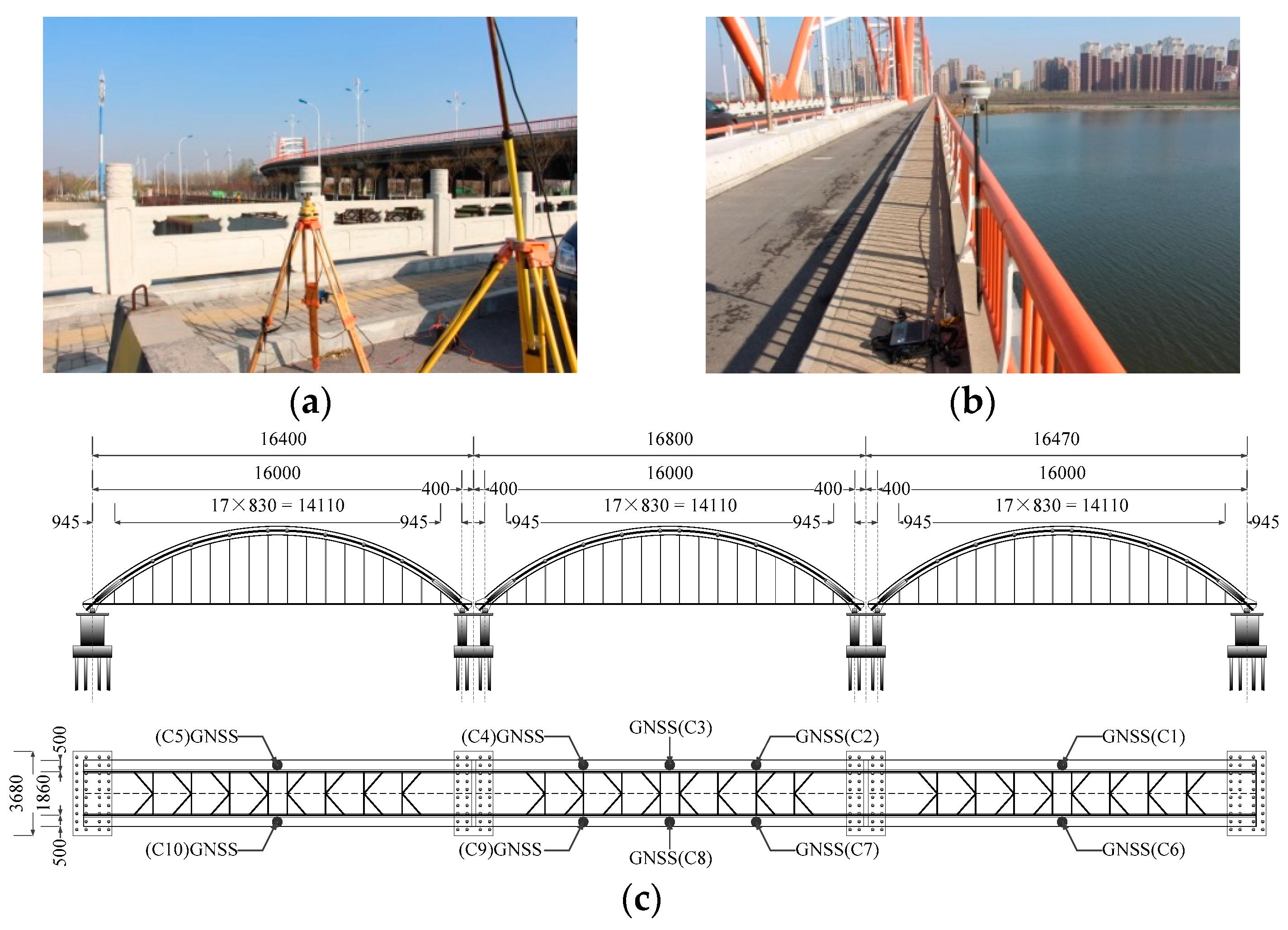
5.1. Bridge Description and Test Plan
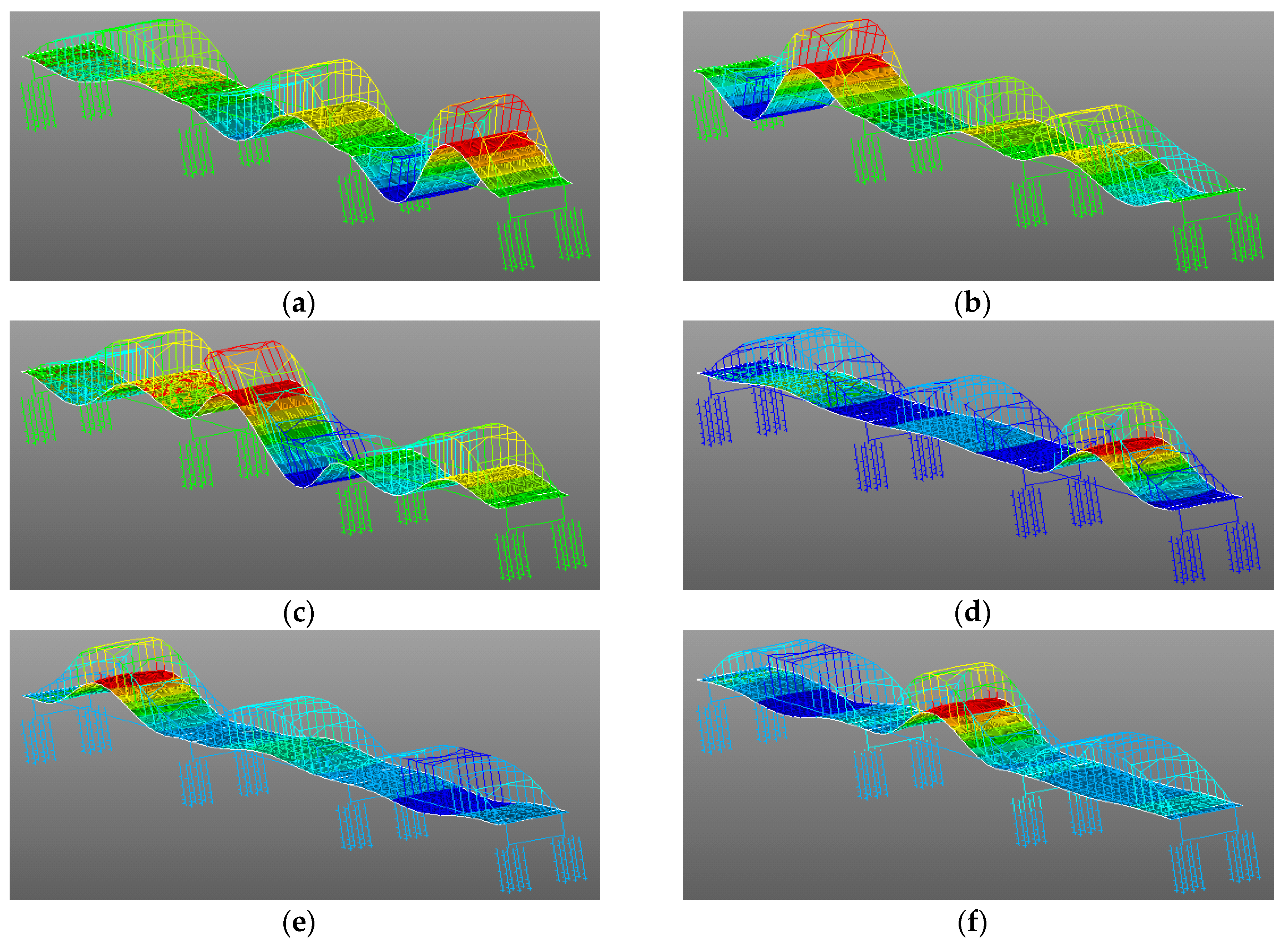
5.2. FEM of the Bridge
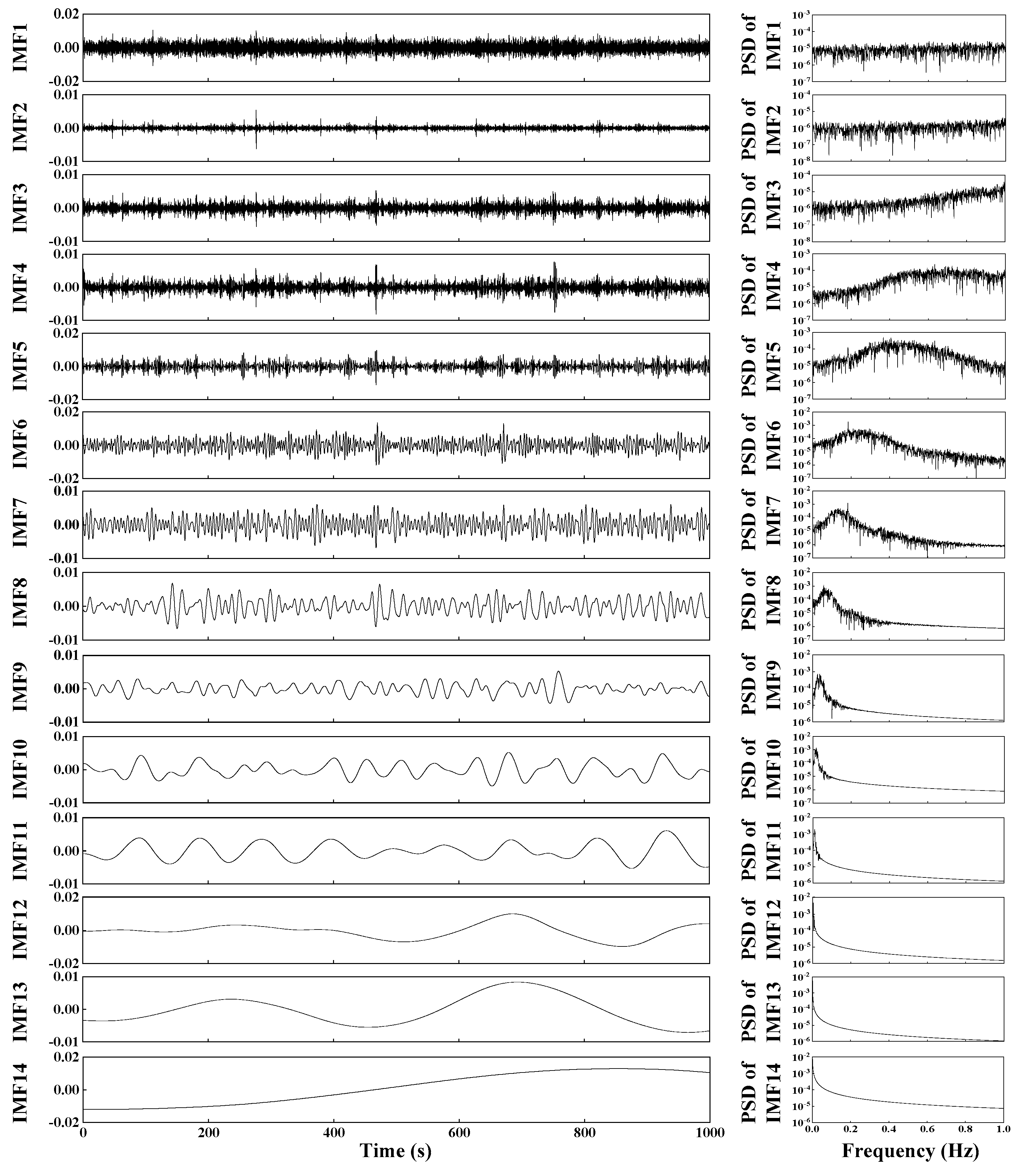
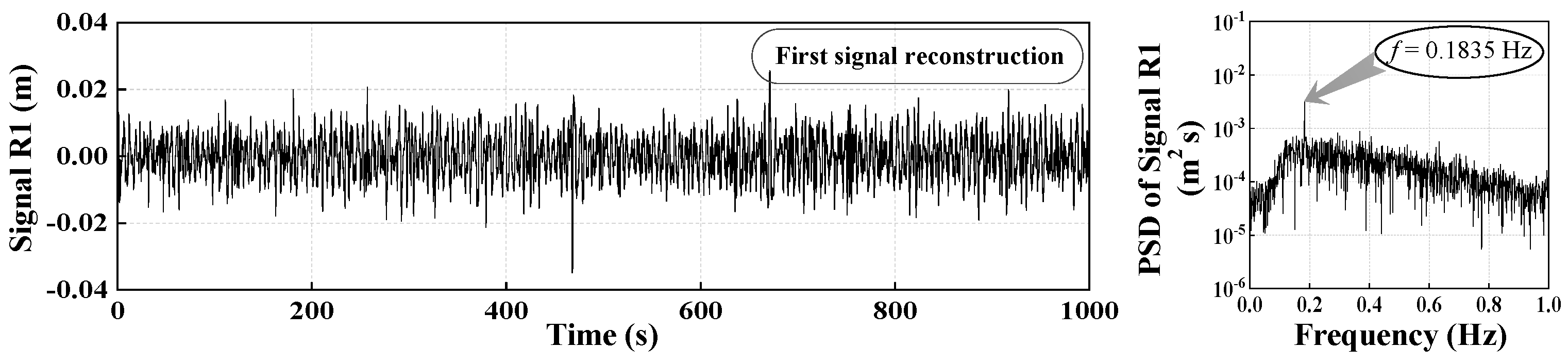
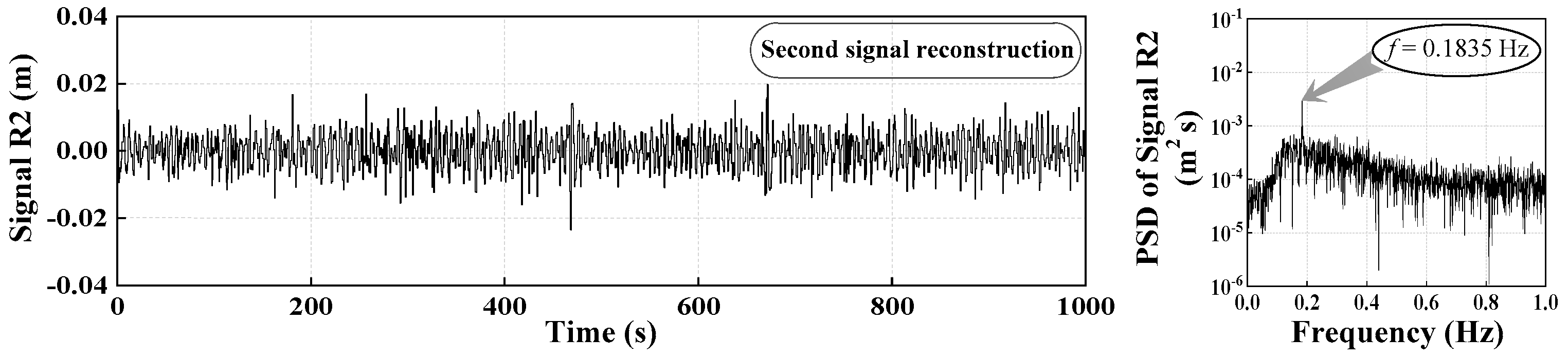
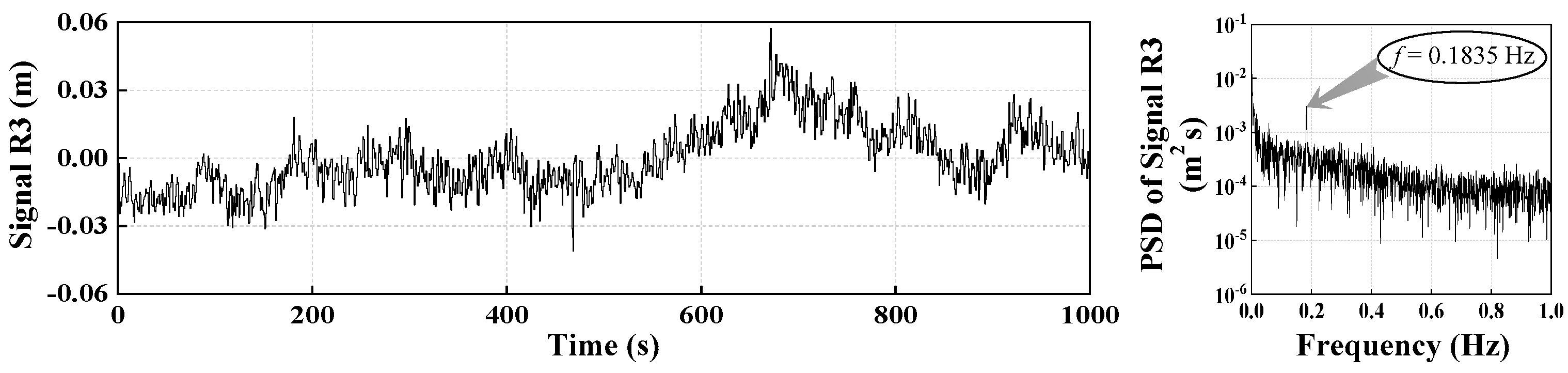
5.3. Vibration Signal Analysis
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Piombo, B.A.D.; Fasana, A.; Marchesiello, S.; Ruzzene, M. Modelling and identification of the dynamic response of a supported bridge. Mech. Syst. Signal Process. 2000, 14, 75–89. [Google Scholar] [CrossRef]
- Fenerci, A.; Øiseth, O.; Rønnquist, A. Long-term monitoring of wind field characteristics and dynamic response of a long-span suspension bridge in complex terrain. Eng. Struct. 2017, 147, 269–284. [Google Scholar] [CrossRef]
- Masri, S.F.; Sheng, L.H.; Caffrey, J.P.; Nigbor, R.L.; Wahbeh, M.; Abdel-Ghaffar, A.M. Application of a web-enabled real-time structural health monitoring system for civil infrastructure systems. Smart Mater. Struct. 2004, 13, 1269–1283. [Google Scholar] [CrossRef]
- Lee, J.J.; Shinozuka, M. A vision-based system for remote sensing of bridge displacement. NDT E Int. 2006, 39, 425–431. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Song, G.B.; Guo, Q. Detection of Shifts in GPS Measurements for a Long-Span Bridge Using CUSUM Chart. Int. J. Struct. Stab. Dyn. 2016, 16, 1640024. [Google Scholar] [CrossRef]
- Górski, P. Investigation of dynamic characteristics of tall industrial chimney based on GPS measurements using Random Decrement Method. Eng. Struct. 2015, 83, 30–49. [Google Scholar] [CrossRef]
- Kalkan, Y.; Potts, L.V.; Bilgi, S. Assessment of vertical deformation of the atatürk dam using geodetic observations. J. Surv. Eng. 2016, 142, 04015011. [Google Scholar] [CrossRef]
- Xiong, C.B.; Niu, Y.B.; Li, Z. An investigation of the dynamic characteristics of super high-rise buildings using real-time kinematic–global navigation satellite system technology. Adv. Struct. Eng. 2018, 21, 783–792. [Google Scholar] [CrossRef]
- Niu, Y.B.; Xiong, C.B. Analysis of the dynamic characteristics of a suspension bridge based on RTK-GNSS measurement combining EEMD and a wavelet packet technique. Meas. Sci. Technol. 2018, 29, 085103. [Google Scholar] [CrossRef]
- Xiong, C.B.; Niu, Y.B. Investigation of the dynamic behavior of a super high-rise structure using RTK-GNSS technique. KSCE J. Civ. Eng. 2019, 23, 654–665. [Google Scholar] [CrossRef]
- Ince, C.D.; Sahin, M. Real-time deformation monitoring with GPS and Kalman Filter. J. Earth Planets Space 2000, 52, 837–840. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5, 8328–8341. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Kurt, M.; Eriten, M.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Strongly nonlinear beats in the dynamics of an elastic system with a strong local stiffness nonlinearity: Analysis and identification. J. Sound Vib. 2014, 333, 2054–2072. [Google Scholar] [CrossRef]
- Kurt, M.; Chen, H.; Lee, Y.S.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Nonlinear system identification of the dynamics of a vibro-impact beam: Numerical results. Arch. Appl. Mech. 2012, 82, 1461–1479. [Google Scholar] [CrossRef]
- Moore, K.J.; Kurt, M.; Eriten, M.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Wavelet-bounded empirical mode decomposition for vibro-impact analysis. Nonlinear Dyn. 2018, 93, 1559–1577. [Google Scholar] [CrossRef]
- Moore, K.J.; Kurt, M.; Eriten, M.; McFarland, D.M.; Bergman, L.A.; Vakakis, A.F. Wavelet-bounded empirical mode decomposition for measured time series analysis. Mech. Syst. Signal Process. 2018, 99, 14–29. [Google Scholar] [CrossRef]
- Kijecwski, T.; Kareem, A. Wavelet transforms for systems identification in civil engineering. Comput.-Aided Civ. Inf. 2003, 18, 339–355. [Google Scholar] [CrossRef]
- Giaouris, D.; Fincth, J.W. De-noising using wavelets on electric drive applications. Electr. Power Syst. Res. 2008, 78, 559–565. [Google Scholar] [CrossRef]
- Liu, F.; Ruan, X.E. Wavelet-based diffusion approaches for signal de-noising. Signal Process 2007, 87, 1138–1146. [Google Scholar] [CrossRef]
- Perez-Ramirez, C.A.; Jaen-Cuellar, A.Y.; Valtierra-Rodriguez, M.; Dominguez-Gonzalez, A.; Osornio-Rios, R.A.; Romero-Troncoso, R.J.; Amezquita-Sanchez, J.P. A two-step strategy for system identification of civil structures for structural health monitoring using wavelet transform and genetic algorithms. Appl. Sci. 2017, 7, 111. [Google Scholar] [CrossRef]
- Zhang, X.; Song, K.; Li, C.G.; Yang, L.X. A novel approach for the estimation of doubly spread acoustic channels based on wavelet transform. Appl. Sci. 2018, 8, 38. [Google Scholar] [CrossRef]
- Farzad, H.; Wasim, O.; Mohamed, G. Roller bearing acoustic signature extraction by wavelet packet transform, applications in fault detection and size estimation. Appl. Acoust. 2016, 104, 101–118. [Google Scholar]
- Lau, L. Wavelet packets based denoising method for measurement domain repeat-time multipath filtering in GPS static high-precision positioning. GPS Solut. 2017, 21, 461–474. [Google Scholar] [CrossRef]
- Ding, Y.L.; Li, A.Q.; Deng, Y. Structural Damage Warning of a Long-Span Cable-Stayed Bridge Using Novelty Detection Technique Based on Wavelet Packet Analysis. Adv. Struct. Eng. 2010, 13, 291–298. [Google Scholar] [CrossRef]
- García-Plaza, E.; Núñez, P.J. Application of the wavelet packet transform to vibration signals for surface roughness monitoring in CNC turning operations. Mech. Syst. Signal Process. 2018, 98, 902–919. [Google Scholar] [CrossRef]
- Ding, Y.L.; Li, A.Q. Structural health monitoring of long-span suspension bridges using wavelet packet analysis. Earthq. Eng. Eng. Vib. 2007, 6, 289–294. [Google Scholar] [CrossRef]
- Sirca, G.F.; Adeli, H. System identification in structural engineering. Sci. Iran. 2012, 19, 1355–1364. [Google Scholar] [CrossRef]
- Wang, X.; Wu, Z.S. Modal damping evaluation of hybrid FRP cable with smart dampers for long-span cable-stayed bridges. Compos. Struct. 2011, 93, 1231–1238. [Google Scholar] [CrossRef]
- Tamura, Y.; Yoshida, A.; Zhang, L. Damping in buildings and estimation techniques. In Proceedings of the 6th Asia-Pacific Conference on Wind Engineering, Seoul, Korea, 12–14 September 2005; pp. 193–214. [Google Scholar]
- Asmussen, J.C.; Ibrahim, R.; Brincker, R. Random decrement: Identification of structures subjected to ambient excitation. In Proceedings of the 16th International Modal Analysis Conference, Santa Barbara, CA, USA, 2–5 February 1998; pp. 914–921. [Google Scholar]
- Lin, C.S.; Chiang, D.Y. Modal identification from nonstationary ambient vibration data using random decrement algorithm. Comput. Struct. 2013, 119, 104–114. [Google Scholar] [CrossRef]
- Ibrahim, S.R. Random decrement technique for modal identification of structures. J. Spacecr. Rocket. 2012, 14, 696. [Google Scholar] [CrossRef]
- Lin, C.S.; Chiang, D.Y. A modified random decrement technique for modal identification from nonstationary ambient response data only. J. Mech. Sci. Technol. 2012, 26, 1687–1696. [Google Scholar] [CrossRef]
- Kim, Y.; Park, S.G. Wet damping estimation of the scaled segmented hull model using the random decrement technique. Ocean Eng. 2014, 75, 71–80. [Google Scholar] [CrossRef]
- Modak, S.V.; Rawal, C.; Kundra, T.K. Harmonics elimination algorithm for operational modal analysis using random decrement technique. Mech. Syst. Signal Process. 2010, 24, 922–944. [Google Scholar] [CrossRef]
- Vandiver, J.K.; Dunwoody, A.B.; Campbell, R.B.; Cook, M.F. A mathematical basis for the random decrement vibration signature analysis technique. ASME J. Mech. Des. 1982, 104, 307–313. [Google Scholar] [CrossRef]
- Ku, C.J.; Cermak, J.E.; Chou, L.S. Random decrement-based method for modal parameter identification of a dynamic system using acceleration responses. J. Wind Eng. Ind. Aerodyn. 2007, 95, 389–410. [Google Scholar] [CrossRef]
- Yang, J.C.S.; Dagalakis, N.G.; Everstine, G.C.; Wang, Y.F. Measurement of structural damping using the random decrement technique. Shock Vib. Bull. 1983, 53, 63–71. [Google Scholar]




| CEEMDAN | WP | CEEMDAN-WP | |
|---|---|---|---|
| SNR | 9.7908 | 9.3499 | 10.2086 |
| RMSE (cm) | 0.3187 | 0.3258 | 0.3121 |
| Steel Tube and Wind Brace | Concrete Inside the Steel Tube | Crossbeam and Stringer | Tie Bar | Bridge Deck | Pier Column | |
|---|---|---|---|---|---|---|
| Elasticity modulus (Pa) | 2.1 × 1011 | 3.5 × 1010 | 3.0 × 1010 | 2.1 × 1011 | 2.85 × 1010 | 3.3 × 1010 |
| Density (kg/m3) | 7800 | 2600 | 2600 | 7800 | 2500 | 2600 |
| Poisson coefficient | 0.3 | 0.1667 | 0.1667 | 0.3 | 0.1667 | 0.1667 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, C.; Yu, L.; Niu, Y. Dynamic Parameter Identification of a Long-Span Arch Bridge Based on GNSS-RTK Combined with CEEMDAN-WP Analysis. Appl. Sci. 2019, 9, 1301. https://doi.org/10.3390/app9071301
Xiong C, Yu L, Niu Y. Dynamic Parameter Identification of a Long-Span Arch Bridge Based on GNSS-RTK Combined with CEEMDAN-WP Analysis. Applied Sciences. 2019; 9(7):1301. https://doi.org/10.3390/app9071301
Chicago/Turabian StyleXiong, Chunbao, Lina Yu, and Yanbo Niu. 2019. "Dynamic Parameter Identification of a Long-Span Arch Bridge Based on GNSS-RTK Combined with CEEMDAN-WP Analysis" Applied Sciences 9, no. 7: 1301. https://doi.org/10.3390/app9071301
APA StyleXiong, C., Yu, L., & Niu, Y. (2019). Dynamic Parameter Identification of a Long-Span Arch Bridge Based on GNSS-RTK Combined with CEEMDAN-WP Analysis. Applied Sciences, 9(7), 1301. https://doi.org/10.3390/app9071301





