Resilient Modulus—Physical Parameters Relationship of Improved Red Clay by Dynamic Tri-Axial Test
Abstract
:1. Introduction
2. Material Properties and Testing Method
2.1. Materials
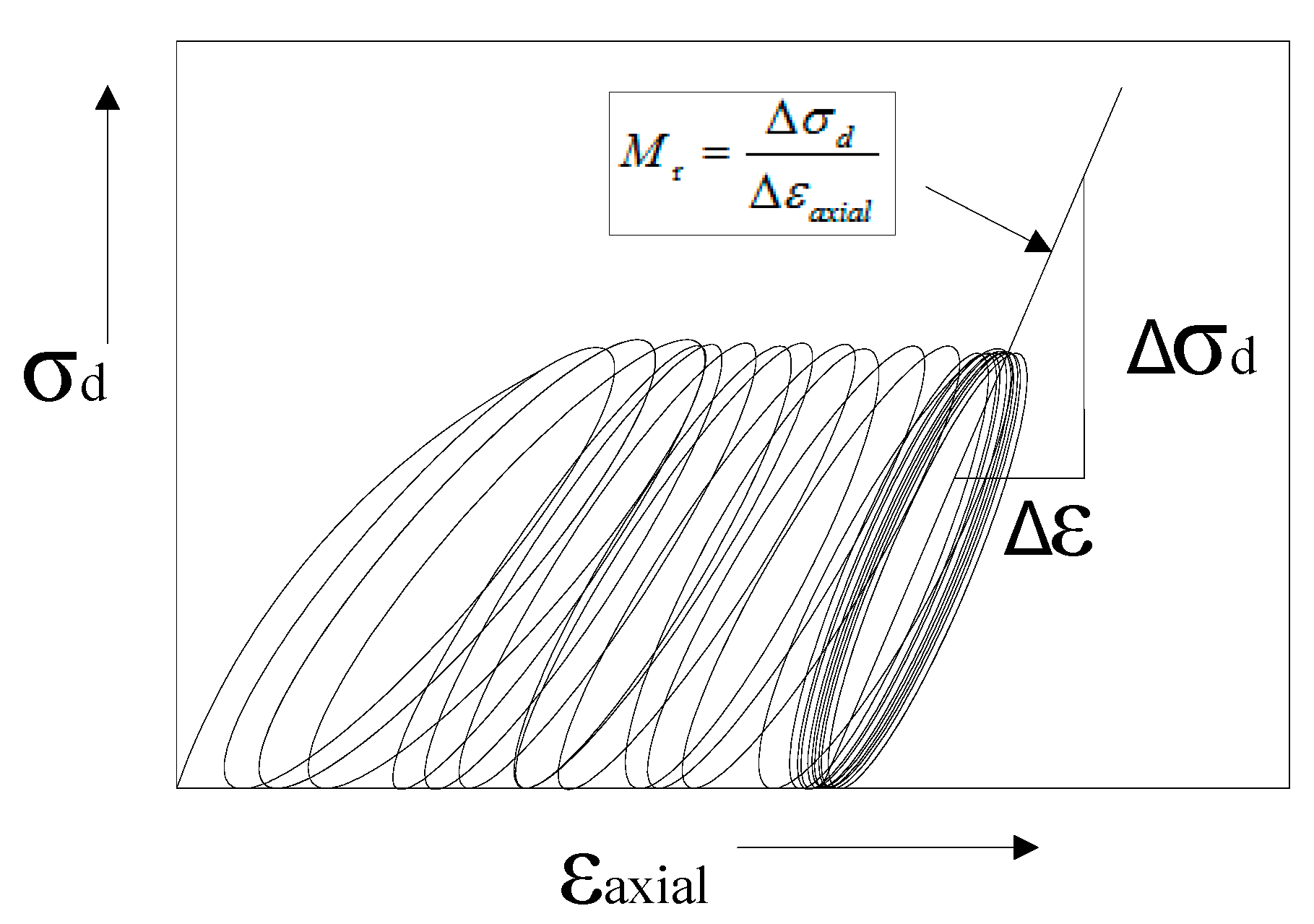
2.2. Testing Method
3. Analysis of Results
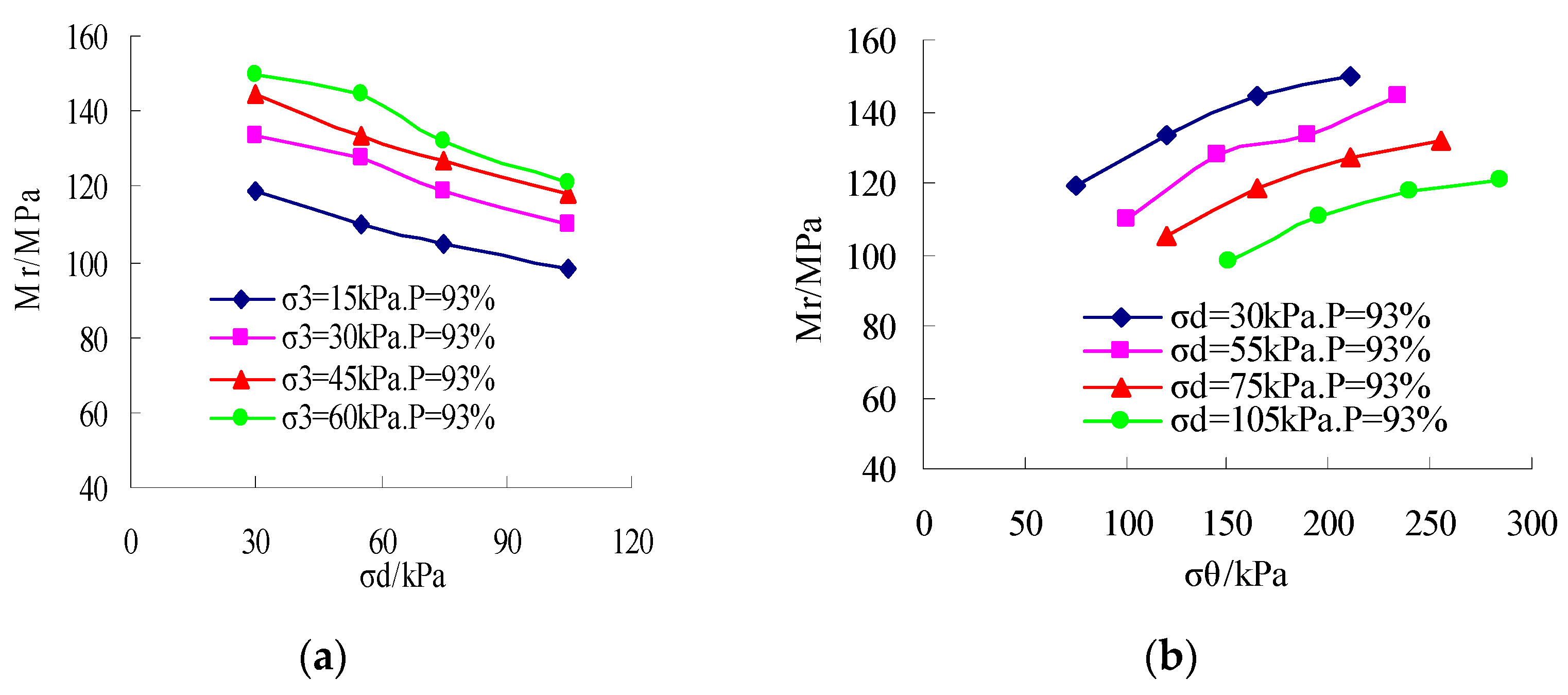
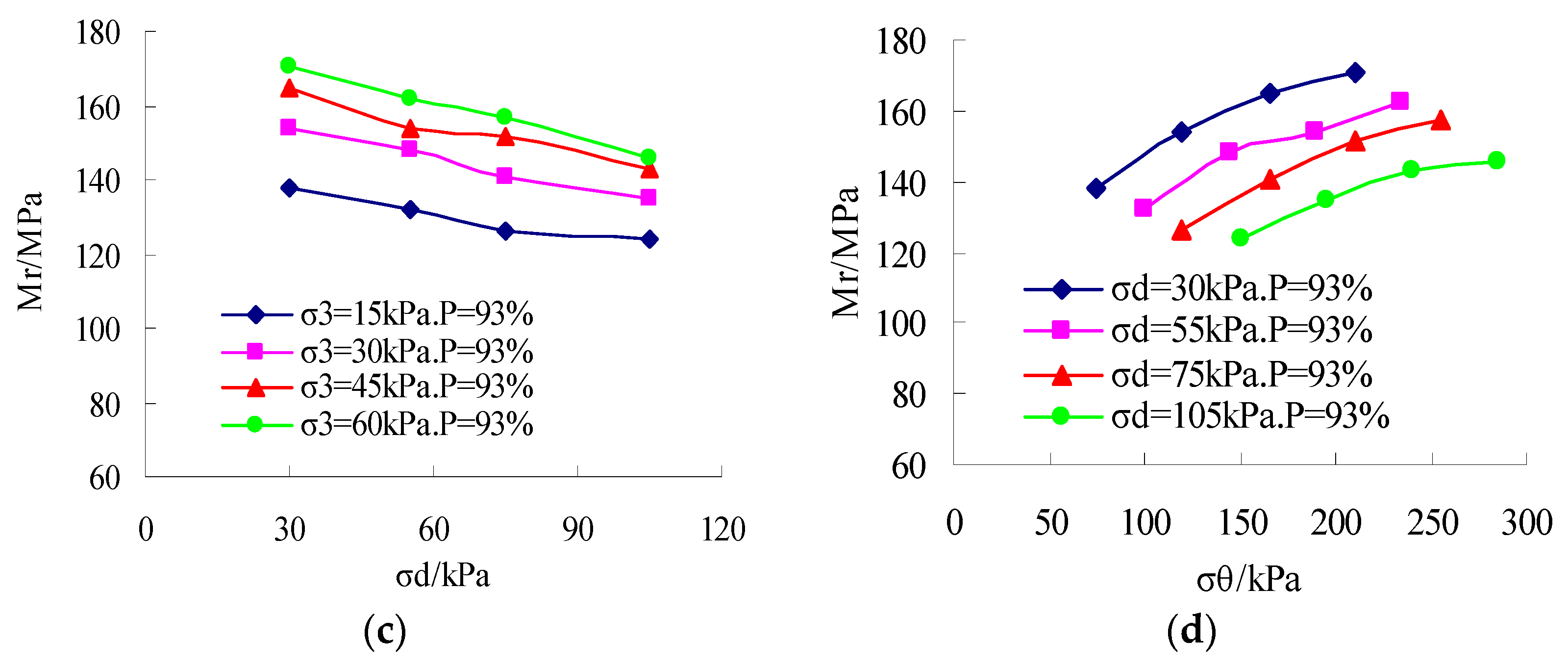
3.1. Influence of Stress State on Resilient Modulus
3.2. Prediction Models of Resilient Modulus
3.2.1. Uzan-Witczak Model
3.2.2. Andrei Model
3.2.3. Ni Model
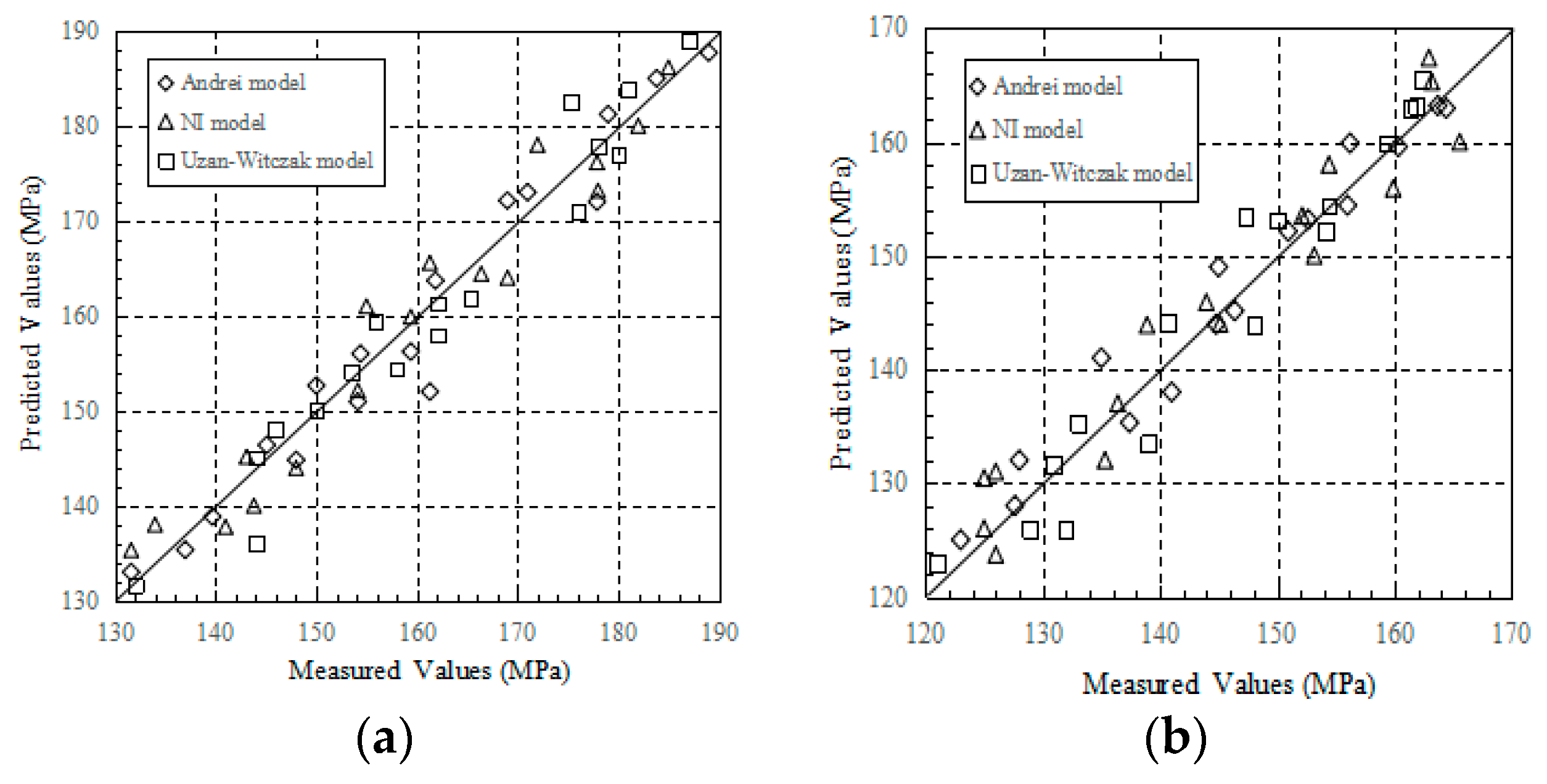
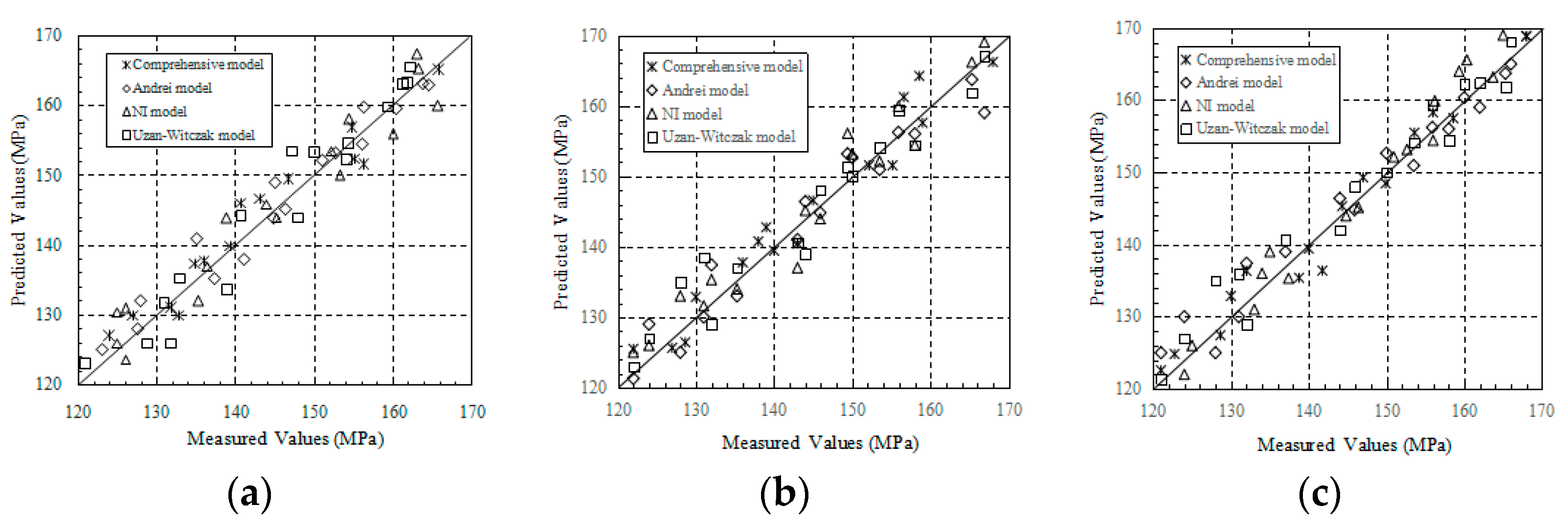
3.3. Regression Analysis Results
4. The Dependence of Resilient Modulus on Material Properties
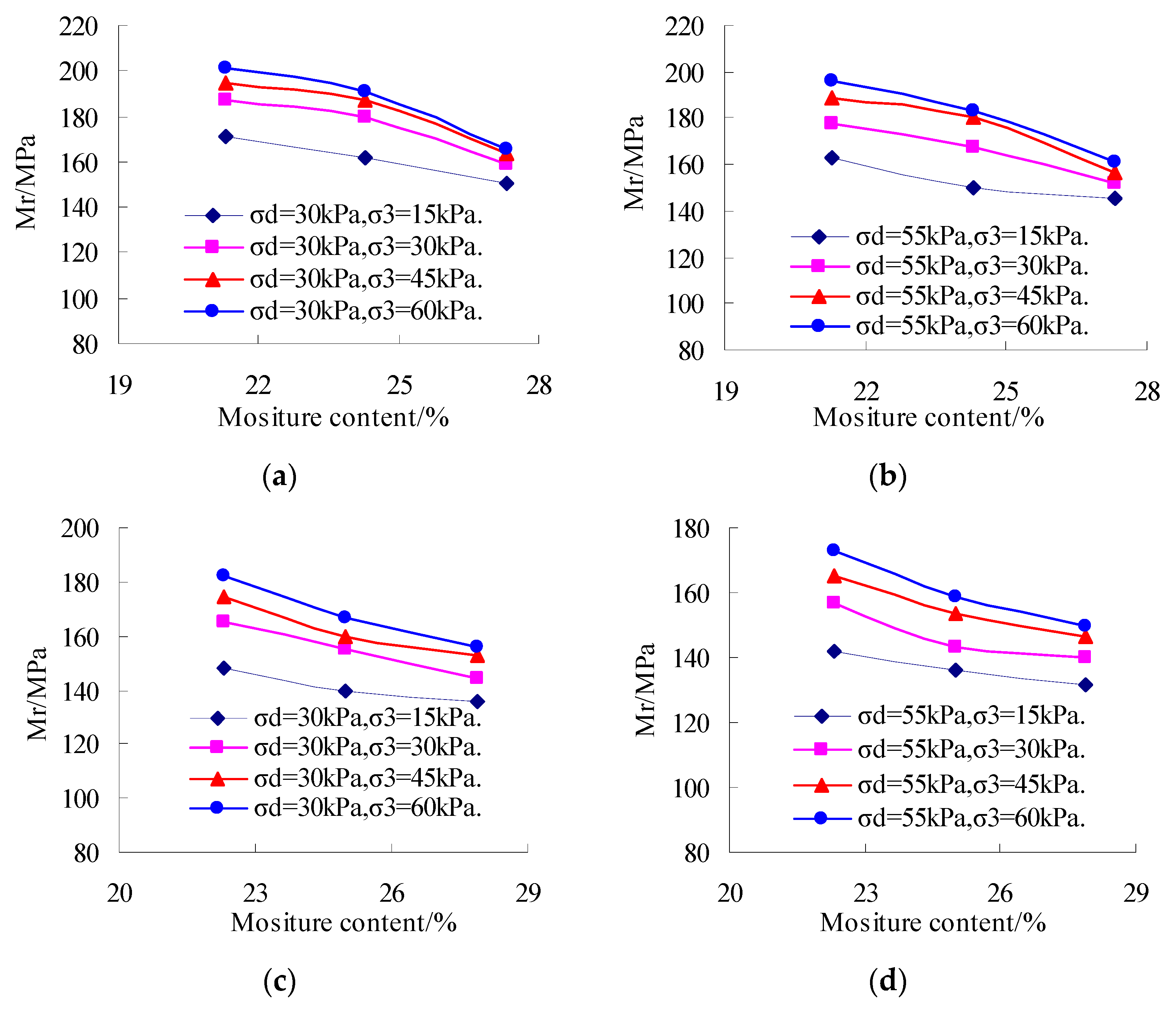
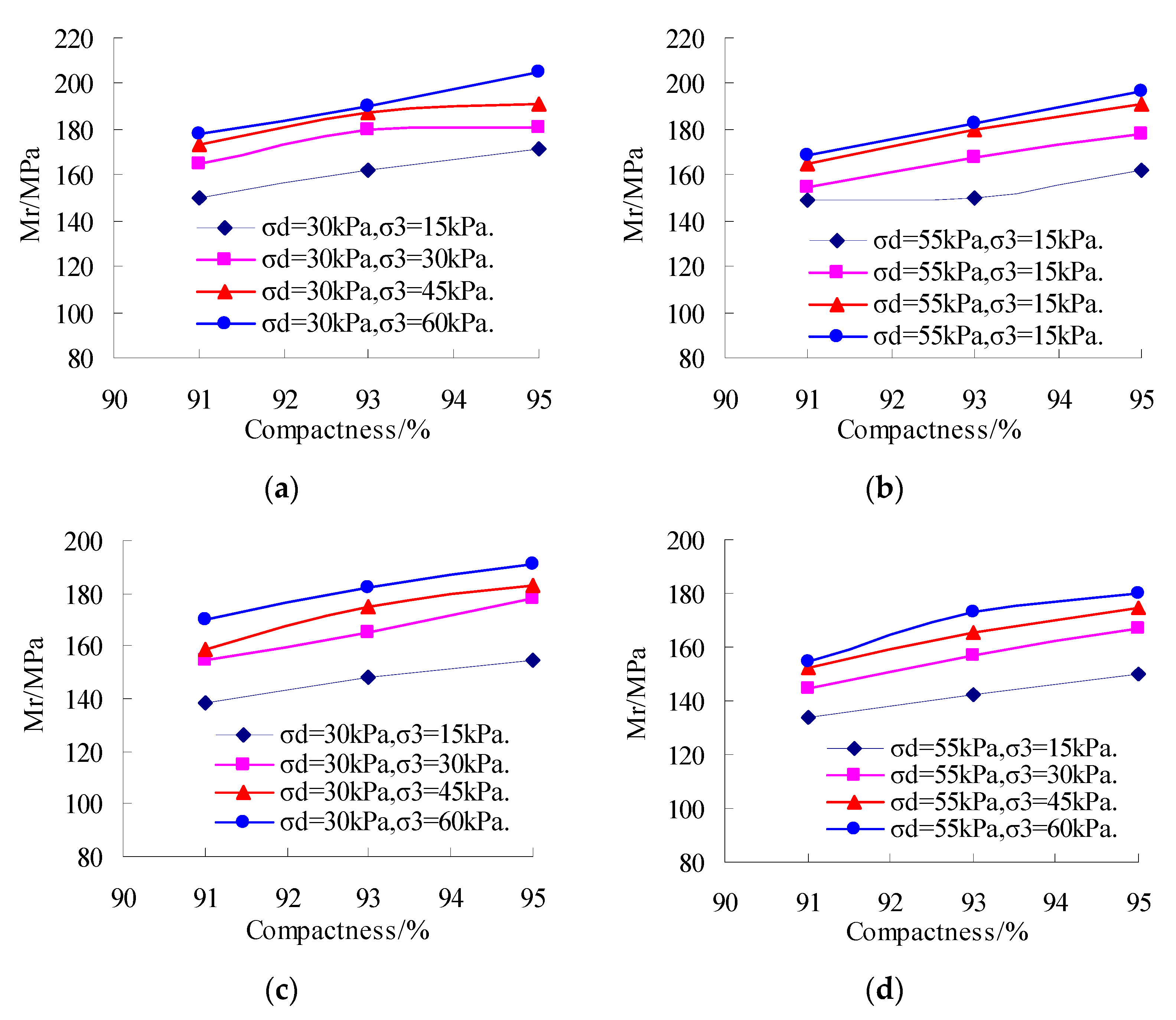
4.1. The Influence of Moisture Content and Compactness on Resilient Modulus
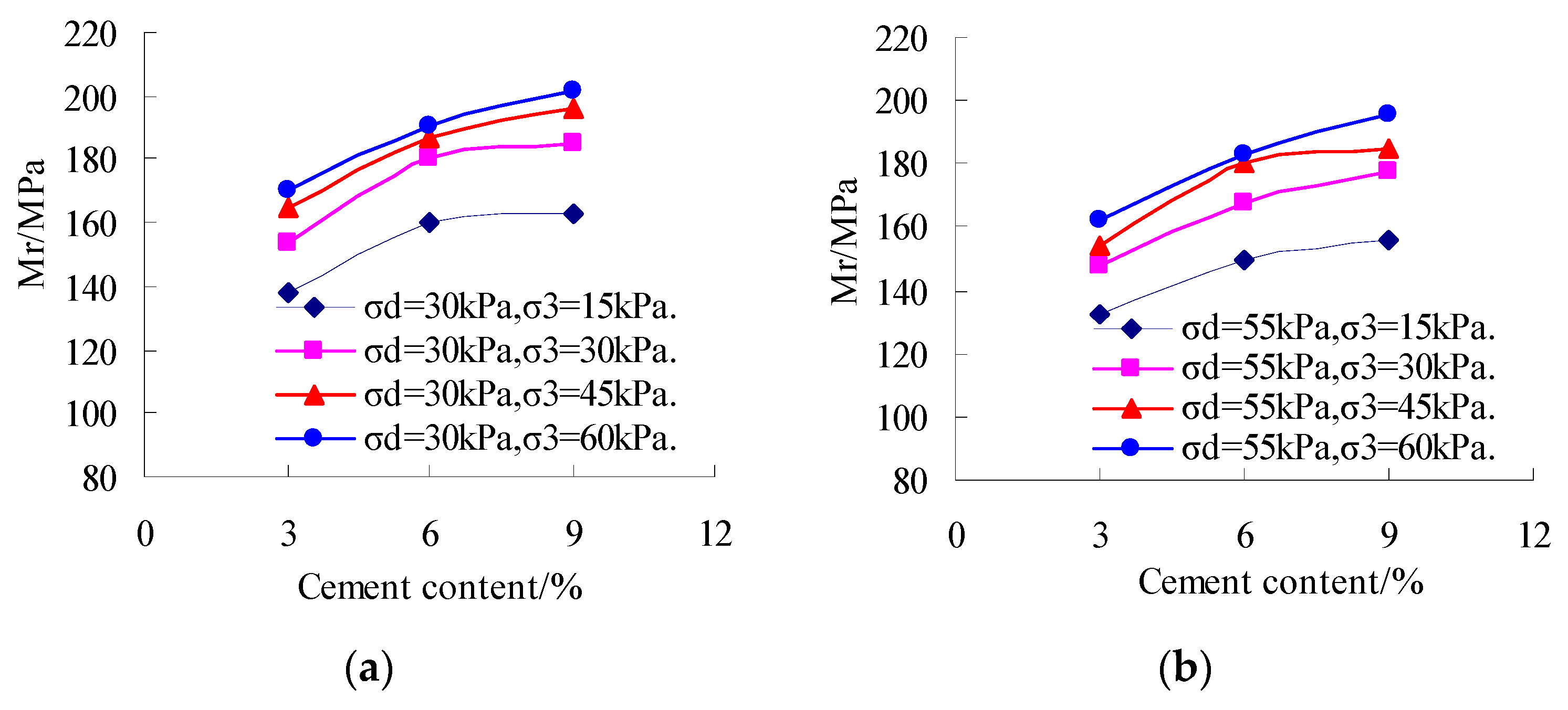
4.2. The Influence of Additive Content on Resilient Modulus
4.3. New Comprehensive Prediction Model
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Li, Z.Y.; Dong, C.; Zou, J.R.; Zou, W.L. Research on experiment and prediction model of dynamic resilient modulus of laterite soil in Southern Hunan. Rock Soil Mech. 2015, 36, 1840–1846. [Google Scholar]
- Wang, Y.X.; Lin, H.; Zhao, Y.L.; Li, X.; Guo, P.P.; Liu, Y. Analysis of fracturing characteristics of unconfined rock plate under edge on impact loading. Eur. J. Environ. Civ. Eng. 2019. [Google Scholar] [CrossRef]
- Wu, F.; Chen, J.; Zou, Q.L. A nonlinear creep damage model for salt rock. Int. J. Damage Mech. 2018, 1–14. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhang, L.Y.; Wang, W.J.; Wan, W.; Ma, W.H. Separation of elastoviscoplastic strains of rock and a nonlinear creep model. Int. J. Geomech. 2018, 04017129. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhang, L.Y.; Wang, W.J.; Wan, W.; Li, S.Q.; Ma, W.H.; Wang, Y.X. Creep behavior of intact and cracked limestone under multi-level loading and unloading cycles. Rock Mech. Rock Eng. 2017, 50, 1409–1424. [Google Scholar] [CrossRef]
- Qiu, X.; Yang, Q.; Wang, B.R.; Luo, X.H. Prediction Model of Dynamic Resilient Modulus of Cohesive Subgrade Soil Based on Triaxial Test System. Key Eng. Mater. 2013, 579–580, 873–876. [Google Scholar] [CrossRef]
- Lin, H.; Wang, H.; Fan, X.; Cao, P.; Zhou, K. Particle size distribution effects on deformation properties of graded aggregate base under cyclic loading. Eur. J. Environ. Civ. Eng. 2018. [Google Scholar] [CrossRef]
- Zheng, H.; Li, T.; Shen, J.; Xu, C.; Sun, H.; Lü, Q. The effects of blast damage zone thickness on rock slope stability. Eng. Geol. 2018, 246, 19–27. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Pu, C.Z.; Cao, R.H.; Jiang, T.T.; Huang, G. The stability and roof-support optimization of roadways passing through unfavorable geological bodies using advanced detection and monitoring methods, among others, in the Sanmenxia Bauxite Mine in China’s Henan Province. Bull. Eng. Geol. Environ. 2019. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhang, L.Y.; Wang, W.J.; Tang, J.Z.; Lin, H.; Wan, W. Transient pulse test and morphological analysis of single rock fractures. Int. J. Rock Mech. Min. Sci. 2017, 91, 139–154. [Google Scholar] [CrossRef]
- Cao, R.H.; Cao, P.; Lin, H.; Ma, G.; Chen, Y. Failure characteristics of intermittent fissures under a compressive-shear test: Experimental and numerical analyses. Theor. Appl. Fract. Mech. 2018, 96, 740–757. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, H. Consistency analysis of Hoek-Brown and equivalent Mohr-coulomb parameters in calculating slope safety factor. Bull. Eng. Geol. Environ. 2018. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Tang, J.Z.; Chen, Y.; Zhang, L.Y.; Wang, W.J.; Liao, J.P. Hydromechanical coupling tests for mechanical and permeability characteristics of fractured limestone in complete stress–strain process. Environ. Earth Sci. 2017, 76, 1–18. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Luo, S.L.; Wang, Y.X.; Wang, W.J.; Zhang, L.Y.; Wan, W. Numerical Analysis of Karst Water Inrush and a Criterion for Establishing the Width of Water-resistant Rock Pillars. Mine Water Environ. 2017, 36, 508–519. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Zhang, L.Y.; Wang, W.J.; Pu, C.Z.; Wan, W.; Tang, J.Z. Cracking and Stress–Strain Behavior of Rock-Like Material Containing Two Flaws Under Uniaxial Compression. Rock Mech. Rock Eng. 2016, 49, 2665–2687. [Google Scholar] [CrossRef]
- Zhao, Y.L.; Wang, Y.X.; Wang, W.J.; Wan, W.; Tang, J.Z. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment. Int. J. Rock Mech. Min. Sci. 2017, 93, 66–75. [Google Scholar] [CrossRef]
- Fan, X.; Lin, H.; Lai, H.P.; Cao, R.H.; Liu, J. Numerical analysis of the compressive and shear failure behavior of rock containing multi-intermittent joints. C. R. Méc. 2019, 347, 33–48. [Google Scholar] [CrossRef]
- Wang, Y.X.; Guo, P.P.; Li, X.; Lin, H.; Liu, Y.; Yuan, H.P. Behavior of Fiber-Reinforced and Lime-Stabilized Clayey Soil in Triaxial Tests. Appl. Sci. 2019, 9, 900. [Google Scholar] [CrossRef]
- Fan, X.; Li, K.H.; Lai, H.P.; Xie, Y.L.; Cao, R.H. Internal stress distribution and cracking around flaws and openings of rock block under uniaxial compression: A particle mechanics approach. Comput. Geotech. 2018, 102, 28–38. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Mitri, H.S. Evaluation method of rockburst: State-of-the-art literature review. Tunn. Undergr. Space Technol. 2018, 81, 632–659. [Google Scholar] [CrossRef]
- Wang, Y.X.; Guo, P.P.; Ren, W.X.; Yuan, B.X.; Yuan, H.P.; Zhao, Y.L.; Shan, S.B.; Cao, P. Laboratory Investigation on Strength Characteristics of Expansive Soil Treated with Jute Fiber Reinforcement. Int. J. Geomech. 2017, 17, 04017101. [Google Scholar] [CrossRef]
- Wang, Y.X.; Guo, P.P.; Dai, F.; Li, X.; Zhao, Y.L.; Liu, Y. Behavior and modeling of fiber-reinforced clay under triaxial compression by combining the superposition method with the energy-based homogenization technique. Int. J. Geomech. 2018, 18, 04018172. [Google Scholar] [CrossRef]
- Liu, B.C.; Li, C.J.; Pan, Z.Y.; Zhang, B.H. Laboratory test for mechanical properties of Guilin red clay mixed with cement. J. Eng. Geol. 2012, 20, 633–638. [Google Scholar]
- Wang, D.; Wang, H.; Jiang, Y. Water immersion-induced strength performance of solidified soils with reactive MgO—A green and low carbon binder. J. Test. Eval. (ASTM) 2019, 47. [Google Scholar] [CrossRef]
- Lin, H.; Xiong, W.; Cao, P. Stability of soil nailed slope using strength reduction method. Eur. J. Environ. Civ. Eng. 2013, 17, 872–885. [Google Scholar] [CrossRef]
- Tan, Y.Z.; Zheng, A.; Wu, P.; Fu, W. Effect of aggregate soil size on California bearing ratio values of laterite soil. Rock Soil Mech. 2013, 34, 1242–1246. [Google Scholar]
- Wang, D.; Du, Y.; Xiao, J. Shear properties of stabilized loess using novel reactive magnesia-bearing binders. J. Mater. Civ. Eng. (ASCE) 2019. [Google Scholar] [CrossRef]
- Meng, J.; Cao, P.; Huang, J.; Lin, H.; Chen, Y.; Cao, R. Second-order cone pro- gramming formulation of discontinuous deformation analysis. Int. J. Numer. Methods Eng. 2019, 1–15. [Google Scholar] [CrossRef]
- Wang, H.; Nie, W.; Cheng, W.M.; Liu, Q.; Jin, H. Effects of air volume ratio parameters on air curtain dust suppression in a rock tunnel’s fully-mechanized working face. Adv. Powder Technol. 2018, 29, 230–244. [Google Scholar] [CrossRef]
- Seed, H.B.; Chan, C.K.; Lee, C.E. Resilience characteristics of subgrade soils and their relation to fatigue failures in asphalt pavements. In Proceedings of the International Conference on Structural Design of Asphalt Pavement, Ann Arbor, MI, USA, 20–24 August 1962; pp. 611–636. [Google Scholar]
- Ba, M.; Fall, M.; Samb, F.; Sarr, D.; Ndiaye, M. Resilient Modulus of Unbound Aggregate Base Courses from Senegal (West Africa). Open J. Civ. Eng. 2011, 1, 1–6. [Google Scholar] [CrossRef]
- AASHTO. Guide for Design of Pavement Structures; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2002. [Google Scholar]
- Shen, J.; Wan, L.; Zuo, J. Non-linear shear strength model for Coal Rocks. Rock Mech. Rock Eng. 2019. [Google Scholar] [CrossRef]
- Huang, F.; Shen, J.; Cai, M.; Xu, C. An empirical UCS model for anisotropic blocky rock masses. Rock Mech. Rock Eng. 2019. [Google Scholar] [CrossRef]
- Shen, J.; Jimenez, R. Predicting the shear strength parameters of sandstone using genetic programming. B Eng. Geol. Environ. 2018, 77, 1647–1662. [Google Scholar] [CrossRef]
- Seed, H.B.; Mitry, F.G.; Monismith, C.L.; Chan, C.K. Prediction of Flexible Pavement Deflections from Laboratory Repeated Load Tests; National Academy of Sciences National Academy of Engineering: Washington, DC, USA, 1967. [Google Scholar]
- Uzan, J. Characterization of Granular Materials; Transportation Research Record 1022; National Research Council: Washington, DC, USA, 1985; pp. 52–59. [Google Scholar]
- Witczak, M.; Uzan, J. The Universal Airport Design System, Report I of IV. Granular Material Characterization; University of Maryland: College Park, MD, USA, 1988. [Google Scholar]
- Uzan, J. Characterization of Clayey Subgrade Materials for Mechanistic Design of Flexible Pavements; Transportation Research Record 1629; Transportation Research Board: Washington, DC, USA, 1998; pp. 188–196. [Google Scholar]
- Andrei, D. Development of a Harmonized Test Protocol for the Resilient Modulus of Unbound Materials Used in Pavement Design. Master’s Thesis, University of Maryland, College Park, MD, USA, 1999. [Google Scholar]
- Ni, B.; Hopkins, T.C.; Sun, L.; Beckham, T.L. Modeling the resilient modulus of soils. In Proceedings of the 6th International Conference on the Bearing Capacity of Roads, Railways and Airfields, Lisbon, Portugal, 24–26 June 2002; pp. 1131–1142.
- Ozel, M.R.; Mohajerani, A. Resilient Modulus of a Stabilised Fine-grained Subgrade Soil. Aust. Geomech. J. 2011, 36, 75–86. [Google Scholar]
- Li, Z.Y.; Zou, J.R.; Dong, C. Study on Prediction Model of Dynamic Resilient Modulus of Cohesive Subgrade Soils Considering Moisture Variation. Appl. Mech. Mater. 2014, 488–489, 411–416. [Google Scholar] [CrossRef]
- Bao, T.N.; Mohajerani, A. Resilient Modulus of Fine-grained Soil and a Simple Testing and Calculation Method for Determining an Average Resilient Modulus Value for Pavement Design. Transp. Geotech. 2016, 7, 59–70. [Google Scholar]
- Wang, H.; Lin, H.; Cao, P. Correlation of UCS Rating with Schmidt Hammer Surface Hardness for Rock Mass Classification. Rock Mech. Rock Eng. 2017, 50, 195–203. [Google Scholar] [CrossRef]
- Liu, Q.; Nie, W.; Yun, H.; Peng, H.T.; Liu, C.Q.; Wei, C.H. Research on tunnel ventilation systems: Dust diffusion and pollution behavior by air curtains based on CFD technology and field measurement. Build. Environ. 2019, 147, 444–460. [Google Scholar] [CrossRef]
- Hua, Y.; Nie, W.; Cai, P.; Liu, Y.H.; Peng, H.T.; Liu, Q. Pattern characterization concerning spatial and temporal evolution of dust pollution associated with two typical ventilation methods at fully mechanized excavation faces in rock tunnels. Powder Technol. 2018, 334, 117–131. [Google Scholar] [CrossRef]
- Wang, Y.X.; Guo, P.P.; Lin, H.; Li, X.; Zhao, Y.L.; Yuan, B.X.; Liu, Y.; Cao, P. Numerical Analysis of Fiber-Reinforced Soils based on the Equivalent Additional Stress Concept. Int. J. Geomech. 2019, in press. [Google Scholar]
- Chen, R.; Ge, Y.H.; Chen, Z.K.; Liu, J.; Zhao, Y.R.; Li, Z.H. Analytical Solution for One-dimensional Contaminant Diffusion through Unsaturated Soils Beneath. Geomembrane. J. Hydrol. 2019, 568, 260–274. [Google Scholar] [CrossRef]
- Chen, R.; Huang, J.W.; Chen, Z.K.; Xu, Y.; Liu, J.; Ge, Y.H. Effect of Root Density of Wheat and Okra on Hydraulic Properties of an Unsaturated Compacted Loam. Eur. J. Soil Sci. 2019. [Google Scholar] [CrossRef]
- Lu, M.M.; Jing, H.W.; Zhou, A.N.; Xie, K.H. Analytical models for consolidation of combined composite ground improved by impervious columns and vertical drains. Int. J. Numer. Anal. Methods Geomech. 2018, 42, 871–888. [Google Scholar] [CrossRef]
- Lu, M.M.; Sloan, S.W.; Indraratna, B.; Jing, H.W.; Xie, K.H. A new analytical model for consolidation with multiple vertical drains. Int. J. Numer. Anal. Methods Geomech. 2016, 40, 1623–1640. [Google Scholar] [CrossRef]
- Yang, S.B.; Nie, W.; Lv, S.S.; Liu, Z.Q.; Peng, H.T.; Ma, X.; Cai, P.; Xu, C.W. Effects of spraying pressure and installation angle of nozzles on atomization characteristics of external spraying system at a fully-mechanized mining face. Powder Technol. 2019, 343, 754–764. [Google Scholar] [CrossRef]
- Lu, M.M.; Jing, H.W.; Zhou, Y.; Xie, K.H. General analytical model for consolidation of stone columns-reinforced ground and combined composite ground. Int. J. Geomechan. (ASCE) 2017, 17, 04016131. [Google Scholar] [CrossRef]
- Cai, P.; Nie, W.; Chen, D.W.; Yang, S.B.; Liu, Z.Q. Effect of air flowrate on pollutant dispersion pattern of coal dust particles at fully mechanized mining face based on numerical simulation. Fuel 2019, 239, 623–635. [Google Scholar] [CrossRef]
- Bao, Q.; Nie, W.; Liu, C.Q.; Liu, Y.H.; Zhang, H.H.; Wang, H.K.; Jin, H. Preparation and Characterization of a Binary-Graft-Based, Water-Absorbing Dust Suppressant for Coal Transportation. J. Appl. Polym. Sci. 2019, 135. [Google Scholar] [CrossRef]
- Jin, H.; Nie, W.; Zhang, H.H.; Liu, Y.H.; Bao, Q.; Wang, H.K. The Preparation and Characterization of a Novel Environmentally-Friendly Coal Dust Suppressant. J. Appl. Polym. Sci. 2019. [Google Scholar] [CrossRef]
- Wang, Y.X.; Shan, S.B.; Zhang, C.S.; Guo, P.P. Seismic response of tunnel lining structure in a thick expansive soil stratum. Tunn. Undergr. Space Technol. 2019, 88, 250–259. [Google Scholar] [CrossRef]
- Yuan, B.X.; Sun, M.; Wang, Y.X.; Zhai, L.H.; Luo, Q.Z. A full 3D displacement measuring system for 3D displacement field of soil around a laterally loaded pile in transparent soil. Int. J. Geomech. 2019. [Google Scholar] [CrossRef]
- Yuan, B.X.; Xu, K.; Wang, Y.X.; Chen, R.; Luo, Q.Z. Investigation of deflection of a laterally loaded pile and soil deformation using the PIV technique. Int. J. Geomech. 2017, 17, 04016138. [Google Scholar] [CrossRef]
- Wang, D.; Wang, H.; Di, S. Mechanical properties and microstructure of magnesia-fly ash pastes. Road Mater. Pavement Des. 2019. [Google Scholar] [CrossRef]
- Wang, D.; Zentar, R.; Abriak, N.E. Durability and swelling of solidified/stabilized dredged marine soils with class F fly ash, cement and lime. J. Mater. Civ. Eng. (ASCE) 2018, 30, 04018013. [Google Scholar] [CrossRef]
- Wang, D.; Zentar, R.; Abriak, N.E.; Di, S.J. Long-term mechanical performance of marine sediments solidified with cement, lime and fly ash. Mar. Georesour. Geotechnol. 2018, 36, 123–130. [Google Scholar] [CrossRef]
- Wang, M.; Shi, X.; Zhou, J.; Qiu, X. Multi-planar detection optimization algorithm for the interval charging structure of large-diameter long hole blasting design based on rock fragmentation aspects. Eng. Optim. 2018, 50, 2177–2191. [Google Scholar] [CrossRef]
- Peng, H.; Nie, W.; Cai, P.; Liu, Q.; Liu, Z.Q. Development of a novel wind-assisted centralized spraying dedusting device for dust suppression in a fully mechanized mining face. Environ. Sci. Pollut. Res. 2018, 1–16. [Google Scholar] [CrossRef]
- Cao, R.; Cao, P.; Lin, H.; Fan, X.; Zhang, C.; Liu, T. Crack Initiation, Propagation, and Failure Characteristics of Jointed Rock or Rock-Like Specimens: A Review. Adv. Civ. Eng. 2019, 2019, 6975751. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Nie, W.; Peng, H.T.; Yang, S.B.; Chen, D.W.; Liu, Q. The effects of the spraying pressure and nozzle orifice diameter on the atomizing rules and dust suppression performances of an external spraying system in a fully-mechanized excavation face. Powder Technol. 2019, in press. [Google Scholar]
- Lekarp, F.; Isacsson, U.; Dawson, A. Resilient Response of Unbound Aggregates. J. Transp. Eng. 2000, 126, 66–75. [Google Scholar] [CrossRef]
- Hopkins, T.C.; Beckham, T.L.; Sun, C. Resilient Modulus of Compacted Crushed Stone Aggregate Bases; Research Report KTC-05-27/SPR-229-01-1F; Kentucky Transportation Center, College of Engineering, University of Kentucky: Lexington, KY, USA, 2001; p. 89. [Google Scholar]
- Ba, M.; Fall, M.; Sall, O.A.; Samb, F. Effect of Compaction Moisture Content on the Resilient Modulus of Unbound Aggregates from Senegal (west Africa). Geomaterials 2012, 2, 19–23. [Google Scholar] [CrossRef]
- May, R.W.; Witczak, M.W. Effective Granular Modulus to Model Pavement Response; Transportation Research Record 810; Transportation Research Board: Washington, DC, USA, 1981; pp. 1–9. [Google Scholar]
- Lu, M.M.; Li, D.X.; Jing, H.W.; Deng, Y.B. Analytical solution for consolidation of band-shaped drain based on an equivalent annular drain. Int. J. Geomech. 2019. [Google Scholar] [CrossRef]
- Butterfield, R. Dimensional analysis for geotechnical engineers. Geotechnique 1999, 49, 357–366. [Google Scholar] [CrossRef]


| Samples | Grain Density | Natural Dry Density | Maximum Dry Density | Optimum Moisture Content | Liquid Limit | Plastic Limit | <0.075mm Grain Size |
|---|---|---|---|---|---|---|---|
| /(g/cm) | /(g/cm) | /(g/cm) | /% | /% | /% | Soil particle content/% | |
| Red clay | 2.72 | 1.28 | 1.73 | 27.8 | 52.6 | 30.7 | 90 |
| Constituents | SiO2 | Al2O3 | Fe2O3 | K2O | MgO | CaO | Na2O | LOI |
|---|---|---|---|---|---|---|---|---|
| Content(%) | 40.27 | 32.65 | 18.52 | 2.51 | 0.91 | 0.72 | 0.24 | 4.18 |
| Mineral | Mineral Compositions/(%) | ||||
|---|---|---|---|---|---|
| Al2Si2O5(OH)4 | Al(OH)3 | FeO(OH) | SiO2 | Deviation | |
| Content(%) | 60.87 | 11.72 | 13.13 | 11.96 | −2.32 |
| Cement Content/% | Optimum Moisture Content/% | Maximum Dry Density/(g/cm3) | Lime Content/% | Optimum Moisture Content/% | Maximum Dry Density/(g/cm3) |
|---|---|---|---|---|---|
| 3 | 25.6 | 1.75 | 3 | 26.2 | 1.74 |
| 6 | 24.3 | 1.76 | 6 | 25.1 | 1.75 |
| 9 | 23.2 | 1.78 | 9 | 24.2 | 1.76 |
| (a) Improved red clay with 3% cement | ||||||
| Source of Variation | Variance Sum | Degree of Freedom | Mean Square Error | F Value | Critical Value a = 0.05 | Significance |
| Deviatoric stress | 2397.41 | 3 | 799.136 | 134.39 | 3.86 | Significant |
| Confining pressure | 1832.63 | 3 | 610.877 | 102.73 | 3.86 | Significant |
| Error | 53.52 | 9 | 5.946 | |||
| Sum | 4283.56 | 15 | ||||
| (b) Improved red clay with 3% lime | ||||||
| Source of Variation | Variance Sum | Degree of Freedom | Mean Square Error | F Value | Critical Value a = 0.05 | Significance |
| Deviatoric stress | 1853.83 | 3 | 617.942 | 178.36 | 3.86 | Significant |
| Confining pressure | 1870.63 | 3 | 623.544 | 179.98 | 3.86 | Significant |
| Error | 31.18 | 9 | 3.465 | |||
| Sum | 3755.64 | 15 | ||||
| Additive Content | Compactness/% | Moisture Content/% | Uzan-Witczak Model | NI Model | Andrei Model | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| k1 | k2 | k3 | R2 | k1 | k2 | k3 | R2 | k1 | k2 | k3 | R2 | |||
| C6% | 93 | OMC minus 3% | 139.6 | 0.2047 | −0.2176 | 0.9260 | 1791.6 | 0.5045 | −0.3637 | 0.9556 | 2033.8 | 0.1974 | −0.9476 | 0.9618 |
| OMC | 148.88 | 0.1953 | −0.2225 | 0.9146 | 1733 | 0.5054 | −0.4431 | 0.9421 | 1960.5 | 0.1999 | −1.0855 | 0.9569 | ||
| OMC plus 3% | 152.38 | 0.1083 | −0.1391 | 0.9191 | 1585 | 0.2844 | −0.2882 | 0.9669 | 1697.6 | 0.1116 | −0.6782 | 0.9739 | ||
| L6% | OMC minus 3% | 123.97 | 0.2168 | −0.2198 | 0.9375 | 1578.1 | 0.5632 | −0.4147 | 0.9718 | 1816.1 | 0.2214 | −1.0717 | 0.9812 | |
| OMC | 149.13 | 0.1901 | −0.2585 | 0.934 | 1513 | 0.5253 | −0.5224 | 0.9782 | 1716.3 | 0.2016 | −1.2226 | 0.9721 | ||
| OMC minus 3% | 129.48 | 0.1445 | −0.1667 | 0.9182 | 1439.2 | 0.3776 | −0.3333 | 0.9662 | 1579.2 | 0.1489 | −0.8169 | 0.9788 | ||
| C6% | 91 | OMC | 155.61 | 0.1811 | −0.2402 | 0.8621 | 1667.8 | 0.4873 | −0.5172 | 0.9342 | 1874.8 | 0.189 | −1.1987 | 0.9434 |
| 93 | 148.88 | 0.1953 | −0.2225 | 0.9146 | 1733 | 0.5054 | −0.4431 | 0.9421 | 1960.5 | 0.1999 | −1.0855 | 0.9569 | ||
| 95 | 165.93 | 0.198 | −0.2418 | 0.8084 | 1851.3 | 0.5399 | −0.5119 | 0.9005 | 2112.9 | 0.2086 | −1.2227 | 0.909 | ||
| L6% | 91 | 115.10 | 0.2107 | −0.2136 | 0.9266 | 1446.8 | 0.557 | −0.3953 | 0.962 | 1664 | 0.2123 | −1.0225 | 0.9374 | |
| 93 | 149.13 | 0.1901 | −0.2585 | 0.934 | 1513 | 0.5253 | −0.5224 | 0.9782 | 1716.3 | 0.2016 | −1.2226 | 0.9721 | ||
| 95 | 144.19 | 0.2147 | −0.244 | 0.8937 | 1708 | 0.5644 | −0.4923 | 0.945 | 1961.7 | 0.2216 | −1.2071 | 0.96 | ||
| C3% | 93 | OMC | 94.43 | 0.2335 | −0.1859 | 0.9596 | 1405 | 0.5954 | −0.2959 | 0.9664 | 1637.3 | 0.236 | −0.8898 | 0.9753 |
| C6% | 148.88 | 0.1953 | −0.2225 | 0.9146 | 1733 | 0.5054 | −0.4431 | 0.9421 | 1960.5 | 0.1999 | −1.0855 | 0.9569 | ||
| C9% | 107.73 | 0.2577 | −0.2073 | 0.9224 | 1655.5 | 0.6738 | −0.3373 | 0.9656 | 1969.8 | 0.2615 | −1.0027 | 0.9514 | ||
| L3% | 86.24 | 0.2671 | −0.2462 | 0.9399 | 1241.3 | 0.6923 | −0.4427 | 0.9681 | 1477.3 | 0.2719 | −1.1974 | 0.974 | ||
| L6% | 149.13 | 0.1901 | −0.2585 | 0.934 | 1513 | 0.5253 | −0.5224 | 0.9782 | 1716.3 | 0.2016 | −1.2226 | 0.9721 | ||
| L9% | 155.61 | 0.1885 | −0.2449 | 0.9156 | 1658.2 | 0.4997 | −0.5133 | 0.9545 | 1868.9 | 0.1928 | −1.1943 | 0.9543 | ||
| Mass Stress θ/kPa | Octahedral Shear Stress/kPa | Measured Data/Mpa | Resilient Modulus | |||||
|---|---|---|---|---|---|---|---|---|
| Andrei Model | NI Model | Uzan-Witczak Model | ||||||
| Predicted Value/Mpa | Error/% | Predicted Value/Mpa | Error/% | Predicted Value/Mpa | Error/% | |||
| 75 | 14.14 | 160 | 160.3371 | 0.2102 | 165.572 | 3.3653 | 162.302 | 1.4184 |
| 100 | 25.93 | 150 | 152.6465 | 1.7338 | 153.1579 | 2.0618 | 150.0214 | 0.0143 |
| 120 | 35.36 | 144 | 146.379 | 1.6252 | 145.1393 | 0.785 | 145.0932 | 0.7534 |
| 150 | 49.5 | 132 | 137.405 | 3.9336 | 135.3122 | 2.4479 | 140.6242 | 6.1328 |
| 120 | 14.14 | 180 | 176.1317 | 2.1962 | 176.1559 | 2.1822 | 177.9052 | 1.1775 |
| 145 | 25.93 | 167.4 | 164.4161 | 1.8148 | 162.9482 | 2.732 | 161.3126 | 3.7736 |
| 165 | 35.36 | 158 | 156.0003 | 1.2819 | 154.4171 | 2.3203 | 154.4036 | 2.3292 |
| 195 | 49.5 | 145.9 | 144.8037 | 0.7571 | 143.9618 | 1.3463 | 148.0175 | 1.4306 |
| 165 | 14.14 | 187 | 187.7086 | 0.3775 | 186.1511 | 0.456 | 189.3211 | 1.226 |
| 190 | 25.93 | 180 | 173.5441 | 3.7201 | 172.194 | 4.5333 | 170.0567 | 5.847 |
| 210 | 35.36 | 165.3 | 163.705 | 0.9743 | 163.1788 | 1.2999 | 161.8498 | 2.1317 |
| 240 | 49.5 | 153.5 | 150.9406 | 1.6956 | 152.1303 | 0.9003 | 154.1433 | 0.4173 |
| 210 | 14.14 | 190.5 | 196.9794 | 3.2894 | 195.6467 | 2.6306 | 198.4513 | 4.0067 |
| 235 | 25.93 | 182.7 | 181.077 | 0.8963 | 180.9776 | 0.9517 | 177.2649 | 3.0661 |
| 255 | 35.36 | 166 | 170.1836 | 2.4583 | 171.5026 | 3.2084 | 168.1048 | 1.2521 |
| 285 | 49.5 | 155.9 | 156.2159 | 0.2022 | 159.8905 | 2.4958 | 159.4045 | 2.1985 |
| Additive | Comprehensive Prediction Model Regression Equation | R2 |
|---|---|---|
| Cement | 0.84 | |
| Lime | 0.86 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, H.; Li, W.; Wang, Y.; Lin, H.; Liu, Y. Resilient Modulus—Physical Parameters Relationship of Improved Red Clay by Dynamic Tri-Axial Test. Appl. Sci. 2019, 9, 1155. https://doi.org/10.3390/app9061155
Yuan H, Li W, Wang Y, Lin H, Liu Y. Resilient Modulus—Physical Parameters Relationship of Improved Red Clay by Dynamic Tri-Axial Test. Applied Sciences. 2019; 9(6):1155. https://doi.org/10.3390/app9061155
Chicago/Turabian StyleYuan, Haiping, Weiqiang Li, Yixian Wang, Hang Lin, and Yan Liu. 2019. "Resilient Modulus—Physical Parameters Relationship of Improved Red Clay by Dynamic Tri-Axial Test" Applied Sciences 9, no. 6: 1155. https://doi.org/10.3390/app9061155
APA StyleYuan, H., Li, W., Wang, Y., Lin, H., & Liu, Y. (2019). Resilient Modulus—Physical Parameters Relationship of Improved Red Clay by Dynamic Tri-Axial Test. Applied Sciences, 9(6), 1155. https://doi.org/10.3390/app9061155







