Voltage/Frequency Deviations Control via Distributed Battery Energy Storage System Considering State of Charge
Abstract
:1. Introduction
- (1)
- The proposed coordinated control algorithm firstly calculates the required power for voltage and frequency deviation control, respectively, and then compares the two values and obtains an optimal regulating power for simultaneously solving the voltage and frequency deviation, which reduces the number of BESSs charging and discharging cycles, and improves the life time of the batteries.
- (2)
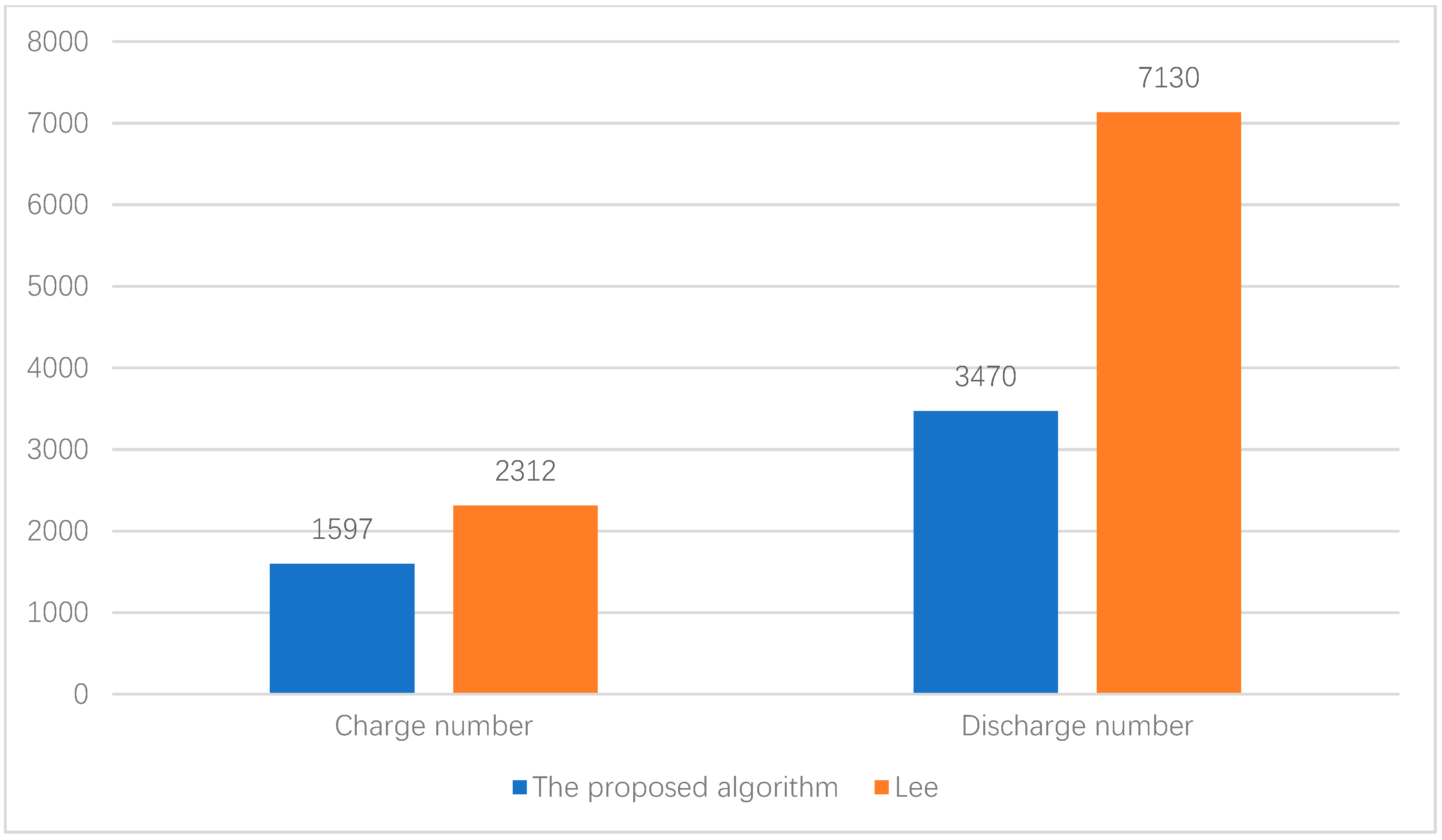
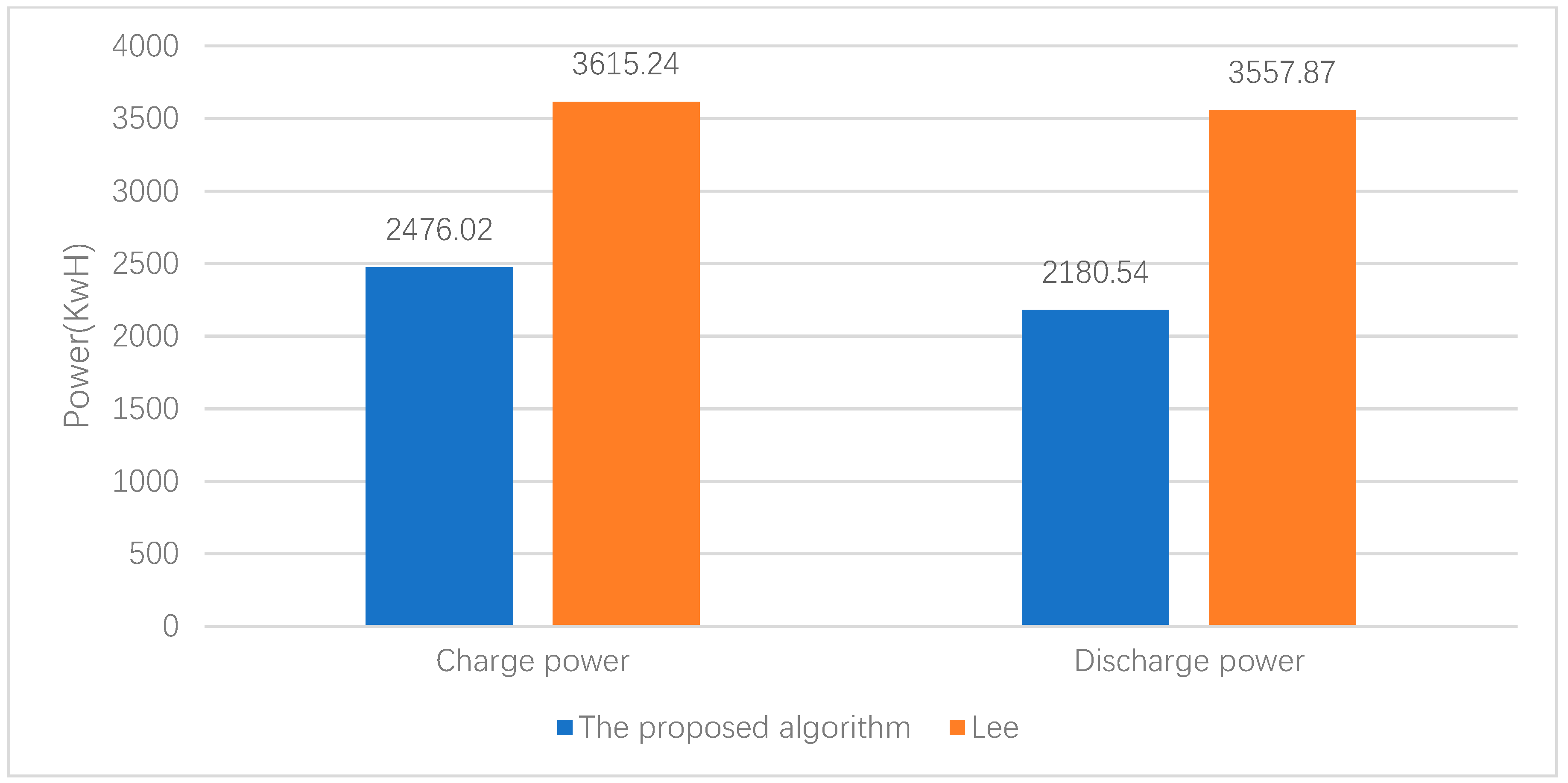
- The proposed method is compared with Lee’s algorithm [29] through the case studies. In Lee’s algorithm, the voltage and frequency regulation by BESSs are operated in a sequential order, which operates the BESSs more frequently. The results of the case study illustrate that a smaller number of charging/discharging cycles and better SOC control can be achieved by our proposed algorithm.
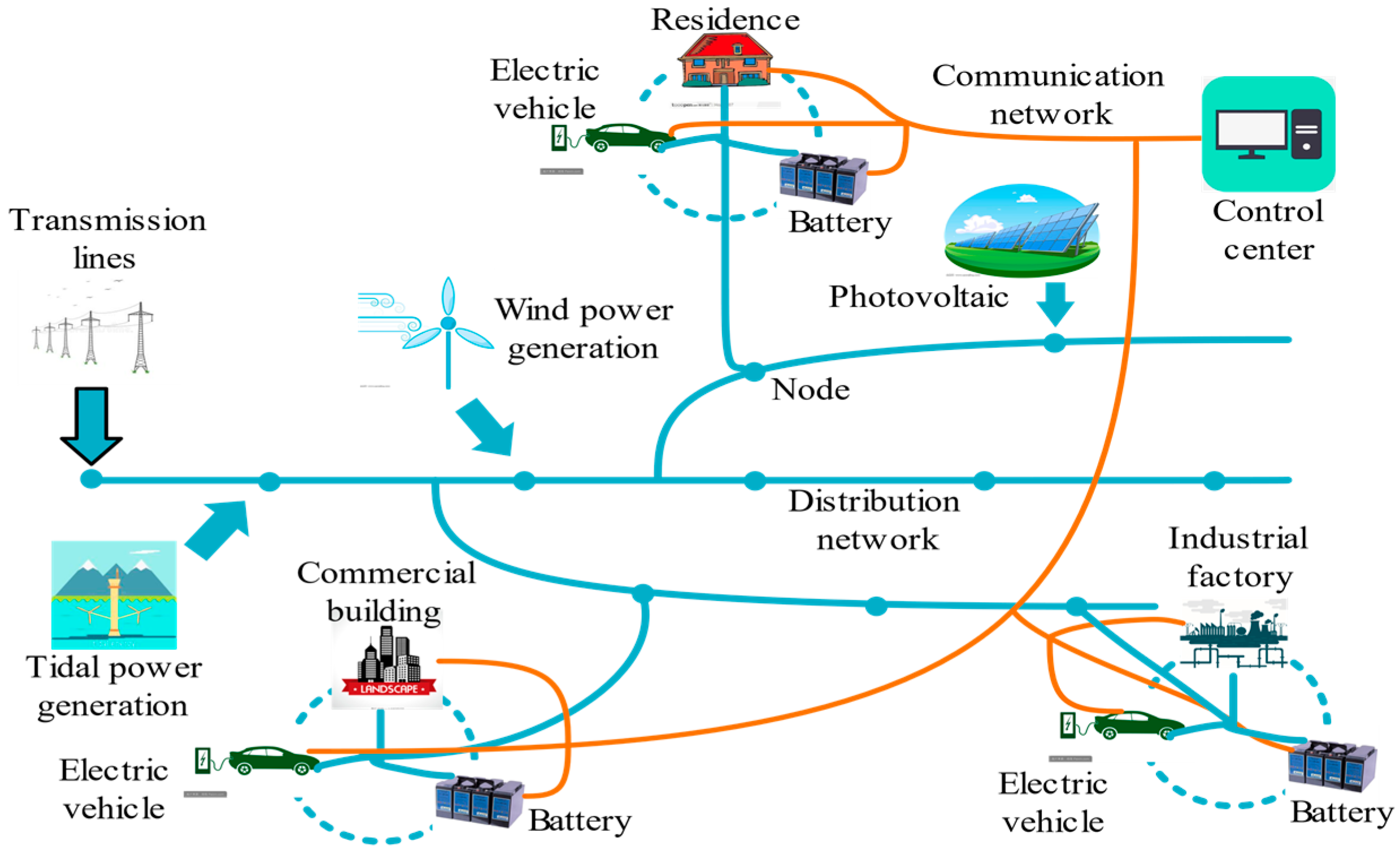
2. System Framework of Distribution System with DGs and BESSs
3. Proposed Collaborative Control Algorithm
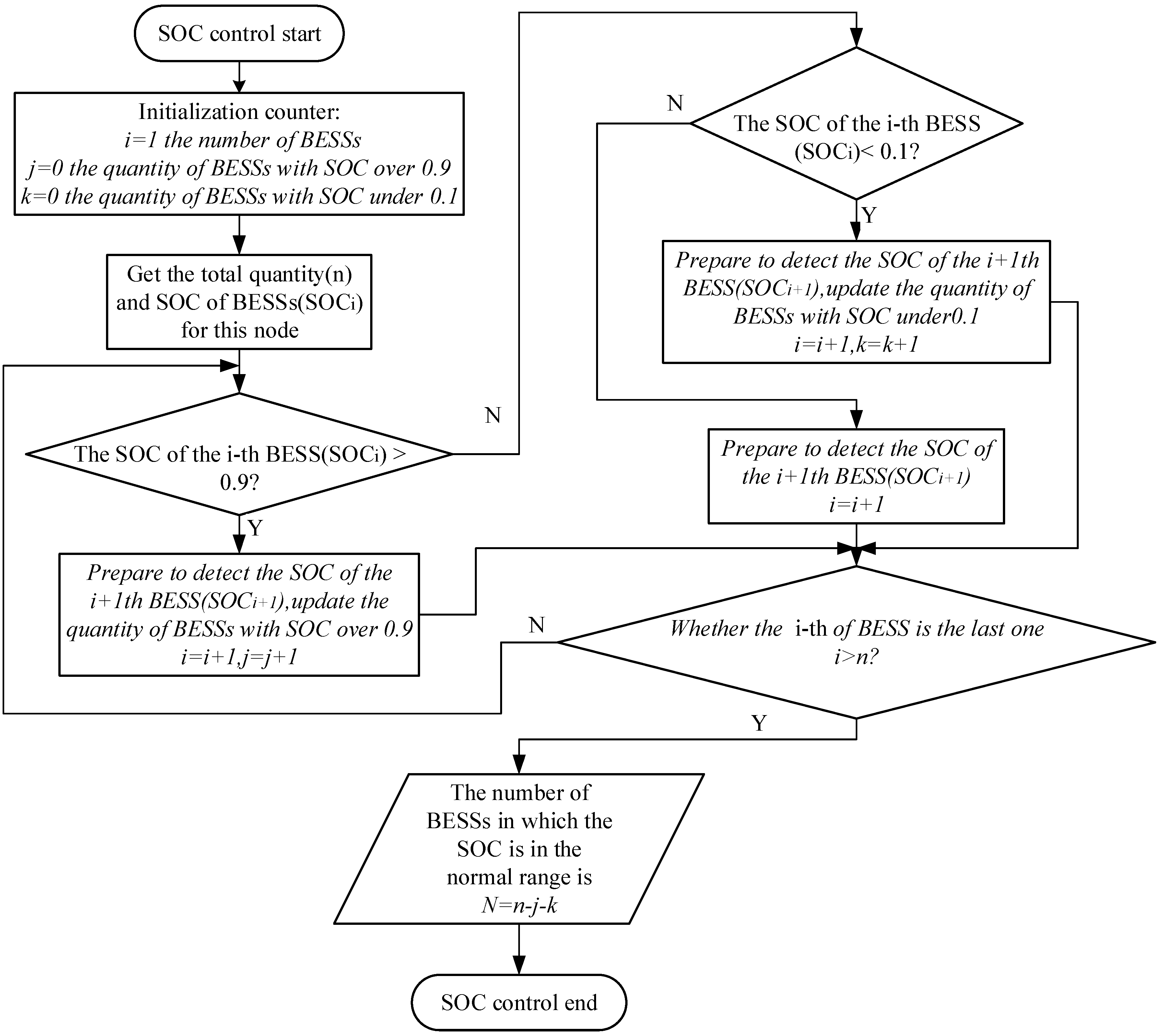
3.1. Full-time SOC Control
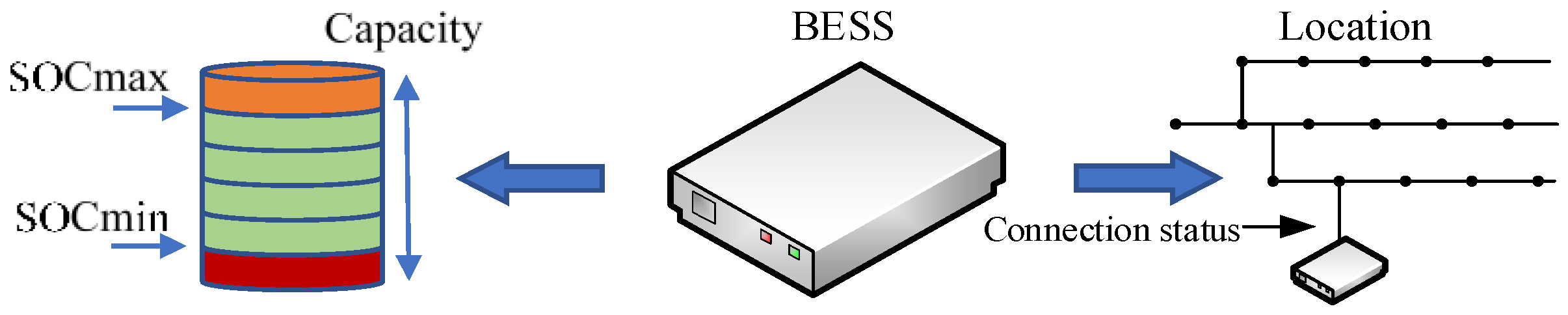
- SOC dynamicswhere is the SOC at time t; and is the capacity of the battery, and is the charging and discharging power of battery, respectively.
- SOC limitswhere and are the minimum and the maximum SOC, respectively.
- Power limitswhere , and , are the minimum and the maximum charging, discharging power, respectively.
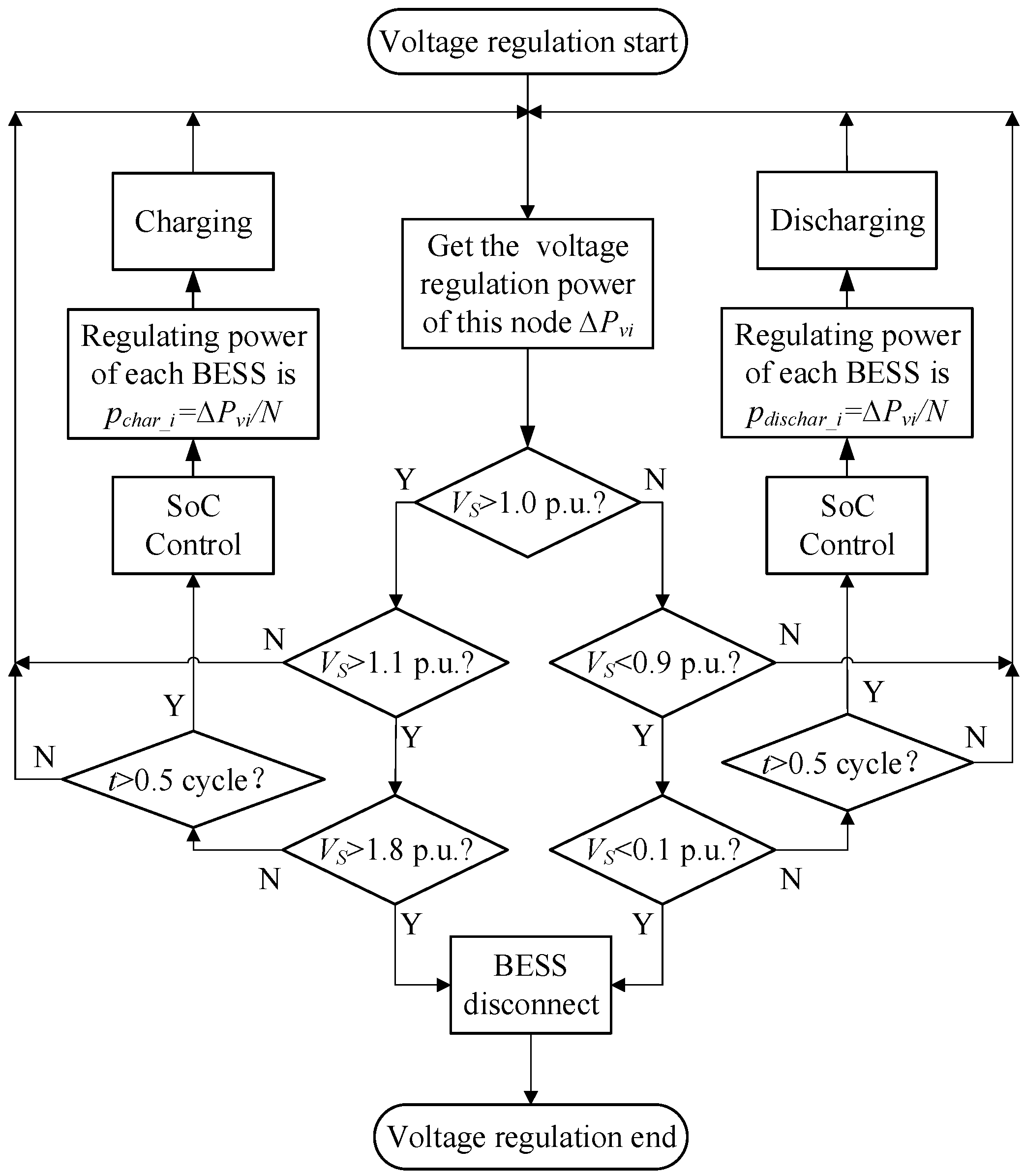
3.2. Independent Voltage Regulation Algorithm
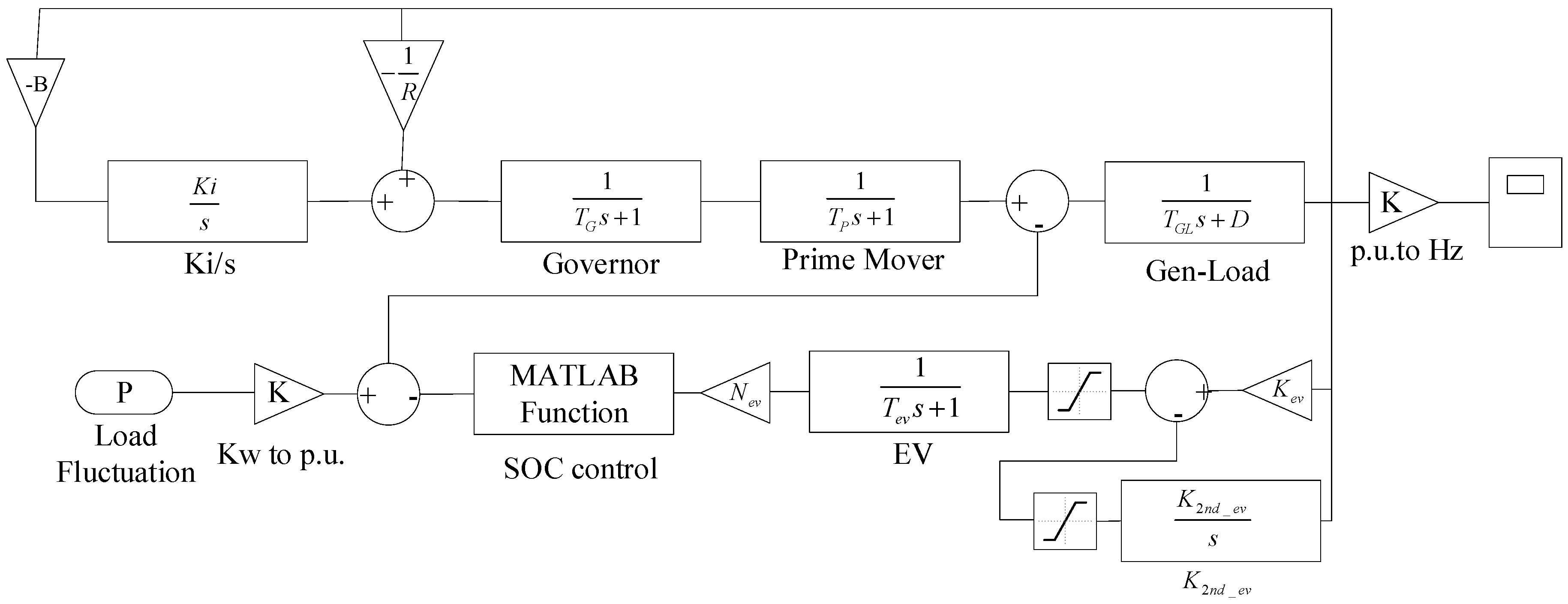
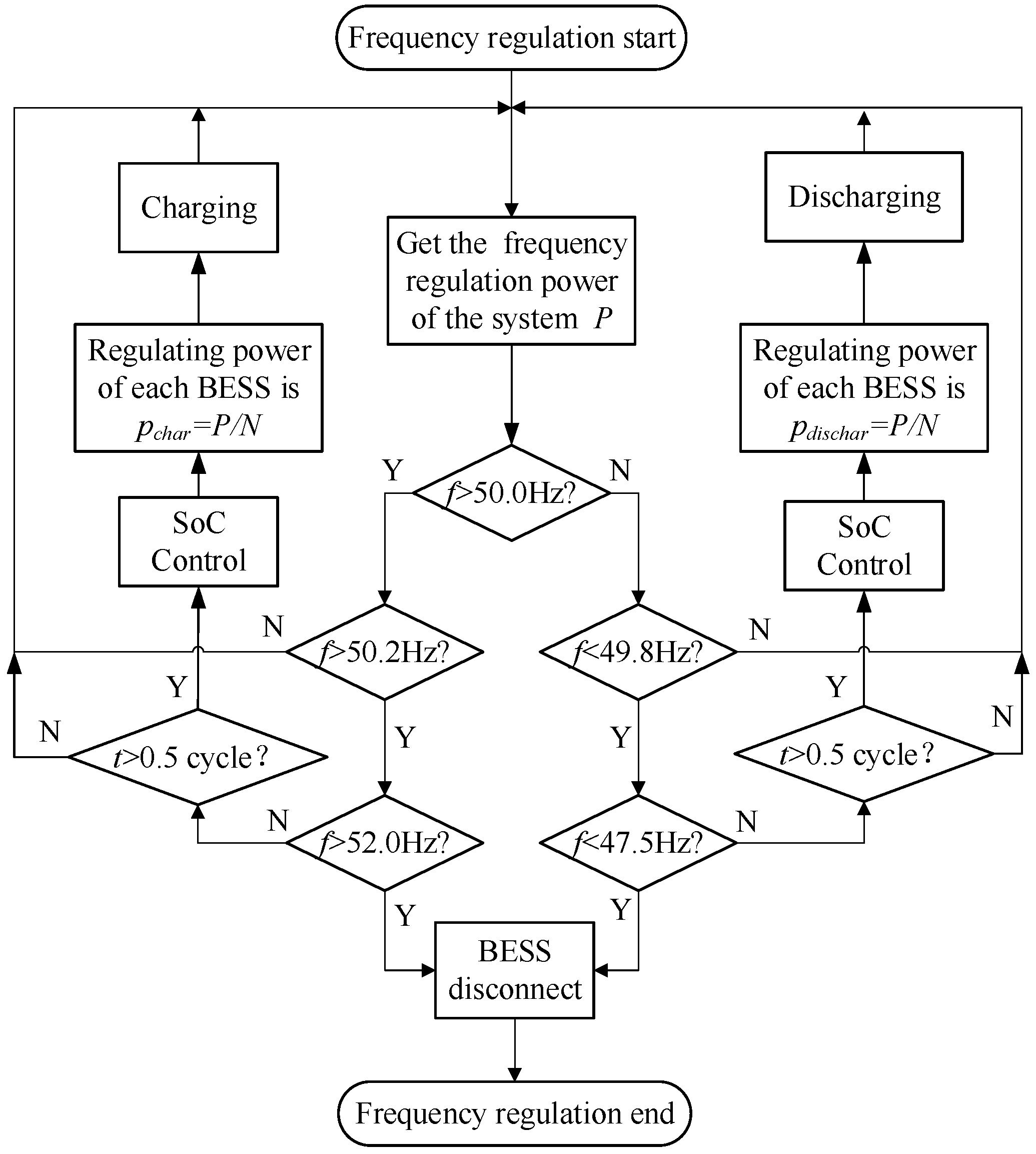
3.3. Independent Frequency Regulation Algorithm
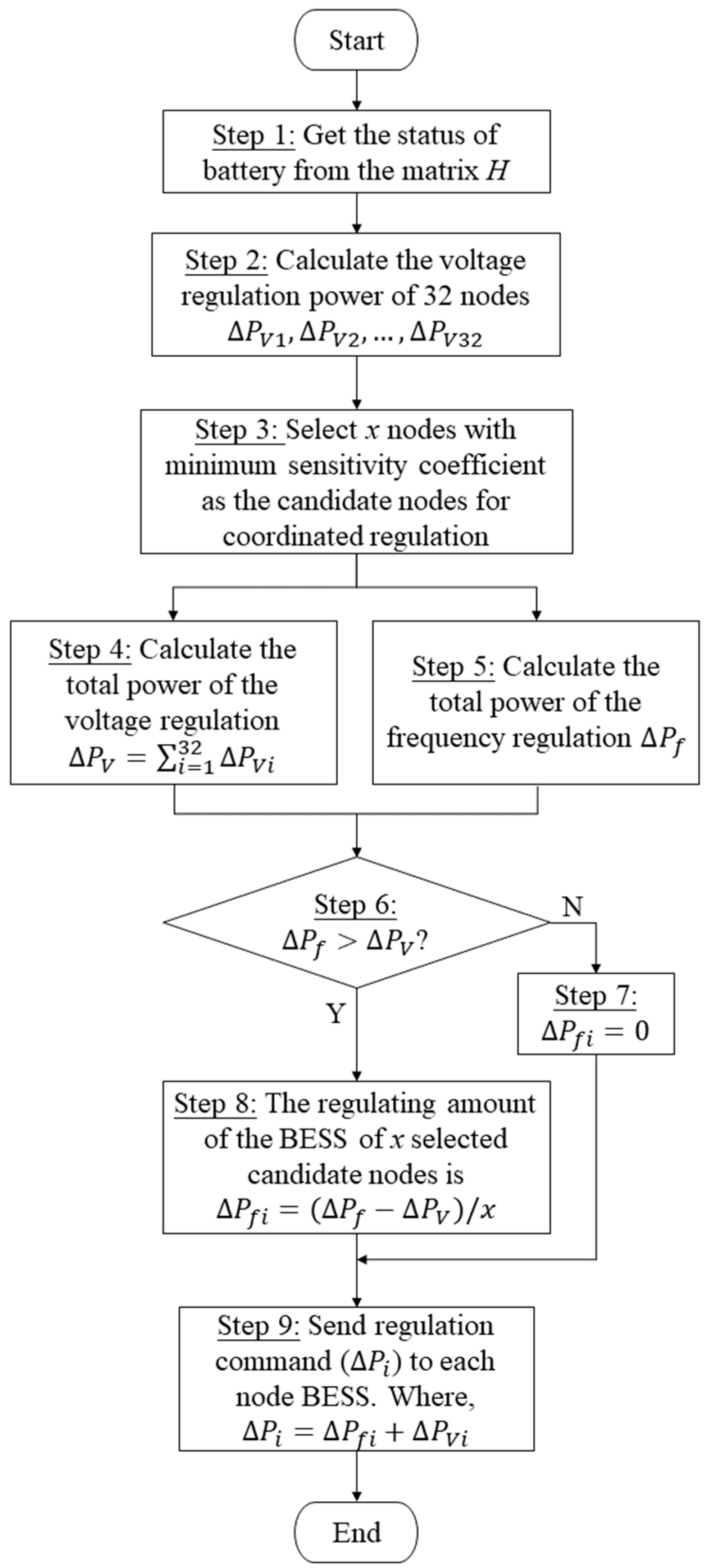
3.4. Coordinated Voltage and Freguency Regulation Algorithm
4. Test and Result Analysis
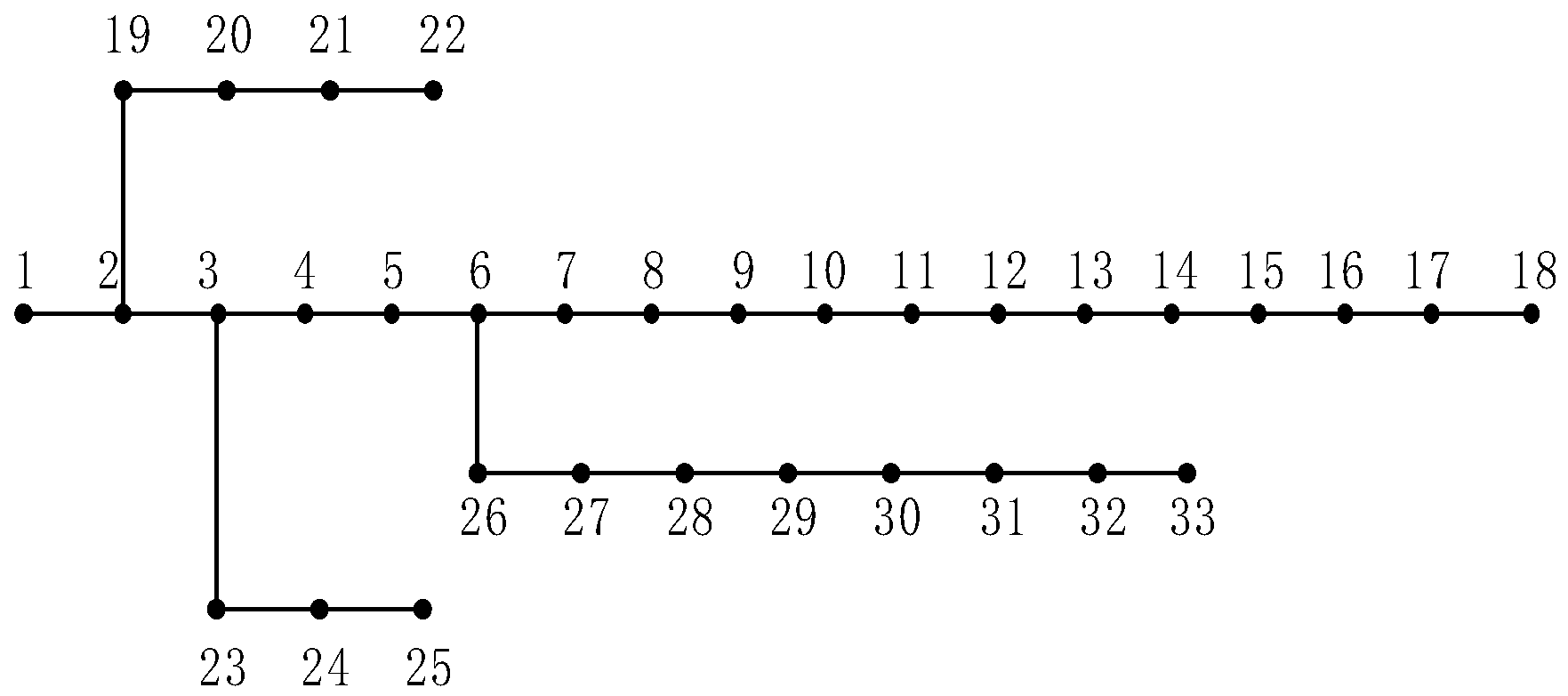
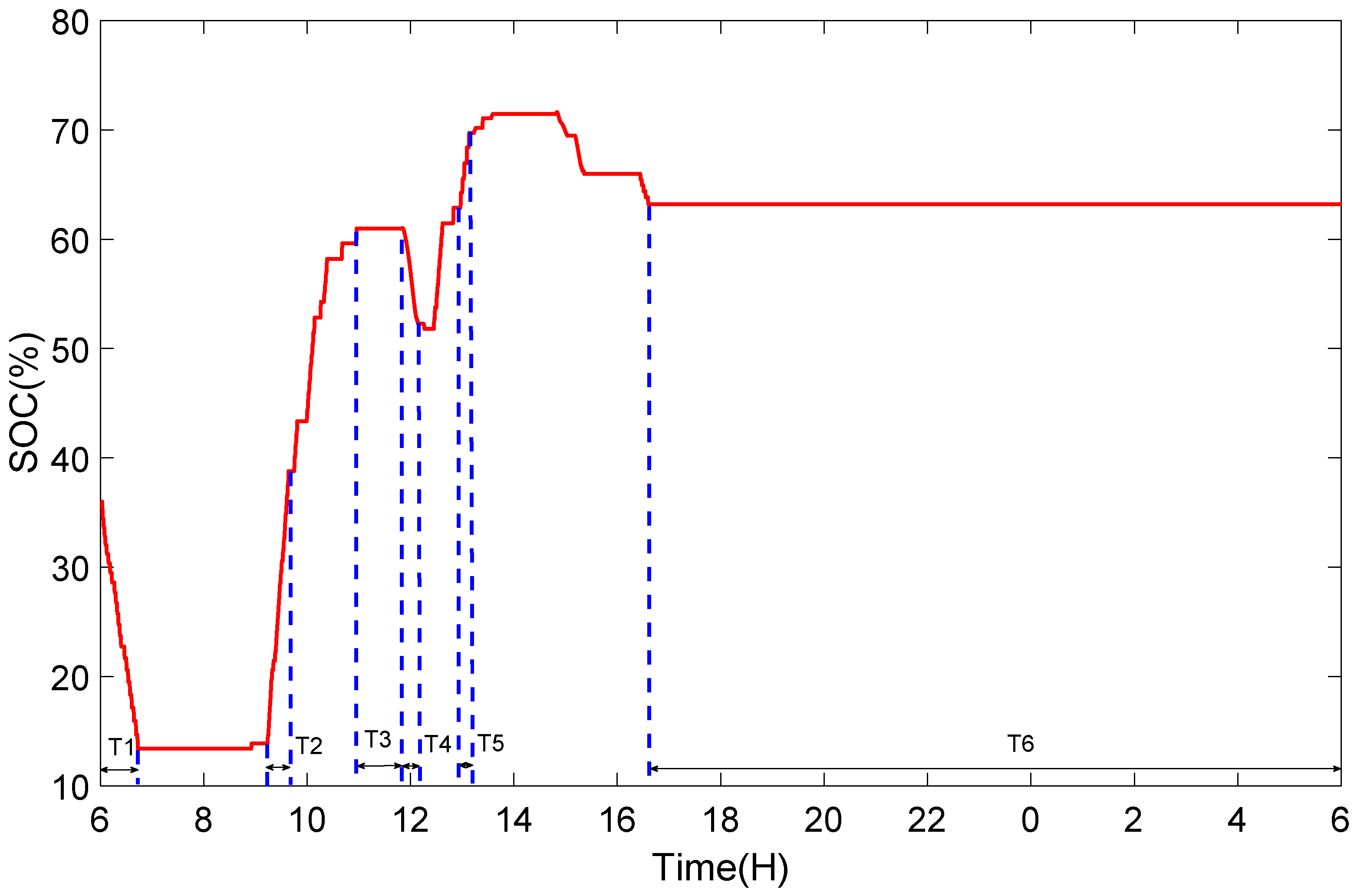
4.1. Test Model and Parameters
- (1)
- T3, T6: Standby period, voltage and frequency are in the normal range, and no regulation required.
- (2)
- T1, T4: Discharging period, BESS is discharged power
- (3)
- T2, T5: Charging period, BESS is charged power from the power system.
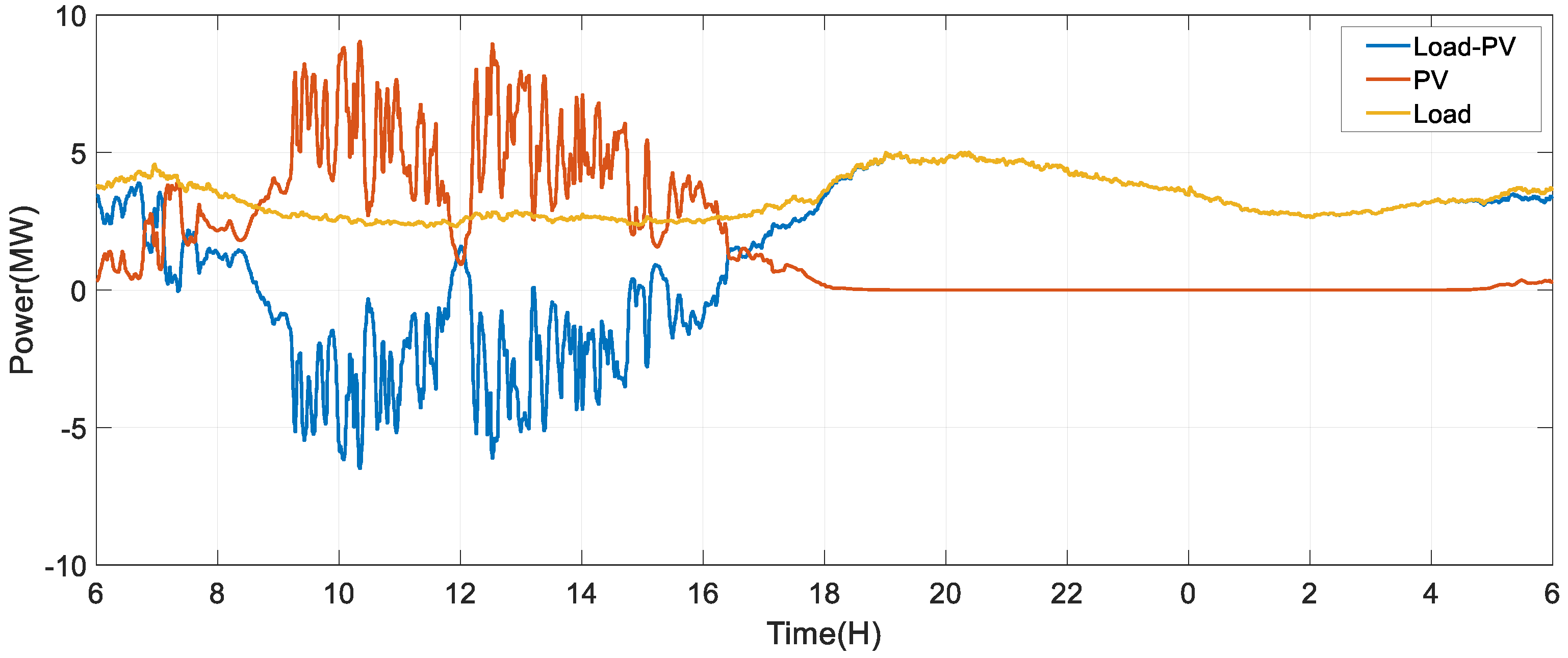
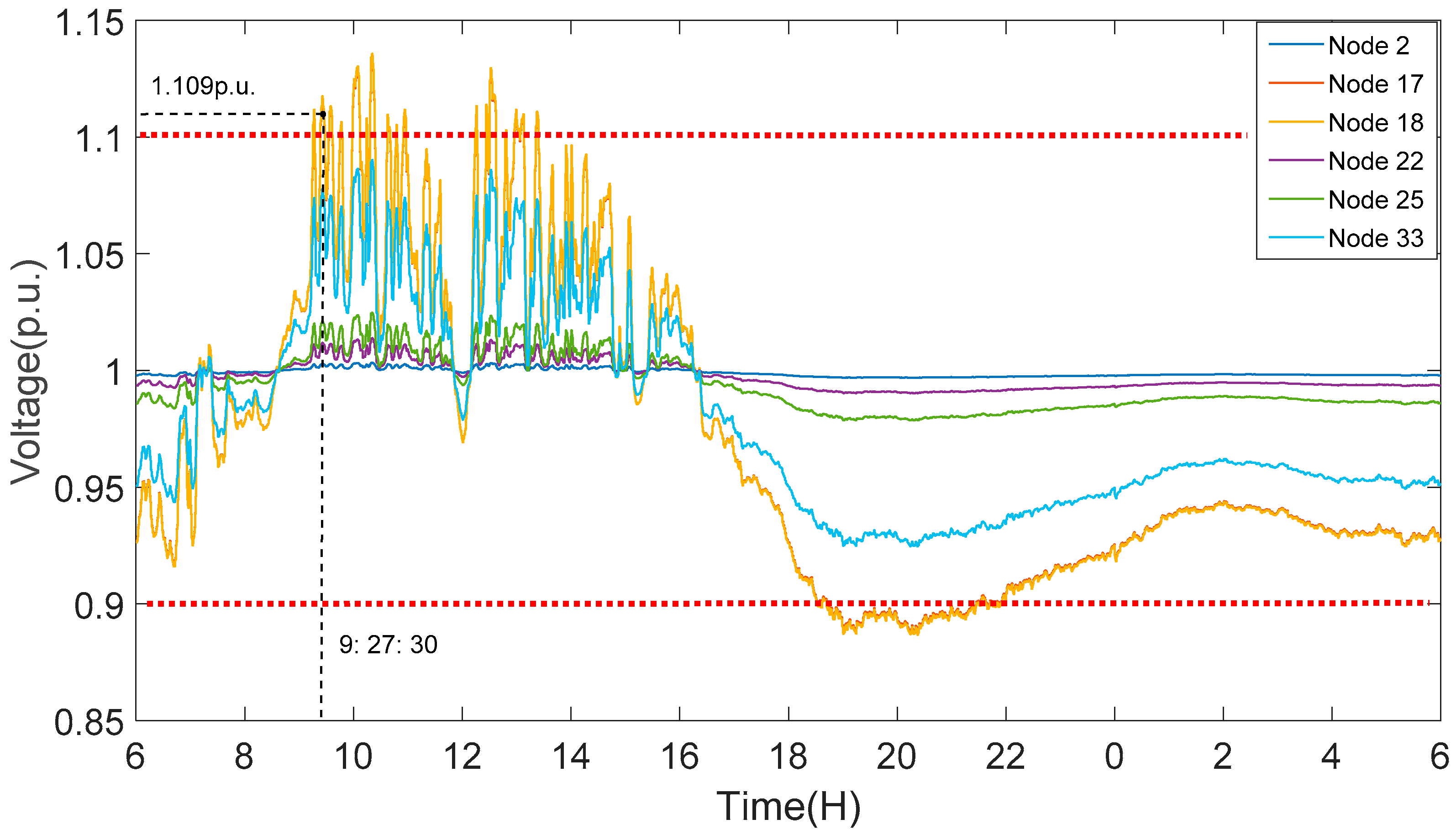
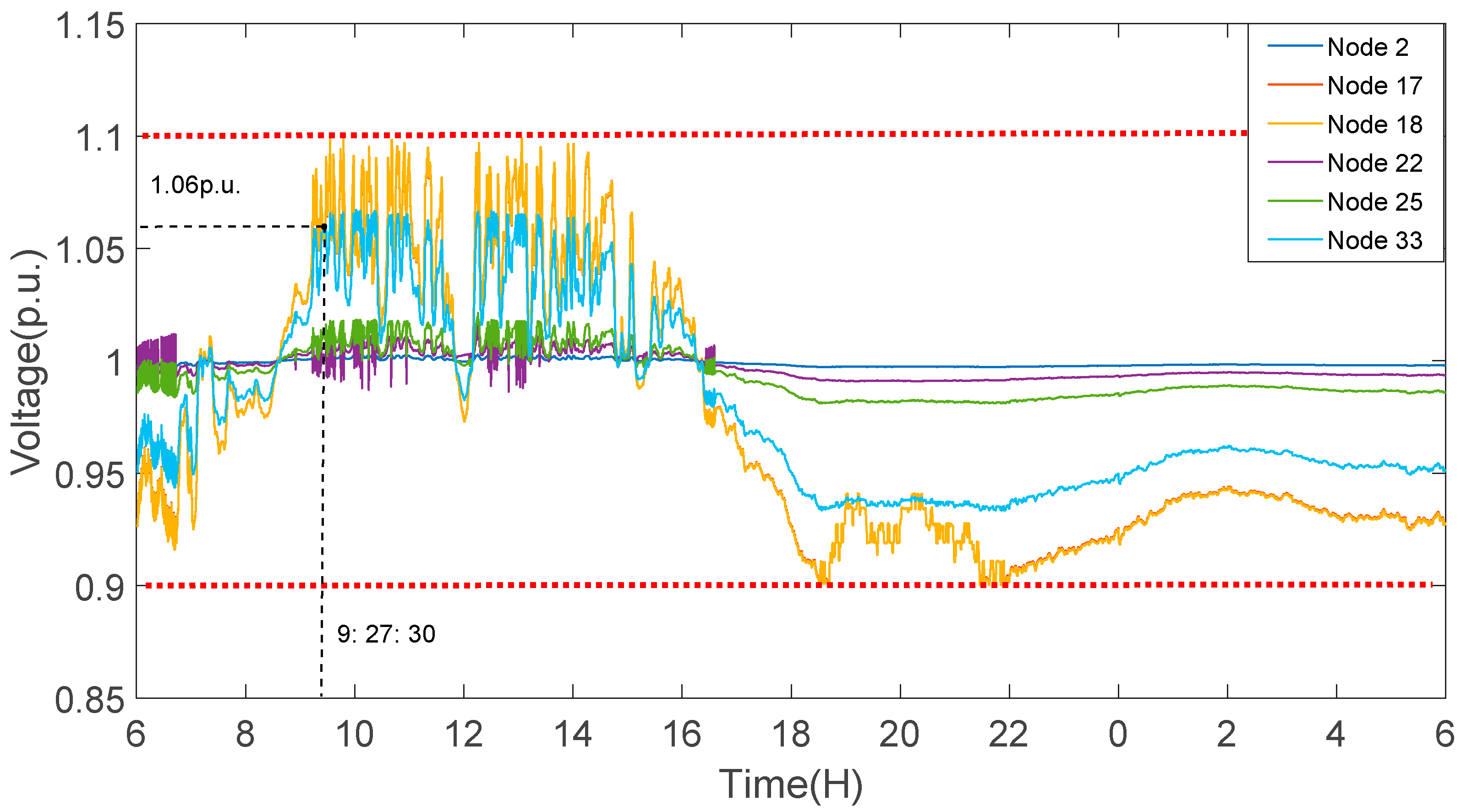
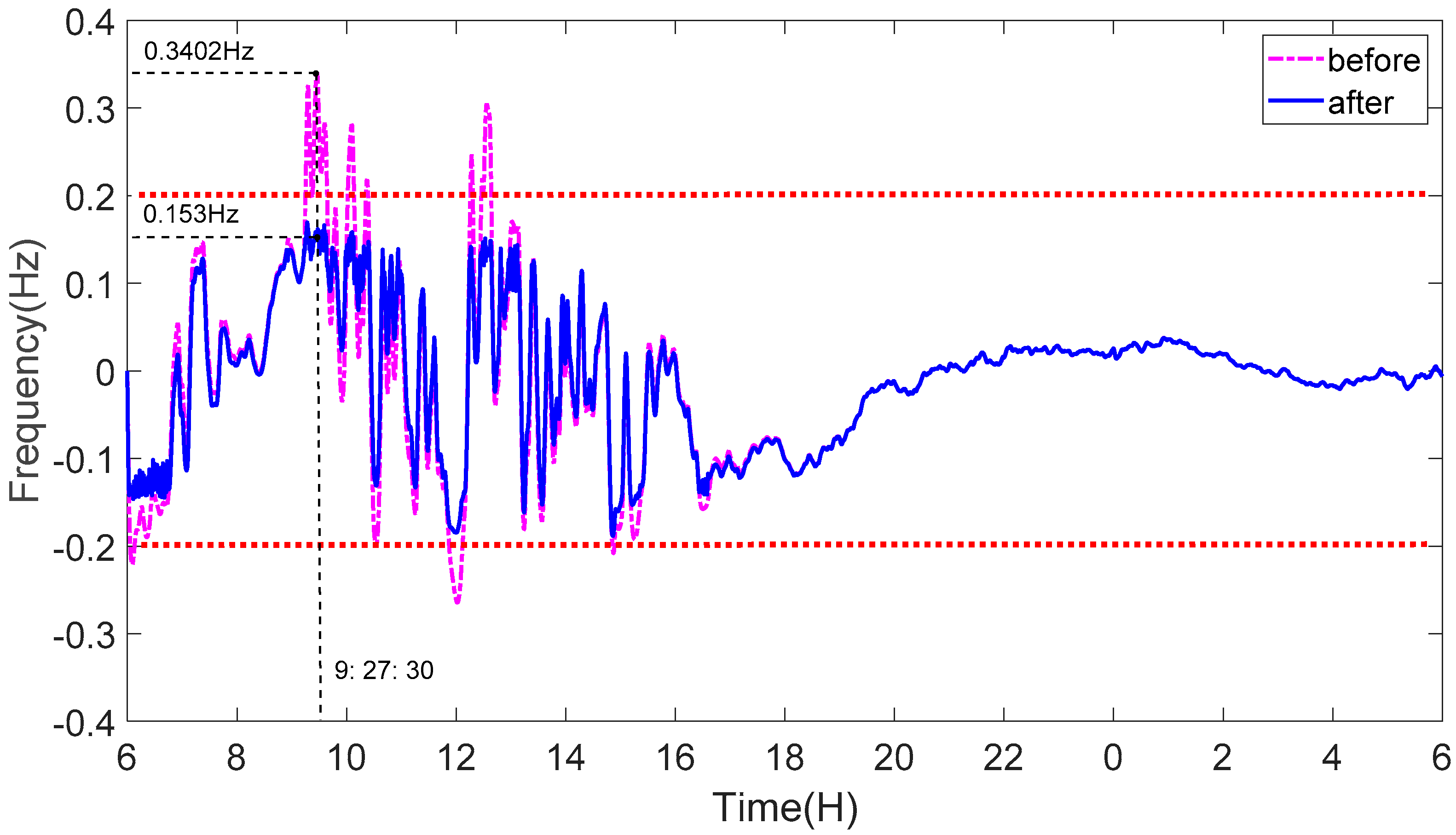
4.2. Result Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Wada, K.; Yokoyama, A. Load frequency control using distributed batteries on the demand side with communication characteristics. In Proceedings of the 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe), Berlin, Germany, 14–17 October 2012; pp. 1–8. [Google Scholar]
- Hepbasli, A. A key review on exergetic analysis and assessment of renewable energy resources for a sustainable future. Renew. Sustain. Energy Rev. 2008, 12, 593–661. [Google Scholar] [CrossRef]
- Palmer, M.D.; Uehara, T.; Shigenobu, R.; Matayoshi, H.; Senjyu, T.; Datta, M. Suppression of power system voltage and frequency fluctuations by decentralized controllable loads. J. Renew. Sustain. Energy 2016, 8, 045905. [Google Scholar] [CrossRef]
- Liu, H.; Yang, Y.; Qi, J.; Li, J.; Wei, H.; Li, P. Frequency droop control with scheduled charging of electric vehicles. IET Gener. Transm. Distrib. 2017, 11, 649–656. [Google Scholar] [CrossRef]
- Hui, H.; Ding, Y.; Zheng, M. Equivalent Modeling of Inverter Air Conditioners for Providing Frequency Regulation Service. IEEE Trans. Ind. Electron. 2018, 66, 1413–1423. [Google Scholar] [CrossRef]
- Palensky, P.; Dietmar, D. Demand side management: Demand response, intelligent energy systems, and smart loads. IEEE Trans. Ind. Informat. 2011, 7, 381–388. [Google Scholar] [CrossRef]
- Long, C.; Ochoa, L.F. Voltage control of PV-rich LV networks: OLTC-fitted transformer and capacitor banks. IEEE Trans. Power Syst. 2016, 31, 4016–4025. [Google Scholar] [CrossRef]
- Ji, H.; Wang, C.; Li, P.; Zhao, J.; Song, G.; Ding, F.; Wu, J. A centralized-based method to determine the local voltage control strategies of distributed generator operation in active distribution networks. Appl. Energy 2018, 228, 2024–2036. [Google Scholar] [CrossRef]
- Liu, C.; Ma, X.; Zhou, M.; Wu, J.; Long, C. Electrical Power and Energy Systems An event-trigger two-stage architecture for voltage control in distribution systems. Int. J. Electr. Power Energy Syst. 2018, 95, 577–584. [Google Scholar] [CrossRef]
- Li, C.; Disfani, V.R.; Pecenak, Z.K.; Mohajeryami, S.; Kleissl, J. Optimal OLTC voltage control scheme to enable high solar penetrations. Electr. Power Syst. Res. 2018, 160, 318–326. [Google Scholar] [CrossRef]
- Yu, L.; Czarkowski, D.; De León, F. Optimal distributed voltage regulation for secondary networks with DGs. IEEE Trans. Smart Grid 2012, 3, 959–967. [Google Scholar] [CrossRef]
- Bedawy, A.; Yorino, N.; Mahmoud, K. Management of voltage regulators in unbalanced distribution networks using voltage/tap sensitivity analysis. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; pp. 363–367. [Google Scholar]
- Daratha, N.; Das, B.; Sharma, J. Coordination Between OLTC and SVC for Voltage Regulation in Unbalanced Distribution System Distributed Generation. IEEE Trans. Power Syst. 2014, 29, 289–299. [Google Scholar] [CrossRef]
- Mahmud, N.; Zahedi, A.; Rahman, M.S. An event-triggered distributed coordinated voltage control strategy for large grid-tied PV system with battery energy storage. In Proceedings of the 2017 Australasian Universities Power Engineering Conference (AUPEC), Melbourne, Australia, 19–22 November 2017. [Google Scholar]
- Tina, G.M.; Garozzo, D.; Siano, P. Scheduling of PV inverter reactive power set-point and battery charge/discharge profile for voltage regulation in low voltage networks. Int. J. Electr. Power Energy Syst. 2018, 107, 131–139. [Google Scholar] [CrossRef]
- Nayeripour, M.; Fallahzadeh-Abarghouei, H.; Waffenschmidt, E.; Hasanvand, S. Coordinated online voltage management of distributed generation using network partitioning. Electr. Power Syst. Res. 2016, 141, 202–209. [Google Scholar] [CrossRef]
- Zakariazadeh, A.; Homaee, O.; Jadid, S.; Siano, P. A new approach for real time voltage control using demand response in an automated distribution system. Appl. Energy 2014, 117, 157–166. [Google Scholar] [CrossRef]
- Liu, X.; Aichhorn, A.; Liu, L.; Li, H. Coordinated control of distributed energy storage system with tap changer transformers for voltage rise mitigation under high photovoltaic penetration. IEEE Trans. Smart Grid 2012, 3, 897–906. [Google Scholar] [CrossRef]
- Akhil, A.A.; Huff, G.; Currier, A.B.; Kaun, B.C.; Rastler, D.M.; Chen, S.B.; Cotter, A.L.; Bradshaw, D.T.; Gauntlett, W.D. DOE/EPRI 2013 Electricity Storage Handbook in Collaboration with NRECA; Sandia National Laboratories: Albuquerque, NM, USA, 2013.
- Mercier, P.; Cherkaoui, R.; Oudalov, A. Optimizing a Battery Energy Storage System for Frequency Control Application in an Isolated Power System. IEEE Trans. Power Syst. 2009, 24, 1469–1477. [Google Scholar] [CrossRef]
- Oudalov, A.; Chartouni, D.; Ohler, C. Optimizing a Battery Energy Storage System for Primary Frequency Control. IEEE Trans. Power Syst. 2007, 22, 1259–1266. [Google Scholar] [CrossRef]
- Singh, B.; Hussain, A. Application of Battery Energy Storage System (BESS) in Voltage Control and Damping of Power Oscillations. In Proceedings of the 2010 5th International Conference on Industrial and Information Systems, Mangalore, India, 29 July–1 August 2010; 514–519; pp. 514–519. [Google Scholar]
- Serban, I.; Teodorescu, R.; Marinescu, C. Energy storage systems impact on the short-term frequency stability of distributed autonomous microgrids, an analysis using aggregate models. IET Renew. Power Gener. 2013, 7, 531–539. [Google Scholar] [CrossRef]
- Papic, I. Simulation Model for Discharging a Lead-Acid Battery Energy Storage System for Load Leveling. IEEE Trans. Energy Convers. 2006, 21, 608–615. [Google Scholar] [CrossRef]
- Wang, Q.; Choi, S.S. The Design of Battery Energy Storage System in a Unified Power-Flow Control Scheme. IEEE Trans. Power Deliv. 2008, 23, 1015–1024. [Google Scholar] [CrossRef]
- Wei, Z.; Moon, B.Y.; Joo, Y.H. Smooth Wind Power Fluctuation Based on Battery Energy Storage S ystem for Wind Farm. J. Electr. Eng. Technol. 2014, 9, 2134–2141. [Google Scholar] [CrossRef]
- Li, X.; Hui, D.; Lai, X. Battery Energy Storage Station (BESS)-Based Smoothing Control of Photovoltaic (PV) and Wind Power Generation Fluctuations. IEEE Trans. Sustain. Energy 2013, 4, 464–473. [Google Scholar] [CrossRef]
- Serban, I.; Marinescu, C. Control Strategy of Three-Phase Battery Energy Storage Systems for Frequency Support in Microgrids and with Uninterrupted Supply of Local Loads. IEEE Trans. Power Electron. 2014, 29, 5010–5020. [Google Scholar] [CrossRef]
- Lee, S.-J.; Kim, J.-H.; Kim, C.-H.; Kim, S.-K.; Kim, E.-S.; Kim, D.-U.; Mehmood, K.K.; Khan, S.U. Coordinated Control Algorithm for Distributed Battery Energy Storage Systems for Mitigating Voltage and Frequency Deviations. IEEE Trans. Smart Grid 2016, 7, 1713–1722. [Google Scholar] [CrossRef]
- Rebours, Y.G.; Kirschen, D.S.; Trotignon, M.; Rossignol, S. A Survey of Frequency and Voltage Control Ancillary Services—Part I: Technical Features. IEEE Trans. Power Syst. 2007, 22, 350–357. [Google Scholar] [CrossRef]
- Gordijn, J.; Akkermans, H. Designing and Evaluating E-Business Models. IEEE Intell. Syst. 2001, 16, 11–17. [Google Scholar] [CrossRef]
- Teng, F.; Strbac, G. Business cases for energy storage with multiple service provision. J. Mod. Power Syst. Clean Energy 2016, 4, 615–625. [Google Scholar] [CrossRef]
- Siano, P.; Sarno, D. Assessing the benefits of residential demand response in a real time distribution energy market. Appl. Energy 2016, 161, 533–551. [Google Scholar] [CrossRef]
- Sidhu, A.S.; Pollitt, M.G.; Anaya, K.L. A social cost benefit analysis of grid-scale electrical energy storage projects: A case study. Appl. Energy 2018, 212, 881–894. [Google Scholar] [CrossRef]
- Rebours, Y.G.; Kirschen, D.S.; Trotignon, M.; Rossignol, S. A survey of frequency and voltage control ancillary services—part II: Economic features. IEEE Trans. Power Syst. 2007, 22, 358–366. [Google Scholar] [CrossRef]
- Arcuri, B.; Spataru, C.; Barrett, M. Evaluation of ice thermal energy storage (ITES) for commercial buildings in cities in Brazil. Sustain. Cities Soc. 2017, 29, 178–192. [Google Scholar] [CrossRef]
- Smith, J.G.; Hensley, G.; Ray, L. IEEE Recommended Practice for Monitoring Electric Power Quality. IEEE Std. 1995, 1159–1995. [Google Scholar]
- Demirok, E.; Gonz, P.C.; Frederiksen, K.H.B.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local Reactive Power Control Methods for Overvoltage Prevention of Distributed Solar Inverters in Low-Voltage Grids. IEEE J. Photovoltaics 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Wang, S.; Chen, S.; Ge, L.; Wu, L. Distributed Generation Hosting Capacity Evaluation for Distribution Systems Considering the Robust Optimal Operation of OLTC and SVC. IEEE Trans. Sustain. Energy 2016, 7, 1111–1123. [Google Scholar] [CrossRef]
- Xie, Q.; Hara, R.; Kita, H.; Tanaka, E. Coordinated control of OLTC and multi-CEMSs for overvoltage prevention in power distribution system. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 692–701. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, Y.; Shentu, X.; Xie, Q.; Ding, Y. Voltage/Frequency Deviations Control via Distributed Battery Energy Storage System Considering State of Charge. Appl. Sci. 2019, 9, 1148. https://doi.org/10.3390/app9061148
Hua Y, Shentu X, Xie Q, Ding Y. Voltage/Frequency Deviations Control via Distributed Battery Energy Storage System Considering State of Charge. Applied Sciences. 2019; 9(6):1148. https://doi.org/10.3390/app9061148
Chicago/Turabian StyleHua, Yongzhu, Xiangrong Shentu, Qiangqiang Xie, and Yi Ding. 2019. "Voltage/Frequency Deviations Control via Distributed Battery Energy Storage System Considering State of Charge" Applied Sciences 9, no. 6: 1148. https://doi.org/10.3390/app9061148
APA StyleHua, Y., Shentu, X., Xie, Q., & Ding, Y. (2019). Voltage/Frequency Deviations Control via Distributed Battery Energy Storage System Considering State of Charge. Applied Sciences, 9(6), 1148. https://doi.org/10.3390/app9061148





