Characteristics of Partially Coherent Circular Flattened Gaussian Vortex Beams in Turbulent Biological Tissues
Abstract
:1. Introduction
2. Partially Coherent Circular Flattened Gaussian Vortex Beams Propagating in a Turbulent Biological Tissue
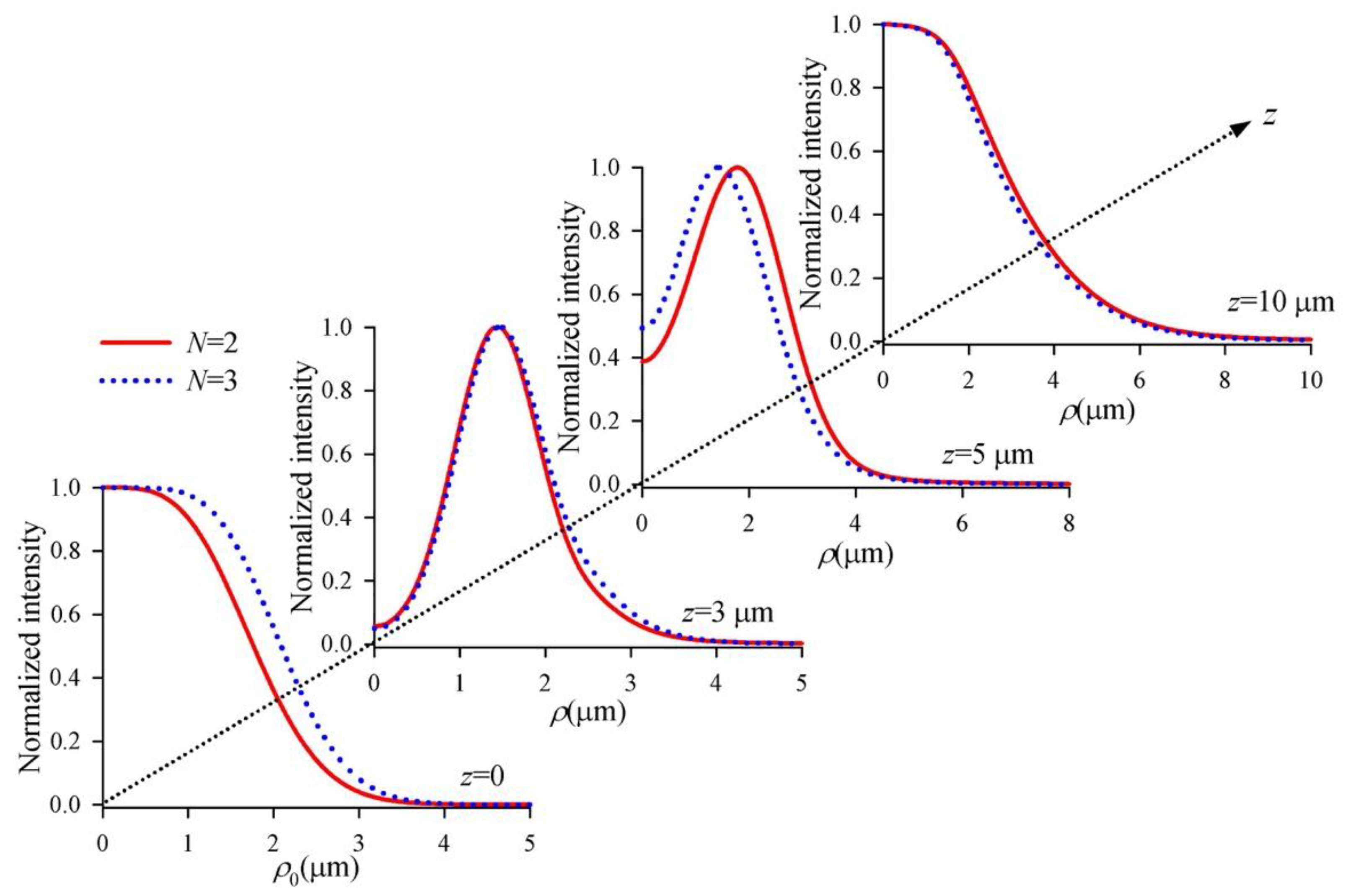
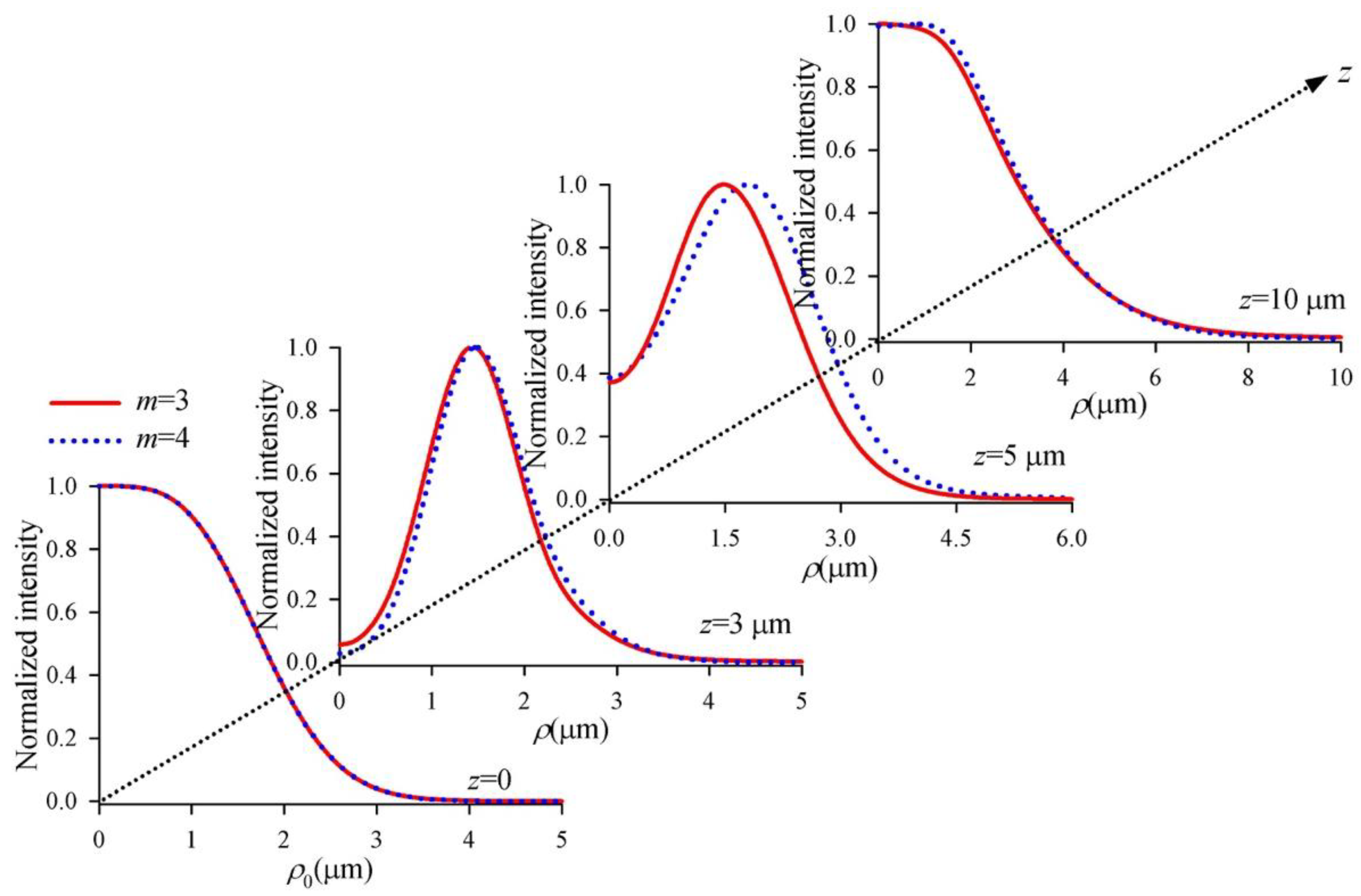
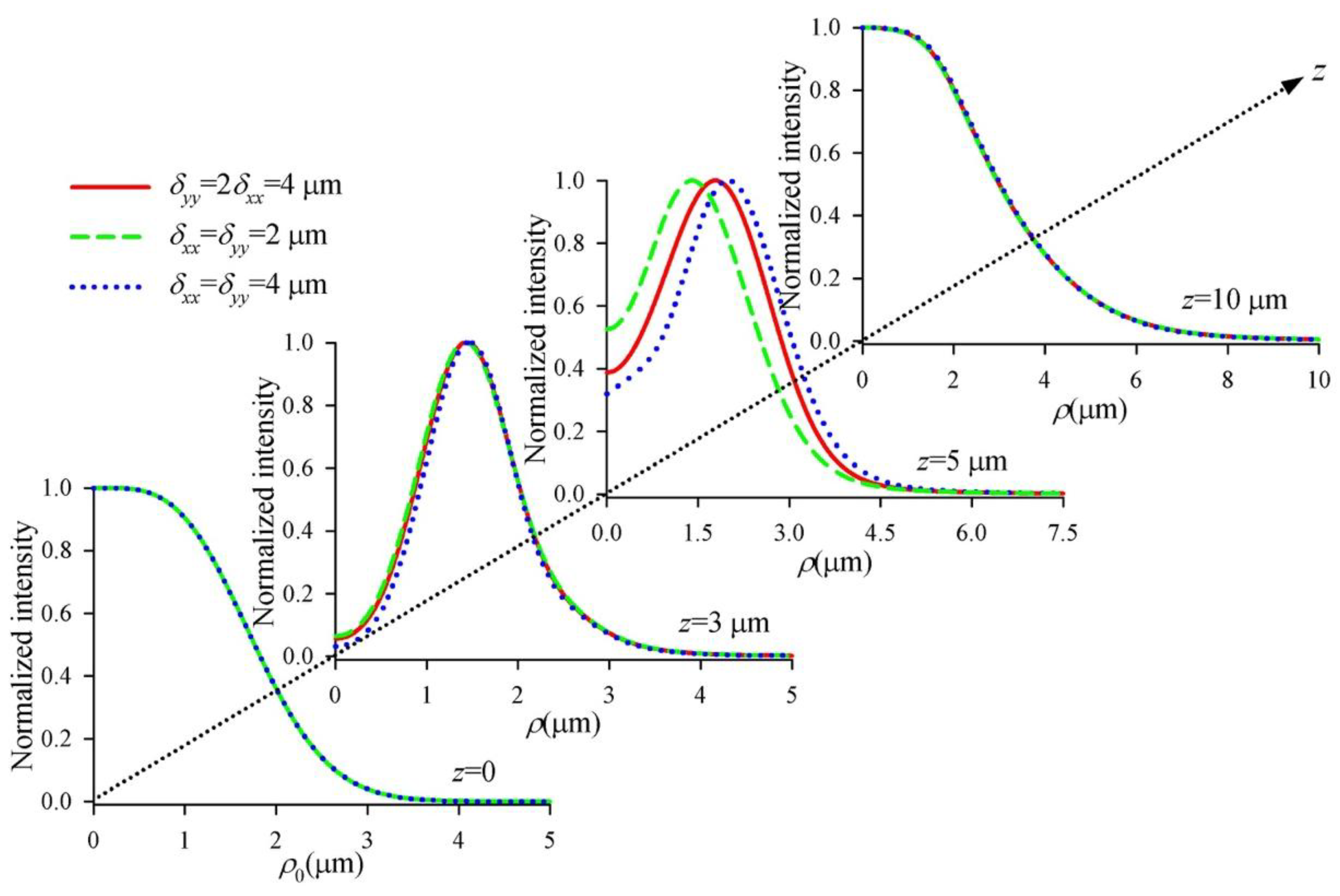
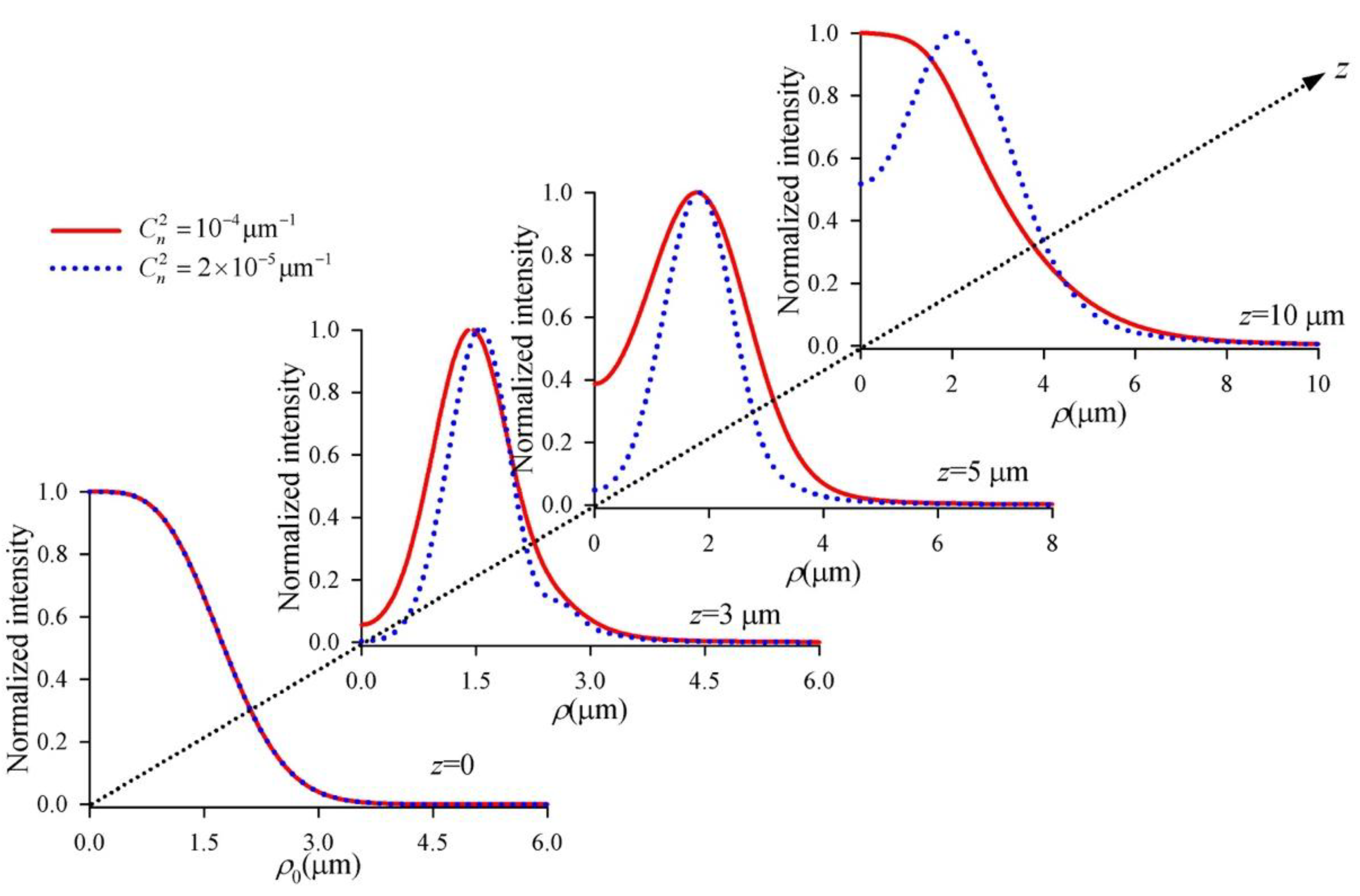
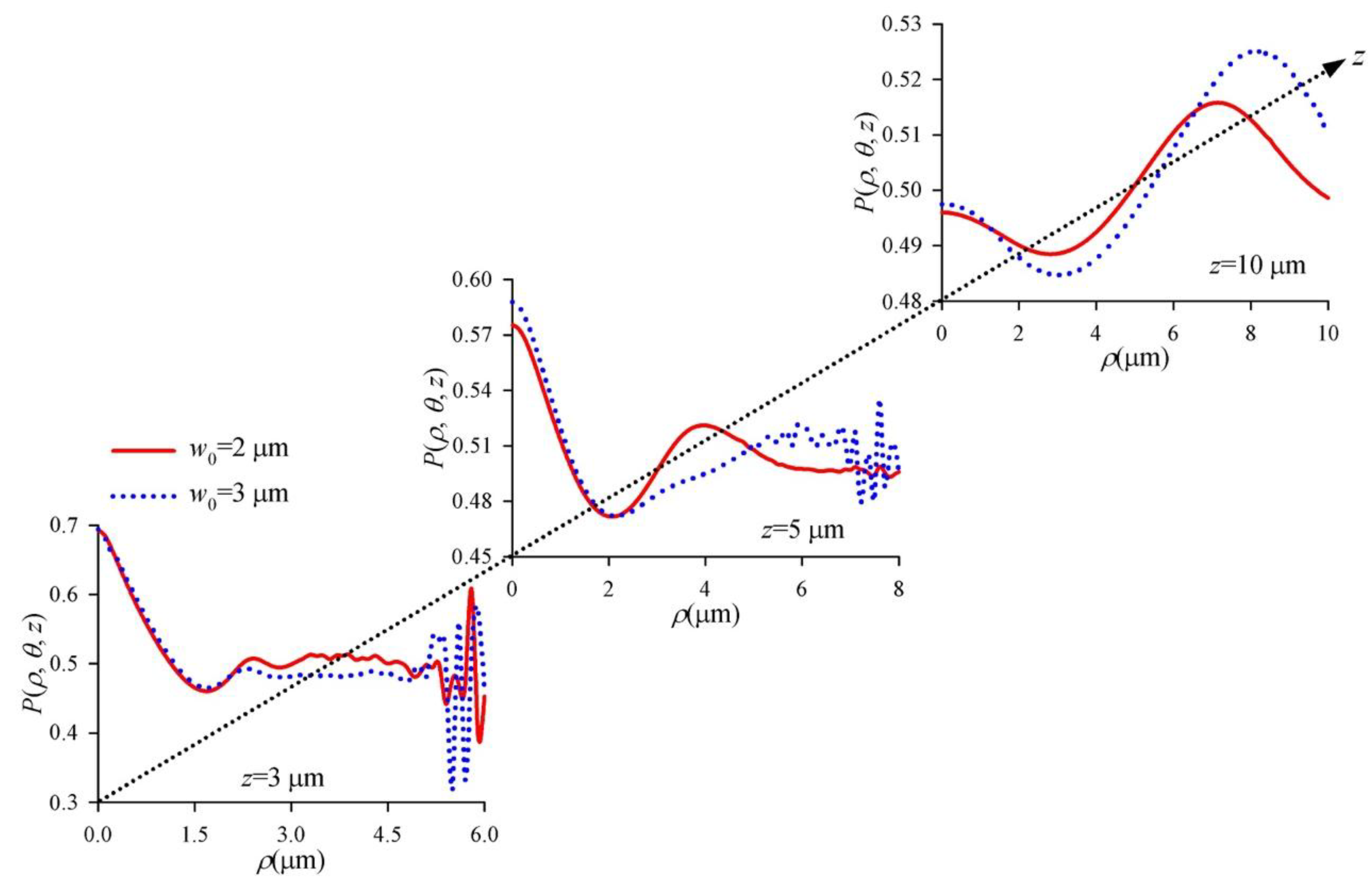
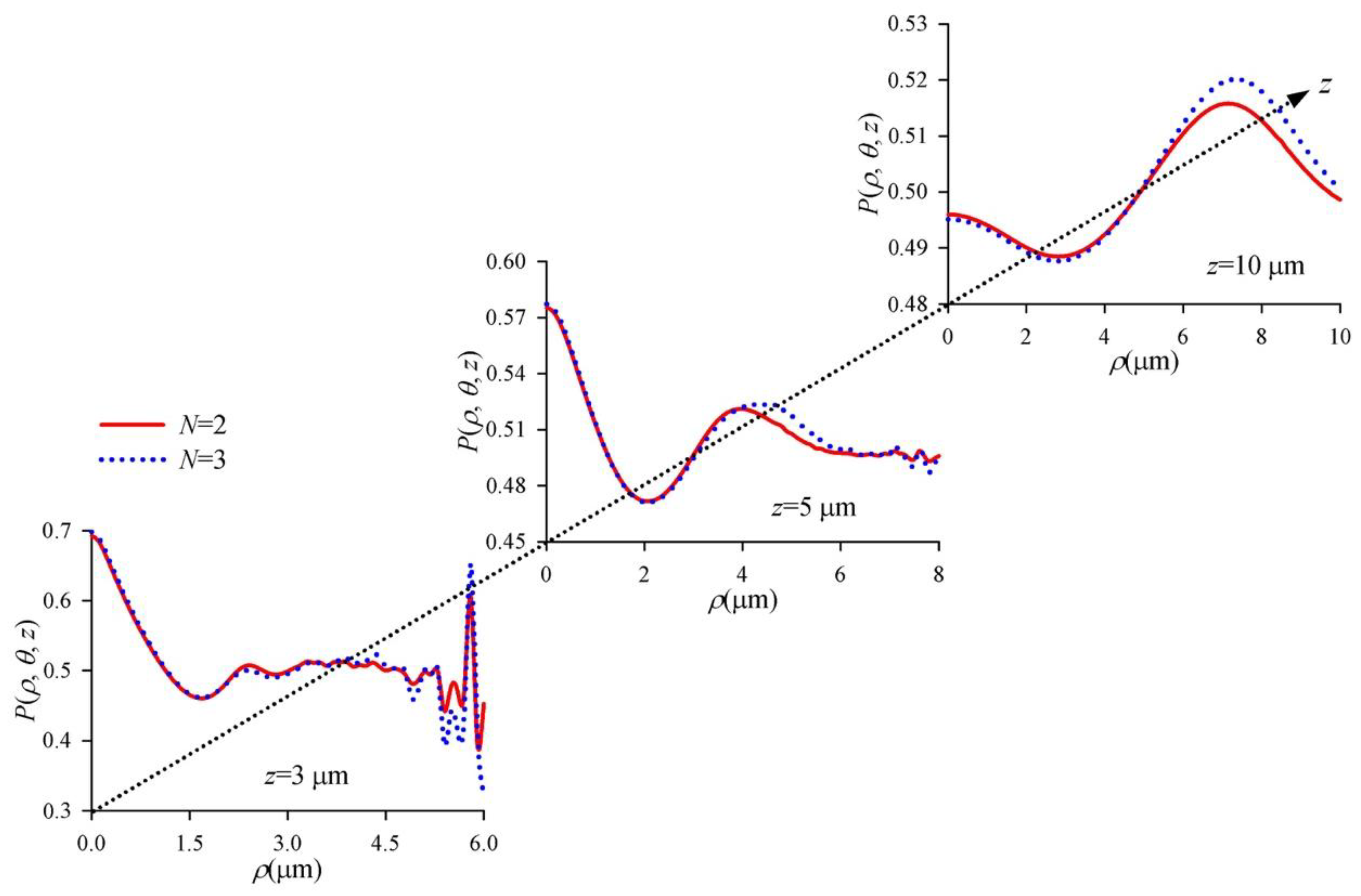
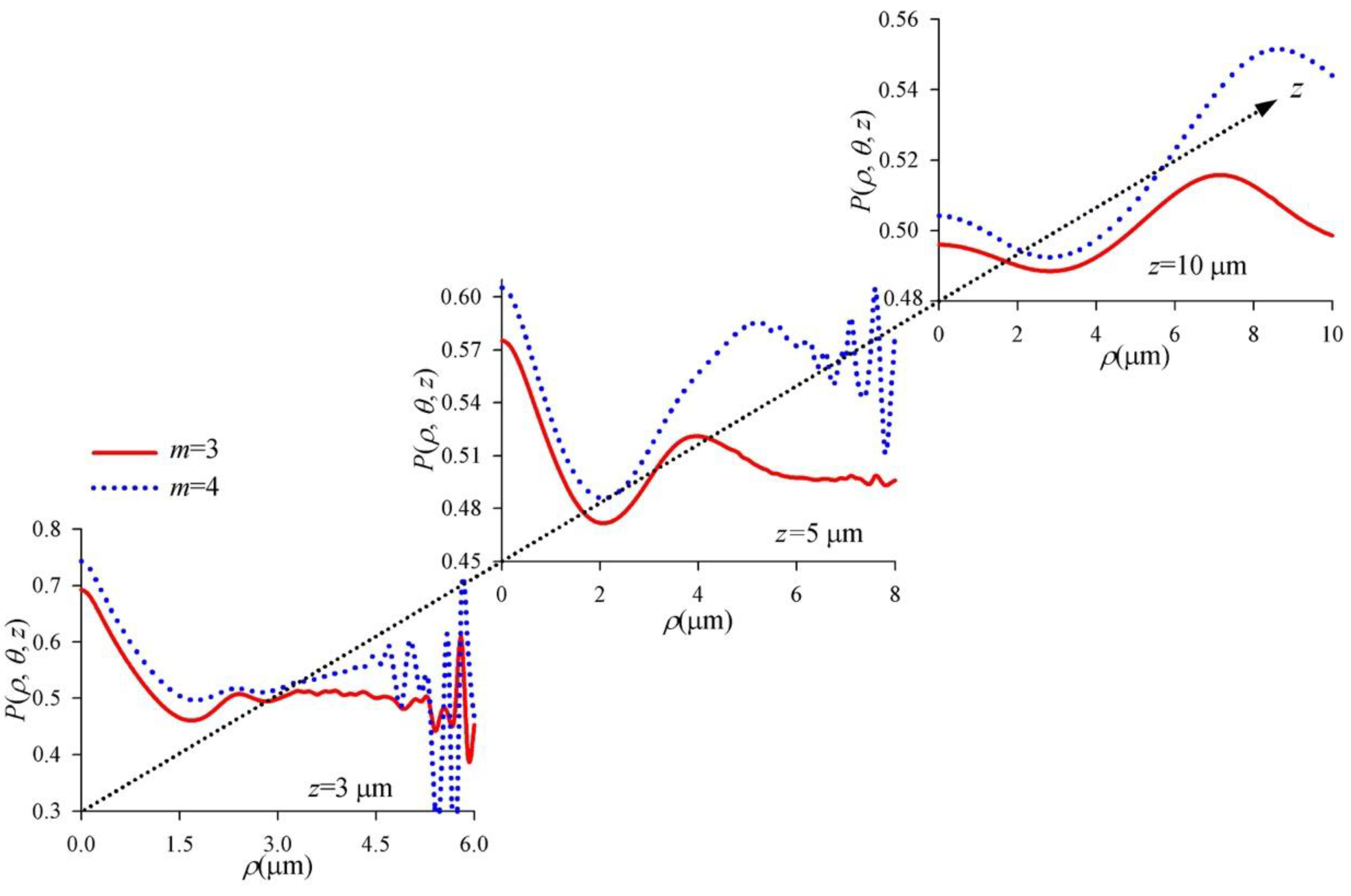
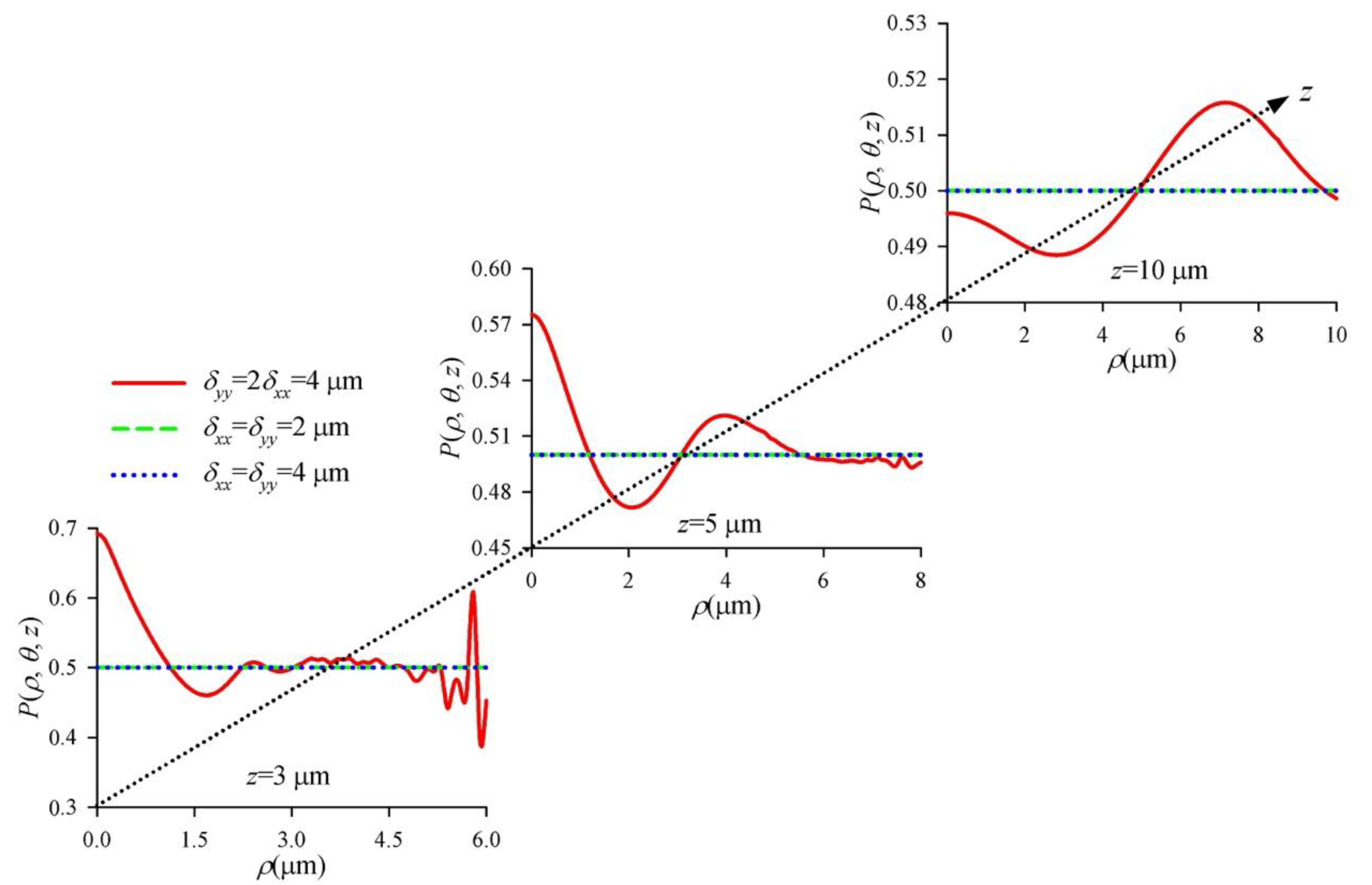
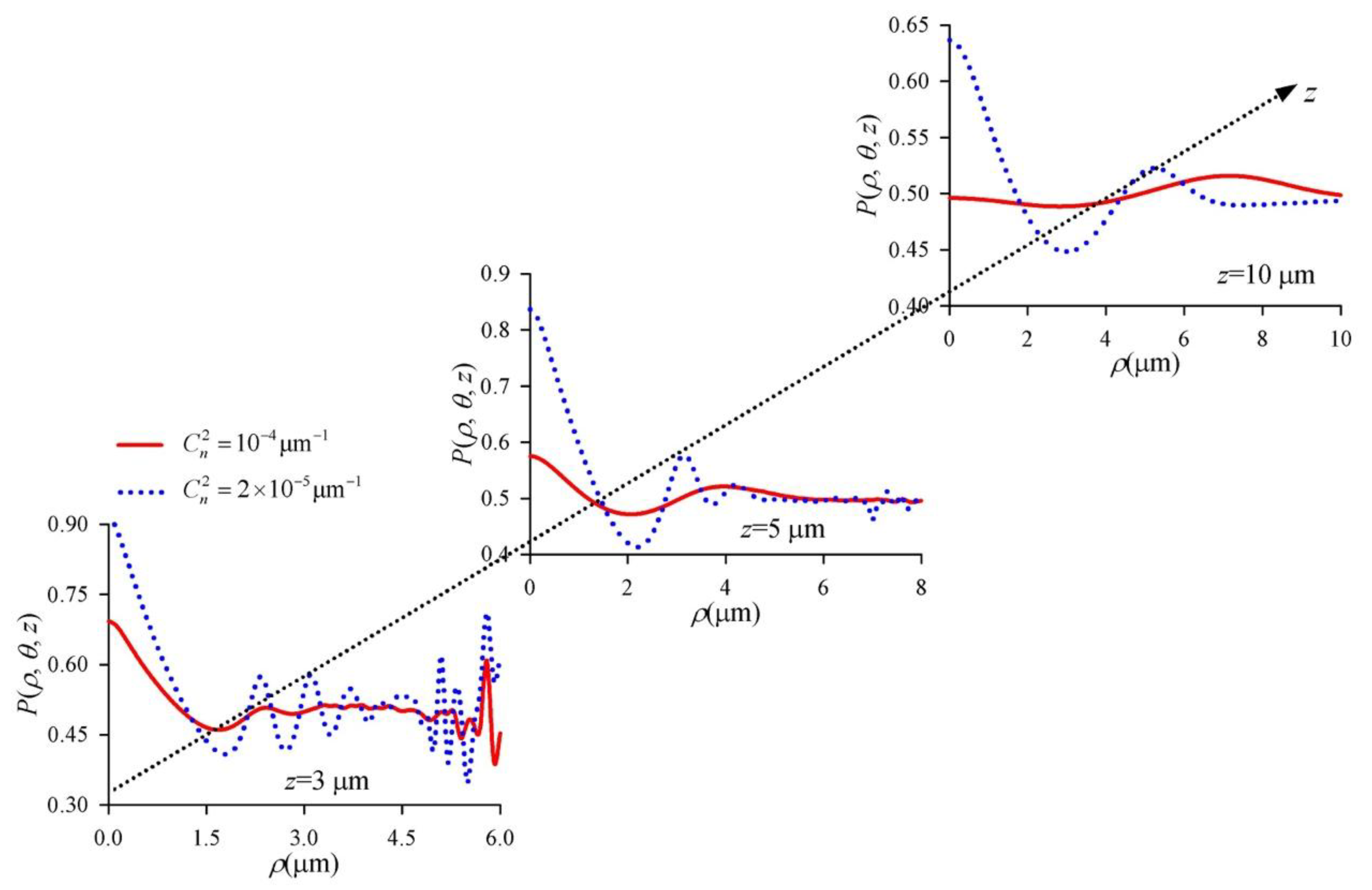
3. Numerical Simulation and Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Amarande, S.A. Beam propagation factor and the kurtosis parameter of flattened Gaussian beams. Opt. Commun. 1996, 129, 311–317. [Google Scholar] [CrossRef]
- Bagini, V.; Borghi, R.; Gori, F.; Pacileo, A.M.; Santarsiero, M.; Ambrosini, D.; Spagnolo, G.S. Propagation of axially symmetric flattened Gaussian beams. J. Opt. Soc. Am. A 1996, 13, 1385–1394. [Google Scholar] [CrossRef]
- Borghi, R.; Santarsiero, M.; Vicalvi, S. Focal shift of focused flat-topped beams. Opt. Commun. 1998, 154, 243–248. [Google Scholar] [CrossRef]
- Cai, Y.; Lin, Q. Properties of a flattened Gaussian beam in the fractional Fourier transform plane. J. Opt. A Pure Appl. Opt. 2003, 5, 272–275. [Google Scholar] [CrossRef]
- Mao, H.; Zhao, D.; Jing, F.; Liu, H.; Wei, X. Propagation characteristics of the kurtosis parameters of flat-topped beams passing through fractional Fourier transformation systems with a spherically aberrated lens. J. Opt. A Pure Appl. Opt. 2004, 6, 640–650. [Google Scholar] [CrossRef]
- Zhu, S.; Li, Z. Theoretical and experimental studies of the spectral changes of a focused polychromatic partially coherent flat-topped beam. Appl. Phys. B 2015, 118, 481–487. [Google Scholar] [CrossRef]
- Huang, Z.; Lin, H.; Wang, J.; Li, M.; Xu, D.; Zhang, R.; We, X. Laser coupling of the numerous flattened Gaussian beams in the fiber-based ICF laser driver. Fusion Eng. Des. 2013, 88, 65–69. [Google Scholar] [CrossRef]
- Lü, B.; Luo, S.; Zhang, B. Propagation of flattened Gaussian beams with rectangular symmetry passing through a paraxial optical ABCD system. Opt. Commun. 1999, 164, 1–6. [Google Scholar] [CrossRef]
- Ibnchaikh, M.; Belafhal, A. Closed-term propagation expression of flattened Gaussian beams through an apertured ABCD optical system. Opt. Commun. 2001, 193, 73–79. [Google Scholar] [CrossRef]
- Ji, X.; Lü, B. Propagation of a flattened Gaussian beam through multi-apertured optical ABCD systems. Optik 2003, 114, 394–400. [Google Scholar] [CrossRef]
- Zhou, N.; Zeng, G.; Hu, L. Algorithms for flattened Gaussian beams passing through apertured and unapertured paraxial ABCD optical systems. Opt. Commun. 2004, 240, 299–306. [Google Scholar] [CrossRef]
- Jiang, H.; Zhao, D.; Mei, Z. Propagation characteristics of the rectangular flattened Gaussian beams through circular apertured and misaligned optical systems. Opt. Commun. 2006, 260, 1–7. [Google Scholar] [CrossRef]
- Hu, L.; Cai, Y. Analytical formula for a circular flattened Gaussian beam propagating through a misaligned paraxial ABCD optical system. Phys. Lett. A 2006, 360, 394–399. [Google Scholar] [CrossRef]
- Lu, X.; Cai, Y. Analytical formulas for a circular or non-circular flat-topped beam propagating through an apertured paraxial optical system. Opt. Commun. 2007, 269, 39–46. [Google Scholar] [CrossRef]
- Cai, Y. Propagation of various flat-topped beams in a turbulent atmosphere. J. Opt. A Pure Appl. Opt. 2006, 8, 537–545. [Google Scholar] [CrossRef]
- Eyyubŏglu, H.T.; Arpali, C.; Baykal, Y. Flat topped beams and their characteristics in turbulent media. Opt. Express 2006, 14, 4196–4207. [Google Scholar] [CrossRef] [PubMed]
- Baykal, Y.; Eyyubŏglu, H.T. Scintillation index of flat-topped Gaussian beams. Appl. Opt. 2006, 45, 3793–3797. [Google Scholar] [CrossRef] [PubMed]
- Baykal, Y.; Eyyubŏglu, H.T. Scintillations of incoherent flat-topped Gaussian source field in turbulence. Appl. Opt. 2007, 46, 5044–5050. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y. Scintillation properties of non-circular flat-topped beams. J. Opt. A Pure Appl. Opt. 2008, 10, 075003. [Google Scholar] [CrossRef]
- Alavinejad, M.; Ghafary, B.; Kashani, F.D. Analysis of the propagation of flat-topped beam with various beam orders through turbulent atmosphere. Opt. Laser Eng. 2008, 46, 1–5. [Google Scholar] [CrossRef]
- Zeng, Z.; Luo, X.; Xia, A.; Zhang, Y.; Cao, B. Inner scale effect on scintillation index of flat-topped beam in non-Kolmogorov weak turbulence. Appl. Opt. 2015, 54, 2630–2638. [Google Scholar] [CrossRef] [PubMed]
- Ata, Y.; Baykal, Y. Flat-topped beam transmittance in anisotropic non-Kolmogorov turbulent marine atmosphere. Opt. Eng. 2017, 56, 104107. [Google Scholar] [CrossRef]
- Golmohammady, S.; Ghafary, B. Stokes parameters of phase-locked partially coherent flat-topped array laser beams propagating through turbulent atmosphere. Laser Phys. 2016, 26, 066201. [Google Scholar] [CrossRef]
- Yousefi, M.; Kashani, F.D.; Mashal, A. Analyzing the average intensity distribution and beam width evolution of phase-locked partially coherent radial flat-topped array laser beams in oceanic turbulence. Laser Phys. 2017, 27, 026202. [Google Scholar] [CrossRef]
- Wang, F.; Cai, Y. Experimental generation of a partially coherent flat-topped beam. Opt. Lett. 2008, 33, 1795–1797. [Google Scholar] [CrossRef] [PubMed]
- Hendriks, A.; Naidoo, D.; Roux, F.S.; López-Mariscal, C.; Forbes, A. The generation of flat-top beams by complex amplitude modulation with a phase-only spatial light modulator. Proc. SPIE 2012, 8490, 849006. [Google Scholar]
- Ojeda-Castañeda, J.; Saavedra, G.; Lopez-Olazagasti, E. Supergaussian beams of continuous order as GRIN modes. Opt. Commun. 1993, 102, 21–24. [Google Scholar] [CrossRef]
- Gori, F. Flattened Gaussian beams. Opt. Commun. 1994, 107, 335–341. [Google Scholar] [CrossRef]
- Cai, Y.; Lin, Q. Light beams with elliptical flat-topped profiles. J. Opt. A Pure Appl. Opt. 2004, 6, 390–395. [Google Scholar]
- Borghi, R. Uniform approximation of paraxial flat-topped beams. J. Opt. Soc. Am. A 2015, 30, 1099–1106. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. Light beams with flat-topped profiles. Opt. Lett. 2002, 27, 1007–1009. [Google Scholar] [CrossRef] [PubMed]
- Li, Y. New expressions for flat-topped light beams. Opt. Commun. 2002, 206, 225–234. [Google Scholar] [CrossRef]
- Chu, X.; Ni, Y.; Zhou, G. Propagation analysis of flattened circular Gaussian beams with a circular aperture in turbulent atmosphere. Opt. Commun. 2007, 274, 274–280. [Google Scholar] [CrossRef]
- Chu, X.; Liu, Z.; Wu, Y. The propagation of a flattened circular Gaussian beam through an optical system in turbulent atmosphere. Appl. Phys. B 2008, 92, 119–122. [Google Scholar] [CrossRef]
- Zhou, G.; Chu, X. Analytic vectorial structure of circular flattened Gaussian beams. Appl. Phys. B 2011, 102, 215–224. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Wang, F.; Cai, Y.; Ma, X. Circular partially coherent flattened Gaussian beam. Opt. Lasers Eng. 2011, 49, 481–489. [Google Scholar] [CrossRef]
- Xu, M.; Alfano, R.R. Fractal mechanisms of light scattering in biological tissue and cells. Opt. Lett. 2005, 22, 3051–3053. [Google Scholar] [CrossRef]
- Xu, M. Plum pudding random medium model of biological tissue toward remote microscopy from spectroscopic light scattering. Biomed. Opt. Express 2017, 8, 2879–2895. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Zhao, D. The statistical properties of anisotropic electromagnetic beams passing through the biological tissues. Opt. Commun. 2012, 285, 4152–4156. [Google Scholar] [CrossRef]
- Luo, M.; Chen, Q.; Hua, L.; Zhao, D. Propagation of stochastic electromagnetic vortex beams through the turbulent biological tissues. Phys. Lett. A 2014, 378, 308–314. [Google Scholar] [CrossRef]
- Wu, Y.; Zhang, Y.; Wang, Q.; Hu, Z. Average intensity and spreading of partially coherent model beams propagating in a turbulent biological tissue. J. Quant. Spectrosc. Ra 2016, 184, 308–315. [Google Scholar] [CrossRef]
- Baykal, Y.; Arpali, C.; Arpali, S.A. Scintillation index of optical spherical wave propagating through biological tissue. J. Mod. Opt. 2017, 64, 138–142. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
- Zhou, G.; Ru, G. Propagation of a Lorentz-Gauss vortex beam in a turbulent atmosphere. PIER 2013, 143, 143–163. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: New York, NY, USA, 1980. [Google Scholar]



© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, Y.; Zhou, Y.; Zhou, G.; Chen, R. Characteristics of Partially Coherent Circular Flattened Gaussian Vortex Beams in Turbulent Biological Tissues. Appl. Sci. 2019, 9, 969. https://doi.org/10.3390/app9050969
Ni Y, Zhou Y, Zhou G, Chen R. Characteristics of Partially Coherent Circular Flattened Gaussian Vortex Beams in Turbulent Biological Tissues. Applied Sciences. 2019; 9(5):969. https://doi.org/10.3390/app9050969
Chicago/Turabian StyleNi, Yongzhou, Yimin Zhou, Guoquan Zhou, and Ruipin Chen. 2019. "Characteristics of Partially Coherent Circular Flattened Gaussian Vortex Beams in Turbulent Biological Tissues" Applied Sciences 9, no. 5: 969. https://doi.org/10.3390/app9050969
APA StyleNi, Y., Zhou, Y., Zhou, G., & Chen, R. (2019). Characteristics of Partially Coherent Circular Flattened Gaussian Vortex Beams in Turbulent Biological Tissues. Applied Sciences, 9(5), 969. https://doi.org/10.3390/app9050969





