1. Introduction
Wind-generated energy is increasingly being used as a power source worldwide, and this has resulted in the need for the enhanced reliability and so-called “sustainability” of wind turbines. Wind turbine systems must continuously generate the required amount of electrical power, depending on the available wind speed, grid demand, and possible malfunctions [
1].
Therefore, potential faults affecting the process must be properly detected and managed before causing the deterioration of the nominal working conditions of the plant or becoming critical issues. Wind turbines with large rotors (i.e., of megawatt size) are very expensive systems; they should be highly available and reliable in order to maximize the generated energy (at a reduced cost) and minimize Operation and Maintenance (O&M) services. In fact, most of the cost of the produced energy is from the installation cost of the wind turbine, but unplanned O&M costs could increase it by about 30%, particularly when offshore wind turbines are considered [
2].
To this end, many wind turbine systems include conservative technologies that protect against faults, which normally lead to a plant shutdown while awaiting O&M services. Hence, more effective solutions for managing faults are required to improve wind turbine features, particularly in faulty situations. Such features would prevent critical failures that may affect other wind turbine components, thus avoiding the unplanned replacement of functional parts and increased O&M costs.
It is beneficial to keep maintenance costs as low as possible, decrease downtime, and consequently increase the amount of captured power and improve reliability despite the presence of faults [
3]. Fault Detection and Isolation (FDI) techniques are powerful methods for this purpose. The fault information captured by FDI units can be used to optimize maintenance procedures via remote diagnosis [
4]. The use of FDI renders the equipment robust to the considered faults and, as a result, maintains the performance of the wind turbine at the desired level, even with the occurrence of faults. Therefore, maintenance requirements and downtime will decrease, and the reliability of power generation will improve. Therefore, the final cost is kept as low as possible [
5,
6].
FDI designs for wind turbines have been significantly developed over the last decade. Most of the works in this field have been motivated by competitions conducted by kk-electronic a/c and MathWorks from 2009–2016 [
4,
7]. Accordingly, the number of studies and consequent publications has increased considerably, and the subject is intensively researched worldwide [
8]. However, there are only a few available review papers in this field [
7,
9].
Hardware redundancy involves equipping components, such as sensors and actuators, with physically-identical counterparts to generate so-called residual signatures, which contain information on the possible fault. This approach increases the weight, occupied space, data acquisition complexity, and therefore, the final design cost. These issues are very problematic for offshore wind turbines. In contrast, software redundancy or computer-based FDI techniques have been developed for wind turbines throughout the last decade to overcome the aforementioned problems [
1]. A mathematical model of a wind turbine is used to generate redundant signals and, accordingly, residuals.
The most challenging issue, which should be considered in wind turbine FDI schemes, is that wind speed is poorly measured by anemometers due to the spatial/temporal effective wind speed distribution over the blade plane, turbulence, wind shear, and tower shadow effects. Therefore, wind speed is considered an an unknown disturbance, as is the consequent aerodynamic torque. Furthermore, FDI schemes should be robust to the considerable noise present in sensor measurements [
4,
7].
The most commonly-adopted model-based FDI techniques for wind turbines are the parity relation method and observer design [
10]. However, these approaches require accurate mathematical models to simulate the dynamic behaviors of the process under diagnosis [
11]. These methods do not require high-resolution signals, so there is no need for data acquisition hardware or installation of additional sensors. However, it is quite challenging to design an effective model that mimics real-world applications. Therefore, data-driven approaches, such as Neural Networks (NN) and fuzzy inference systems, can be used for wind turbine FDI designs. In fact, these artificial intelligence systems provide the best tools to represent the nonlinear and partially-known behavior of wind turbines [
12]. The designed prototype is fed with actual/estimated inputs (i.e., those of the wind turbine) to generate redundant outputs. Some other works have proposed the use of this data-driven learning scheme for wind turbine FDI, and it has been considered and applied to different wind turbine components, e.g., gearboxes, generator faults, and pitch faults [
10].
As an alternative approach, fault information can be directly extracted/inferred using this method, which relies on the design of an accurate a priori knowledge-based network, e.g., Adaptive Neuro-Fuzzy Inference System (ANFIS) or Fuzzy Inference System (FIS). Accordingly, expert knowledge must be included in the design, whether for numerical rules or fuzzy if/then linguistic rules. One of the advantages of fuzzy logic and fuzzy membership representation is that the uncertain measurement of the wind speed provided by the anemometer can be directly used [
8]. Classification methods are also utilized for rotor imbalance/aerodynamic asymmetry fault diagnosis [
13].
Therefore, the main contribution of this work is the development of viable and reliable solutions for the fault diagnosis of an offshore wind turbine model. The design of fault-tolerant controllers is not considered in this paper, but it would likely rely on the same tools considered here. In fact, the fault diagnosis module provides information on the faulty conditions of the system so that the controller activity can compensate. In particular, the FDI task was accomplished here by using fault estimators, which were obtained via these data-driven approaches, as they also offer effective tools for managing limited knowledge of the process dynamics, together with noise and disturbance effects.
The first data-driven solution addressed in this paper relies on fuzzy Takagi–Sugeno models [
14], which are derived from a clustering algorithm, followed by an identification procedure [
15]. The second solution exploits NN to describe the nonlinear analytical links between measurement and fault signals. The chosen network architecture belongs to the Nonlinear AutoRegressive with eXogenous (NARX) input prototype, which can describe dynamic relationships over time. The training of the neural fault estimators exploits a standard training algorithm that processes the acquired data [
16].
The developed fault diagnosis strategies were verified by means of a high-fidelity simulator that describes the normal and faulty behavior of a wind turbine plant. The achieved performances were verified in the presence of uncertainty and disturbance effects, thus validating the reliability and robustness features of the proposed schemes. Their effectiveness, which was further tested using a Hardware-In-the-Loop (HIL) test rig, suggests further investigation of more realistic applications of the proposed schemes.
It is worth noting the rationale underlying the proposal of these tools for the fault diagnosis of wind turbines. When a mathematical description of a plant subject to diagnosis can be included in the FDI design phase, model-based techniques yield the best performances. However, when modeling errors and disturbances are present, the learning phase exploited by the considered data-driven solutions leads to results that are better than those from model-based schemes. In fact, NN and fuzzy models use the learning accumulated from data-driven offline simulations, even if the training stage can be computationally heavy.
This work is organized as follows.
Section 2 describes the offshore wind turbine simulator.
Section 3 illustrates the fault diagnosis methodologies that rely on fuzzy and NN prototypes. The obtained results are summarized in
Section 4, taking into account simulated and real-time conditions. Finally,
Section 5 ends the paper by outlining the key achievements of the study and providing suggestions for future research issues.
2. Wind Turbine Simulator and Fault Model
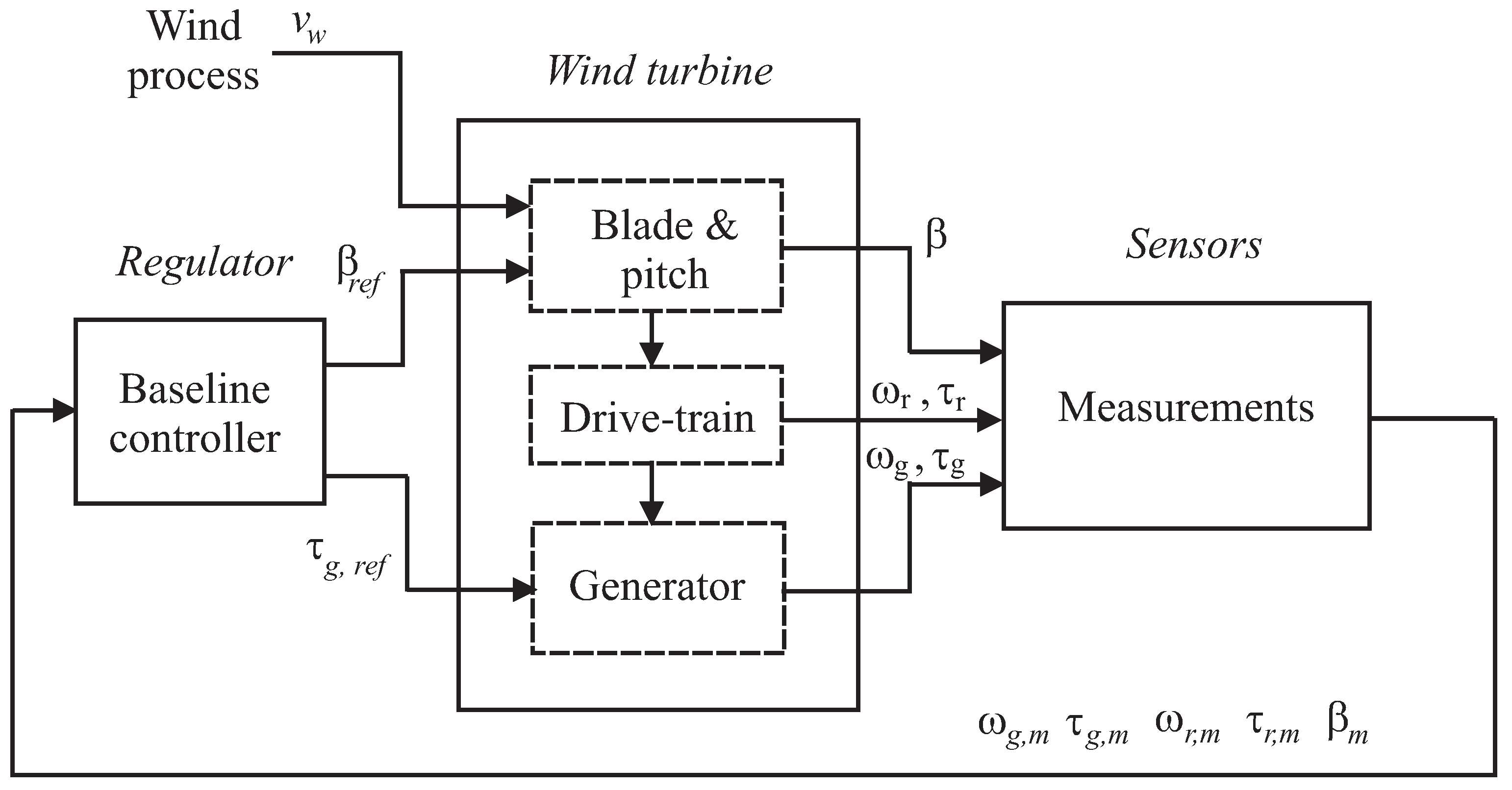
The three-bladed horizontal-axis wind turbine model considered in this work follows the principle that wind power activates the wind turbine blades, which leads to the rotation of the low-speed rotor shaft. In order to increase its rotational speed to that which is generally required by the generator, a gearbox with a drivetrain is included in the system. A more detailed description of this benchmark is given in [
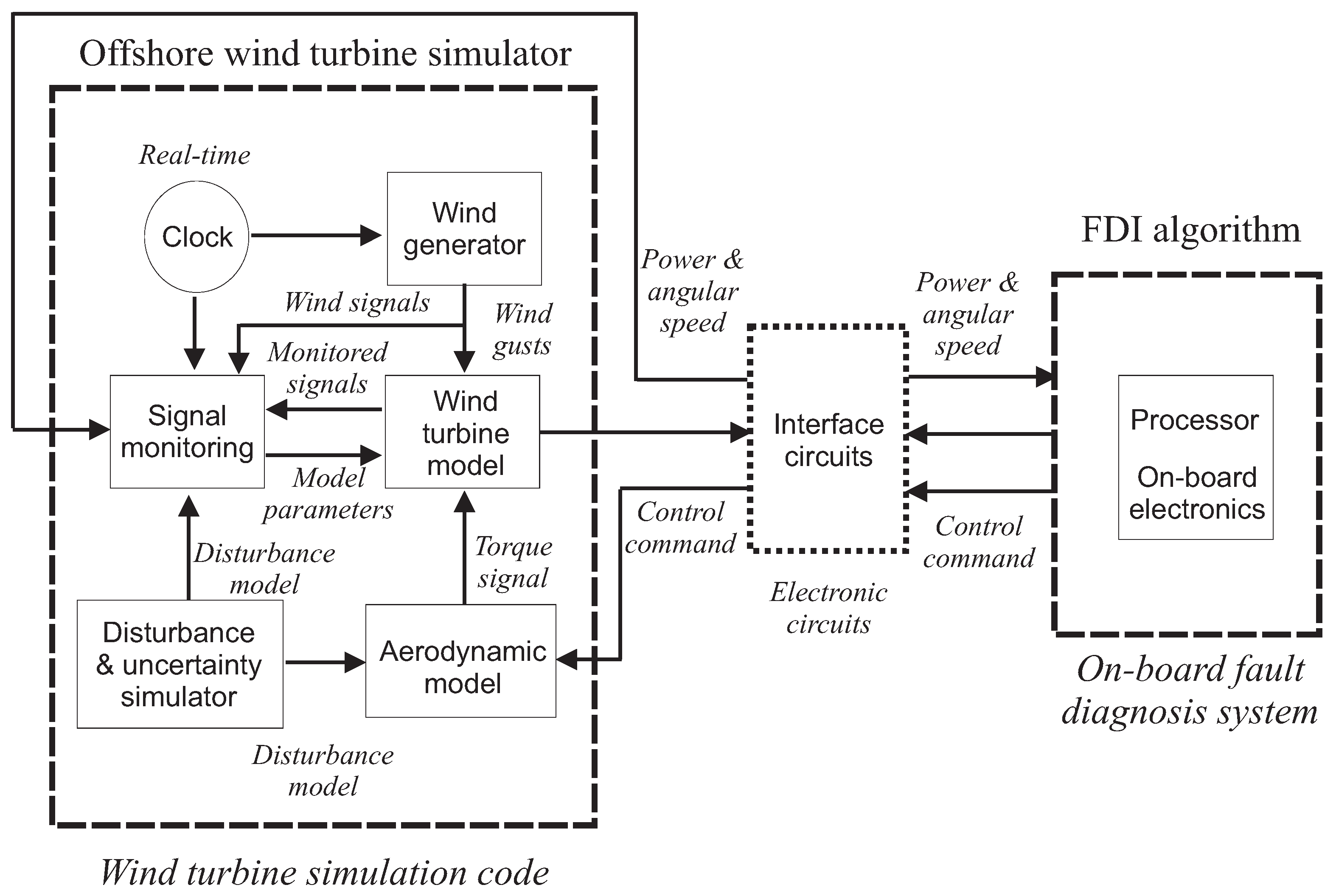
7], and its schematic diagram is presented in
Figure 1.
The wind turbine simulator has two controlled outputs, i.e., the generator rotational speed
and its generated power
. The wind turbine model is controlled by means of two actuated inputs, i.e., the generator torque
and the blade pitch angle
. The latter signal controls the actuators of the blades, which are implemented by hydraulic drives [
7].
Several other measurements are acquired from the wind turbine benchmark: the signal
represents the rotor speed, and
is the reference torque. Moreover, the aerodynamic torque signal
is computed from the wind speed
, which is usually available with limited accuracy. In fact, the wind field is not uniform around the wind turbine rotor plane, especially for large rotor systems. Moreover, anemometers measuring this variable are mounted behind the rotor on the nacelle. Therefore, the wind speed measurement
is affected by the interference between the blades and the nacelle, as well as the turbulence around the rotor plane. The alteration of the wind speed measurement
with respect to its nominal value around the rotor plane represents an uncertainty in the wind turbine model and a disturbance term in the control design [
7].
Finally, as sketched in
Figure 1, the signals generated by the wind turbine system are assumed to be acquired through the measurement block, whose objective is to simulate the real behavior of the sensors and actuators. Therefore, the measured signals are modeled as the sum of their actual values and white Gaussian process terms. Moreover, the wind turbine simulator includes a baseline controller, represented by standard PID regulators that regulate the generated power on the basis of the actual wind speed, as shown in [
4,
7].
The wind turbine simulator also includes the generation of three different typical fault cases: sensor, actuator, and system faults [
4,
7]. The sensor faults are generated as additive signals on the affected measurements. As an example, the faulty sensor of the pitch angle
provides the wrong measurement of the blade orientation, and if not handled, the controller cannot fully track the power reference signal. On the other hand, actuator faults lead to the alteration of the input and output descriptions of the pitch angle and the generator torque models by modifying their dynamics. In this way, a pressure drop in the hydraulic circuit of the pitch actuator and an electronic breakdown in the converter device are simulated, respectively. Finally, a system fault affects the drivetrain of the turbine, which is described as a slow variation in the friction coefficient over time. This can be caused by wear and tear of the mechanical parts over time.
This scenario is summarized in
Table 1, which also reports the measured signals that are affected by these nine faults.
The overall model of the wind turbine process is represented as a nonlinear continuous-time function
that describes the evolution of the turbine state vector
excited by the input vector
:
where, in this case, the state of the system is considered equal to the outputs of the wind turbine system, i.e., the rotor speed, the generator speed, and the generated power:
On the other hand, the input vector,
consists of the measurements of the three pitch angles from the three redundant sensors, as well as the measured torque. These signals are sampled with a sample time
T in order to acquire a total of
N measurements
,
with
, in order to implement the data-driven fault diagnosis solutions proposed in this paper.
It is worth noting that, as highlighted in
Section 3, the effect of the faults considered in
Table 1 is assumed to be generated by equivalent signals added to the input and output measurements. This approach was formerly proposed by the authors of [
17]. Moreover, this assumption is also known as Errors-In-Variables (EIV) modeling, which is exploited in the dynamic system identification framework [
18].
3. Fault Diagnosis Techniques: Fuzzy Systems and Neural Networks
In order to solve the fault diagnosis problem, this work assumes that the wind turbine system is affected by equivalent additive faults on the input and output measurements, as well as measurement errors, as described by the relations in Equation (
2):
where
and
represent the actual process variables;
and
are the measurements acquired by the sensors; and
and
describe the measurement errors. Note that, according to the relations in Equation (
2), it is assumed that the fault signals
and
have equivalent additive effects. These functions are different from zero only in the presence of faults. In general, the vector
has
r components, i.e., the number of process inputs, while
has
m elements, i.e., the number of process outputs.
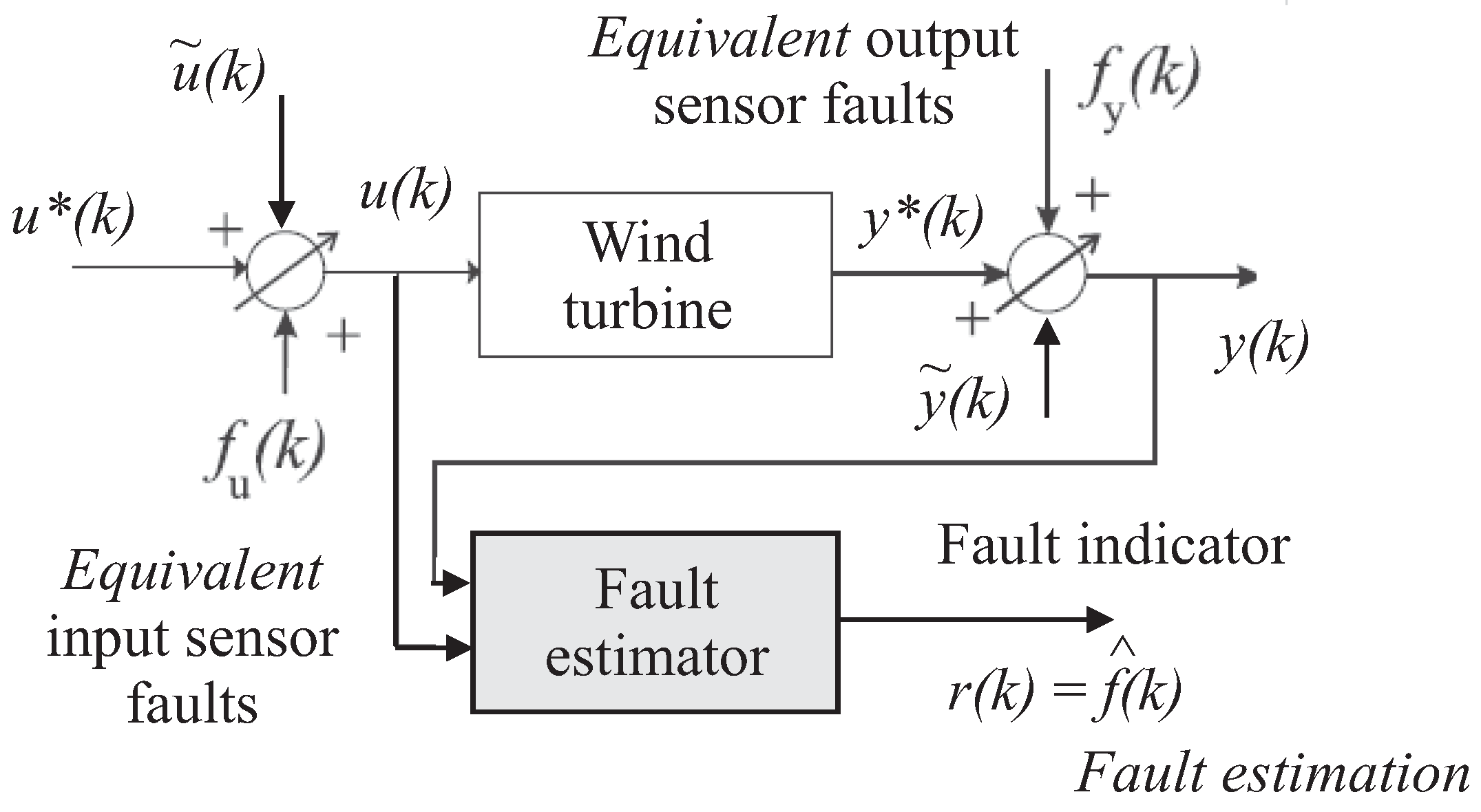
This work suggests exploiting fuzzy system and NN structures in order to provide an online estimation
of the fault signals
and
. Hence, as shown in
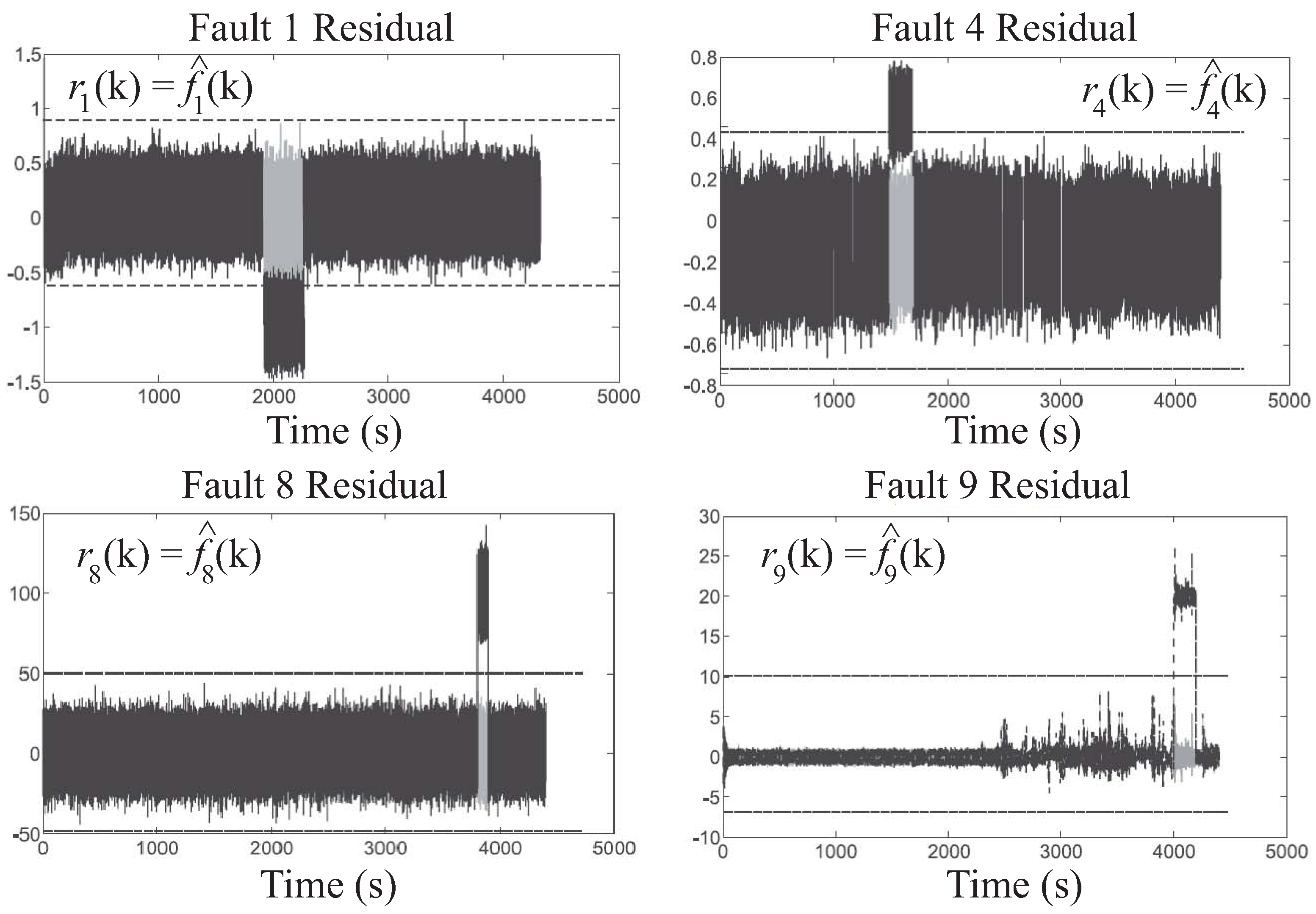
Figure 2, the diagnostic residuals
are equal to the estimated fault signals,
, as in Equation (
3):
The variable
is the fault vector, i.e.,
. Therefore, the general fault estimate
is equal to the
component of the fault vectors
or
in Equation (
2), with
. This residual generation scheme is represented in
Figure 2.
Figure 2 shows that, in general, the residual generators are fed by the input and output measurements
and
. The occurrence of the
fault can be simply detected using the threshold logic of Equation (
4) applied to the
residual
[
11]:
with
representing the
component of the vector
. Its mean
and variance
values are computed in a fault-free condition from
N samples according to the relations in Equation (
5):
Note that the parameter
represents a variable that has to be properly tuned in order to separate the fault-free from the faulty conditions effectively, as shown in
Section 4. Once the fault detection phase is complete, the fault isolation task is directly obtained by means of the bank of estimators depicted in
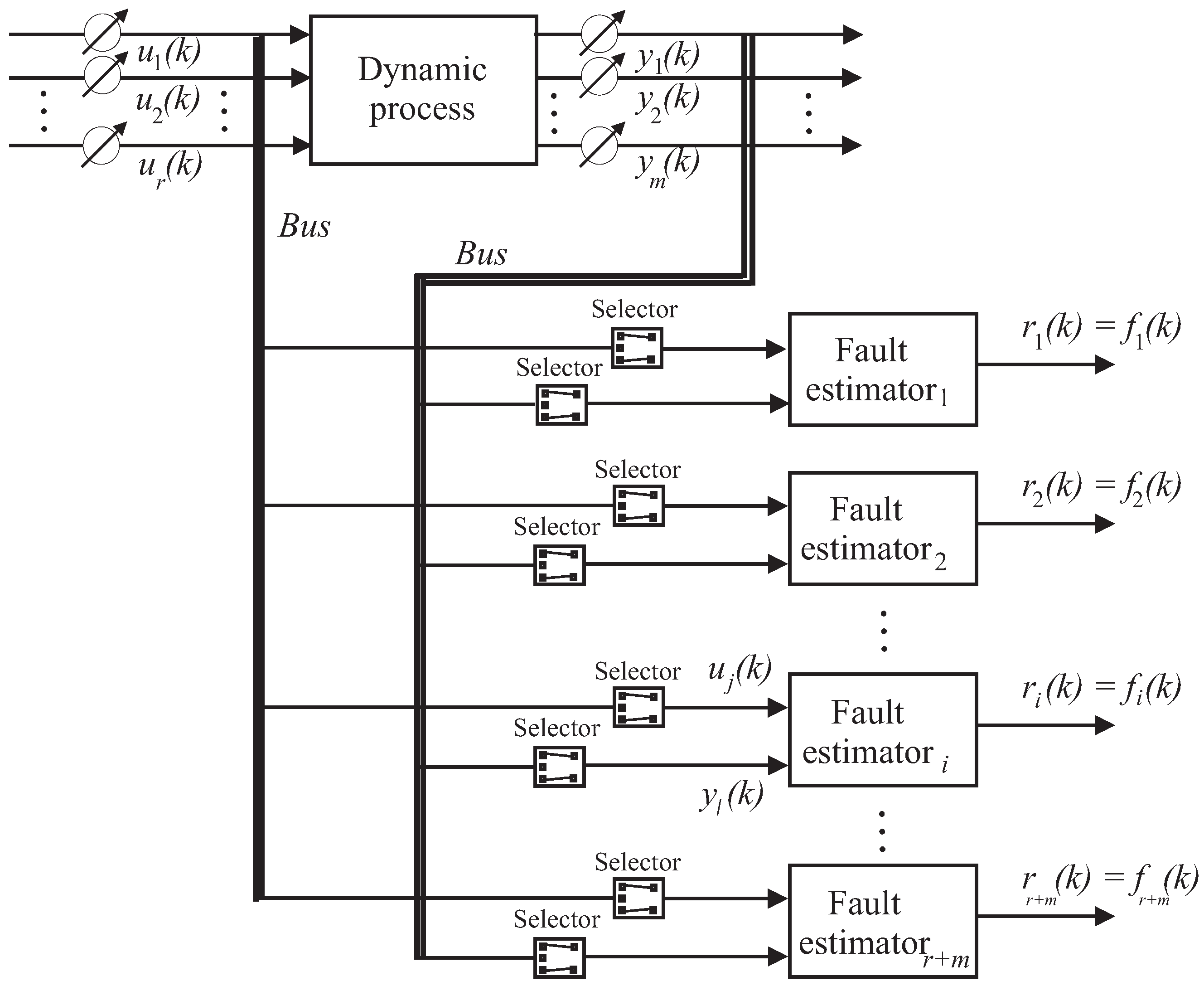
Figure 3.
According to the scheme depicted in
Figure 3, the number of estimators in the bank is equal to the number of faults that have to be diagnosed, i.e.,
. In general, the
estimator is driven by the input and output signals
and
. However, its inputs
and output
are selected in order to be selectively sensitive to the particular fault
. To this end, the design of these fault estimators is enhanced by the fault sensitivity analysis procedure reported in
Section 3.
The first method proposed in this paper for designing fault estimators relies on Takagi–Sugeno (TS) models [
19]. This approach was formerly addressed in [
14] for the approximation of nonlinear Multiple-Input Single-Output (MISO) dynamic systems with arbitrary accuracy. The general fault estimator
has the form of Equation (
6):
The TS fuzzy model results are described as discrete-time linear AutoRegressive models with eXogenous input (ARX) of order
o, in which the regressor vector has the form of Equation (
7):
where
and
are the components of the actual system input and output vectors
and
that are selected using the fault sensitivity analysis proposed in
Section 3. The variable
k represents the time step, with
. The parameters of the TS fuzzy model in Equation (
6) are collected into the vector:
where the
coefficients refer to the output samples, while the
coefficients are associated with the input ones.
This work proposes to solve the derivation of the TS models as a system identification problems from the noisy data of Equation (
2). In particular, the design of the bank of fault estimators in
Figure 3 requires the estimation of the consequent parameters
and
of Equation (
8).
Note that the design method proposed in this work exploits the direct identification of the TS fuzzy models of Equation (
6). In particular, the fuzzy model structure, i.e., the number of rules
, the antecedents, and the fuzzy membership functions
in Equation (
6), are derived by means of the Fuzzy Modeling and Identification (FMID) toolbox implemented in the MATLAB environment [
14]. Moreover, the computation of the TS model parameters in Equation (
8) was solved by the authors in [
20] as an EIV estimation problem, as highlighted by the relations in Equation (
2). On the other hand, the FMID toolbox uses the Gustafson–Kessel (GK) clustering method [
14] to perform a partition of input–output data into a proper number
of regions (clusters), where the
model of Equation (
6) is valid. This model is thus obtained after the selection of the model order
o and the number of clusters
. The FMID toolbox also determines the antecedent degrees of fulfillment
in Equation (
6), which are derived with a curve fitting method [
14].
This paper proposes a different data-driven approach that is based on NN, which is exploited to implement the scheme shown in
Figure 3. According to this scheme, a bank of NN is used to reconstruct the faults affecting the system under diagnosis using a proper set of input and output measurements. The structure proposed in this work consists of a feedforward multilayer perceptron NN with three layers [
21]. Moreover, this study suggests the use of a quasi-static NN, as it represents a suitable tool to predict dynamic relationships between the input–output measurements and the considered fault function
with arbitrary accuracy [
21].
Therefore, the
neural fault estimator in
Figure 3 is described by the relation in Equation (
9):
where
and
are the general
and
components of the measured inputs and outputs
and
, respectively, that are selected via the fault sensitivity analysis tool.
and
represent the number of delays of the input and the output samples.
is the function realized by the static NN, which depends on the number of neurons and their weights.
The NN exploited in this study uses sigmoidal activation functions for the neurons in both the input and the hidden layers, while a linear one is used in the output layer. The number of neurons and delays (
and
) is selected to obtain suitable fault estimation errors after the NN training from the data acquired from the system under diagnosis. In particular, the NN training is performed by generating a proper number of data,
N, which are partitioned into the training, validation, and test sets, as required by the Levenberg–Marquardt back-propagation algorithm [
21].
Fault Sensitivity Analysis
The design of the fault diagnosis schemes proposed in this paper and represented in
Figure 3 is enhanced by the tool presented here. It consists of a fault sensitivity analysis that is performed on the measurements acquired from the wind turbine simulator. The procedure aims to define the most sensitive measurements
and
with respect to the general fault
considered in
Section 2.
According to the assumption of Equation (
2), the considered fault signals
have been injected into the wind turbine simulator, and only single faults may occur. Then, the Relative-Mean-Squared Errors (RMSEs) between the fault-free and faulty signals acquired from the simulator are computed. In this way, the most sensitive signals
and
are selected for each fault
i. The achieved results are summarized in
Table 2.
In particular, the fault sensitivity analysis follows the selection algorithm, which relies on the normalized sensitivity function
of Equation (
10),
with:
and:
In fact, represents the effect of the considered fault case with respect to the measured signal , with . The subscripts “f” and “n” indicate the faulty and the fault-free cases, respectively. Therefore, the measurement that is most affected by the considered fault is the value of , which, in this case, is equal to one. Otherwise, smaller values of indicate that is not affected by that fault.
The complete results of the fault sensitivity analysis are summarized in
Table 3.
This method represents a key feature of the proposed approach to fault diagnosis. In fact, the fault estimators of the bank of
Figure 3 are designed by exploiting a reduced number of input signals
and
. It also leads to a noteworthy simplification of the complexity and the computational cost of the identification and training phases of the fuzzy and NN models, respectively.
Note finally that the fault sensitivity analysis was performed by considering one fault at a time. The case of multiple faults was not considered here, as the wind turbine benchmark simulates the occurrence of single faults only, as described in [
4,
7]. However, the case of multiple faults occurring at the same time could be considered, even if a different fault sensitivity analysis has to be executed.