Quantification of Active Structural Path for Vibration Reduction Control of Plate Structure under Sinusoidal Excitation
Abstract
:1. Introduction
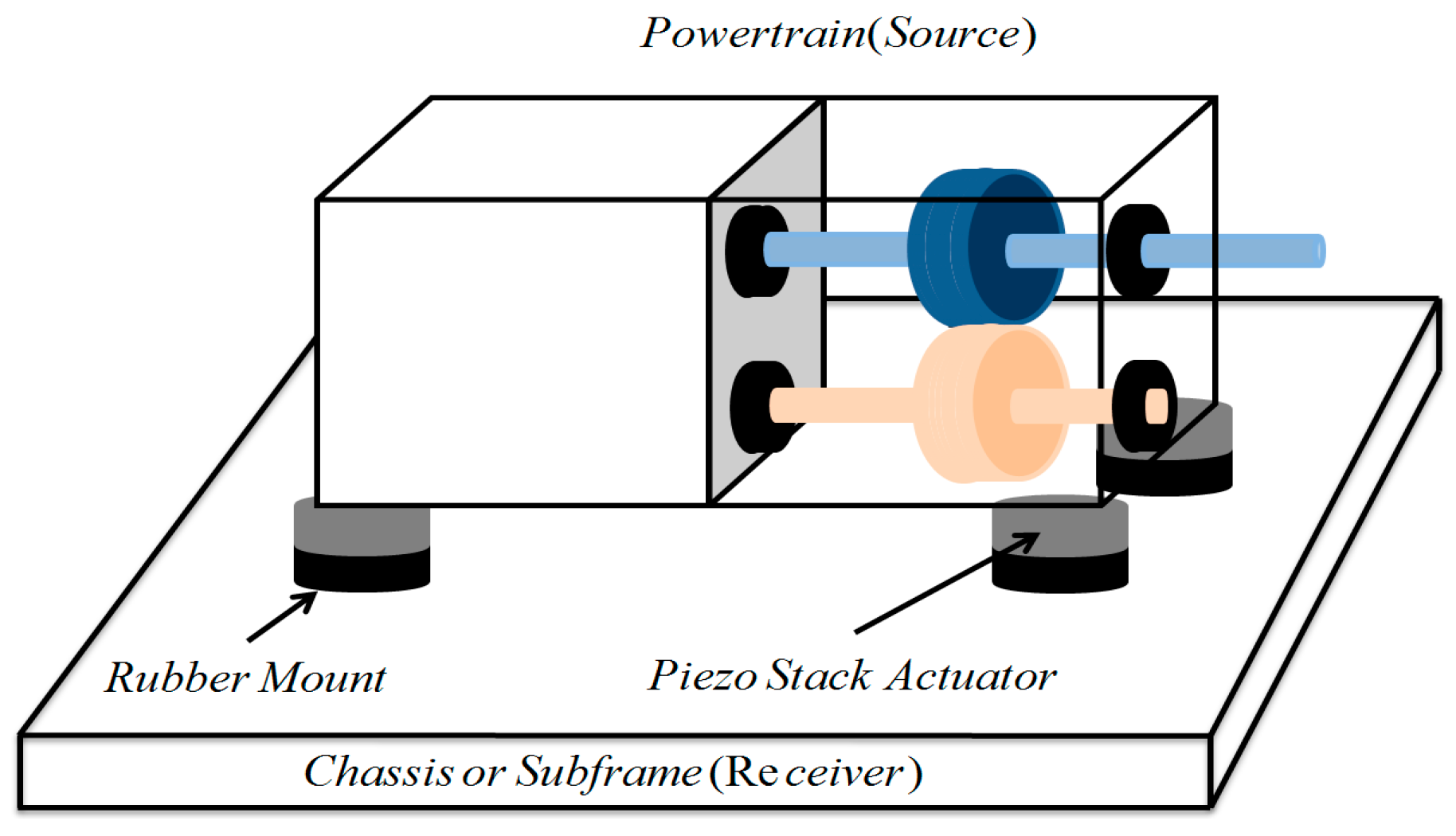
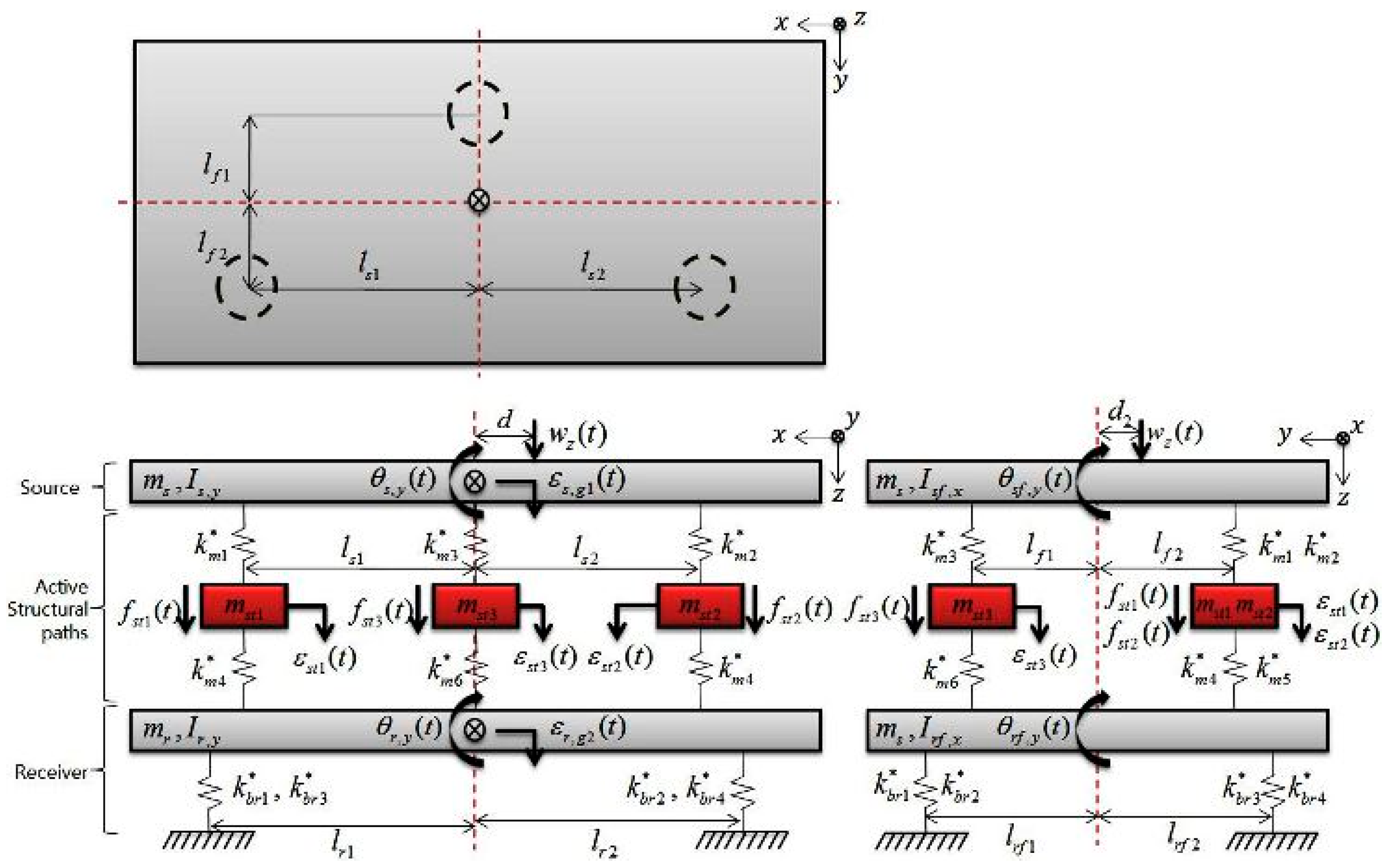
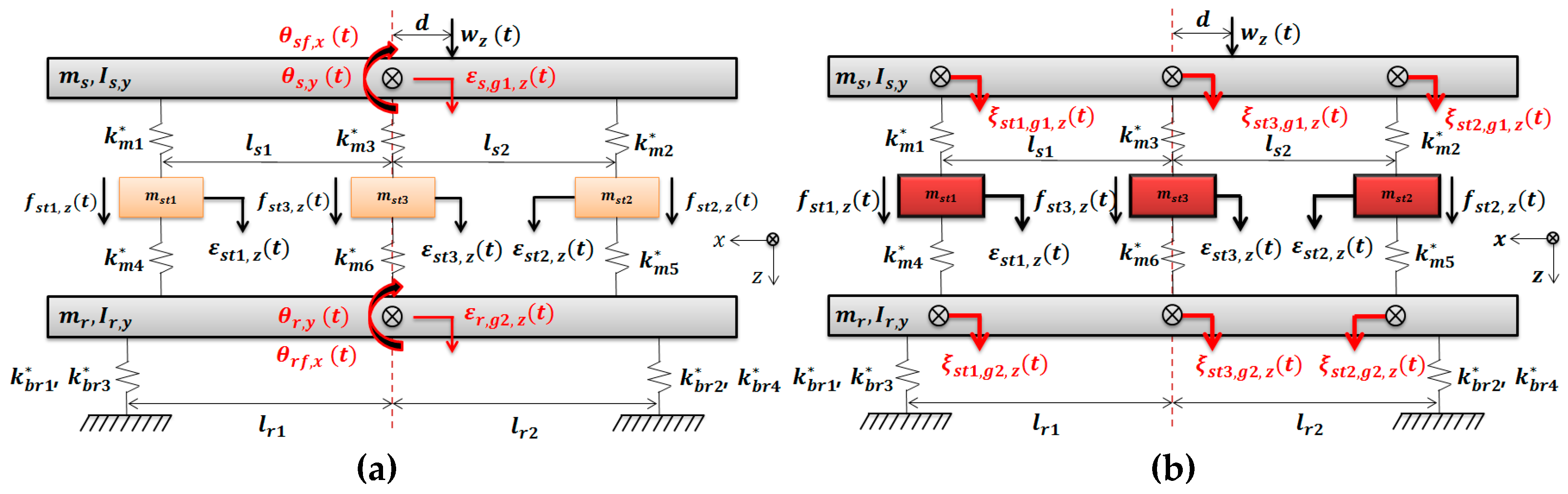
2. Modeling of Mounting System
2.1. 9-DOF Modeling
2.2. Calculation of Actuator Amplitude and Phase
3. Validation Using the Numerical Simulation
3.1. Simulation Overview
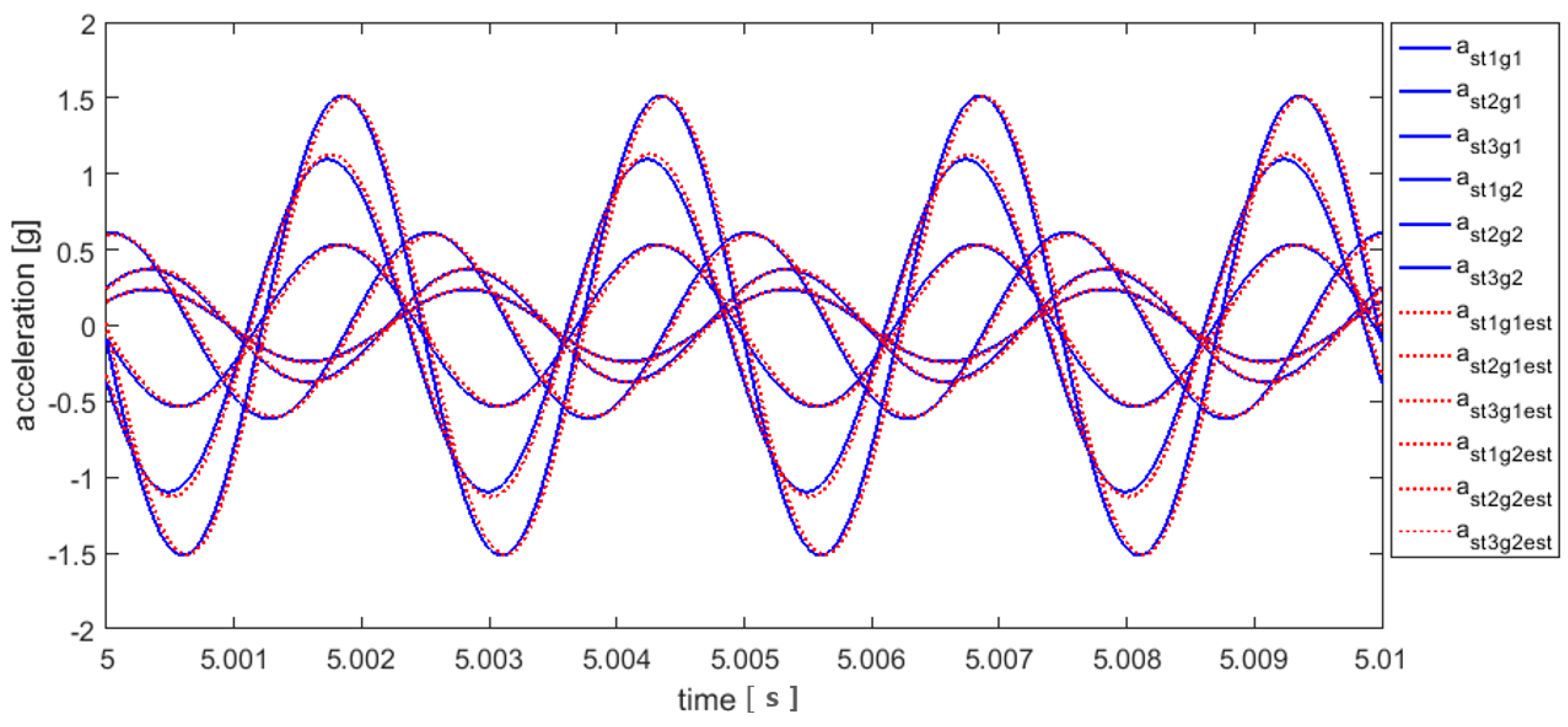
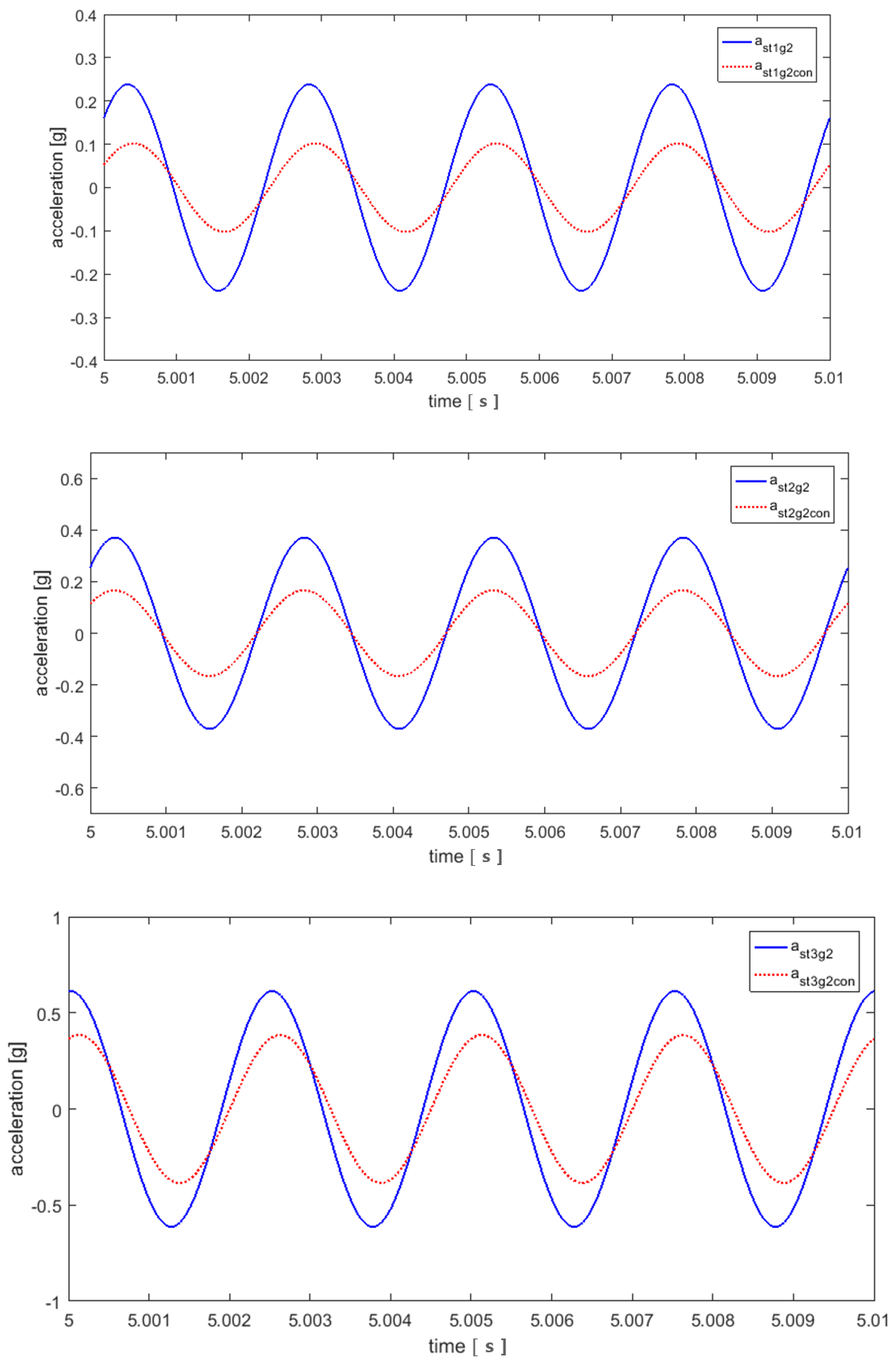
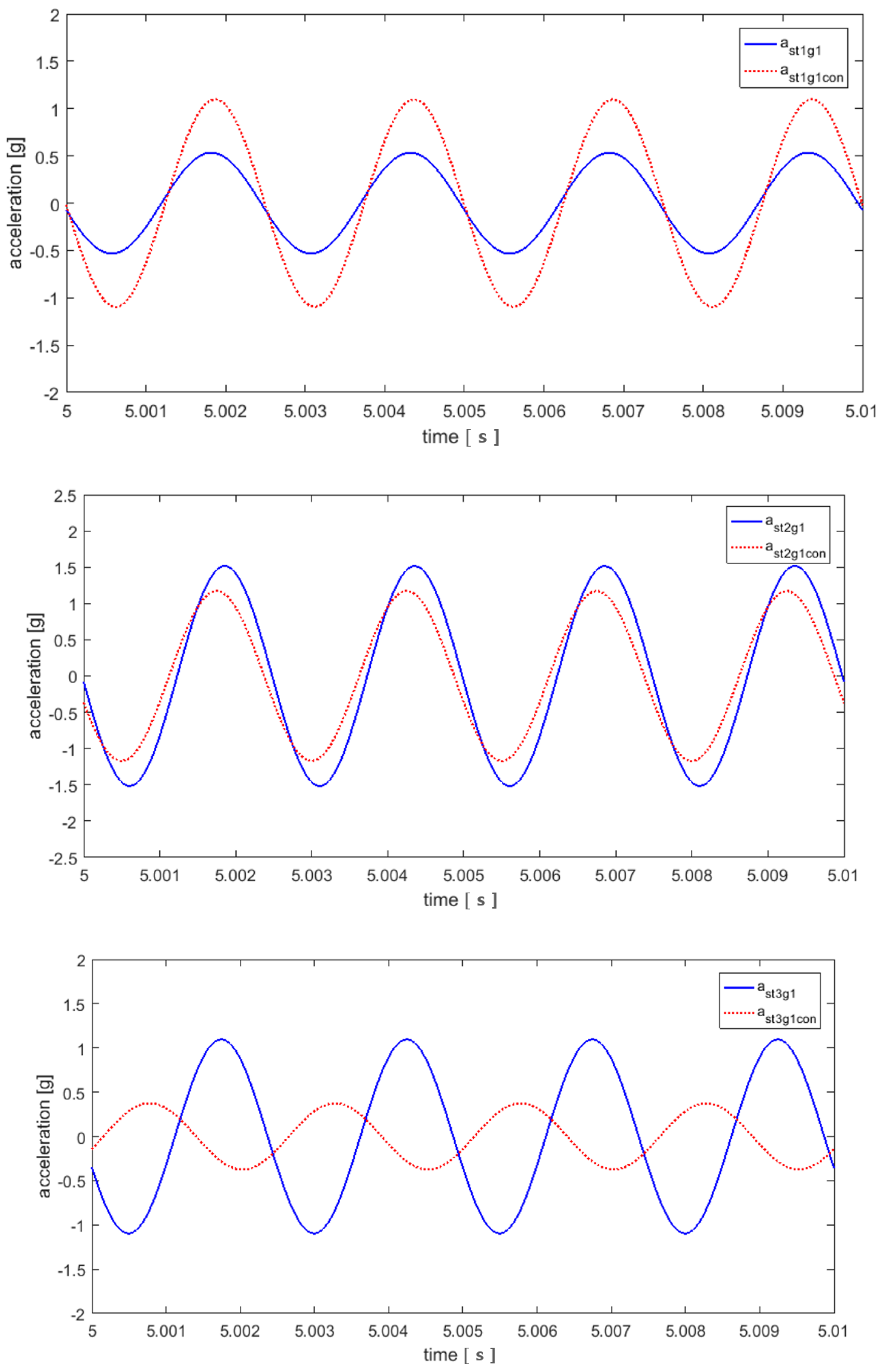
3.2. Control Using the Calculated Amplitude and Phase
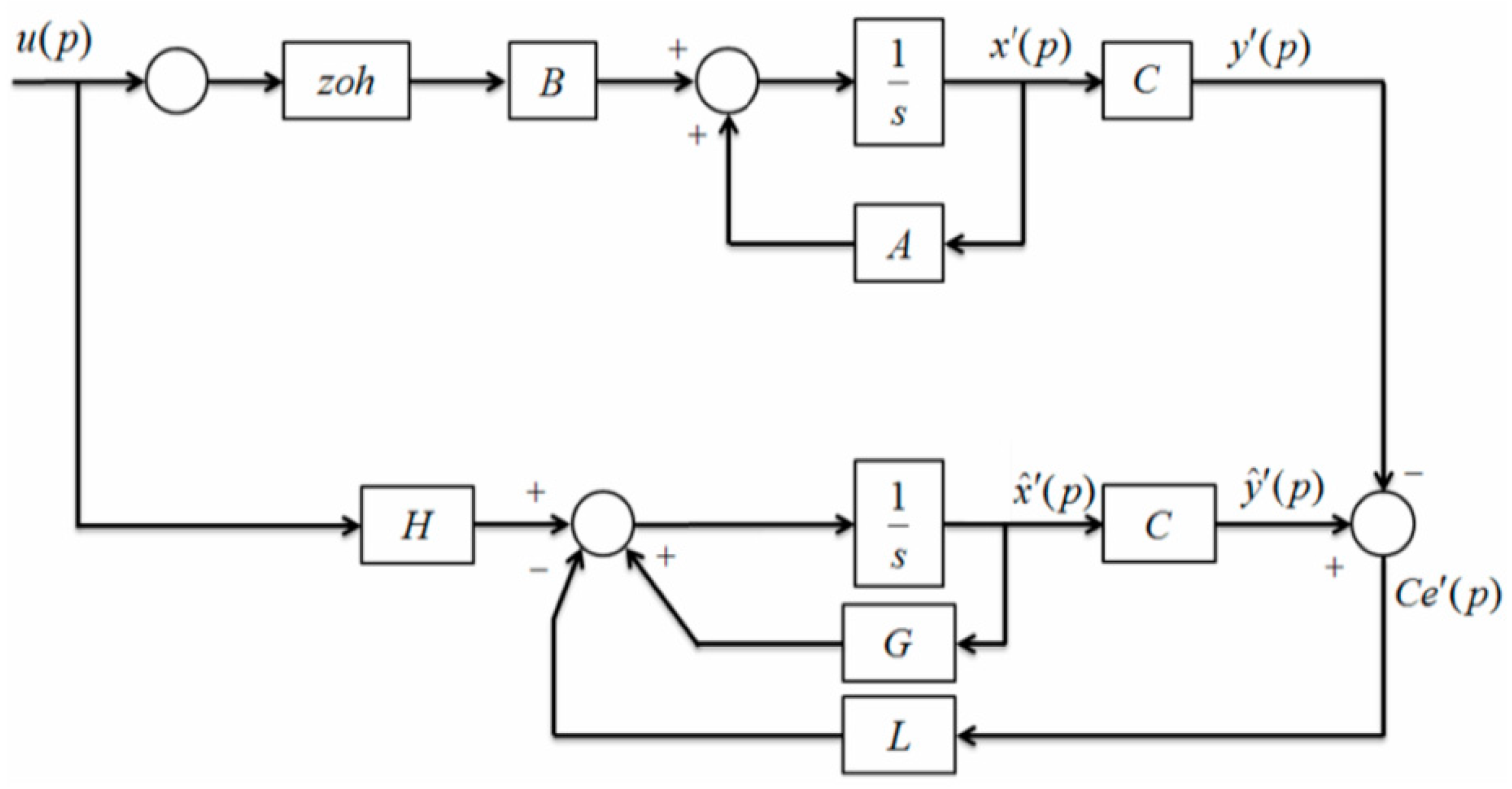
3.3. Control Using the NLMS Algorithm
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Minak, G.; Fragassa, C.; De Camargo, F.V. A Brief Review on Determinant Aspects in Energy Efficient Solar Car Design and Manufacturing. In Proceedings of the International Conference on Sustainable Design and Manufacturing, Bologna, Italy, 26–28 April 2017; Volume 68, pp. 847–856. [Google Scholar]
- Hosseini, A.M.; Arzanpour, S.; Golnaraghi, F.; Parameswaran, A.M. Solenoid actuator design and modeling with application in engine vibration isolators. J. Vib. Control 2012, 19, 1015–1023. [Google Scholar] [CrossRef]
- Tang, X.; Yang, W.; Hu, X.; Zhang, D. A novel simplified model for torsional vibration analysis of a series-parallel hybrid electric vehicle. Mech. Syst. Signal Process. 2017, 85, 329–338. [Google Scholar] [CrossRef]
- Kraus, R.; Herold, S.; Millitzer, J.; Jungblut, T. Development of Active Engine Mounts Based on Piezo Actuators. ATZ Worldw. 2014, 116, 46–51. [Google Scholar] [CrossRef]
- Harun, M.H.; Azhari, M.A.; Yunos, M.R.M.; Yamin, A.K.M. Characterization of a Magnetorheological Fluid Damper Applied to Semi-Active Engine Mounting System. In Proceedings of the 6th ECCOMAS Conference on Smart Structures and Materials, Glasgow, UK, 11–15 June 2018; Volume 5, pp. 2448–2459. [Google Scholar]
- Hausberg, F.; Scheiblegger, C.; Pfeffer, P.; Plöchl, M.; Hecker, S.; Rupp, M. Experimental and analytical study of secondart path variations in active engine mounts. J. Sound Vib. 2015, 340, 22–38. [Google Scholar] [CrossRef]
- Yang, T.; Suai, Z.; Sun, Y.; Zhu, M.; Xiao, Y.; Liu, X.; Du, J.; Jin, G.; Liu, Z. Active vibration isolation system for a diesel engine. Noise Control Eng. J. 2012, 60, 267–282. [Google Scholar] [CrossRef]
- Sun, W.; Li, Y.; Huang, J.; Zhang, N. Vibration effect and control of In-Wheel Switched Reluctance Motor for electric vehicle. J. Sound Vib. 2015, 338, 105–120. [Google Scholar] [CrossRef]
- Chae, H.D.; Choi, S.-B. A new vibration isolation bed stage with magnetorheological dampers for ambulance vehicles. Smart Mater. Struct. 2014, 24, 17001. [Google Scholar] [CrossRef]
- Jeon, J.; Han, Y.-M.; Lee, D.-Y.; Choi, S.-B. Vibration control of the engine body of a vehicle utilizing the magnetorheological roll mount and the piezostack right-hand mount. Proc. Inst. Mech. Eng. D J. Autom. Eng. 2013, 227, 1562–1577. [Google Scholar] [CrossRef]
- Fakhari, V.; Choi, S.-B.; Cho, C.-H. A new robust adaptive controller for vibration control of active engine mount subjected to large uncertainties. Smart Mater. Struct. 2015, 24, 45044. [Google Scholar] [CrossRef]
- Elahinia, M.; Ciocanel, C.; Nguyen, T.M.; Wang, S. MR- and ER-Based Semiactive Engine Mounts: A Review. Smart Mater. Res. 2013, 2013, 1–21. [Google Scholar] [CrossRef]
- Wu, W.; Chen, X.; Shan, Y. Analysis and experiment of a vibration isolator using a novel magnetic spring with negative stiffness. J. Sound Vib. 2014, 333, 2958–2970. [Google Scholar] [CrossRef]
- Truong, T.Q.; Ahn, K.K. A new type of semi-active hydraulic engine mount using controllable area of inertia track. J. Sound Vib. 2010, 329, 247–260. [Google Scholar] [CrossRef]
- Kamada, T.; Fujita, T.; Hatayama, T.; Arikabe, T.; Murai, N.; Aizawa, S.; Tohyama, K. Active vibration control of frame structures with smart structures using piezoelectric actuators (Vibration control by control of bending moments of columns). Smart Mater. Struct. 1997, 6, 448–456. [Google Scholar] [CrossRef]
- Loukil, T.; Bareille, O.; Ichchou, M.; Haddar, M. A low power consumption control scheme: Application to a piezostack-based active mount. Front. Mech. Eng. 2013, 8, 383–389. [Google Scholar] [CrossRef]
- Sui, L.; Xiong, X.; Shi, G. Piezoelectric Actuator Design and Application on Active Vibration Control. Phys. Procedia 2012, 25, 1388–1396. [Google Scholar] [CrossRef]
- Herold, S.; Kraus, R.; Millitzer, J.; de Rue, G. Vibration control of a medium-sized vehicle by a novel active engine mount. In Proceedings of the 4th PT PIESA Symposium, Nuremberg, Germany, 26 April 2013. [Google Scholar]
- Bartel, T.; Herold, S.; Mayer, D.; Melz, T. Development and testing of active vibration control systems with piezoelectric actuators. In Proceedings of the 6th Eccomas Conference on Smart Structures and Materials, Torino, Italy, 24–26 June 2013. [Google Scholar]
- Liette, J.; Dreyer, J.T.; Singh, R. Interaction between two active structural paths for source mass motion control over mid-frequency range. J. Sound Vib. 2014, 333, 2369–2385. [Google Scholar] [CrossRef]



| Variable | Values | Units | Variable | Values | Units |
|---|---|---|---|---|---|
| Source | |||
| Original | |||
| All actuators turned on | |||
| Receiver | |||
| Original | |||
| All actuators turned on |
| Source | |||
| Original | |||
| Control using the NLMS | |||
| Receiver | |||
| Original | |||
| Control using the NLMS |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, D.; Kim, B. Quantification of Active Structural Path for Vibration Reduction Control of Plate Structure under Sinusoidal Excitation. Appl. Sci. 2019, 9, 711. https://doi.org/10.3390/app9040711
Hong D, Kim B. Quantification of Active Structural Path for Vibration Reduction Control of Plate Structure under Sinusoidal Excitation. Applied Sciences. 2019; 9(4):711. https://doi.org/10.3390/app9040711
Chicago/Turabian StyleHong, Dongwoo, and Byeongil Kim. 2019. "Quantification of Active Structural Path for Vibration Reduction Control of Plate Structure under Sinusoidal Excitation" Applied Sciences 9, no. 4: 711. https://doi.org/10.3390/app9040711
APA StyleHong, D., & Kim, B. (2019). Quantification of Active Structural Path for Vibration Reduction Control of Plate Structure under Sinusoidal Excitation. Applied Sciences, 9(4), 711. https://doi.org/10.3390/app9040711




