Peridynamic Modeling of Mode-I Delamination Growth in Double Cantilever Composite Beam Test: A Two-Dimensional Modeling Using Revised Energy-Based Failure Criteria
Abstract
:1. Introduction
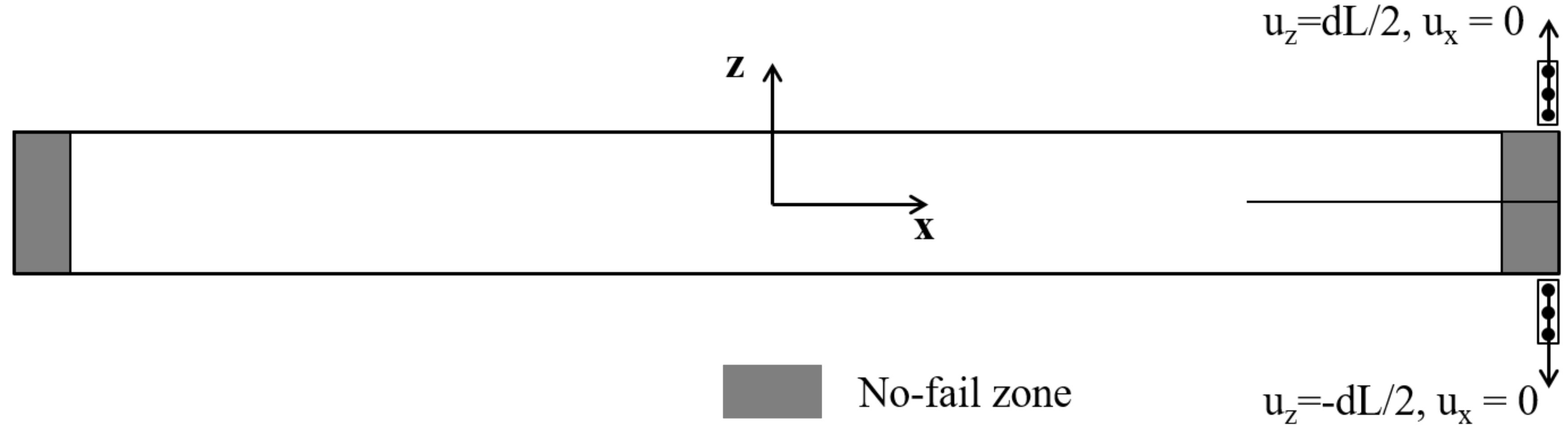
2. Two-Dimensional Ordinary State-Based Peridynamic Model for DCB Modeling
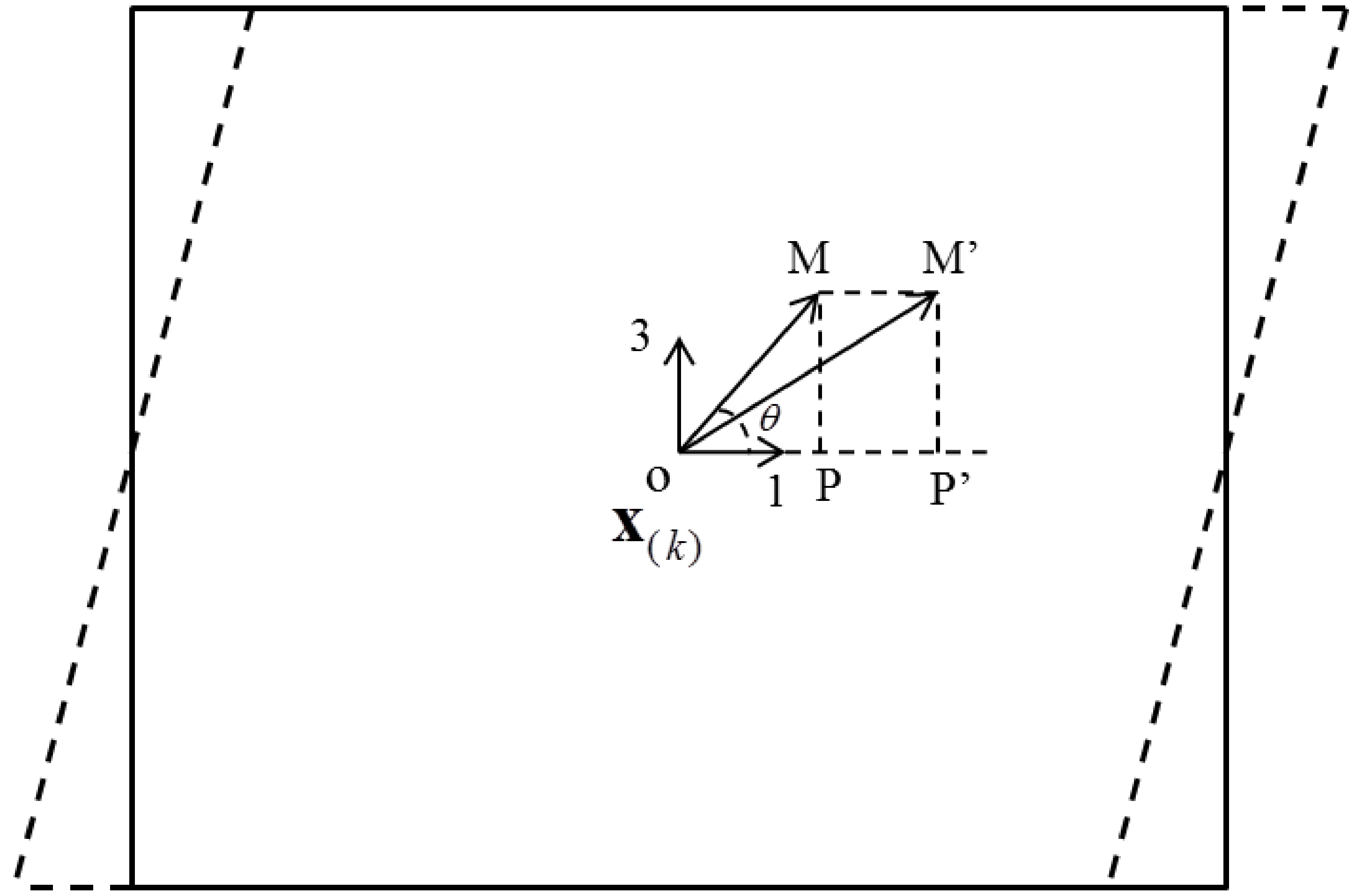
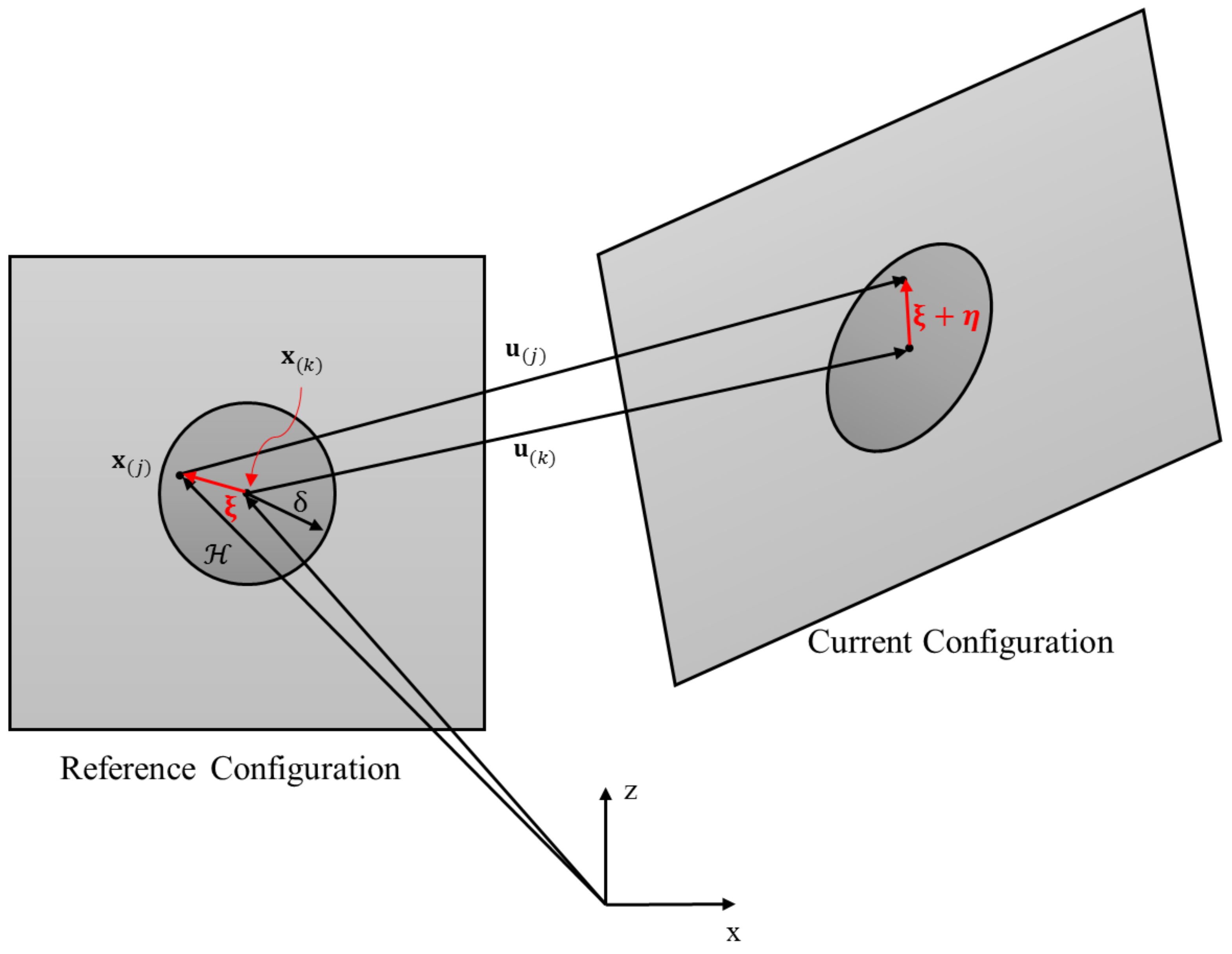
2.1. Governing Equation
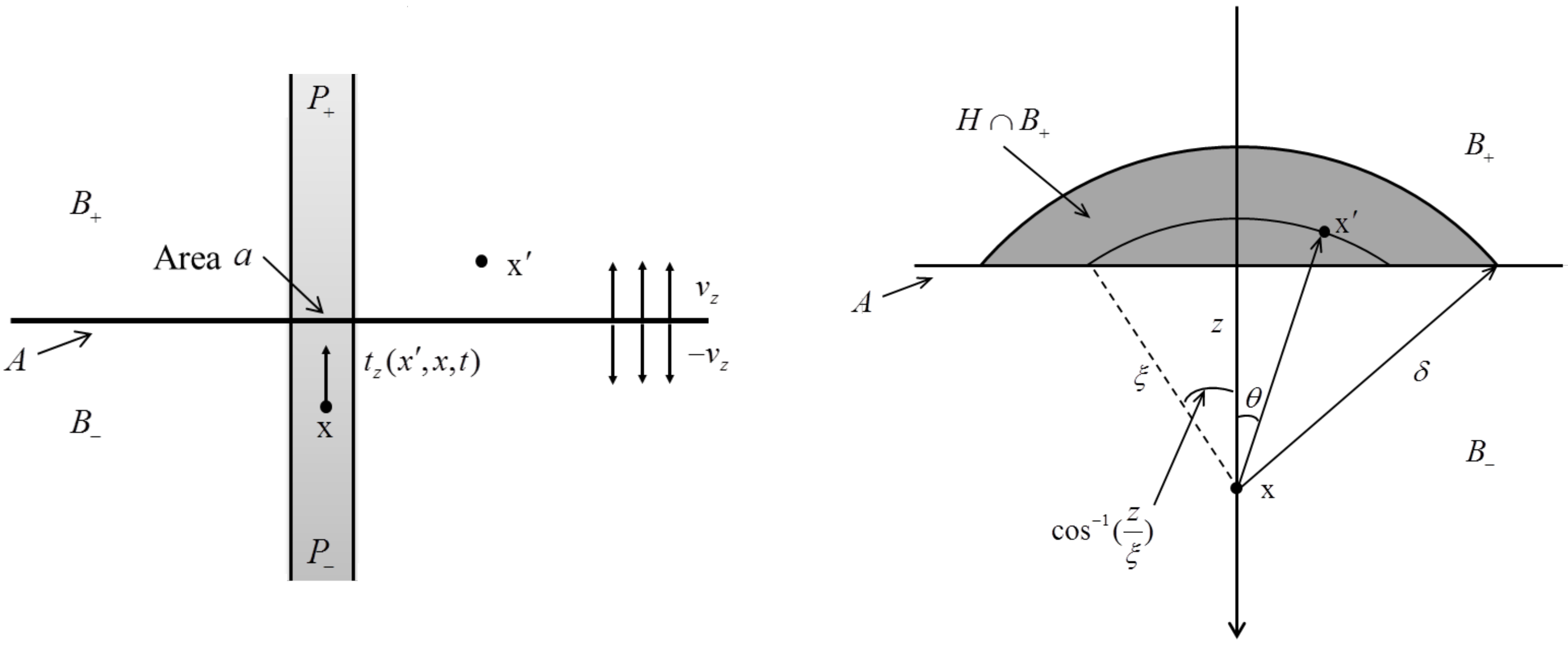
2.2. Revised Energy-Based Failure Criteria
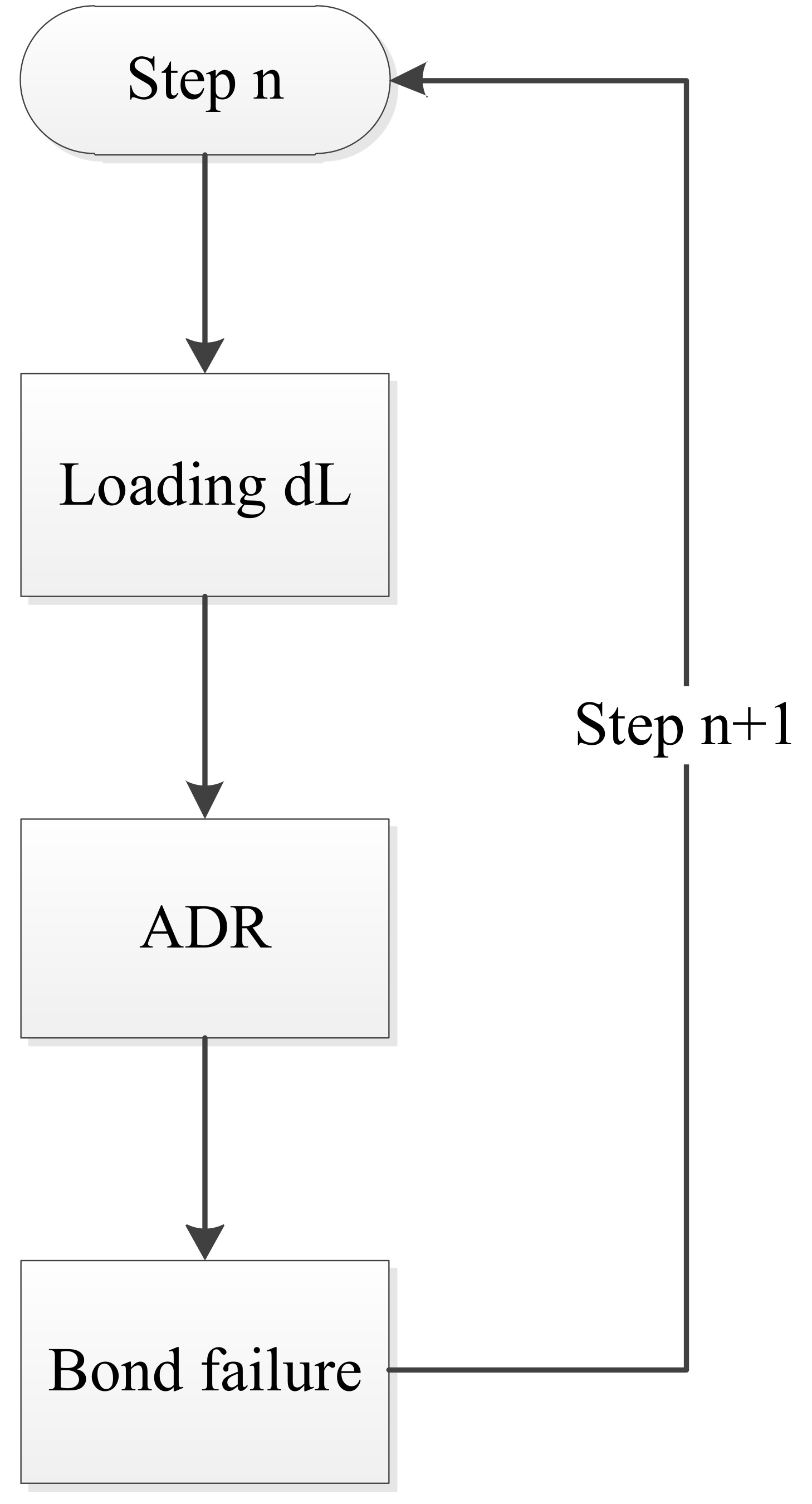
2.3. Numerical Implementation
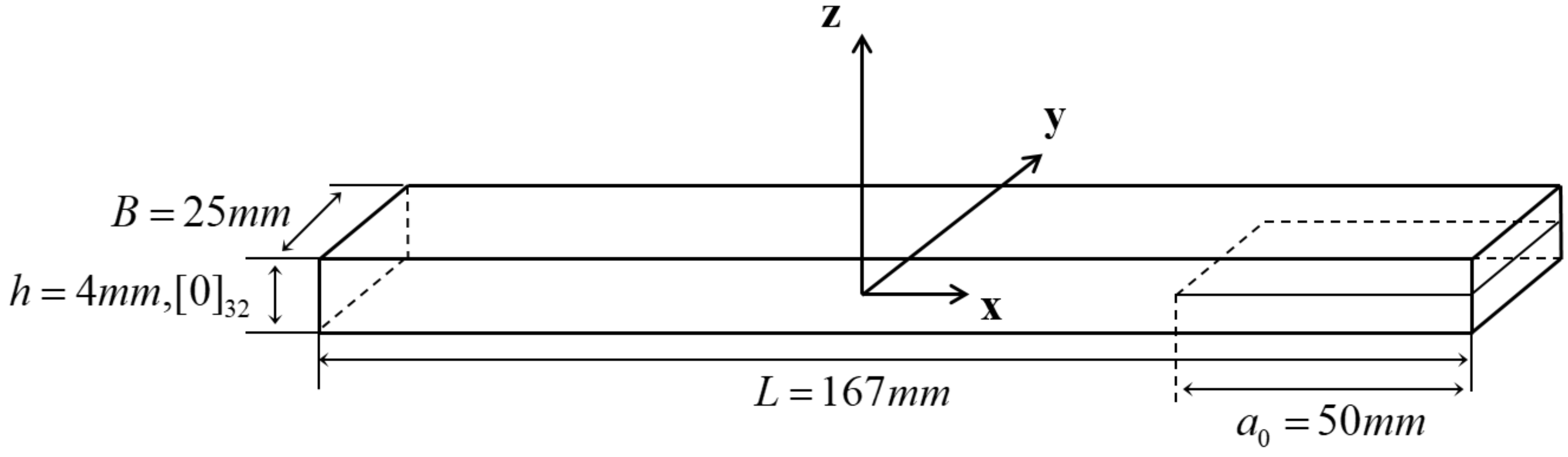
3. Experimental Setup and Results
4. Numerical Results and Discussion
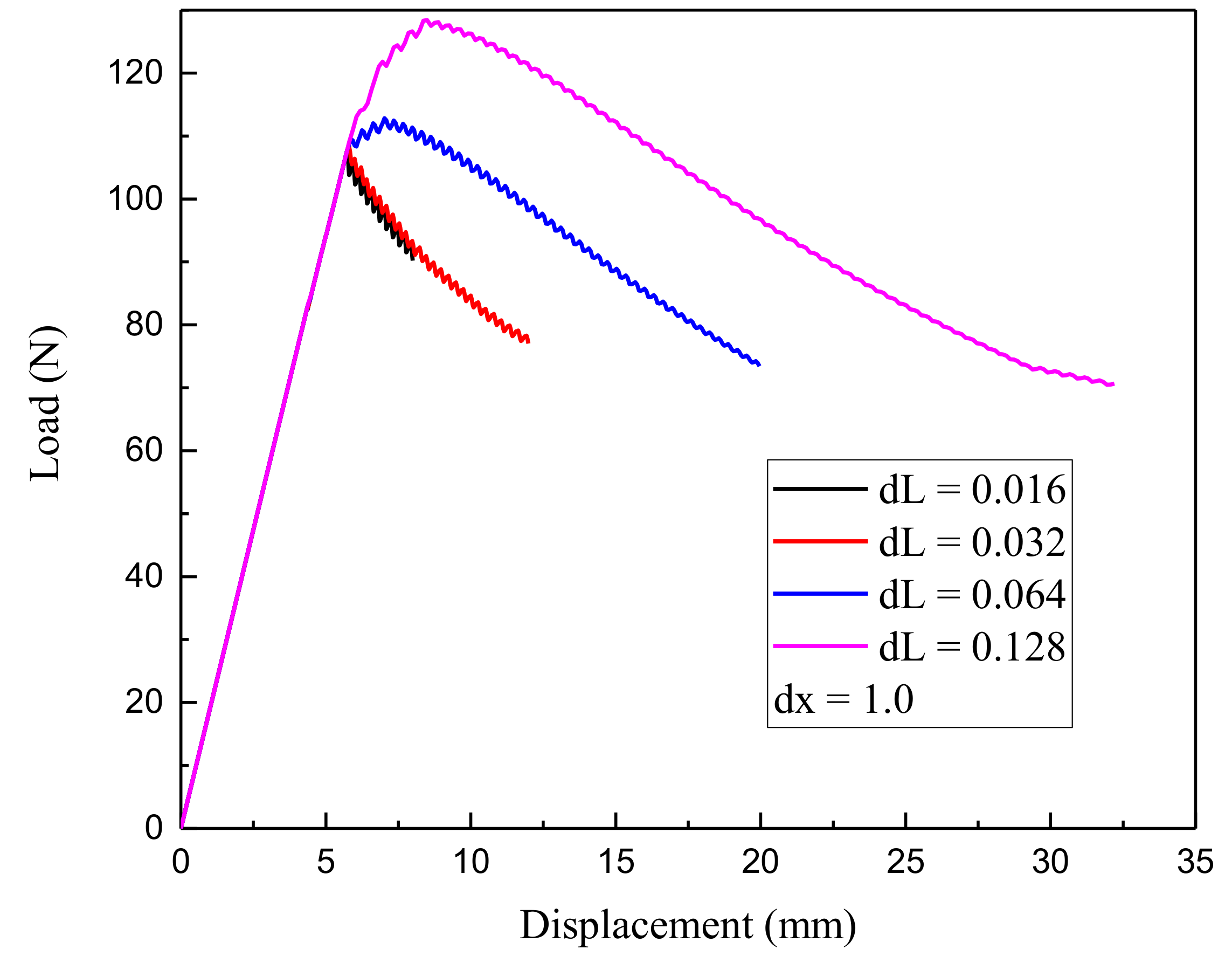
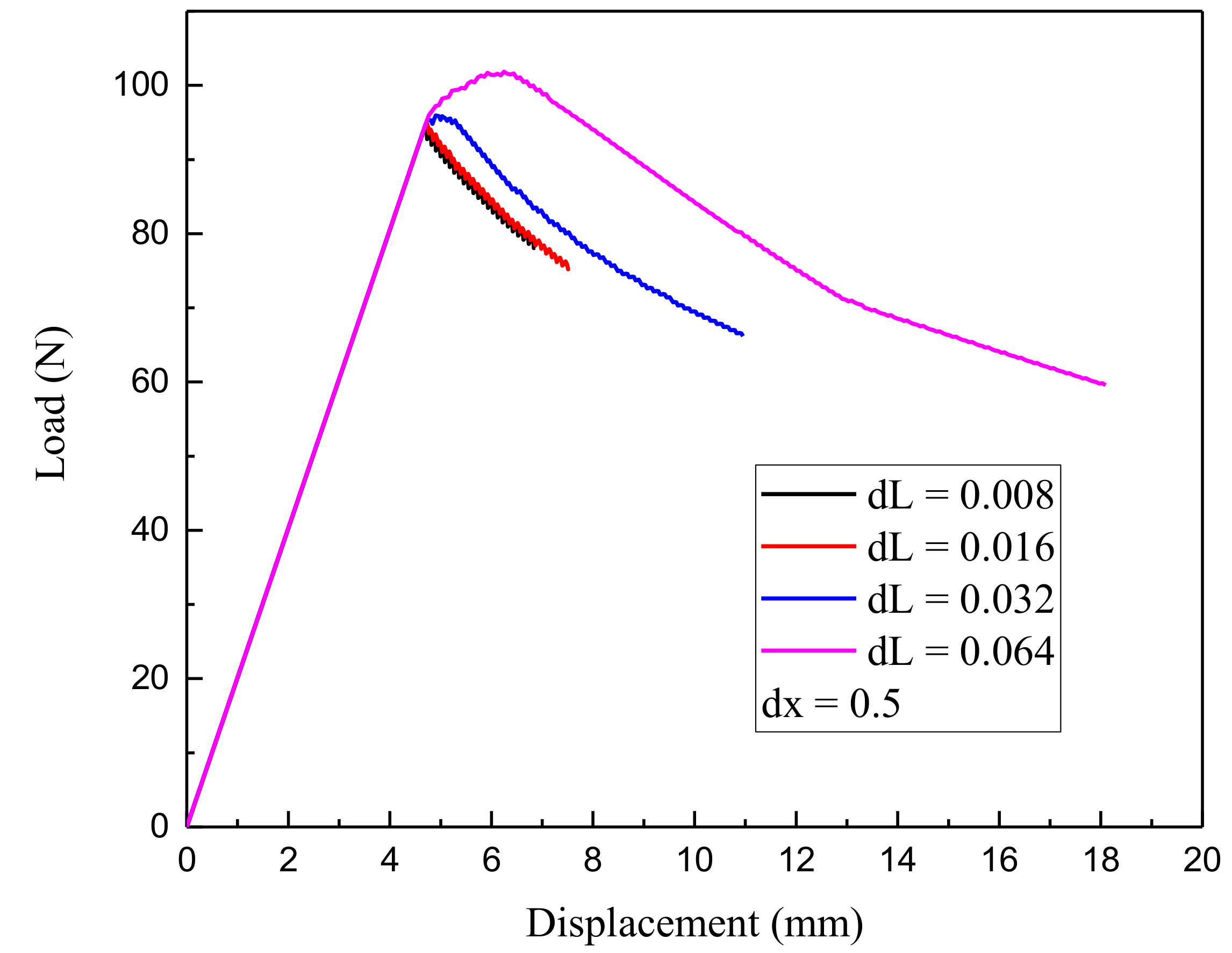
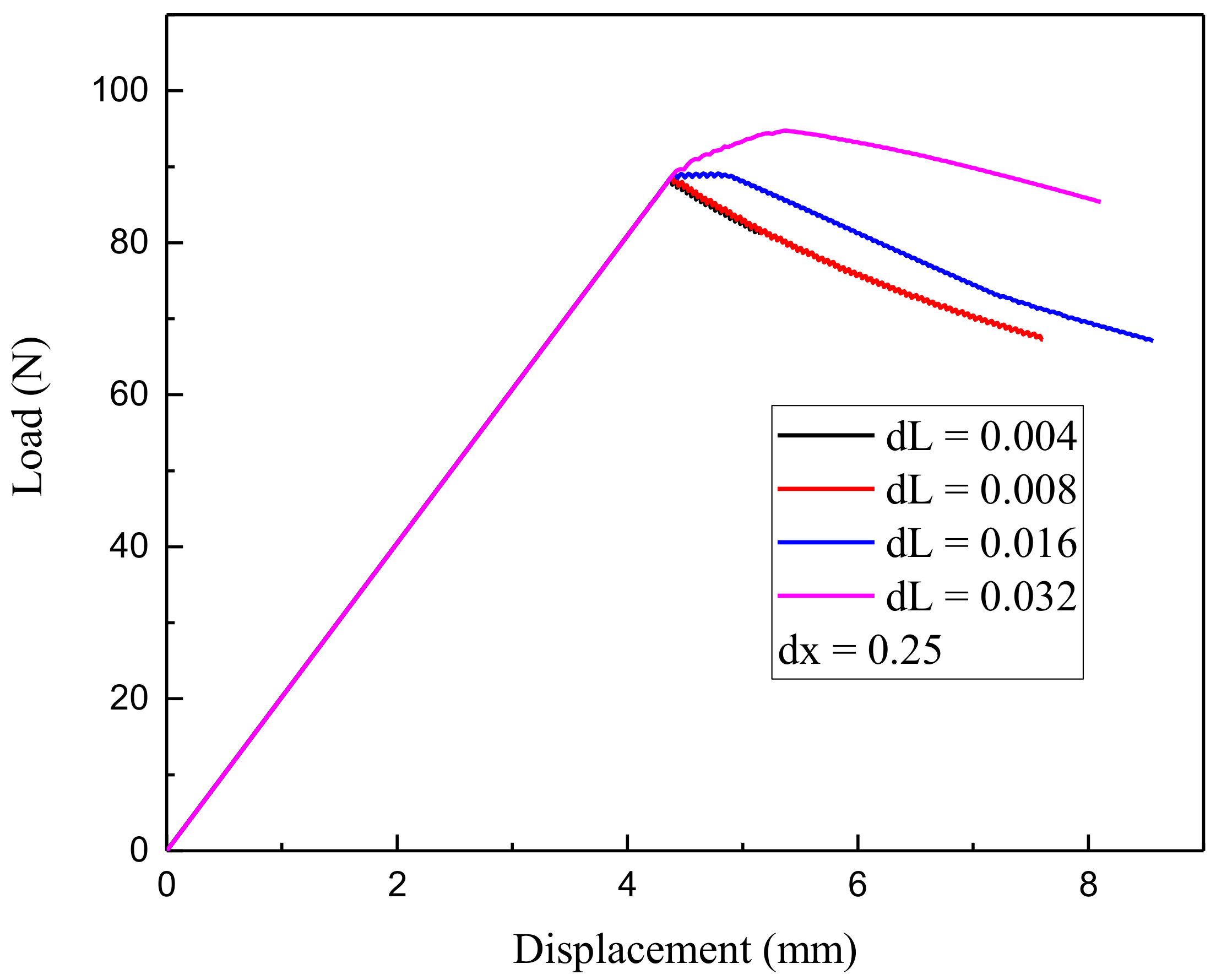
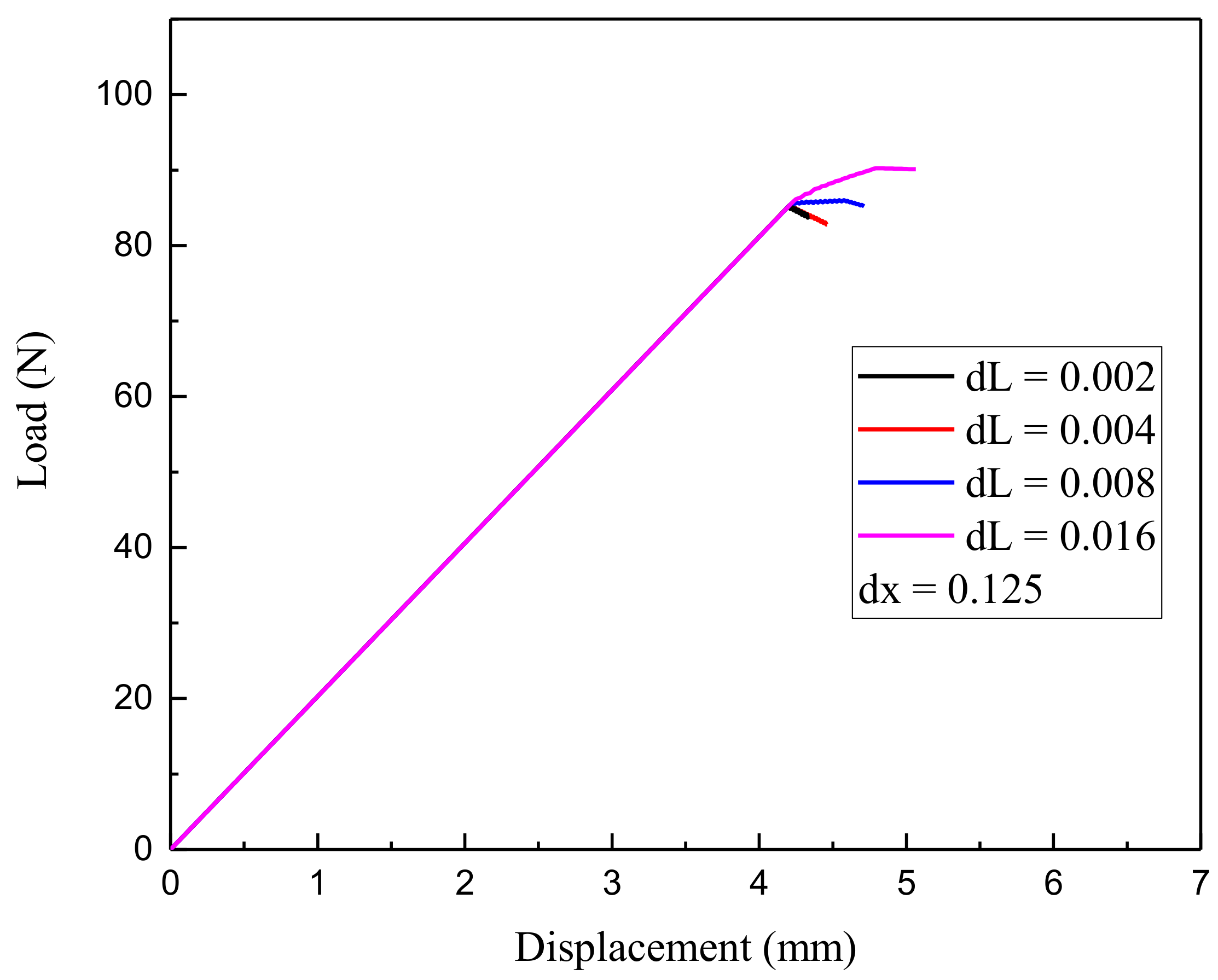
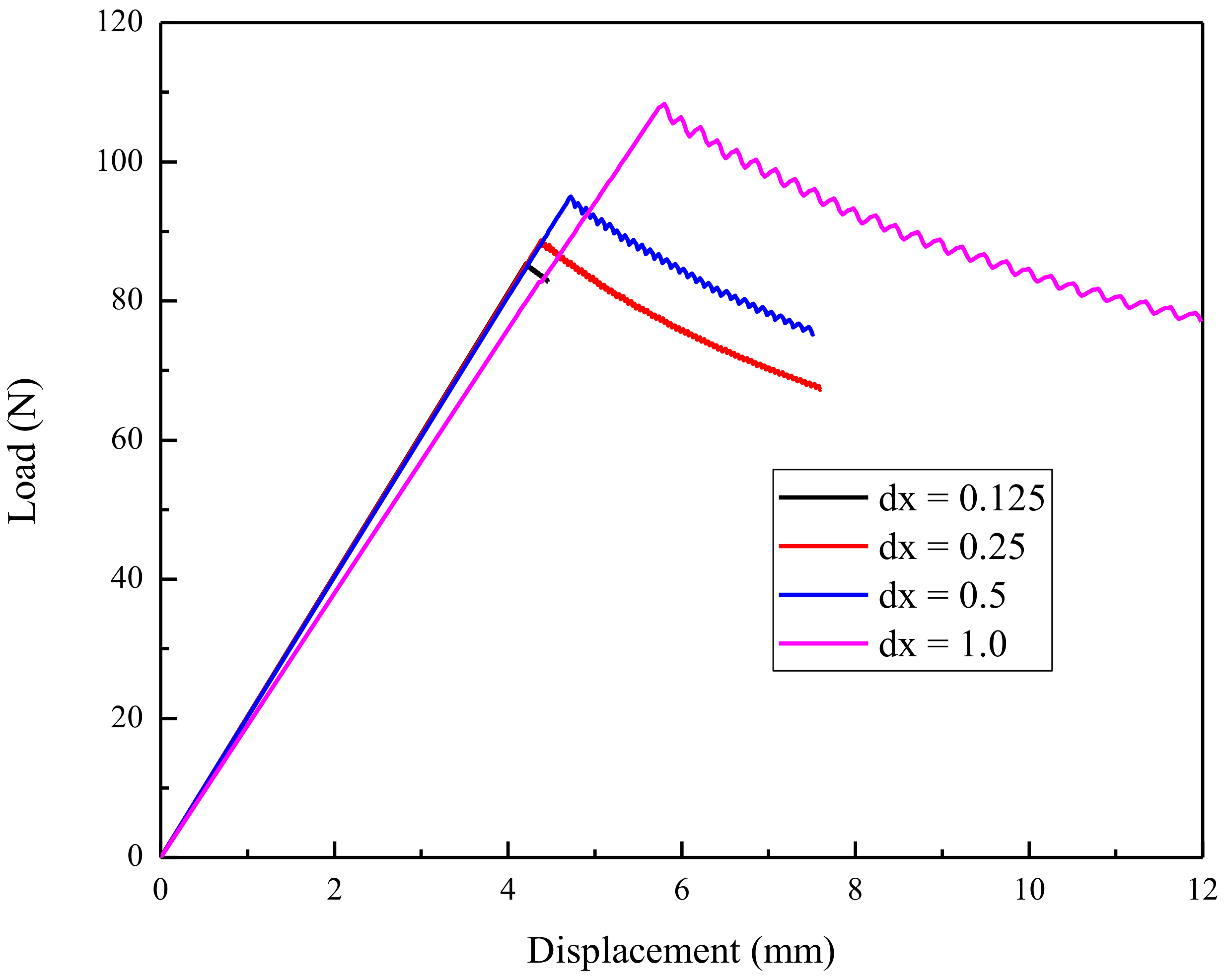
4.1. Loading Increment Convergence Analysis and Grid Spacing Influence Study
- (1)
- For dx = 1.0, dL: 0.128, 0.064, 0.032, 0.016 (mm);
- (2)
- For dx = 0.5, dL: 0.064, 0.032, 0.016, 0.008 (mm);
- (3)
- For dx = 0.25, dL: 0.032, 0.016, 0.008, 0.004 (mm);
- (4)
- For dx = 0.125, dL: 0.016, 0.008, 0.004, 0.002 (mm).
4.2. Comparison of Load–Displacement Curve and Delamination Growth Process
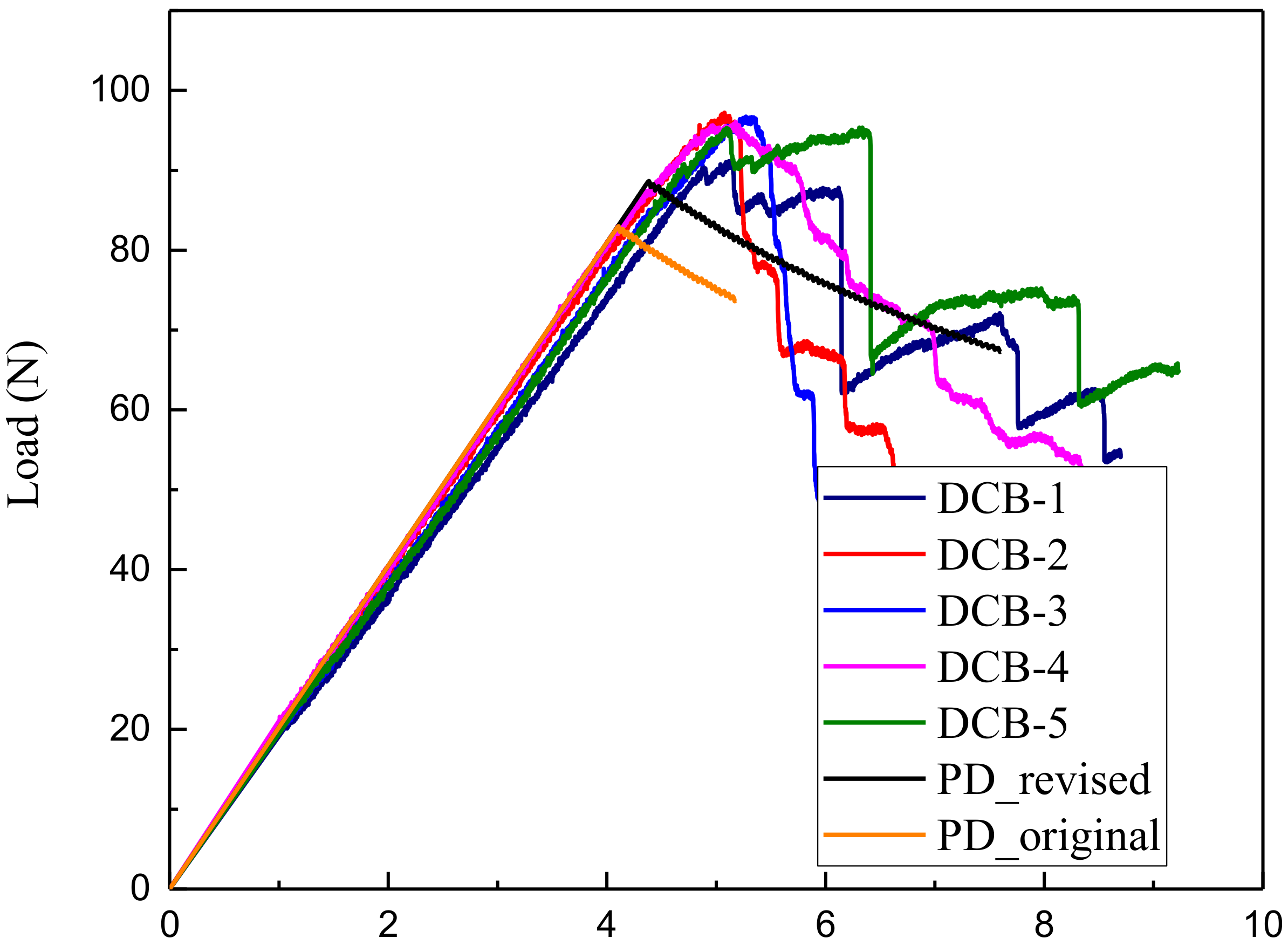
4.3. Comparison of Numerical Modeling Using Revised and Original Energy-Based Failure Criteria
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Stiffness Matrix of DCB Composite Specimen in x–z Direction
Appendix A.2. Derivation Procedure of PD Material Parameters
References
- Alfano, G.; Crisfield, M.A. Finite element interface models for the delamination analysis of laminated composites: Mechanical and computational issues. Int. J. Numer. Methods Eng. 2001, 50, 1701–1736. [Google Scholar] [CrossRef]
- Camanho, P.P.; Vila, C.G.D.; Ambur, D.R. Numerical Simulation of Delamination Growth in Composite Materials; NASA Technical Paper 211041; NASA: Washington, DC, USA, 2001; pp. 1–24.
- Camanho, P.P.; Dávila, C.G.; De Moura, M.F. Numerical simulation of mixed-mode progressive delamination in composite materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar] [CrossRef]
- Meo, M.; Thieulot, E. Delamination modelling in a double cantilever beam. Compos. Struct. 2005, 71, 429–434. [Google Scholar] [CrossRef]
- Zhao, L.; Zhi, J.; Zhang, J.; Liu, Z.; Hu, N. XFEM simulation of delamination in composite laminates. Compos. Part A Appl. Sci. Manuf. 2016, 80, 61–71. [Google Scholar] [CrossRef]
- Kim, S.H.; Kim, C.G. Optimal design of composite stiffened panel with cohesive elements using micro-genetic algorithm. J. Compos. Mater. 2008, 42, 2259–2273. [Google Scholar] [CrossRef]
- Orifici, A.C.; Shah, S.A.; Herszberg, I.; Kotler, A.; Weller, T. Failure analysis in postbuckled composite T-sections. Compos. Struct. 2008, 86, 146–153. [Google Scholar] [CrossRef]
- Riccio, A.; Raimondo, A.; Di Felice, G.; Scaramuzzino, F. A numerical procedure for the simulation of skin-stringer debonding growth in stiffened composite panels. Aerosp. Sci. Technol. 2014, 39, 307–314. [Google Scholar] [CrossRef]
- Oterkus, E.; Madenci, E. Peridynamic Theory for Damage Initiation and Growth in Composite Laminate. Key Eng. Mater. 2012, 488–489, 355–358. [Google Scholar] [CrossRef]
- Xu, J.; Askari, A.; Weckner, O.; Silling, S. Peridynamic Analysis of Impact Damage in Composite Laminates. J. Aerosp. Eng. 2008, 21, 187–194. [Google Scholar] [CrossRef]
- Askari, E.; Xu, J.; Silling, S. Peridynamic Analysis of Damage and Failure in Composites. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2006; pp. 1–12. [Google Scholar]
- Hu, Y.L.; De Carvalho, N.V.; Madenci, E. Peridynamic modeling of delamination growth in composite laminates. Compos. Struct. 2015, 132, 610–620. [Google Scholar] [CrossRef]
- Silling, S.A.; Epton, M.; Weckner, O.; Xu, J.; Askari, E. Peridynamic states and constitutive modeling. J. Elast. 2007, 88, 151–184. [Google Scholar] [CrossRef]
- Silling, S.A. Reformulation of elasticity theory for discontinuities and long-range forces. J. Mech. Phys. Solids 2000, 48, 175–209. [Google Scholar] [CrossRef] [Green Version]
- Silling, S.A.; Lehoucq, R.B. Peridynamic Theory of Solid Mechanics. In Advances in Applied Mechanics; Aref, H., VanDerGiessen, E., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 73–168. [Google Scholar]
- Diyaroglu, C.; Oterkus, E.; Madenci, E.; Rabczuk, T.; Siddiq, A. Peridynamic modeling of composite laminates under explosive loading. Compos. Struct. 2016, 144, 14–23. [Google Scholar] [CrossRef] [Green Version]
- Oterkus, E.; Madenci, E. Peridynamic Analysis of Fiber Reinforced Composite Materials. J. Mech. Mater. Struct. 2012, 7, 45–84. [Google Scholar] [CrossRef]
- Oterkus, E.; Madenci, E.; Weckner, O.; Silling, S.; Bogert, P.; Tessler, A. Combined finite element and peridynamic analyses for predicting failure in a stiffened composite curved panel with a central slot. Compos. Struct. 2012, 94, 839–850. [Google Scholar] [CrossRef]
- Oterkus, E.; Barut, A.; Madenci, E. Damage Growth Prediction from Loaded Composite Fastener Holes by Using Peridynamic Theory. In Proceedings of the 51th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, FL, USA, 12–15 April 2010. Paper No.2010-3026. [Google Scholar]
- Hu, Y.; Yu, Y.; Wang, H. Peridynamic analytical method for progressive damage in notched composite laminates. Compos. Struct. 2014, 108, 801–810. [Google Scholar] [CrossRef]
- Hu, Y.L.; Madenci, E. Bond-based peridynamic modeling of composite laminates with arbitrary fiber orientation and stacking sequence. Compos. Struct. 2016, 153, 139–175. [Google Scholar] [CrossRef]
- Hu, Y.; Madenci, E.; Phan, N.D. Peridynamics for Predicting Tensile and Compressive Strength of Notched Composites. In Proceedings of the 57th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, San Diego, CA, USA, 4–8 January 2016; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2016. [Google Scholar]
- Hu, Y.L.; Madenci, E. Peridynamics for fatigue life and residual strength prediction of composite laminates. Compos. Struct. 2017, 160, 169–184. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Shokrieh, M.M.; Camanho, P.P. Finite element modeling of mode I delamination growth in laminated DCB specimens with R-curve effects. Compos. Part B Eng. 2013, 45, 897–903. [Google Scholar] [CrossRef]
- Shanmugam, V.; Penmetsa, R.; Tuegel, E.; Clay, S. Stochastic modeling of delamination growth in unidirectional composite DCB specimens using cohesive zone models. Compos. Struct. 2013, 102, 38–60. [Google Scholar] [CrossRef]
- Krueger, R. A summary of benchmark examples to assess the performance of quasi-static delamination propagation prediction capabilities in finite element codes. J. Compos. Mater. 2015, 49, 3297–3316. [Google Scholar] [CrossRef]
- Madenci, E.; Oterkus, E. Peridynamic Theory and Its Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Silling, S.A.; Askari, E. A meshfree method based on the peridynamic model of solid mechanics. Comput. Struct. 2005, 83, 1526–1535. [Google Scholar] [CrossRef]
- Kilic, B.; Madenci, E. An adaptive dynamic relaxation method for quasi-static simulations using the peridynamic theory. Theor. Appl. Fract. Mech. 2010, 53, 194–204. [Google Scholar] [CrossRef]
- Breitenfeld, M.S.; Geubelle, P.H.; Weckner, O.; Silling, S.A. Non-ordinary state-based peridynamic analysis of stationary crack problems. Comput. Methods Appl. Mech. Eng. 2014, 272, 233–250. [Google Scholar] [CrossRef]
- Ni, T.; Zaccariotto, M.; Zhu, Q.-Z.; Galvanetto, U. Static solution of crack propagation problems in Peridynamics. Comput. Methods Appl. Mech. Eng. 2019, 346, 126–151. [Google Scholar] [CrossRef]
- Fatica, M.; Ruetsch, G. CUDA Fortran for Scientists and Engineers: Best Practices for Efficient CUDA Fortran Programming; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- ASTM: D5528-13: Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; American Society for Testing and Materials: West Conshohocken, PA, USA, 2013.
- Beckmann, R.; Mella, R.; Wenman, M.R. Mesh and timestep sensitivity of fracture from thermal strains using peridynamics implemented in Abaqus. Comput. Methods Appl. Mech. Eng. 2013, 263, 71–80. [Google Scholar] [CrossRef]
- Henke, S.F.; Shanbhag, S. Mesh sensitivity in peridynamic simulations. Comput. Phys. Commun. 2014, 185, 181–193. [Google Scholar] [CrossRef]
- Steward, R.J.; Jeon, B. Decoupling strength and grid resolution. In Proceedings of the 18th U.S. National Congress for Theoretical and Applied Mechanics, Chicago, IL, USA, 4–9 June 2018. [Google Scholar]

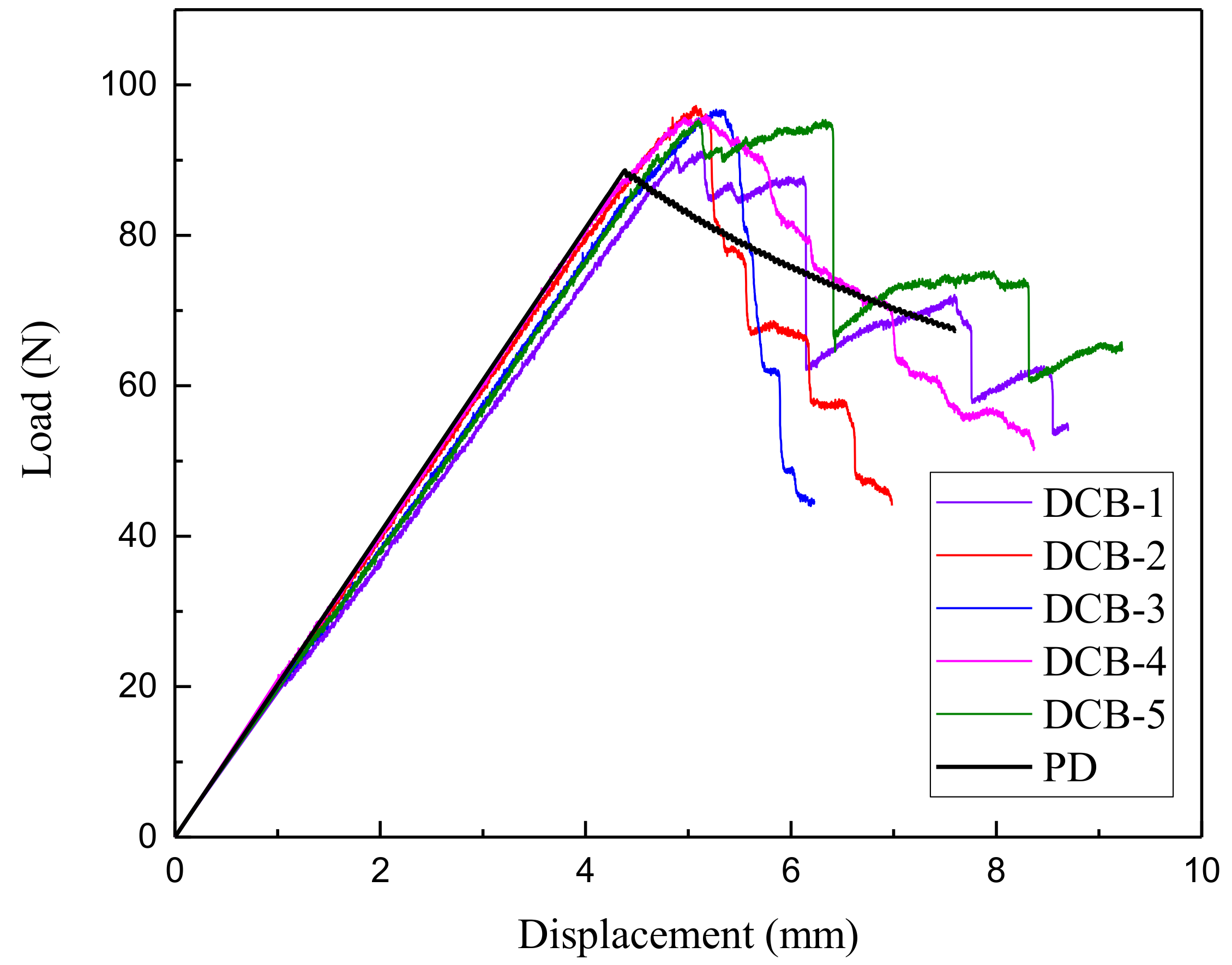
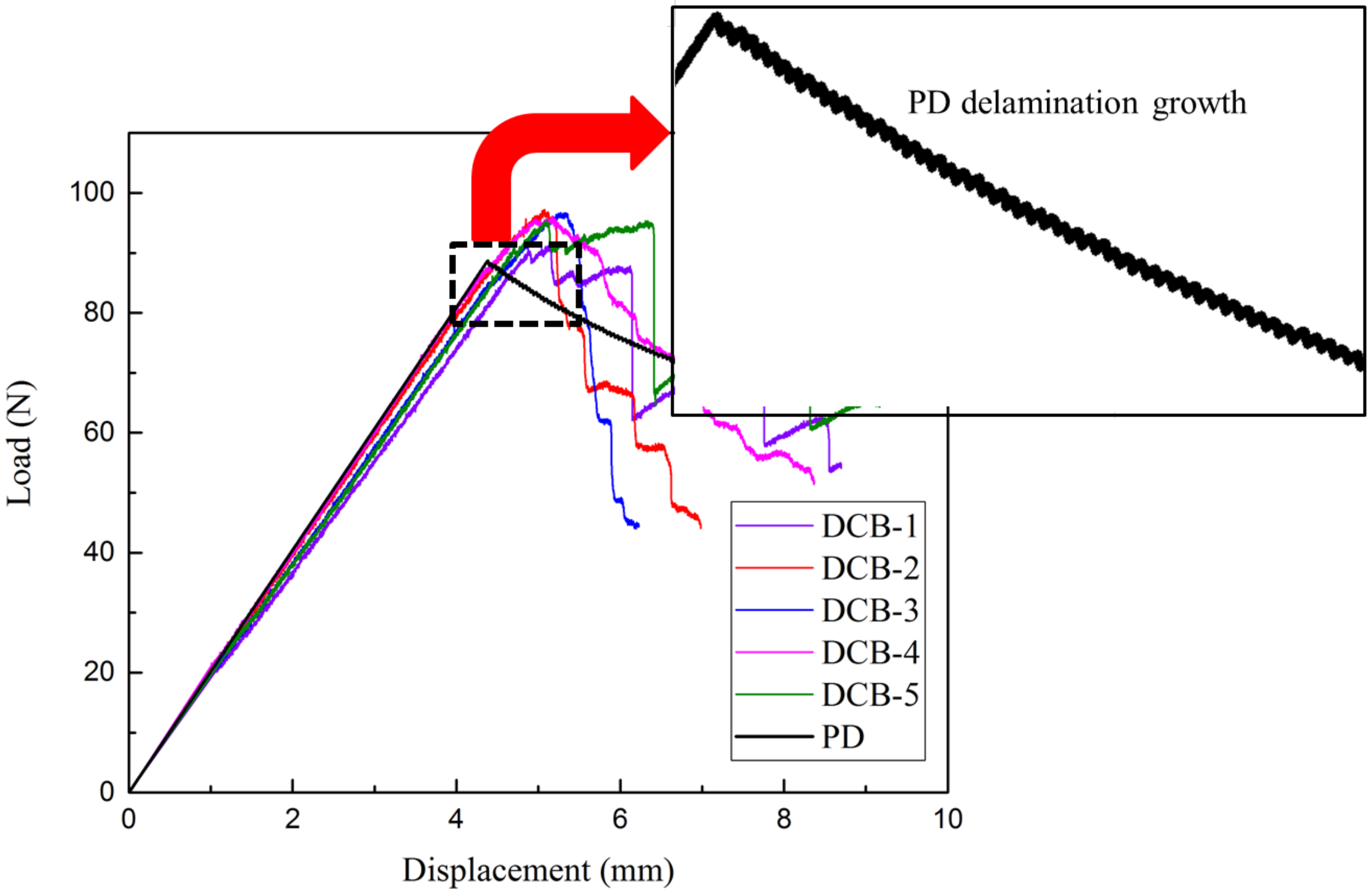
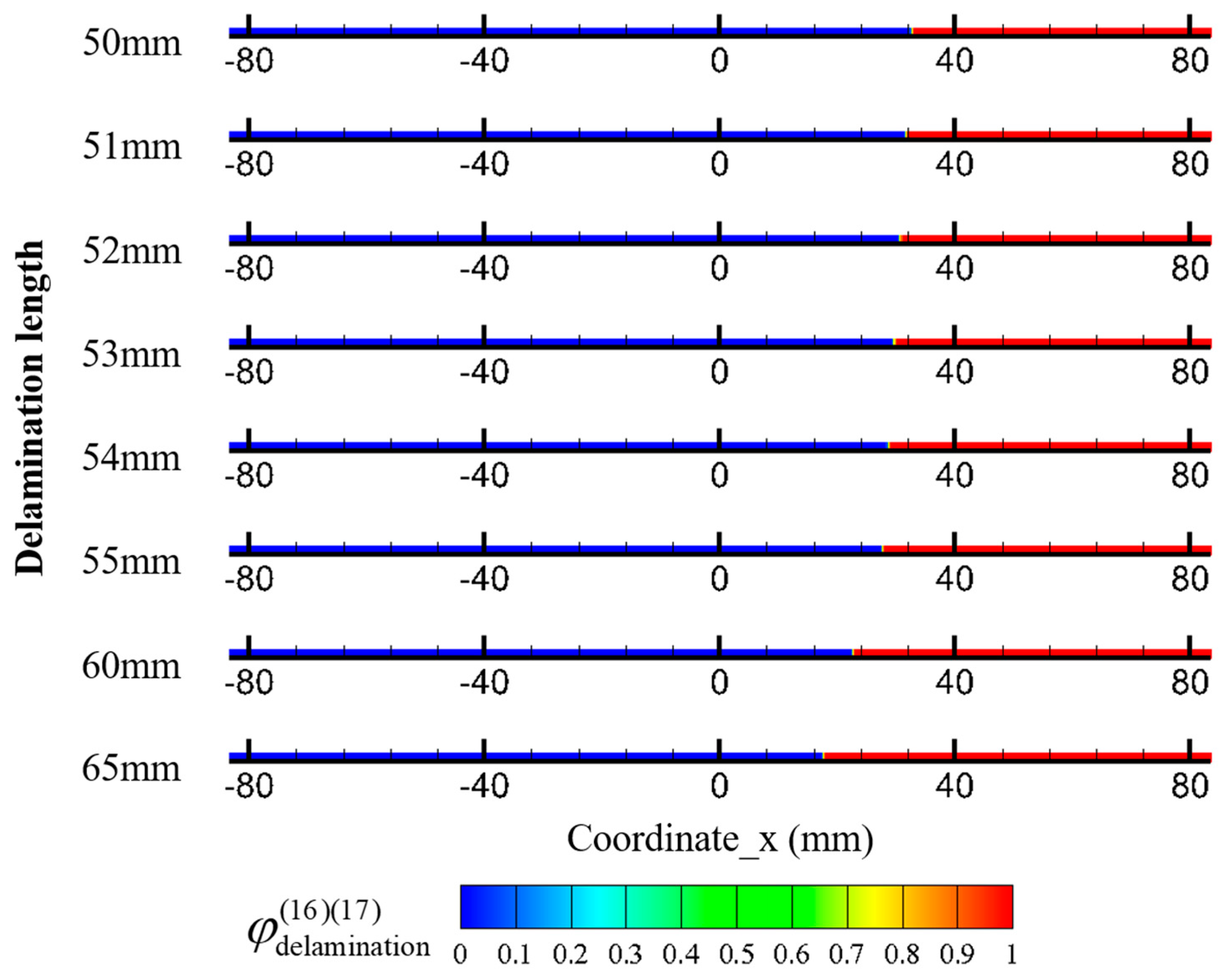
| DELL (mm) | DCB-1 | DCB-2 | DCB-3 | DCB-4 | DCB-5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Disp. (mm) | Load (N) | Disp. (mm) | Load (N) | Disp. (mm) | Load (N) | Disp. (mm) | Load (N) | Disp. (mm) | Load (N) | |
| 50 | 4.77 | 88.04 | 5.07 | 97.22 | 5.52 | 86.16 | 5.27 | 94.29 | 4.79 | 91.07 |
| 51 | 5.17 | 87.59 | 5.23 | 86.22 | 5.59 | 79.09 | 5.27 | 94.29 | 5.24 | 91.09 |
| 52 | 5.18 | 85.84 | 5.26 | 82.09 | 5.60 | 77.87 | 5.75 | 89.35 | 5.34 | 90.19 |
| 53 | 5.20 | 85.23 | 5.29 | 81.60 | 5.62 | 77.53 | 5.75 | 89.35 | 5.62 | 92.44 |
| 54 | 5.26 | 85.60 | 5.30 | 80.78 | 5.65 | 72.54 | 5.75 | 89.35 | 5.62 | 92.44 |
| 55 | 5.54 | 84.56 | 5.34 | 80.10 | 5.67 | 69.59 | 5.96 | 81.77 | 6.02 | 93.91 |
| 60 | 6.15 | 62.19 | 5.52 | 77.25 | 5.89 | 55.74 | 6.47 | 74.20 | 6.42 | 66.33 |
| 65 | 6.79 | 68.00 | 6.15 | 66.52 | 6.03 | 47.80 | 7.13 | 62.66 | 8.12 | 73.22 |
| 127 | 7.9 | 4.2 | 0.32 | 0.512 |
| DELL (mm) | Experimental Avg. | PD | Difference | |||
|---|---|---|---|---|---|---|
| Disp. (mm) | Load (N) | Disp. (mm) | Load (N) | Disp. (mm) | Load (N) | |
| 50 | 5.09 | 91.35 | 4.39 | 88.66 | −13.78% | −2.95% |
| 51 | 5.30 | 87.66 | 4.55 | 87.16 | −14.10% | −0.57% |
| 52 | 5.43 | 85.07 | 4.72 | 85.64 | −13.00% | 0.67% |
| 53 | 5.49 | 85.23 | 4.89 | 84.13 | −11.00% | −1.30% |
| 54 | 5.52 | 84.14 | 5.06 | 82.62 | −8.29% | −1.81% |
| 55 | 5.70 | 81.99 | 5.23 | 81.24 | −8.26% | −0.91% |
| 60 | 6.09 | 67.14 | 6.16 | 75.05 | 1.16% | 11.78% |
| 65 | 6.84 | 63.64 | 7.16 | 69.72 | 4.66% | 9.55% |
| Comparison | Experimental Avg. | PD_original | PD_revised |
|---|---|---|---|
| Max load | 95.29 | 82.97 | 88.66 |
| Difference | / | −12.93% | −6.96% |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.-W.; Guo, S.; Li, H.; Wang, H. Peridynamic Modeling of Mode-I Delamination Growth in Double Cantilever Composite Beam Test: A Two-Dimensional Modeling Using Revised Energy-Based Failure Criteria. Appl. Sci. 2019, 9, 656. https://doi.org/10.3390/app9040656
Jiang X-W, Guo S, Li H, Wang H. Peridynamic Modeling of Mode-I Delamination Growth in Double Cantilever Composite Beam Test: A Two-Dimensional Modeling Using Revised Energy-Based Failure Criteria. Applied Sciences. 2019; 9(4):656. https://doi.org/10.3390/app9040656
Chicago/Turabian StyleJiang, Xiao-Wei, Shijun Guo, Hao Li, and Hai Wang. 2019. "Peridynamic Modeling of Mode-I Delamination Growth in Double Cantilever Composite Beam Test: A Two-Dimensional Modeling Using Revised Energy-Based Failure Criteria" Applied Sciences 9, no. 4: 656. https://doi.org/10.3390/app9040656
APA StyleJiang, X.-W., Guo, S., Li, H., & Wang, H. (2019). Peridynamic Modeling of Mode-I Delamination Growth in Double Cantilever Composite Beam Test: A Two-Dimensional Modeling Using Revised Energy-Based Failure Criteria. Applied Sciences, 9(4), 656. https://doi.org/10.3390/app9040656