Lifetime Prognosis of Lithium-Ion Batteries Through Novel Accelerated Degradation Measurements and a Combined Gamma Process and Monte Carlo Method
Abstract
:Featured Applications
Abstract
1. Introduction
2. Method
2.1. Physical-Based Reliability Model
2.2. Gamma Process Model
- y(0) = 0
- the increments ∆y(t) = y(t + ) − y(t) are independent
- ∆y(t) has a gamma distribution G(α, β), with the probability density function (PDF) defined by
2.3. Monte Carlo Simulation
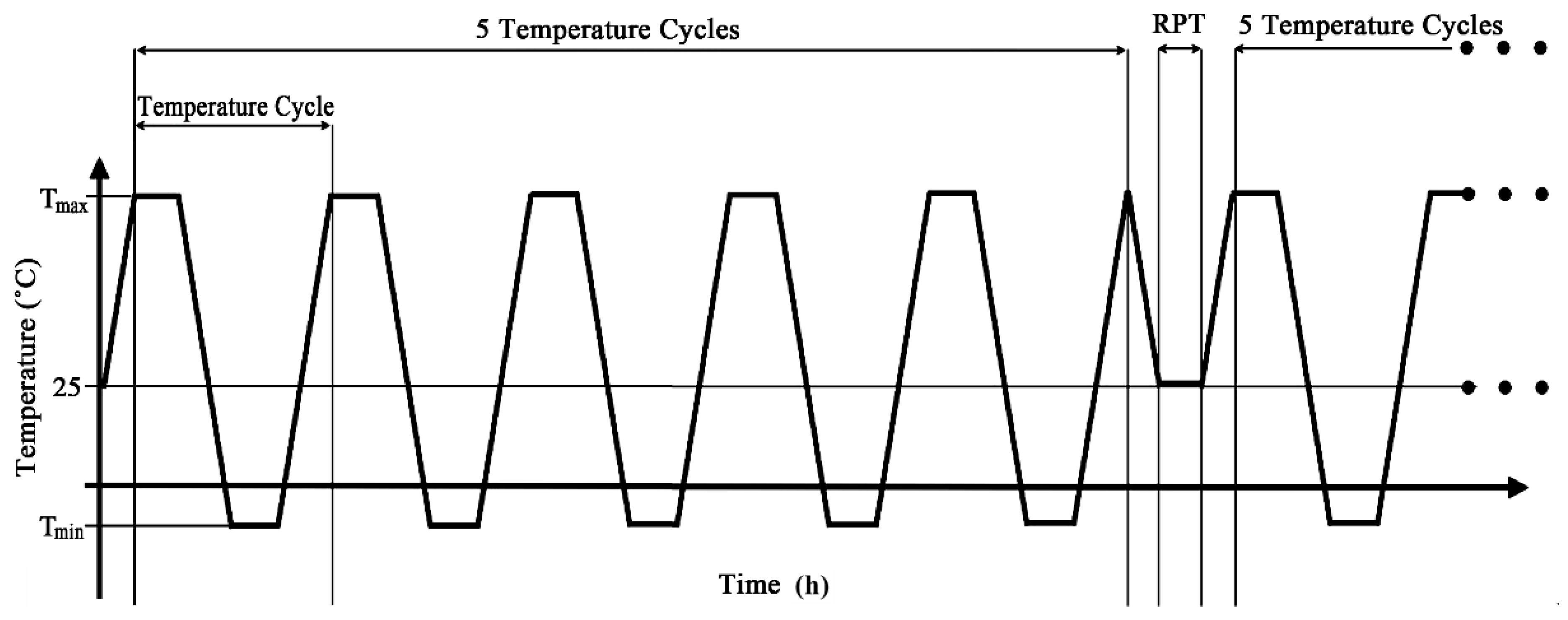
3. Experiment
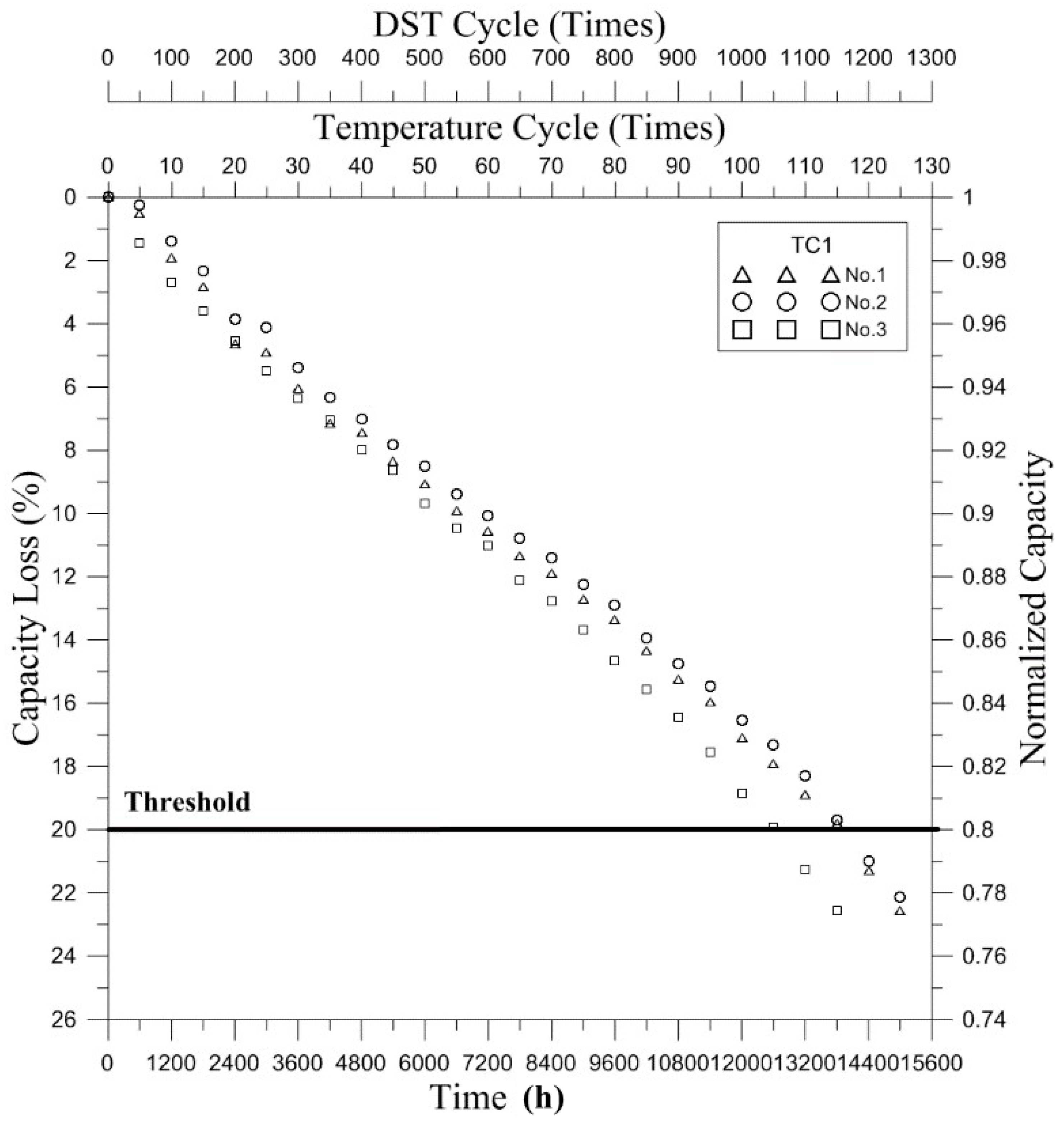
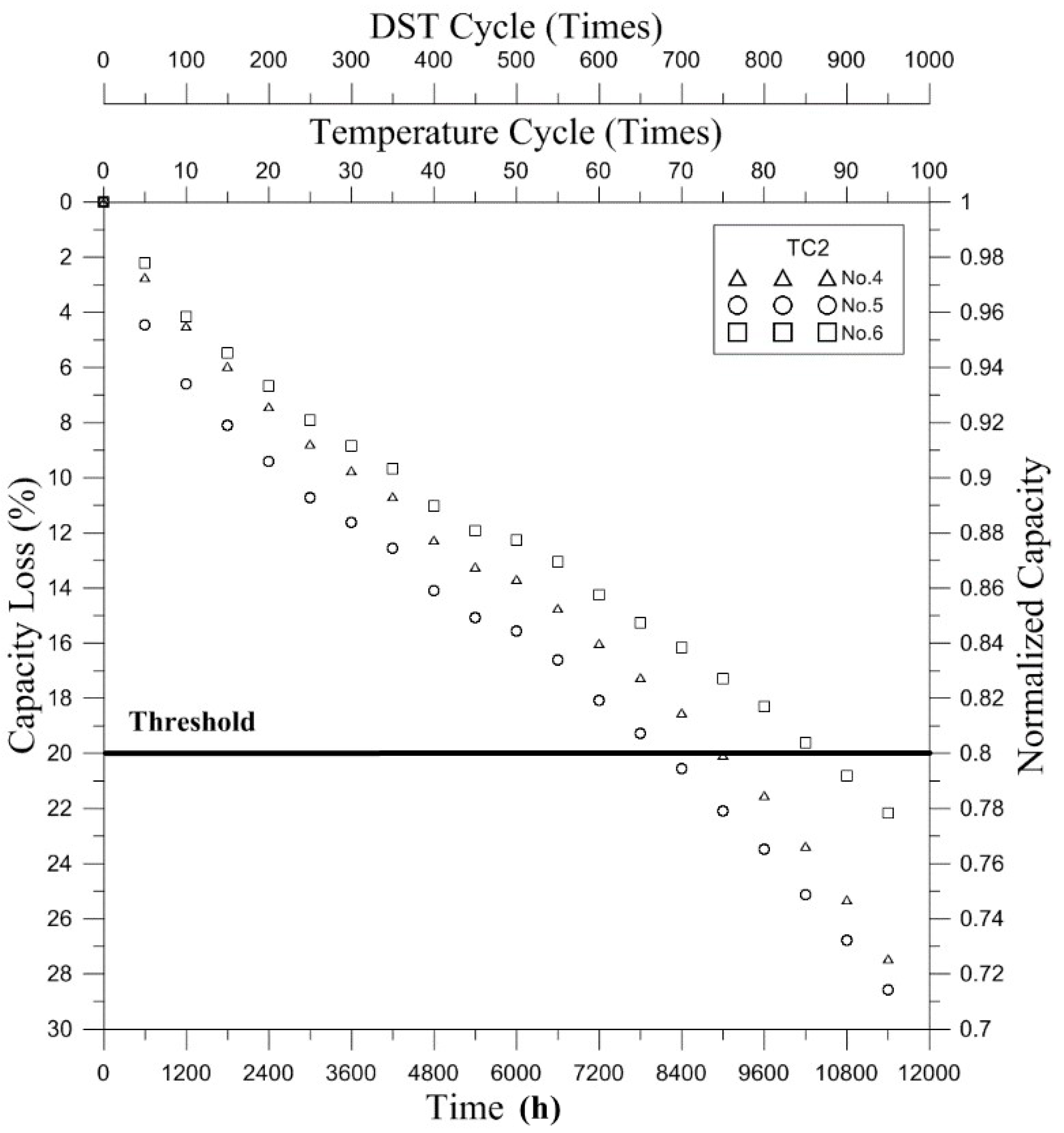
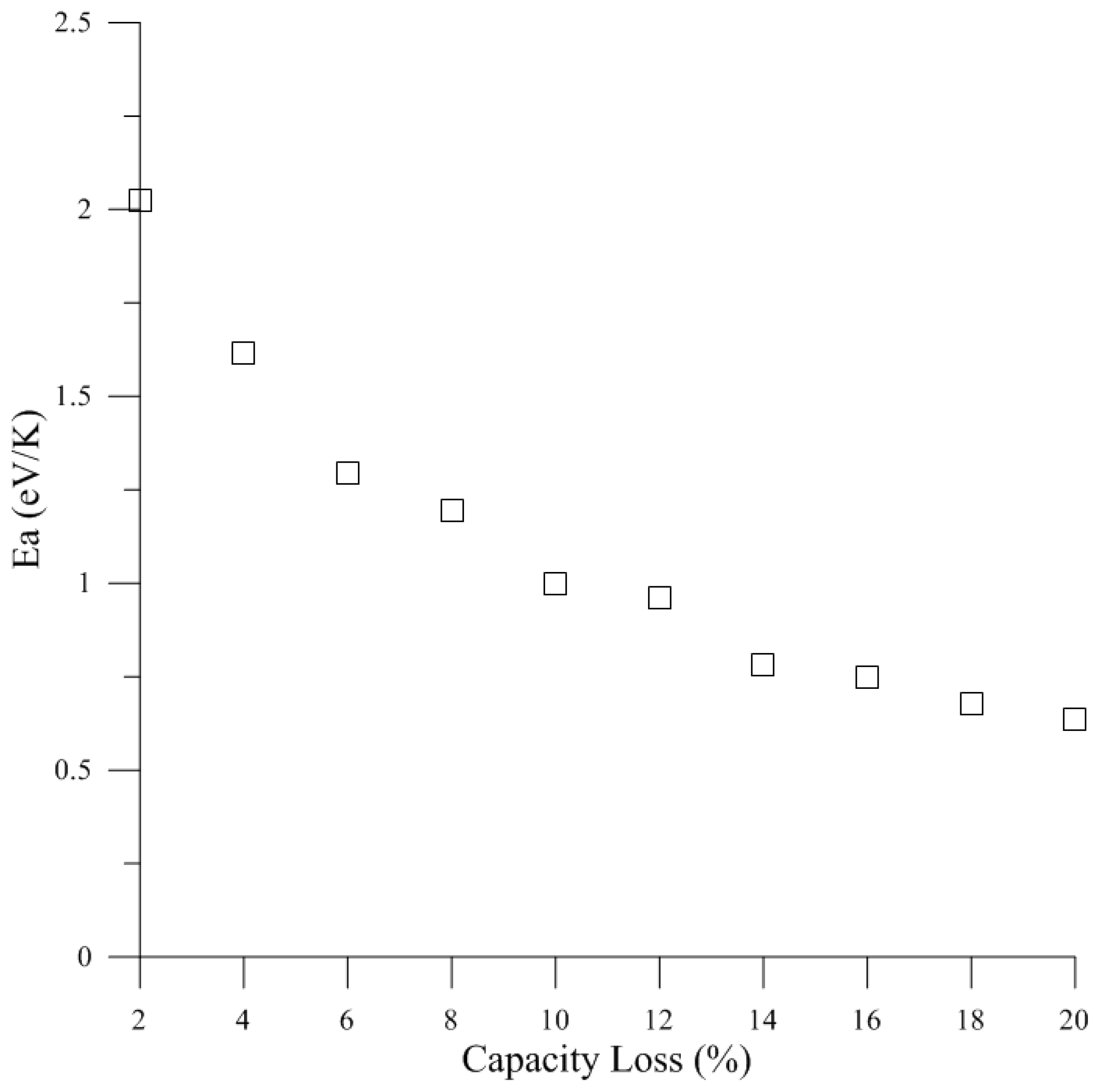
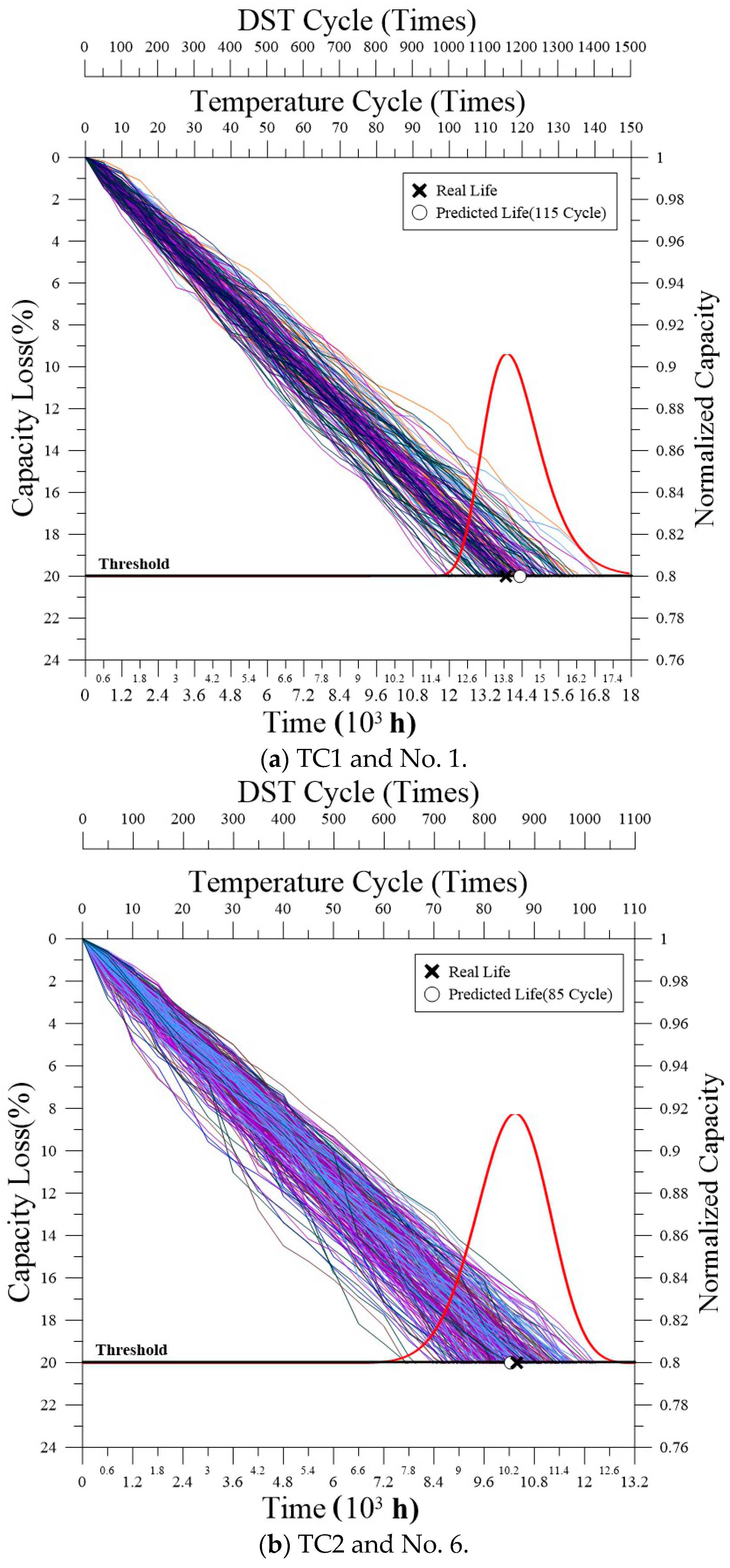
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Santhanagopalan, S.; Zhang, Q.; Kumaresan, K.; White, R.E. Parameter estimation and life modeling of lithium-ion cells. J. Electrochem. Soc. 2008, 155, A345–A353. [Google Scholar] [CrossRef]
- Thomas, E.V.; Case, H.; Doughty, D.; Jungst, R.; Nagasubramanian, G.; Roth, E. Accelerated power degradation of li-ion cells. J. Power Sources 2003, 124, 254–260. [Google Scholar] [CrossRef]
- Spotnitz, R. Simulation of capacity fade in lithium-ion batteries. J. Power Sources 2003, 113, 72–80. [Google Scholar] [CrossRef]
- Hoog, J.; Timmermans, J.; Ioan-Stroe, D.; Swierczynski, M.; Jaguemont, J.; Goutam, S.; Omar, N.; Mierlo, J.; Bossche, P. Combined cycling and calendar capacity fade modeling of a Nickel-Manganese-Cobalt Oxide Cell with real-life profile validation. Appl. Energy 2017, 200, 47–61. [Google Scholar] [CrossRef]
- Sutter, L.; Berckmans, G.; Marinaro, M.; Smekens, J.; Firouz, Y.; Wohlfahrt-Mehrens, M.; Mierlo JOmar, N. Comprehensive aging analysis ofvolumetric constrained Lithium-ion pouch cells with high concentration silicon-alloy anodes. Energies 2018, 11, 2948. [Google Scholar] [CrossRef]
- Oldham, H.; Myland, J. Fundamentals of Electrochemical Science; Academic: San Diego, CA, USA, 1994. [Google Scholar]
- Shiao, C.C.; Chung, K.J. Accelerated degradation assessment of 18650 li-ion batteries. In Proceedings of the IEEE 2012 International Symposium on Computer, Consumer, and Control, Taichung, Taiwan, 4–6 June 2012; pp. 930–933. [Google Scholar]
- Rong, P.; Pedram, M. An analytical model for predicting the remaining battery capacity of lithium-ion batteries. IEEE Trans. VLSI Syst. 2006, 14, 441–451. [Google Scholar] [CrossRef]
- Armand, J.M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar]
- Ramadass, P.; Haran, B.; Gomadam, P.; White, R.; Popov, B. Development of first principles capacity fade model for li-ion cells. J. Electrochem. Soc. 2004, 151, A196–A203. [Google Scholar] [CrossRef]
- Christensen, J.; Newman, J. Effect of anode film resistance on the charge/discharge capacity of a lithium-ion battery. J. Electrochem. Soc. 2003, 150, A1416–A1420. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Ning, G.; White, R.; Popov, B. A generalized cycle life model of rechargeable li-ion batteries. Electrochim. Acta 2006, 51, 2012–2022. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chung, K.J.; Hsiao, C.C. A Novel Double Dynamic Stress Accelerated Degradation Test to Evaluate Power Fade of Batteries for Electric Vehicles. In Intelligent Technologies and Engineering Systems; Lecture Notes of Electrical Engineering; Springer: New York, NY, USA, 2013; Volume 234, pp. 161–168. [Google Scholar]
- Wu, Q.; Yang, J.; Wang, J.; Xue, L. Reliability analysis of degradation with a new independent increment process. J. Mech. Sci. Technol. 2014, 28, 3971–3976. [Google Scholar] [CrossRef]
- Wei, H.; Dietrich, D.L. An alternative degradation reliability modeling approach using maximum likelihood estimation. IEEE Trans. Reliab. 2005, 54, 310–317. [Google Scholar]
- Weaver, B.P.; Meeker, W.Q. Methods for planning repeated measures accelerated degradation tests. Appl. Stoch. Models Bus. Ind. 2014, 30, 658–671. [Google Scholar] [CrossRef]
- Whitmore, G.A. Estimating degradation by a Wiener diffusion process subjected to measurement error. Lifetime Data Anal. 1995, 1, 307–319. [Google Scholar] [CrossRef] [PubMed]
- Park, C.; Padgett, W.J. Accelerated degradation models for failure based on geometric Brownian motion and Gamma processes. Lifetime Data Anal. 2005, 11, 511–527. [Google Scholar] [CrossRef] [PubMed]
- Tsai, C.; Tseng, S.; Balakrishnan, N. Optimal design for degradation tests based on Gamma processes with random effects. IEEE. Trans. Reliab. 2012, 61, 604–613. [Google Scholar] [CrossRef]
- Norris, K.C.; Landzberg, A.H. Reliability of Controlled Collapse Interconnections. IBM J. Res. Dev. 1969, 13, 266–271. [Google Scholar] [CrossRef]
- Baussaron, J.; Mihaela, B.; Leo, G.; Fabrice, G.; Paul, S. Reliability assessment based on degradation measurement: How to compare some models. Reliab. Eng. Syst. Saf. 2014, 131, 236–241. [Google Scholar] [CrossRef]
- Wang, H.; Xu, T.; Mi, Q. Lifetime prediction based on Gamma processes from accelerated degradation data. Chin. J. Aeronaut. 2015, 28, 172–179. [Google Scholar] [CrossRef]
- O’connor, P.D.T.; Kleyner, A. Practical Reliability Engineering, 5th ed.; Wiley: Hoboken, NJ, USA, 2012; pp. 109–119. [Google Scholar]
- Omar, N.; Daowd, M.; Hegazy, O.; Mulder, G.; Timmermans, J.; Coosemans, T.; Bossche, P.; Mierlo, J. Standardization work for BEV and HEV applications: Critical appraisal of recent traction battery documents. Energies 2012, 5, 138–156. [Google Scholar] [CrossRef]
- USABC. Electric Vehicle Battery Test Procedures Manual; Rev. 2; USABC and DOE National Laboratories Personnel: Idaho Falls, ID, USA, 1996.
- Ruiz, V.; Persio, F. Standards for the Performance and Durability Assessment of Electric Vehicle Batteries; JRC Tech. Reports; EU: Luxembourg, 2018. [Google Scholar]
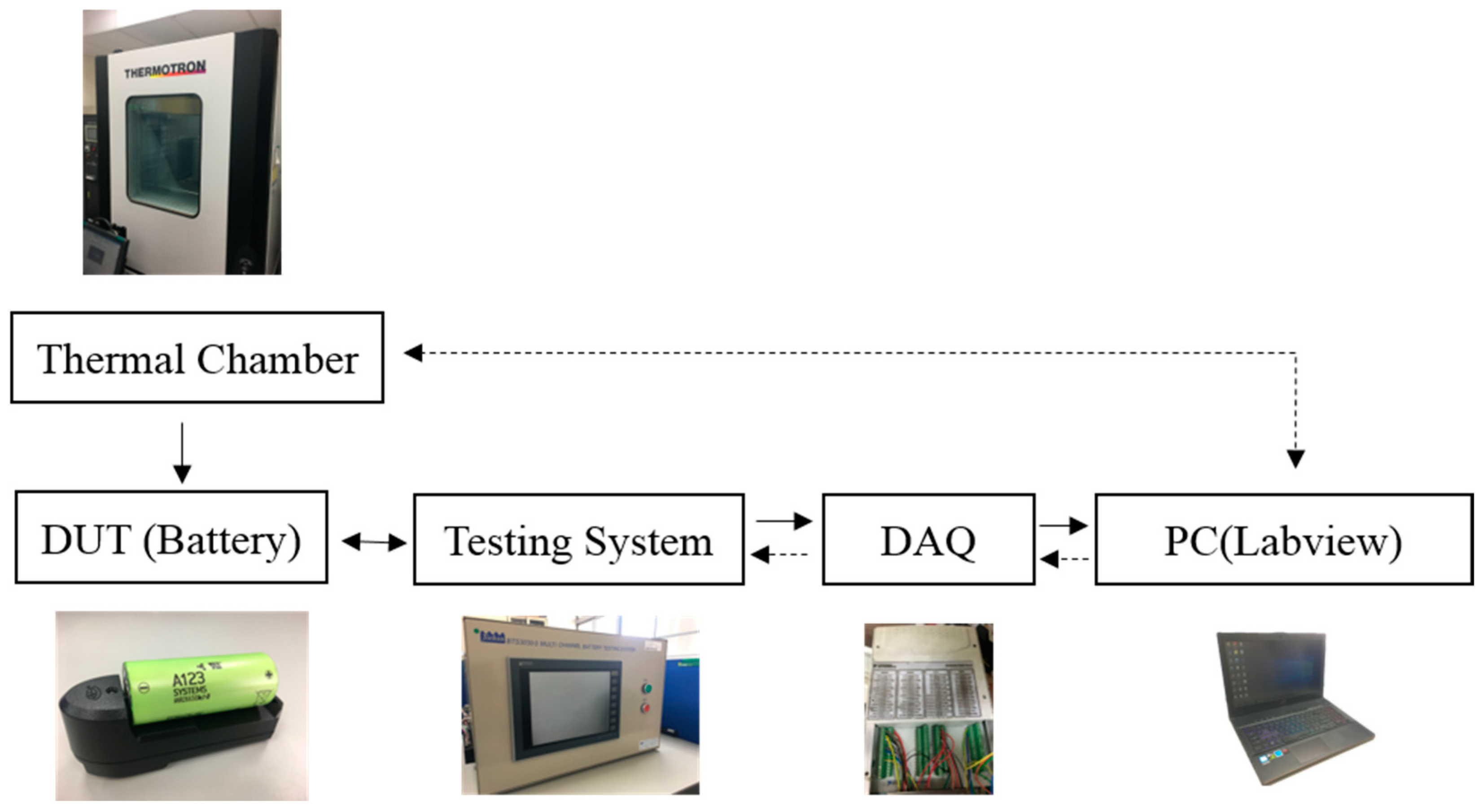


| Cell Brand and Series # | Nominal Voltage | Geometry | Weight | Nominal Capacity | Dimensions | Operation Temperature |
|---|---|---|---|---|---|---|
| A123 ANR26650 | 3.3 V | Cylinder | 76 g | 2300 mAh | 25.85 mm × 65.2 mm | −30 °C ~ 55 °C |
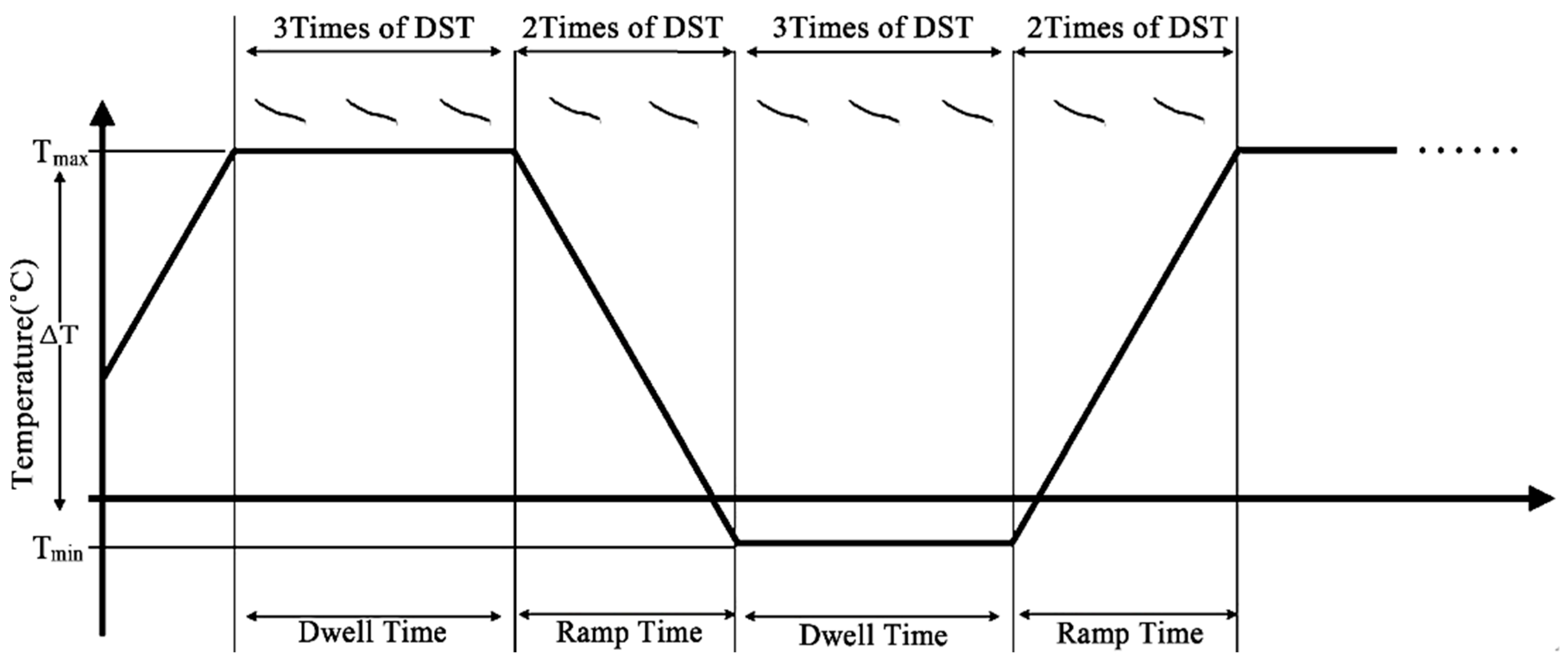
| Test Parameters | TC1 | TC2 |
|---|---|---|
| Tmax, °C | 55 | 60 |
| Tmin, °C | −15 | −10 |
| Temperature Range ΔT, °C | 70 | 70 |
| Dwell Time, h | 35 | 35 |
| Ramp Time, h | 25 | 25 |
| Ramp Rate, °C/h | 2.76 | 2.76 |
| Cycle Duration, day | 5 | 5 |
| Frequency of Usage, cycles/day | 0.2 | 0.2 |
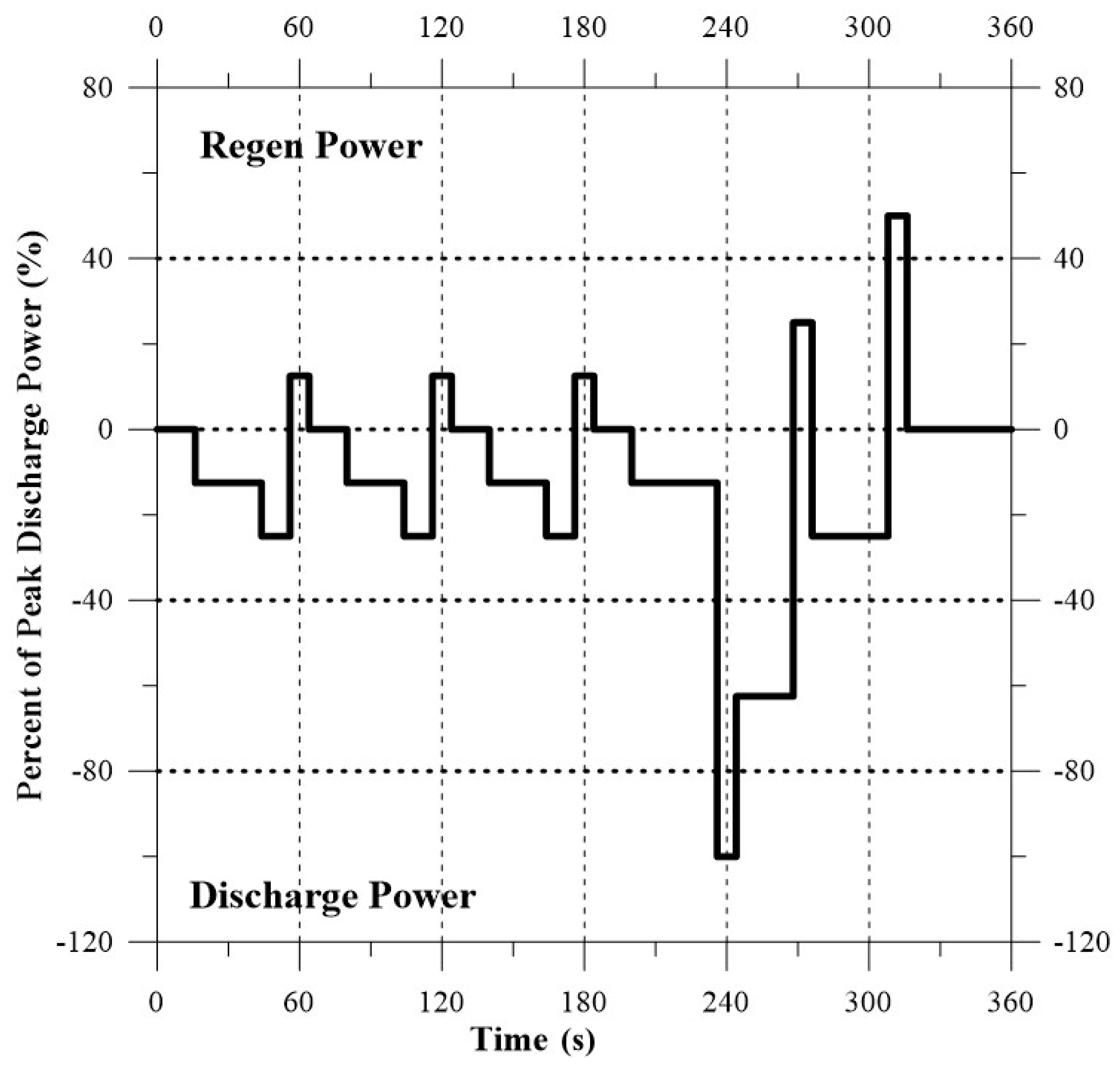
| Step | Time (s) | % | Step | Time (s) | % |
|---|---|---|---|---|---|
| 1 | 16 | 0 | 11 | 12 | −25 |
| 2 | 28 | −12.5 | 12 | 8 | 12.5 |
| 3 | 12 | −25 | 13 | 16 | 0 |
| 4 | 8 | 12.5 | 14 | 36 | −12.5 |
| 5 | 16 | 0 | 15 | 8 | −100 |
| 6 | 24 | −12.5 | 16 | 24 | −62.5 |
| 7 | 12 | −25 | 17 | 8 | 25 |
| 8 | 8 | 12.5 | 18 | 32 | −25 |
| 9 | 16 | 0 | 19 | 8 | 50 |
| 10 | 24 | −12.5 | 20 | 44 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.-C.; Chung, K.-J. Lifetime Prognosis of Lithium-Ion Batteries Through Novel Accelerated Degradation Measurements and a Combined Gamma Process and Monte Carlo Method. Appl. Sci. 2019, 9, 559. https://doi.org/10.3390/app9030559
Lin Y-C, Chung K-J. Lifetime Prognosis of Lithium-Ion Batteries Through Novel Accelerated Degradation Measurements and a Combined Gamma Process and Monte Carlo Method. Applied Sciences. 2019; 9(3):559. https://doi.org/10.3390/app9030559
Chicago/Turabian StyleLin, Yu-Chang, and Kuan-Jung Chung. 2019. "Lifetime Prognosis of Lithium-Ion Batteries Through Novel Accelerated Degradation Measurements and a Combined Gamma Process and Monte Carlo Method" Applied Sciences 9, no. 3: 559. https://doi.org/10.3390/app9030559
APA StyleLin, Y.-C., & Chung, K.-J. (2019). Lifetime Prognosis of Lithium-Ion Batteries Through Novel Accelerated Degradation Measurements and a Combined Gamma Process and Monte Carlo Method. Applied Sciences, 9(3), 559. https://doi.org/10.3390/app9030559




