Analytical Solutions for the Propagation of UltraShort and UltraSharp Pulses in Dispersive Media
Abstract
:1. Introduction
2. Generic Dispersion Analysis
3. Fundamental Dispersion Theorems
3.1. Pulse Boosting and Decaying
3.2. Pulse Chirping
4. Gaussian Pulse
4.1. Boosted Gaussian
4.2. Chirped Gaussian
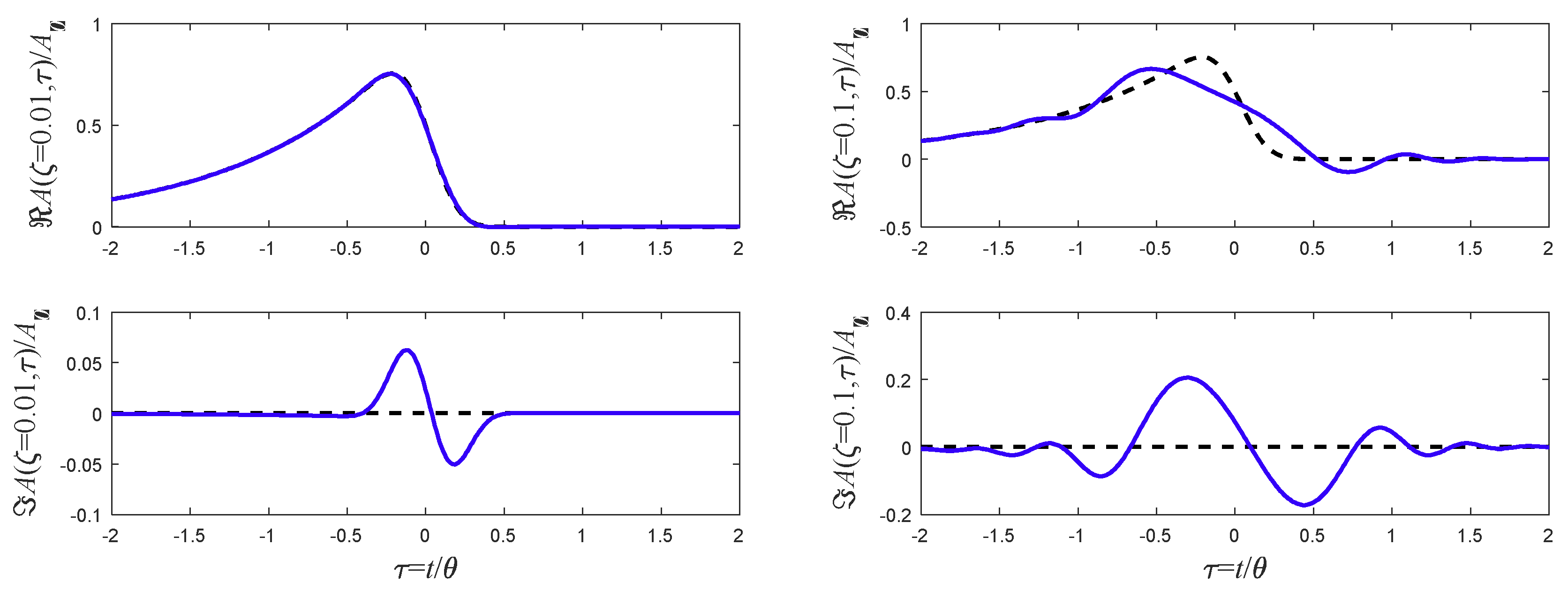
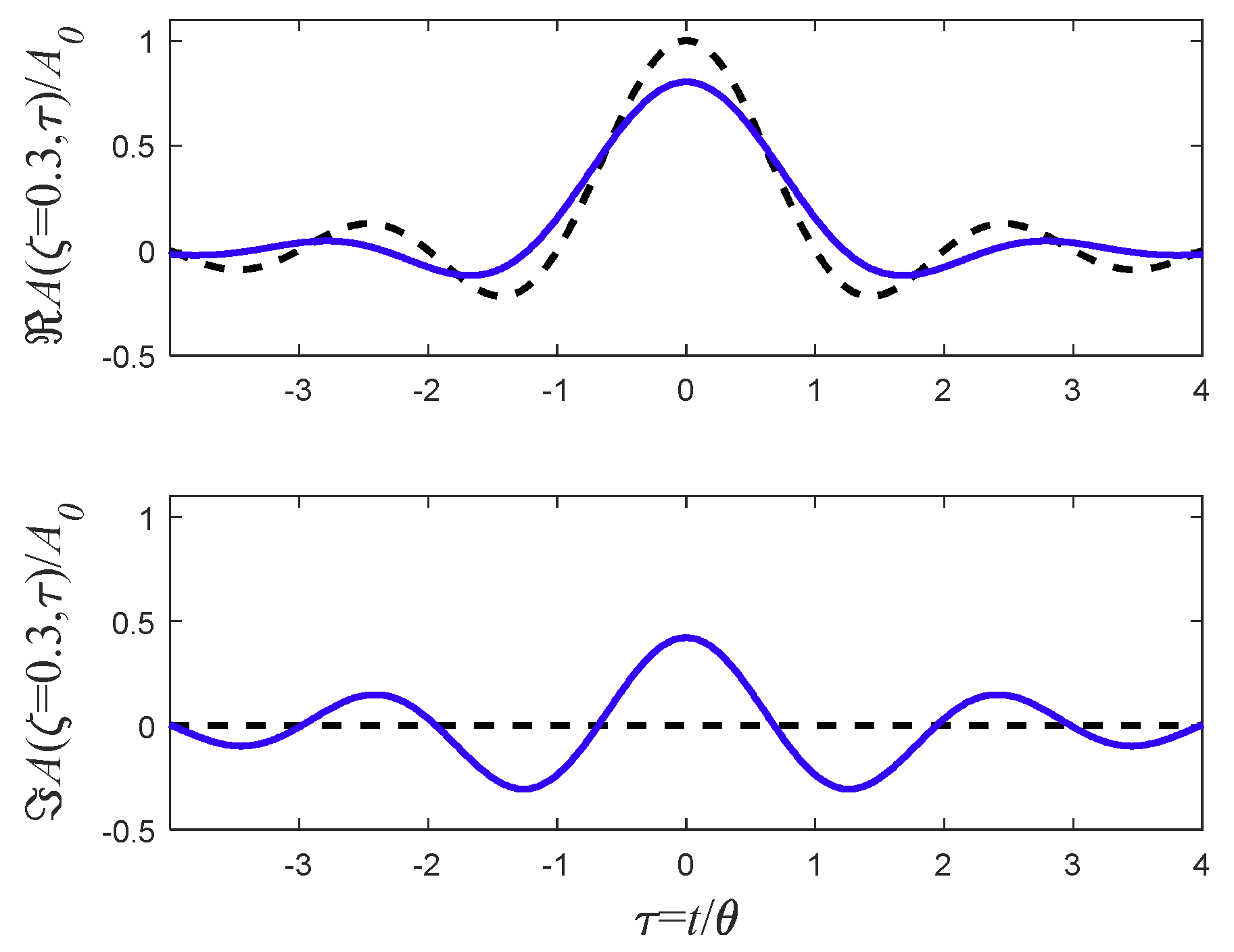
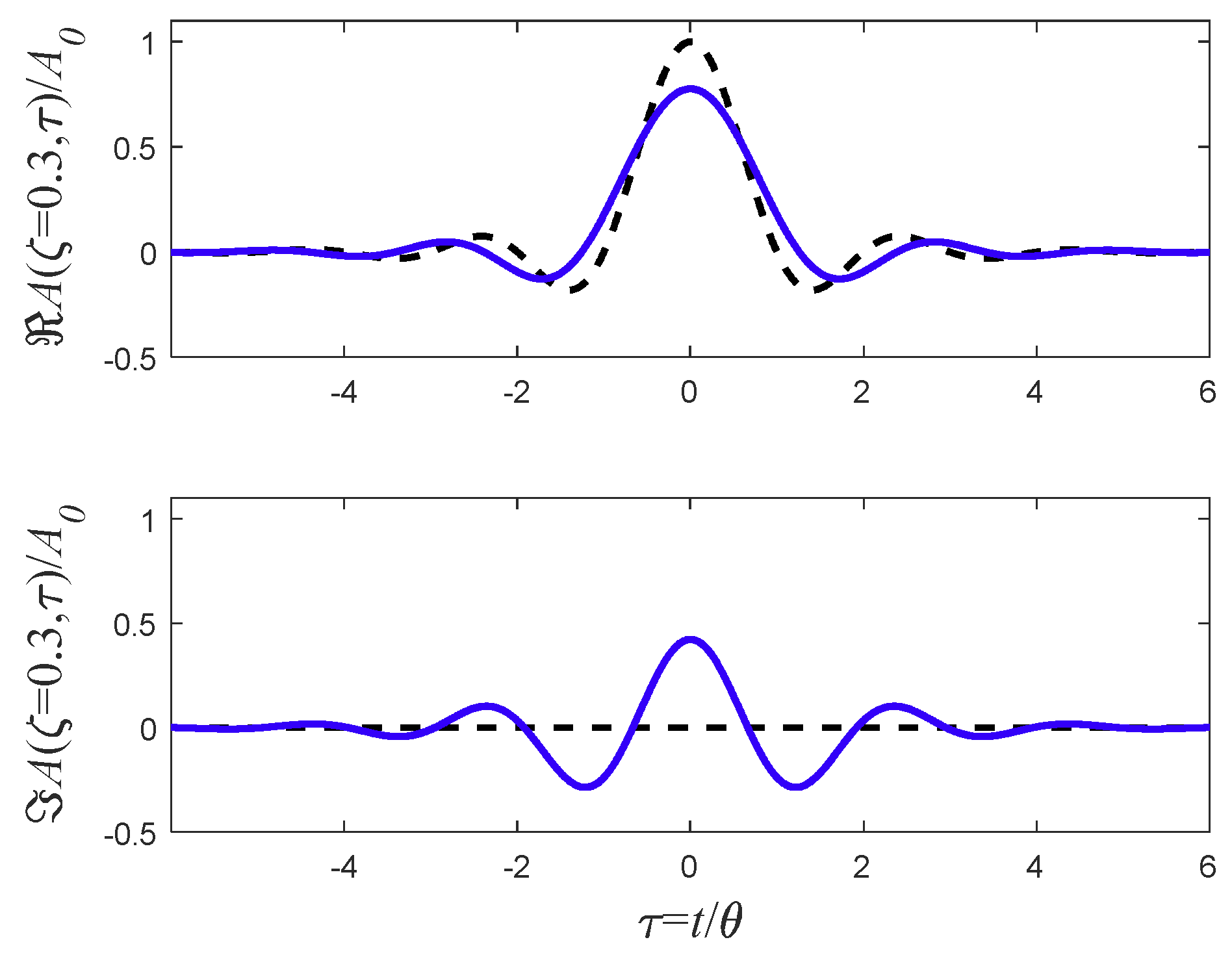
5. Singular Pulses
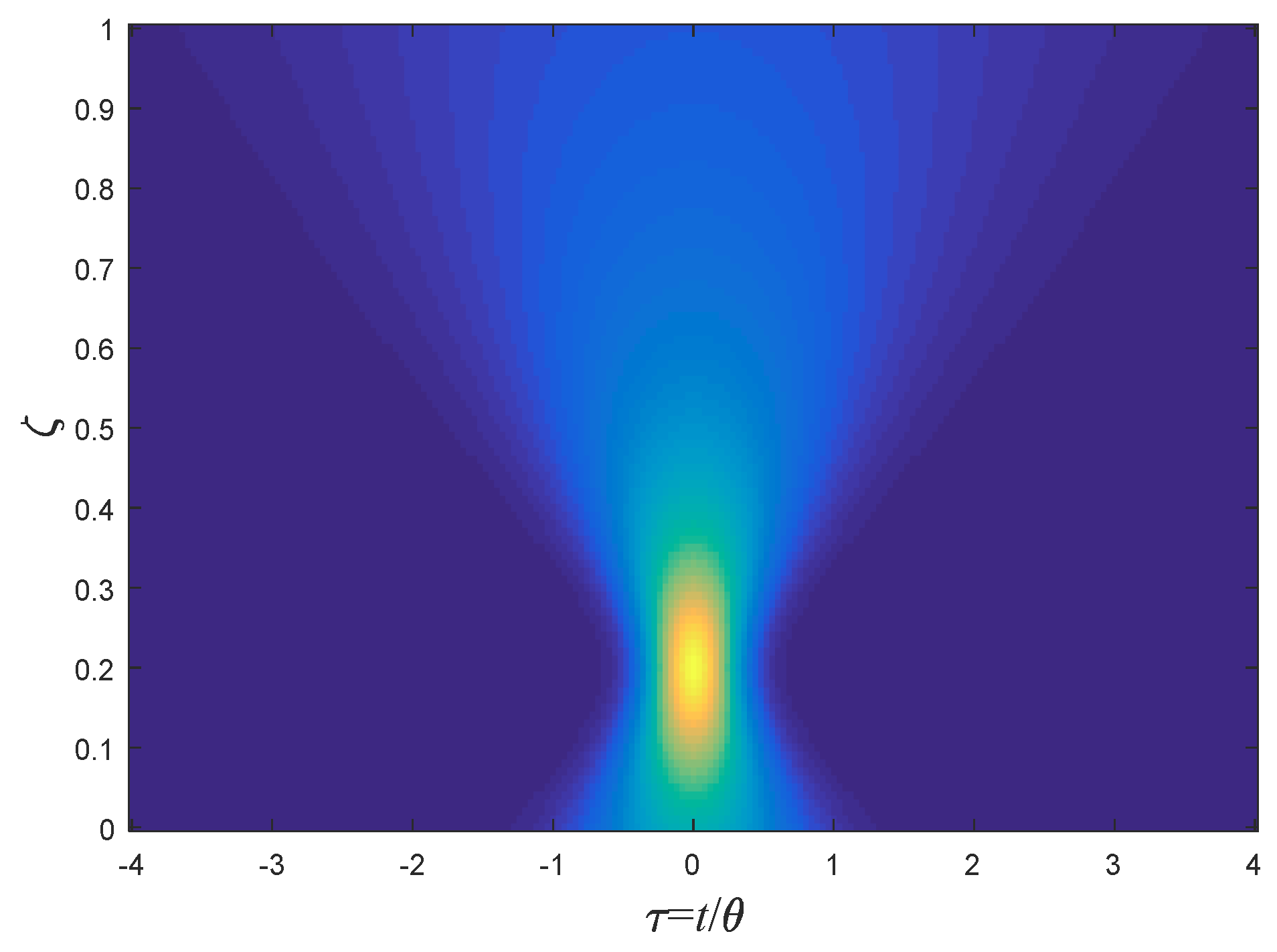
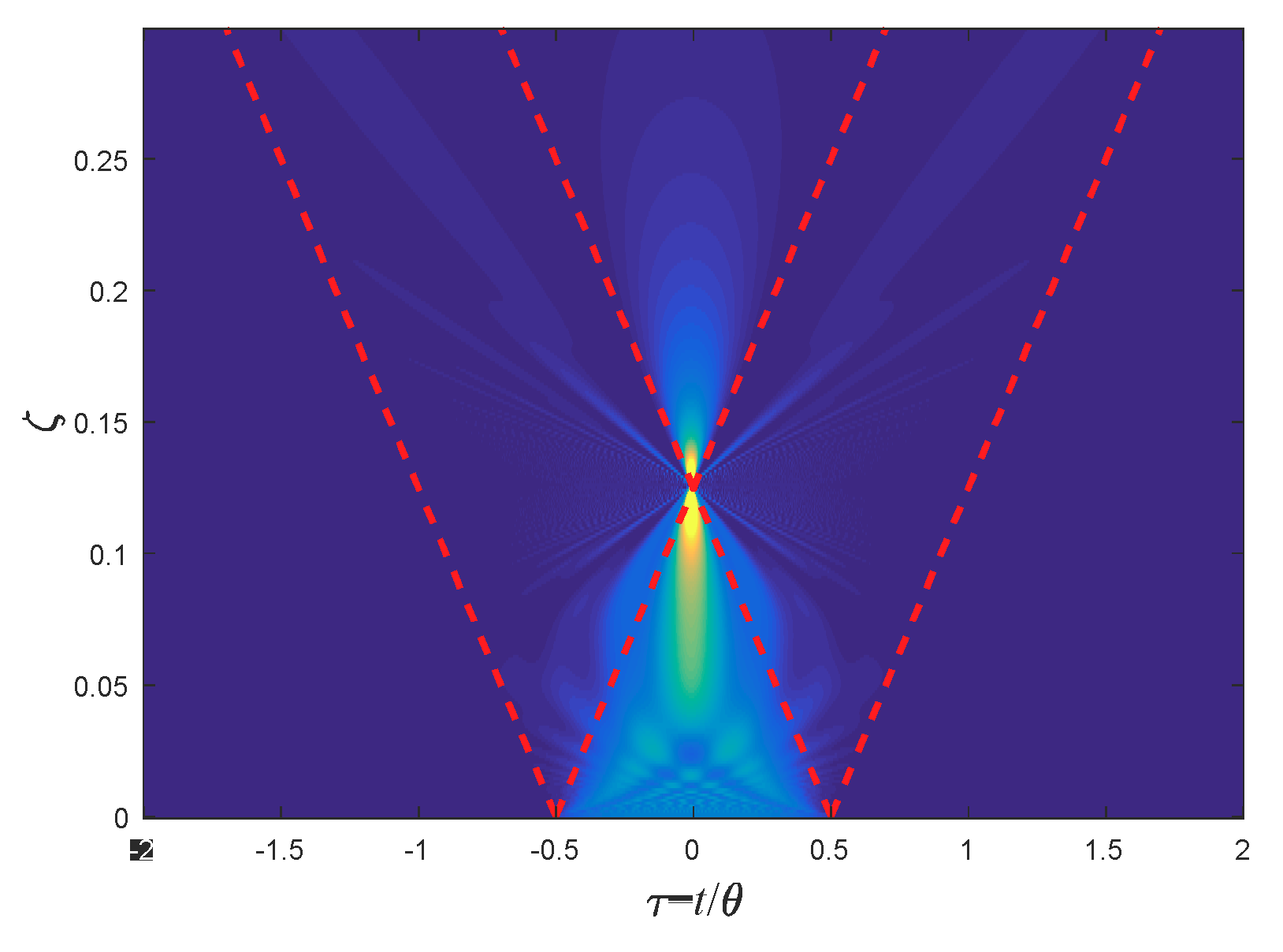
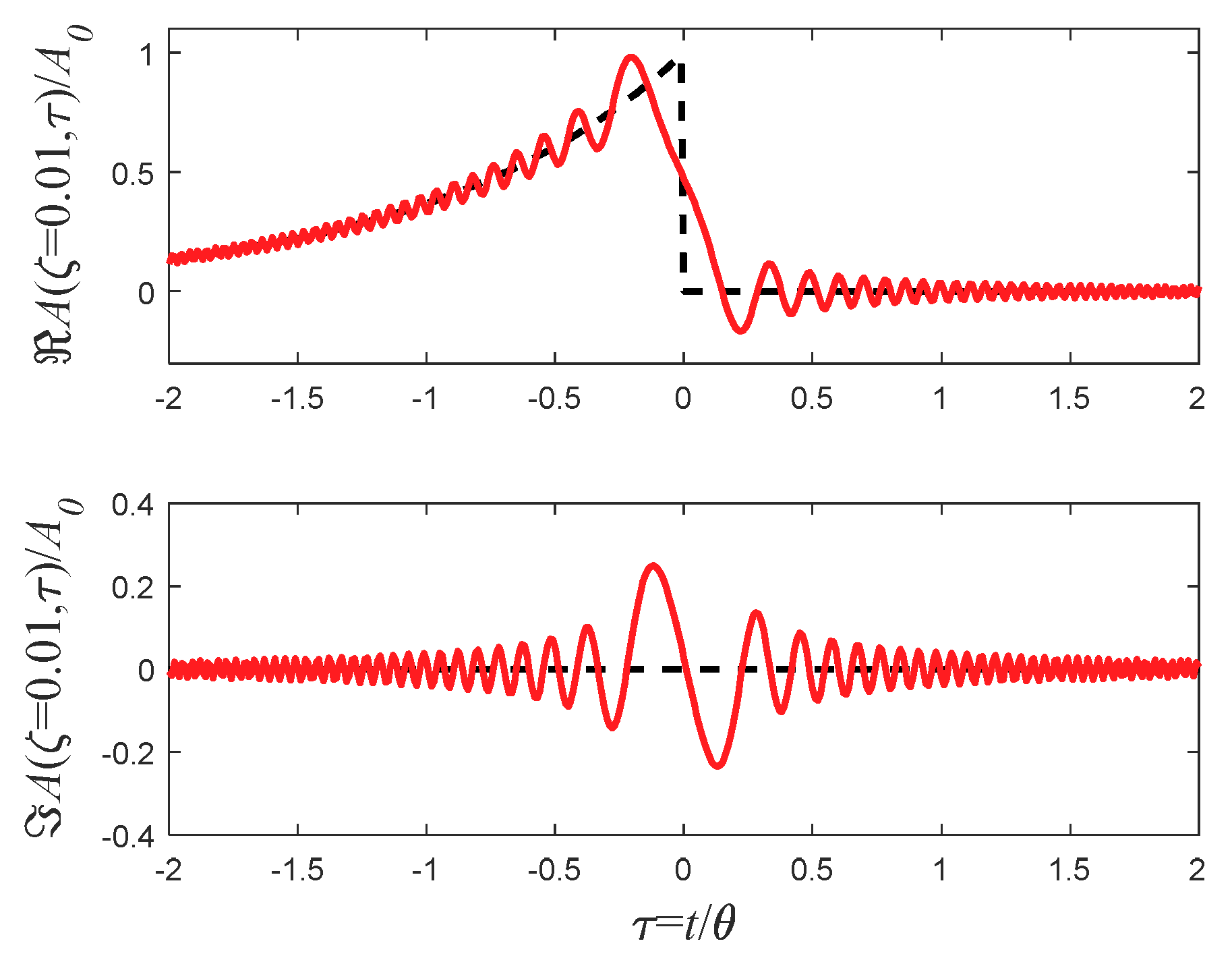
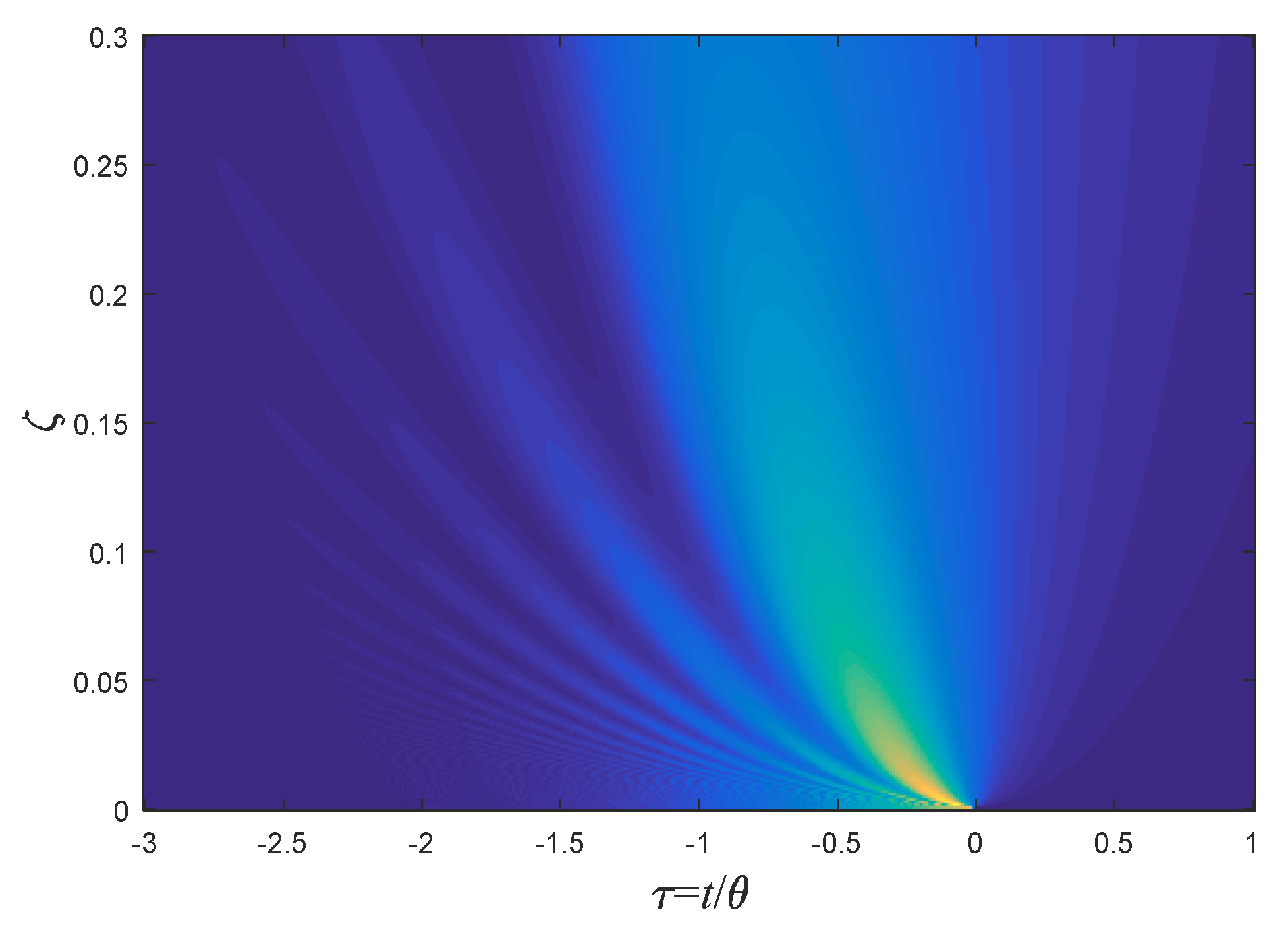
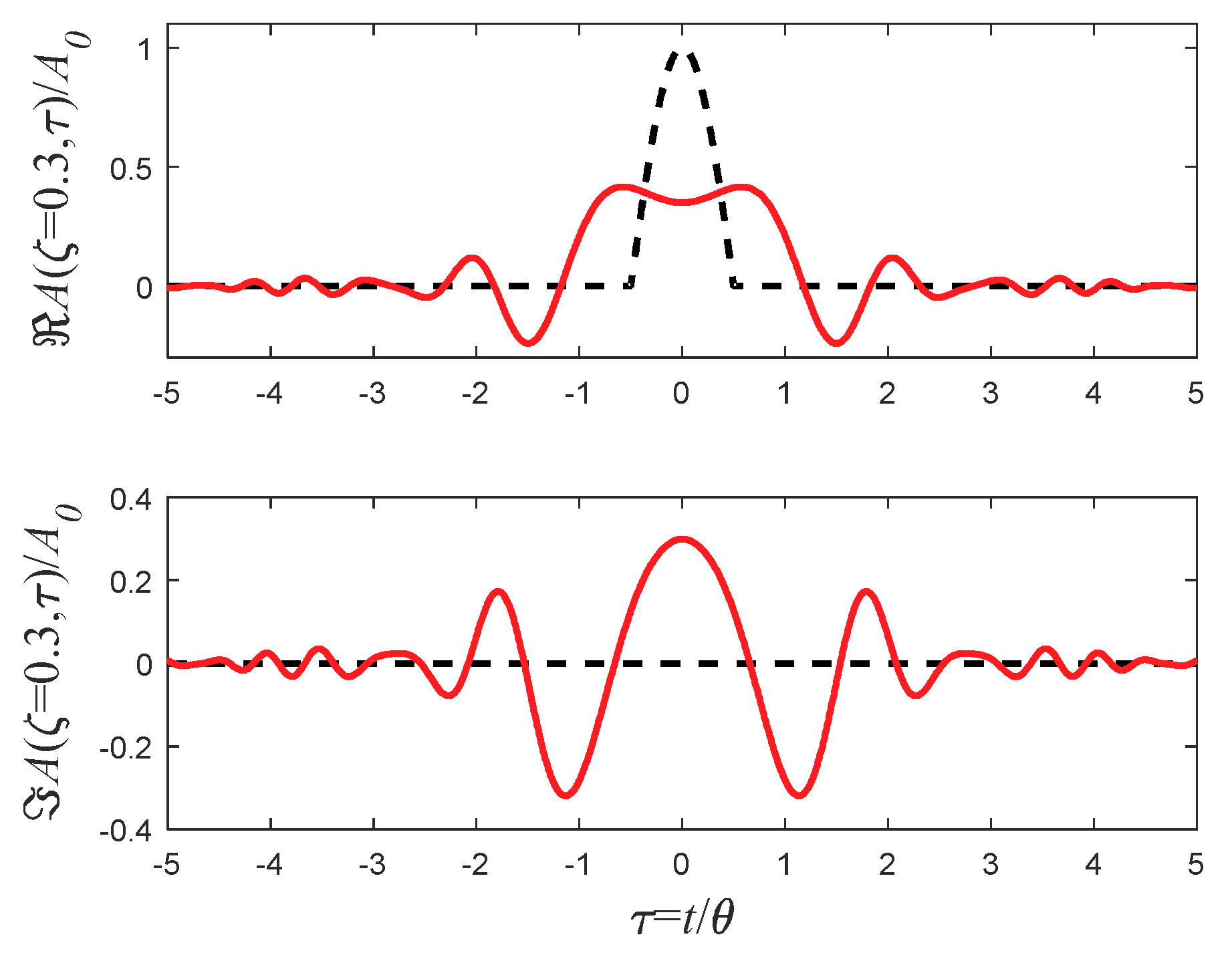
5.1. The Step Function
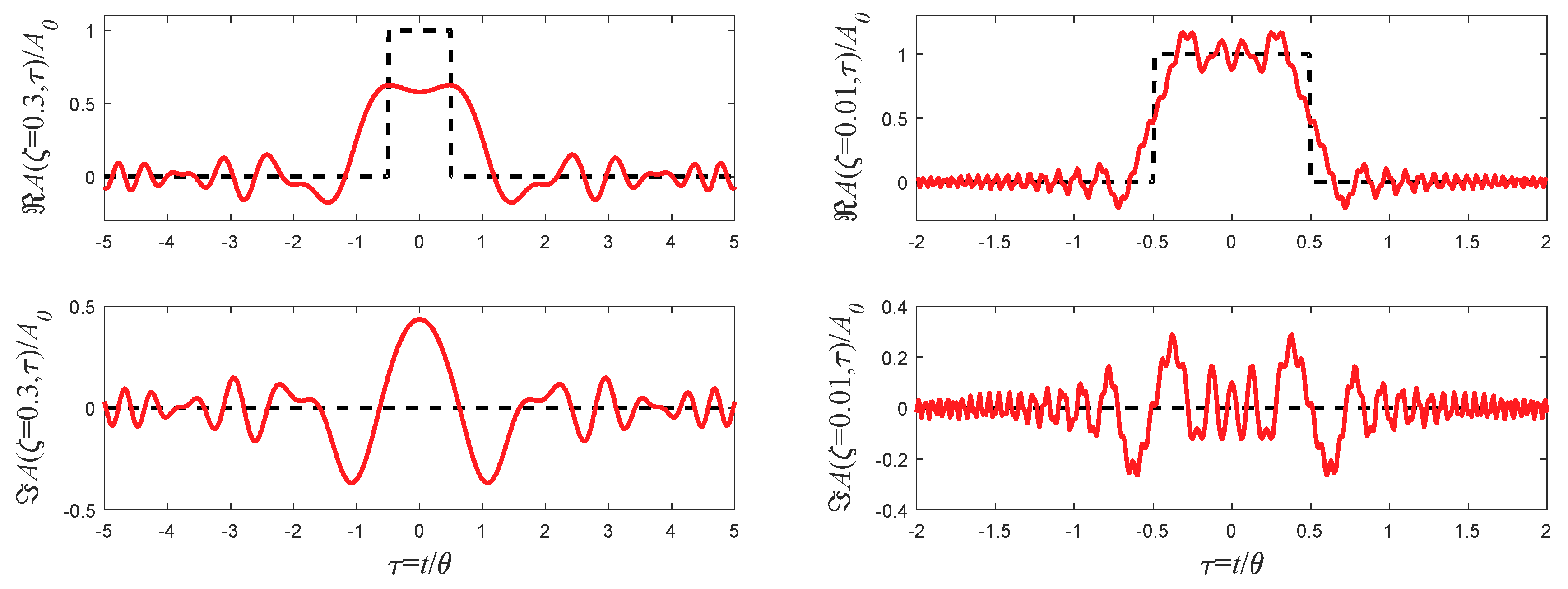
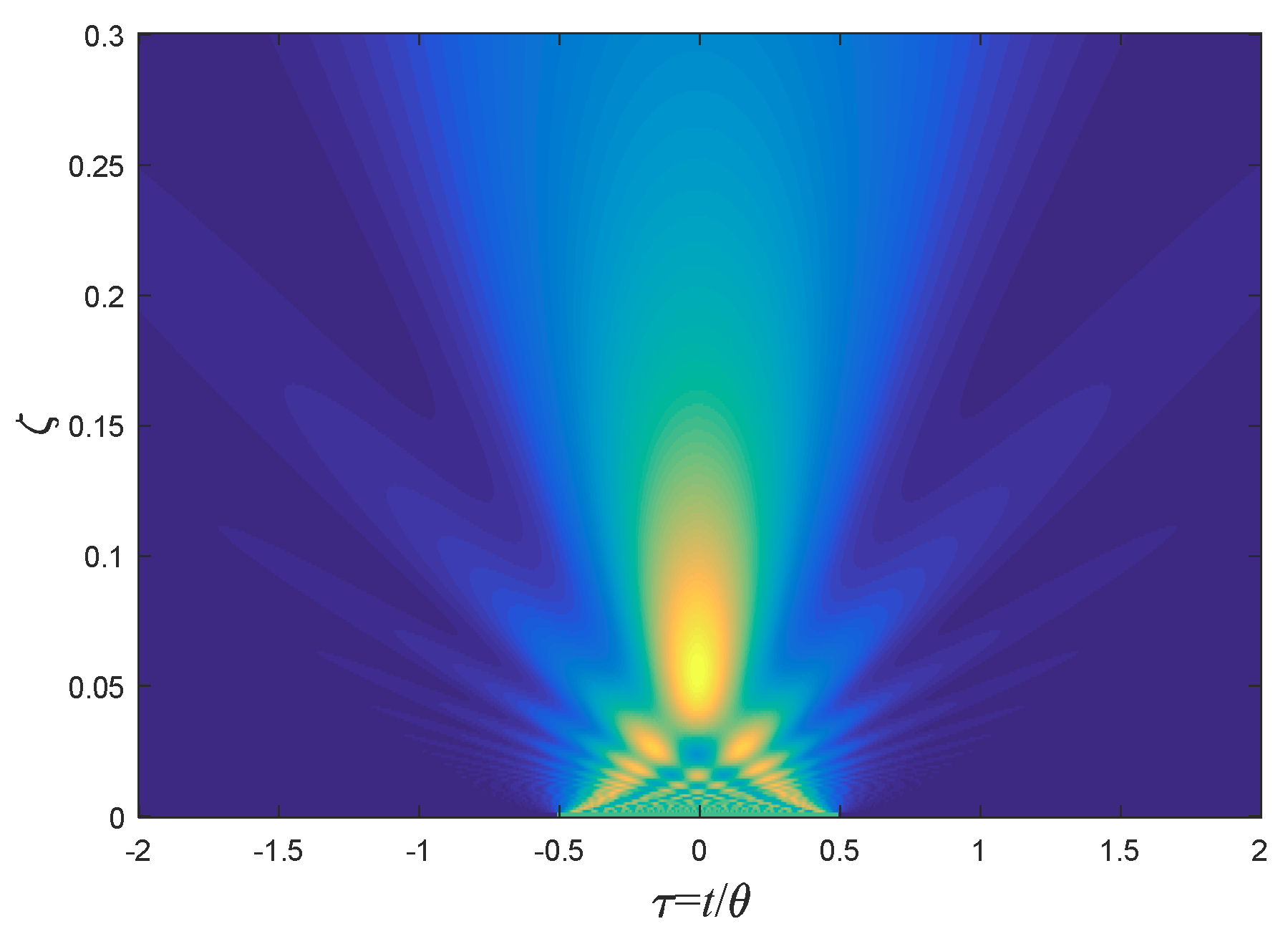
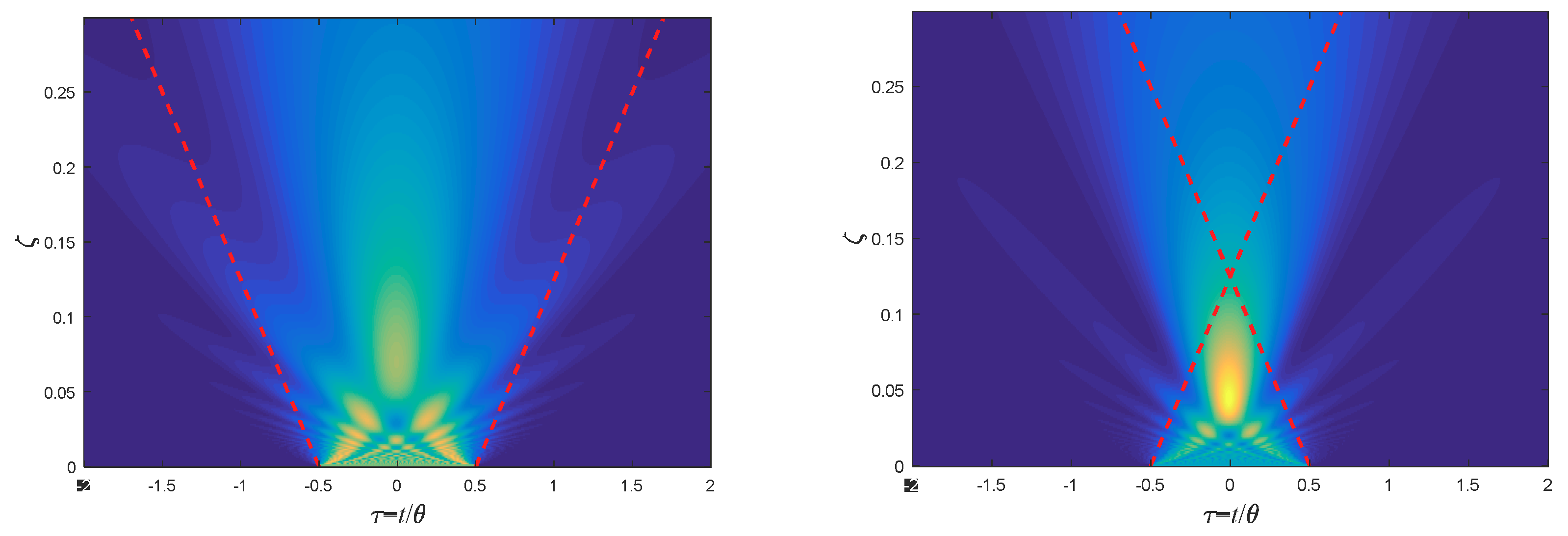
5.2. Rectangular Pulses
5.3. Chirped Rectangular Pulses
5.4. Exponential Pulse
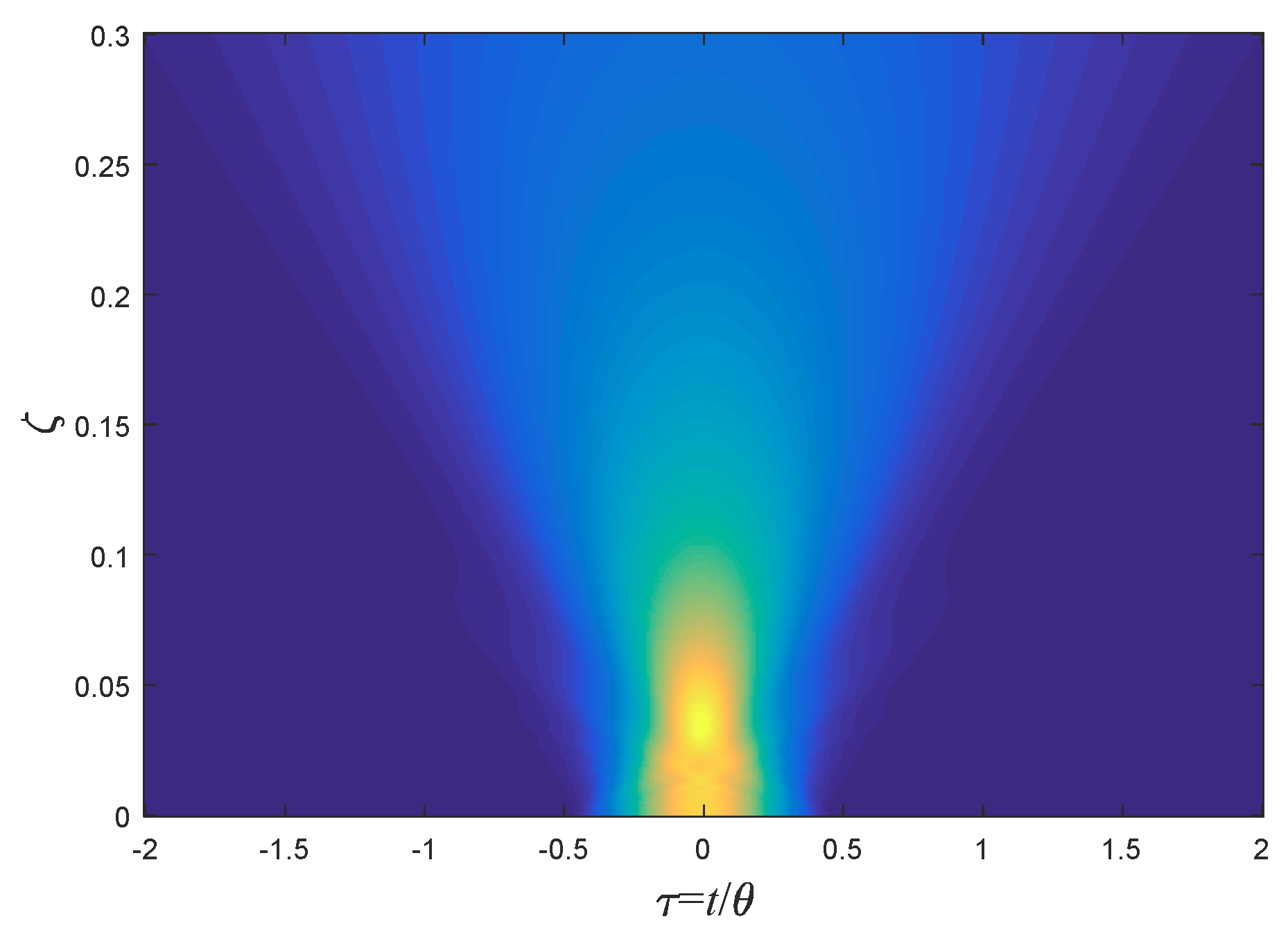
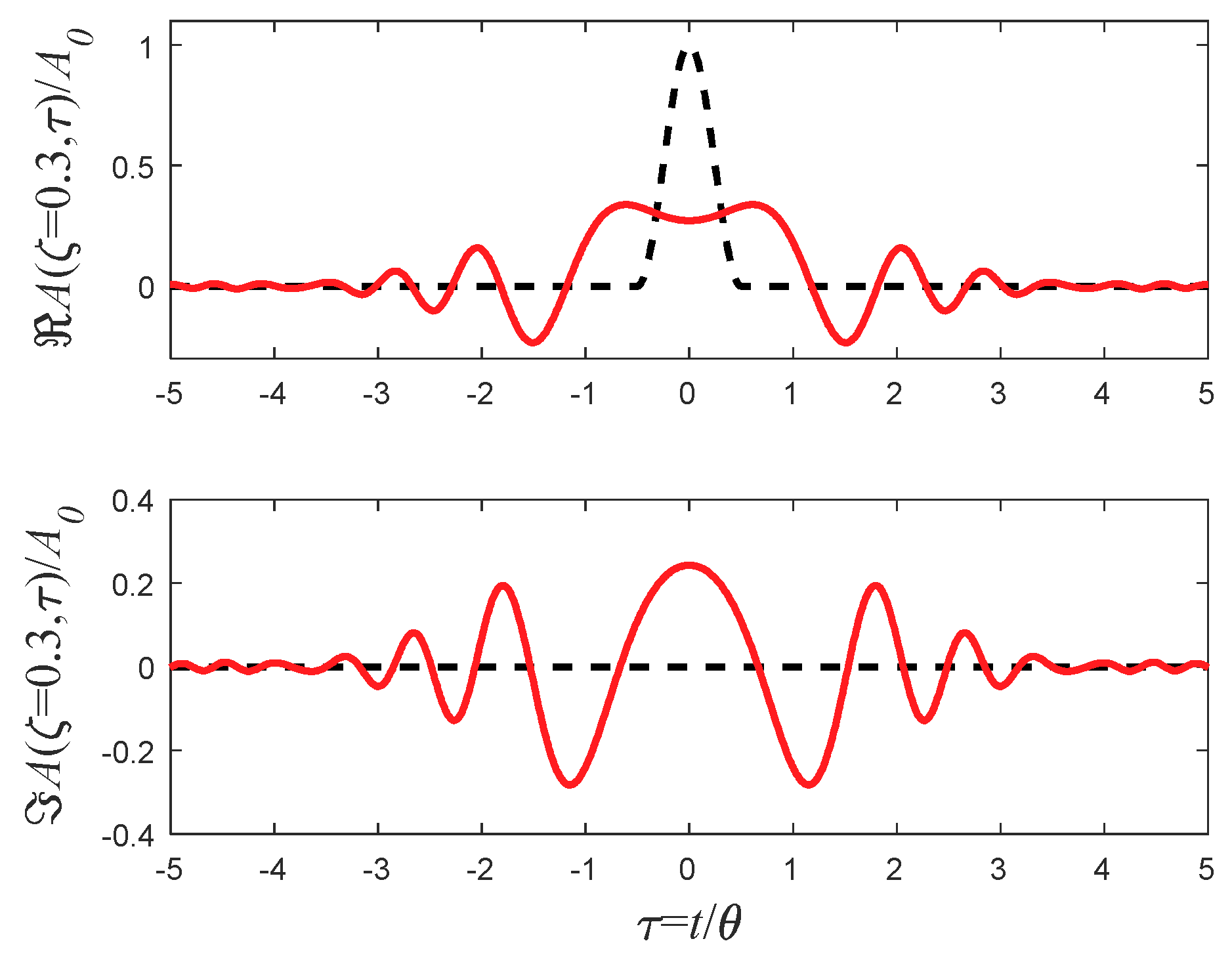
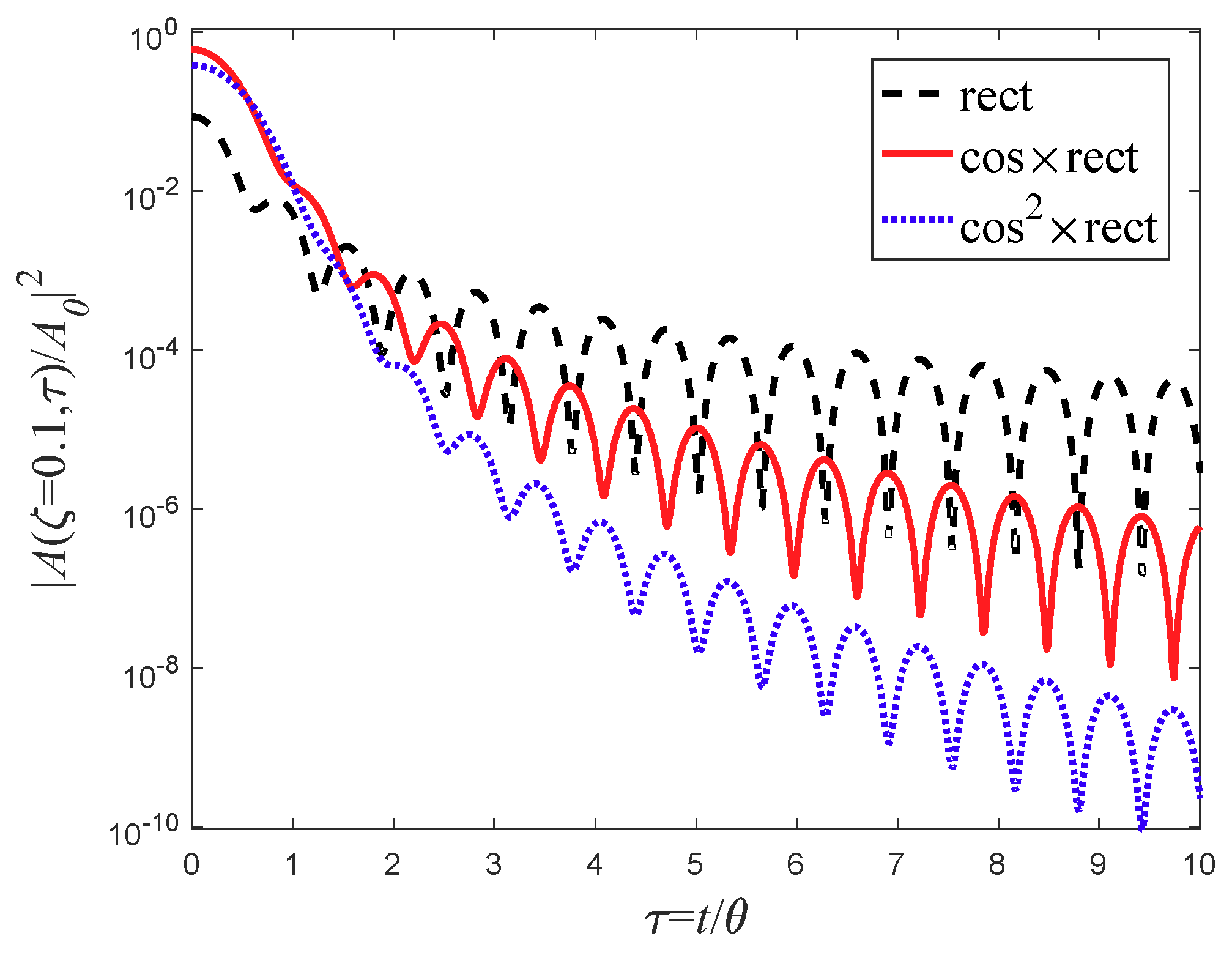
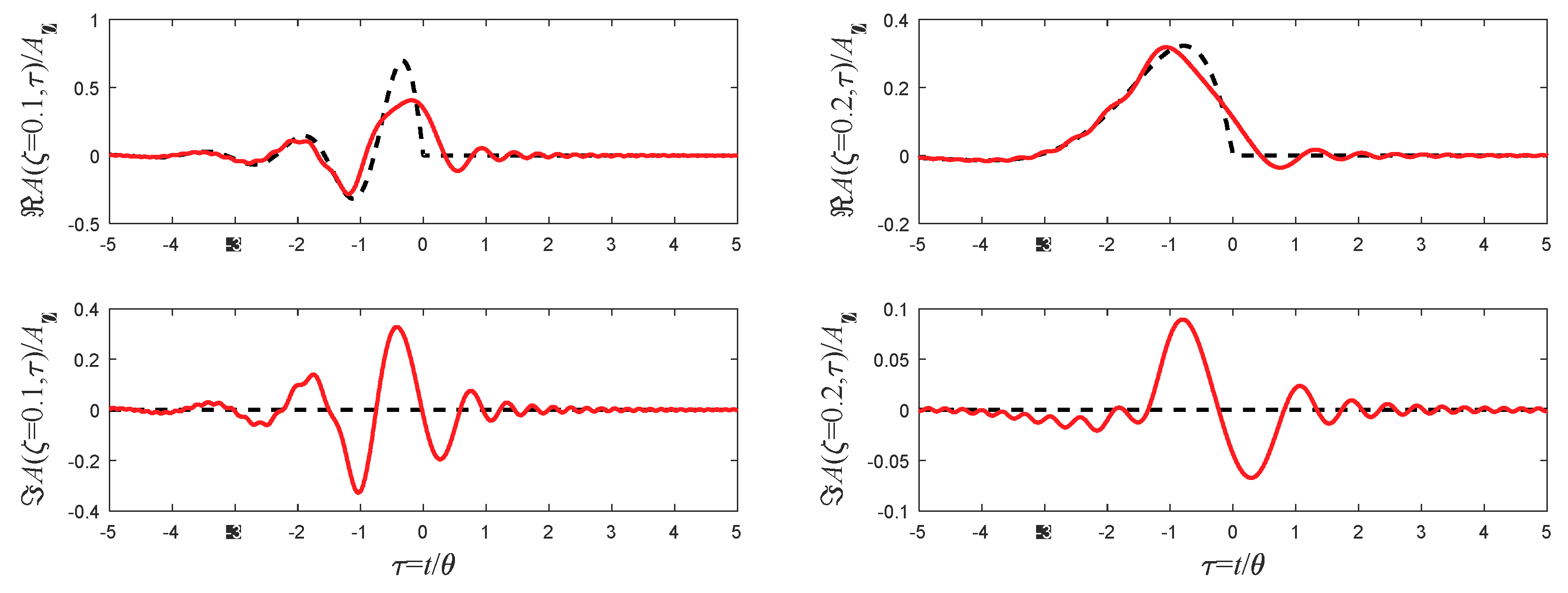
5.5. Cosine Pulse
5.6. Square Cosine Pulse
5.7. Generalization and Applicable Examples
6. Smooth Pulses
6.1. Smooth Step Function
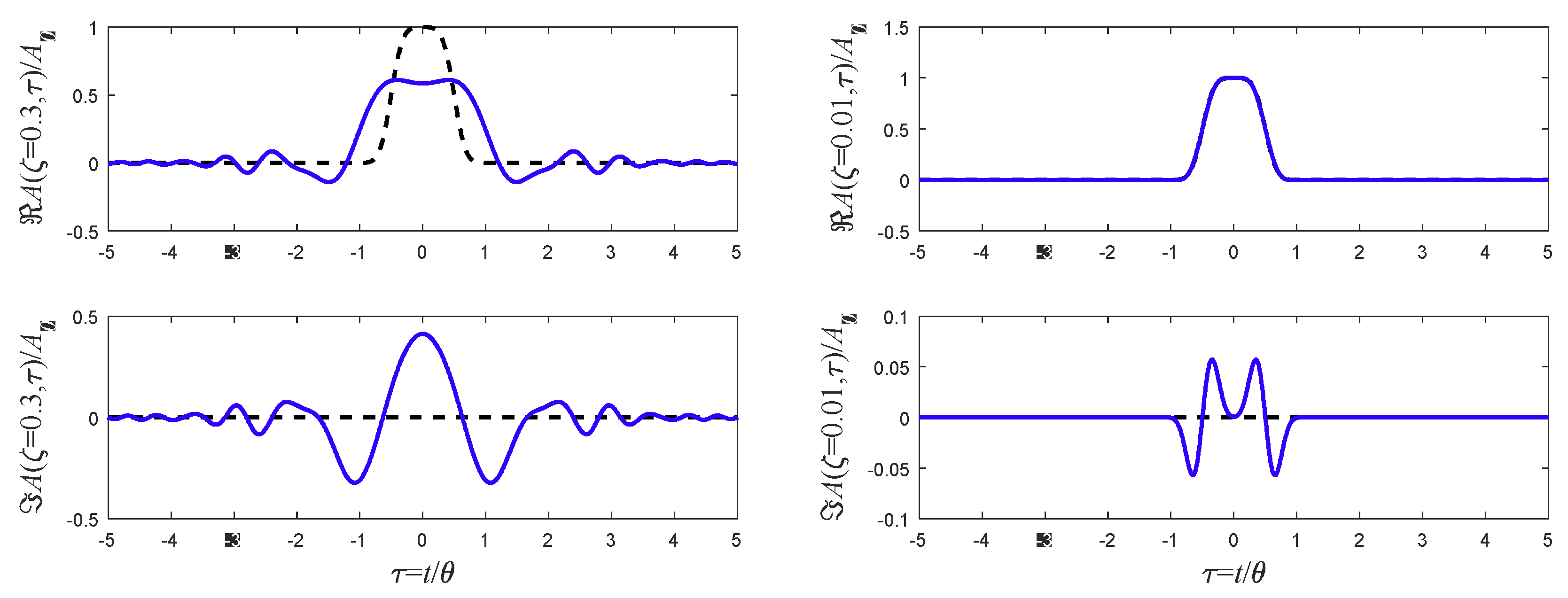
6.2. Smooth Rectangular Pulse
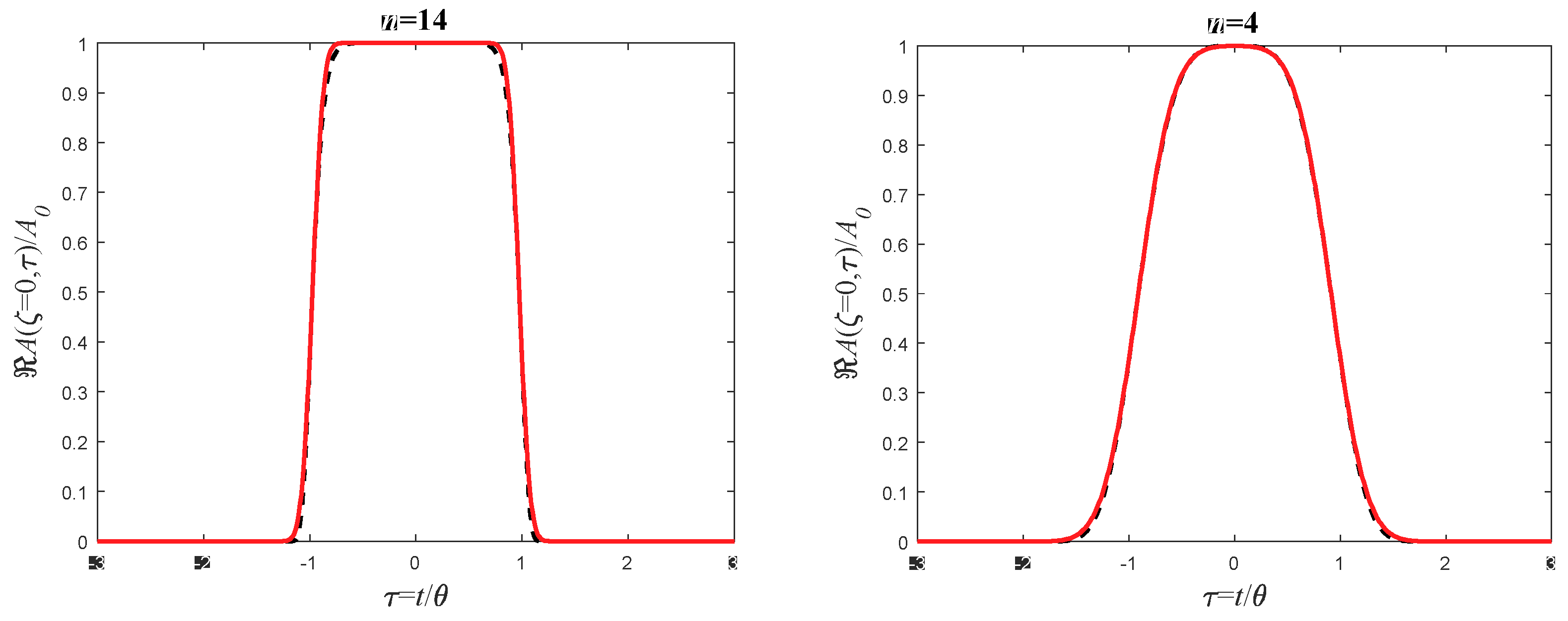
6.3. Relations to Super-Gaussian Pulses
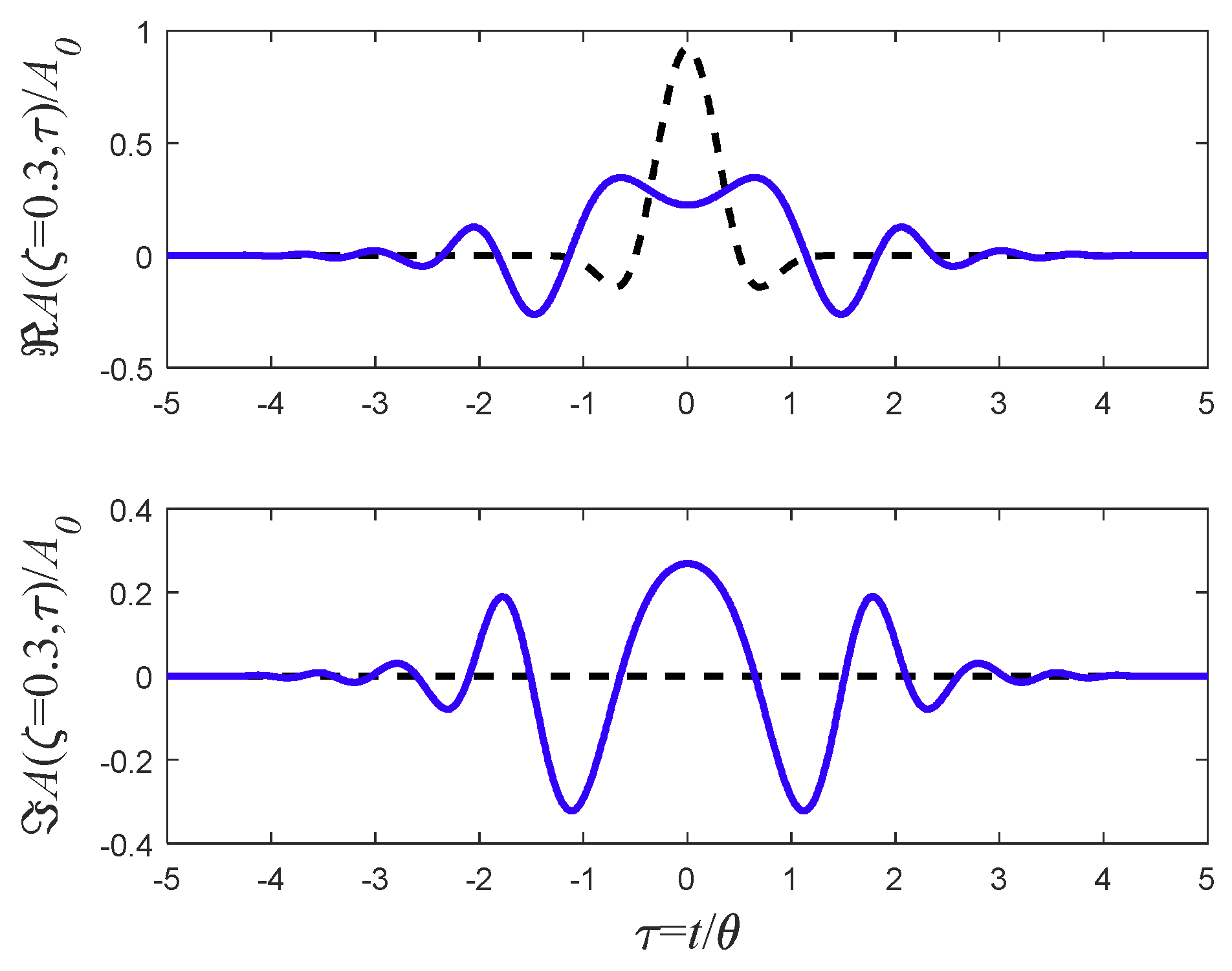
6.4. Chirped Smooth Rectangular Pulse
6.5. Smooth Cosine Pulse
6.6. Smooth Exponential Pulse
7. Singular Pulses in the Spectral Domain
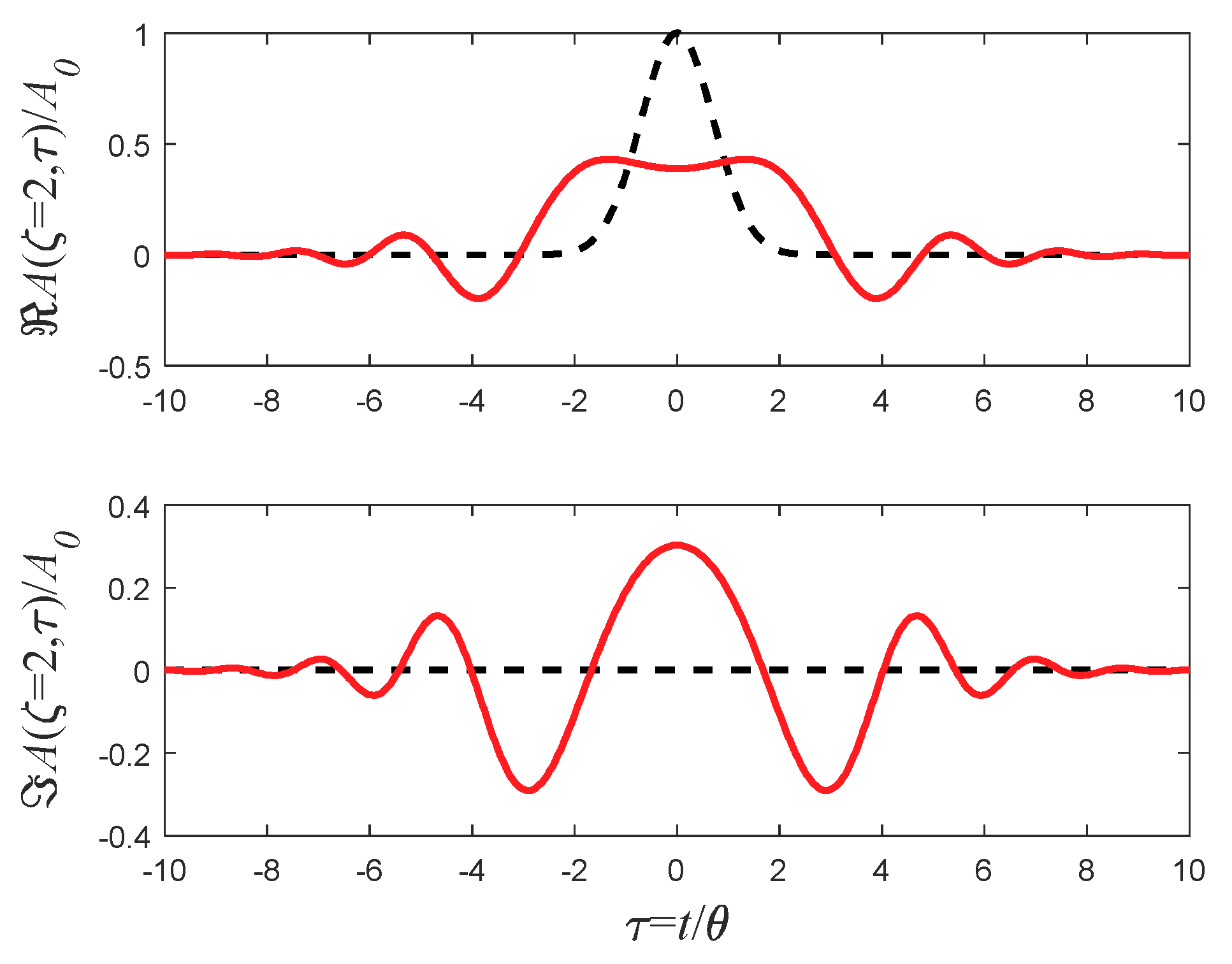
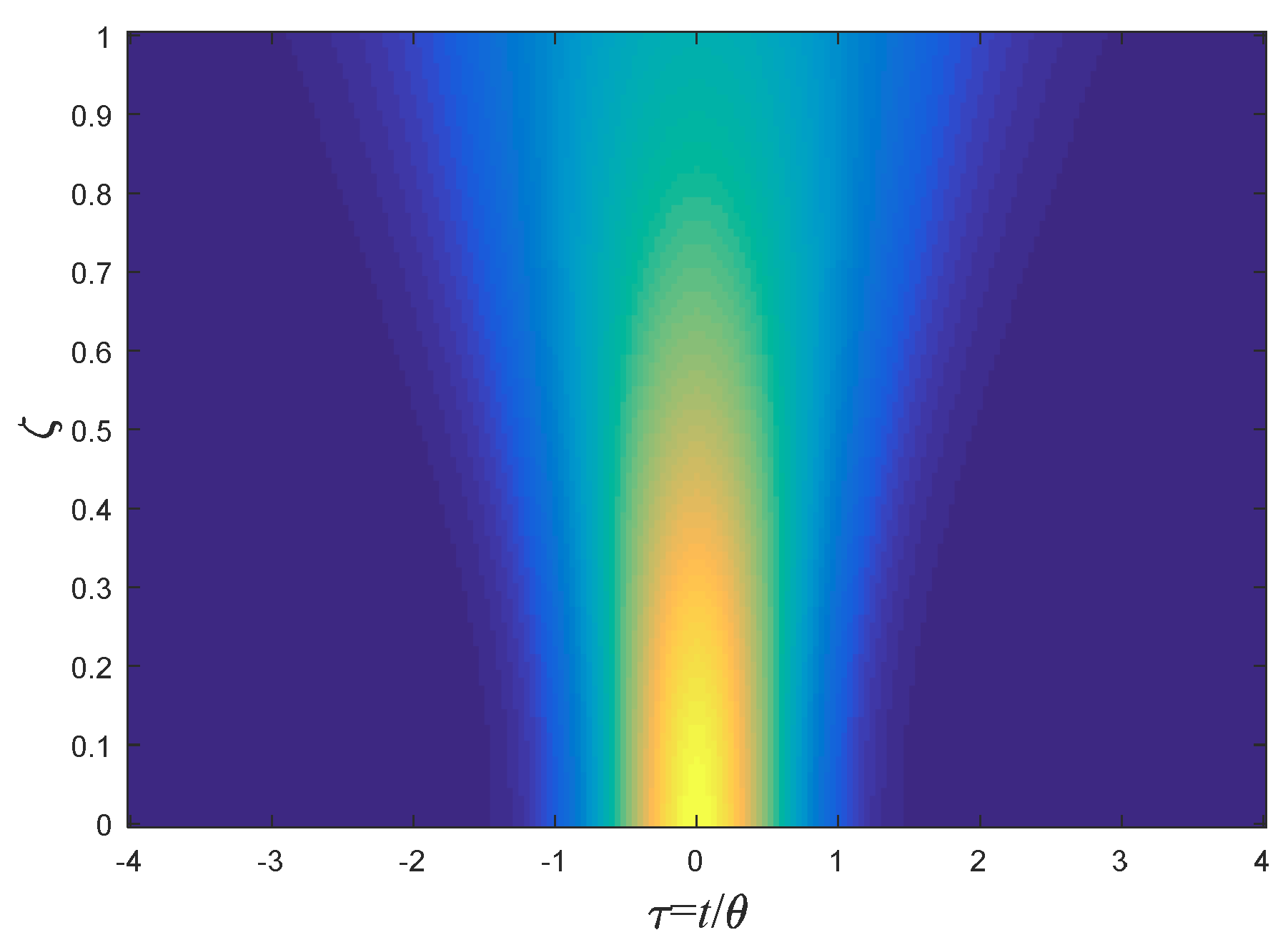
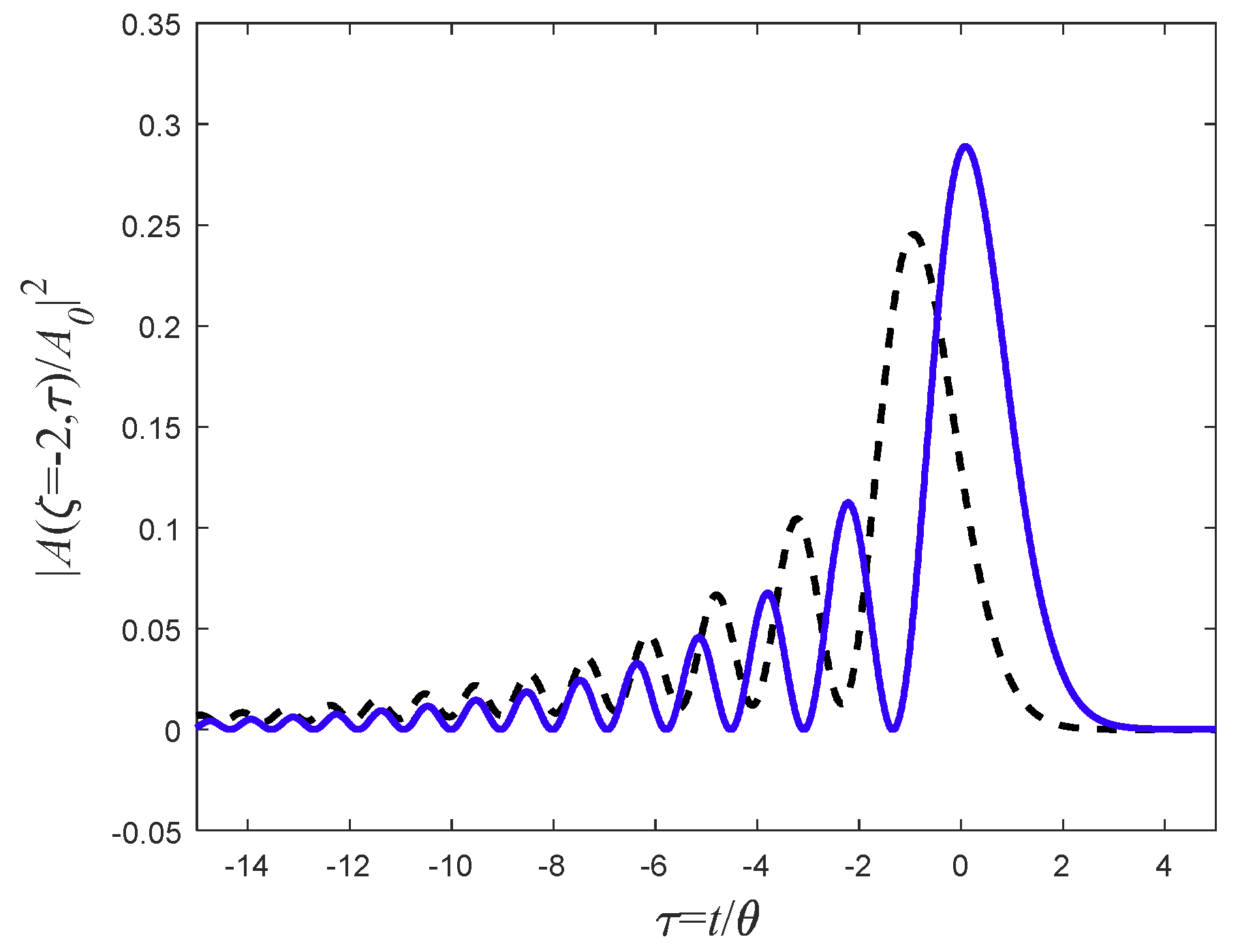
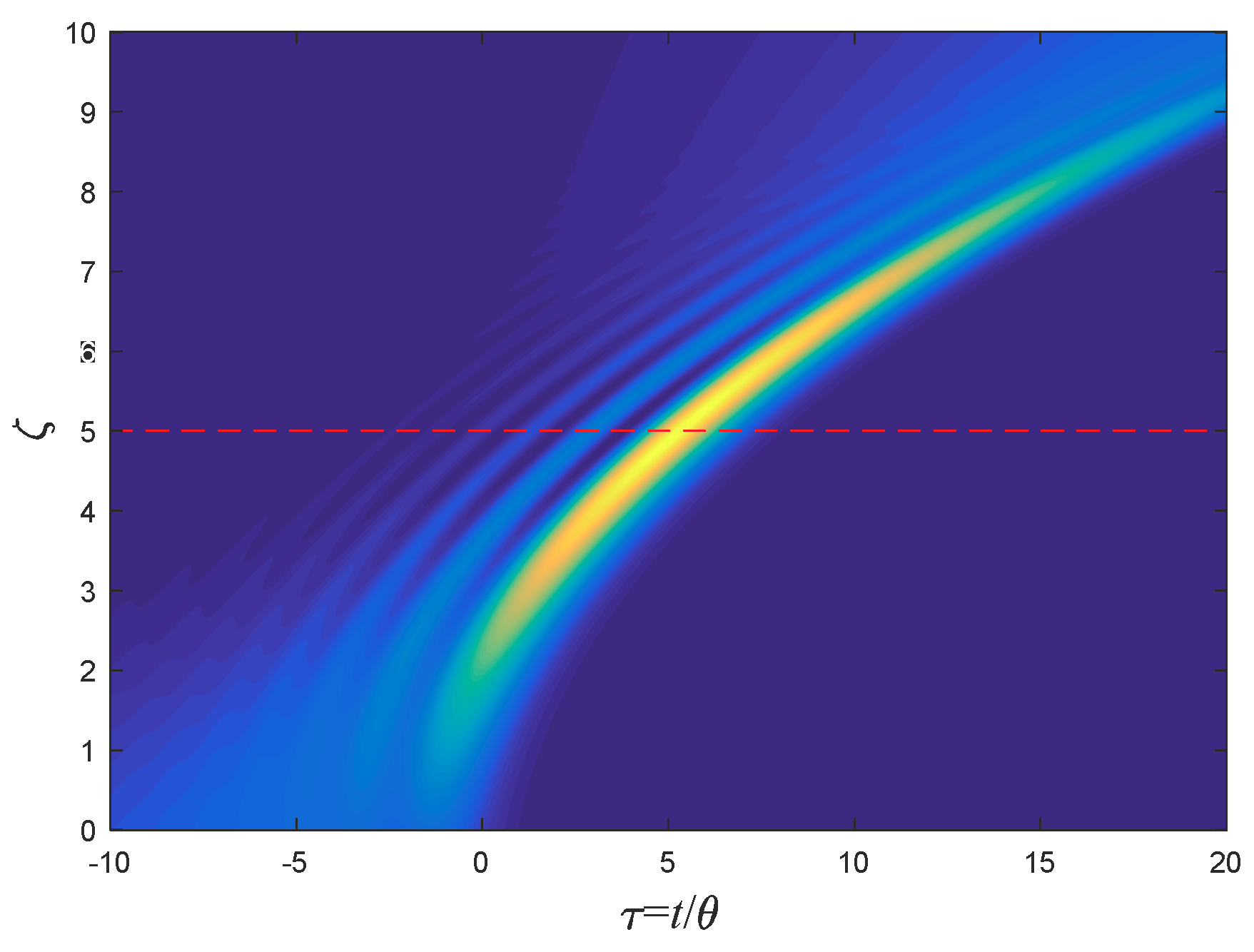
7.1. The ideal Nyquist-Sinc Pulse
7.2. Nyquist Sinc Pulse with Smooth Spectrum
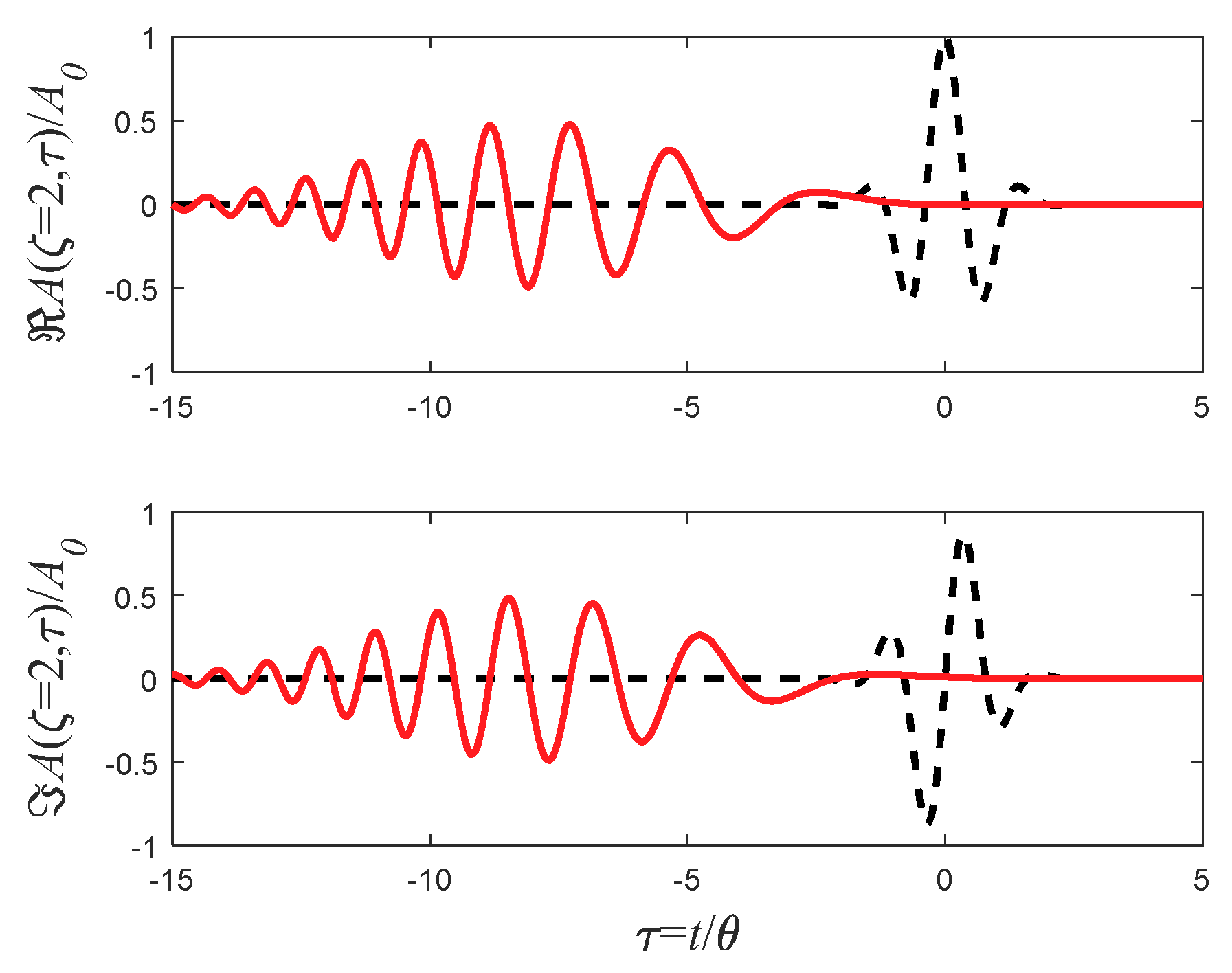
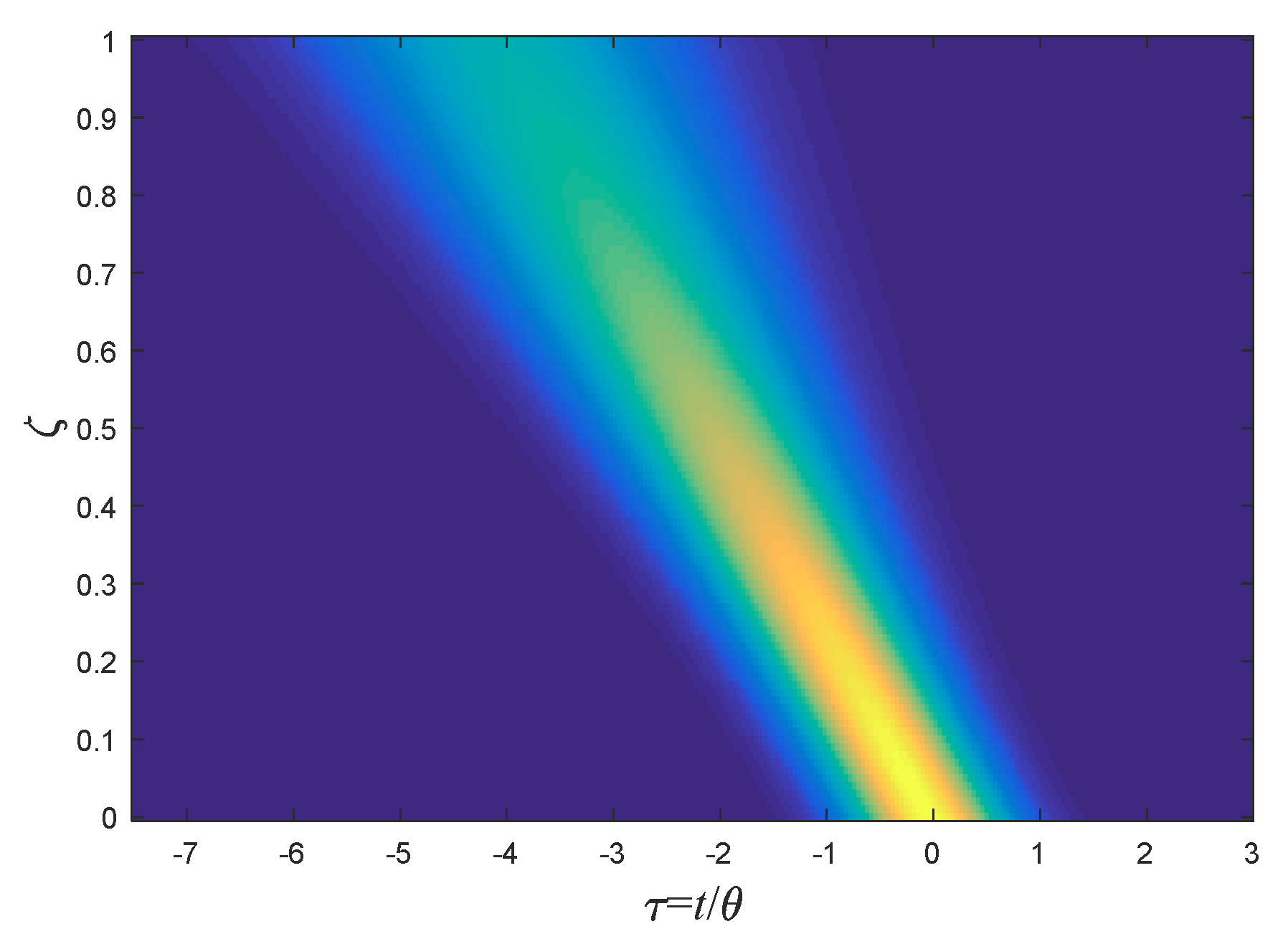
8. Undistorted Airy Pulses
8.1. Undistorted Ideal Accelerating Pulses
8.2. Physical Accelerating Pulse
8.3. Attenuation Compensating Airy Pulse
8.4. Physical Attenuation Compensating Airy Pulse
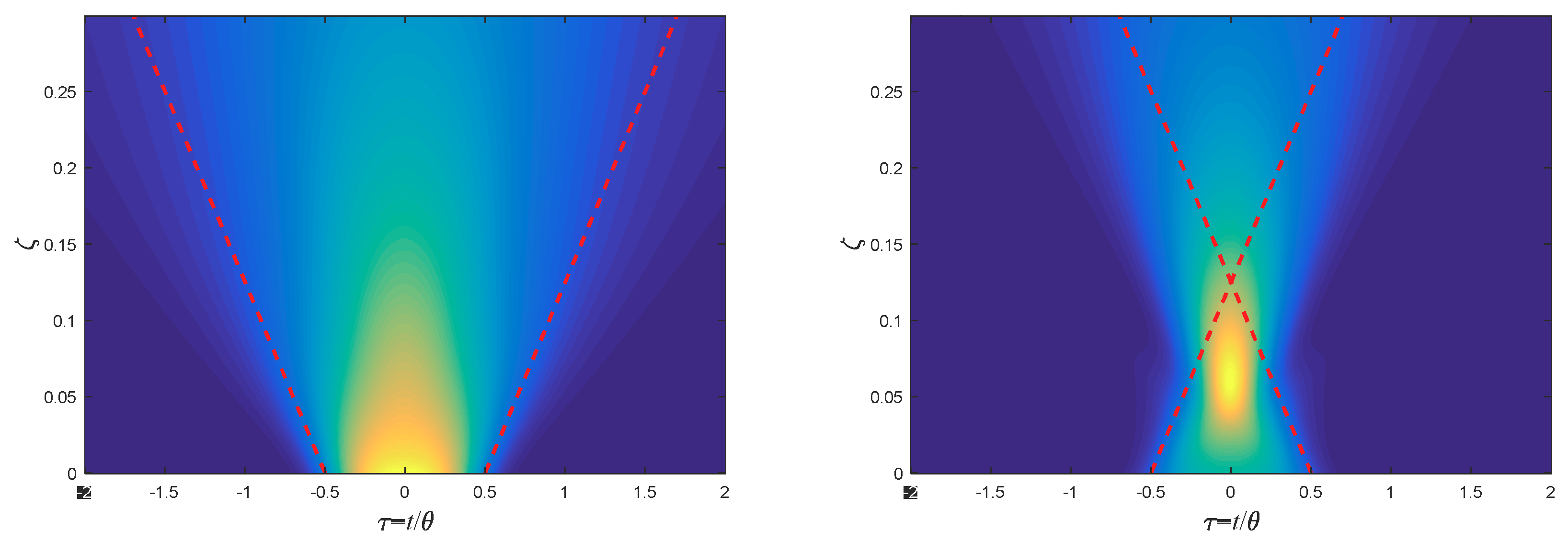
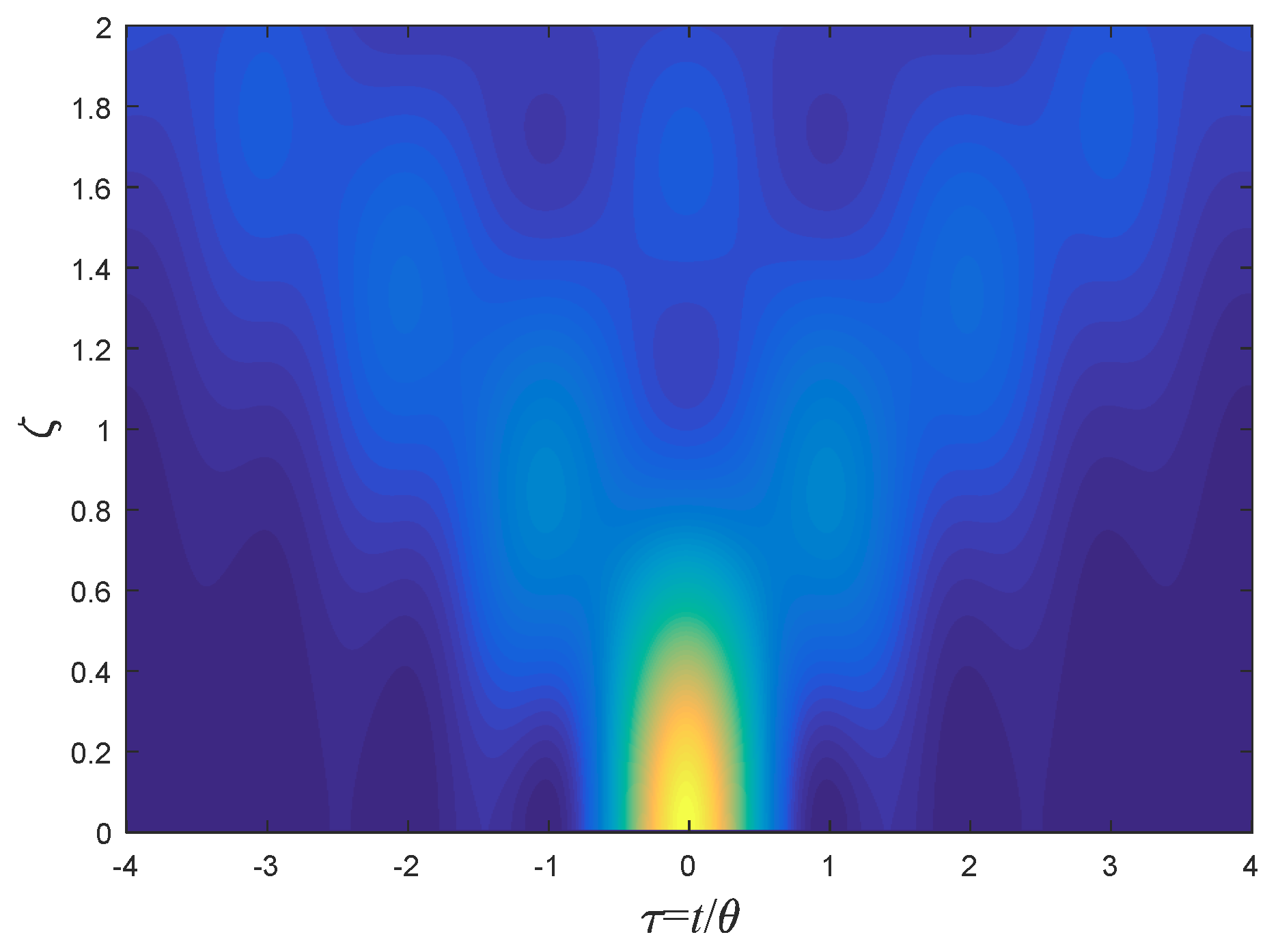
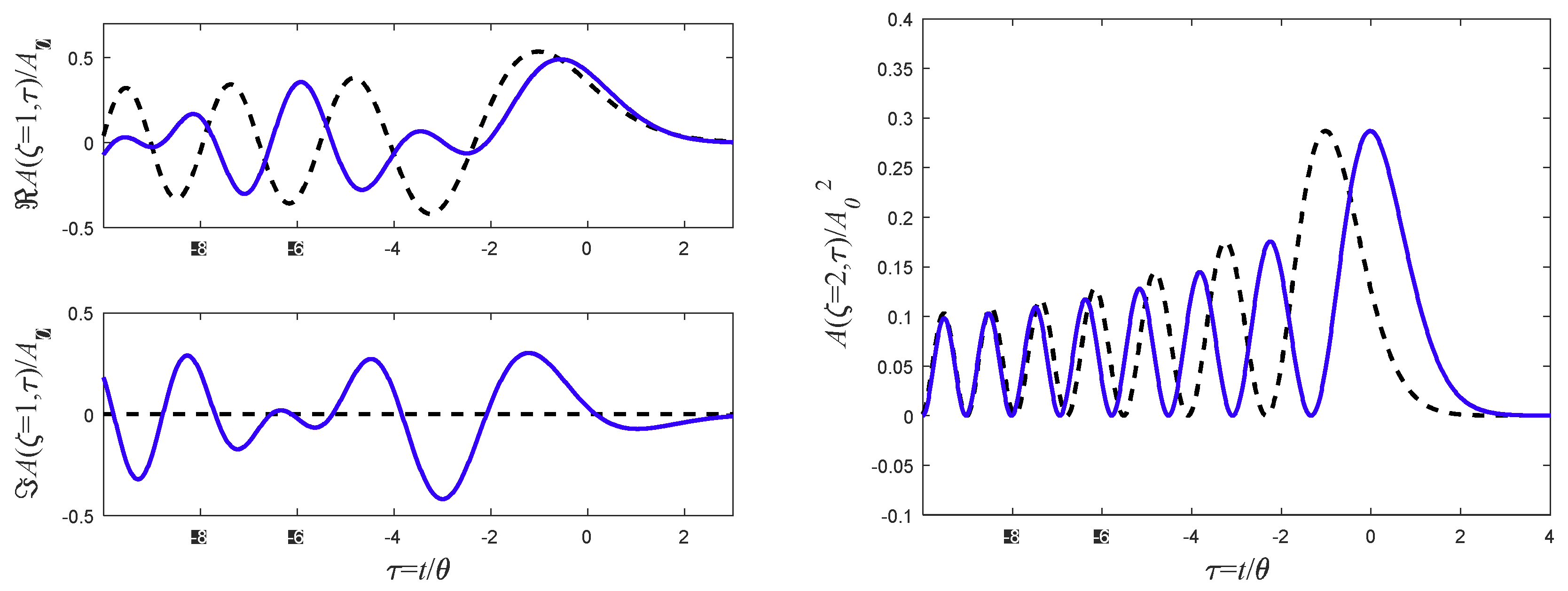
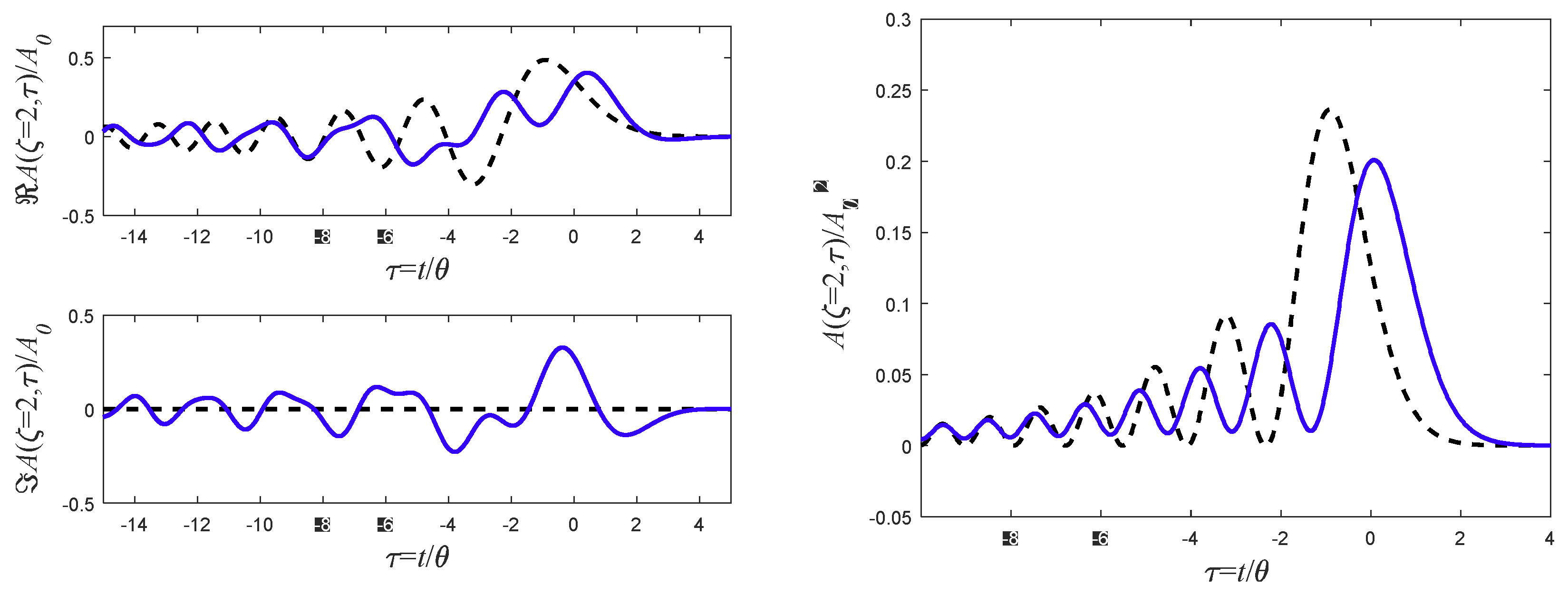
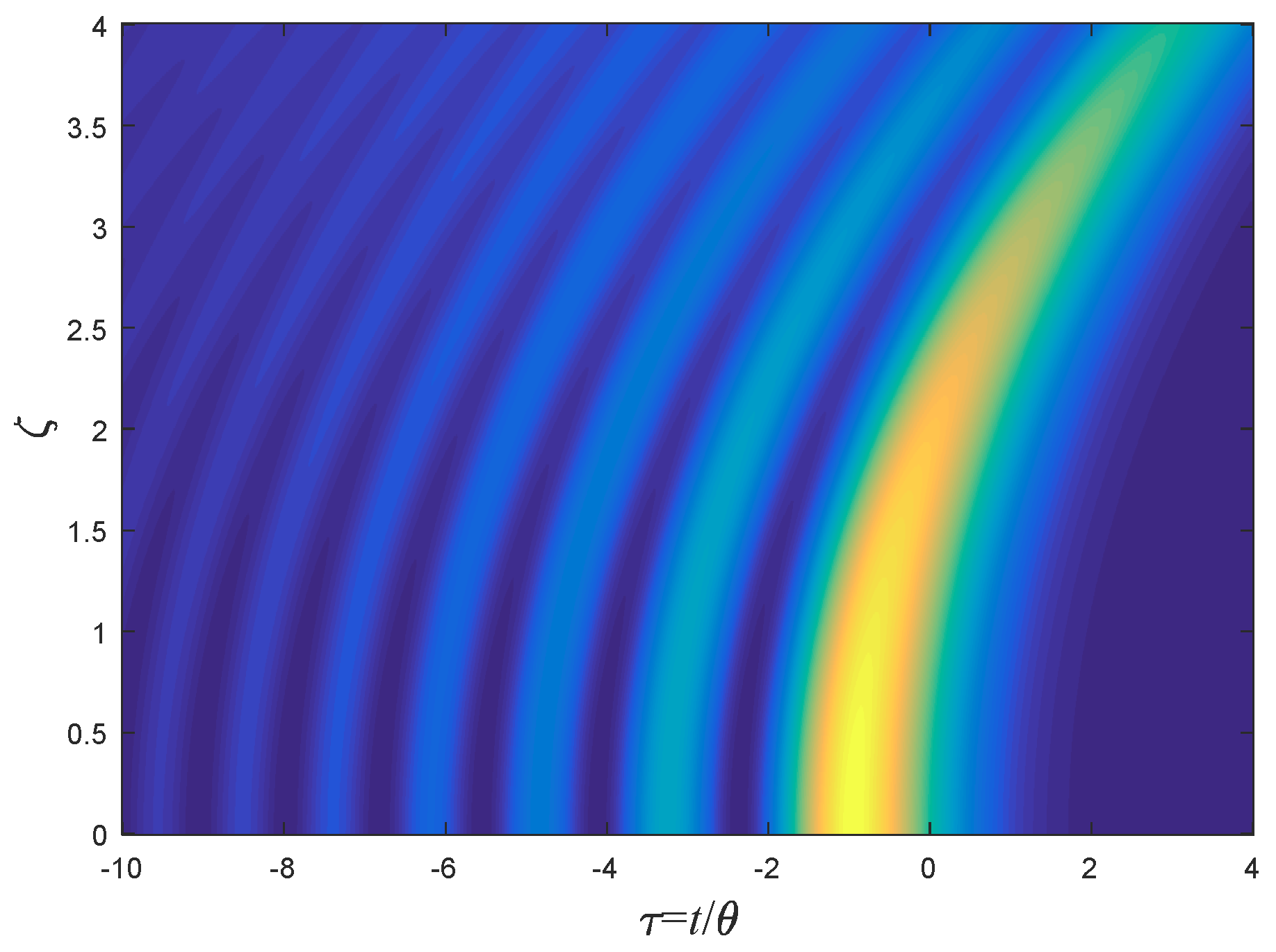
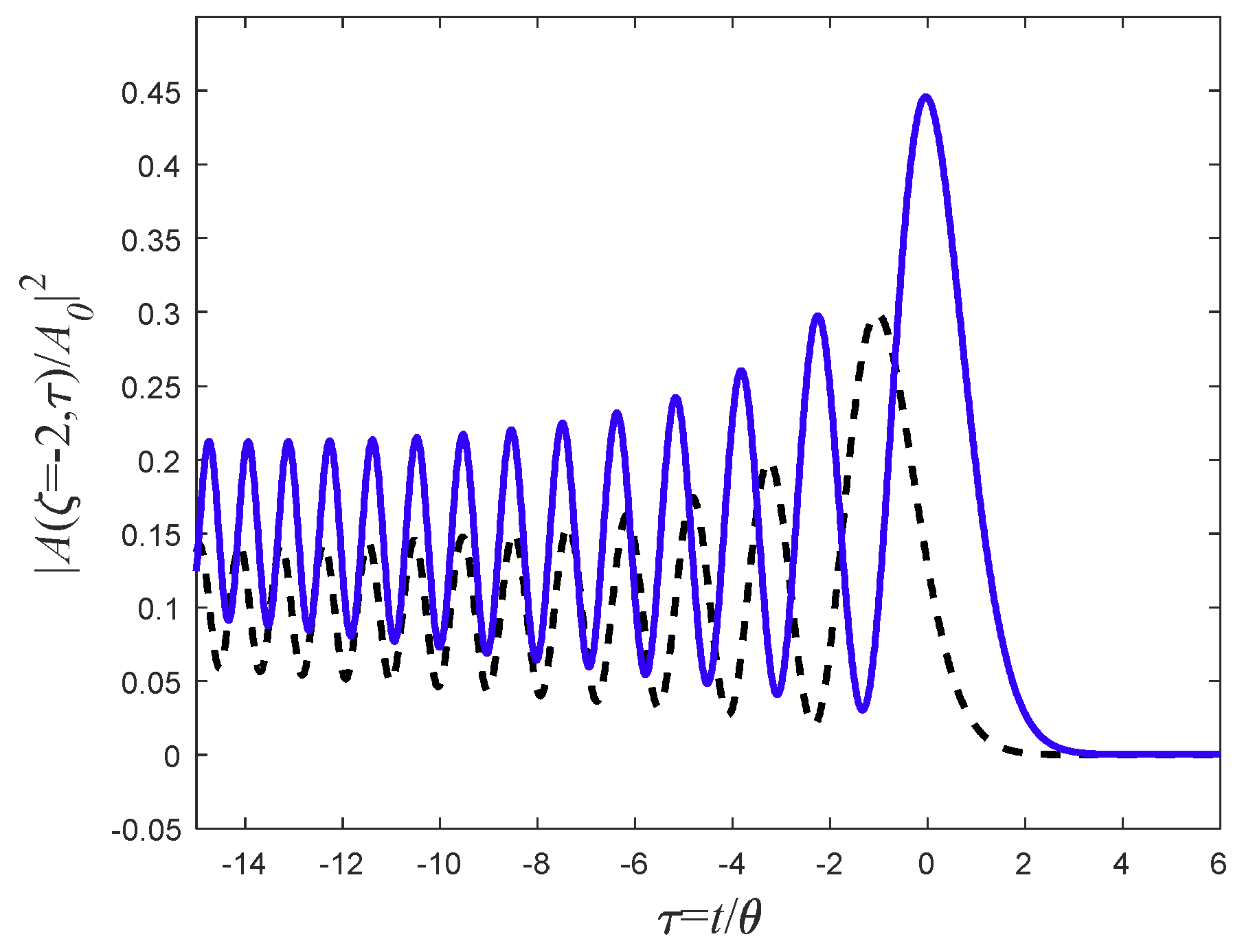
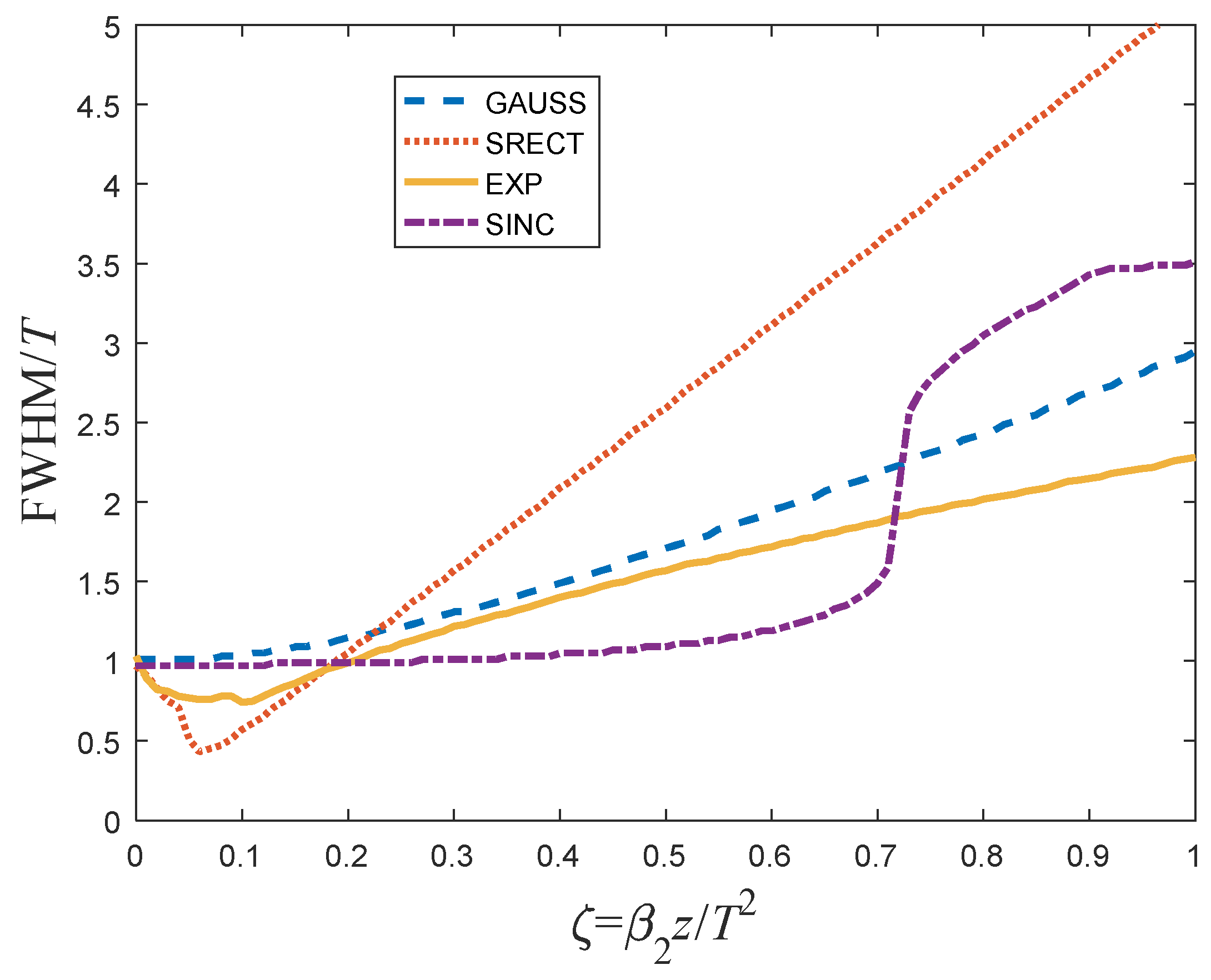
9. Pulse Broadening Comparison
10. Discussion and Conclusions
Funding
Conflicts of Interest
Appendix A. Proof of Equation (3)
Appendix B. Proof of Equation (6)
Appendix C. Proof of Equation (10)
References
- Zevallos, M.E.; Gayen, S.K.; Das, B.B.; Alrubaiee, M.; Alfano, R.R. Picosecond Electronic Time-Gated Imaging of Bones in Tissues. IEEE J. Sel. Top. Quantum Electron. 1999, 5, 916–922. [Google Scholar] [CrossRef]
- Gayen, S.K.; Alfano, R.R. Emerging optical biomedical imaging techniques. Opt. Photon. News 1996, 7, 17–22. [Google Scholar] [CrossRef]
- Das, B.B.; Yoo, K.M.; Alfano, R.R. Ultrafast time-gated imaging in thick tissues: A step toward optical mammography. Opt. Lett. 1993, 18, 1092–1094. [Google Scholar] [CrossRef] [PubMed]
- Marom, D.M.; Sun, P.C.; Fainman, Y. Communication with ultrashort pulses and parallel-to-serial and serial-to-parallel converters. In Proceedings of the LEOS ‘97, 10th Annual Meeting IEEE Lasers and Electro-Optics Society, San Francisco, CA, USA, 10–13 November 1997. [Google Scholar]
- Amiri, I.S.; Ahmad, H. Optical Soliton Communication Using Ultra-Short Pulses; Springer: Singapore, 2015. [Google Scholar]
- Yamaoka, Y.; Harada, Y.; Sakakura, M.; Minamikawa, T.; Nishino, S.; Maehara, S.; Hamano, S.; Tanaka, H.; Takamatsu, T. Photoacoustic microscopy using ultrashort pulses with two different pulse durations. Opt. Express 2014, 22, 17063–17072. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, H.C.; Arne, Y.B.; Alvin, C.L.; Yeh, T. Imaging embryonic development with ultrashort pulse microscopy. Opt. Eng. 2014, 53, 051506. [Google Scholar] [CrossRef]
- Technical Note: The Effect of Dispersion on Ultrashort Pulses. Newport Corporation (2018). Available online: https://www.newport.com/n/the-effect-of-dispersion-on-ultrashort-pulses (accessed on 10 January 2018).
- Sindhu, T.G.; Bisht, P.B.; Rajesh, R.J.; Satyanarayana, M.V. Effect of higher order nonlinear dispersion on ultrashort pulse evolution in a fiber laser. Microw. Opt. Technol. Lett. 2001, 28, 196–198. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Xi, P.; Ren, Q. Origin and effect of high-order dispersion in ultrashort pulse multiphoton microscopy in the 10 fs regime. Appl. Opt. 2010, 49, 6703–6709. [Google Scholar] [CrossRef] [PubMed]
- Granot, E. Fundamental dispersion limit for spectrally bounded On-Off-Keying communication channels and its implications to Quantum Mechanics and the Paraxial Approximation. Europhys. Lett. 2012, 100, 44004. [Google Scholar] [CrossRef]
- Granot, E. Information Loss in Quantum Dynamics. In Advanced Technologies of Quantum Key Distribution; INTECH: Rijeka, Croatia, 2017. [Google Scholar]
- Wollenhaupt, M.; Assion, A.; Baumert, T. Femtosecond Laser Pulses: Linear Properties, Manipulation, Generation and Measurement. Chap. 12. In Hanbookd of Laser and Optics; Träger, F., Ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Agrawal, G.P. Fiber-Optic Communications Systems, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2002. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Ali, R.; Hamza, M.Y. Propagation behavior of super-Gaussian pulse in dispersive and nonlinear regimes of optical communication systems. In Proceedings of the International Conference on Emerging Technologies (ICET 2016), Islamabad, Pakistan, 18–19 October 2016. [Google Scholar]
- Anderson, D.; Lisak, M. Propagation characteristics of frequency-chirped super-Gaussian optical pulses. Opt. Lett. 1986, 11, 569–571. [Google Scholar] [CrossRef]
- Zhang, L.; Li, C.; Zhong, H.; Xu, C.; Lei, D.; Li, Y.; Fan, D. Propagation dynamics of super-Gaussian beams in fractional Schrödinger equation: From linear to nonlinear regimes. Opt. Express 2016, 24, 14406–14418. [Google Scholar] [CrossRef]
- Moshinsky, M. Diffraction in time. Phys. Rev. 1952, 88, 625–631. [Google Scholar] [CrossRef]
- Del Campo, A.; Garcia-Calderon, G.; Muga, J.G. Quantum Transients. Phys. Rep. 2009, 476, 1–50. [Google Scholar] [CrossRef]
- Berry, M.V. Quantum fractals in boxes. J. Phys. A Math. Gen. 1996, 29, 6617–6629. [Google Scholar] [CrossRef]
- Granot, E.; Marchewka, A. Generic Short-Time Propagation of Sharp-Boundaries Wave Packets. Europhys. Lett. 2005, 72, 341–347. [Google Scholar] [CrossRef]
- Granot, E.; Luz, E.; Marchewka, A. Generic pattern formation of sharp-boundaries pulses propagation in dispersive media. J. Opt. Soc. Am. B 2012, 29, 763–768. [Google Scholar] [CrossRef]
- Granot, E.; Marchewka, A. Emergence of currents as a transient quantum effect in nonequilibrium systems. Phys. Rev. A 2011, 84, 032110–032115. [Google Scholar] [CrossRef]
- Marciano, S.; Ben-Ezra, S.; Granot, E. Eavesdropping and Network Analyzing Using Network Dispersion. Appl. Phys. Res. 2015, 7, 27. [Google Scholar] [CrossRef]
- Soto, M.A.; Alem, M.; Shoaie, M.A.; Vedadi, A.; Brès, C.-S.; Thévenaz, L.; Schneider, T. Optical sinc-shaped Nyquist pulses of exceptional quality. Nat. Commun. 2013, 4, 2898. [Google Scholar] [CrossRef]
- Schmogrow, R.; Bouziane, R.; Meyer, M.; Milder, P.A.; Schindler, P.C.; Killey, R.I.; Bayvel, P.; Koos, C.; Freude, W.; Leuthold, J. Real-time OFDM or Nyquist pulse generation—Which performs better with limited resources? Opt. Express 2012, 20, B543. [Google Scholar] [CrossRef]
- Hirooka, T.; Ruan, P.; Guan, P.; Nakazawa, M. Highly dispersion-tolerant 160 Gbaud optical Nyquist pulse TDM transmission over 525 km. Opt. Express 2012, 20, 15001–15007. [Google Scholar] [CrossRef]
- Hirooka, T.; Nakazawa, M. Linear and nonlinear propagation of optical Nyquist pulses in fibers. Opt. Express 2012, 20, 19836–19849. [Google Scholar] [CrossRef] [PubMed]
- Schmogrow, R.; Hillerkuss, D.; Wolf, S.; Bäuerle, B.; Winter, M.; Kleinow, P.; Nebendahl, B.; Dippon, T.; Schindler, P.C.; Koos, C.; et al. 512QAM Nyquist sinc-pulse transmission at 54 Gbit/s in an optical bandwidth of 3 GHz. Opt. Express 2012, 20, 6439–6447. [Google Scholar] [CrossRef] [PubMed]
- Bosco, G.; Carena, A.; Curri, V.; Poggiolini, P.; Forghieri, F. Performance limits of Nyquist-WDM and CO-OFDM in high-speed PM-QPSK systems. IEEE Phot. Technol. Lett. 2010, 22, 1129–1131. [Google Scholar] [CrossRef]
- Berry, M.V.; Balázs, N.L. Nonspreading wave packets. Am. J. Phys. 1979, 47, 264–267. [Google Scholar] [CrossRef]
- Siviloglou, G.A.; Broky, J.; Dogariu, A.; Christodoulides, D.N. Observation of Accelerating Airy Beams. Phys. Rev. Lett. 2007, 99, 213901. [Google Scholar] [CrossRef] [PubMed]
- Bandres, M.A. Accelerating beams. Opt. Lett. 2009, 34, 3791–3793. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, A. Handbook of Mathematical Functions; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Siviloglou, G.A.; Christodoulides, D.N. Accelerating finite energy Airy beams. Opt. Lett. 2007, 32, 979. [Google Scholar] [CrossRef] [PubMed]
- Preciado, M.A.; Dholakia, K.; Mazilu, M. Generation of attenuation-compensating Airy beams. Opt. Lett. 2014, 39, 4950–4953. [Google Scholar] [CrossRef]
- Preciado, M.A.; Sugden, K. Proposal and design of airy-based rocket pulses for invariant propagation in lossy dispersive media. Opt. Lett. 2012, 37, 4970–4972. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Granot, E. Analytical Solutions for the Propagation of UltraShort and UltraSharp Pulses in Dispersive Media. Appl. Sci. 2019, 9, 527. https://doi.org/10.3390/app9030527
Granot E. Analytical Solutions for the Propagation of UltraShort and UltraSharp Pulses in Dispersive Media. Applied Sciences. 2019; 9(3):527. https://doi.org/10.3390/app9030527
Chicago/Turabian StyleGranot, Er’el. 2019. "Analytical Solutions for the Propagation of UltraShort and UltraSharp Pulses in Dispersive Media" Applied Sciences 9, no. 3: 527. https://doi.org/10.3390/app9030527
APA StyleGranot, E. (2019). Analytical Solutions for the Propagation of UltraShort and UltraSharp Pulses in Dispersive Media. Applied Sciences, 9(3), 527. https://doi.org/10.3390/app9030527




