Abstract
In order to meet the requirement of secure image communication in a resource-constrained network environment, a novel lightweight chaotic image encryption scheme based on permutation and diffusion has been proposed. It was claimed that this scheme can resist differential attacks, statistical attacks, etc. However, the original encryption scheme is found to be vulnerable and insecure to chosen-plaintext attack (CPA). In this paper, the original encryption scheme is analyzed comprehensively and attacked successfully. Only by choosing a full zero image as the chosen-plaintext of the diffusion phase, the encrypted image can be restored into permutation-only phase, and by applying the other chosen images as the chosen-plaintexts of the permutation phase, the map matrix which is equivalent to the secret key of the permutation phase can be further revealed. Experiments and analysis verify the feasibility of our proposed attack strategy.
1. Introduction
With the development of Internet and information technology, ever-increasing multimedia data is emerging in our daily lives. Among multimedia data, digital image carrying information in a visualized manner has become a widely used data format. Many of these digital images in networks may be involved in personal privacy, military secrets, trade secrets, and even national security. If such digital images are intercepted by some unauthorized users, serious security disasters can occur. Thus, it is essential to protect private images with some effective solutions [1,2,3,4]. Image encryption [5,6,7], which aims at preventing unauthorized access by converting the data into an unrecognized form, has been a well-known effective and popular method to secure them.
Among different types of image encryption algorithms, the Chaos-based cryptosystem is particularly efficient and popular in image processing fields as it has many significant characteristics such as ergodicity, unpredictability, and initial state sensitivity [8,9,10,11]. In general, the existing chaotic systems can be partitioned into two primary types: one dimension (1D) maps [9] and high dimension (HD) maps [11]. 1D chaotic maps often have simple structures and low computational complexity; thus, it is efficient and easy to generate pseudorandom sequence during image cryptography. However, they face some potential drawbacks like vulnerability and limited chaotic ranges [12,13]. The demanding for higher level of security of image cryptosystems motivates researchers to extend 1D maps to HD chaotic maps. Generally speaking, HD maps have larger chaotic ranges and at least two variables to acquire better chaotic behaviors. These properties also make their chaotic orbits more unpredictable, and thus lead to a higher security for cryptosystems. However, higher computational overhead and implementation difficulty of these HD chaotic maps make them impractical for resource-limited devises as well [14,15,16]. Thus, to balance chaotic behaviors and computational cost, it is necessary and vital to develop such a scheme, which not only ensures larger key space to resist brute attack and key sensitivity to control parameters, but also can be implemented in a low computational overhead.
To meet the demanding for practical scenarios, a novel and lightweight chaotic image encryption scheme using 2D dimension Baker’s map has been proposed for secure communication [17]. The image cryptography algorithm [17] under study, involves the use of Permutation–Diffusion based on Fridrich’s structure. First, based on the two sets of initial settings— and —of 2D Baker’s map, the key matrices and , both used for the permutation phase, and the diffusion key (random number), used for the diffusion phase, are obtained. Then, in the permutation phase, the original plaintext is permuted based on the generated key matrices and ; the permuted plaintext is further diffused by the XOR operation between the matrix and the permuted plaintext . The original cryptosystem can provide good security for image to some degree; nevertheless, the simple XOR operation of the diffusion phase is insecure enough since it can be completely cracked by using only one time of CPA. In turn, the permutation phase can be further broken with the other CPA attack proposed by the state-of-the-art works [18]. Based on the above, the original encryption design may be not suitable for privacy protection with higher level of security requirements.
The main contributions of this paper are as follows.
- (1)
- We propose a feasible attack strategy that can completely break the original Permutation–Diffusion based image cryptosystem with high security and low computational overhead, which is especially applicable for secure image communication in the resource-constrained modern network environment.
- (2)
- Our cryptanalysis is also efficient with little computing, especially in the case of attack permutation phase where the equivalent rule for any complex scrambling method can be obtained. The proposed method is instructive for cryptanalysis researches of other image encryption schemes with a structure of permutation–diffusion.
- (3)
- The corresponding improvements are proposed by analyzing the complexity and security of the original encryption scheme [17], which will provide a useful reference for the development of image cryptosystem.
2. Review of the Original Scheme
A general flowchart of the original scheme is presented in Figure 1. As shown in Figure 1, the encryption design of the original scheme is composed of two processes: the permutation phase and diffusion phase. The permutation phase scrambles the original pixels by swapping the pixel values in the original image with the element values in the key matrices and , which can be carried out due to the superiority of the 2D Baker’s map, i.e., it can perform one-to-one the unit square onto itself. The diffusion phase further diffuses the permuted pixels by XORing a random matrix that depends on a random number generated by the initial setting, constant value matrix of the permuted plaintext .
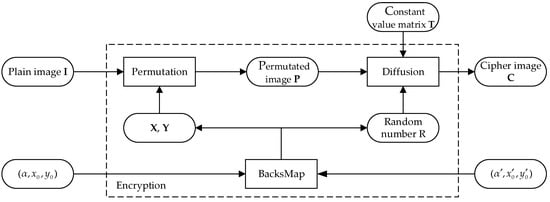
Figure 1.
A general illustration of the original scheme.
In the following, we discuss the permutation and diffusion phases of the original scheme in detail. Let denote a grayscale plaintext image with the size of and let and denote the 2D Baker’s map function and the swap function, respectively. The details of the pixel scramble and diffusion of the original plaintext are as follows.
Step 1: Input the plaintext image and compute the key matrices and using the map function .
Step 2: Scramble the original plaintext by swapping it with to generate the permuted image , as shown in (2).
where and meet the conditions and , respectively; and satisfy the conditions and .
Step 3: Compute the random number by using the map function again, and compute the matrix used to diffuse the permuted plaintext .
Step 4: Diffuse the permuted image by performing XOR operation on the permuted image , the matrix , and the constant value matrix controlled by the image sizes and the position of each pixel directly.
Until now, we have obtained the permuted and diffused image, i.e., the final ciphertext image .
3. Cryptanalysis of the Original Scheme
According to Kerchoff’s principle [19], the security of a cryptosystem only relies on the secret keys, regardless of the algorithm design and complexity of the cryptosystem. From the perspective of cryptanalysts, they know everything about the cryptosystem except for the secrecy of the key. Thus, after knowledge of the cryptographic algorithm, one can easily carry out cryptanalysis if there exist some possible loopholes in original cryptosystems.
In order to collapse the encryption scheme [17], a general framework of the proposed attack strategy is presented in Figure 2. As presented in Figure 2, the total cryptanalysis processes of the presented attack strategy include Attack 1 and Attack 2. Attack 1 is used to acquire the secret key of the original diffusion phase so as to retrieve the permutation-only image ; with the help of the revealed diffusion key , Attack 2 is further adopted to obtain the permutation rule of the original permutation phase. If one has knowledge of the permutation rule , he/she can recover the plaintext image accurately, i.e., the deciphering image; as such, the original cryptosystem can be completely collapsed. In the following, we will discuss the cryptanalysis process in detail.
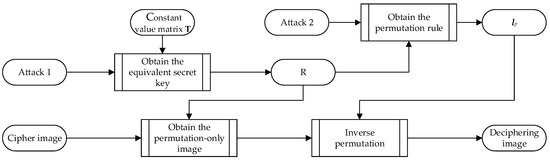
Figure 2.
A framework of the proposed attack strategy.
3.1. Obtain the Equivalent Secret Key
In this section, we discuss how to obtain the secret key R of the original diffusion phase in detail. For the original diffusion process, even if it employs the superiority, such as larger key space and key sensitivity of the 2D Baker’s map to diffuse the permuted image, the key equivalent that is functionally equal to the secret key of the diffusion phase can be easily obtained with a CPA attack (called the zero image as the chosen plaintext), as shown in the flowchart of Figure 3. Furthermore, the cipher image generated by encrypting the full zero image is exactly the key equivalent of the original diffusion phase, which will be discussed in detail next. With the help of the known constant value matrix , the correct secret key can be revealed completely.

Figure 3.
Flowchart on obtaining the secret key .
According to the assumption of chosen-plaintext that the plaintext is chosen in advance and its corresponding ciphertext can be generated from the chosen-plaintext, let a full zero image act as the chosen-plaintext image . Note: all of the existing permutation algorithms will lose their efficacies if a full zero image is used to act as the plaintext image. Therefore, after the original permutation phase, the permuted image of the chosen-plaintext image is still itself. For the diffusion phase, although we do not know the secret key used in the diffusion phase, the diffusion algorithm is public and available. Thus, according to (3), (4) and the permuted image , we have
Based on the above (6), the matrix has become a matrix in which all element values equal to the random number generated by Bake’s map or its equivalent; in other word, the plaintext-related process of the original scheme has become invalid. Then, with the assistance of (5), the matrix and the permuted plaintext image , the ciphertext image can be obtained as
where is a constant value matrix relying on an image size and its pixel position; or rather, it can be available by anyone who wants to know the content of the matrix. The obtained ciphertext image is the final encryption resultant of the chosen-plaintext image , and it is known and available according to the assumption of chosen-plaintext. Apparently, the ciphertext image only relies on the matrix ; also, the matrix is exactly decided by the random number or its equivalent. Thus, ciphertext image is the key equivalent of the diffusion phase. By further XORing the known constant value matrix , as show in (8), the correct diffusion key of the original diffusion phase can be completely revealed.
For clarity, we also provide the process of revealing the diffusion key . As depicted in Algorithm 1, the diffusion key can be easily obtained by using the full zero plain image and the constant value matrix , which also provides the indicator of a large loophole existing in the original cryptosystem.
| Algorithm 1 Obtain the secret key R |
| Input: Full zero plain image I0 |
| Output: The secret key R |
| 1: procedure Key(I0) |
| 2: M, N ← size(I0) // Get the size of the plain image |
| 3: T ← zeros(M, N) |
| 4: for i from 1 to M |
| 5: for j from 1 to N |
| 6: T(i, j) ← mod(M/i + N/j, 256) // Obtain the constant matrix |
| 7: end |
| 8: end |
| 9: C ← encryption(I0) // Obtain the ciphertext image |
| 10: R ← bitxor(T, C) |
| 11: end procedure |
After revealing the diffusion key , the permutation-only image can be obtained by decrypting the final ciphertext image , which is the encryption resultant of the exploited test image in the original cryptosystem. Algorithm 2 depicts the generation of permutation-only image in detail. Apparently, the permutation-only image can be successfully obtained.
| Algorithm 2 Obtain the permutation rule lp |
| Input: N pairs of permutation-only images of chosen images |
| Output: Permutation rule lp and B |
| 1: procedure Rule(P1, P2, …, Pn) // Define a function to obtain the permutation rule |
| 2: M, N ← size(P1) // Get the size of the image |
| 3: B ← zeros(M, N) |
| 4: for i from 1 to M |
| 5: for j from 1 to N |
| 6: B(i, j) ← P1(i, j) * 256 + P2(i, j) |
| 7: end |
| 8: end |
| 9: lp ← reshape(B, 1, M * N) // Turn the matrix into a vector |
| 10: end procedure |
3.2. Obtain the Permutation Rule
Having attacked the diffusion phase of the original scheme, the final encrypted resultant generated by the original cryptosystem could be restored into permutation-only phase. In this section, we further analyze and attack the permutation phase of the original scheme so as to retrieve the original plaintext image. The flowchart structure of revealing the permutation rule is presented in Figure 4. First, n pairs of plain images are chosen as the chosen-plaintext images. Based on the original cryptosystem, we can easily obtain their corresponding final cipher images . With the help of the diffusion key revealed in the previous section, we can obtain the permutation rule , which is composed of . Next, the detailed analysis process of revealing the permutation rule will be described.
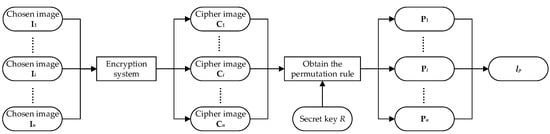
Figure 4.
Flowchart on obtaining the permutation rule .
For the permutation process of the original cryptosystem, both the key space and key sensitivity are reliable and effective; it is almost impossible to obtain the key directly from the permutation phase. Nevertheless, the map matrix which is equivalent to the secret key of the permutation phase can be revealed by using the state-of-the-art work [18], which will be discussed in the following. Note that for any of the existing scrambling algorithms, they cannot modify the pixel values of an image, but merely scramble the pixel positions. Therefore, if one can utilize some possible means to uniquely identify a pixel position, the permutation rules of all permutation-only cryptosystems will be revealed accurately and efficiently under any conditions (regardless of the cryptosystem structures). The assumption has been successfully implemented in recent proposed the state-of-the-art work [18], which can completely determine the correct plaintext elements by utilizing a deterministic method. For a plain image of size , which acts as the test image in original cryptosystem, the position of each pixel row by row in the plaintext image can be determined by a dimension vector . According to the Lemma 1 of Jolfaei et al.’s work [18], the number of the chosen-plaintext images to break any of the existing permutation-only cryptosystems is , which can be formulized as follows.
where denotes the number of locations, i.e., the size of an image; denotes the number of all entries, and there will be 256 entries for an image of 8 bit in depth. In the following, we will discuss two concrete cases to completely determine the correct plaintext elements of the permutation-only cryptosystem on the basis of (9).
Case 1: If the size of a plaintext image I is , only two chosen plaintext images— and —will be chosen to obtain the permutation rule. The following will give some related analyses.
For the plaintext image of size which will be restored using the two chosen plaintext images and , the position vector of all pixels in the plaintext image can be rearranged row by row in the matrix , as shown in (10), where each element includes two digits in base 256 across the character set to express the position of .
where the element is exactly the position of the position vector .
Since the pixel value in the original plaintext image varies from 0 to 255, i.e., all of the entries in (9), we can obtain the two matrices with entries by splitting matrix into two bit-plane images. Actually, the bit-plane images are exactly the chosen plaintext images and mentioned above, as shown in (11,12).
Based on above, the pixel position vector of the original plaintext image has completely relied on and . In the following, we only need to generate the pixel position vector of the permutation-only image by recovering the final ciphertext image of the original plaintext image into the permutation-only phase, the permutation rule of the original permutation phase will be able to be revealed. Here, the final ciphertext image——includes two parts— and (encrypted by the original permutation and diffusion phases). Furthermore, the pixel position vector of permutation-only image is indirectly determined by and . With the help of the generated diffusion key , the ciphertext images and can be easily restored to the permutation-only images and ; the position vector of permutation-only image is exactly the combination resultant of the two obtained and is exactly the position vector of the permutation-only image . Therefore, the permutation rule has been revealed, which can be seen in Algorithm 3.
| Algorithm 3 Proposed diffusion attack algorithm |
| Input: A known ciphertext image C, full zero plain image I0 |
| Output: The permutation-only image P of known ciphertext image C |
| 1: procedure De_ diffusion(C, I0) |
| 2: M, N ← size (C) // Get the size of the image |
| 3: R ← Key (I0) // Invoke algorithm 1 to obtain the key R |
| 4: r ← 0 |
| 5: for i from 1 to M |
| 6: for j from 1 to N |
| 7: r ← mod(C(i−1, j−1) + R, 256) |
| 8: P(i, j) ← bitxor(r, C(i, j)) |
| 9: T(i, j) ← mod(M/i + N/j, 256) // Obtain the constant matrix |
| 10: end |
| 11: end |
| 12: P ← bitxor(P, T) // Return the permutation-only image |
| 13: end procedure |
In Algorithm 3, one can easily find that a one-to-one map between the permutation rule and the position vector of the original plaintext has been established. For clarity, Figure 4 further illustrates the map between permutation rule and the position vector of the original plaintext image. As depicted in Figure 5, we reshape the chosen-plaintext images— and —into the position vector of the original plaintext image in the top half part, and and into the position vector of the permutation-only images in the upper half part, respectively. Obviously, one can deterministically find out all of the correct plaintext elements by one-to-one mapping all pixels of the permutation-only image into the original plain image.
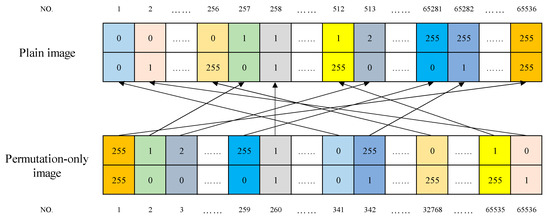
Figure 5.
A schematic diagram of permutation correspondence.
Case 2: If the size of a plaintext image is , only three chosen plaintext images will be required to obtain the permutation rule . For the plaintext image of size which will be restored using three chose plaintext images, the position vector of all pixels in the plaintext image can be rearranged row by row in the matrix , where each element includes three digits in base across the character set to express the position of .
In a similar manner, the permutation rule of the original cryptosystem can also be revealed by the three chosen-plaintext images. Here, we will not describe the similar process again.
Once permutation rule is accurately revealed, the exploited test image——in the original cryptosystem can be restored by decrypting the permutation-only image . Algorithm 4 also describes the generation of the exploited test image in the original cryptosystem in detail. Apparently, the permutation-only image can be successfully obtained.
| Algorithm 4 Proposed confusion attack algorithm |
| Input: The permutation-only image P, and n pairs of permutation-only images of chosen images |
| Output: The deciphering image I |
| 1: procedure De_ confusion(P, P1, P2, …, Pn) |
| 2: M, N ← size(P) // Get the size of the image |
| 3: I ← zeros(M, N) |
| 4: lp, B ← Rule(P1, P2, …, Pn) // Invoke algorithm 2 to obtain the permutation rule |
| 5: x, y ← 0 |
| 6: for i from 1 to M |
| 7: for j from 1 to N |
| 8: x ← floor(B(i, j) / M) + 1 // Obtain the original row number |
| 9: y ← mod(B(i, j), M) // Obtain the original column number |
| 10: I(x, y) ← P(i, j) // Return the permutation-only image |
| 11: end |
| 12: end |
| 13: end procedure |
For clarity and the ease explanation, Figure 6 shows the process of chosen-plaintext attack for obtaining the permutation rule . In Figure 6, the first, second, and third columns represent plaintext, final ciphertext, and permutation-only images, respectively; Figure 6(a1,b1) represents the two original chosen-plaintext images; Figure 6(a2,b2) represents the final ciphertext image of Figure 6(a1,b1) encrypted by the original cryptosystem; and Figure 6(a3,b3) is the permutation-only images obtained by decrypting the final ciphertext images Figure 6(a2,b2) with the revealed diffusion secret key R in the previous section. Once the permutation-only images are obtained, the original plaintext image can be found by one-to-one maps the permuted positions into the original positions, as mentioned above. In addition, the element of the first pixel position of the original plaintext image is also marked for analyzing the permutation rule of the original scheme. After obtaining the permutation-only image, the element of the first pixel position of the original plaintext image has been scrambled into position in the permutation-only image, indicating that based on Jolfaei et al.’s work [18], a one-to-one map can be successfully established.

Figure 6.
Chosen-plaintext attack for obtaining the permutation rule: images from the first column to the last are plain, cipher, and permutated images, respectively; images from the first row to the last are color, selected images, respectively.
3.3. Summary of the Attack Strategy
In this section, the total attack process, including revealing the diffusion key and the permutation rule , is briefly summarized as follows.
- Step 1: According to Algorithm 1, obtain the secret key or equivalent key via a known full zero image (Attack 1) as stated in Section 3.1.
- Step 2: Obtain permutation rule using the following substeps.
- Determine the number of chosen images (Attack 2) according to (9).
- According to Algorithm 2, obtain the permutation-only images of chosen images with the diffusion key .
- According to Algorithm 3, obtain the permutation rule with the permutation-only images.
- Step 3: Invoke Algorithm 3 to obtain the permutation-only image of the final ciphertext image.
- Step 4: Invoke Algorithm 4 to obtain the deciphering image of the final ciphertext image.
In addition, the effectiveness of the proposed attack strategy is verified by a series of simulation experiments. All of the experiments were executed on a personal computer equipped with an Intel(R) Core(TM) i7-7500U 2.90 GHz CPU and 8 GB memory capacity. MATLAB R2016b was used for the simulations. The most typical representatives with the size of , including ‘Lena’, ‘Peppers’, ‘Chemical plant’, complete black, and complete white image, were tested for verification. The original test images in Figure 7(a1–e1) were firstly encrypted by the original cryptosystem, and the final encrypted resultants are shown in Figure 7(a2,b2,c2,d2,e2), respectively. Based on this, we can attack the final encrypted resultants step by step by using the obtained diffusion key and the permutation rule . Specifically, by utilizing CPA, i.e., the Algorithm 1 mentioned above, the final the final encrypted resultants can be restored into the permutation-only images, as shown in Figure 7(a3–e3). With the help of the obtained permutation rule , i.e., the Algorithm 2 mentioned before, these permutation-only images can be further restored the original plaintext images, as shown in Figure 7(a4–c4), which are completely identical the original plaintext images by observing the XOR operation resultants between the original images and the restored ones, as shown in Figure 7(a5–d5). Therefore, the proposed attack strategy is effective.

Figure 7.
The effectiveness of the proposed cryptanalysis: images from column 1 to column 5 show plain images, cipher images, retrieved permutation-only images, final recovered images, and XOR results for column 1 and column 4, respectively.
For the solid gray image that has the same pixel value such as complete black image shown in Figure 7(d1) and complete white image shown in Figure 7(e1), their ciphertext images shown in Figure 7(d2,e2) show a hierarchy of symmetry from the diagonal. Additionally, their permutation-only images shown in Figure 7(d3,e3) are the same as the final recovered images shown in Figure 7(d4,e4). Therefore, it is proved that the original encryption scheme does not applicable to this kind of solid gray images. Because scrambling does not work on images with the same pixel values, it is easy to obtain the secret key. Nevertheless, our proposed strategy is still effective for this kind of solid gray images.
3.4. Computational Complexity Analysis
In the proposed cryptanalysis structure, the original diffusion phase can be cracked with only one full zero image, and the original permutation phase can be broken by chosen-plaintext images. Thus, the total plaintext images are required to collapse the original cryptosystem, which is acceptable for the requirements of the computational complexity and cryptanalysis feasibility. In addition, The running times of attacking permutation and diffusion phases for different sizes of images, including , , and , are also shown in Table 1. From Table 1, one can easily find that given an image size (), the average running times for attacking permutation and diffusion are 0.4249 and 2.4225 (1.6362 and 8.2446), respectively; the average running times for breaking the total cryptosystem is 2.8473 (9.8808 for ). Therefore, the proposed attack strategy is satisfactory in terms of executive efficiency. In addition, as expected, the running time is increased with the increase of the size of an image; in other words, the proposed attack strategy can be applicable for breaking the cryptosystem with an image of any size.

Table 1.
Execution time (seconds).
4. Conclusions
This paper has proposed a novel means of attacking the recent proposed 2D chaotic encryption scheme. The original cryptosystem is based on permutation–diffusion structure, and its security merely relies on two permutation key matrices— and —and an diffusion key . We found the cryptosystem has potential vulnerability for resistance against CPA attacks. In this paper, the total chosen-plaintext images can completely collapse the original cryptosystem: one full zero image was used for breaking the original diffusion phase and plaintext images used for cracking the original permutation phase. Experiments has verified the feasibility the proposed attack strategy, especially applicable for images with any sizes.
Additionally, it is clear from the above discussion that the methods may be effective to improve the security of the original encryption scheme. (1) Associate the key with the plain image closely to reduce the possibility of violent attacks; the key is dynamic, and each plain image corresponds to a set of keys. (2) Add a substitute phase before the original diffusion phase to protect against chosen plaintext attacks to a certain extent. (3) Improve encryption structures, such as diffusion between row circular shift and column circular shift, increasing the number of pixels for boundary substitution and so on. Actually, the complexity and security of encryption schemes mainly depends on the structure of the encryption scheme and the choice of the key, which are difficult to preserve at the same time. Therefore, sometimes there is a trade-off between the security and complexity of encryption schemes.
Author Contributions
Conceptualization, M.L.; Methodology, M.L.; Software, K.Z.; Validation, H.R.; Formal Analysis, H.F.; Investigation, H.R.; Writing—Original Draft Preparation, K.Z. and H.R.; Writing—Review and Editing, H.F.; Visualization, K.Z.; Supervision, H.F.; Funding Acquisition, M.L. and H.F.
Funding
This research was funded by the National Natural Science Foundation of China (Grant nos., 61602158, U1604154), the Science and Technology Research Project of Henan Province (Grant no., 182102210374), the Science Foundation for the Excellent Youth Scholars of Henan Normal University (Grant no., YQ201607), and the PhD Scientific Research Foundation of Henan Normal University (Grant no., 5101119170143).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Li, X.W.; Lee, I.K. Robust copyright protection using multiple ownership watermarks. Opt. Express 2015, 23, 3035–3046. [Google Scholar]
- Fan, H.; Li, M.; Liu, D.; An, K. Cryptanalysis of a plaintext-related chaotic RGB image encryption scheme using total plain image characteristics. Multimed. Tools Appl. 2018, 77, 20103–20127. [Google Scholar]
- Wang, X.; Wang, Q.; Zhang, Y. A fast image algorithm based on rows and columns switch. Nonlinear Dyn. 2015, 79, 1141–1149. [Google Scholar]
- Li, M.; Ren, H.; Zhang, E.; Wang, W.; Sun, L.; Xiao, D. A VQ-Based Joint Fingerprinting and Decryption Scheme for Secure and Efficient Image Distribution. Secur. Commun. Netw. 2018, 2018, 4313769. [Google Scholar]
- Cambareri, V.; Mangia, M.; Pareschi, F.; Rovatti, R.; Setti, G. Low-Complexity Multiclass Encryption by Compressed Sensing. IEEE Trans. Signal Process. 2015, 63, 1. [Google Scholar]
- Zhang, L.Y.; Liu, Y.; Pareschi, F.; Zhang, Y.; Wong, K.-W.; Rovatti, R.; Setti, G. On the security of a class of diffusion mechanisms for image encryption. IEEE Trans. Cybern. 2018, 48, 1163–1175. [Google Scholar]
- Zheng, P.; Huang, J. Efficient Encrypted Images Filtering and Transform Coding with Walsh-Hadamard Transform and Parallelization. IEEE Trans. Image Process. 2018, 27, 2541–2556. [Google Scholar]
- Ping, P.; Wu, J.; Mao, Y.; Xu, F.; Fan, J. Design of image cipher using life-like cellular automata and chaotic map. Signal Process. 2018, 150, 233–247. [Google Scholar]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar]
- Li, M.; Xiao, D.; Liu, H.; Bai, S. A recoverable chaos-based fragile watermarking with high PSNR preservation. Secur. Commun. Netw. 2016, 9, 2371–2386. [Google Scholar]
- Hua, Z.; Jin, F.; Xu, B.; Huang, H. 2D Logistic-Sine-Coupling Map for Image Encryption. Signal Process. 2018, 149, 148–161. [Google Scholar]
- Li, M.; Liu, S.; Niu, L.; Liu, H. Cryptanalyzing a chaotic encryption algorithm for highly auto correlated data. Opt. Laser Technol. 2016, 86, 33–38. [Google Scholar]
- Dhall, S.; Pal, S.K.; Sharma, K. Cryptanalysis of image encryption scheme based on a new 1D chaotic system. Signal Process. 2018, 146, 22–32. [Google Scholar]
- Sun, Y.; Luo, H.; Das, S.K. A trust-based framework for fault-tolerant data aggregation in wireless multimedia sensor networks. IEEE Trans. Dependable Secur. Comput. 2012, 9, 785–797. [Google Scholar]
- Luo, H.; Luo, J.; Liu, Y.; Das, S. Adaptive data fusion for energy efficient routing in wireless sensor networks. IEEE Trans. Comput. 2006, 55, 1286–1299. [Google Scholar]
- Zhao, D.; Li, X.Y.; Ma, H. How to crowdsource tasks truthfully without sacrificing utility: Online incentive mechanisms with budget constraint. In Proceedings of the IEEE INFOCOM 2014-IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014. [Google Scholar]
- Mondal, B.; Kumar, P.; Singh, S. A chaotic permutation and diffusion based image encryption algorithm for secure communications. Multimed. Tools Appl. 2018, 77, 31177–31198. [Google Scholar]
- Jolfaei, A.; Wu, X.W.; Muthukkumarasamy, V. On the Security of Permutation-Only Image Encryption Schemes. IEEE Trans. Inf. Forensics Secur. 2015, 11, 235–246. [Google Scholar]
- Kerckhoffs, A. La cryptographie militaire. J. Des Sci. Mil. 1883, 4, 161–191. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).