Development and Evaluation of Crack Band Model Implemented Progressive Failure Analysis Method for Notched Composite Laminate
Abstract
Featured Application
Abstract
1. Introduction
2. Development of Progressive Failure Analysis
2.1. Progressive Failure Analysis
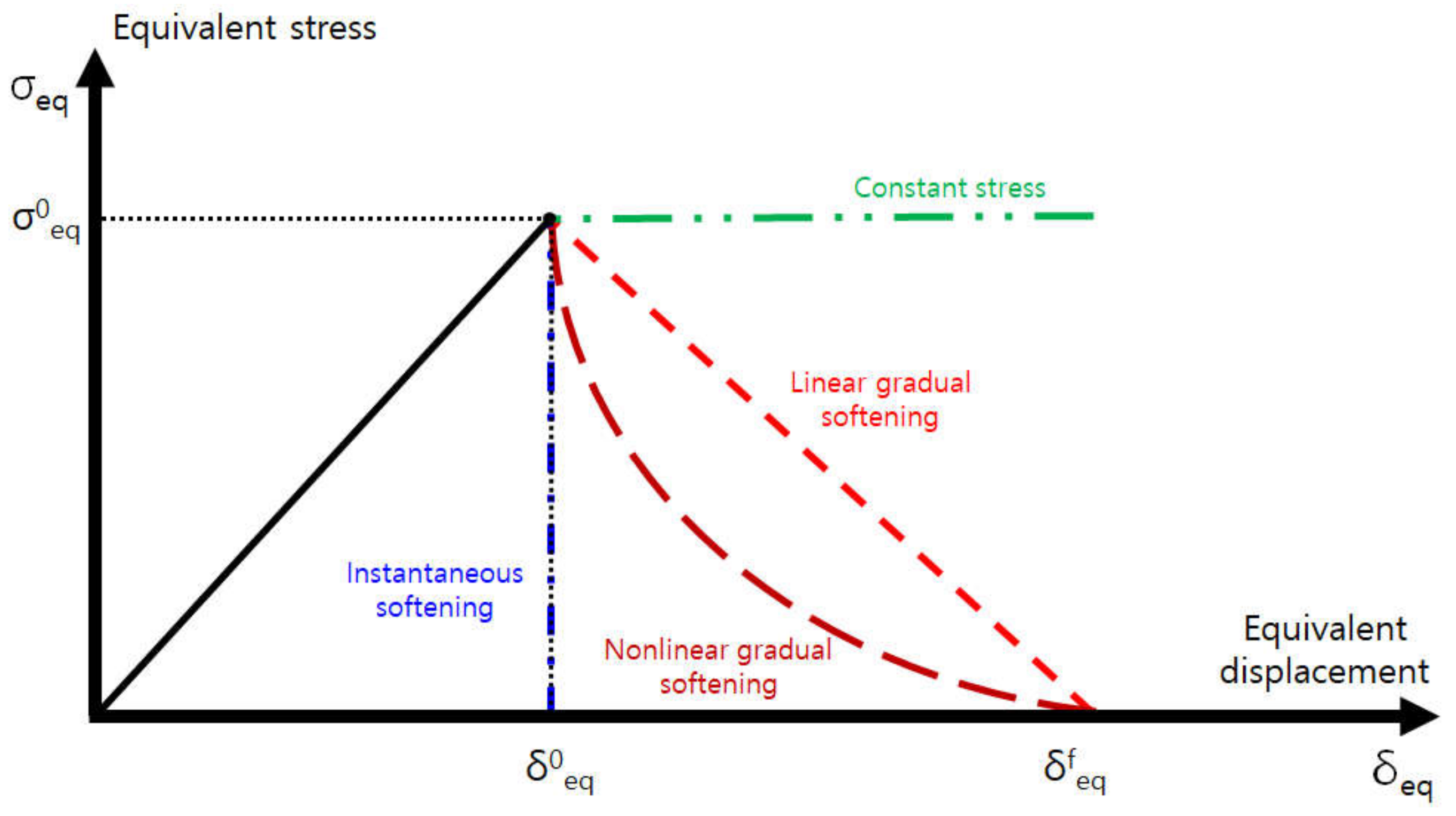
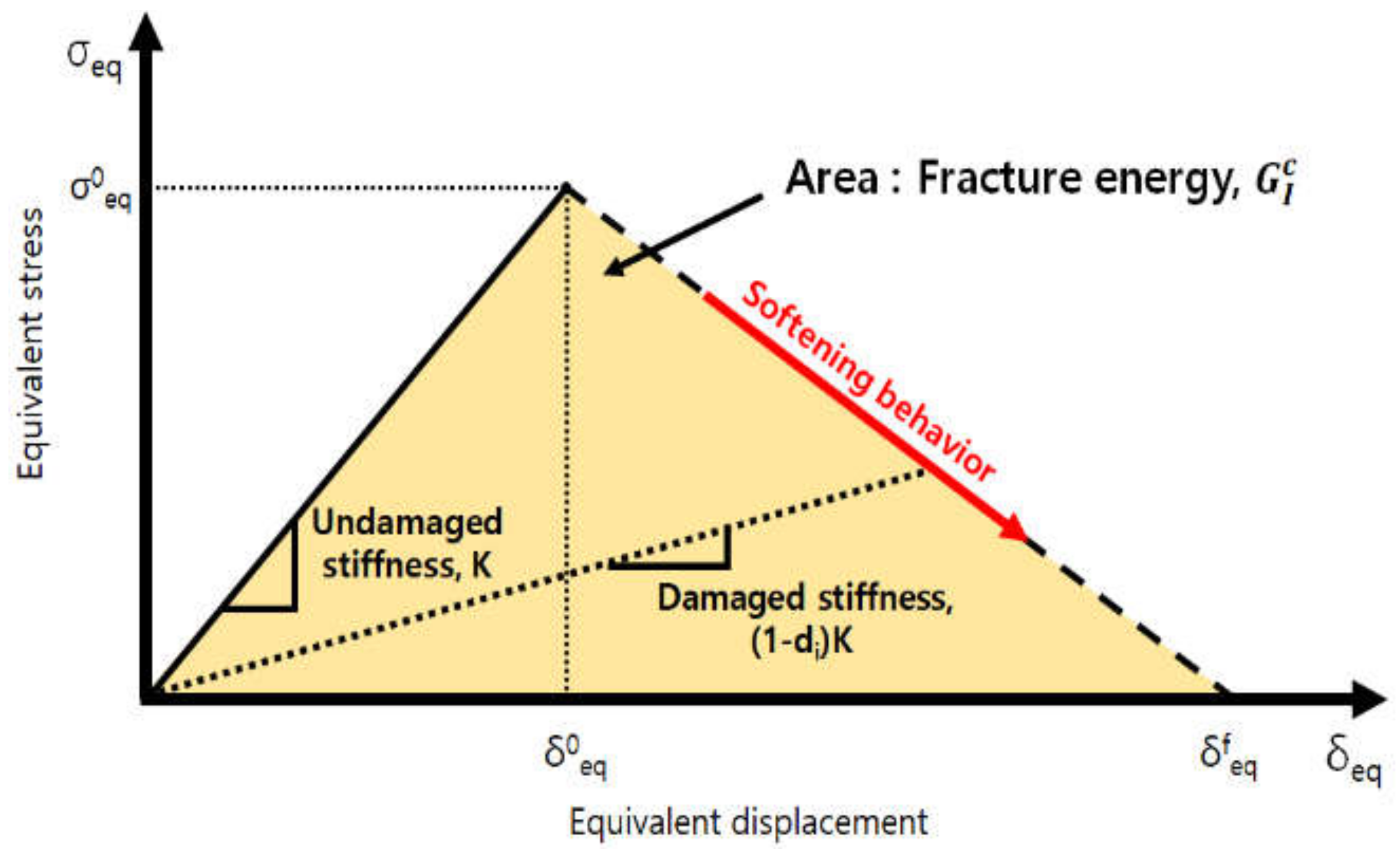
2.2. Damage Initiation and Evolution
3. Material and Test Procedures
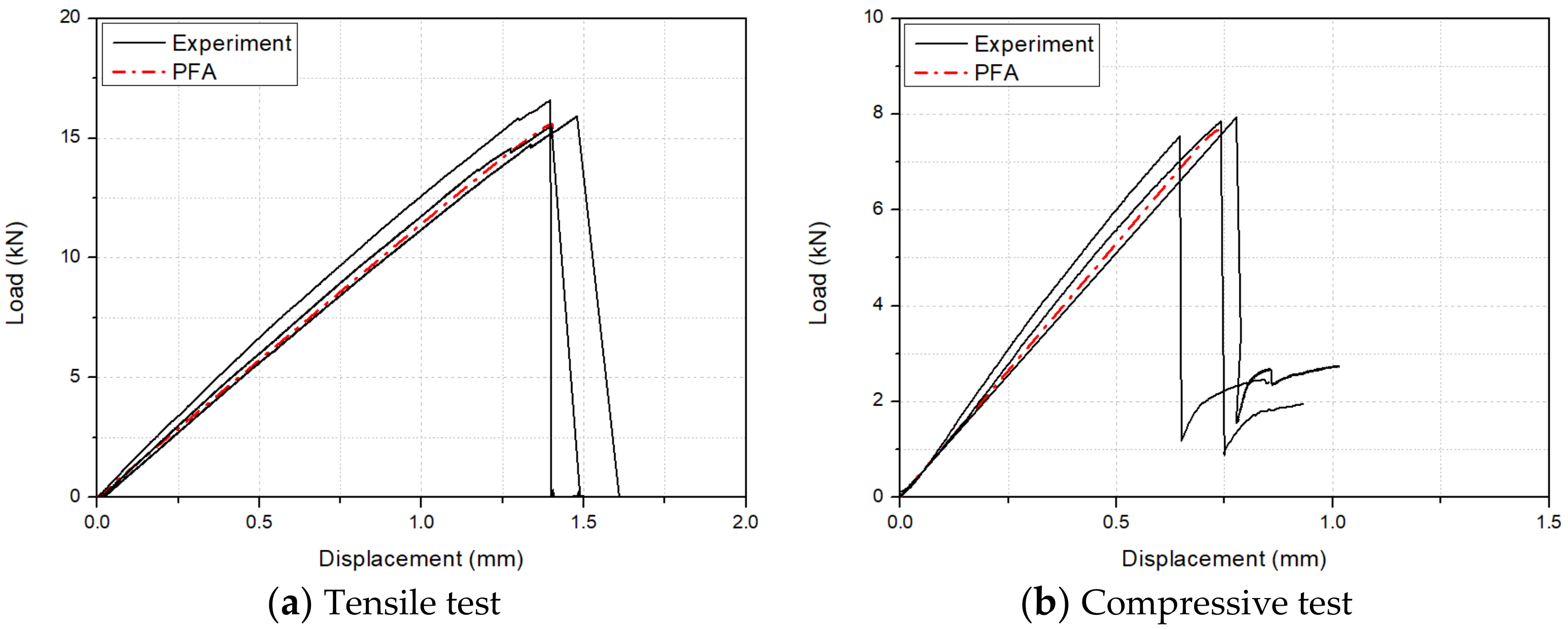
3.1. Composite Material and Test Specimen
3.2. Test Procedures
3.3. FEM Procedures
4. Results
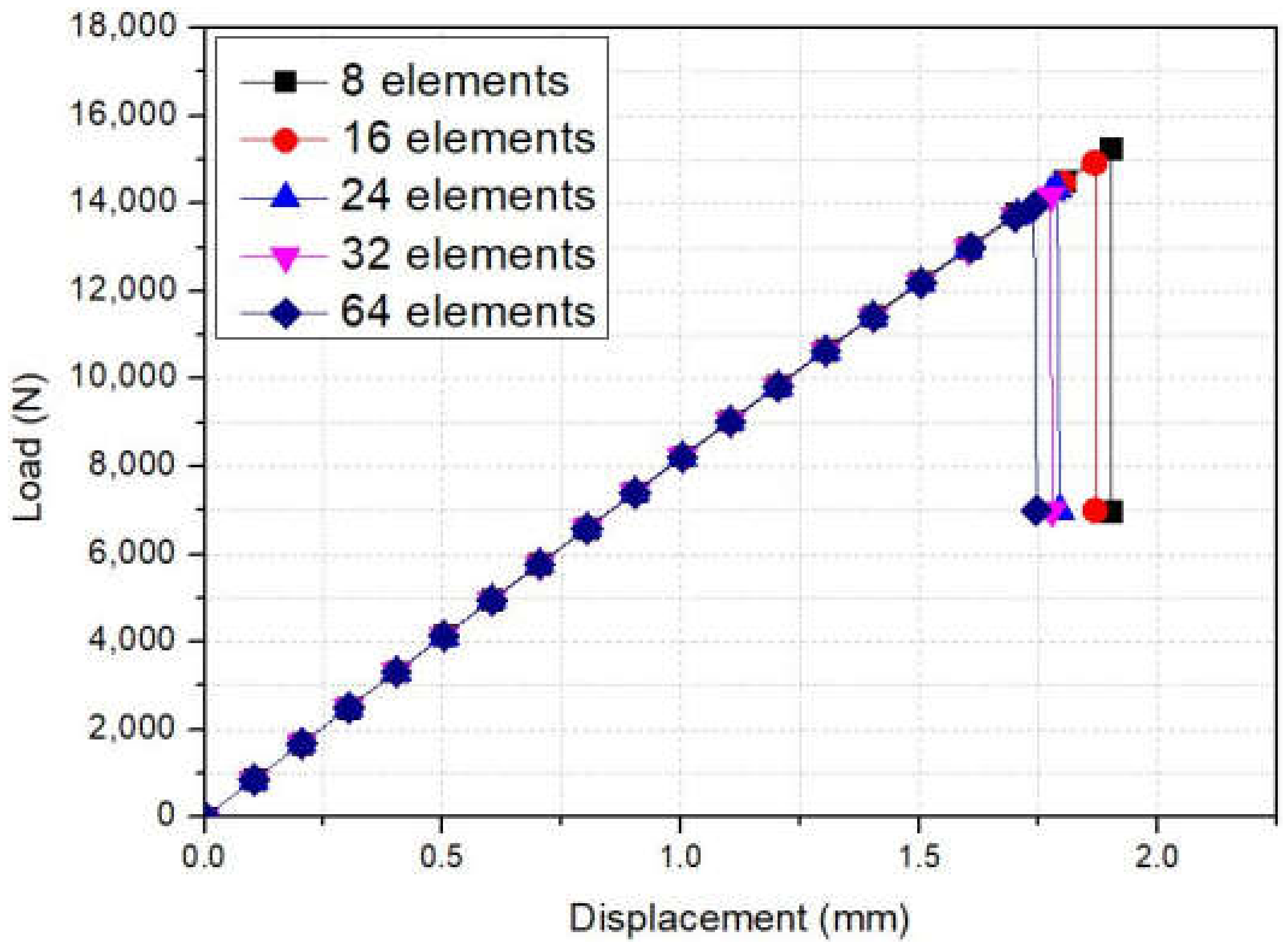
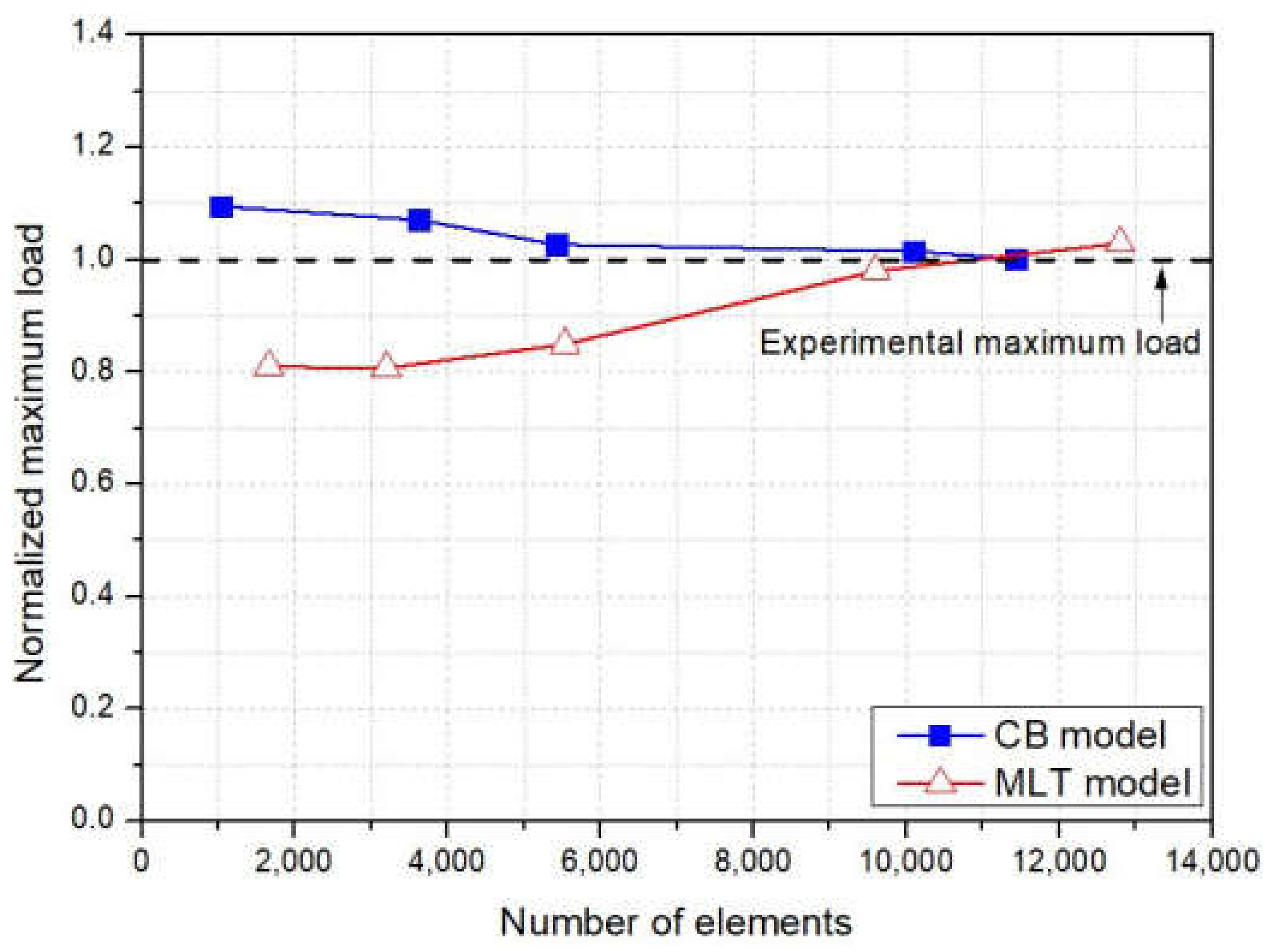
4.1. Mesh Dependency Study
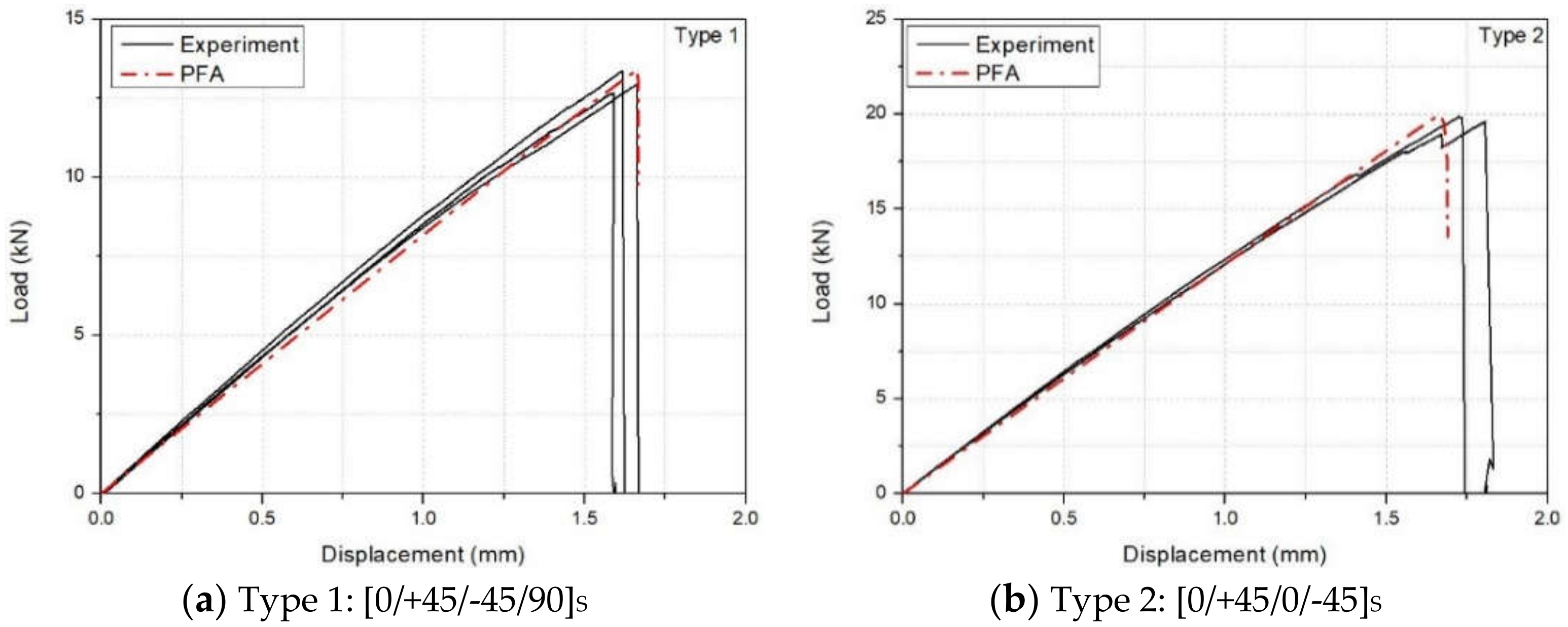
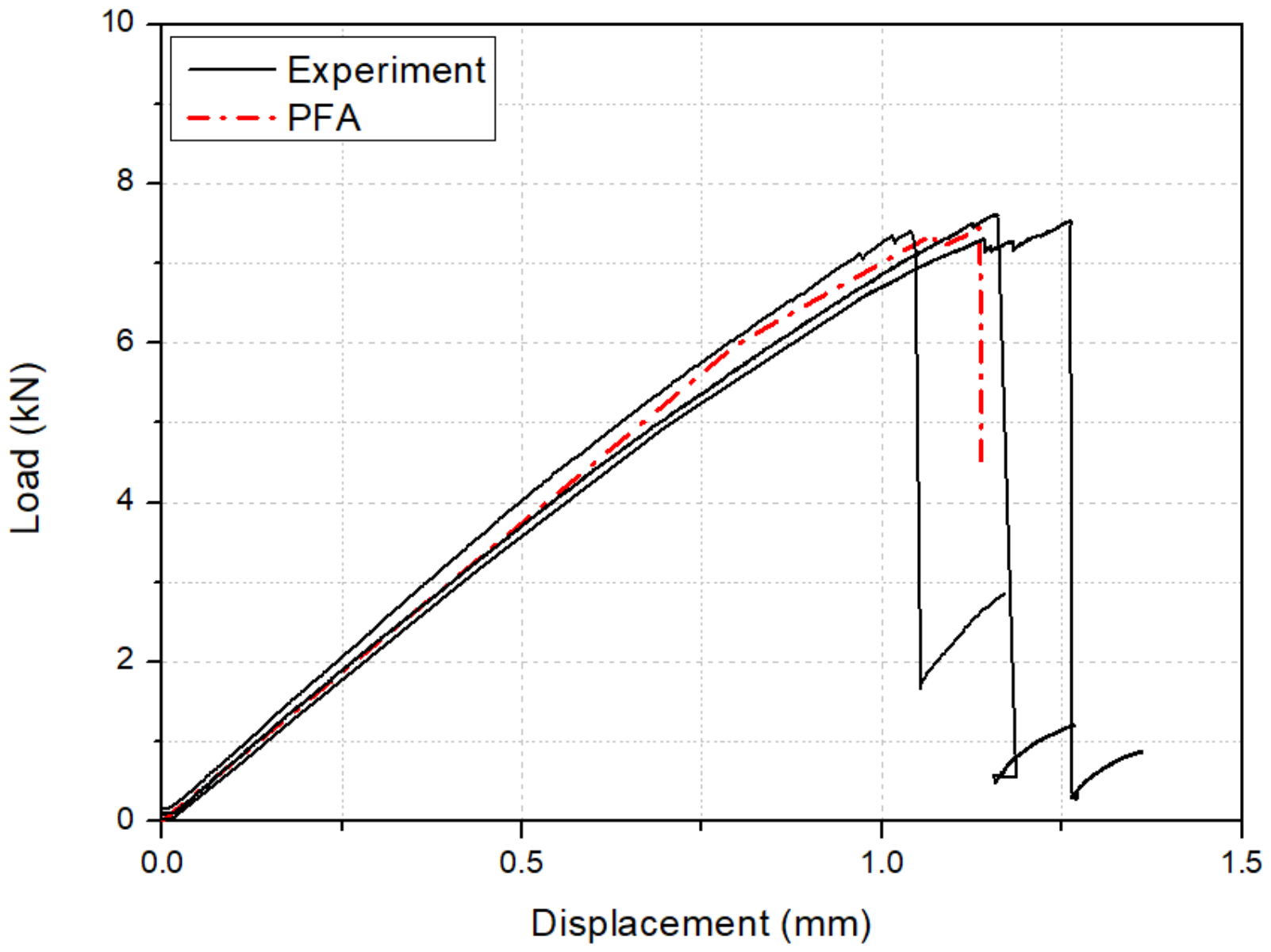
4.2. Evaluation of Load-Displacement Behavior
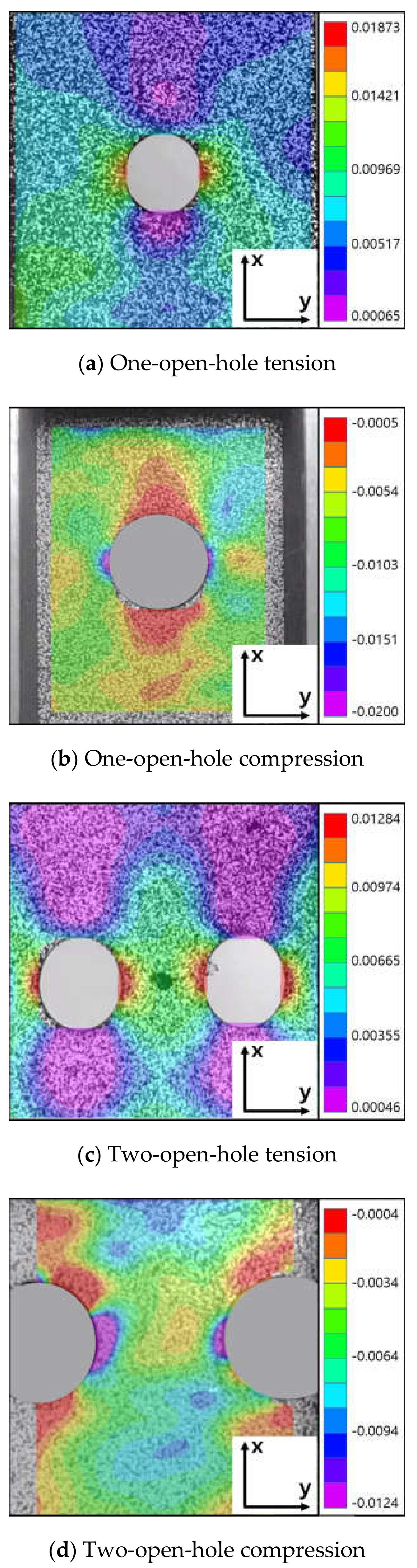
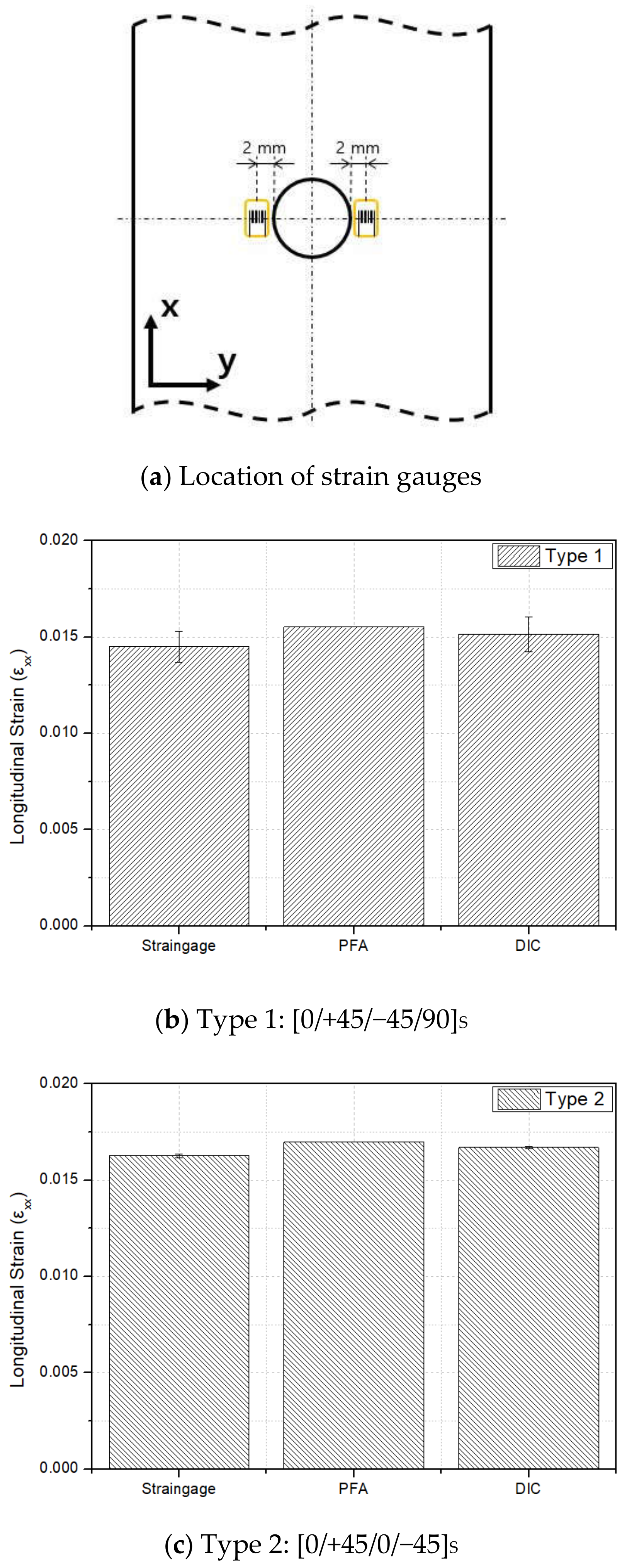
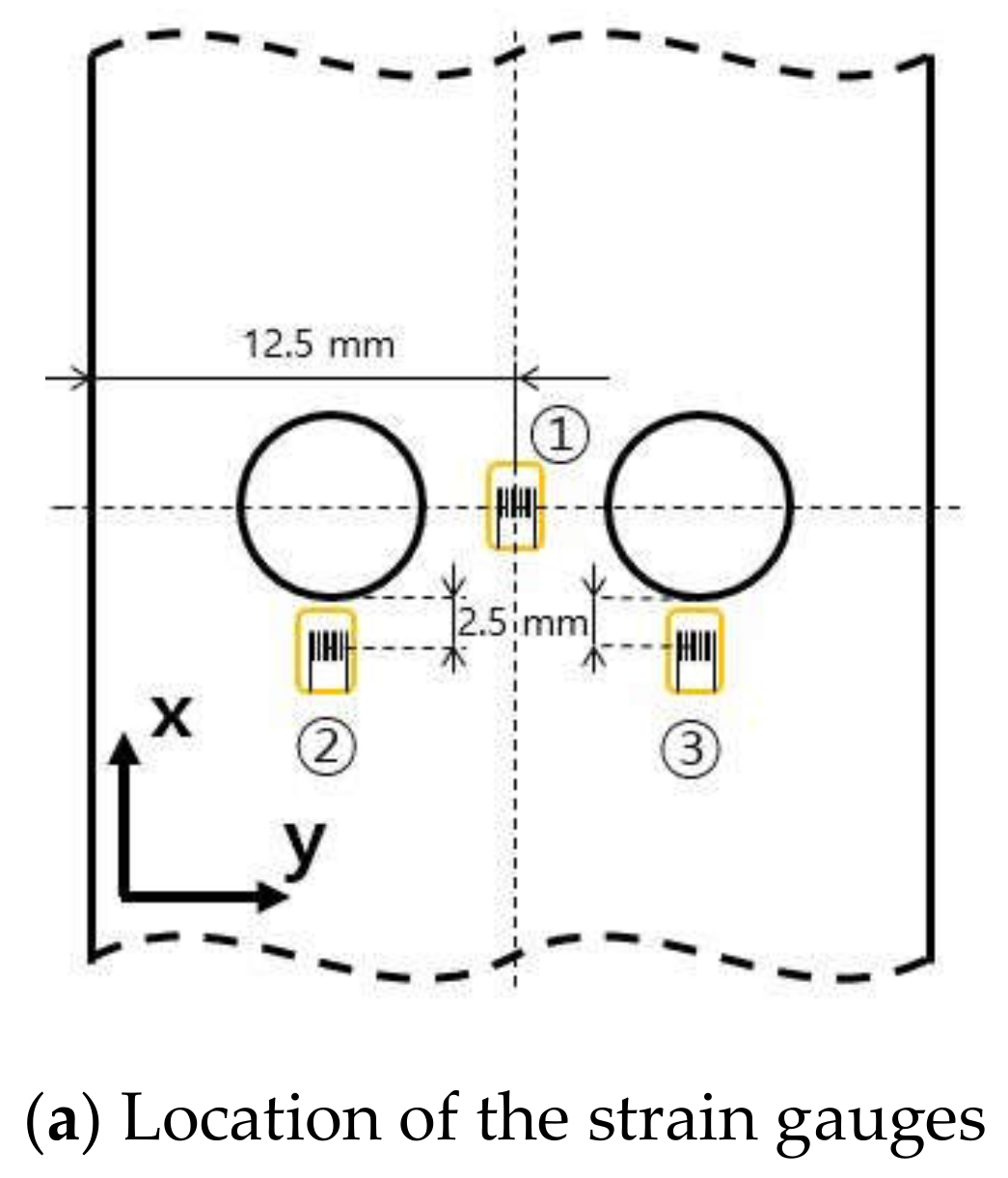
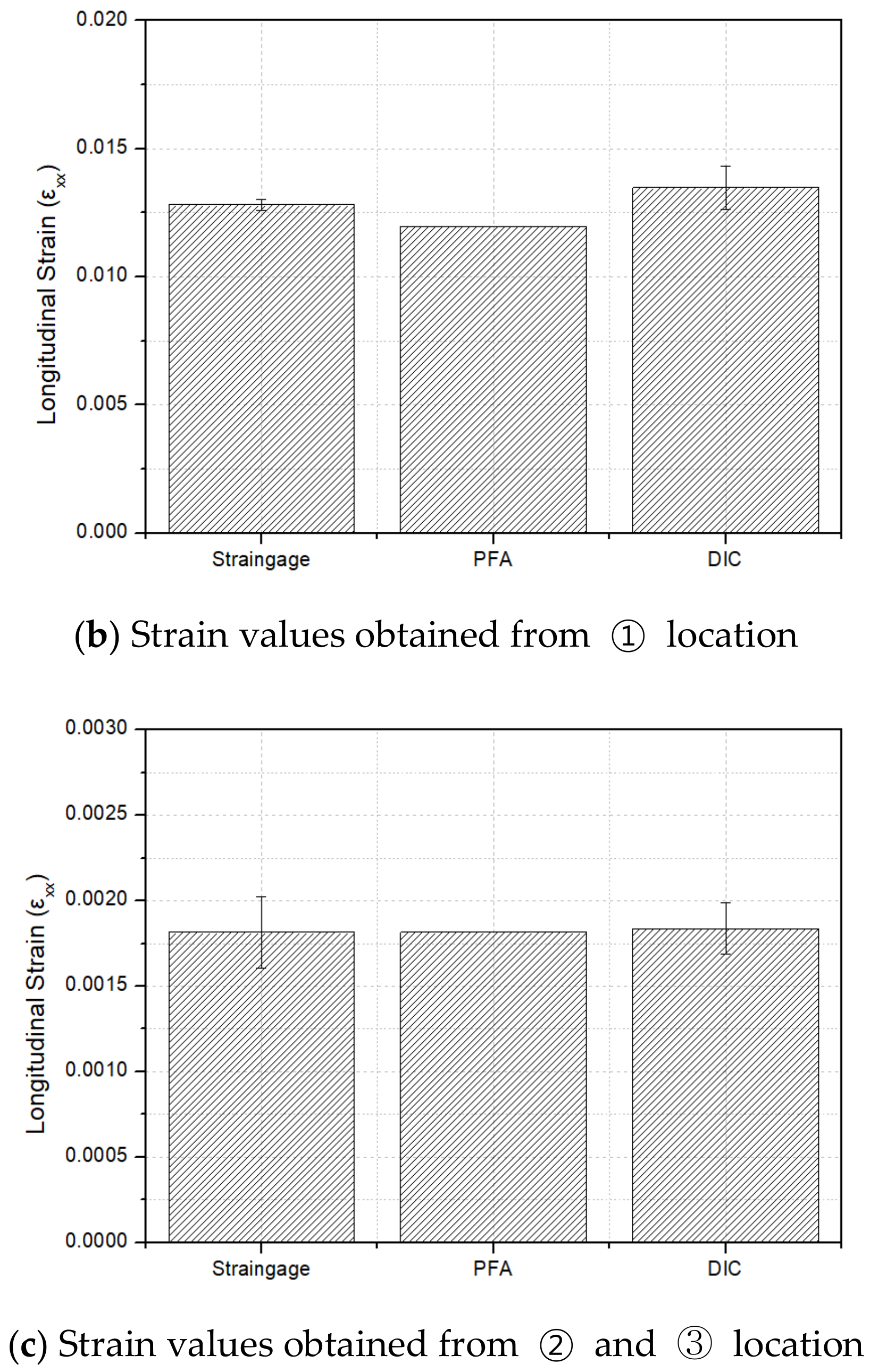
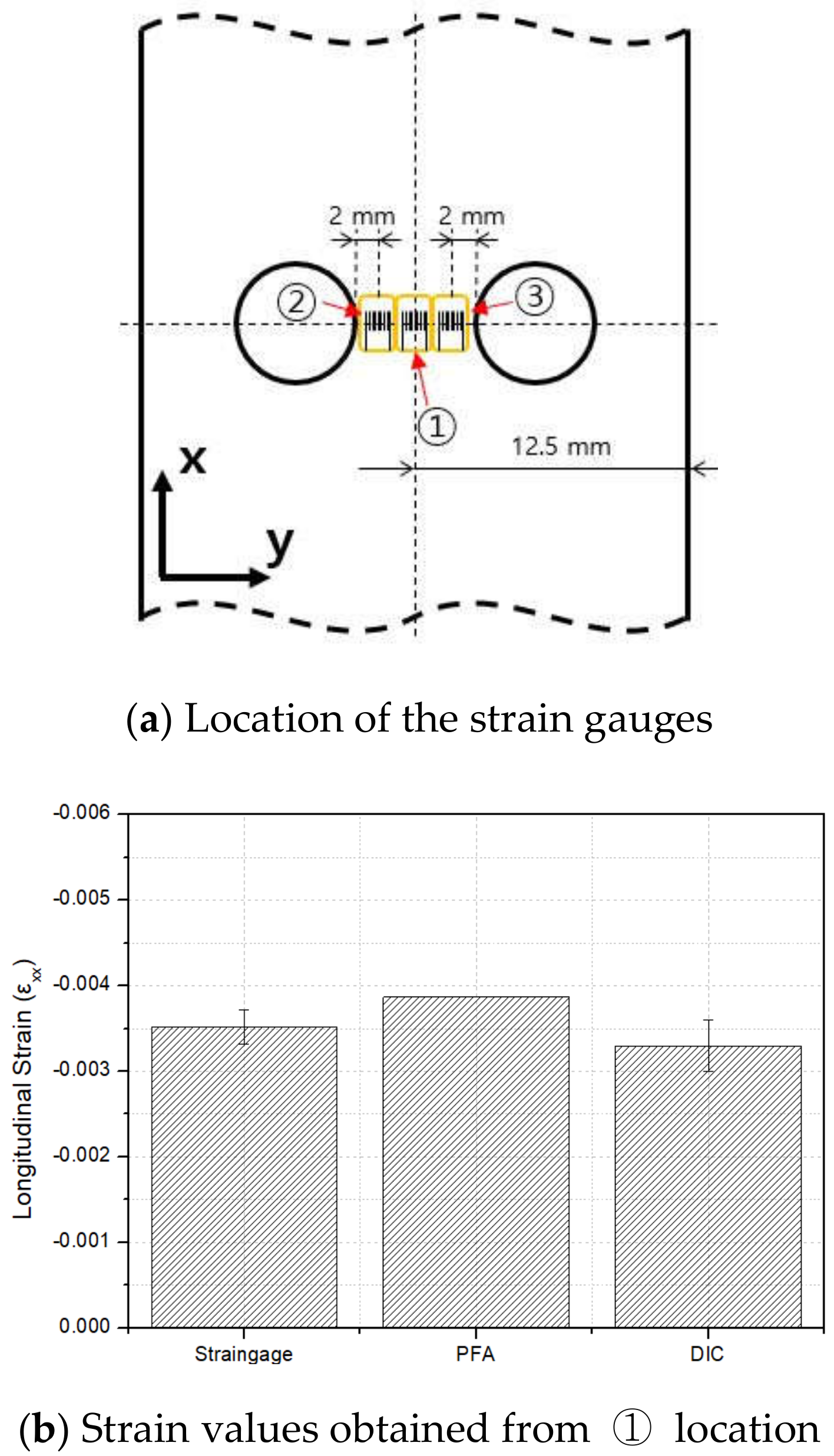
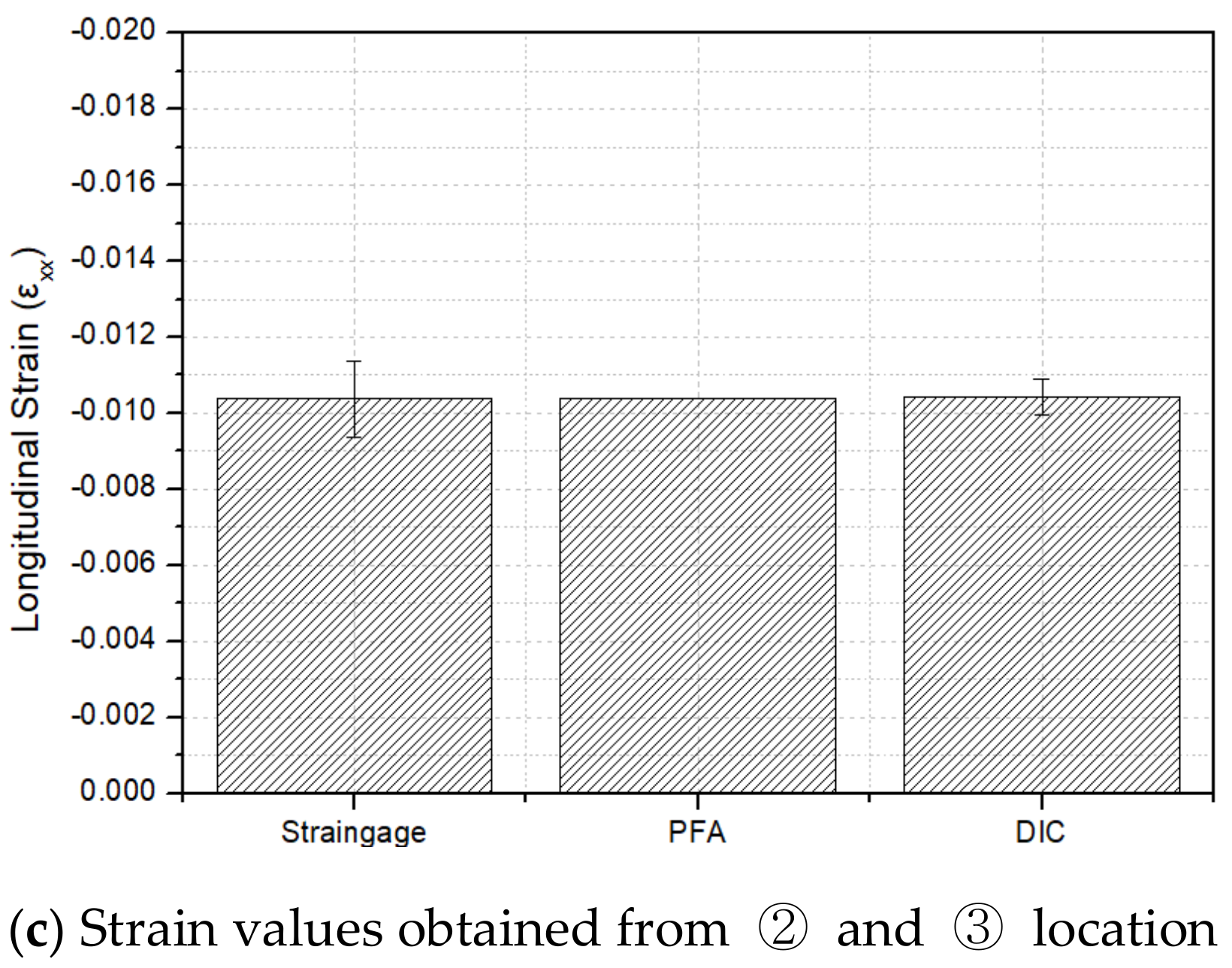
4.3. Evaluation of Strain Behavior
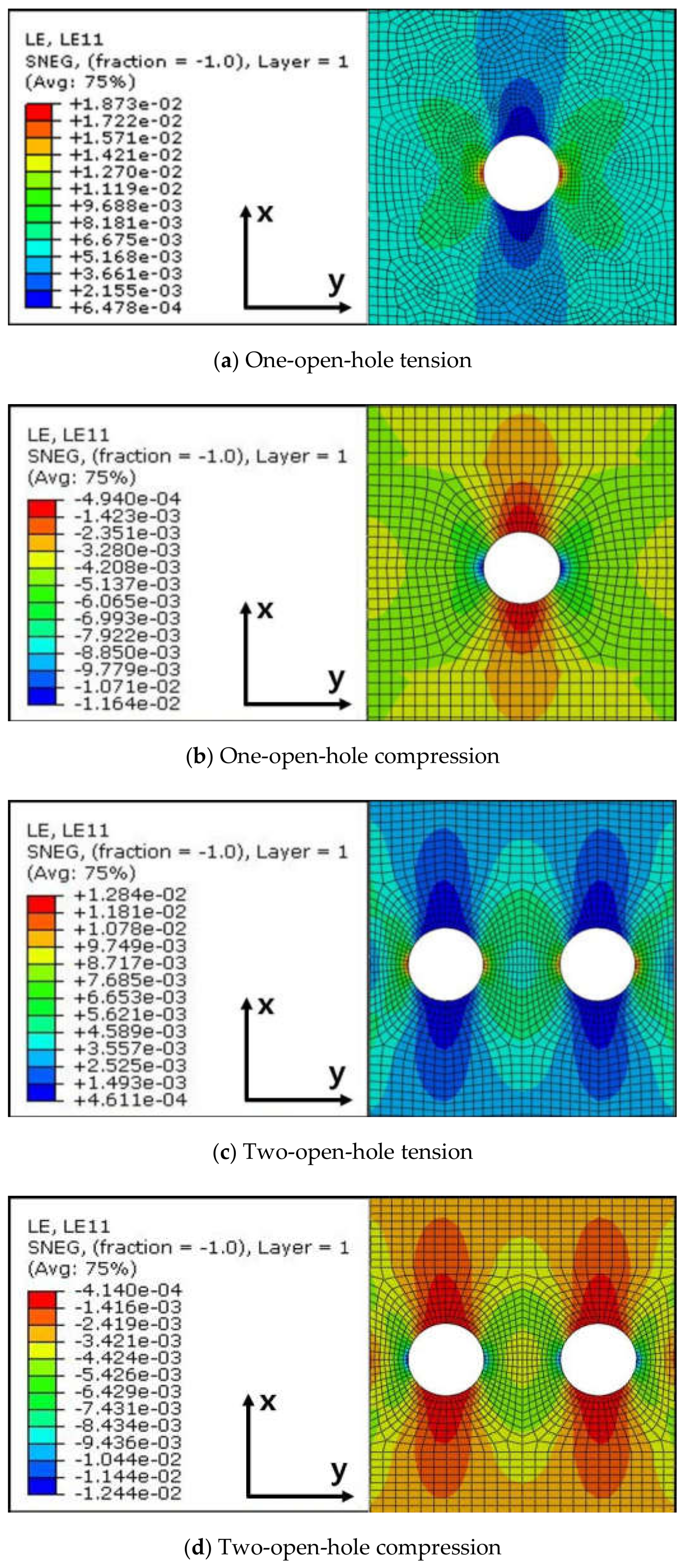
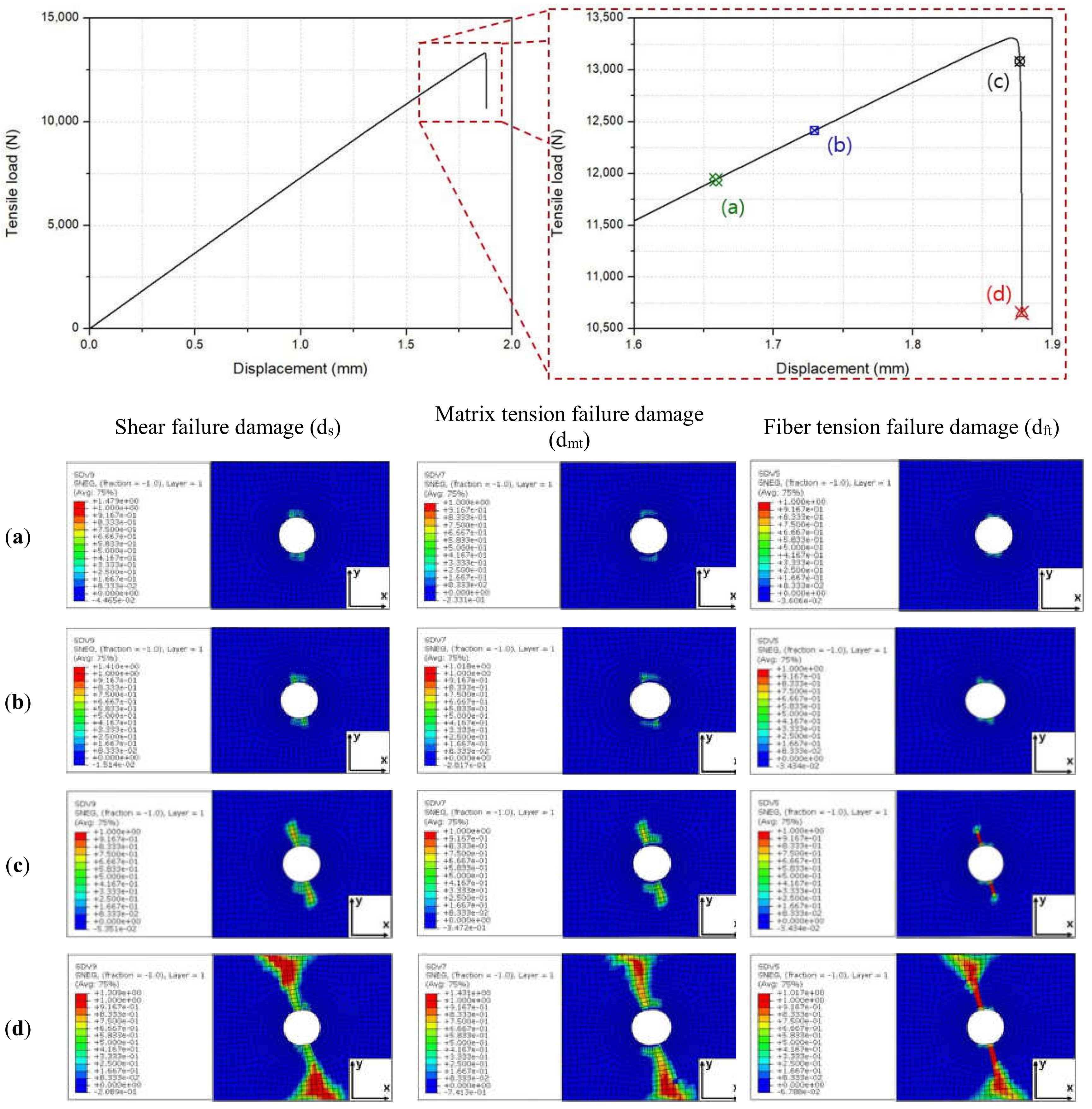
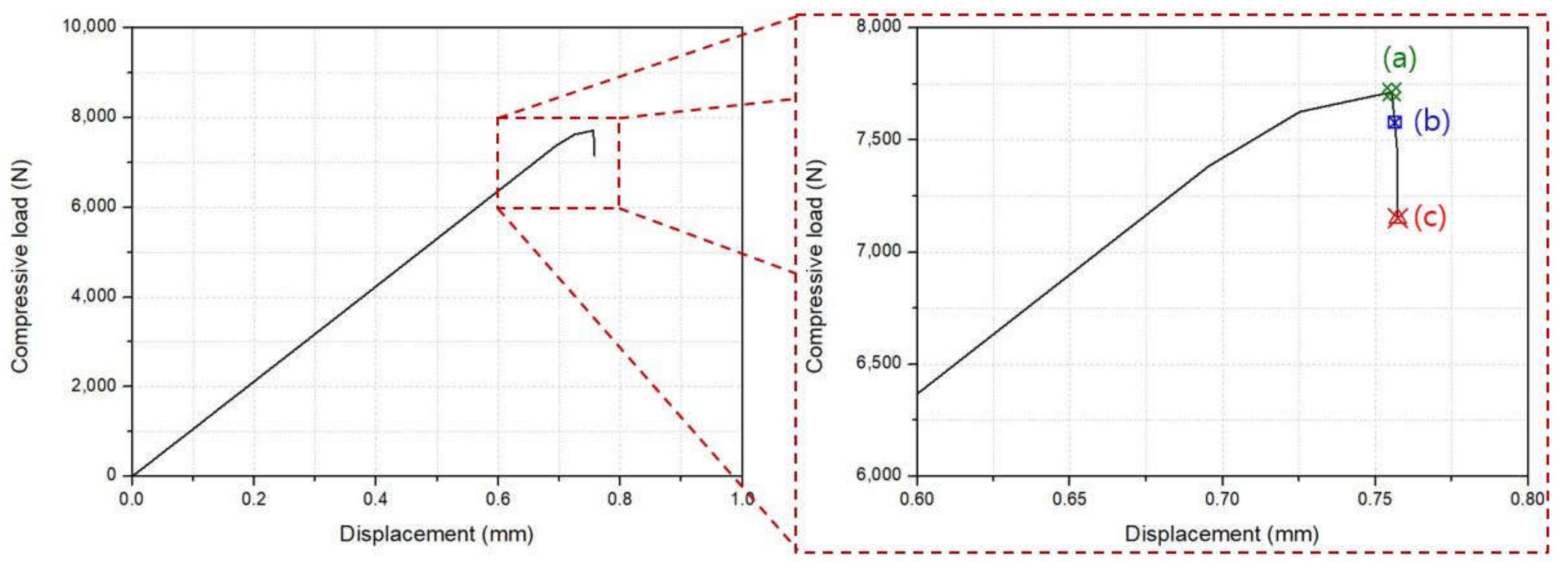
4.4. Failure Behavior Observation
5. Conclusions
- (1)
- The developed PFA model demonstrated results that were less-mesh-dependent in comparison to the MLT-PFA model that has been used in various studies. The lower mesh dependency occurred because each element failed when considering the constant fracture energy regardless of the element size when using the damage variable in the crack-band-model.
- (2)
- The analysis results were in good agreement with the experimental ones regardless of the stacking sequences, the number of notches, and the loading direction. This conclusion was determined by examining the load-displacement behavior and the strain distribution of the PFA results while doing a comparison to the experimental results.
- (3)
- Using the developed PFA model, the failure behavior of the composite laminate containing open holes was studied. Tensile failure behavior shows a final load-drop induced from the fiber failure damage while the compressive failure behavior shows that the final load-drop occurred by shear and matrix failure damage. The different fracture mechanism according to the loading direction was confirmed by comparing the fractured specimens.
Author Contributions
Funding
Conflicts of Interest
References
- Skvortsov, A.; MacGillivray, I.; Sharma, G.S.; Kessissoglou, N. Sound scattering by a lattice of resonant inclusions in a soft medium. Phys. Rev. E 2019, 99, 063006. [Google Scholar] [CrossRef]
- Matzenmiller, A.; Lubliner, J.; Taylor, R.L. A constitutive model for anisotropic damage in fiber-composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Chang, F.K.; Chang, K.Y. A progressive damage model for laminated composites containing stress concentrations. J. Compos. Mater. 1987, 21, 834–855. [Google Scholar] [CrossRef]
- Su, Z.C.; Tay, T.E.; Ridha, M.; Chen, B.Y. Progressive damage modeling of open-hole composite laminates under compression. Compos. Struct. 2015, 122, 507–517. [Google Scholar] [CrossRef]
- Chen, B.Y.; Tay, T.E.; Maiz, P.M.; Pinho, S.T. Numerical analysis of size effects on open-hole tensile composite laminates. Compos. Part. A Appl. Sci. Manuf. 2013, 47, 52–62. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Oh, B.H. Crack band theory for fracture of concrete. Matér. Constr. 1983, 16, 155–177. [Google Scholar] [CrossRef]
- Lapczyk, I.; Hurtado, J.U. Progressive damage modeling in fiber-reinforced materials. Compos. Part. A Appl. Sci. Manuf. 2007, 38, 2333–2341. [Google Scholar] [CrossRef]
- Riccio, A.; Costanzo, C.D.; Gennaro, P.D.; Sellitto, A.; Raimondo, A. Intra-laminar progressive failure analysis of composite laminates with a large notch damage. Eng. Fail. Anal. 2017, 73, 97–112. [Google Scholar] [CrossRef]
- Kodagali, K. Progressive Failure Analysis of composite Materials using the Puck Failure Criteria. Master’s Thesis, College of Engineering and Computing, University of South Carolina, Columbia, SC, USA, 2017. [Google Scholar]
- Jiang, Y. Measurement of J-integral Values of Dental Ceramics by Digital Image Correlation. Master’s Thesis, Department of Mechanical Engineering, Case Western Reserve University, Cleveland, OH, USA, 2016. [Google Scholar]
- Catalanotti, G.; Camanho, P.P.; Xavier, J.; Dávila, C.G.; Marques, A.T. Measurement of resistance curves in the longitudinal failure of composites using digital image correlation. Compos. Sci. Technol. 2010, 70, 1986–1993. [Google Scholar] [CrossRef]
- Camanho, P.P.; Ercin, G.H.; Catalanotti, G.; Mahdi, S.; Linde, P. A finite fracture mechanics model for the prediction of the open-hole strength of composite laminates. Compos. Part. A Appl. Sci. Manuf. 2012, 43, 1219–1225. [Google Scholar] [CrossRef]
- Bao, H.; Liu, G. Progressive failure analysis on scaled open-hole tensile composite laminates. Compos. Struct. 2016, 50, 173–180. [Google Scholar] [CrossRef]
- Joseph, A.P.K.; Davinson, P.; Waas, A.M. Open hole and filled hole progressive damage and failure analysis of composite laminates with a countersunk hole. Compos. Struct. 2018, 203, 523–538. [Google Scholar] [CrossRef]
- Tohaga, V.; Skovsgaard, S.P.H.; Jensen, H.M. Micromechanics of kink band formation in open-hole fibre composites under compressive loading. Compos. Part. B Eng. 2018, 149, 66–73. [Google Scholar] [CrossRef]
- Pierron, F.; Green, B.; Wisnom, M.R. Full-field assessment of the damage process of laminated composite open-hole tensile specimens. Part I: Methodology. Compos. Part. A Appl. Sci. Manuf. 2007, 38, 2307–2320. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, J.; Sun, Y.; Tian, K. Experimental and numerical investigation of open hole carbon fiber composite laminates under compression with three different stacking sequences. J. Mater. Res. Technol. 2019, 8, 2957–2968. [Google Scholar] [CrossRef]
- Caminero, M.A.; Lopez-Pedrosa, M.; Pinna, C.; Soutis, C. Damage monitoring and analysis of composite laminates with an open hole and adhesively repairs using digital image correlation. Compos. Part. B Eng. 2013, 53, 76–91. [Google Scholar] [CrossRef]
- Moure, M.M.; Otero, F.; Garcia-Castillo, S.K.; Sanchez-Saez, S.; Barbero, E.; Barbero, E.J. Damage evolution in open-hole laminated composite plates subjected to in-plane loads. Compos. Struct. 2015, 133, 1048–1057. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, X.; Wu, T. Damage characteristics of open-hole laminated composites subjected to longitudinal loads. Compos. Struct. 2019, 230, 111474. [Google Scholar] [CrossRef]
- Liu, H.; Falzon, B.G.; Li, S.; Tan, W.; Liu, J.; Chai, H.; Blackman, B.R.K.; Dear, J.P. Compressive failure of woven fabric reinforced thermoplastic composites with an open-hole: An experimental and numerical study. Compos. Struct. 2019, 213, 108–117. [Google Scholar] [CrossRef]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A fatigue failure criterion for fiber-reinforced materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Standard, A.S.T.M. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM D3039/D3039M-14; ASTM International: Philadelphia, PA, USA, 2014. [Google Scholar]
- Standard, A.S.T.M. Standard Test Method for Compressive Properties of Polymer Matrix Composite Materials with Unsupported Gage Section by Shear Loading; ASTM D3410/D3410M-16; ASTM International: Philadelphia, PA, USA, 2016. [Google Scholar]
- Standard, A.S.T.M. Standard Test Method for Shear Properties of Composite Materials by the V-Notched Beam Method; ASTM D5379/D5379M-12; ASTM International: Philadelphia, PA, USA, 2012. [Google Scholar]
- Pinho, S.T.; Robinson, P.; Iannucci, L. Fracture toughness of the tensile and compressive fibre failure modes in laminated composites. Compos. Sci. Technol. 2006, 66, 2069–2079. [Google Scholar] [CrossRef]
- Laffan, M.J.; Pinho, S.T.; Robinson, P.; Iannucci, L. Measurement of the in situ ply fracture toughness associated with mode I fibre tensile failure in FRP. Part I: Data reduction. Compos. Sci. Technol. 2010, 70, 606–613. [Google Scholar] [CrossRef]
- Laffan, M.J.; Pinho, S.T.; Robinson, P.; Iannucci, L. Measurement of the in situ ply fracture toughness associated with mode I fibre tensile failure in FRP. Part II: Size and lay-up effects. Compos. Sci. Technol. 2010, 70, 614–621. [Google Scholar] [CrossRef]
- Standard, A.S.T.M. Standard Test Method for Open-Hole Compressive Strength of Polymer Matrix Composite Laminates; ASTM D6484/D6484M-14; ASTM International: Philadelphia, PA, USA, 2014. [Google Scholar]
- Hundley, J.M.; Hahn, H.T.; Yang, J.M.; Facciano, A.B. Three-dimensional progressive failure analysis of bolted titanium graphite fiber metal laminate joints. J. Compos. Mater. 2011, 45, 751–769. [Google Scholar] [CrossRef]
- Wang, Y.; Tong, M.; Zhu, S. Three Dimensional Continuum Damage Mechanics Model of Progressive Failure Analysis in Fibre-Reinforced Composite Laminates. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009; p. 2629. [Google Scholar]
- Jung, K.H.; Kim, D.H.; Kim, H.J.; Park, S.H.; Jhang, K.Y.; Kim, H.S. Finite element analysis of a low-velocity impact test for glass fiber-reinforced polypropylene composites considering mixed-mode interlaminar fracture toughness. Compos. Struct. 2017, 160, 446–456. [Google Scholar] [CrossRef]
- Paiva, J.M.F.D.; Mayer, S.; Rezende, M.C. Evaluation of Mechanical Properties of Four Different Carbon/Epoxy Composites Used in Aeronautical Field. Mat. Res. 2005, 8, 91–97. [Google Scholar] [CrossRef]
- Gutkin, R.; Pinho, S.T. Combining damage and friction to model compressive damage growth in fibre-reinforced composites. J. Compos. Mater. 2015, 49, 2483–2495. [Google Scholar] [CrossRef]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Sound absorption by rubber coatings with periodic voids and hard inclusions. Appl. Acoust. 2019, 143, 200–210. [Google Scholar] [CrossRef]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Sound transmission through a periodically voided soft elastic medium submerged in water. Wave Motion 2017, 70, 101–112. [Google Scholar] [CrossRef]
- Sharma, G.S.; Skvortsov, A.; MacGillivray, I.; Kessissoglou, N. Acoustic performance of periodic steel cylinders embedded in a viscoelastic medium. J. Sound Vib. 2019, 443, 652–665. [Google Scholar] [CrossRef]







| Property | Symbol | Units | Value |
|---|---|---|---|
| Longitudinal modulus | GPa | 147.7 | |
| Transverse modulus | GPa | 8.52 | |
| Shear modulus | GPa | 4.59 | |
| Poisson’s ratio | - | 0.3 | |
| Longitudinal tensile strength | MPa | 2737 | |
| Transverse tensile strength | MPa | 1600 | |
| Longitudinal compressive strength | MPa | 51.32 | |
| Transverse compressive strength | MPa | 201.08 | |
| Shear strength | MPa | 81.0 | |
| Fiber tensile fracture energy | kN/m2 | 180 | |
| Fiber compressive fracture energy | kN/m2 | 100 | |
| Matrix tensile fracture energy | kN/m2 | 0.30 | |
| Matrix compressive fracture energy | kN/m2 | 1.71 |
| Specimen Type | Stacking Sequence |
|---|---|
| Type 1 | [0/+45/−45/90]s |
| Type 2 | [0/+45/0/−45]s |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, D.; Kim, S.; Kim, J.; Doh, Y. Development and Evaluation of Crack Band Model Implemented Progressive Failure Analysis Method for Notched Composite Laminate. Appl. Sci. 2019, 9, 5572. https://doi.org/10.3390/app9245572
Yoon D, Kim S, Kim J, Doh Y. Development and Evaluation of Crack Band Model Implemented Progressive Failure Analysis Method for Notched Composite Laminate. Applied Sciences. 2019; 9(24):5572. https://doi.org/10.3390/app9245572
Chicago/Turabian StyleYoon, Donghyun, Sangdeok Kim, Jaehoon Kim, and Youngdae Doh. 2019. "Development and Evaluation of Crack Band Model Implemented Progressive Failure Analysis Method for Notched Composite Laminate" Applied Sciences 9, no. 24: 5572. https://doi.org/10.3390/app9245572
APA StyleYoon, D., Kim, S., Kim, J., & Doh, Y. (2019). Development and Evaluation of Crack Band Model Implemented Progressive Failure Analysis Method for Notched Composite Laminate. Applied Sciences, 9(24), 5572. https://doi.org/10.3390/app9245572





