Reliability Modelling and Evaluation for LTD System Based on Load-Sharing Model
Abstract
1. Introduction
2. Reliability Model of a Linear Transformer Driver (LTD) System
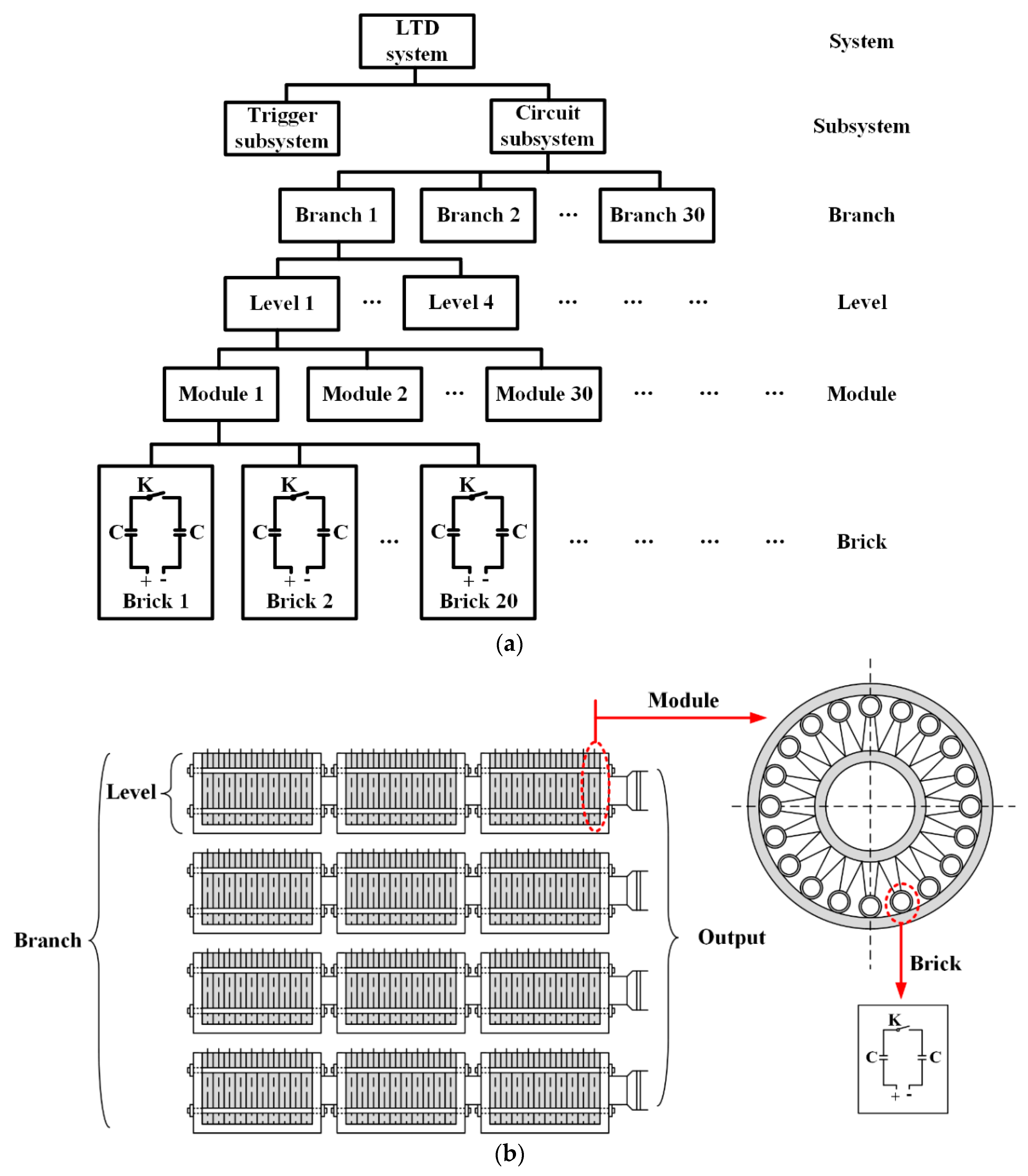
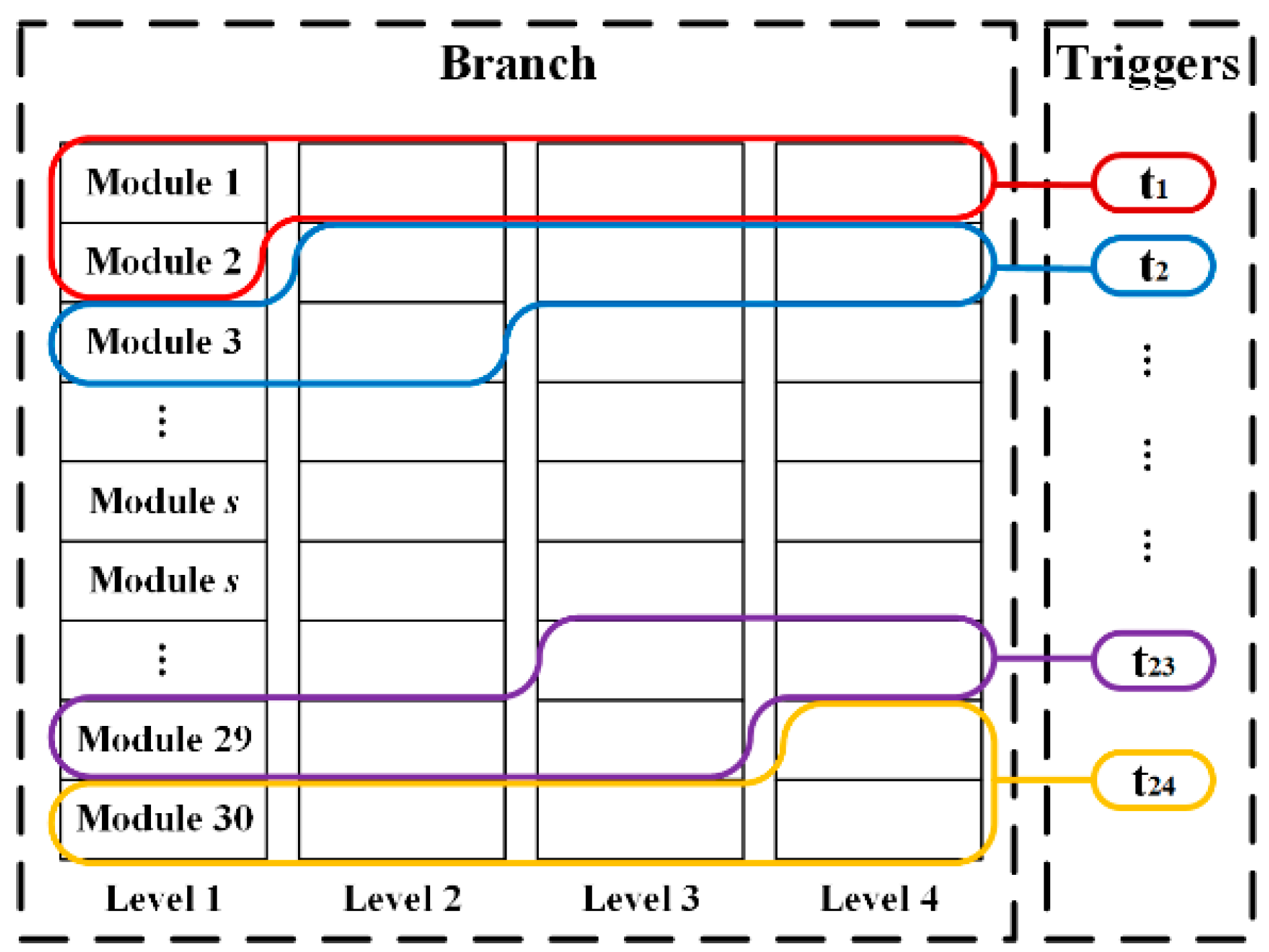
2.1. LTD System Description
- Subsystem: any branch failure will cause the subsystem failure.
- Branch: any level failure in a branch will cause the branch failure.
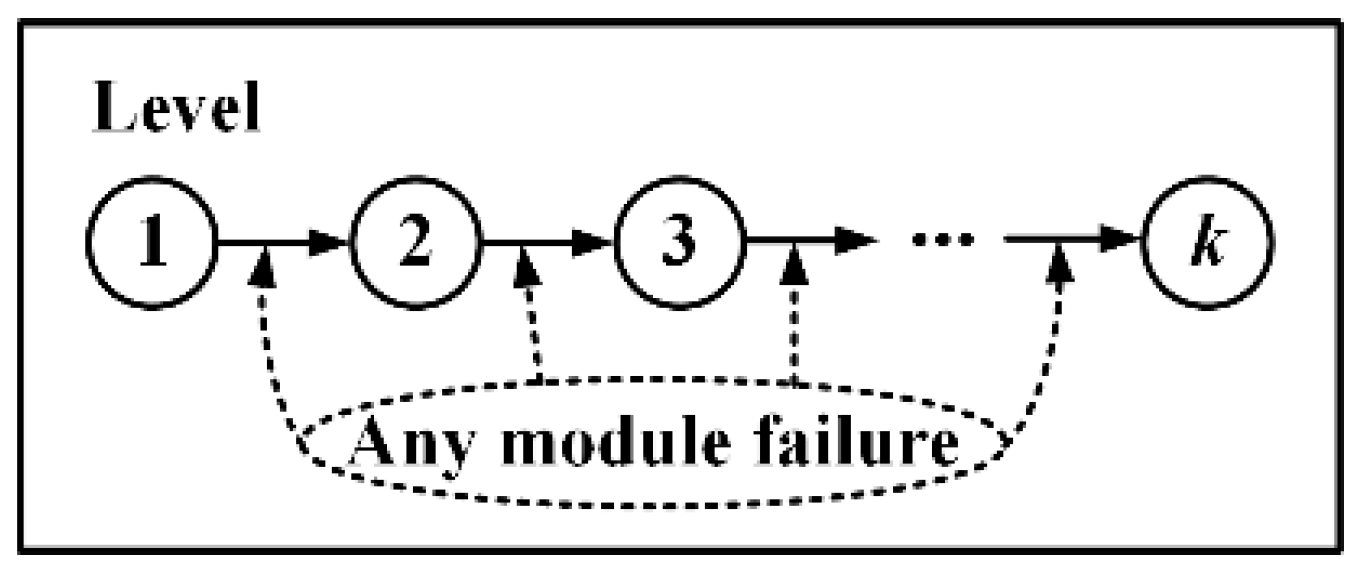
- Level: when there are more than modules failed in a level, the level is judged to fail.
- Module: any brick failure in a module will cause the module failure.
- Brick: both the switch self-discharge and the capacitor insulation damage will cause the brick failure, but we only consider the switch self-discharge in the subsequent analysis because it is always the more common reasons.
2.2. System Reliability Model
3. Load-Sharing Based Voltage Redistribution Mechanism for Modules in Each Level
3.1. Equal Load-Sharing Rule
3.2. Linear Load-Sharing Rule
3.3. Exponential Load-Sharing Rule
3.4. Local-Equal Load-Sharing Rule
4. Numerical Simulation and Analysis
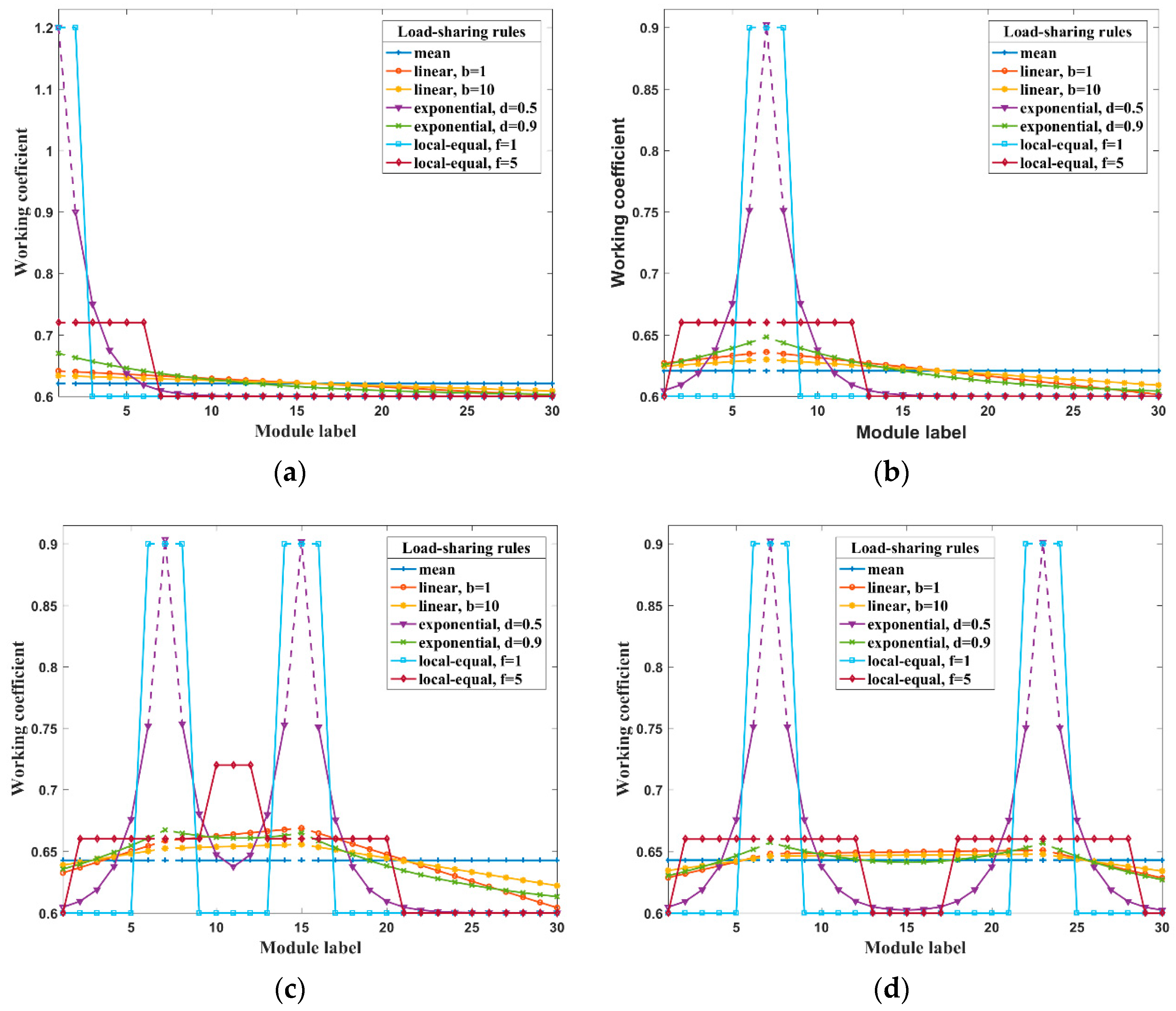
4.1. Effect Analysis of Different Load-Sharing Rules on the Modules in a Level
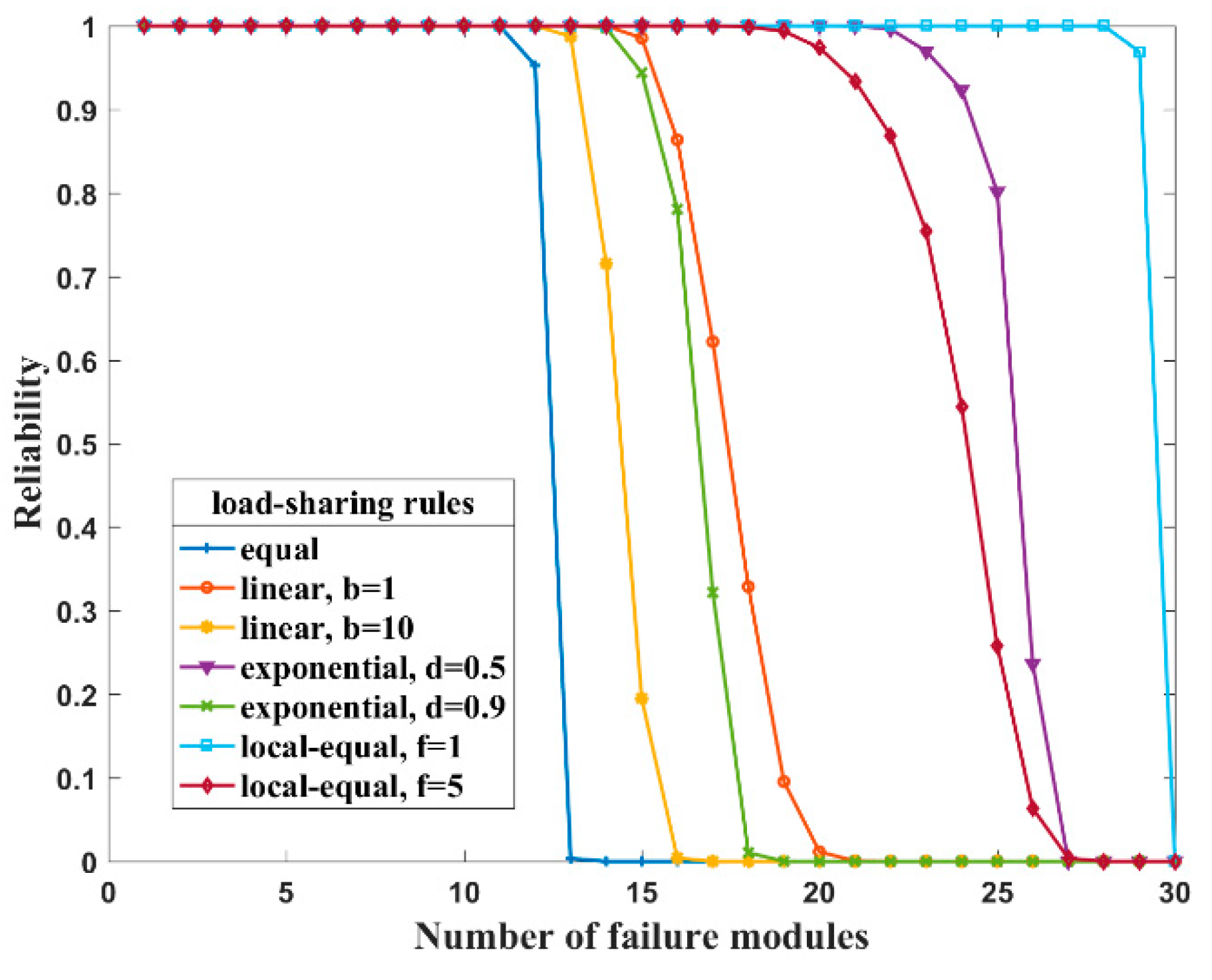
4.2. Load-Sharing Based Level Reliability Analysis with the Increasing Number of Failure Modules
- When just a few modules fail, there are nearly no differences in the impact of different load-sharing rules on the level of condition reliability, namely the early stage of reliability degradation curve is almost overlapped.
- With the continuously increase of the failure modules, all the reliability degradation curve will drop significantly but the point at which the curve begins to decrease obviously and the corresponding decreasing rate is greatly affected by the load-sharing rule. The more sensitive to the distance factor the load-sharing rule is, the slower the level reliability is degraded. Accordingly, the curve of the equal rule is the first one to decrease with a sharp rate.
- In the later stage of the reliability curve, almost all the loads are shared by the few remaining modules, thus the failure rates of each module are quite high and the level reliability is close to 0.
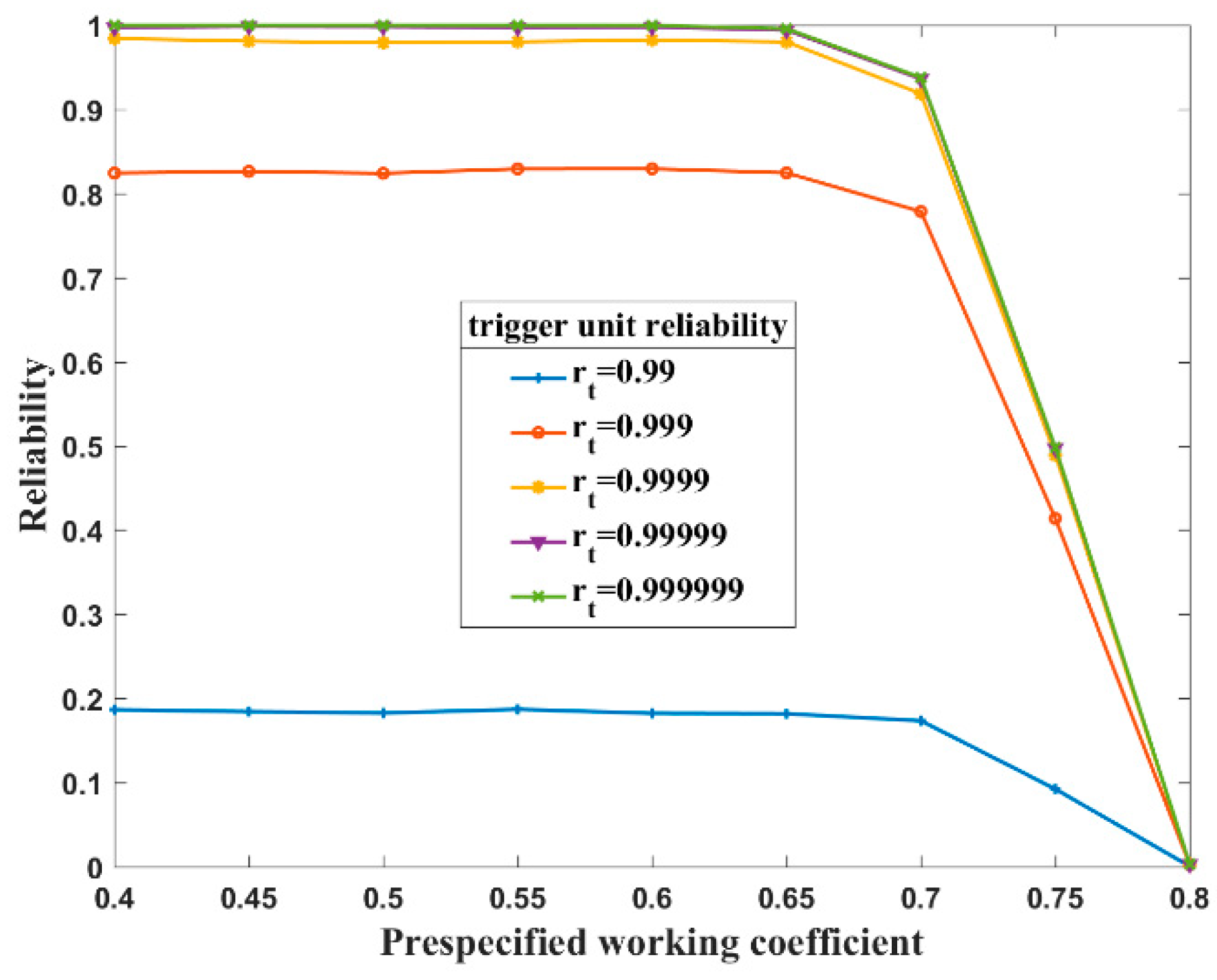
4.3. System Reliability Analysis with a Special Trigger Strategy Considered
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stygar, W.A.; Cuneo, M.E.; Headley, D.I.; Ives, H.C.; Leeper, R.J.; Mazarakis, M.G.; Olson, C.L.; Porter, J.L.; Wagoner, T.C.; Woodworth, J.R. Architecture of petawatt-class z-pinch accelerators. Phys. Rev. Accel. Beams 2006, 10, 536–550. [Google Scholar]
- Jiang, W. Review of solid-state linear transformer driver technology. Matter Radiat. Extrem. 2018, 3, 159–164. [Google Scholar] [CrossRef]
- Stygar, W.A.; Awe, T.J.; Bailey, J.E.; Bennett, N.L.; Breden, E.W.; Campbell, E.M.; Clark, R.E.; Cooper, R.A.; Cuneo, M.E.; Ennis, J.B.; et al. Conceptual designs of two petawatt-class pulsed-power accelerators for high-energy-density-physics experiments. Phys. Rev. Spec. Top.-Accel. Beams 2015, 18, 110401. [Google Scholar] [CrossRef]
- Smith, I.D. Induction voltage adders and the induction accelerator family. Phys. Rev. Spec. Top.-Accel. Beams 2004, 7, 705–707. [Google Scholar] [CrossRef]
- Kim, A.A.; Mazarakis, M.G.; Sinebryukhov, V.A.; Kovalchuk, B.M.; Visir, V.A.; Volkov, S.N.; Bayol, F.; Bastrikov, A.N.; Durakov, V.G.; Frolov, S.V.; et al. Development and tests of fast 1-MA linear transformer driver stages. Phys. Rev. Spec. Top.-Accel. Beams 2009, 12, 050402. [Google Scholar] [CrossRef]
- Mazarakis, M.G.; Fowler, W.E.; LeChien, K.L.; Long, F.W.; Matzen, M.K.; McDaniel, D.H.; McKee, R.G.; Olson, C.L.; Porter, J.L.; Rogowski, S.T.; et al. High-Current Linear Transformer Driver Development at Sandia National Laboratories. IEEE Trans. Plasma Sci. 2010, 38, 704–713. [Google Scholar] [CrossRef]
- Spielman, R.B.; Froula, D.H.; Brent, G.; Campbell, E.M.; Reisman, D.B.; Savage, M.E.; Shoup, M.J.; Stygar, W.A.; Wisher, M.L. Conceptual design of a 15-TW pulsed-power accelerator for high-energy-density–physics experiments. Matter Radiat. Extrem. 2017, 2, 204–223. [Google Scholar] [CrossRef]
- Bastrikov, A.N.; Vizir, V.A.; Volkov, S.N.; Durakov, V.G.; Efremov, A.M.; Zorin, V.B.; Kim, A.A.; Kovalchuk, B.M.; Kumpjak, E.V.; Loginov, S.V.; et al. Primary energy storages based on linear transformer stages. Laser Part. Beams 2003, 21, 295–299. [Google Scholar] [CrossRef]
- Zhang, P.; Sun, J.; Sun, F.; Qiu, A.; Sun, J.; Hu, Y.; Cong, P. Simulation Analysis of a Pulsed Compact FLTD System for Large-Area Hard X-Ray Sources. IEEE Trans. Plasma Sci. 2016, 44, 803–807. [Google Scholar] [CrossRef]
- Collier, L.; Dickens, J.; Mankowski, J.; Neuber, A. Performance Analysis of an All Solid-State Linear Transformer Driver. IEEE Trans. Plasma Sci. 2017, 45, 1755–1761. [Google Scholar] [CrossRef]
- Li, J.; Chen, W.; Li, J.; Jiang, W.; Zhong, X.; Gou, Y. Robust Design for Linear Transformer Driver System. IEEE Trans. Plasma Sci. 2015, 43, 3406–3411. [Google Scholar] [CrossRef]
- Leckbee, J.J.; Maenchen, J.E.; Johnson, D.L.; Portillo, S.; VanDeValde, D.M.; Rose, D.V.; Oliver, B.V. Design, Simulation, and Fault Analysis of a 6.5-MV LTD for Flash X-Ray Radiography. IEEE Trans. Plasma Sci. 2006, 34, 1888–1899. [Google Scholar] [CrossRef]
- Kapur, K.C.; Lamberson, L.R. Reliability in Engineering Design; John Wiley & Sons: New York, NY, USA, 1977. [Google Scholar]
- Griffith, W.S. Optimal Reliability Modeling: Principles and Applications. Technometrics 2012, 46, 112. [Google Scholar] [CrossRef]
- Boddu, P.; Xing, L. Reliability evaluation and optimization of series–parallel systems with k-out-of-n: G subsystems and mixed redundancy types. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2013, 227, 187–198. [Google Scholar] [CrossRef]
- Daniels, H.E. The statistical theory of the strength of bundles of threads. Proc. A 1945, 183, 405–435. [Google Scholar]
- Yamamoto, W.; Jin, L.; Suzuki, K. Optimal allocations for load-sharing k-out-of-n: F systems. J. Stat. Plan. Inference 2009, 139, 1777–1781. [Google Scholar] [CrossRef]
- Zhang, N.; Fouladirad, M.; Barros, A. Maintenance analysis of a two-component load-sharing system. Reliab. Eng. Syst. Saf. 2017, 167, 67–74. [Google Scholar] [CrossRef]
- Kim, K.O. Optimal number of components in a load-sharing system for maximizing reliability. J. Korean Stat. Soc. 2018, 47, 32–40. [Google Scholar] [CrossRef]
- Shao, J.; Lamberson, L.R. Modeling a shared-load k-out-of-n: G system. IEEE Trans. Reliab. 1991, 40, 205–209. [Google Scholar] [CrossRef]
- Liu, H. Reliability of a load-sharing k-out-of-n: G system: Non-iid components with arbitrary distributions. IEEE Trans. Reliab. 1998, 47, 279–284. [Google Scholar]
- Jiakai, C.; Yan, H.; Wei, W. Reliability analysis and optimization of equal load-sharing k-out-of-n phased-mission systems. Eksploat. I Niezawodn.-Maint. Reliab. 2015, 17, 250–259. [Google Scholar] [CrossRef][Green Version]
- Amari, S.V.; Bergman, R. Reliability Analysis of k-out-of-n Load-Sharing Systems; Reliability & Maintainability Symposium: Washington, DC, USA; IEEE: Washington, DC, USA, 2008; pp. 440–445. [Google Scholar]
- Yang, C.; Zeng, S.; Guo, J. Reliability Analysis of Load-Sharing K-out-of-N System Considering Component Degradation. Math. Probl. Eng. 2015, 2015, 1–10. [Google Scholar]
- Li, Y.; Chen, Y.; Yu, X. A Failure Mechanism Cumulative Model for Reliability Evaluation of a k-out-of-n System with Load Sharing Effect. IEEE Access 2017, 7, 2210–2222. [Google Scholar]
- Zhang, J.; Zhao, Y.; Ma, X. A new reliability analysis method for load-sharing k-out-of-n: F system based on load-strength model. Reliab. Eng. Syst. Saf. 2019, 182, 152–165. [Google Scholar] [CrossRef]
- Kvam, P.H.; Pe, A.E. Estimating Load-Sharing Properties in a Dynamic Reliability System. J. Am. Stat. Assoc. 2005, 100, 262–272. [Google Scholar] [CrossRef] [PubMed]
- Park, C. Parameter estimation for the reliability of load-sharing systems. IIE Trans. 2010, 42, 753–765. [Google Scholar] [CrossRef]
- Harlow, D.G.; Phoenix, S.L. The Chain-of-Bundles Probability Model For the Strength of Fibrous Materials I: Analysis and Conjectures. J. Compos. Mater. 1978, 12, 195–214. [Google Scholar] [CrossRef]
- Durham, S.D.; Lynch, J.D.; Padgett, W.J.; Horan, T.J.; Owen, W.J.; Surles, J. Localized Load-sharing Rules and Markov-Weibull Fibers. J. Compos. Mater. 1997, 31, 1856–1882. [Google Scholar] [CrossRef]
- Suprasad, A.V.; Krishna, M.B.; Hoang, P. Tampered Failure Rate Load-Sharing Systems: Status and Perspectives. In Handbook of Performability Engineering; Springer: London, UK, 2008. [Google Scholar]
- Singh, B.; Sharma, K.K.; Kumar, A. Analyzing the dynamic system model with discrete failure time distribution. Stat. Methods Appl. 2009, 18, 521–542. [Google Scholar] [CrossRef]
- Ji, C.; Zhou, L.; Jiao, J.; Ren, F.; Chen, L.; Jiang, J.; Zhao, Y. Reliability of large device analysis. High Power Laser Part. Beams 2018, 30, 045003. [Google Scholar]
- Liu, X. Breakdown Characteristics of Gas Switch and Its Influence on the Output Parameters of Fast Linear Transformer Driver. Ph.D. Thesis, Xi’an Jiaotong University, Xi’an, China, 2010. [Google Scholar]
- Zeng, Z. Introduction to Practical Pulse Technology; Shaanxi Science and Technology Press: Shanxi, China, 2003. [Google Scholar]
- Kaminskiy, M.P.; Krivtsov, V.V. A Simple Procedure for Bayesian Estimation of the Weibull Distribution. IEEE Trans. Reliab. 2005, 54, 612–616. [Google Scholar] [CrossRef]
- Cousineau, D. Fitting the three-parameter weibull distribution: Review and evaluation of existing and new methods. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 281–288. [Google Scholar] [CrossRef]
- Pretorius, A.H.; Van Wijk, J.J. Visual analysis of multivariate state transition graphs. IEEE Trans. Vis. Comput. Graph. 2006, 12, 685–692. [Google Scholar] [CrossRef] [PubMed]
- Ren, F.; Jiao, J.; Hu, Y.; Zhao, T.; Zhou, L. Reliability Evaluation for Complex Systems with Load Sharing and Failure Dependence: A Case Study on LTD; International Conference on Reliability Systems Engineering: Beijing, China; IEEE, Beijing, China, 2017; pp. 1–6. [Google Scholar]
| Order | Name | Abbreviation |
|---|---|---|
| 1 | circuit subsystem | |
| 2 | branch | |
| 3 | level | |
| 4 | module | |
| 5 | brick/circuit unit | |
| 6 | switch | sw |
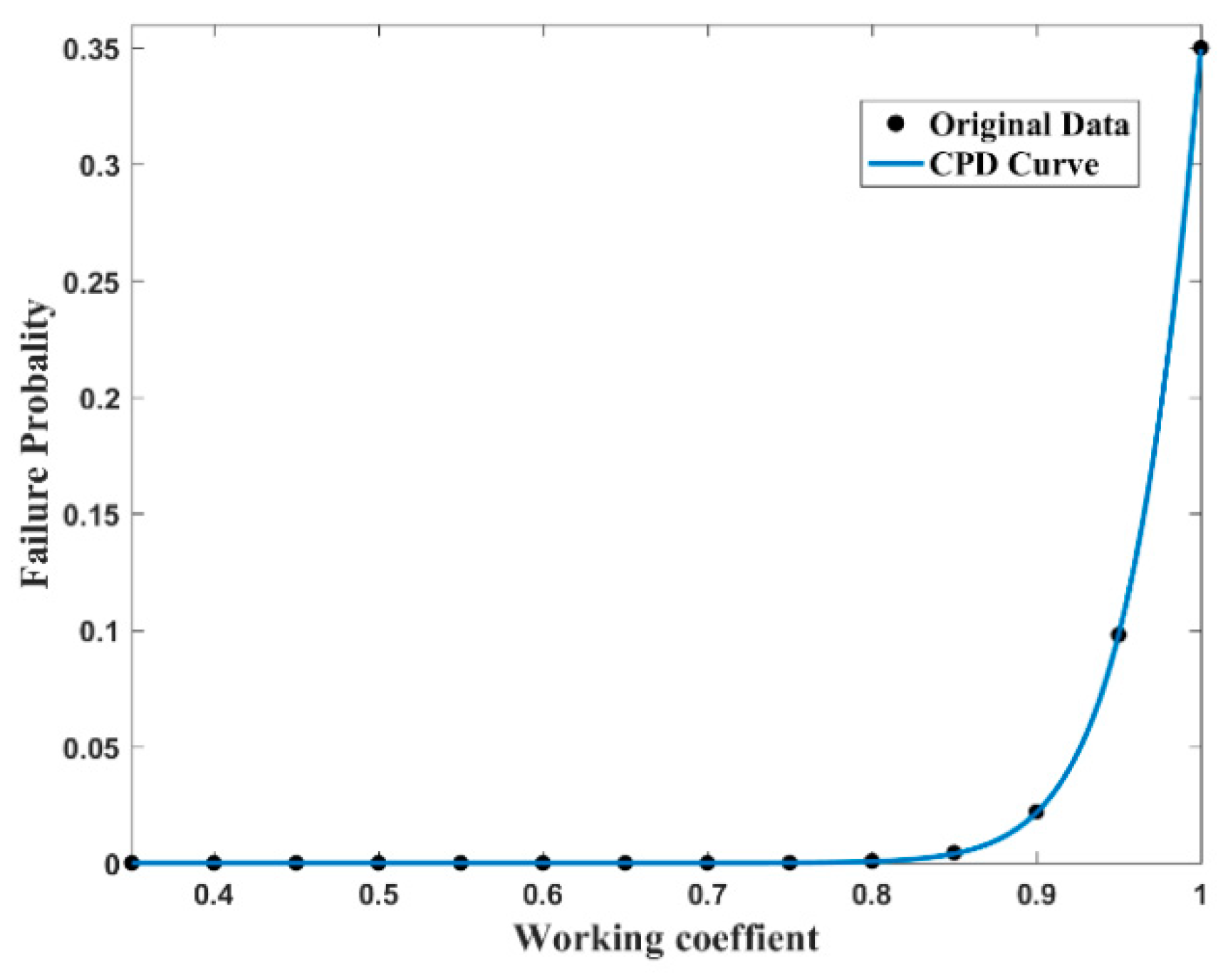
| Working Coefficient (%) | Failure Probability | Working Coefficient (%) | Failure Probability |
|---|---|---|---|
| 35 | 0 | 70 | 1.40 × 10−5 |
| 40 | 2.00 × 10−14 | 75 | 1.10 × 10−4 |
| 45 | 3.10 × 10−12 | 80 | 7.70 × 10−4 |
| 50 | 1.70 × 10−10 | 85 | 4.40 × 10−3 |
| 55 | 5.30 × 10−9 | 90 | 0.022 |
| 60 | 1.00 × 10−7 | 95 | 0.098 |
| 65 | 1.40 × 10−6 | 100 | 0.35 |
| Simulation Flow: calculate the statistical reliability |
|---|
| Input:numS (sample time) Output: conRL (statistical reliability array) Begin 01: Initalization: construct an Array variable sumR to save all the simulation results 02: for i = 1 to numS 03: construct an Array variable sum to save the single simulation result 04: calculate the module failure rate Array FM 05: update the Array variable sum 06: for j = 1 to threshold 07: generate a random variable η according to FM to reflect the failure 08: update the module failure rate Array FM 09: update the Array variable sum 10: end for 11: sumR = sum+sumR; 12: end for 13: conRL = sumR/numS; End |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, J.; Zhao, T.; Jiao, J.; Chen, Z.; Ren, F. Reliability Modelling and Evaluation for LTD System Based on Load-Sharing Model. Appl. Sci. 2019, 9, 5528. https://doi.org/10.3390/app9245528
Chu J, Zhao T, Jiao J, Chen Z, Ren F. Reliability Modelling and Evaluation for LTD System Based on Load-Sharing Model. Applied Sciences. 2019; 9(24):5528. https://doi.org/10.3390/app9245528
Chicago/Turabian StyleChu, Jiayun, Tingdi Zhao, Jian Jiao, Zhiwei Chen, and Fuchun Ren. 2019. "Reliability Modelling and Evaluation for LTD System Based on Load-Sharing Model" Applied Sciences 9, no. 24: 5528. https://doi.org/10.3390/app9245528
APA StyleChu, J., Zhao, T., Jiao, J., Chen, Z., & Ren, F. (2019). Reliability Modelling and Evaluation for LTD System Based on Load-Sharing Model. Applied Sciences, 9(24), 5528. https://doi.org/10.3390/app9245528





