Featured Application
The developed fully simulation-based melting point prediction method facilitates the design of novel green ionic liquids.
Abstract
In this work, we introduce a simulation-based method for predicting the melting point of ionic liquids without prior knowledge of their crystal structure. We run molecular dynamics simulations of biofriendly, choline cation-based ionic liquids and apply the method to predict their melting point. The root-mean-square error of the predicted values is below 24 K. We advocate that such precision is sufficient for designing ionic liquids with relatively low melting points. The workflow for simulations is available for everyone and can be adopted for any species from the wide chemical space of ionic liquids.
1. Introduction
The past decades have seen a steep increase of interest in ionic liquids (IL) such as solvents and electrolytes. ILs are commonly defined as salts that are liquid under 100 °C and are entirely composed of ions [1]. Due to their ionic character, they exhibit several desirable properties, for example, negligible vapor pressure, tunable polarity and high charge density. Moreover, there is a large number of different ions that can potentially yield an IL, which allows the fine-tuning of its properties for various applications [1]. Due to high thermal and (electro)chemical stability [2,3,4] some ILs are especially suitable candidates for energy applications, where higher cell voltage directly translates into increased energy density [5]. Furthermore, ILs are widely utilized as catalysts, lubricants, solvents in organic synthesis and countless other applications [6]. However, common ILs containing imidazolium cations and fluorinated anions are far from being biofriendly, which prevents their use in medicine and biotechnology [7]. For example, there is an increasing interest for usage of electroactive polymer actuators containing IL electrolytes in various medical devices [8,9,10].
On the one hand, it is true that the stability and low volatility of ILs decrease the risk of pollution by evaporation. On the other hand, even ILs of the latest generation are still toxic and often non-biodegradable. For example, fluorinated and cyano-based anions can emit hydrofluoric acid and hydrogen cyanide, respectively [7]. Toxicity depends on both cation and anion and thus less toxic ions have been considered. In case of anion, increase in the hydrophilicity as well as exclusion of fluoride- and cyano-substituents generally results in practically harmless and more biodegradable ILs [7]. In case of cation, toxicity is strongly influenced by alkyl chain length—shorter alkyl chains increase hydrophilicity and result in more benign ILs [7]. Petkovic et al. showed that choline cation is considerably less toxic than other traditional quaternary nitrogen based cations [11]. The primary drawback of introducing a more biofriendly ion to an IL composition is the resulting higher melting point; in many cases, the IL turns solid at ambient temperatures [11].
The experimental data on melting points of the biofriendly choline ILs is scarce and sometimes inconsistent due to variable water content and the presence of anion conjugated acid in the salt [12,13]. For example, for choline acetate [11,14,15] and choline citrate [16,17] significantly different melting points have been reported. Herewith, any experimental high-throughput characterization of promising ILs is unacceptably time-consuming—evaporation of water in vacuo, extraction or crystallization of ILs require much time and effort. A computational approach to the assessment of ILs properties looks most appealing. Previously, the melting points of ILs were computationally predicted with molecular dynamics (MD) simulations and quantitative structure-activity relationship (QSAR) models [18]. An overview of these methods is given in the discussion section. Their comparison reveals that the most accurate is the so-called pseudo supercritical path (PSCP) method, which has a significant limitation—requirement for the knowledge of the IL crystal structure [19,20].
In this study, we have developed simulation-based melting point prediction method for ILs with unknown crystal structure. Using this method, we have computationally investigated fourteen biofriendly, choline cation-based ILs and choline bis[(trifluoromethyl)sulfonyl]imide (TFSI). We have validated the predicted results against experimental melting points, which were available in the literature and/or measured in the current work.
2. Materials and Methods
2.1. Models
The choice of anions was made based on low toxicity and biodegradability of the corresponding ILs. We paired choline cation with fourteen biofriendly carboxylic acid, benzoic acid and sulfonimide-derived anions displayed in Figure 1. The harmful TFSI anion was included for comparison purpose and because choline TFSI is relatively well studied in the literature.
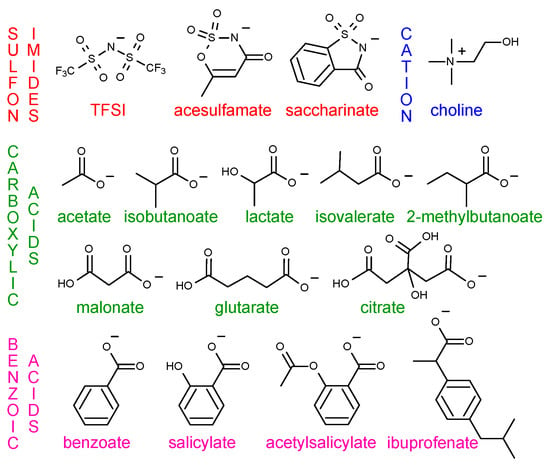
Figure 1.
2-D chemical structures of the studied anions and choline cation. TFSI corresponds to bis[(trifluoromethyl)sulfonyl]imide.
To the best of our knowledge, the crystal structure is known only for choline acetate, choline acesulfamate, choline saccharinate and choline TFSI among the studied ILs [21,22,23,24]. Thus, for each IL, we generated a solid phase using Coulombic potential wells inspired by the PSCP method [19,20]. The solid phases were then heated and their melting points were determined by the change in the self-diffusion coefficient of the ions. The developed method is summarized in Figure 2 and explained in detail in the following sections. An example workflow is also available online in Reference [25].

Figure 2.
Schematical workflow of the developed melting point prediction method. Ionic liquids are packed, structurized with Coulombic potential wells, heated from 175 to 475 K and the melting points are then estimated from diffusion coefficient (D) temperature (T) dependence.
2.2. Simulations Details
The MD simulations were run using the GROMACS code (GROMACS 5.1.4, Uppsala University, Uppsala, Sweden, 2016) with a time step 0.5 fs. The cut-off length of 1.3 nm for Lennard-Jones and electrostatic interactions was used. The OPLS-AA (All Atom Optimized Potentials for Liquid Simulations) force field with refitted partial charges was employed as discussed in Section 2.6. The force field parameters along with the refitted partial charges are available online in Reference [25]. The number of IL ions in systems was varied so that the packed solid phase lattice, which is discussed in the next section, would extend more than 2.8 nm in all dimensions to accommodate at least 128 or at most 350 ion pairs. Two different initial densities were tested for each IL, which were assumed from the IL or corresponding anion acid densities. Sulfonimides were packed at 1.4 kg/dm3 and 1.6 kg/dm3; carboxylic and benzoic acids were packed at 1.0 kg/dm3, 1.2 kg/dm3 or 1.4 kg/dm3. This density determined only the initial package density as in the later simulations an ensemble was used.
2.3. Solid Phase Structures
The starting structures were generated randomly with the Packmol (Packmol 1.1.2.272, University of Campinas, São Paulo, Brazil, 2009) algorithm [26]. First, these structures were equilibriated in a short MD run with the steep integrator. Subsequently, the solid phases were obtained in 200 ps simulations, where the temperature was changed from 1000 K to 1 K in 100 ps and then kept at 1 K for 100 ps.
200 ps, or even 200 μs, is too short timescale for the formation of a realistic solid phase—a process that is known to be problematic and time-consuming for the ILs in experiments. The necessary macroscopic timescales are practically unreachable in simulations. Thus, Coulombic potentials wells were added to the system to facilitate the generation of more ordered solid phase structures. Similar approach was used in the PSCP method by Eike et al. to obtain a single known solid phase during a cycle of simulations for the purposes of melting point prediction [19,20].
In contrast to the PSCP method, in this work, as the placement of ions in the real solid phase was unknown for our ILs, eight different potential well lattices were constructed for each IL. Different lattices were generated by the combination of CsCl and NaCl ionic lattices with 3:2:2, 3:3:2, 3:3:3 and 4:3:2 lattice vector ratios. Thus, all subsequent simulations were conducted with eight differently packed systems for each IL. Even though cubic or orthorombic initial lattices were used, the ions were not explicitly restricted to be at the centers of potential wells even if it was the most energetically favored. Also ions were allowed to relax prior to annealing simulations, so that the IL lattice could adapt any of the Bravais lattices.
A potential well is a virtual site which interacts with the rest of the system only through a linear Coulombic potential. The linear potential scaling from distance is important to avoid the forces to approach infinity at close distances since they have no Lennard–Jones repulsion. The presence of the potential wells enable the use of elevated temperatures without the decomposition of an ordered lattice. The elevated temperatures are beneficial for allowing ions to overcome rotational energy barriers in short amounts of time, after which the system is cooled down.
After the initial structuring, six subsequent 500 ps-long simulations were run again with potential wells. In simulations one, three and five only the anions were allowed to move while the positions of the cations were restrained. In simulations two, four and six the cations moved while the anions were restrained. The temperature control was similar to the initial potential well simulation: the temperature was decreased from 1000 K to 1 K within 400 ps and was kept there for the final 100 ps. However, weaker potential wells were used in each consecutive simulation so that the yielded solid phase structure could improve iteratively as the perturbation from the potential wells was weaker. An iterative approach and using position restrictions is necessary for obtaining a more organized solid phase, because the position of every ion in the system depends on all other ions.
2.4. Annealing Simulations
The potential wells were removed from the system and the obtained solid phases were equilibriated at 175 K for 2.5 ns with an ensemble. Then the temperature was increased to 475 K over 30 ns (). The simulations were run at 1 bar with the compressibility of . The isotropic Berendsen pressure coupling algorithm and the velocity rescaling temperature coupling algorithm were used. The cut-off for van der Waals and electrostatic interactions was 1.3 nm. The particle-mesh Ewald model was used to account for the long-range electrostatic interactions with 0.10 nm Fourier spacing. The resulting trajectories were used to predict the melting points of the systems.
2.5. Melting Point Prediction
Throughout the annealing simulations, the mean square displacement of particles was calculated. From the mean square displacement the average diffusion coefficients were estimated for every consecutive 10 ps time-frame. This approach does not provide accurate diffusion coefficients, as they are usually simulated over longer time-frames at constant temperature. However, the approach allows to monitor the relative change of the diffusion coefficient during annealing. At first approximation, the diffusion coefficient, D, follows the Arrhenius’ equation:
where denotes the diffusion activation energy, R is universal gas constant and T is temperature. Assuming that for a given phase the diffusion mechanism does not change with the temperature, we take that the diffusion coefficient depends linearly on the inverse temperature. As the liquid and solid phases have markedly different pre-exponent factors () and activation energies, melting can be identified during an annealing simulation by a significant change in slope of the D–T dependence.
Melting points were identified for all systems as the point between the solid and liquid phase D–T dependencies. The solid and liquid phase D–T dependencies were linearized according to a few criteria: (1) the regions were distributed so that the sum of the correlation coefficients of both phases () was maximum; (2) systems with no distinct change in slope were excluded as there may have been only one phase throughout the simulation; (3) systems with moderate and low correlation of the solid and liquid phase fits ( and ) were excluded from the analysis. Subsequently, the melting point of the highest melting solid phase of each IL was reported as the predicted melting point of the corresponding IL.
2.6. Force Fields and Partial Charges
The OPLS-AA force field was employed. The force field parameters for choline and TFSI ions were obtained from References [27,28]. The rest of the force fields were developed using the generic OPLS-AA atom types. The Ligandbook repository was used as the starting point for most anions [29]. The force fields that were used in the final method are available in Reference [25].
Ion charges in MD are often taken as ±1e. As charge distribution is expected to be a dominant factor for ILs, where Coulombic forces dominate, such approximation would introduce a large error. The first estimation of the atomic partial charges was made with single point DFT (density functional theory) calculations of single ions in vacuum. CHELPG (charges from electrostatic potentials using a grid based method) charges were chosen as they are developed to accurately reproduce the electrostatic potential [30]. The calculations were done on PBE/Def2-SVP level [31,32] with the Orca (Orca 4.0.0.2, Max Planck Institute for Chemical Energy Conversion, Mülheim an der Ruhr, Germany, 2017) quantum chemical program suite [33]. As the GHELPG analysis does not depend much on the basis set, one of the simplest option (Def2-SVP) was chosen. For the same reason PBE density functional, showing a moderate performance on ILs [34,35], was used.
The CHELPG charges were utilized in MD simulations to construct solid phases using potential wells as described in the previous sections. Potential wells were removed and after a 2.5 ns period of relaxation, snapshots of the systems were taken. These snapshots served as starting points for semi-empirical GFN2-xTB (GFN2-xTB 5.9, Universität Bonn, Bonn, Germany, 2018) calculations [36,37]. Instead of CHELPG charges, Hirshfeld partial charges were extracted from the single point GFN2-xTB calculations as the CHELPG method is not available in the GFN2-xTB code. New atomic partial charges were calculated by averaging the charges of the corresponding atoms within all differently packed systems of the same IL. The ions that were further than 15 Å from the geometrical centre of the box were excluded, because the GFN2-xTB calculations were run without periodic boundary conditions and thus such ions might have been affected by the boundary effects.
Finally, the obtained averaged charges were inserted into the force fields and the workflow was restarted using the new charges. This approach yields more realistic atomic charge distribution for condensed phases than gas-phase DFT calculations of single ions.
2.7. Experimental
The ILs experimentally studied in the current work were synthesized by neutralization of choline bicarbonate solution with the respective acids [15]. Structures of the obtained ILs were confirmed by 1H nuclear magnetic resonance (NMR) spectroscopy (Bruker Avance II 400 MHz, Bruker Corporation, Billerica, MA, USA) using D2O as the solvent. The water content of the choline ILs was determined by Karl Fischer coulometric titration (Metrohm 756 KF Coulometer, Metrohm AG, Herisau, Switzerland). All the used chemicals were purchased from Sigma-Aldrich, St. Louis, MO, USA.
The experimental measurements of normal melting points () were done on a NETZSCH DSC 204 F1 Phoenix® (NETZSCH Group, Selb, Germany) differential scanning calorimeter (DSC). Samples were placed in aluminum pans and heated under nitrogen with a temperature screening rate of . The reported melting points correspond to the endothermic peak maximum temperatures. The uncertainty of measurement was ±1 K.
3. Results
3.1. Experimental Results
Several simulated ILs were synthesized and characterized experimentally in the current work to better validate the simulation results. We prioritized ILs with missing values (e.g., choline 2-methylbutanoate, choline isovalerate) and those with conflicting values in the literature (choline acetate [11,14,15], choline citrate [16,17]). The glass transition temperatures () and melting points (), obtained with differential scanning calorimetry, are compiled in Table 1. The water content in the synthesized ILs is also provided in Table 1.

Table 1.
The experimental glass transition temperatures and melting points of choline cation-based ionic liquids measured with differential scanning calorimetry (DSC). T range indicates the scanned temperature range. Water content was measured with Karl Fischer titration.
3.2. Predicted Melting Points
For each IL, the solid phases were packed and the systems determining the melting points were identified to the criteria defined in the methods section. Following this, solid and liquid phase linear fits were made. For example, Figure 3 displays the D–T dependence of choline ibuprofenate solid phase during annealing along with the fitted lines—red for solid phase and green for liquid phase. Similar plots for all of the studied ILs are provided in the Supplementary Materials.
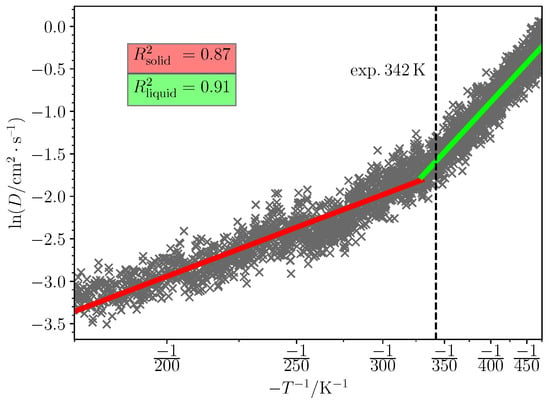
Figure 3.
The diffusion coefficient (D) dependence on temperature (T) during annealing simulation of choline ibuprofenate. The solid phase was packed at 1.2 kg/dm3 density with potential wells in CsCl lattice with 4:3:2 vector ratio. Red, green and the dotted line indicate respectively the fitted solid phase region, the fitted liquid phase region and the experimental melting point.
It is evident from Figure 3 that although the liquid and solid phases’ fit is quite strong, the phase transition from solid to liquid introduces a slightly curved region. A more severe example of non-linearity among the simulated systems is choline saccharinate (Figure 4).
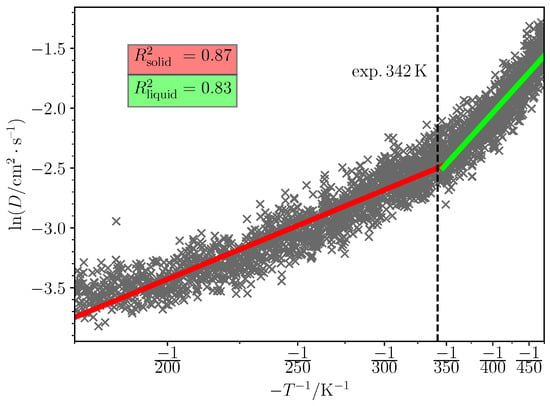
Figure 4.
The diffusion coefficient (D) dependence on temperature (T) during annealing simulation of Choline Saccharinate. The solid phase was packed at 1.6 kg/dm3 density with potential wells in NaCl lattice with 3:2:2 vector ratio. Red, green and the dotted line indicate respectively the fitted solid phase region, the fitted liquid phase region and the experimental melting point.
This phenomenon occurs most likely due to the presence of more than one competing diffusion mechanism. In this case, the D–T dependence cannot be properly linearized using the Arrhenius’ equation (Equation (1)), as different mechanisms may have different activation energies and pre-exponent factors .
Regardless of whether this situation arises in pure phases, it is unavoidable at phase transfer conditions where different phases and/or their transition states coexist. Given an infinitely long simulation, the melting process goes to completion at a discrete temperature provided that the system is crystalline. However, at simulation size and time scales, melting occurs over a range of temperatures. The diffusion mechanism is different and complex during the time when the system has begun to melt, but its structure is still dependent on the initial solid phase. This effect is manifested as non-linearity in the D–T dependence and it lowers the accuracy of the melting point prediction.
Despite the described non-linearity, the prediction of melting points is possible through an assumption, that melting point is the temperature at which the fitted solid phase dependence ends. The system at the end of the solid fit may be a complex transitional phase instead of a proper solid or liquid phase, but the end-point can still be mathematically determined. To increase robustness, we excluded from analysis systems with correlation coefficients below 0.7 and 0.9 for the solid and liquid phase fits, respectively. This way we avoided systems with large non-linearity and oscillations at phase transition. For choline saccharinate, a 0.7 minimum liquid phase fit was allowed, as none of its systems produced a liquid phase fit of above 0.9. Note that simulations with different partial charges or temperature rates have weaker correlations requiring lower thresholds.
Melting points were found as the intersection point of solid and liquid phase fits. The predicted melting points are presented in Table 2. The root-mean-square error of the predicted melting points is 18–24 K, depending on the choice of the experimental reference. It is seen that the experimental results can significantly vary among themselves, which is probably caused by different heating rates used in differential scanning calorimetry and more importantly the presence of impurities (incl. water), on which the data often remains unpublished. Regardless of the choice of reference value, the mean error of 2–10 K indicates a positive skew in the predicted values, for example, the prediction method tends to slightly overestimate the melting points.

Table 2.
The experimental and predicted melting points () of choline cation-based ionic liquids and their difference ().
3.3. Annealing Temperature Rate Effect
To be assured that the hysteresis effect does not affect our determined melting “onset” temperatures, we carried out annealing simulations with different temperature rates for those solid phases that yielded the predicted melting points. If the delayed phase transition, that we observe as non-linearity in D–T dependencies, is accompanied by superheating, then the predicted melting point should strongly depend on the simulation temperature increase regime.
As can be seen in Figure 5, the annealing temperature rate indeed influences the evaluated melting point values. For most ILs, these values seem to converge, but for Choline Acesulfamate and Choline 2-Methylbutanoate the resulting dependence was unclear. Within subgroups shown in Figure 5A–D, except for these two ILs, the order of predicted agrees with the experimental one. In case of superheating due to hysteresis, faster temperature rates should systematically produce higher melting point estimates which is not the case for our systems. Hence, it is possible that there is a hysteresis effect, but it does not severely affect our obtained results.
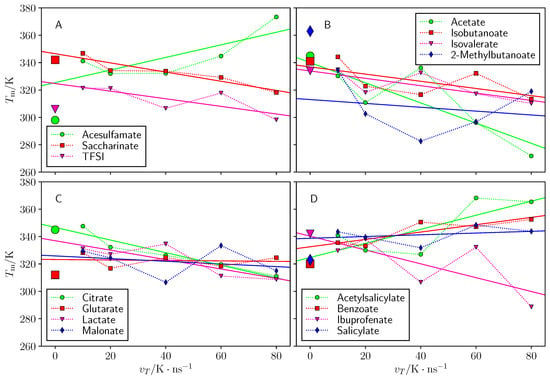
Figure 5.
The predicted melting point () dependence on temperature rate () for: (A) choline sulfonimides, (B) choline carboxylates (with one carboxyl group), (C) choline carboxylates (with two carboxyl groups) and (D) choline benzoates. Large markers at correspond to experimental values. Solid regression lines extrapolate between different temperature rates.
Interestingly, in most cases faster temperature rates tended to yield underestimated predictions rather overestimated predictions, while the latter would be the expected if superheating effect occurred. We can speculate that rapid heating either causes local overheating or the velocity rescaling temperature coupling algorithm misbehaves at such extreme conditions. In any case it is concluded, that the temperature rate of used in this work is sufficient to provide accurate results.
A linear regression line was added to Figure 5 to indicate trend in predicted melting point when the rate of melting is slowed. The most straightforward albeit expensive way to minimize the effect of hysteresis is to conduct longer simulations. Another way is to conduct simulations with different and not necessarily slower duration and extrapolate the results. We added a regression line to simulations with different time rates in Figure 5 to enable the estimation of extrapolated melting point by their intercept values at .
The root-mean-squared error of the extrapolated melting points prediction was 19–23 K, which is almost identical to the error of the regular predictions (18–24 K). It appears that most regression lines in Figure 5 tend to steer close to the experimental values than predictions at , but there is a severe outlier—choline 2-methylbutanoate. With the exclusion of choline 2-methylbutanoate the root-mean-squared error of the extrapolated predictions is 12–18 K (17–22 K for regular predictions). Individual melting points predicted from the extrapolated results are found in Table S1 in the Supplementary Materials.
3.4. The Choice of Partial Charges
Throughout the development of the melting point prediction method, the partial charge distribution was established as a key factor. It is often approximated in the MD studies, that the ionic charges are ±1 e. Following this example, the CHELPG atomic charges were calculated for single ions in vacuum with DFT on PBE/Def2-SVP level. Using the obtained atomic charges, the determined melting point values were severely overestimated (Table 3). The melting point estimations improved for some cases when all CHELPG charges were scaled by a factor of 0.8 to account for the possibility of partial charge transfer [41].

Table 3.
The experimental and predicted melting points () of choline cation-based ionic liquids. Predictions are done with different partial charges: calculated with DFT, calculated with DFT and then scaled with 0.8 and averaged charges from GFN2-xTB calculation of solid phase.
It is natural that lower charges lead to decrease in melting point, because the Coulombic interactions become weaker. However, arbitrarily reducing the partial charges is not justifiable and still led to overestimated melting point predictions. Partial charge transfer manifests itself in DFT calculations of large sets of ion pairs [30,42,43]. Yet, as previous studies have shown, larger associates are require to obtain more realistic ionic charges and partial charge distributions within ions [44,45]. Thus, we calculated partial charges in IL clusters using the GFN2-xTB method and Hirshfeld partitioning scheme. These charges, when incorporated into the force fields, yielding more accurate melting point predictions in most of the cases (Table 3). The cluster geometries for the GFN2-xTB calculations were extracted from the workflow simulation trajectories obtained with CHELPG charges.
4. Discussion
The prediction of IL melting point was performed before with varying success via quantitative structure–property relationship (QSPR) or MD-based [18] approach. In QSPR methods, several simple descriptors are correlated to the melting point. Numerous QSPR [46,47,48,49,50,51,52] and other statistical models [53,54] were assembled, with perhaps the most impressive being a work by Torrecilla et al., who report a mean prediction error of only 1.30% [46]. However, the QSPR and QSAR-based models have an intrinsic shortcoming—they are reliable as far as the characterized substances are similar to those of the training set that were used to build the model. Therefore, they are not best suited for screening for novel compounds or for studying more complex systems, for example, mixtures of ILs.
There are several MD-based methods for melting point determination such as the free-energy based PSCP method [19,20,55], hysteresis method [56], voids method [57,58] and solid–liquid interface method [59]. They are in principle more reliable and universally applicable than the QSPR methods [18]. In practice, they have a severe limitation—requirement for the crystal structure data. The main motivation for the melting point prediction of ILs is to identify new low melting ILs prior to their synthesis. If the prediction method requires crystal structure data, then it makes synthesis and crystallization of the IL inevitable. At that point, a little effort put in measuring the melting point makes the post-prediction useless.
Our method does not require the knowledge of IL crystal structure. Instead, the solid phases are packed with the help of Coulombic potential wells. Differently from the PSCP method [19,20,55], where the wells are placed in known lattice vertices, we simulate different lattices and choose the highest melting point.
Our analysis of D–T dependencies can be considered direct as opposed to constructing phase transition free energy cycles as is done in PSCP. The authors of the PSCP method, Zhang and Maginn claimed that direct prediction of melting points of ILs is not accurate due to the superheating phenomenon which leads to severe overestimation of the melting points [18]. Contrary to that claim, in our results (Table 2), there is a relatively small skew (2–10 K mean average error) towards higher predicted values. In addition, we did not observe clear superheating hysteresis when changing the temperature rate of annealing simulations (Figure 5). Interestingly, faster temperature rates did yield inaccurate results, but they tended to underestimate rather than overestimate the melting points. This might be happen due to local overheating or problems with the temperature coupling algorithm at more rapid temperature rates. Conducting annealing simulations with different temperature rates also yields a slightly more accurate prediction for most cases. This was shown with the regression lines in Figure 5 via extrapolation towards temperature rate of , which would correspond to an infinitely slow annealing.
Another factor, which did lead to markedly overestimated results for our method, was using inaccurate partial charges. In the work by Zhang and Maginn [18], the IL force field charges used to test different methods were obtained similarly to our initial DFT CHELPG charges, where the ionic charges are forced to be ±1 e. In current work, we observed large errors when using these partial charges (Table 3). The situation improved slightly with scaling the charges uniformly down with the factor of 0.8—a typical value obtained in DFT calculations [43,60]. Arbitrary down-scaling is better than using charges of unity, but an accurate charge distribution is also required as demonstrated in the previous works [61,62,63]. The error of our predicted melting points greatly decreased when the charges were extracted from calculations with clusters instead of single ions. In this work, we have used GFN-xTB2 semi-empirical calculations to estimate charges in condensed phases, but perhaps even more accurate charges can be extracted from ab initio MD if required (see e.g., Reference [55]).
Another viable alternative is to use polarizable force fields to circumvent the need for such static partial charges altogether. Previously, this was shown to have a significant effect on interactions between ions in aqueous solutions [64,65,66,67,68] and the dynamics of the ILs [69,70,71,72]. Running simulations with polarizable force field was not feasible in current work, because polarizable force fields were not readily available for all studied ILs. Nevertheless, recent progress in the development of transferable polarizable force fields reassures that in the nearest future the presented method for predicting melting points could be applied to a larger set of ionic liquids without the need to refine charges.
5. Conclusions
This work introduces an MD-based method for estimating the melting points of ILs. While the method is suitable for any ionic compound, we have focused on the melting point of biofriendly choline ILs. Application of these liquids requires them to be liquid at ambient temperature, yet most of them tend to be solid. We have tested the developed method on 15 ILs comprising of choline cation and various biofriendly anions.
Compared to previously published methods, the accuracy of our method is excellent with a root-mean-square error of only 18–24 K. Moreover, compared to other approaches, our method has a relevant advantage—it does not require the knowledge of the crystal structure nor does it depend on the choice of a training set as QSPR-based methods do. Hence, our method is useful for the discovery of ionic compounds for example, for computational screening and characterization of novel biofriendly ILs prior to their synthesis. Instead of replicating an experimental crystal, the solid phases in our method are constructed with the help of Coulombic potential wells. The potential well positions are systematically varied for each IL to create optimal structures which are then melted in annealing simulations. Melting point is then determined via analysis of the dependence of the annealing simulation.
Direct melting point determination methods such as ours have previously received criticism that they suffer from overheating due to hysteresis resulting in overestimated melting points. On varying the temperature rate of melting simulations, we observed no clear overheating tendency. However, we did observe significant overestimation of predicted melting points when inaccurate charges partial charge distribution was used, for example, when charges were extracted from the DFT calculations of single ions. We obtained significantly better melting point predictions only after using partial charges extracted from semi-empirical calculations of condensed phase. This indicates that both the effective ionic charges and the charge distributions within ions are detrimental for accurate simulation of ILs.
The publicly available automated workflow in Reference [25], which implements the developed method, can be readily extended to other ILs and their mixtures. As similar calculations are readily parallelizable, the only practical limitation is the availability of the force fields. We believe that that disadvantage is minor, as it is being eliminated with the development of novel transferable force field parameters.
Supplementary Materials
The following are available online at https://www.mdpi.com/2076-3417/9/24/5367/s1, Figure S1: D–T dependence of Choline Acetate, Figure S2: D–T dependence of Choline Acesulfamate, Figure S3: D–T dependence of Choline Acetylsalicylate, Figure S4: D–T dependence of Choline Benzoate, Figure S5: D–T dependence of Choline Citrate, Figure S6: D–T dependence of Choline Glutarate, Figure S7: D–T dependence of Choline Ibuprofenate, Figure S8: D–T dependence of Choline Isobutanoate, Figure S9: D–T dependence of Choline Isovalerate, Figure S10: D–T dependence of Choline Lactate, Figure S11: D–T dependence of Choline Malonate, Figure S12: D–T dependence of Choline 2-Methylbutanoate, Figure S13: D–T dependence of Choline Saccharinate, Figure S14: D–T dependence of Choline Salicylate, Figure S15: D–T dependence of Choline TFSI, Table S1 Experimental, predicted and extrapolated melting points.
Author Contributions
Conceptualization, K.P.-E. and V.I.; methodology, K.K.; software, K.K.; validation, F.E., K.K.; formal analysis, K.K.; investigation, F.E. and K.K.; resources, K.P.-E. and V.I.; data curation, K.K.; writing—original draft preparation, F.E. and K.K.; writing—review and editing, K.P.-E. and V.I.; visualization, K.K.; supervision, K.P.-E. and V.I.; project administration, K.P.-E. and V.I.; funding acquisition, K.P.-E. and V.I.
Funding
The EU supported this research through the European Regional Development Fund (TK141 “Advanced materials and high-technology devices for energy recuperation systems”), Estonian Institutional Research Grant IUT20-13, Estonian Personal Research Project PUT1107, and the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 793377 (BIOACT). Computational results were obtained in part using the High Performance Computing Center of the University of Tartu and in part using the EPSRC funded ARCHIE-WeSt High Performance Computer (www.archie-west.ac.uk, EPSRC grant no. EP/K000586/1).
Acknowledgments
The authors would like to thank Wasserscheid’s work group at Friedrich-Alexander University Erlangen-Nürnberg for the help with the DSC measurements.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IL | ionic liquid |
| MD | molecular dynamics |
| QSAR | quantitative strucutre–activity relationship |
| PSCP | pseudo supercritical path model |
| TFSI | bis[(trifluoromethyl)sulfonyl]imide |
| OPLS-AA | optimized potentials for liquid simulations for all atoms, a molecular dynamics force field |
| NVT | a molecular dynamics ensemble where the amount of particles, volume and temperature are constant |
| NPT | a molecular dynamics ensemble where the amount of particles, pressure and temperature are constant |
| DFT | density functional theory |
| CHELPG | charges from electrostatic potentials using a grid based method |
| GFN2-xTB | Grimme’s semi empirical tight binding method |
| QSPR | quantitative structure–property relationship |
References
- Fedorov, M.V.; Kornyshev, A.A. Ionic Liquids at Electrified Interfaces. Chem. Rev. 2014, 114, 2978–3036. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, M.; Thomas, M.L.; Zhang, S.; Ueno, K.; Yasuda, T.; Dokko, K. Application of Ionic Liquids to Energy Storage and Conversion Materials and Devices. Chem. Rev. 2017, 117, 7190–7239. [Google Scholar] [CrossRef] [PubMed]
- De Vos, N.; Maton, C.; Stevens, C.V. Electrochemical Stability of Ionic Liquids: General Influences and Degradation Mechanisms. ChemElectroChem 2014, 1, 1258–1270. [Google Scholar] [CrossRef]
- Maton, C.; De Vos, N.; Stevens, C.V. Ionic liquid thermal stabilities: decomposition mechanisms and analysis tools. Chem. Soc. Rev. 2013, 42, 5963–5977. [Google Scholar] [CrossRef] [PubMed]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy applications of ionic liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef]
- Plechkova, N.V.; Seddon, K.R. Applications of ionic liquids in the chemical industry. Chem. Soc. Rev. 2008, 37, 123–150. [Google Scholar] [CrossRef]
- Amde, M.; Liu, J.F.; Pang, L. Environmental application, fate, effects, and concerns of ionic liquids: A review. Environ. Sci. Technol. 2015, 49, 12611–12627. [Google Scholar] [CrossRef]
- Bubak, G.; Gendron, D.; Ceseracciu, L.; Ansaldo, A.; Ricci, D. Parylene-Coated Ionic Liquid-Carbon Nanotube Actuators for User-Safe Haptic Devices. ACS Appl. Mater. Interfaces 2015, 7, 15542–15550. [Google Scholar] [CrossRef]
- Rinne, P.; Põldsalu, I.; Johanson, U.; Tamm, T.; Põhako-Esko, K.; Punning, A.; van den Ende, D.; Aabloo, A. Encapsulation of ionic electromechanically active polymer actuators. Smart Mater. Struct. 2019, 28, 074002. [Google Scholar] [CrossRef]
- Shoa, T.; Madden, J.D.; Munce, N.R.; Yang, V.X.D. Steerable Catheters. In Biomedical Applications of Electroactive Polymer Actuators; Carpi, F., Smela, E., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2009; pp. 229–248. [Google Scholar] [CrossRef]
- Petkovic, M.; Ferguson, J.L.; Gunaratne, H.N.; Ferreira, R.; Leitao, M.C.; Seddon, K.R.; Rebelo, L.P.N.; Pereira, C.S. Novel biocompatible cholinium-based ionic liquids—Toxicity and biodegradability. Green Chem. 2010, 12, 643–649. [Google Scholar] [CrossRef]
- Aakeröy, C.B.; Fasulo, M.E.; Desper, J. Cocrystal or Salt: Does It Really Matter? Mol. Pharm. 2007, 4, 317–322. [Google Scholar] [CrossRef] [PubMed]
- Abbott, A.P.; Boothby, D.; Capper, G.; Davies, D.L.; Rasheed, R.K. Deep Eutectic Solvents Formed between Choline Chloride and Carboxylic Acids: Versatile Alternatives to Ionic Liquids. J. Am. Chem. Soc. 2004, 126, 9142–9147. [Google Scholar] [CrossRef] [PubMed]
- Fukaya, Y.; Iizuka, Y.; Sekikawa, K.; Ohno, H. Bio ionic liquids: Room temperature ionic liquids composed wholly of biomaterials. Green Chem. 2007, 9, 1155–1157. [Google Scholar] [CrossRef]
- Muhammad, N.; Hossain, M.I.; Man, Z.; El-Harbawi, M.; Bustam, M.A.; Noaman, Y.A.; Mohamed Alitheen, N.B.; Ng, M.K.; Hefter, G.; Yin, C.Y. Synthesis and Physical Properties of Choline Carboxylate Ionic Liquids. J. Chem. Eng. Data 2012, 57, 2191–2196. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Pei, Y.; Wang, J.; He, M. Design of environmentally friendly ionic liquid aqueous two-phase systems for the efficient and high activity extraction of proteins. Green Chem. 2012, 14, 2941–2950. [Google Scholar] [CrossRef]
- Mourao, T.; Tome, L.C.; Florindo, C.; Rebelo, L.P.N.; Marrucho, I.M. Understanding the Role of Cholinium Carboxylate Ionic Liquids in PEG-Based Aqueous Biphasic Systems. ACS Sustain. Chem. Eng. 2014, 2, 2426–2434. [Google Scholar] [CrossRef]
- Zhang, Y.; Maginn, E.J. A comparison of methods for melting point calculation using molecular dynamics simulations. J. Chem. Phys. 2012, 136, 144116. [Google Scholar] [CrossRef]
- Eike, D.M.; Maginn, E.J. Atomistic simulation of solid-liquid coexistence for molecular systems: Application to triazole and benzene. J. Chem. Phys. 2006, 124, 164503. [Google Scholar] [CrossRef]
- Eike, D.M.; Brennecke, J.F.; Maginn, E.J. Toward a robust and general molecular simulation method for computing solid-liquid coexistence. J. Chem. Phys. 2005, 122, 014115. [Google Scholar] [CrossRef]
- Pereira, J.F.; Barber, P.S.; Kelley, S.P.; Berton, P.; Rogers, R.D. Double salt ionic liquids based on 1-ethyl-3-methylimidazolium acetate and hydroxyl-functionalized ammonium acetates: Strong effects of weak interactions. Phys. Chem. Chem. Phys. 2017, 19, 26934–26943. [Google Scholar] [CrossRef]
- Brünig, T.; Krekić, K.; Bruhn, C.; Pietschnig, R. Calorimetric Studies and Structural Aspects of Ionic Liquids in Designing Sorption Materials for Thermal Energy Storage. Chem. Eur. J. 2016, 22, 16200–16212. [Google Scholar] [CrossRef]
- Nockemann, P.; Thijs, B.; Driesen, K.; Janssen, C.R.; Van Hecke, K.; Van Meervelt, L.; Kossmann, S.; Kirchner, B.; Binnemans, K. Choline Saccharinate and Choline Acesulfamate: Ionic Liquids with Low Toxicities. J. Phys. Chem. B 2007, 111, 5254–5263. [Google Scholar] [CrossRef]
- Villanueva, M.; Parajo, J.; Sanchez, P.B.; Garcia, J.; Salgado, J. Liquid range temperature of ionic liquids as potential working fluids for absorption heat pumps. J. Chem. Thermodyn. 2015, 91, 127–135. [Google Scholar] [CrossRef]
- Karu, K. GitHub Repository of the Force Fields and Workflow Used in: Predicting Melting Points of Biofriendly Choline-Based Ionic Liquids with Molecular Dynamics. Available online: https://github.com/vilab-tartu/MP-FFs (accessed on 12 October 2019).
- Martinez, L.; Andrade, R.; Birgin, E.G.; Martinez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Sambasivarao, S.V.; Acevedo, O. Development of OPLS-AA Force Field Parameters for 68 Unique Ionic Liquids. J. Chem. Theory Comput. 2009, 5, 1038–1050. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Deschamps, J.; Padua, A.A.H. Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 2038–2047. [Google Scholar] [CrossRef]
- Domanski, J.; Beckstein, O.; Iorga, B.I. Ligandbook—An online repository for small and drug-like molecule force field parameters. Bioinformatics 2017, 33, 1747–1749. [Google Scholar] [CrossRef]
- Rigby, J.; Izgorodina, E.I. Assessment of atomic partial charge schemes for polarisation and charge transfer effects in ionic liquids. Phys. Chem. Chem. Phys. 2013, 15, 1632–1646. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Zahn, S.; MacFarlane, D.; Izgorodina, E.I. Assessment of Kohn-Sham Density Functional Theory and Moller-Plesset Perturbation Theory for Ionic Liquids. Phys. Chem. Chem. Phys. 2013, 15, 13664–13675. [Google Scholar] [CrossRef] [PubMed]
- Karu, K.; Mišin, M.; Ers, H.; Sun, J.; Ivaništšev, V. Performance of SCAN density functional for a set of ionic liquid ion pairs. Int. J. Quantum Chem. 2018, 118, e25582. [Google Scholar] [CrossRef]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Bannwarth, C.; Shushkov, P. A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All spd-Block Elements (Z = 1–86). J. Chem. Theory Comput. 2017, 13, 1989–2009. [Google Scholar] [CrossRef]
- Rengstl, D.; Fischer, V.; Kunz, W. Low-melting mixtures based on choline ionic liquids. Phys. Chem. Chem. Phys. 2014, 16, 22815–22822. [Google Scholar] [CrossRef]
- Diogo, H.P.; Moura Ramos, J.J. Study of the thermal behavior of choline ibuprofenate using differential scanning calorimetry and hot-stage microscopy. J. Mol. Struct. 2014, 1078, 174–180. [Google Scholar] [CrossRef]
- Wolf, J.; Aboody, R. Choline salicylate: A new and more rapidly absorbed durg for salicylate therapy. Int. Record. Med. 1960, 173, 234–241. [Google Scholar]
- Schröder, C. Comparing reduced partial charge models with polarizable simulations of ionic liquids. Phys. Chem. Chem. Phys. 2012, 14, 3089–3102. [Google Scholar] [CrossRef]
- Lage-Estebanez, I.; Ruzanov, A.; de la Vega, J.M.G.; Fedorov, M.V.; Ivaništšev, V.B. Self-interaction error in DFT-based modelling of ionic liquids. Phys. Chem. Chem. Phys. 2016, 18, 2175–2182. [Google Scholar] [CrossRef]
- Karu, K.; Ruzanov, A.; Ers, H.; Ivaništšev, V.; Lage-Estebanez, I.; de la Vega, J.M.G. Predictions of Physicochemical Properties of Ionic Liquids with DFT. Computation 2016, 4, 25. [Google Scholar] [CrossRef]
- Dommert, F.; Wendler, K.; Berger, R.; Delle Site, L.; Holm, C. Force Fields for Studying the Structure and Dynamics of Ionic Liquids: A Critical Review of Recent Developments. ChemPhysChem 2012, 13, 1625–1637. [Google Scholar] [CrossRef] [PubMed]
- Kirchner, B.; Malberg, F.; Firaha, D.S.; Hollóczki, O. Ion pairing in ionic liquids. J. Phys. Condens. Matter. 2015, 27, 463002. [Google Scholar] [CrossRef] [PubMed]
- Torrecilla, J.S.; Rodriguez, F.; Bravo, J.L.; Rothenberg, G.; Seddon, K.R.; Lopez-Martin, I. Optimising an artificial neural network for predicting the melting point of ionic liquids. Phys. Chem. Chem. Phys. 2008, 10, 5826–5831. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Jain, R.; Lomaka, A.; Petrukhin, R.; Karelson, M.; Visser, A.E.; Rogers, R.D. Correlation of the Melting Points of Potential Ionic Liquids (Imidazolium Bromides and Benzimidazolium Bromides) Using the CODESSA Program. J. Chem. Inf. Comput. Sci. 2002, 42, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Lomaka, A.; Petrukhin, R.; Jain, R.; Karelson, M.; Visser, A.E.; Rogers, R.D. QSPR Correlation of the Melting Point for Pyridinium Bromides, Potential Ionic Liquids. J. Chem. Inf. Comput. Sci. 2002, 42, 71–74. [Google Scholar] [CrossRef]
- Varnek, A.; Kireeva, N.; Tetko, I.V.; Baskin, I.I.; Solovev, V.P. Exhaustive QSPR Studies of a Large Diverse Set of Ionic Liquids: How Accurately Can We Predict Melting Points? J. Chem. Inf. Model. 2007, 47, 1111–1122. [Google Scholar] [CrossRef]
- Trohalaki, S.; Pachter, R. Prediction of Melting Points for Ionic Liquids. QSAR Comb. Sci. 2005, 24, 485–490. [Google Scholar] [CrossRef]
- Venkatraman, V.; Evjen, S.; Knuutila, H.K.; Fiksdahl, A.; Alsberg, B.K. Predicting ionic liquid melting points using machine learning. J. Mol. Liq. 2018, 264, 318–326. [Google Scholar] [CrossRef]
- Eike, D.M.; Brennecke, J.F.; Maginn, E.J. Predicting melting points of quaternary ammonium ionic liquids. Green Chem. 2003, 5, 323–328. [Google Scholar] [CrossRef]
- Preiss, U.; Bulut, S.; Krossing, I. In Silico Prediction of the Melting Points of Ionic Liquids from Thermodynamic Considerations: A Case Study on 67 Salts with a Melting Point Range of 337 C. J. Phys. Chem. B 2010, 114, 11133–11140. [Google Scholar] [CrossRef] [PubMed]
- Lazzus, J.A. A group contribution method to predict the melting point of ionic liquids. Fluid Phase Equilib. 2012, 313, 1–6. [Google Scholar] [CrossRef]
- Zhang, Y.; Maginn, E.J. The effect of C2 substitution on melting point and liquid phase dynamics of imidazolium based-ionic liquids: Insights from molecular dynamics simulations. Phys. Chem. Chem. Phys. 2012, 14, 12157–12164. [Google Scholar] [CrossRef] [PubMed]
- Luo, S.N.; Ahrens, T.J. Superheating systematics of crystalline solids. Appl. Phys. Lett. 2003, 82, 1836–1838. [Google Scholar] [CrossRef]
- Phillpot, S.R.; Lutsko, J.F.; Wolf, D.; Yip, S. Molecular-dynamics study of lattice-defect-nucleated melting in silicon. Phys. Rev. B 1989, 40, 2831–2840. [Google Scholar] [CrossRef]
- Lutsko, J.F.; Wolf, D.; Phillpot, S.R.; Yip, S. Molecular-dynamics study of lattice-defect-nucleated melting in metals using an embedded-atom-method potential. Phys. Rev. B 1989, 40, 2841–2855. [Google Scholar] [CrossRef]
- Morris, J.R.; Wang, C.Z.; Ho, K.M.; Chan, C.T. Melting line of aluminum from simulations of coexisting phases. Phys. Rev. B 1994, 49, 3109–3115. [Google Scholar] [CrossRef]
- Mondal, A.; Balasubramanian, S. Quantitative Prediction of Physical Properties of Imidazolium Based Room Temperature Ionic Liquids through Determination of Condensed Phase Site Charges: A Refined Force Field. J. Phys. Chem. B 2014, 118, 3409–3422. [Google Scholar] [CrossRef]
- Gieldon, A.; Bobrowski, M.; Bielicka-Gieldon, A.; Czaplewski, C. Theoretical calculation of the physico-chemical properties of 1-butyl-4-methylpyridinium based ionic liquids. J. Mol. Liq. 2017, 225, 467–474. [Google Scholar] [CrossRef]
- Zhang, Y.; Maginn, E.J. A Simple AIMD Approach to Derive Atomic Charges for Condensed Phase Simulation of Ionic Liquids. J. Phys. Chem. B 2012, 116, 10036–10048. [Google Scholar] [CrossRef]
- Schroder, C.; Rudas, T.; Neumayr, G.; Benkner, S.; Steinhauser, O. On the collective network of ionic liquid/water mixtures. I. Orientational structure. J. Chem. Phys. 2007, 127, 234503. [Google Scholar] [CrossRef] [PubMed]
- Jungwirth, P.; Tobias, D.J. Ions at the Air/Water Interface. J. Phys. Chem. B 2002, 106, 6361–6373. [Google Scholar] [CrossRef]
- Jungwirth, P.; Winter, B. Ions at Aqueous Interfaces: From Water Surface to Hydrated Proteins. Annu. Rev. Phys. Chem. 2008, 59, 343–366. [Google Scholar] [CrossRef] [PubMed]
- Minofar, B.; Vácha, R.; Wahab, A.; Mahiuddin, S.; Kunz, W.; Jungwirth, P. Propensity for the Air/Water Interface and Ion Pairing in Magnesium Acetate vs Magnesium Nitrate Solutions: Molecular Dynamics Simulations and Surface Tension Measurements. J. Phys. Chem. B 2006, 110, 15939–15944. [Google Scholar] [CrossRef]
- Petersen, P.B.; Saykally, R.J.; Mucha, M.; Jungwirth, P. Enhanced Concentration of Polarizable Anions at the Liquid Water Surface: SHG Spectroscopy and MD Simulations of Sodium Thiocyanide. J. Phys. Chem. B 2005, 109, 10915–10921. [Google Scholar] [CrossRef]
- Picálek, J.; Minofar, B.; Kolafa, J.; Jungwirth, P. Aqueous solutions of ionic liquids: Study of the solution/vapor interface using molecular dynamics simulations. Phys. Chem. Chem. Phys. 2008, 10, 5765. [Google Scholar] [CrossRef]
- Bedrov, D.; Piquemal, J.P.; Borodin, O.; MacKerell, A.D.; Roux, B.; Schröder, C. Molecular Dynamics Simulations of Ionic Liquids and Electrolytes Using Polarizable Force Fields. Chem. Rev. 2019, 119, 7940–7995. [Google Scholar] [CrossRef]
- Salanne, M. Simulations of room temperature ionic liquids: From polarizable to coarse-grained force fields. Phys. Chem. Chem. Phys. 2015, 17, 14270–14279. [Google Scholar] [CrossRef]
- Pádua, A.A.H. Resolving dispersion and induction components for polarisable molecular simulations of ionic liquids. J. Chem. Phys. 2017, 146, 204501. [Google Scholar] [CrossRef]
- Bernardes, C.E.S.; Shimizu, K.; Lopes, J.N.C.; Marquetand, P.; Heid, E.; Steinhauser, O.; Schröder, C. Additive polarizabilities in ionic liquids. Phys. Chem. Chem. Phys. 2016, 18, 1665–1670. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).