Quantifying the Predictability and Efficiency of the Cointegrated Ethanol and Agricultural Commodities Price Series
Abstract
1. Introduction
2. Data and Methodology
2.1. Detrended Fluctuation Analysis and Hurst Exponent
- ,
- , for a random walk (Bm). The TS has no long memory process,
- , for a persistent (long memory or correlated) process that leads to the concept of the fBm, and
- , for an antipersistent (short-term memory, anticorrelated) process.
2.2. Fractal Dimension
- ;
- , for a random walk (Bm) such that the TS has no long memory process and no local anticorrelations;
- , corresponds to a persistence (long memory or correlated) process that leads to the concept of the fBm;
- , for an antipersistent process (short-term memory, anticorrelated).
2.2.1. Hall-Wood Estimator
2.2.2. Robust Genton Estimator
2.3. Market Efficiency Measure
2.4. Lyapunov Method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| TS | Time series |
| CEPEA | Center for Advanced Studies on Applied Economics/University of Sao Paulo |
| ETH | Brazilian ethanol |
| SUG | Sugar |
| COT | Cotton |
| LCA | Live cattle |
| ARA | Arabica coffee |
| ROB | Robusta coffee |
| COR | Corn |
| SOY | Soybean |
| Sub-period 1 | |
| Sub-period 2 | |
| Sub-period 3 | |
| Sub-period 4 | |
| Sub-period 5 | |
| DFA | Detrended Fluctuation Analysis |
| Efficiency Index |
References
- Goldemberg, J. Ethanol for a Sustainable Energy Future. Science 2007, 315, 808–810. [Google Scholar] [CrossRef] [PubMed]
- Goldemberg, J.; Coelho, S.T.; Guardabassi, P. The sustainability of ethanol production from sugarcane. Energy Policy 2008, 36, 2086–2097. [Google Scholar] [CrossRef]
- Coelho, S.T.; Goldemberg, J.; Lucon, O.; Guardabassi, P. Brazilian sugarcane ethanol: Lessons learned. Energy Sustain. Dev. 2006, 10, 26–39. [Google Scholar] [CrossRef]
- Lapola, D.M.; Schaldach, R.; Alcamo, J.; Bondeau, A.; Koch, J.; Koelking, C.; Priess, J.A. Indirect land-use changes can overcome carbon savings from biofuels in Brazil. Proc. Natl. Acad. Sci. USA 2010, 107, 3388–3393. [Google Scholar] [CrossRef] [PubMed]
- De Cerqueira Leite, R.C.; Leal, M.R.L.V.; Cortez, L.A.B.; Griffin, W.M.; Scandiffio, M.I.G. Can Brazil replace 5% of the 2025 gasoline world demand with ethanol? Energy 2009, 34, 655–661. [Google Scholar] [CrossRef]
- Fargione, J.; Hill, J.; Tilman, D.; Polasky, S.; Hawthorne, P. Land Clearing and the Biofuel Carbon Debt. Science 2008, 319, 1235–1238. [Google Scholar] [CrossRef]
- Debnath, D.; Whistance, J.; Thompson, W.; Binfield, J. Complement or substitute: Ethanol’s uncertain relationship with gasoline under alternative petroleum price and policy scenarios. Appl. Energy 2017, 191, 385–397. [Google Scholar] [CrossRef]
- Moreira, J.R. Sugarcane for energy—Recent results and progress in Brazil. Energy Sustain. Dev. 2000, 4, 43–54. [Google Scholar] [CrossRef]
- Janda, K.; Kristoufek, L. The Relationship between Fuel and Food Prices: Methods, Outcomes, and Lessons for Commodity Price Risk Management. In CAMA Working Paper 2019; Centre for Applied Macroeconomic Analysis, Crawford School of Public Policy, The Australian National University: Canberra, Australia, 2019; pp. 1–58. [Google Scholar] [CrossRef]
- Santos, G.R.; Garcia, E.A.; Shikida, P.F.A. A Crise na produção do etanol e as interfaces com as políticas públicas. Radar 2015, 39, 27–38. [Google Scholar]
- Albarracín, E.S.; Gamboa, J.C.R.; Marques, E.C.M.; Stosic, T. Complexity analysis of Brazilian agriculture and energy market. Phys. A Stat. Mech. Appl. 2019, 523, 933–941. [Google Scholar] [CrossRef]
- Du, X.; Carriquiry, M.A. Flex-fuel vehicle adoption and dynamics of ethanol prices: Lessons from Brazil. Energy Policy 2013, 59, 507–512. [Google Scholar] [CrossRef]
- Quintino, D.D.; David, S.A. Quantitative analysis of feasibility of hydrous ethanol futures contracts in Brazil. Energy Econ. 2013, 40, 927–935. [Google Scholar] [CrossRef]
- Murari, T.; Filho, A.; Pereira, E.; Ferreira, P.; Pitombo, S.; Pereira, H.B.B.; Santos, A.A.B.; Moret, M.A. Comparative Analysis between Hydrous Ethanol and Gasoline C Pricing in Brazilian Retail Market. Sustainability 2019, 11, 4719. [Google Scholar] [CrossRef]
- Serra, T.; Zilberman, D. Biofuel-related price transmission literature: A review. Energy Econ. 2013, 37, 141–151. [Google Scholar] [CrossRef]
- Quintino, D.D.; David, S.A.; Vian, C.E.d.F. Analysis of the relationship between ethanol spot and futures prices in Brazil. Int. J. Financ. Stud. 2017, 5, 11. [Google Scholar] [CrossRef]
- Laurini, M.P. The spatio-temporal dynamics of ethanol/gasoline price ratio in Brazil. Renew. Sustain. Energy Rev. 2017, 70, 1–12. [Google Scholar] [CrossRef]
- Ghoddusi, H. Blending under uncertainty: Real options analysis of ethanol plants and biofuels mandates. Energy Econ. 2017, 61, 110–120. [Google Scholar] [CrossRef]
- David, S.A.; Inacio, C.M.C., Jr.; Machado, J.A.T. Ethanol Prices and Agricultural Commodities: An Investigation of Their Relationship. Mathematics 2019, 7, 774. [Google Scholar] [CrossRef]
- Al-Maadid, A.; Caporale, G.M.; Spagnolo, F.; Spagnolo, N. Spillovers between food and energy prices and structural breaks. Int. Econ. 2017, 150, 1–18. [Google Scholar] [CrossRef]
- Bentivoglio, D.; Finco, A.; Bacchi, M. Interdependencies between Biofuel, Fuel and Food Prices: The Case of the Brazilian Ethanol Market. Energies 2016, 9, 464. [Google Scholar] [CrossRef]
- Capitani, D.H.D.; Junior, J.C.C.; Tonin, J.M. Integration and hedging efficiency between Brazilian and U.S. ethanol markets. Rev. Contemp. Econ. Gest. 2018, 16, 93–117. [Google Scholar] [CrossRef]
- Dutta, A. Cointegration and nonlinear causality among ethanol-related prices: Evidence from Brazil. GCB Bioenergy 2018, 10, 335–342. [Google Scholar] [CrossRef]
- Saghaian, S.H.; Nemati, M.W.C.; Chen, B. Asymmetric price volatility transmission between U.S. biofuel, corn, and oil markets. J. Agric. Resour. Econ. 2018, 43, 46–60. [Google Scholar] [CrossRef]
- Qiu, C.; Colson, G.; Escalante, C.; Wetzstein, M. Considering macroeconomic indicators in the food before fuel nexus. Energy Econ. 2012, 34, 2021–2028. [Google Scholar] [CrossRef]
- Bastianin, A.; Galeotti, M.; Manera, M. Causality and predictability in distribution: The ethanol—Food price relation revisited. Energy Econ. 2014, 42, 152–160. [Google Scholar] [CrossRef]
- Bastianin, A.; Galeotti, M.; Manera, M. Ethanol and field crops: Is there a price connection? Food Policy 2016, 63, 53–61. [Google Scholar] [CrossRef]
- Kristoufek, L.; Janda, K.; Zilberman, D. Comovements of ethanol-related prices: Evidence from Brazil and the USA. GCB Bioenergy 2016, 8, 346–356. [Google Scholar] [CrossRef]
- Serra, T.; Zilberman, D.G.J.M.; Goodwin, B.K. Nonlinearities in the U.S. corn-ethanol-oil-gasoline price system. Agric. Econ. 2011, 42, 35–45. [Google Scholar] [CrossRef]
- Carpio, L.G.T. The effects of oil price volatility on ethanol, gasoline, and sugar price forecasts. Energy 2019, 181, 1012–1022. [Google Scholar] [CrossRef]
- Serra, T.; Zilberman, D.; Gil, J. Price volatility in ethanol markets. Eur. Rev. Agric. Econ. 2010, 38, 259–280. [Google Scholar] [CrossRef]
- Cabrera, B.L.; Schulz, F. Volatility linkages between energy and agricultural commodity prices. Energy Econ. 2016, 54, 190–203. [Google Scholar] [CrossRef]
- Rafiq, S.; Bloch, H. Explaining commodity prices through asymmetric oil shocks: Evidence from nonlinear models. Resour. Policy 2016, 50, 34–48. [Google Scholar] [CrossRef]
- Rosa, F.; Vasciaveo, M. Volatility in US and Italian agricultural markets, interactions and policy evaluation. In Proceedings of the European Association of Agricultural Economists 123rd Seminar, Dublin, Ireland, 23–24 February 2012. [Google Scholar] [CrossRef]
- Piot-Lepetit, I.; M’Barek, R. Methods to Analyse Agricultural Commodity Price Volatility; Piot-Lepetit, I., M’Barek, R., Eds.; Springer: New York, NY, USA, 2011; pp. 1–11. [Google Scholar] [CrossRef]
- Rahman, U.; Markel, E.; English, B.C. The Economics of Biofuel Policies: Impacts on Price Volatility in Grain and Oilseed Markets. Aust. J. Agric. Resour. Econ. 2017, 61, E11–E13. [Google Scholar] [CrossRef]
- Földvári, P.; van Leeuwen, B. What can price volatility tell us about market efficiency? Conditional heteroscedasticity in historical commodity price series. Cliometrica 2011, 5, 165–186. [Google Scholar] [CrossRef][Green Version]
- Bryce, R.; Sprague, K.B. Revisiting detrended fluctuation analysis. Sci. Rep. 2012, 2, 315. [Google Scholar] [CrossRef] [PubMed]
- Hurst, H.E. The long-term dependence in stock returns. Trans. Am. Soc. Civ. Eng. 1951, 116, 770–799. [Google Scholar]
- Gneiting, T.; Ševčíková, H.; Percival, D.B. Estimators of fractal dimension: Assessing the roughness of time series and spatial data. Stat. Sci. 2012, 247–277. [Google Scholar] [CrossRef]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Kristoufek, L.; Vosvrda, M. Measuring capital market efficiency: Global and local correlations structure. Phys. A Stat. Mech. Appl. 2013, 392, 184–193. [Google Scholar] [CrossRef]
- Teng, Y.; Shang, P. Detrended fluctuation analysis based on higher-order moments of financial time series. Phys. A Stat. Mech. Appl. 2018, 490, 311–322. [Google Scholar] [CrossRef]
- Shang, P.; Lu, Y.; Kamae, S. Detecting long-range correlations of traffic time series with multifractal detrended fluctuation analysis. Chaos Solitons Fractals 2008, 36, 82–90. [Google Scholar] [CrossRef]
- David, S.A.; Quintino, D.D.; Inacio, C.M.C., Jr.; Machado, J.A.T. Fractional dynamic behavior in ethanol prices series. J. Comput. Appl. Math. 2018, 339, 85–93. [Google Scholar] [CrossRef]
- Ayadi, O.F.; Williams, J.; Hyman, L.M. Fractional dynamic behavior in Forcados Oil Price Series: An application of detrended fluctuation analysis. Energy Sustain. Dev. 2009, 13, 11–17. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Joyeux, R. An introduction to long-memory time series models and fractional differencing. J. Time Ser. Anal. 1980, 1, 15–29. [Google Scholar] [CrossRef]
- Cizeau, P.; Liu, Y.; Meyer, M.; Peng, C.K.; Stanley, H.E. Volatility distribution in the S&P500 stock index. Phys. A Stat. Mech. Appl. 1997, 245, 441–445. [Google Scholar] [CrossRef]
- Ausloos, M.; Vandewalle, N.; Boveroux, P.; Minguet, A.; Ivanova, K. Applications of statistical physics to economic and financial topics. Phys. A Stat. Mech. Appl. 1999, 274, 229–240. [Google Scholar] [CrossRef]
- Di Matteo, T.; Aste, T.; Dacorogna, M.M. Scaling behaviors in differently developed markets. Phys. A Stat. Mech. Appl. 2003, 324, 183–188. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Statistical methodology for nonperiodic cycles: From the covariance to R/S analysis. In Annals of Economic and Social Measurement, Volume 1, Number 3; NBER: Cambridge, MA, USA, 1972; pp. 259–290. [Google Scholar]
- Mandelbrot, B.B.; Wallis, J.R. Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence. Water Resour. Res. 1969, 5, 967–988. [Google Scholar] [CrossRef]
- Welch, P. The use of fast Fourier transform for the estimation of power spectra: A method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef]
- Roerink, G.J.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar] [CrossRef]
- Carbone, A. Detrending moving average algorithm: A brief review. Dimension 2009, 49, 59. [Google Scholar] [CrossRef]
- Xu, L.; Ivanov, P.C.; Hu, K.; Chen, Z.; Carbone, A.; Stanley, H.E. Quantifying signals with power-law correlations: A comparative study of detrended fluctuation analysis and detrended moving average techniques. Phys. Rev. E 2005, 71, 051101. [Google Scholar] [CrossRef] [PubMed]
- Simonsen, I.; Hansen, A.; Nes, O.M. Determination of the Hurst exponent by use of wavelet transforms. Phys. Rev. E 1998, 58, 2779. [Google Scholar] [CrossRef]
- Percival, D.B.; Walden, A.T. Wavelet Methods for Time Series Analysis; Cambridge University Press: Cambridge, UK, 2006; Volume 4. [Google Scholar]
- Peng, C.K.; Buldyrev, S.V.; Havlin, S.; Simons, M.; Stanley, H.E.; Goldberger, A.L. Mosaic organization of DNA nucleotides. Phys. Rev. E 1994, 49, 1685–1689. [Google Scholar] [CrossRef] [PubMed]
- Shieh, S.J. Long memory and sampling frequencies: Evidence in stock index futures markets. Int. J. Theor. Appl. Financ. 2006, 9, 787–799. [Google Scholar] [CrossRef]
- Tarnopolski, M. On the relationship between the Hurst exponent, the ratio of the mean square successive difference to the variance, and the number of turning points. Phys. A Stat. Mech. Appl. 2016, 461, 662–673. [Google Scholar] [CrossRef]
- Serinaldi, F. Use and misuse of some Hurst parameter estimators applied to stationary and nonstationary financial time series. Phys. A Stat. Mech. Appl. 2010, 389, 2770–2781. [Google Scholar] [CrossRef]
- Peters, E.E. Chaos and Order in the Capital Markets: A New View of Cycles, Prices, and Market Volatility; John Wiley & Sons: Hoboken, NJ, USA, 1996; Volume 1. [Google Scholar]
- Kristoufek, L. How are rescaled range analyses affected by different memory and distributional properties? A Monte Carlo study. Phys. A Stat. Mech. Appl. 2012, 391, 4252–4260. [Google Scholar] [CrossRef]
- Hall, P.; Wood, A. On the performance of box-counting estimators of fractal dimension. Biometrika 1993, 80, 246–251. [Google Scholar] [CrossRef]
- Genton, M.G. Variogram fitting by generalized least squares using an explicit formula for the covariance structure. Math. Geol. 1998, 30, 323–345. [Google Scholar] [CrossRef]
- Kristoufek, L.; Vosvrda, M. Commodity futures and market efficiency. Energy Econ. 2014, 42, 50–57. [Google Scholar] [CrossRef]
- Wolf, A. Quantifying chaos with Lyapunov exponents. Chaos 1986, 16, 273–290. [Google Scholar]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003; Volume 69. [Google Scholar]
- Bryant, P.; Brown, R.; Abarbanel, H.D.I. Lyapunov exponents from observed time series. Phys. Rev. Lett. 1990, 65, 1523–1526. [Google Scholar] [CrossRef] [PubMed]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Hanias, M.; Magafas, L.; Stavrinides, S. Chaotic Analysis of Gold Price Index. J. Eng. Sci. Technol. Rev. 2015, 8, 16–18. [Google Scholar] [CrossRef]
- Casdagli, M. Nonlinear prediction of chaotic time series. Phys. D Nonlinear Phenom. 1989, 35, 335–356. [Google Scholar] [CrossRef]
- Jiang, Y.; Nie, H.; Ruan, W. Time-varying long-term memory in Bitcoin market. Financ. Res. Lett. 2018, 25, 280–284. [Google Scholar] [CrossRef]
- Sensoy, A.; Tabak, B.M. Dynamic efficiency of stock markets and exchange rates. Int. Rev. Financ. Anal. 2016, 47, 353–371. [Google Scholar] [CrossRef]
- Nigatu, G.; Adjemian, M.K. The U.S. Role in the Price Determination of Major Agricultural Commodities. In Proceedings of the 2017 Allied Social Sciences Association (ASSA) Annual Meeting, Chicago, IL, USA, 6–8 January 2017. [Google Scholar] [CrossRef]
- Costa, S.M.A.L.; Ferreira Filho, J.B.d.S. Commercial liberalization in Brazil and integration in the markets of agricultural commodities: The cotton, corn and rice markets. Rev. Econ. E Sociol. Rural 2000, 38, 183–210. [Google Scholar]
- Mattos, F.; Garcia, P. Price discovery in thinly traded markets: Cash and Futures relationships in Brazilian agricultural futures markets. In Proceedings of the NCR-134 Conference on Applied Commodity Price Analysis, Forecasting, and Market Risk Management, St. Louis, MO, USA, 19–20 April 2004. [Google Scholar]
- Bohl, M.T.; Gross, C.; Souza, W. The role of emerging economies in the global price formation process of commodities: Evidence from Brazilian and U.S. coffee markets. Int. Rev. Econ. Financ. 2019, 60, 203–215. [Google Scholar] [CrossRef]

| Pairs | Tests | Periods | |||||
|---|---|---|---|---|---|---|---|
| Full-Period | |||||||
| ETH-SUG | Max-Eigen | 13.90 * | 11.52 | 6.80 | 13.34 | 7.72 | 8.55 |
| Trace | 17.67 | 18.61 * | 10.37 | 15.51 | 8.60 | 11.13 | |
| ETH-COT | Max-Eigen | 21.1 *** | 14.87 * | 5.57 | 8.63 | 7.61 | 10.51 |
| Trace | 26.6 *** | 19.24 * | 7.95 | 9.35 | 10.85 | 14.95 | |
| ETH-ARA | Max-Eigen | 9.88 | 10.34 | 4.27 | 9.61 | 11.66 | 9.87 |
| Trace | 13.56 | 11.34 | 7.56 | 18.75 * | 14.55 | 14.56 | |
| ETH-ROB | Max-Eigen | 14.30 * | 15.18 * | 3.81 | 8.33 | 6.88 | 13.15 |
| Trace | 17.47 | 18.94 * | 5.25 | 12.82 | 10.24 | 19.16 * | |
| ETH-COR | Max-Eigen | 14.05 * | 12.02 | 7.31 | 15.02 * | 4.88 | 11.03 |
| Trace | 18.05 * | 16.99 | 10.77 | 17.92 * | 6.51 | 14.45 | |
| ETH-LCA | Max-Eigen | 11.43 | 12.65 | 8.40 | 13.72 | 5.58 | 7.33 |
| Trace | 14.23 | 14.51 | 10.47 | 20.75 *** | 6.64 | 10.39 | |
| ETH-SOY | Max-Eigen | 10.63 | 11.57 | 7.54 | 8.70 | 8.94 | 7.41 |
| Trace | 15.43 | 13.08 | 11.38 | 9.57 | 13.14 | 9.47 | |
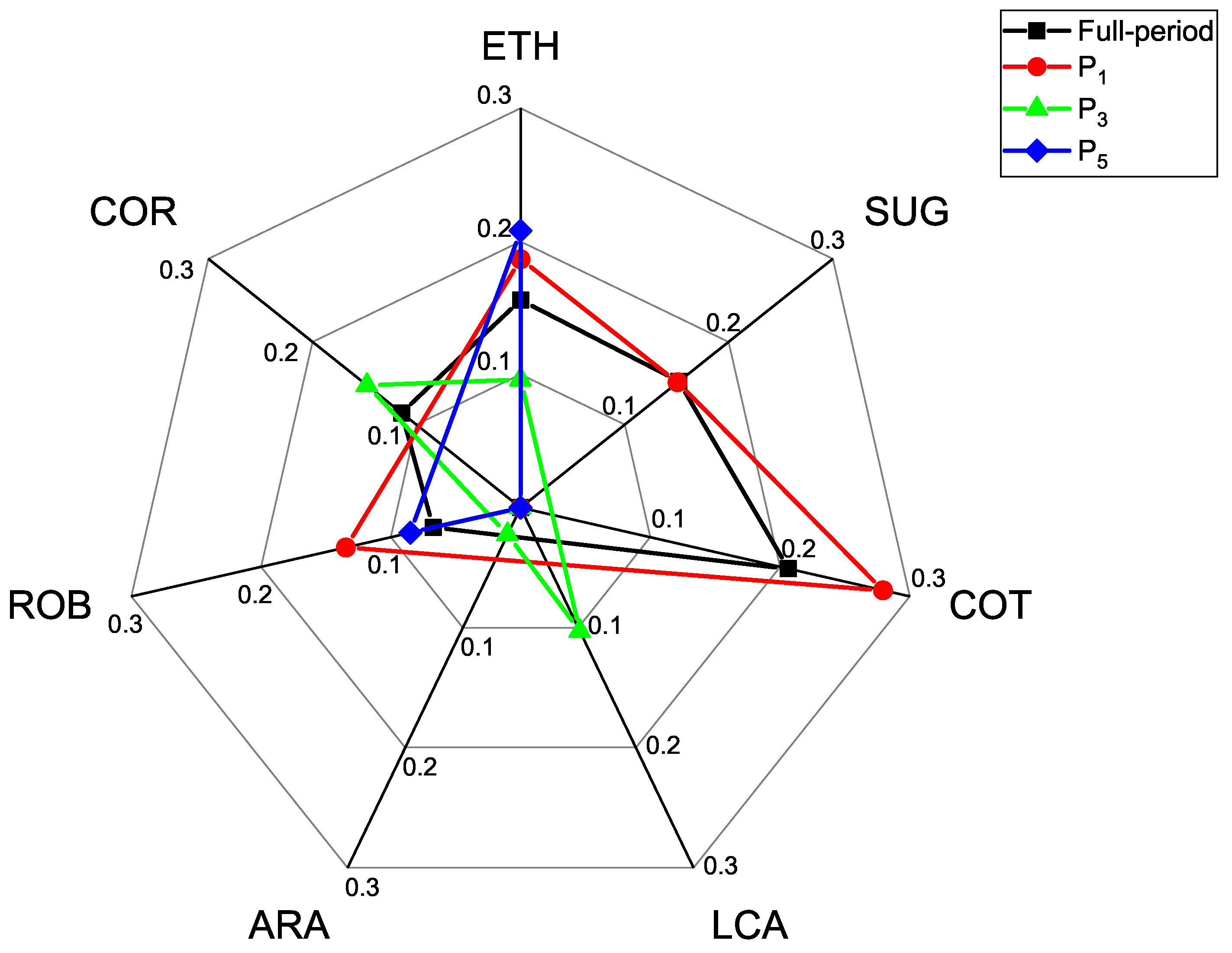
| Commodities | Hurst (H) | Fractal Dimension () | EI | Lyapunov () | (days) | |
|---|---|---|---|---|---|---|
| Full-period | SUG | 0.7381 | 1.3105 | 0.1521 | 0.2026 | 4.9371 |
| COT | 0.7167 | 1.1491 | 0.2062 | 0.1697 | 5.8917 | |
| ETH | 0.6175 | 1.2113 | 0.1559 | 0.3075 | 3.2520 | |
| COR | 0.6211 | 1.3063 | 0.1142 | 0.2181 | 4.5844 | |
| ROB | 0.6318 | 1.4737 | 0.0672 | 0.2923 | 3.4216 | |
| SUG | 0.7614 | 1.3487 | 0.1510 | 0.1901 | 5.2598 | |
| COT | 0.7884 | 1.0215 | 0.2794 | 0.3868 | 2.5856 | |
| ETH | 0.6585 | 1.1620 | 0.1867 | 0.4444 | 2.2501 | |
| ROB | 0.7610 | 1.5675 | 0.1348 | 0.5672 | 1.7632 | |
| ARA | 0.4820 | 1.4590 | 0.0224 | 0.3876 | 2.5803 | |
| LCA | 0.7030 | 1.5318 | 0.1027 | 0.3605 | 2.7740 | |
| ETH | 0.5840 | 1.3271 | 0.0961 | 0.2935 | 3.4075 | |
| COR | 0.6988 | 1.2816 | 0.1477 | 0.2497 | 4.0053 | |
| ETH | 0.6699 | 1.4989 | 0.0849 | 0.1576 | 6.3472 | |
| ROB | 0.7271 | 1.1515 | 0.2080 | 0.2684 | 3.7265 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
David, S.A.; Inácio, C.M.C., Jr.; Tenreiro Machado, J.A. Quantifying the Predictability and Efficiency of the Cointegrated Ethanol and Agricultural Commodities Price Series. Appl. Sci. 2019, 9, 5303. https://doi.org/10.3390/app9245303
David SA, Inácio CMC Jr., Tenreiro Machado JA. Quantifying the Predictability and Efficiency of the Cointegrated Ethanol and Agricultural Commodities Price Series. Applied Sciences. 2019; 9(24):5303. https://doi.org/10.3390/app9245303
Chicago/Turabian StyleDavid, Sergio Adriani, Claudio M. C. Inácio, Jr., and José António Tenreiro Machado. 2019. "Quantifying the Predictability and Efficiency of the Cointegrated Ethanol and Agricultural Commodities Price Series" Applied Sciences 9, no. 24: 5303. https://doi.org/10.3390/app9245303
APA StyleDavid, S. A., Inácio, C. M. C., Jr., & Tenreiro Machado, J. A. (2019). Quantifying the Predictability and Efficiency of the Cointegrated Ethanol and Agricultural Commodities Price Series. Applied Sciences, 9(24), 5303. https://doi.org/10.3390/app9245303







