Shear Load-Displacement Curves of PVA Fiber-Reinforced Engineered Cementitious Composite Expansion Joints in Steel Bridges
Abstract
Featured Application
Abstract
1. Introduction
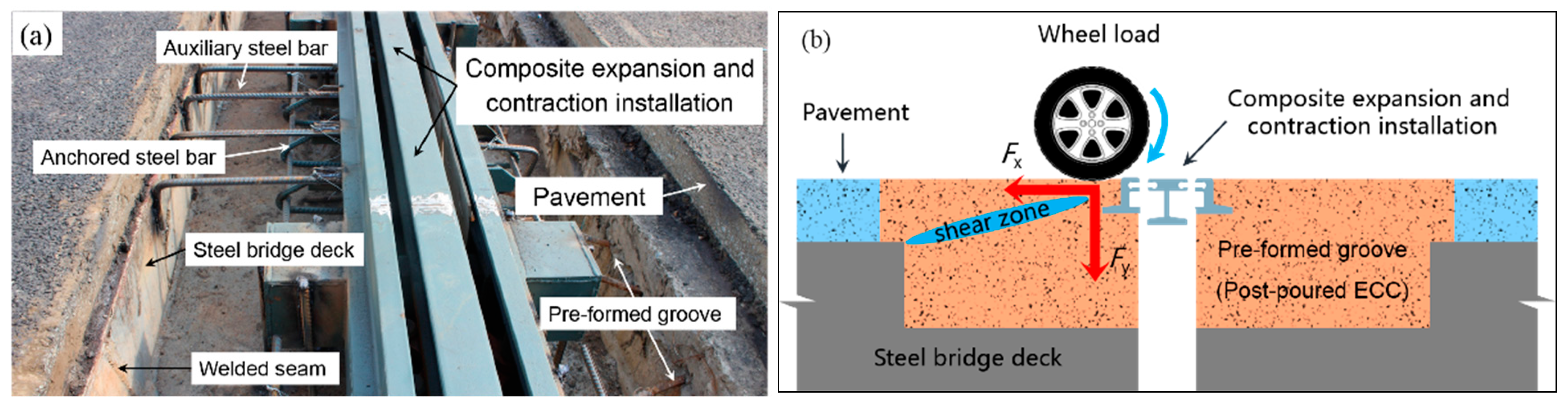
2. Engineering Application and Experimental Design
Engineering Application
3. Mathematical Problem and Numerical Analysis Models
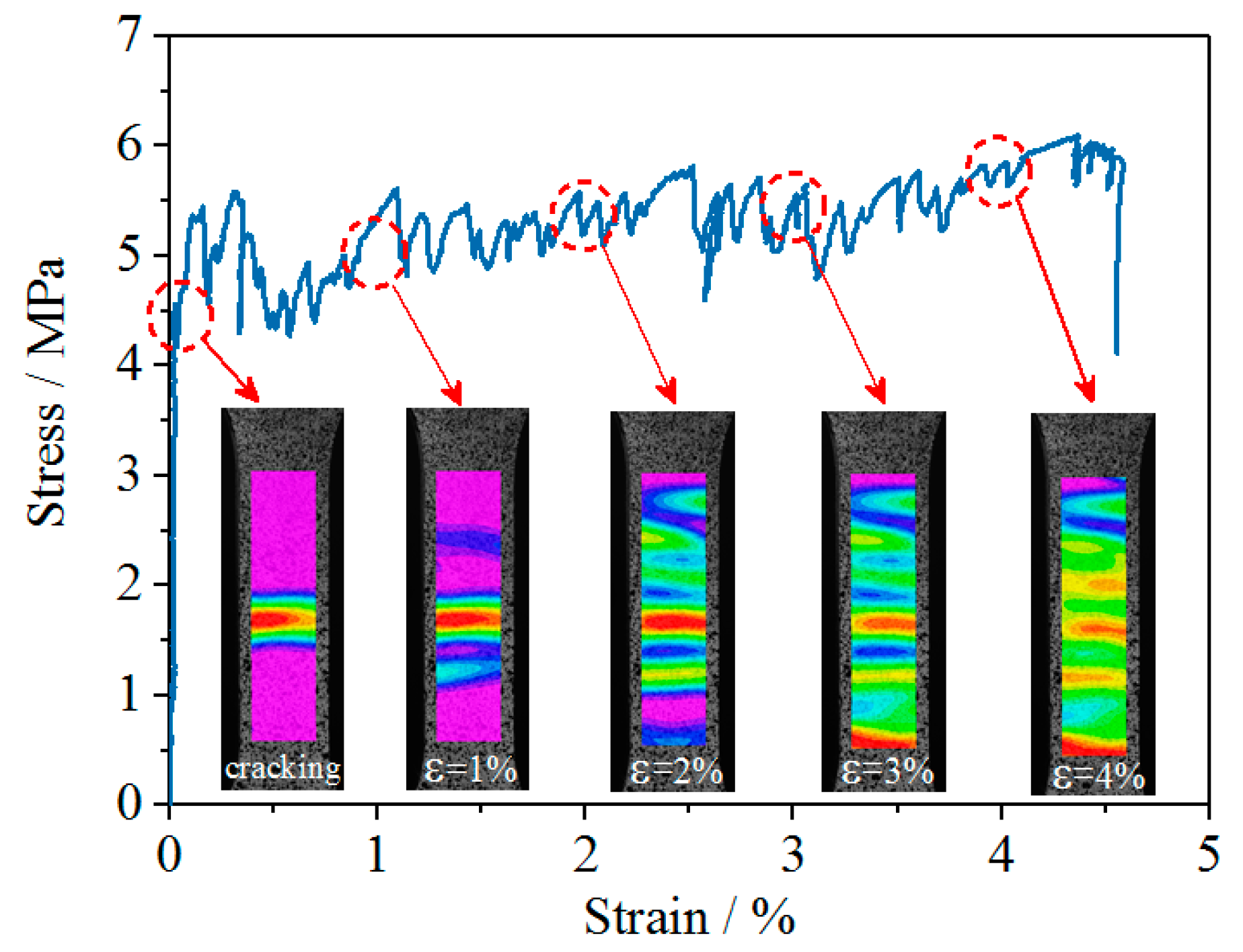
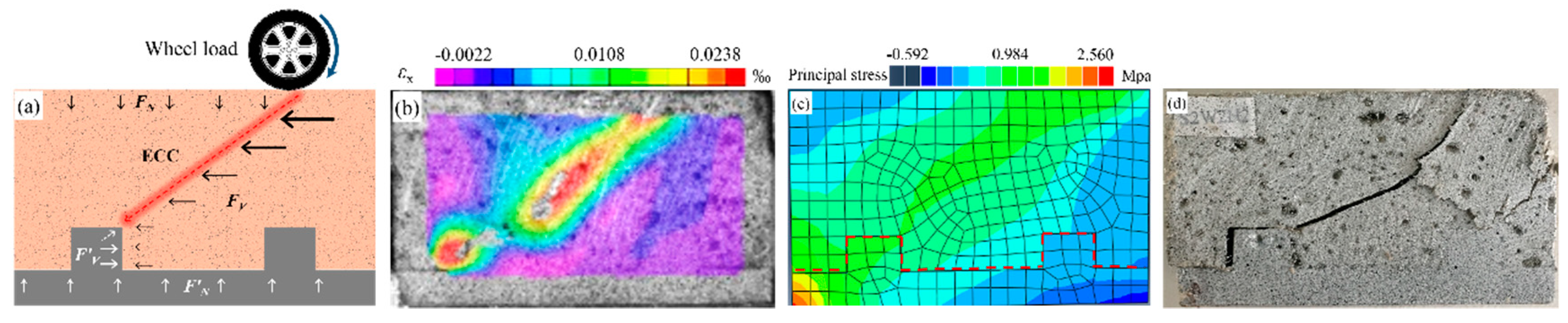
3.1. Shear Failure Characteristics
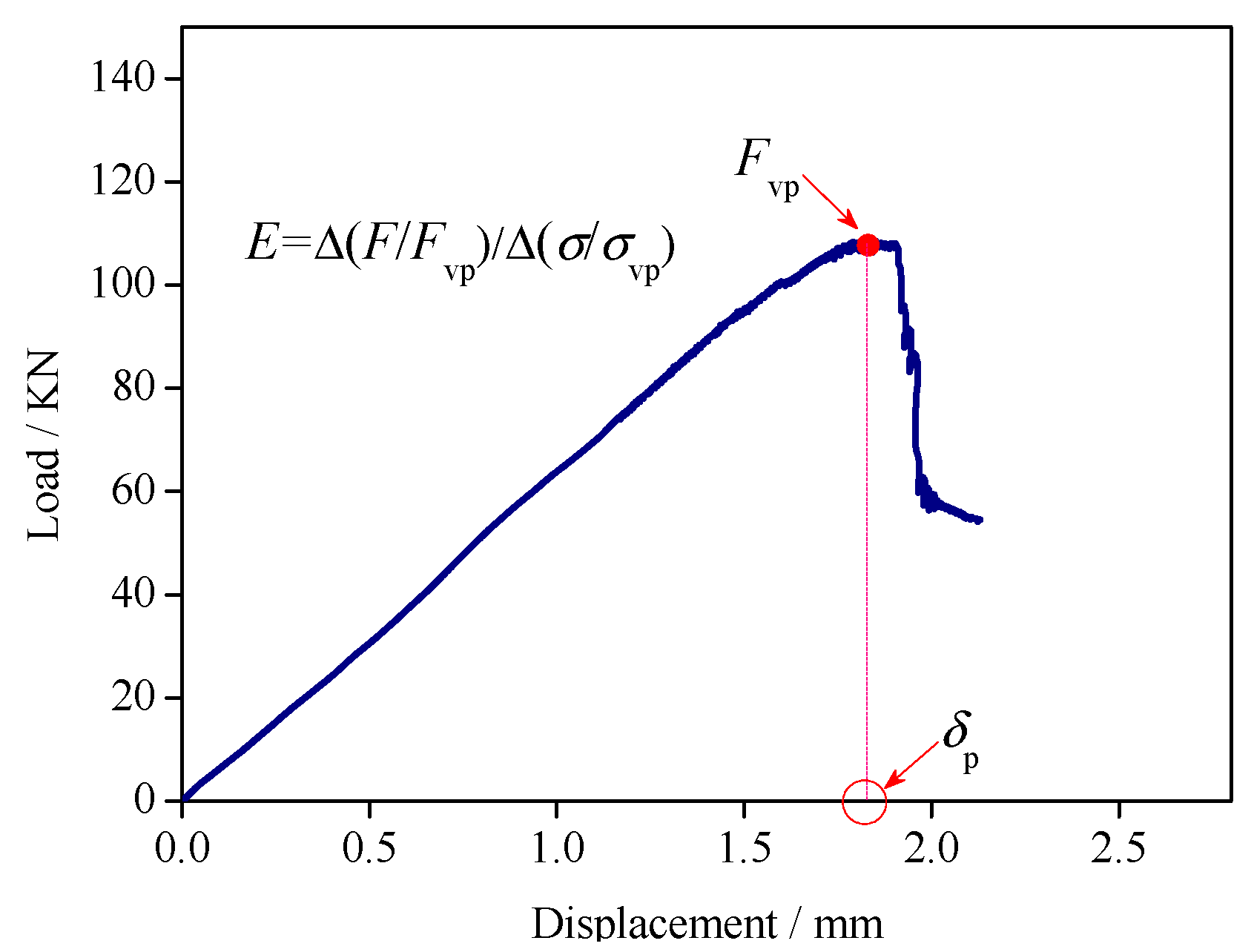
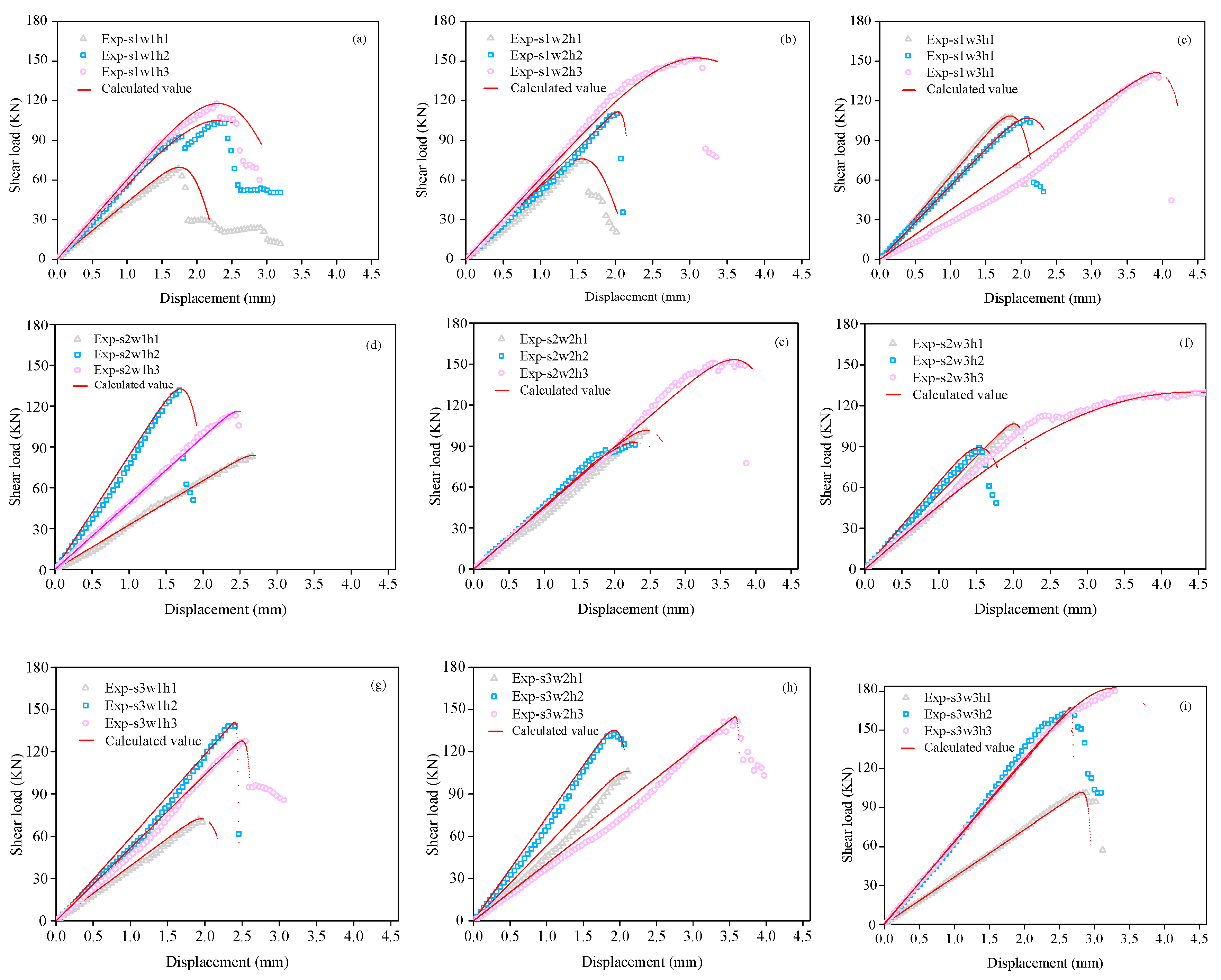
3.2. Shear Load-Displacement Curve
3.3. Peak Shear Load Fvp
3.4. Peak Shear Displacement δp
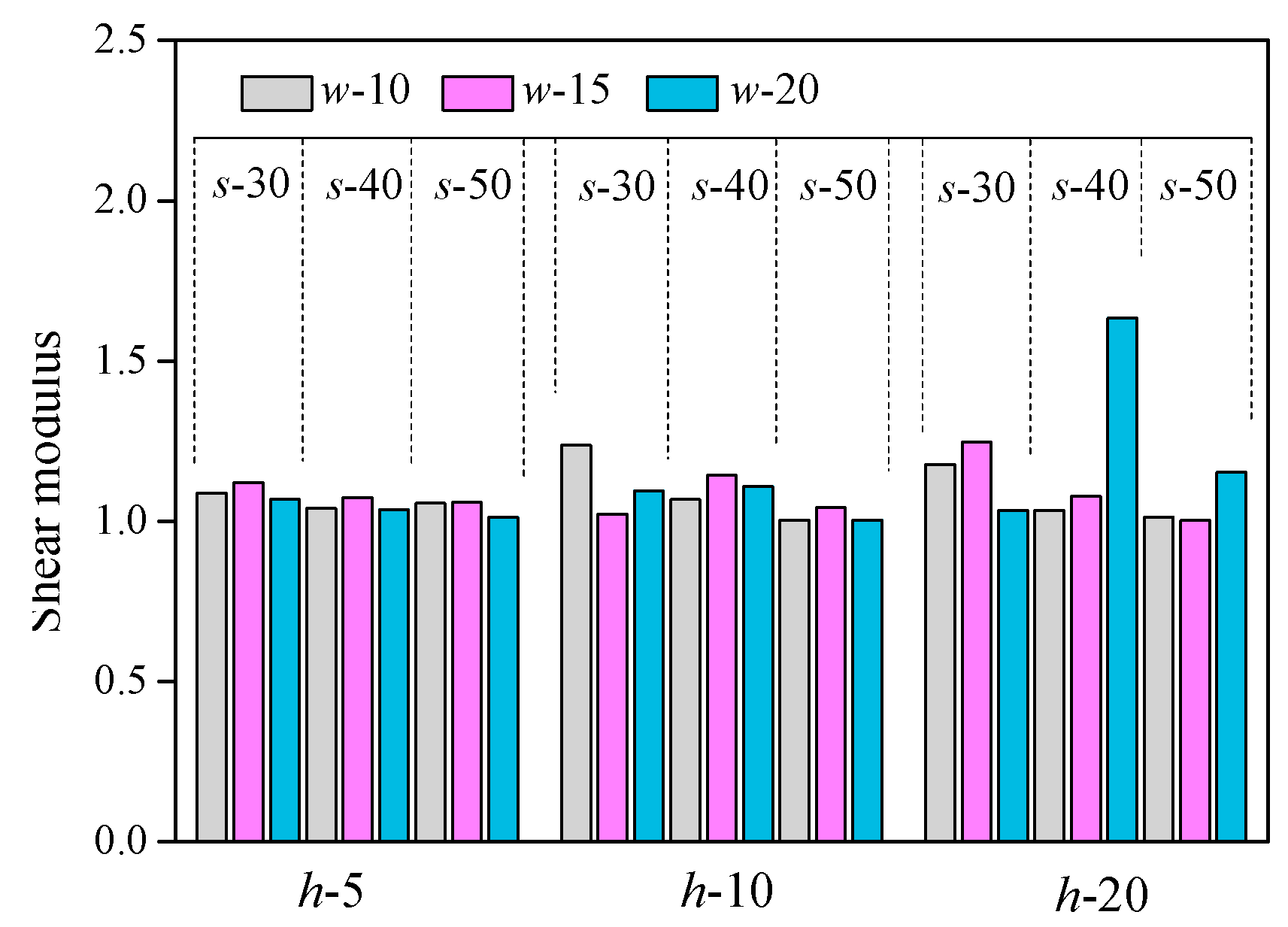
3.5. Shear Modulus
4. Shear Load-Displacement Curves Model and Analysis
4.1. Curve Model
4.2. Calculation Results and Analysis
5. Conclusions
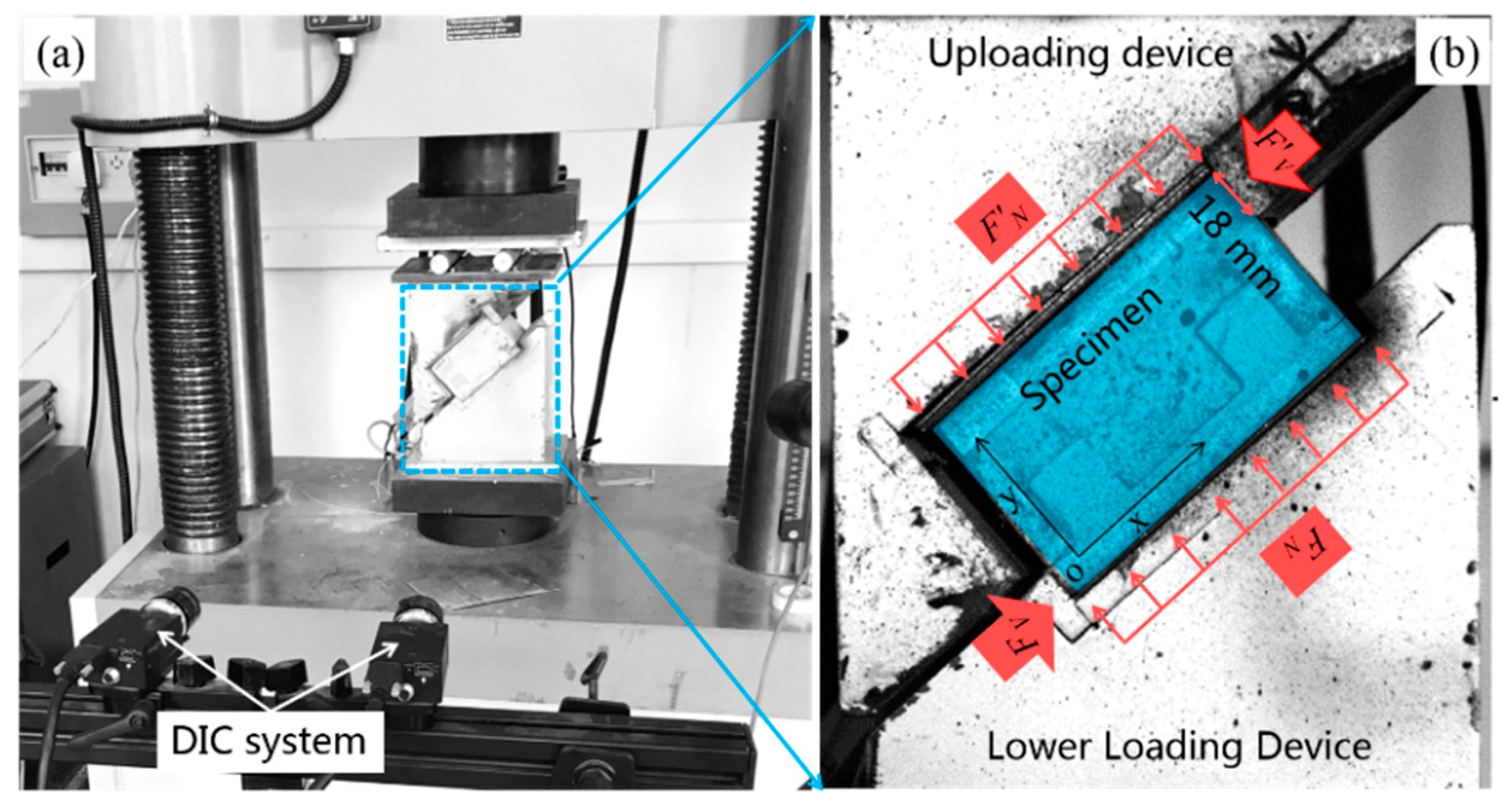
- The failure mode of the specimens was diagonal shear failure, and the ultimate failure mode was diagonal shear crack of the ECC material. The strain field εx and stress field σx nephogram based on the DIC could well describe the failure mode of the composite structure specimens, which was consistent with the experimental results.
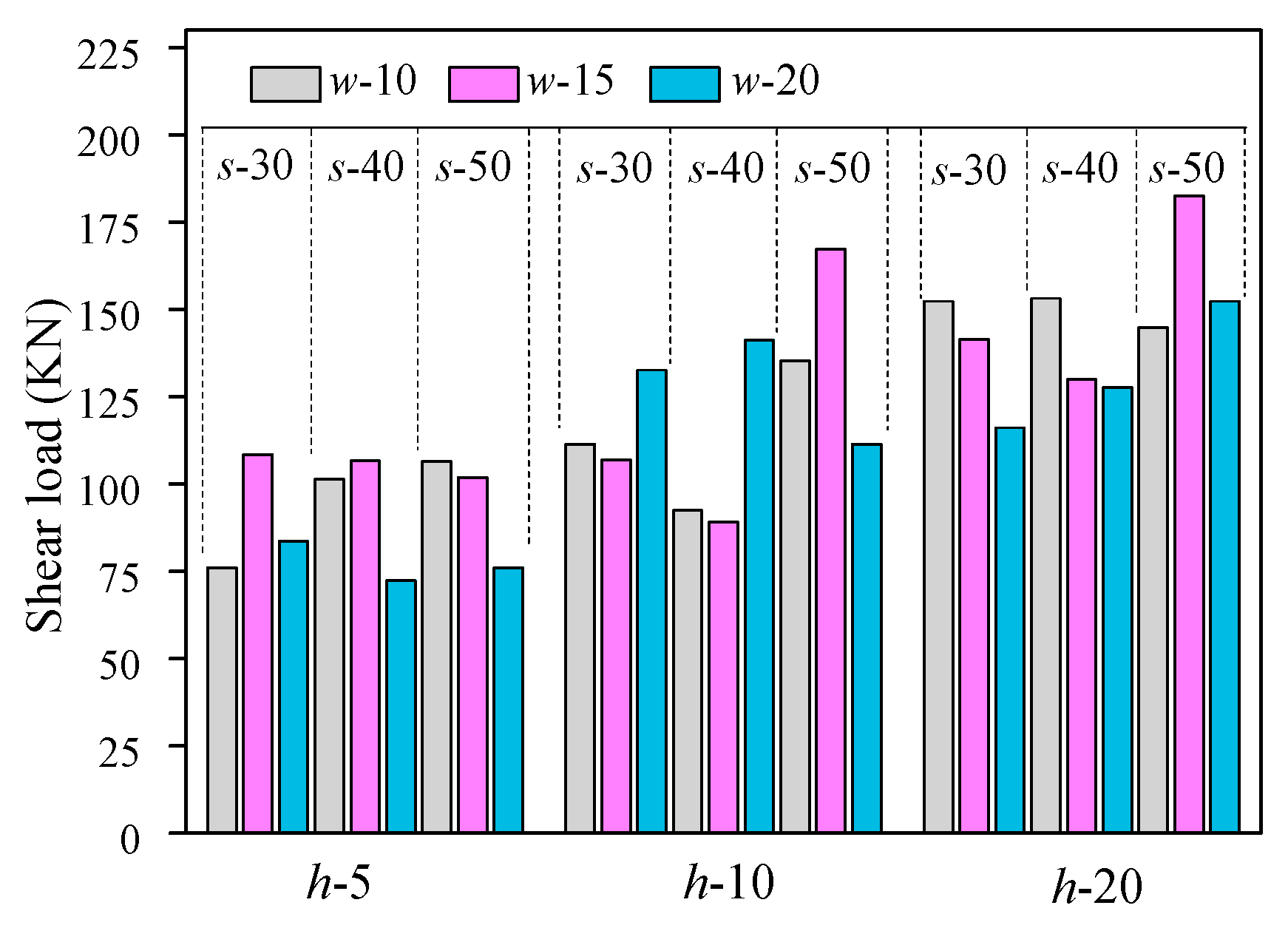
- Based on the calculation of the Fv-δ curves of 27 groups of composite structure specimens, the test parameter H had a significant influence on the curve mechanical properties. When H was 20 mm (the maximum value of test), the characteristic values of shear displacement and the peak shear load were the largest. The effect of W and S on the shear mechanical properties exhibited no clear regularity.
- The Fv-δ curve model of the ECC/steel composite structure specimens based on continuous damage mechanics and the Weibull distribution theory was in good agreement with the experimental values. It can be used for the shear design of ECC expansion joints.
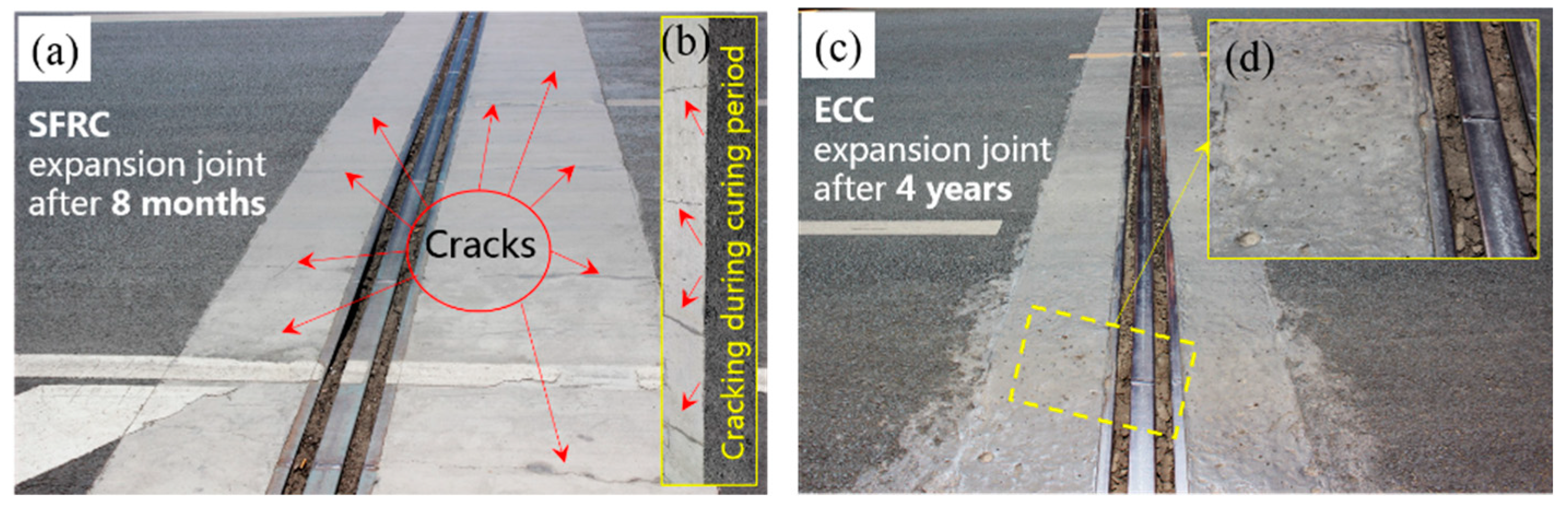
- After four years of operation, the ECC bridge expansion joint demonstration project completed by our team in the early stage achieved good results. This promotes the application of ECC in engineering.
Author Contributions
Funding
Conflicts of Interest
References
- Guo, T.; Huang, L.Y.; Liu, J.; Zou, Y. Damage mechanism of control springs in modular expansion joints of long-span bridge. J. Bridge Eng. 2018, 23, 04018038. [Google Scholar] [CrossRef]
- Ma, J.; Sun, S.Z.; Qi, Y. Review on China’s bridge engineering research. China J. Highw. Transp. 2014, 27, 1–96. [Google Scholar]
- Mascio, P.D.; Loprencipe, G.; Moretti, L.; Puzzo, L.; Zoccali, P. Bridge expansion joint in road transition curve: Effects assessment on heavy vehicles. Appl. Sci. Basel. 2017, 7, 599. [Google Scholar] [CrossRef]
- Yang, Y. Research of Rapid Repair Materials for Bridge Expansion Joints Rehabilitation. Doctoral Dissertation, Chongqing Jiaotong University, Chongqing, China, 2017. [Google Scholar]
- Ajwad, A.; Qureshi, L.A.; Tahir, F.; Hussain, J. Investigation regarding bridge expansion joints deterioration in pakistan and its remedial measures. Tech. J. UET Taxila. 2014, 19, 34–39. [Google Scholar]
- Deng, L.; Yan, W.; Zhu, Q. Vehicle impact on the deck slab of concrete box-girder bridges due to damaged expansion joints. J. Bridge Eng. 2015, 21, 06015006. [Google Scholar] [CrossRef]
- Quinn, B.H.; Civjan, S.A. Assessment of bridge joint performance in the northeastern states. Transport. Res. Rec. 2016, 2550, 46–53. [Google Scholar] [CrossRef]
- Lachinger, S.; Strauss, A.; Kwapisz, M.; Zimmermann, T. Evaluation of expansion joints in Austria. In Proceedings of the 37th IABSE Madrid Symposium Report, Madrid, Spain, September 2014; pp. 2961–2968. [Google Scholar]
- Lima, J.M.; Brito, J. Inspection survey of 150 expansion joints in road bridges. Eng. Struct. 2009, 31, 1077–1084. [Google Scholar] [CrossRef]
- Chang, L.M.; Lee, Y.J. Evaluation of performance of bridge deck expansion joints. J. Perform. Constr. Fac. 2002, 16, 3–9. [Google Scholar] [CrossRef]
- Balakumaran, S.S.G.; O’Neill, K.; Springer, T.C.; Adam, M.A. Elastomeric concrete plug joints: A new durable bridge expansion joint design. Transp. Res. Rec. 2017, 2642, 18–25. [Google Scholar] [CrossRef]
- Yu, T.L.; Li, C.Y.; Wu, S.G. Performance of polymer modified asphalt bridge expansion joints in low-temperature regions. J. Perform. Constr. Fac. 2009, 23, 227–233. [Google Scholar] [CrossRef]
- Zhou, M.; Lu, W.; Song, J.W.; Lee, G.C. Application of ultra-high performance concrete in bridge engineering. Constr. Build. Mater. 2018, 186, 1256–1267. [Google Scholar] [CrossRef]
- Ren, L.; Liang, M.Y.; Wang, K.; He, Y.; Zhao, G.G. Key performance and application of ultra-high-performance concrete in bridge expansion joint. Bull. Chin. Ceramic. Soc. 2018, 37, 2048–2052. [Google Scholar]
- Li, V.C. High-Performance and multifunctional cement-based composite material. Engineering 2019, 5, 250–260. [Google Scholar] [CrossRef]
- Kang, S.B.; Tan, K.H.; Zhou, X.H.; Yang, B. Experimental investigation on shear strength of engineered cementitious composites. Eng. Struct. 2017, 143, 141–151. [Google Scholar] [CrossRef]
- Hou, M.J.; Hu, K.X.; Yu, J.T.; Dong, S.W.; Xu, S.L. Experimental study on ultra-high ductility cementitious composites applied to link slabs for jointless bridge decks. Compos. Struct. 2018, 204, 167–177. [Google Scholar] [CrossRef]
- Kim, M.J.; Kim, S.; Yoo, D.Y. Hybrid effect of twisted steel and polyethylene fibers on the tensile performance of ultra-high-performance cementitious composites. Polymers 2018, 10, 879. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.G.; Zhang, D.X.; Yan, C.W.; Deng, Y.H. Experimental study on the tensile properties of PVA-ECC with high-calcium fly ash. Bull Chin Ceramic Soc. 2016, 35, 52–60. [Google Scholar]
- Lemaitre, J. How to use damage mechanics. Nucl. Eng. Des. 1984, 80, 233–245. [Google Scholar] [CrossRef]
- Chen, L.; Wang, C.P.; Liu, J.F.; Liu, J.; Wang, J.; Jia, Y.; Shao, J.F. Damage and plastic deformation modeling of Beishan granite under compressive stress conditions. Rock Mech. Rock Eng. 2015, 48, 1623–1633. [Google Scholar] [CrossRef]
- Chi, Y.; Xu, L.H.; Yu, H.S. Constitutive modeling of steel-polypropylene hybrid fiber reinforced concrete using a non-associated plasticity and its numerical implementation. Compos. Struct. 2014, 111, 497–509. [Google Scholar] [CrossRef]
- Lai, Y.M.; Li, J.B.; Li, Q.Z. Study on damage statistical constitutive model and stochastic simulation for warm ice-rich frozen silt. Cold Reg. Sci. Technol. 2012, 71, 102–110. [Google Scholar] [CrossRef]
- Li, Y.; Jia, D.; Rui, Z.; Peng, J.; Fu, C.; Zhang, J. Evaluation method of rock brittleness based on statistical constitutive relations for rock damage. J. Petrol. Sci. Eng. 2017, 153, 123–132. [Google Scholar] [CrossRef]
- Hosseini, E.; Holdsworth, S.; Mazza, E. Stress regime-dependent creep constitutive model considerations in finite element continuum damage mechanics. Int. J. Damage Mech. 2013, 22, 1186–1205. [Google Scholar] [CrossRef]
- Darabi Masoud, K.; Abu Al-Rub Rashid, K.; Masad Eyad, A.; Little Dallas, N. Constitutive modeling of fatigue damage response of asphalt concrete materials with consideration of micro-damage healing. Int. J. Solids Struct. 2013, 50, 2901–2913. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, C.J.; Zhao, M.H.; Li, X.B. Statistical damage constitutive model for rocks considering residual strength. Int. J. Geomech. 2016, 17, 04016033. [Google Scholar] [CrossRef]
- Yu, T.T. Statistical damage constitutive model of quasi-brittle materials. J. Aerosp. Eng. 2009, 22, 95–100. [Google Scholar] [CrossRef]

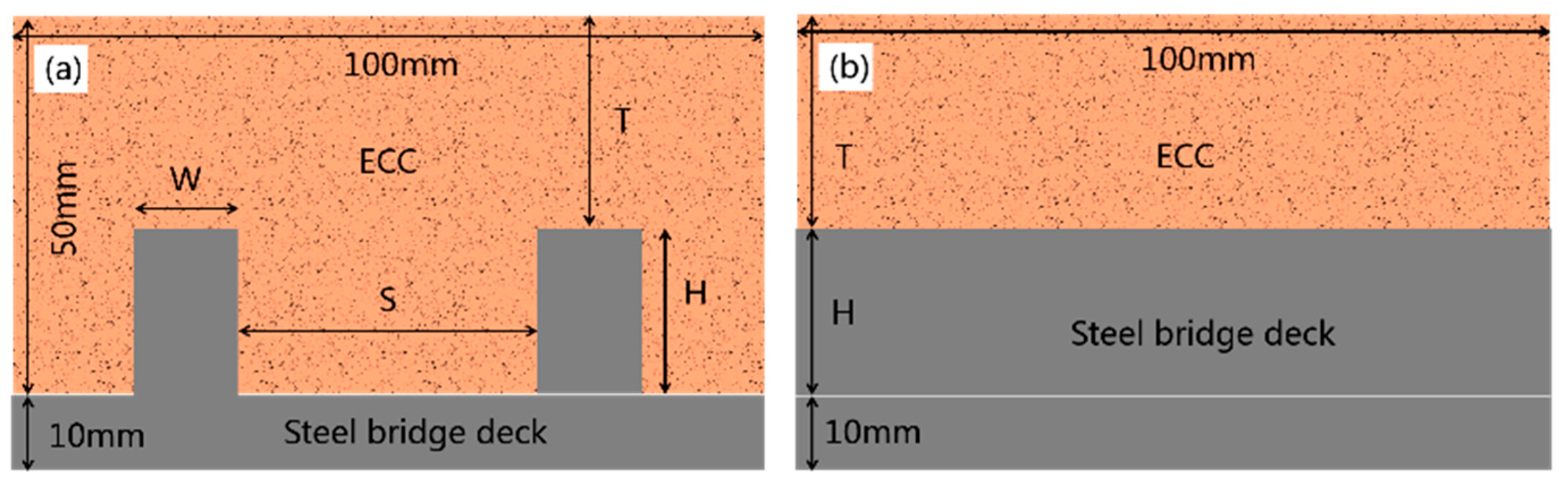

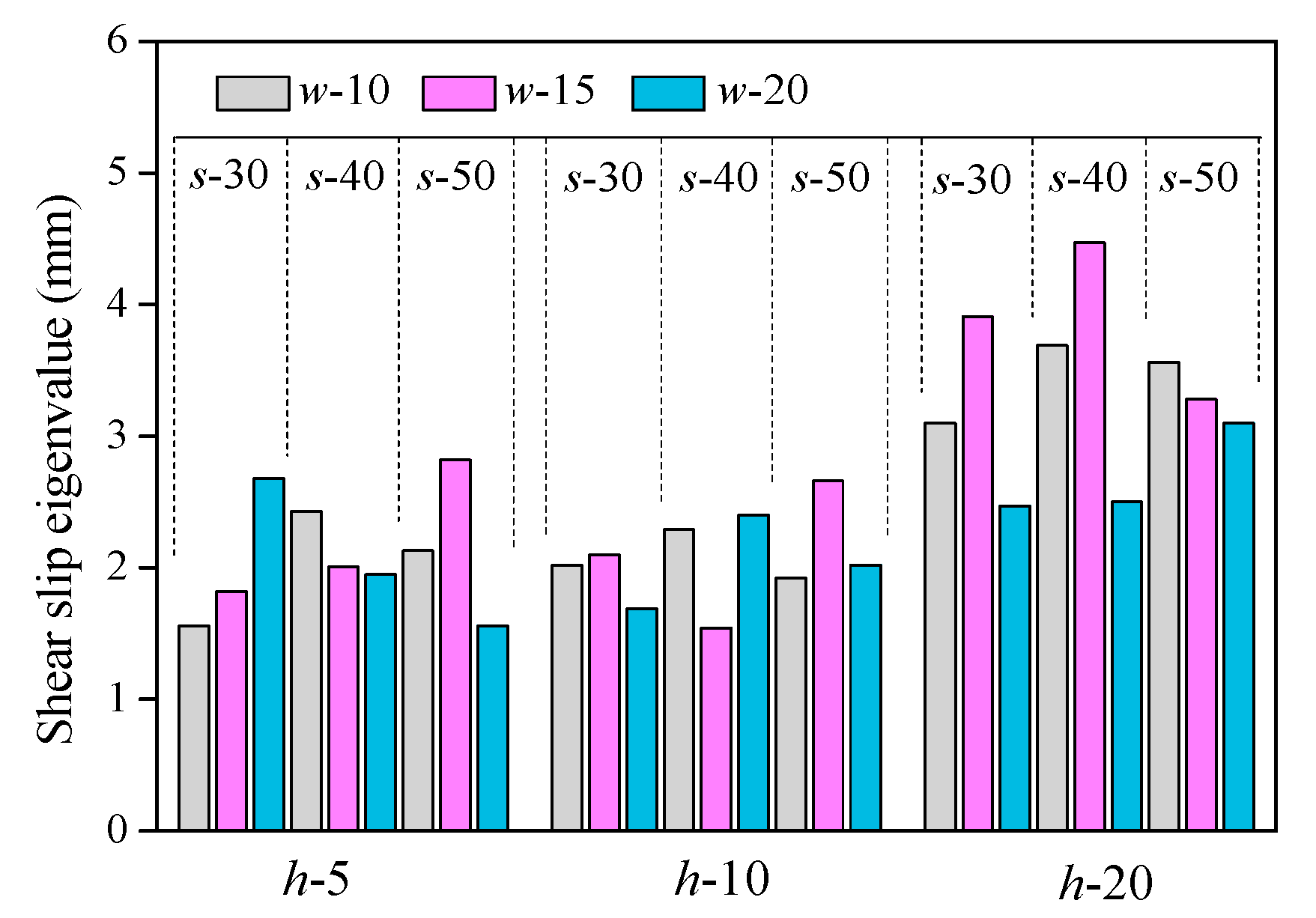
| No. | S | W | H | No. | S | W | H | No. | S | W | H |
|---|---|---|---|---|---|---|---|---|---|---|---|
| s1w1h1 | 30 | 10 | 5 | s1w2h1 | 30 | 15 | 5 | s1w3h1 | 30 | 20 | 5 |
| s1w1h2 | 30 | 10 | 10 | s1w2h2 | 30 | 15 | 10 | s1w3h2 | 30 | 20 | 10 |
| s1w1h3 | 30 | 10 | 20 | s1w2h3 | 30 | 15 | 20 | s1w3h3 | 30 | 20 | 20 |
| s2w1h1 | 40 | 10 | 5 | s2w2h1 | 40 | 15 | 5 | s2w3h1 | 40 | 20 | 5 |
| s2w1h2 | 40 | 10 | 10 | s2w2h2 | 40 | 15 | 10 | s2w3h2 | 40 | 20 | 10 |
| s2w1h3 | 40 | 10 | 20 | s2w2h3 | 40 | 15 | 20 | s2w3h3 | 40 | 20 | 20 |
| s3w1h1 | 50 | 10 | 5 | s3w2h1 | 50 | 15 | 5 | s3w3h1 | 50 | 20 | 5 |
| s3w1h2 | 50 | 10 | 10 | s3w2h2 | 50 | 15 | 10 | s3w3h2 | 50 | 20 | 10 |
| s3w1h3 | 50 | 10 | 20 | s3w2h3 | 50 | 15 | 20 | s3w3h3 | 50 | 20 | 20 |
| Tensile Strength (MPa) | Young’s Modulus (GPa) | Diameter (μm) | Length (mm) | Elongation (%) |
|---|---|---|---|---|
| 1600 | 40 | 40 | 12 | 6 |
| Cement (kg/m3) | Fly Ash (kg/m3) | Silica Sand (kg/m3) | Water (kg/m3) | Water-RAE (kg/m3) | mw/mb (-) | PVA Fiber (vol %) |
|---|---|---|---|---|---|---|
| 378 | 880 | 457 | 302 | 16.37 | 0.24 | 2 |
| Specimens | m | Specimens | m | Specimens | m |
|---|---|---|---|---|---|
| s1w1h1 | 11.89 | s2w1h1 | 25.26 | s3w1h1 | 17.89 |
| s1w1h2 | 4.68 | s2w1h2 | 15.21 | s3w1h2 | 246.33 |
| s1w1h3 | 6.11 | s2w1h3 | 29.32 | s3w1h3 | 76.75 |
| s1w2h1 | 8.70 | s2w2h1 | 13.85 | s3w2h1 | 17.60 |
| s1w2h2 | 44.25 | s2w2h2 | 7.46 | s3w2h2 | 23.82 |
| s1w2h3 | 4.52 | s2w2h3 | 13.30 | s3w2h3 | 291.12 |
| s1w3h1 | 15.02 | s2w3h1 | 27.45 | s3w3h1 | 85.23 |
| s1w3h2 | 10.96 | s2w3h2 | 9.68 | s3w3h2 | 271.54 |
| s1w3h3 | 29.30 | s2w3h3 | 2.04 | s3w3h3 | 7.03 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, L.; Liu, S.; Yan, C.; Zhang, J.; Wang, X. Shear Load-Displacement Curves of PVA Fiber-Reinforced Engineered Cementitious Composite Expansion Joints in Steel Bridges. Appl. Sci. 2019, 9, 5275. https://doi.org/10.3390/app9245275
Yin L, Liu S, Yan C, Zhang J, Wang X. Shear Load-Displacement Curves of PVA Fiber-Reinforced Engineered Cementitious Composite Expansion Joints in Steel Bridges. Applied Sciences. 2019; 9(24):5275. https://doi.org/10.3390/app9245275
Chicago/Turabian StyleYin, Liqiang, Shuguang Liu, Changwang Yan, Ju Zhang, and Xiaoxiao Wang. 2019. "Shear Load-Displacement Curves of PVA Fiber-Reinforced Engineered Cementitious Composite Expansion Joints in Steel Bridges" Applied Sciences 9, no. 24: 5275. https://doi.org/10.3390/app9245275
APA StyleYin, L., Liu, S., Yan, C., Zhang, J., & Wang, X. (2019). Shear Load-Displacement Curves of PVA Fiber-Reinforced Engineered Cementitious Composite Expansion Joints in Steel Bridges. Applied Sciences, 9(24), 5275. https://doi.org/10.3390/app9245275




